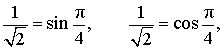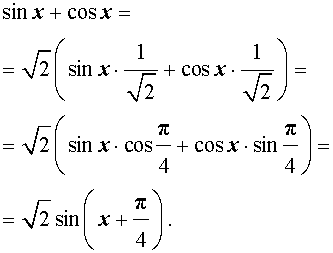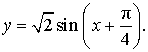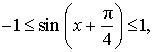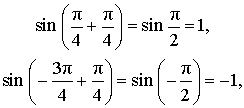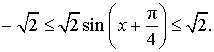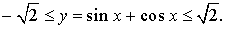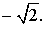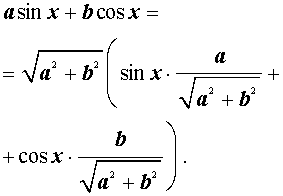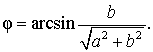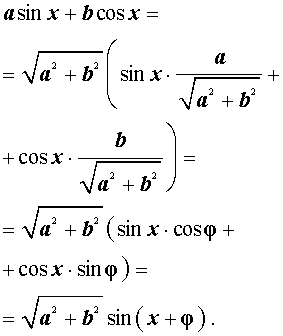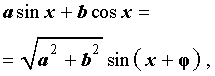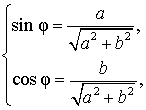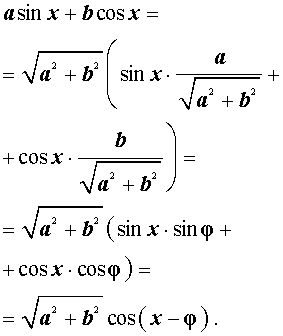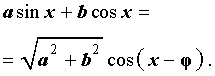Как найти вспомогательный аргумент

Печать страницы

Метод вспомогательного угла в тригонометрических уравнениях

23 октября 2015

На уроках алгебры учителя рассказывают, что существует небольшой (на самом деле — очень даже большой) класс тригонометрических уравнений, которые не решаются стандартными способами — ни через разложение на множители, ни через замену переменной, ни даже через однородные слагаемые. В этом случае в дело вступает принципиально другой подход — метод вспомогательного угла.

Что это за метод и как его применять? Для начала вспомним формулы синуса суммы/разности и косинуса суммы/разности:

[begin{align}& sin left( alpha pm beta right)=sin alpha cos beta pm cos alpha sin beta \& cos left( alpha pm beta right)=cos alpha cos beta mp sin alpha sin beta \end{align}]

Думаю, эти формулы хорошо знакомы вам — из них выводятся формулы двойного аргумента, без которых в тригонометрии вообще никуда. Но давайте теперь рассмотрим простое уравнение:

[3sin x+4cos x=5]

Разделим обе части на 5:

[frac{3}{5}sin x+frac{4}{5}cos x=1]

Заметим, что ${{left( frac{3}{5} right)}^{2}}+{{left( frac{4}{5} right)}^{2}}=1$, а это значит, что обязательно найдётся такой угол $alpha $, для которого эти числа являются соответственно косинусом и синусом. Поэтому наше уравнение перепишется следующим образом:

[begin{align}& cos alpha sin x+sin alpha cos x=1 \& sin left( alpha +x right)=1 \end{align}]

А это уже легко решается, после чего останется лишь выяснить, чему равен угол $alpha $. Как это выяснить, а также как правильно подбирать число для деления обеих частей уравнения (в данном простом примере мы делили на 5) — об этом в сегодняшнем видеоуроке:

Сегодня мы будем разбирать решение тригонометрических уравнений, а, точнее, один-единственный прием, который называется «метод вспомогательного угла». Почему именно этот метод? Просто потому, что за последние два-три дня, когда я занимался с учениками, которым рассказывал о решении тригонометрических уравнений, и мы разбирали, в том числе, метод вспомогательного угла, и все ученики как один допускают одну и ту же ошибку. А ведь метод вообщем-то несложный и, более того, это один из основных приемов в тригонометрии. Поэтому многие тригонометрические задачи иначе как методом вспомогательного угла вообще не решаются.

Поэтому сейчас для начала мы рассмотрим пару простеньких задач, а потом перейдем к задачам посерьезней. Однако все эти они так или иначе потребуют от нас применение метода вспомогательного угла, суть которого я расскажу уже в первой конструкции. 

Решение простых тригонометрических задач

Пример № 1

[cos 2x=sqrt{3}sin 2x-1]

Немного преобразуем наше выражение:

[cos 2x-sqrt{3}sin 2x=-1left| left( -1 right) right.]

[sqrt{3}cdot sin 2x-cos 2x=1]

Как мы будем решать его? Стандартный прием состоит в том, чтобы раскрыть $sin 2x$ и $cos 2x$ по формулам двойного угла, а затем переписать единицу как ${{sin }^{2}}x{{cos }^{2}}x$, получить однородное уравнение, привести его к тангенсам и решить. Однако это долгий и нудный путь, который требует большого объема вычислений.

Предлагаю задуматься вот на чем. У нас есть $sin $ и $cos $. Вспомним формулу косинуса и синуса суммы и разности:

[sin left( alpha pm beta right)=sin alpha cos beta pm cos alpha sin beta ]

[cos left( alpha +beta right)=cos alpha cos beta -sin alpha sin beta ]

[cos left( alpha -beta right)=cos acos beta +sin alpha sin beta ]

Вернемся к нашему примеру. Все сведем к синусу разности. Но для начала уравнение необходимо немного преобразовать. Найдем коэффициент:

[l={{left( sqrt{3} right)}^{2}}+{{left( -1 right)}^{2}}=3+1=4]

[sqrt{l}=2]

$sqrt{l}$ — это тот самый коэффициент, на который необходимо разделить обе части уравнения, чтобы перед синусом и косинусом появились числа, которые сами по себе являются синусами и косинусами. Давайте разделим:

[frac{sqrt{3}}{2}cdot sin 2x-frac{1}{2}cdot cos 2x=frac{1}{2}]

Посмотрим на то, что у нас получилось слева: существует ли такой $sin $ и $cos $, чтобы $cos alpha =frac{sqrt{3}}{2}$, а $sin alpha =frac{1}{2}$? Очевидно существует: $alpha =frac{text{ }!!pi!!text{ }}{6}$. Поэтому мы можем переписать наше выражение следующим образом:

[cos frac{text{ }!!pi!!text{ }}{text{6}}cdot sin 2x-sin frac{text{ }!!pi!!text{ }}{text{6}}cdot cos 2x=frac{1}{2}]

[sin 2xcdot cos frac{text{ }!!pi!!text{ }}{text{6}}-cos 2xcdot sin frac{text{ }!!pi!!text{ }}{text{6}}=frac{1}{2}]

Теперь перед нами формула синуса разности. Мы можем написать так:

[sin left( 2x-frac{text{ }!!pi!!text{ }}{text{6}} right)=frac{1}{2}]

Перед нами простейшая классическая тригонометрическая конструкция. Напомню:

[sin x=a]

[x=arcsin a+2text{ }!!pi!!text{ }n]

[x=text{ }!!pi!!text{ }-arcsin a-2text{ }!!pi!!text{ }n]

Это и запишем для нашего конкретного выражения:

[left[ begin{align}& 2x-frac{text{ }!!pi!!text{ }}{6}=frac{text{ }!!pi!!text{ }}{6}=2text{ }!!pi!!text{ }n \& 2x-frac{text{ }!!pi!!text{ }}{text{6}}=text{ }!!pi!!text{ }-frac{text{ }!!pi!!text{ }}{text{6}}+2text{ }!!pi!!text{ }n \end{align} right.]

[left[ begin{align}& 2x=frac{text{ }!!pi!!text{ }}{3}+2text{ }!!pi!!text{ }n \& 2x=text{ }!!pi!!text{ }+2text{ }!!pi!!text{ }n \end{align} right.]

[]

[left[ begin{align}& x=frac{text{ }!!pi!!text{ }}{6}+text{ }!!pi!!text{ }n \& x=frac{text{ }!!pi!!text{ }}{2}+text{ }!!pi!!text{ }n \end{align} right.]

[nin Z]

Нюансы решения

Итак, что нужно делать, если вам попалось подобный пример:

1. Преобразовать конструкцию, если нужно.
2. Найти поправочный коэффициент, взять из него корень и разделить обе части примера на него.
3. Смотрим, какие значения синуса и косинуса получаются у чисел.
4. Раскладываем уравнение по формулам синуса или косинуса разности или суммы.
5. Решаем простейшее тригонометрическое уравнение.

В связи с этим у внимательных учеников наверняка возникнет два вопроса.

Что нам мешает на этапе нахождения поправочного коэффициента записать $sin $ и $cos $? — Нам мешает основное тригонометрическое тождество. Дело в том, что полученные $sin $ и $cos $, как любые другие при одном и том же аргументе, должны при возведении в квадрат в сумме давать ровно «единицу». В процессе решения нужно быть очень внимательным и не потерять «двойку» перед «иксами».

Метод вспомогательного угла — это инструмент, который помогает свести «некрасивое» уравнение к вполне адекватному и «красивому».

Пример № 2

[sqrt{3}sin 2x+2{{sin }^{2}}x-1=2cos x]

Мы видим, что у нас есть ${{sin }^{2}}x$, поэтому давайте воспользуемся выкладками понижения степеней. Однако прежде чем ними воспользоваться, давайте их выведем. Для этого вспомним, как найти косинус двойного угла:

[cos 2x={{cos }^{2}}x-{{sin }^{2}}x=2{{cos }^{2}}x-1=1-2{{sin }^{2}}x]

Если мы запишем $cos 2x$ в третьем варианте, то получим:

[cos 2x=1-2{{sin }^{2}}x]

[2{{sin }^{2}}x=1-cos 2x]

[{{sin }^{2}}x=frac{1-{{cos }^{2}}x}{x}]

Я выпишу отдельно:

[{{sin }^{2}}x=frac{1-cos 2x}{2}]

То же самое можно сделать и для ${{cos }^{2}}x$:

[{{cos }^{2}}x=frac{1+cos 2x}{2}]

Нам потребуется только первые выкладки. Давайте приступим к работе над задачей:

[sqrt{3}cdot sin 2x+2cdot frac{1-cos 2x}{2}-1=2cos x]

[sqrt{3}cdot sin 2x+1-cos 2x-1=2cos x]

[sqrt{3}cdot sin 2x-cos 2x=2cos x]

Теперь воспользуемся выкладками косинуса разности. Но для начала посчитаем поправку $l$:

[l={{left( sqrt{3} right)}^{2}}+{{left( -1 right)}^{2}}=4]

[sqrt{l}=2]

Перепишем с учетом этого факта:

[frac{sqrt{3}}{2}cdot sin 2x-frac{1}{2}cdot cos 2x=cos x]

В этом случае мы можем записать, что $frac{sqrt{3}}{2}=frac{text{ }!!pi!!text{ }}{3}$, а $frac{1}{2}=cos frac{text{ }!!pi!!text{ }}{3}$. Перепишем:

[sin frac{text{ }!!pi!!text{ }}{text{3}}cdot sin 2x-cos frac{text{ }!!pi!!text{ }}{text{3}}cdot cos 2x=cos x]

[-cos left( frac{text{ }!!pi!!text{ }}{text{3}}+2x right)=cos x]

Внесем «минус» в скобку хитрым способом. Для этого заметим следующее:

[cos left( frac{text{ }!!pi!!text{ }}{text{3}}+2x right)=cos left( text{ }!!pi!!text{ }-text{ }!!pi!!text{ +}frac{text{ }!!pi!!text{ }}{text{3}}+2x right)=]

[=cos left( text{ }!!pi!!text{ }-frac{2text{ }!!pi!!text{ }}{3}+2x right)=cos left( text{ }!!pi!!text{ }+varphi right)=-cos varphi ]

Возвращаемся к нашему выражению и вспоминаем, что в роли $varphi $ у нас выражение $-frac{2text{ }!!pi!!text{ }}{3}+2x$. Поэтому запишем:

[-left( -cos left( -frac{2text{ }!!pi!!text{ }}{3}+2x right) right)=cos x]

[cos left( 2x-frac{2text{ }!!pi!!text{ }}{3} right)=cos x]

Чтобы решить подобною задачу, нужно вспомнить такое:

[cos alpha =cos beta ]

[left[ begin{align}& alpha =beta +2text{ }!!pi!!text{ }n \& alpha =-beta +2text{ }!!pi!!text{ }n \end{align} right.]

Разберемся с нашим примером:

[left[ begin{align}& 2x-frac{2text{ }!!pi!!text{ }}{3}=x+2text{ }!!pi!!text{ }n \& 2x-frac{2text{ }!!pi!!text{ }}{3}=-x+2text{ }!!pi!!text{ }n \end{align} right.]

Давайте посчитаем каждое из этих уравнений:

[x=frac{2text{ }!!pi!!text{ }}{3}+2text{ }!!pi!!text{ }n]

И вторую:

[3x=frac{2text{ }!!pi!!text{ }}{3}+2text{ }!!pi!!text{ }]

[x=frac{2pi }{9}+frac{2pi n}{3}]

Запишем окончательный ответ:

[left[ begin{align}& x=frac{2text{ }!!pi!!text{ }}{3}+2text{ }!!pi!!text{ }n \& x=frac{2text{ }!!pi!!text{ }}{9}+frac{2text{ }!!pi!!text{ }n}{3} \end{align} right.]

Нюансы решения

На самом деле, это выражение решается множеством различных способов, однако именно метод вспомогательного угла является в данном случае оптимальным. Кроме того, на примере данной конструкции хотелось бы обратить ваше внимание еще на несколько интересных приемов и фактов:

• Формулы понижения степеней. Эти формулы не нужно запоминать, однако нужно знать, как их выводить, о чем я вам сегодня и рассказал.
• Решение уравнений вида $cos alpha =cos beta $.
• Добавление «нуля».

Но и это еще не все. До сих пор $sin $ и $cos $, которые мы выводили в качестве дополнительного аргумента, мы считали, что они должны быть положительными. Поэтому сейчас мы решим более сложные задачи.

Разбор более сложных задач

Пример № 1

[sin 3x+4{{sin }^{3}}x+4cos x=5]

Преобразуем первое слагаемое:

[sin 3x=sin left( 2x+x right)=sin 2xcdot cos x+cos 2xcdot sin x]

Второе:

[4{{sin }^{3}}x=4cdot {{sin }^{2}}xcdot sin x=4cdot frac{1-{{cos }^{2}}x}{2}cdot sin x=]

[=2left( 1-cos 2x right)cdot sin x]

А теперь подставим все это в нашу исходную конструкцию:

[sin 2xcos x+cos 2xsin x+2sin x-2cos xsin x+4cos x=5]

[sin 2xcos x-operatorname{cosx}-cos2sin x+2sin x+4cos x=5]

[sin left( 2x-x right)+2sin x+4cos x=5]

[3sin x+4cos x=5]

Давайте введем нашу поправку:

[l=9+16=25]

[sqrt{l}=5]

Записываем:

[frac{3}{5}sin x+frac{4}{5}cos x=1]

Таких $alpha $, для которых $sin $ или $cos $ был бы равен $frac{3}{5}$ и $frac{4}{5}$ в тригонометрической таблице нет. Поэтому давайте просто так и напишем и сведем выражение к синусу суммы:

[sin xcdot cos varphi +cos xcdot sin varphi =1]

[sin left( x+varphi right)=1]

Это частный случай, простейшая тригонометрическая конструкция:

[x+varphi =frac{text{ }!!pi!!text{ }}{2}+2text{ }!!pi!!text{ }n]

[x=frac{text{ }!!pi!!text{ }}{text{2}}-varphi +2text{ }!!pi!!text{ }n]

Осталось найти, чему равен $varphi $. Именно в этом месте многие ученики ошибаются. Дело в том, что на $varphi $ накладываются два требования:

[left{ begin{align}& cos varphi =frac{3}{5} \& sin varphi =frac{4}{5} \end{align} right.]

Начертим радар и посмотрим, где такие значения встречаются:

Возвращаясь к нашему выражению, мы напишем следующее:

[x=frac{text{ }!!pi!!text{ }}{2}-arcsin frac{4}{5}+2text{ }!!pi!!text{ }n]

Но и эту запись можно немного оптимизировать. Поскольку мы знаем следующее:

[alpha :arcsin alpha +arccos alpha =frac{text{ }!!pi!!text{ }}{text{2}},]

то в нашем случае можно записать так:

[x=arccos frac{4}{5}+2text{ }!!pi!!text{ }n]

Пример № 2

Здесь потребуется еще более глубокое понимание методик решения стандартных задач без тригонометрии. Но для решения этого примера мы также используем метод вспомогательного угла.[]

[5+2sin 2x-5cos x=5sin x]

Первое, что бросается в глаза — здесь нет степеней выше первой и поэтому ничего нельзя разложить по формулам разложения степеней. Воспользуется обратными выкладками:

[5+4sin xcos x-5cos x-5sin x=0]

[3+2+4sin xcos x-5left( sin x+cos x right)=0]

Зачем я разложил $5$. Вот смотрите:

[3+2left( 1+2sin xcos x right)-5left( sin xcos x right)=0]

Единицу по основному тригонометрическому тождеству мы можем расписать как ${{sin }^{2}}x+{{cos }^{2}}x$:

[3+2left( {{sin }^{2}}x+2sin xcos x+co{{s}^{2}}x right)-5left( sin x+cos x right)=0]

Что дает нам такая запись? Дело в том, что в первой скобке стоит точный квадрат. Свернем его и получим:

[3+2{{left( sin x+cos x right)}^{2}}-5left( sin x+cos x right)=0]

Предлагаю ввести новую переменную:

[sin x+cos x=t]

В этом случае мы получим выражение:

[3+2{{t}^{2}}-5t=0]

[2{{t}^{2}}-5t+3=0]

[D=25-24=1]

[{{t}_{1}}=frac{5+1}{4}=frac{3}{2}]

[{{t}_{2}}=frac{5-1}{4}=1]

Итого мы получаем:

[left[ begin{align}& sin x+cos x=frac{3}{2} \& sin x+cos x=1 \end{align} right.]

Разумеется, знающие ученики сейчас скажут, что такие конструкции легко решаются с помощью сведения к однородному. Однако мы решим каждое уравнение методом вспомогательного угла. Для этого сначала посчитаем поправку $l$:

[l={{1}^{2}}+{{1}^{2}}=2]

[sqrt{l}=sqrt{2}]

Разделим все на $sqrt{2}$:

[left[ begin{align}& frac{sqrt{2}}{2}sin x+frac{sqrt{2}}{2}cos x=frac{3}{2sqrt{2}} \& frac{sqrt{2}}{2}sin x+frac{sqrt{2}}{2}cos x=frac{sqrt{2}}{2} \end{align} right.]

Все сведем к $cos $:

[cos xcdot cos frac{text{ }!!pi!!text{ }}{4}+sin xsin frac{text{ }!!pi!!text{ }}{text{4}}]

[left[ begin{align}& cos left( x-frac{text{ }!!pi!!text{ }}{text{4}} right)=frac{3}{2sqrt{2}} \& cos left( x-frac{text{ }!!pi!!text{ }}{4} right)=frac{sqrt{2}}{2} \end{align} right.]

Разбираемся с каждым из этих выражений.

Первое уравнение корней не имеет, и для доказательства этого факта нам поможет иррациональность в знаменателе. Заметим следующее:

[sqrt{2}<1,5]

[frac{3}{2sqrt{2}}>frac{3}{3cdot 1,5}=frac{3}{3}=1]

Итого мы четко доказали, что требуется, чтобы $cos left( x-frac{text{ }!!pi!!text{ }}{4} right)$ был равен числу, которое большее «единицы» и, следовательно, у этой конструкции корней нет.

Разбираемся со вторым:

[x-frac{text{ }!!pi!!text{ }}{4}=pm frac{text{ }!!pi!!text{ }}{4}+2text{ }!!pi!!text{ }n]

Решаем эту конструкцию:

[x=frac{text{ }!!pi!!text{ }}{4}pm frac{text{ }!!pi!!text{ }}{text{4}}+2text{ }!!pi!!text{ }n]

В принципе, можно оставить ответ таким, а можно его расписать:

[x=frac{text{ }!!pi!!text{ }}{2}+2text{ }!!pi!!text{ }n]

[x=2text{ }!!pi!!text{ }n]

[nin Z]

Важные моменты

В заключение хотел бы еще раз обратить ваше внимание на работу с «некрасивыми» аргументами, т.е. когда $sin $ и $cos $ не являются табличными значениями. Проблема состоит в том, что если мы утверждаем, что в нашем уравнении $frac{3}{5}$ — это $cos $, а $frac{4}{5}$ — это $sin $, то в итоге, после того как мы решим конструкцию, нужно учитывать оба этих требования. Мы получаем систему из двух уравнений. Если мы не будем это учитывать, то получим следующую ситуацию. В этом случае мы получим две точки и на месте $varphi $ у нас окажется два числа: $arcsin frac{4}{5}$ и $-arcsin frac{4}{5}$, однако последний нас ни в коем случае не устраивает. То же самое будет и с точкой $frac{3}{5}$.

Такая проблема возникает только тогда, когда речь идет о «некрасивых» аргументах. Когда у нас табличные значения, то ничего такого нет.

Надеюсь, сегодняшний урок помог вам разобраться, что такое метод вспомогательного угла и как его применять на примерах разного уровня сложности. Но это не единственный урок, посвященный решению задач методом вспомогательного угла. Поэтому оставайтесь с нами!

Смотрите также:

1. Как решать тригонометрические уравнения? Основные приёмы и методы.
2. Решаем однородные тригонометрические уравнения
3. Задача B8: отрезки и углы в треугольниках
4. Схема Бернулли. Примеры решения задач
5. Деление многочленов уголком
6. Задача B4: вклад в банке и проценты

Метод введения дополнительного угла (Метод введения вспомогательного аргумента)

Рассмотрим метод введения дополнительного угла на примере решения следующей задачи.

ЗАДАЧА . Найти наибольшее и наименьшее значения функции

РЕШЕНИЕ . Заметив, что

преобразуем правую часть формулы (1):

Отсюда вытекает, что выражение (1) можно переписать в виде:

ОТВЕТ . Наибольшее значение функции (1) равно 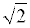, наименьшее значение функции (1) равно

ЗАМЕЧАНИЕ . В рассмотренной задаче угол 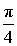и является дополнительным углом.

Теперь докажем формулу дополнительного угла (вспомогательного аргумента) в общем виде. Для этого рассмотрим выражение

где a и b – произвольные, отличные от нуля числа, и преобразуем его:

Введем дополнительный угол (вспомогательный аргумент) φ , у которого:

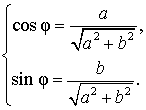(4)

В случае, когда a и b являются положительными числами, в качестве дополнительного угла можно взять, например, угол

Тогда выражение (3) принимает вид:

Таким образом, мы получили формулу

которую и называют формулой дополнительного угла (вспомогательного аргумента).

Если же дополнительный угол, в отличие от формул (4), ввести по формулам

то выражение (3) примет вид

и мы получаем другой вид формулы дополнительного угла:

Тема 19. ТРИГОНОМЕТРИЧЕСКИЕ УРАВНЕНИЯ. Введение вспомогательного аргумента. Методы замены неизвестного. Способ преобразования произведения тригонометрических функций в сумму.
материал для подготовки к егэ (гиа) по алгебре (10 класс) по теме

Актуальной задачей на сегодняшний день является качественная подготовка учащихся к единому государственному экзамену (ЕГЭ) по математике, а также абитуриентов к вступительным экзаменам по математике в вузы, проводимым как в форме письменных контрольных работ, так и в форме тестирований.

Имея многолетний положительный опыт подготовки школьников и абитуриентов к экзаменам по математике, проводимым в разных формах, считаю целесообразным поделиться своими разработками со всеми заинтересованными в них лицами.

Тема 19. «Тригонометрические уравнения. Введение вспомогательного аргумента. Методы замены неизвестного. Способ преобразования произведения тригонометрических функций в сумму» содержит теоретические сведения, систематизированный набор ключевых методов решения типовых задач, сопровождающихся подробным разбором решений. По каждому методу приводятся упражнения с ответами для закрепления изучаемого материала.

Материал будет полезен для использования учителями общеобразовательных учреждений на элективных курсах и факультативных занятиях по математике для подготовки учащихся к ЕГЭ, абитуриентов при подготовке к вступительным экзаменам в вузы.

Скачать:

Вложение	Размер
tema_19._trigonometricheskie_uravneniya.metody_resheniya_7-9.docx	83.21 КБ

Предварительный просмотр:

Тема 19. Тригонометрические уравнения.

Введение вспомогательного аргумента. Методы замены неизвестного.

Способ преобразования произведения тригонометрических функций в сумму.

VII. Введение вспомогательного аргумента.

Этим методом решаются уравнения вида

Уравнение решается по следующему плану:

1) записываем уравнение в виде

Соответствующее значение существует, т.к. выполнено характеристическое свойство

3) уравнение принимает вид то есть – это простейшее уравнение.

Примеры. Решить уравнение.

Решение: тогда Перепишем исходное уравнение в виде . Далее необходимо учесть, что тогда рассматриваемое уравнение можно записать в виде а затем с помощью формулы синуса суммы перейти к уравнению

Тогда уравнение перепишем в виде

Полагая , приходим к уравнению

Так как (или ), то ( ).

1. Найти число корней уравнения на интервале

Подсчитаем число корней, принадлежащих интервалу При

При и корни не принадлежат интервалу следовательно, число корней равно 4.

VIII. Методы замены неизвестного (подстановка).

Применение некоторых замен неизвестного приводит к упрощению соответствующих уравнений.

Примеры. Решить уравнение.

Решение. Сделаем замену, обозначив . Выразим из этой замены , получим . Итак, подставив в уравнение выражения и , получим квадратное уравнение . Следовательно, . Первое уравнение совокупности не имеет решений, так как Решим второе уравнение совокупности.

Замечание . Если тригонометрическое уравнение содержит разность синуса и косинуса и их произведение, то используют замену ,

Решение. Воспользуемся формулой и перепишем данное уравнение иначе

Обозначим . Получаем . Тогда . Второе уравнение совокупности решений не имеет. Решим

1. Ответ:
2. Ответ:
3. Ответ:

IX. Способ преобразования произведения тригонометрических функций в сумму.

Сущность способа поясним на примерах.

Пример. Решить уравнение

Решение. Применим к обеим частям уравнения формулу получим Воспользуемся формулой Получим

1. Ответ:
2. Ответ:
3. Число корней уравнения на интервале равно.

Конспект урока по алгебре на тему “Решение тригонометрических уравнений. Метод введения вспомогательного аргумента”

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

«Актуальность создания школьных служб примирения/медиации в образовательных организациях»

Свидетельство и скидка на обучение каждому участнику

План-конспект урока по предмету

«Решение тригонометрических уравнений.

Метод введения вспомогательного аргумента»

Автор: Ишмухаметова Р.Р.

Конспект урока по теме

«Решение тригонометрических уравнений. Метод введения вспомогательного аргумента»

1. Организационный момент.

Приветствие, создание позитивного эмоционального настроя.

( На уроке учащиеся будут работать в группах, поэтому нужно представить старших групп, рассказать о правилах работы в группе и о самооценке своей работы на уроке.).

У.: У нас сегодня будет с одной стороны обычный урок, т.к. мы с вами будем решать, решать и решать, но с другой стороны он будет и необычным. Как вы думаете почему?

Ответ: открытый урок.

А вот и не угадали. Мы с вами будем решать почти весь урок только одно уравнение. Но об этом немного попозже.

А сейчас давайте вспомним методы решения тригонометрических уравнений.

Ответ: Метод замены переменной, метод разложения на множители вынесением за скобки, метод разложения на множители с помощью формул суммы и разности синусов и косинусов, т.е. преобразование суммы в произведение и решение уравнений с использованием однородности.

(на экране появляются тригонометрические уравнения, учащиеся называют способы решения уравнений и по мере называния способы появляются на экране, справа от столбца уравнений )

sin x + cos x = 0

Б. Метод разложения на множители

sin 5 x – sin x = 0

В. Метод преобразования суммы в произведение

4 sin 2 x – cos x = 1

Г. Метод однородных уравнений

sin 2 x -5 sinxcosx + 6 cos 2 x =0

Работа в группах: 2. 1. Решение задания на соответствие тригонометрических уравнений и методов решения.

Задание группам: соединить стрелочками метод решения и уравнение. Обсуждают в группах, а затем проверяем, спрашиваю например 1 группу, а остальные проверяют и обсуждаем решение.

Даю время 2 мин, на самооценку 1 задания. На экране появляются критерии самооценки:

2.2. Решение данных тригонометрических уравнений и проверка их на доске.

Задание: решить данные тригонометрические уравнения (каждая группа решает все уравнения, но внутри группы распределяют, кто какое будет решать уравнение). Затем каждая группа записать решение на доске и объяснить метод решения одного уравнения на выбор.

Даю время 2 мин на самооценку. На экране появляются критерии самооценки:

2 балл – за решенное уравнение, но с допущенной ошибкой;

1 балл – за недорешенное уравнение;

И плюс 1 балл за ответ у доски.

3. Открытие новых знаний.

3.1.Постановка проблемы: проблемная ситуация с затруднением

Вы смогли выполнить задание?

Почему это задание не получилось?

Мы с вами при решении уравнений чаще всего не сразу видели, какой это способ решения.

Что мы для этого делали?

Сейчас я каждой группе предложу свой метод решения этого уравнения, а вы попробуете, выполнив какие-либо преобразования решить уравнение и отметить решение уравнения на единичном тригонометрическом круге. Затем разберем решение на доске. Если вы не сможете догадаться какое преобразование нужно выполнить, вы можете взять подсказку. Подсказки будут платные. Стоят они 0,5 балла.

Пытаются выполнить задание

не знаем способа решения.

Выполняли какие-либо тригонометрические преобразования

Подсказки напечатаны на карточках и разложены на столе учителя. Метод решения и шпаргалки к этому методу решения уравнения определенного цвета.

3.2. .Обсуждение и решение проблемы по группам.

3.3.Обсуждение проблемы у доски.

Записывают решения на доске и объясняют. Сделать вывод о решении после каждого объяснения.

На экране появляются 5 единичных тригонометрических круга, на которых отмечены решения уравнения.

3.4. Выводы и предложения по решению уравнения.

Почему такое произошло?

-Что мы делаем в этом случае? Как проверить кто прав?

Как выполняется проверка?

4 ответа одинаковые, а один ответ – другой.

Допустили ошибку при решении

или возник посторонний корень при возведении в квадрат

подставить в уравнение и если получим верное равенство, значит, этот корень является решением уравнения.

У.: Давайте выполним проверку корней уравнения. Каждая группа проверит одно решение.

Раздать листы с заданием, какой корень проверить, а затем результат вывешиваем на доску и делаем вывод о достоверности решений.

Вывод: Значения х = 0 и 2П и х = П2 являются решениями уравнения, а значения х = П и х =3 П2 не являются решениями данного уравнения или это так называемые посторонние корни.

У.: почему они возникли и при решении каким способом?

О.: при возведении в квадрат.

У.: Как можно уточнить ответ уравнения или что можно исключить из множества всех действительных чисел?

При каких значениях n у нас получаются верные решения, а при каких – не верные или посторонние?

Ответ: при п четных – верные, а при п нечетных – неверные.

3.5.Введение нового метода решения данного типа уравнения.

Какой способ вам показался новым?

Действительно этот способ для вас новый.

Если назовут несколько способов, то сначала проанализировать какие способы применяли при решении этого уравнения, и только потом этот способ появится как новый.

Сначала обсудить вопрос об общем виде уравнения.

Как вы думаете как в общем виде можно записать уравнение, которое мы решали?

У кого какие идеи, гипотезы?

У кого какие мнения?

Откройте учебники и найдите параграф, где говорится о решении уравнений такого вида. Прочитайте его.

А теперь давайте попробуем составить алгоритм решения уравнений такого вида.

На экране появляется постепенно алгоритм решения уравнения.

a cos x + b sin x = c,

1) делим мы на

2) Уравнение принимает вид

3) Вводим вспомогательный аргумент (угол), такой, что и

Т.о. уравнение можно записать в виде

, а это простейшее тригонометрическое уравнение.

Запишите себе в тетрадь.

Чему равны а, в и с в нашем уравнении?

Как можно получить в нашем случае из а и в

Нужно было решить уравнение sinx + cos x = 1.

Там где делили на

Варианты ответов, но нужно чтобы возник ответ

a cos x + b sin x = c,

делим мы на

=

4. Закрепление изученного материала.

4.1.Работа с учебником по поиску подобных уравнений.

Найдите на с.189 номер с подобным типом уравнений и давайте выберем уравнения, которые будем решать

4.2.Решение найденных уравнений изученным методом.

Выбираем и решаем в зависимости от времени.(№ 625 1,3 или 4)

Ответы записывают на листах и вывешиваем на доску. Анализируем решение и ставим оценки.

5. Подведение итогов.

А как ее мы можем уточнить?

Что мы вводили? Посмотрите в учебнике, на доску.

Так как мы можем уточнить тему

После уточнения вывешиваю тему на доску.

И все таки какой метод из примененных вами вам больше всего понравился?

Как видим этот тип уравнений можно решать любым из данных методов, лишь бы он был вам понятен.

Решение тригонометрических уравнений

Молчание или неточная формулировка

Решение тригонометрических урав

нений. Метод введения вспомогательного аргумента (или угла)

Каждая группа с учетом набранных баллов оценивает свой вклад в работу на уроке.

Проставьте на листе оценки за работу на уроке.

6. Задание для внеаудиторной самостоятельной работы.(появляется на экране)

Прочитать §.36 п.2 и решить № 664.

На «3» – решить новым способом уравнения этого номера.

На «4» – решить 2 способами уравнения этого номера;

На «5» – решить всевозможными способами эти уравнения.

А теперь выразите свое отношение к уроку. Понравился он вам или нет, получили ли вы новые знания, или этот урок оставил вас равнодушными к математике.

Прикрепить к синусоиде (она вывешивается на доску) кружочки желтого, зеленого и коричневого цвета. Желтые крепятся сверху, коричневые – снизу синусоиды, а зеленые на ось Ох.

Посмотрите как мы сегодня поработали . Молодцы!

Спасибо за хорошую работу на уроке. До свидания.

Прочитать §36 п.2

На «3» – решить новым способом уравнения этого номера.

На «4» – решить 2 способами уравнения этого номера;

На «5» – решить всевозможными способами эти уравнения.

Курс повышения квалификации

Дистанционное обучение как современный формат преподавания

• Сейчас обучается 949 человек из 80 регионов

Курс профессиональной переподготовки

Математика: теория и методика преподавания в образовательной организации

• Сейчас обучается 681 человек из 75 регионов

Курс повышения квалификации

Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО

• Сейчас обучается 314 человек из 70 регионов

Ищем педагогов в команду «Инфоурок»

Дистанционные курсы для педагогов

Самые массовые международные дистанционные

Школьные Инфоконкурсы 2022

33 конкурса для учеников 1–11 классов и дошкольников от проекта «Инфоурок»

Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:

5 565 688 материалов в базе

Другие материалы

• 10.09.2018
• 223
• 0

• 10.09.2018
• 165
• 0

• 10.09.2018
• 5033
• 36

• 10.09.2018
• 279
• 2

• 10.09.2018
• 576
• 0

• 10.09.2018
• 1920
• 46

• 10.09.2018
• 304
• 2

• 10.09.2018
• 1066
• 3

Вам будут интересны эти курсы:

Оставьте свой комментарий

Авторизуйтесь, чтобы задавать вопросы.

Добавить в избранное

• 10.09.2018 1424
• DOCX 113.5 кбайт
• 71 скачивание
• Оцените материал:

Настоящий материал опубликован пользователем Ишмухаметова Резеда Расуловна. Инфоурок является информационным посредником и предоставляет пользователям возможность размещать на сайте методические материалы. Всю ответственность за опубликованные материалы, содержащиеся в них сведения, а также за соблюдение авторских прав несут пользователи, загрузившие материал на сайт

Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.

Автор материала

• На сайте: 8 лет и 2 месяца
• Подписчики: 0
• Всего просмотров: 1666
• Всего материалов: 2

Московский институт профессиональной
переподготовки и повышения
квалификации педагогов

Дистанционные курсы
для педагогов

663 курса от 690 рублей

Выбрать курс со скидкой

Выдаём документы
установленного образца!

Учителя о ЕГЭ: секреты успешной подготовки

Время чтения: 11 минут

Профессия педагога на третьем месте по популярности среди абитуриентов

Время чтения: 1 минута

Объявлен конкурс дизайн-проектов для школьных пространств

Время чтения: 2 минуты

Тринадцатилетняя школьница из Индии разработала приложение против буллинга

Время чтения: 1 минута

В Рособрнадзоре рассказали, как будет меняться ЕГЭ

Время чтения: 2 минуты

ЕГЭ в 2022 году будут сдавать почти 737 тыс. человек

Время чтения: 2 минуты

У 76% российских учителей оклад ниже МРОТ

Время чтения: 2 минуты

Подарочные сертификаты

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.

[spoiler title=”источники:”]

http://nsportal.ru/shkola/algebra/library/2014/04/04/tema-19-trigonometricheskie-uravneniya-vvedenie-vspomogatelnogo

http://infourok.ru/konspekt-uroka-po-algebre-na-temu-reshenie-trigonometricheskih-uravneniy-metod-vvedeniya-vspomogatelnogo-argumenta-3223501.html

[/spoiler]

Метод введения дополнительного угла (Метод введения вспомогательного аргумента)

Рассмотрим метод введения дополнительного угла на примере решения следующей задачи.

ЗАДАЧА. Найти наибольшее и наименьшее значения функции

РЕШЕНИЕ. Заметив, что

преобразуем правую часть формулы (1):

Отсюда вытекает, что выражение (1) можно переписать в виде:

Поскольку

причем

то

Следовательно,

ОТВЕТ. Наибольшее значение функции (1) равно , наименьшее значение функции (1) равно

ЗАМЕЧАНИЕ. В рассмотренной задаче угол  и является дополнительным углом.

Теперь докажем формулу дополнительного угла (вспомогательного аргумента) в общем виде. Для этого рассмотрим выражение

где a и b – произвольные, отличные от нуля числа, и преобразуем его:

Введем дополнительный угол (вспомогательный аргумент) φ , у которого:

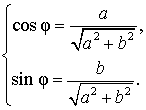(4)

В случае, когда a и b являются положительными числами, в качестве дополнительного угла можно взять, например, угол

Тогда выражение (3) принимает вид:

Таким образом, мы получили формулу

которую и называют формулой дополнительного угла (вспомогательного аргумента).

Если же дополнительный угол, в отличие от формул (4), ввести по формулам

то выражение (3) примет вид

и мы получаем другой вид формулы дополнительного угла:

Ранее мы рассмотрели два способа решения тригонометрических уравнений: сведение к квадратному уравнению с помощью замены переменной, метод разложения на множители левой части уравнения. Среди тригонометрических уравнений выделяют однородные и неоднородные уравнения.

---

---

---

---

Однородное тригонометрическое уравнение первого порядка

Пусть дано уравнение a sin x+b cos x=0

Разделим обе части уравнения на cos x. Получим равносильное уравнение, т. к. cosx≠0, иначе, если cos x=0, то уравнение примет вид a sin x=0, т. е. sin x=0, чего быть не может, по основному тригонометрическому тождеству синус и косинус одного и того же аргумента не могут одновременно обращаться в нуль. После деления на ненулевое выражение исходное уравнение примет вид a tg x+b=0, из которого последовательно находим tg x, а затем переменную x.

---

Решить уравнение sin x+cos x=0.

---

Решение

Разделим обе части уравнения на cosx≠0.

tgx+1=0, откуда x=-π4+πk, k∈Z.

Ответ: -π4+πk, k∈Z.

---

Однородное тригонометрическое уравнение второго порядка

Пусть дано уравнение a sin2x+b sinxcosx+c cos2x=0.

Разделим обе части уравнения на cos2x≠0. Получим равносильное уравнение a tg2x+b tgx+c=0, квадратное относительно tg x. Для дальнейшего решения используем метод замены переменной.

---

Решить уравнение 6cos2x+sin2x-5sinxcosx=0.

---

Решение

Разделим обе части уравнения на cos2x≠0. Уравнение примет вид tg2x-5tgx+6=0. Пусть tg x=t,  тогда  t2-5t+6=0, откуда t1=3, t2=2. Вернемся к исходной переменной:

tgx=3, x=arctg3+πk, k∈Z, или

tgx=2, x=arctg2+πn, n∈Z.

Ответ: arctg3+πk, k∈Z; arctg2+πn, n∈Z.

---

Несложно заметить, что при решении однородного тригонометрического уравнения n-го порядка обе части уравнения делят на косинус аргумента в наибольшей степени.

---

Решить уравнение:

1. 2sinx-5cosx=0;

2. sin2x+3sinxcosx-4cos2x=0.

---

Неоднородные тригонометрические уравнения

---

---

Неоднородные тригонометрические уравнения первого порядка имеют несколько способов решения. Рассмотрим основные из них.

Метод решения неоднородных тригонометрических уравнений первого порядка с помощью формул двойного аргумента

Пусть дано уравнение вида a sinx+b cosx=c, где a≠0, b≠0, c≠0. Применим к нему следующие формулы:

cosx=cos2x2-sin2x2                                        (1)

sinx=2sinx2cosx2                                               (2)

sin2x2+cos2x2=1.                                             (3)

Получаем

a×2sinx2cosx2+b×(cos2x2-sin2x2)=c×(sin2x2+cos2x2).

Раскроем скобки, приведем подобные слагаемые:

(-b-c)sin2x2+2asinx2cosx2+(b-c)cos2x2=0.

А это однородное тригонометрическое уравнение второго порядка, метод решения которого описан выше.

Метод решения неоднородных тригонометрических уравнений первого порядка с помощью универсальной подстановки

Пусть дано уравнение вида a sinx+b cosx=c, где a≠0, b≠0, c≠0. Применим к нему следующие формулы (формулы универсальной подстановки):

sinx=2tgx21+tg2x2,                                        (4)

cosx=1-tg2x21+tg2x2.                                        (5)

Тогда уравнение примет вид:

a×2tgx21+tg2x2+b×1-tg2x21+tg2x2=c,

2a×tgx2+b-b×tg2x2=c+c×tg2x2, или,

(c+b)tg2x2-2a×tgx2+(c-b)=0.

А это тригонометрическое уравнение, квадратное относительно tgx2, которое можно решить, заменив tgx2 другой переменной.

Метод решения неоднородных тригонометрических уравнений с помощью введения вспомогательного аргумента

Пусть дано уравнение вида a sinx+b cosx=c, где a≠0, b≠0, c≠0

Разделим обе части уравнения на a2+b2:

aa2+b2sinx+ba2+b2cosx=ca2+b2.

Пусть sinφ=ba2+b2, cosφ=aa2+b2. Такое число φ существует, т. к. 

(ba2+b2)2+(aa2+b2)2=1, т. е. выполняется равенство

sin2φ+cos2φ=1. Тогда уравнение примет вид

cosφ×sinx+sinφ×cosx=ca2+b2. Применим формулу синуса суммы аргументов: sin(x+φ)=ca2+b2.

---

---

Неоднородные тригонометрические уравнения второго порядка решаются следующим образом: по основному тригонометрическому тождеству представляют единицу как sin2x+cos2x и умножают это выражение на d: asin2x+bsinxcosx+ccos2x=d(sin2x+cos2x). После преобразований получим однородное тригонометрическое уравнение второго порядка.

---

Решить уравнение 3sinx-4cosx=5.

---

Решение

Решим данное уравнение с помощью формул двойного аргумента, применим формулы (1)–(3). Тогда 

6sinx2cosx2-4(cos2x2-sin2x2)=5(cos2x2+sin2x2).

Раскроем скобки, приведем подобные слагаемые:

sin2x2-6sinx2cosx2+9cos2x2=0.

Получили однородное тригонометрическое уравнение второго порядка. Разделим обе части уравнения на cos2x2≠0, тогда tg2x2-6tgx2+9=0. Пусть tgx2=t. Имеем t2-6t+9=0, откуда t=3. Вернемся к исходной переменной: tgx2=3, значит, x=2arctg3+2πk, k∈Z.

Ответ: 2arctg3+2πk, k∈Z.

---

Решить уравнение 4sinx-3cosx=2.

---

Решение

Решим данное уравнение с помощью формул универсальной подстановки, применив формулы (4), (5). Тогда 

4×2tgx21+tg2x2-3×1-tg2x21+tg2x2=2,

8tgx2-3+3tg2x2=2+2tg2x2,

tg2x2+8tgx2-5=0.

Пусть tgx2=t, тогда t2+8t-5=0, откуда t1=-4+21 и t2=-4-21. Вернемся к исходной переменной: 

tgx2=-4+21 или tgx2=-4-21. Тогда

x=2arctg(-4+21)+2πk, k∈Z,

x=2arctg(-4-21)+2πn, n∈Z.

Ответ: 2arctg(-4+21)+2πk, k∈Z, 2arctg(-4-21)+2πn, n∈Z.

---

Решить уравнение cos2x=3sin2x-1.

---

Решение

Перепишем уравнение в виде 3sin2x-cos2x=1.

Решим данное уравнение методом введения вспомогательного аргумента.  Здесь, a=3, b=1, a2+b2=2.

Разделим обе части уравнения на 2: 32sin2x-12cos2x=12. Введем вспомогательный аргумент φ так, чтобы cosφ=32, sinφ=12. Очевидно, что φ=π6. Исходное уравнение можно записать в виде:

cosπ6sin2x-sinπ6cos2x=12, или sin(2x-π6)=12. Это уравнение равносильно совокупности уравнений 2x-π6=π6+2πn, n∈Z и 2x-π6=5π6+2πk, k∈Z. Откуда x=π6+πn, n∈Z и x=π2+πk, k∈Z.

Ответ: π6+πn, n∈Z, π2+πk, k∈Z.

---

Решить уравнение cos4x4+cos4x4+3π4=14.

---

Решение

Воспользуемся формулой понижения степени cos2α2=1+cosα2:

1+cosx222+1+cosx2+3π222=14.

В левой части уравнения применим свойство степени и умножим обе его части на 4:

1+cosx22+1+cosx2+3π22=1.

По формулам приведения cosx2+3π2=sinx2.

После раскрытия скобок, приведения подобных слагаемых, применения основного тригонометрического тождества, получим:

cosx2+sinx2=-1.

Разделим обе части уравнения на 2:

12cosx2+12sinx2=-12.

Зная, что 12=sinπ4=cosπ4, последнее уравнение можно переписать так:

sinπ4cosx2+cosπ4sinx2=-12.

Воспользуемся формулой синуса суммы аргументов:

sin(π4+x2)=-12,

[π4+x2=-π4+2πk, k∈Z,π4+x2=-3π4+2πn, n∈Z, [x2=-π2+2πk, k∈Z,x2=-π+2πn, n∈Z,

[x=-π+4πk, k∈Z,x=-2π+4πn, n∈Z,  или  [x=π+4πk, k∈Z,x=2π+4πn, n∈Z.

Ответ: π+4πk, k∈Z;  2π+4πn, n∈Z.

---

Решить уравнение:

1. sin2x-4sin2x-3cos2x=-5;

2. 5sinx-12cosx=13 методом введения вспомогательного аргумента;

3. 3cosx+2sinx=1 двумя способами (формул двойного аргумента, универсальной подстановки).

---

---

---