Длина
S
дуги гладкой кривой y=
f(x),
содержащейся между двумя точками с
абсциссами x
= a
и x
= b
равна
![]()
Пример
2.1. Вычислить
длину дуги
![]()
,
цепной линии, заданной уравнением

,
от точки x
= 0 до точки
x
= 4.
Решение.
Воспользуемся указанной формулой.
Имеем:

и


Отсюда
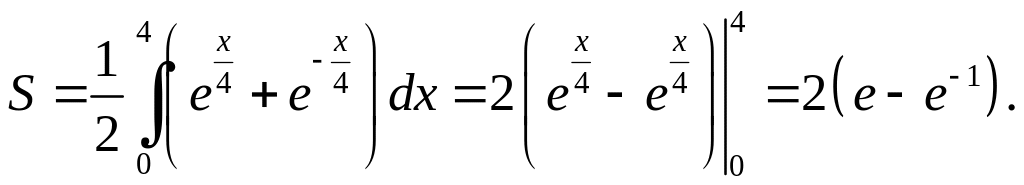
2.2.
Длина дуги кривой, заданной параметрически.
Если
кривая задана уравнениями в параметрической
форме
![]()
,
где
φ (t)
и ψ (t)
– непрерывно дифференцируемые функции,
то длина дуги S
кривой равна

где
t1
и t2
значения параметра, соответствующие
концам дуги.
Пример
2.1.. Вычислить
длину дуги кривой:
![]()
от
t
= 0 до
![]()
Решение.
Дифференцируя по t
параметрические уравнения кривой,
получим
![]()
![]()
Преобразуем
подынтегральную функцию:
![]()
![]()
![]()
![]()
Пользуясь
формулой для длины дуги в параметрическом
виде, получим

2.3. Длина дуги кривой в полярной системе координат
Если
гладкая кривая задана уравнением
![]()
в полярных координатах ρ
и φ,
то длина дуги S
равна

где
α и β –значения полярного угла в крайних
точках дуги.
Пример
2.3. Найти
длину всей кривой
![]()
Вся
кривая описывается точкой (ρ,
φ) при
изменении φ
от 0 до 3π.
Решение.
Имеем
![]()
поэтому
длина всей дуги кривой
![]()

Задачи
для самостоятельного решения.
1.
Определить длину дуги кривой,
![]()
,отсеченной
осью Oх.
Ответ:![]()
2.
Определить длину дуги кривой
![]()
от x=0
до x=1
Ответ:
![]()
3.
Определить длину дуги кривой
![]()
между
точками, абсциссы которых π/2 и π/3.
Ответ:![]()
4.
Определить длину дуги кривой
![]()
от
начала координат до точки, для которой
x=1.
Ответ:
e
– 1.
5.
Определить длину дуги кривой
![]()
от x1=a
до x2=b.
Ответ:
![]()
-
Вычислить
длину дуги кривой
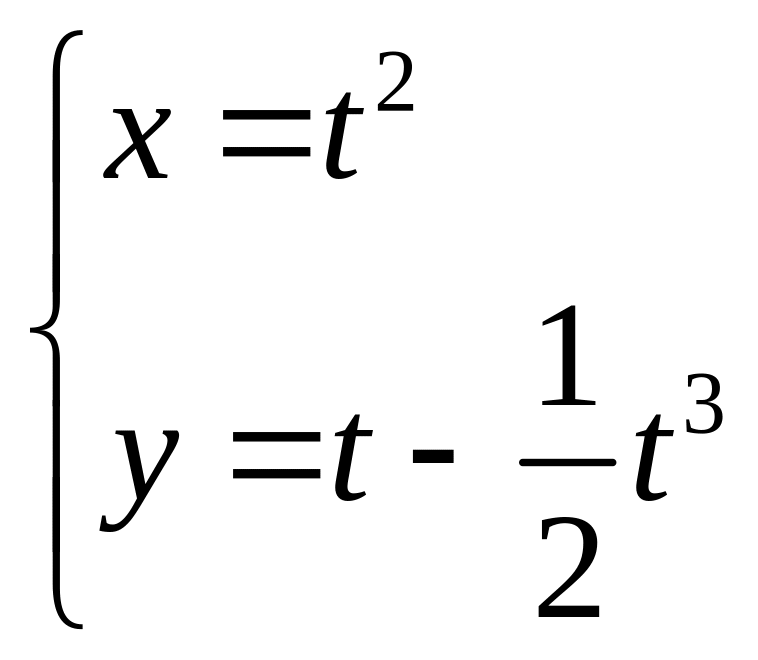
в пределах от 0 до

.
Ответ:
![]()
-
Вычислить
длину дуги кривой

от
t1=0
до t2=π.
Ответ:
![]()
-
Найти
длину развертки окружности
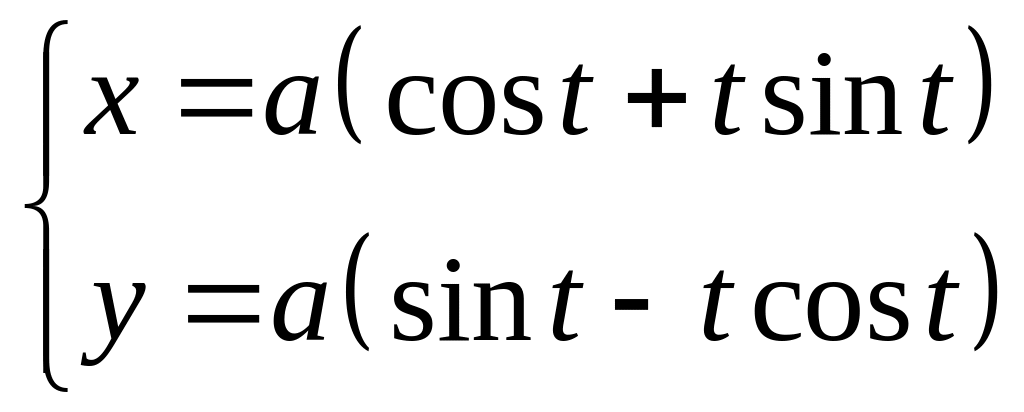
от
t=0
до t=T.
Ответ:
![]()
9.
Найти длину кривой

Ответ:
16a.
10.
Найти всю длину кардиоиды
![]()
Ответ:
8a.
11.
Вычислить длину прямой линии
![]()
в пределах от φ1=0
до φ2=π/2.
Ответ:
![]()
12.
Вычислить длину дуги части параболы
![]()
отсекаемой от параболы вертикальной
прямой, проходящей через полюс.
Ответ:
![]()
.
13.
Вычислить длину кривой
![]()
Ответ:
![]()
Занятие
3.
Вычисление объема тел.
3.I. Объем тела вращения
Объемы
тел, образованных вращением криволинейной
трапеции, ограниченной кривой
![]()
,
осью Ох и
двумя вертикалями х=а
и х=b,
вокруг осей Ох
и Oy,
выражаются соответственно формулами:
1.

2.
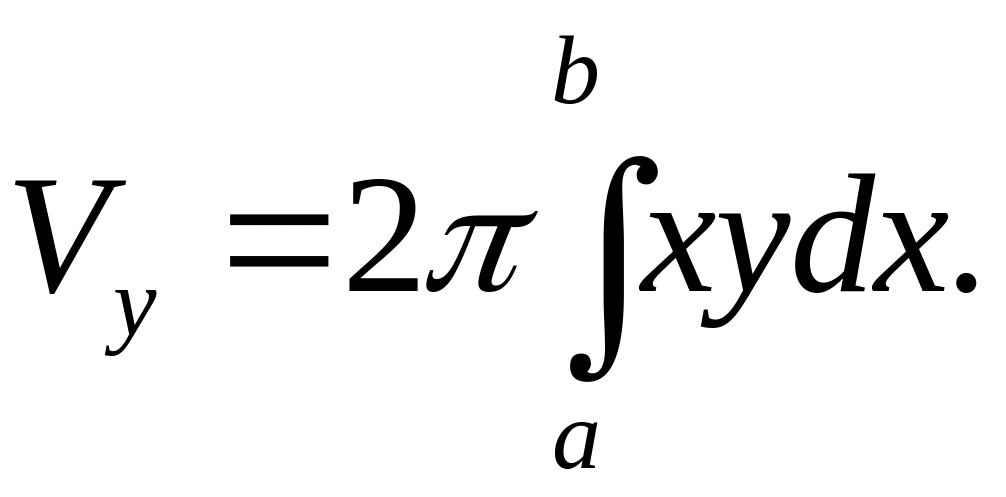
Объем
тела, образованного вращением около
оси Oy
фигуры, ограниченной кривой
![]()
Осью Oy
и двумя прямыми y=c
и y
= d
можно получить
по формуле
![]()
получающейся
из формулы 1. путем перестановки координат
X
и Y.
В
более общем случае объемы тел, образованных
вращением фигуры, ограниченной кривыми
![]()
(причем
![]()
)
и прямыми х=а,
x=b,
вокруг координатных осей Ох
и Oy
соответственно
равны

П
ример
3.1. Вычислить
объем тела, образованного вращением
фигуры вокруг оси Ох,
ограниченной линиями
![]()
,
х=а.
Решение.
Построив параболу
и
прямую х=а,
получим
параболический сегмент ОАВ
(рис.5).
При
вращении его вокруг оси Ох
образуется
сегмент параболоида вращения. Согласно
общим указаниям найдем объем этого
тела.

Пример
3.2. Вычислить
объем тела, образованного вращением
фигуры, ограниченной одной полуволной
синусоиды y=sinx
и отрез-ком
![]()
оси Ох
вокруг оси Oy.
Решение.

![]()
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
30.04.2022503.81 Кб02.doc
- #
- #
30.04.2022381.44 Кб120.doc
- #
- #
- #
- #
- #
- #
- #
- #
$begingroup$
I’m trying to find the entire length of the cardioid $r = 1-costheta$.
Although, I’m not sure how to compute the definite integral for $a$ and $b$, given that the equation is for the length of the arc is this:
$$int^{theta}_{a}sqrt{r^2+left(frac{dr}{dtheta}right)^2}space dtheta$$
Here is my working out:
$sqrt{(1-costheta)^2-sintheta} = 1-2cos left(θright)+cos ^2left(θright)-sin ^2left(θright)$
Hence:
$$int^{theta}_{a}sqrt{left(cos left(θright)-1right)^2-sin ^2left(θright)}space dtheta$$
Though, where would I begin with computing the following integral? I appreciate the support.
asked Mar 3, 2021 at 13:29
![]()
$endgroup$
4
$begingroup$
To find the full length of the cardioid you need to integrate from $0$ to $2pi$:
$$
L=int_0^{2pi}sqrt{(1-costheta)^2color{red}+(sintheta)^2},dtheta=
int_0^{2pi}sqrt{2(1-costheta)},dtheta=int_0^{2pi}2sinfractheta2,dtheta.
$$
Can you take it from here?
answered Mar 3, 2021 at 13:51
useruser
24.4k2 gold badges21 silver badges55 bronze badges
$endgroup$
2
$begingroup$
You could also take (due to symmetry with respect to the polar axis) half the integral:
$$L=2int_0^{pi}sqrt{(1-costheta)^2+(sintheta)^2},dtheta=
4int_0^{pi}sin(theta/2),dtheta=8.$$
answered Apr 26, 2021 at 14:44
$endgroup$
You must log in to answer this question.
Not the answer you’re looking for? Browse other questions tagged
.
Not the answer you’re looking for? Browse other questions tagged
.
Если посмотреть на кардиоиду , что в ссылке, то видим: ось симметрии вертикальная. – то есть ось 0y.
Поэтому можно рассмотреть удвоенную длину левой половины. Я приму для простоты набивки такое уравнение:
[math]r=2(1-sin{t})quad[/math] где [math]t[/math] изменяется от [math]frac{pi}{2},[/math] до [math]frac{3pi}{2},[/math]
Полная длина кривой:
[math]L=2int limits_{frac{pi}{2}}^{frac{3pi}{2}}sqrt{r^2+(r’)^2},dt[/math]
[math]r^2=4(1-sin{t})^=4-8sin{t}+4sin^2{t}[/math]
[math]r’=-2cos{t}, ; , (r’)^2=4cos^2{t}[/math]
Под корнем будет [math]8(1-sin{t})[/math]
Нужно взять такой интеграл:
[math]L=2int limits_{frac{pi}{2}}^{frac{3pi}{2}}sqrt{8(1-sin{t})}, dt=frac{16cos{t}}{sqrt{2(1-sin{t})}} bigg |_{frac{pi}{2}}^{frac{3pi}{2}}=0-(-16)=16[/math]
Бали затруднения с нижним пределом, но взял lim и все выяснилось:
https://www.wolframalpha.com/input/?i=lim(16*cos(x)%2Fsqrt(2-2*sin(x)),x%3Dpi%2F2)
Наталья Игоревна Восковская
Эксперт по предмету «Математика»
Задать вопрос автору статьи
Определение длины дуги кривой
Рассмотрим в пространстве дугу $cup AB$ некоторой кривой. Точками $M_{0} $, $M_{1} $, $M_{2} $, …. , $M_{n-1} $, $M_{n} $ разобьем её на $n$ произвольных последовательных участков. Соединим соседние точки отрезками прямых и получим вписанную в дугу $cup AB$ ломаную, в которой $M_{0} $ совпадает с точкой $A$, а $M_{n} $ совпадает с точкой $B$. Эта ломаная состоит из звеньев $M_{0} M_{1} $, $M_{1} M_{2} $, …. , $M_{i-1} M_{i} $, …. , $M_{n-1} M_{n} $.
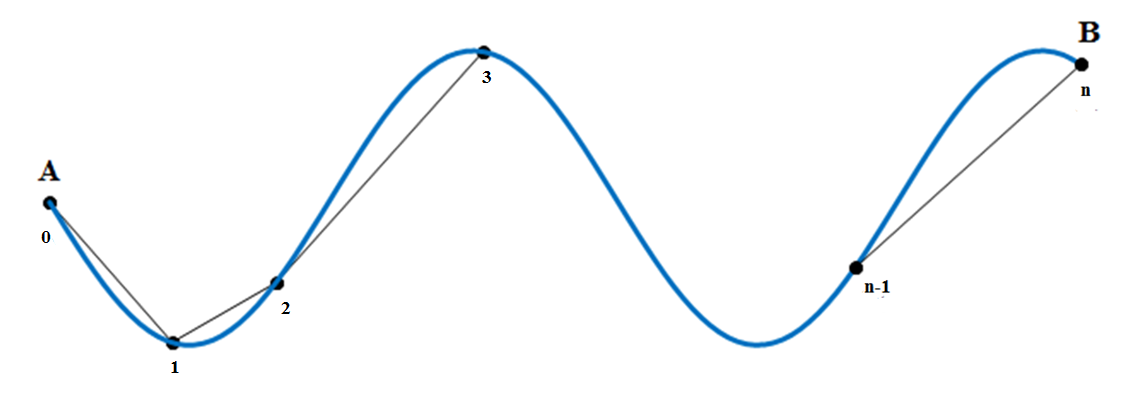
Обозначим длины звеньев этой ломаной следующим образом: длина $M_{0} M_{1} =Delta ; l_{1} $, длина $M_{1} M_{2} =Delta ; l_{2} $, …. , длина $M_{i-1} M_{i} =Delta ; l_{i} $, …. , длина $M_{n-1} M_{n} =Delta ; l_{n} $. Тогда периметр этой ломаной $l_{n} =Delta ; l_{1} +Delta ; l_{2} +ldots +Delta ; l_{i} +ldots +Delta ; l_{n} $ или просто $l_{n} =sum limits _{i=1}^{n}Delta ; l_{i} $.
Будем уменьшать длины всех звеньев за счет увеличения их количества. При этом форма ломаной будет приближается к форме дуги кривой.
На этом основании длина дуги кривой определяется так: длиной $l$ дуги называется предел, к которому стремится периметр вписанной в эту дугу ломаной при неограниченном увеличении числа её звеньев и при стремлении к нулю наибольшей из длин её звеньев.
Соответствующее выражение имеет вид: $l=mathop{lim }limits_{max ; Delta ; l_{i} to 0} sum limits _{i=1}^{n}Delta ; l_{i} $.
Определение
Кривые, для которых этот предел существует, называются спрямляемыми.
Формулы для длины дуги плоской кривой
Пусть кривая задана между своими точками $A$ и $B$ на отрезке $left[a,; bright]$ уравнением в явном виде $y=fleft(xright)$, где $fleft(xright)$ — непрерывная функция с непрерывной первой производной на этом отрезке. В этом случае длина дуги кривой между точками точками $A$ и $B$ вычисляется по формуле $l=int limits _{a}^{b}sqrt{1+y’^{2} } cdot dx $.
«Длина дуги и ее производная» 👇
Задача 1
Найти длину дуги цепной линии $y=frac{1}{2} cdot left(e^{x} +e^{-x} right)$ на отрезке $left[0,; 1right]$.
Находим производную:
[y’=left(frac{1}{2} cdot left(e^{x} +e^{-x} right)right)^{{‘} } =frac{1}{2} cdot left(e^{x} -e^{-x} right).]
Вычисляем:
[1+y’^{2} =1+left(frac{1}{2} cdot left(e^{x} -e^{-x} right)right)^{2} =1+frac{1}{4} cdot left(e^{2cdot x} -2cdot e^{x} cdot e^{-x} +e^{-2cdot x} right)=]
[=1+frac{1}{4} cdot left(e^{2cdot x} -2+e^{-2cdot x} right)=frac{1}{4} cdot left(e^{x} +e^{-x} right)^{2} ;]
[sqrt{1+y’^{2} } =frac{1}{2} cdot left(e^{x} +e^{-x} right).]
Находим длину дуги:
[l=int limits _{a}^{b}sqrt{1+y’^{2} } cdot dx =int limits _{0}^{1}frac{1}{2} cdot left(e^{x} +e^{-x} right)cdot dx =frac{1}{2} cdot left[e^{x} -e^{-x} right]_{0}^{1} =]
[=frac{1}{2} cdot left(left(e^{1} -e^{-1} right)-left(e^{0} -e^{-0} right)right)=frac{e-e^{-1} }{2} .]
Пусть кривая задана параметрическими уравнениями $x=xleft(tright)$ и $y=yleft(tright)$, $alpha le tle beta $. Предположим, что функции $x=xleft(tright)$ и $y=yleft(tright)$ и их производные непрерывны при $alpha le tle beta $, причем $x’left(tright)ne 0$. В этом случае длина дуги кривой вычисляется по формуле $l=int limits _{alpha }^{beta }sqrt{left(x’left(tright)right)^{2} +left(y’left(tright)right)^{2} } cdot dt $.
Задача 2
Найти длину одной арки циклоиды $x=t-sin t$, $y=1-cos t$, $0le tle 2cdot pi $.
Находим производные:
[x’=left(t-sin tright)^{{‘} } =1-cos t; y’=left(1-cos tright)^{{‘} } =sin t.]
Вычисляем:
[left(x’right)^{2} +left(y’right)^{2} =left(1-cos tright)^{2} +left(sin tright)^{2} =2cdot left(1-cos tright)=4cdot sin ^{2} frac{t}{2} .]
Находим длину дуги:
[l=int limits _{0}^{2cdot pi }sqrt{4cdot sin ^{2} frac{t}{2} } cdot dt =2cdot int limits _{0}^{2cdot pi }sin frac{t}{2} cdot dt =-4cdot left[cos frac{t}{2} right]_{0}^{2cdot pi } =]
[=-4cdot left(cos frac{2cdot pi }{2} -cos frac{0}{2} right)=-4cdot left(-1-1right)=8.]
Пусть кривая задана в полярных координатах $rho =rho left(phi right)$, $alpha le phi le beta $. Предположим, что функция $rho =rho left(phi right)$ и её производная непрерывны при $alpha le phi le beta $. В этом случае длина дуги кривой вычисляется по формуле $l=int limits _{alpha }^{beta }sqrt{rho ^{2} +rho ‘^{2} } cdot dphi $.
Задача 3
Найти длину кардиоиды $rho =1+cos phi $.
Так как кардиоида симметрична относительно полярной оси, то изменяя полярный угол $phi $ от $0$ до $pi $, мы получим половину длины кардиоиды.
Находим производную: $rho ‘=-sin phi $.
Вычисляем:
[rho ^{2} +rho ‘^{2} =left(1+cos phi right)^{2} +left(-sin phi right)^{2} =2cdot left(1+cos phi right).]
Находим половину длины кардиоиды:
[frac{l}{2} =int limits _{0}^{pi }sqrt{2cdot left(1+cos phi right)} cdot dphi =2cdot int limits _{0}^{pi }cos frac{phi }{2} cdot dphi =4cdot left[sin frac{phi }{2} right]_{0}^{pi } =4cdot sin frac{pi }{2} =4.]
Полная длина кардиоиды $l=8$.
Производная и дифференциал дуги
Пусть в формуле $l=int limits _{a}^{b}sqrt{1+left(f’left(xright)right)^{2} } cdot dx $ для длины дуги кривой, заданной в виде $y=fleft(xright)$, $ale xle b$, нижняя граница интеграла $a$ остается постоянной, а верхняя граница изменяется и равна $x$.
При этом длина дуги $lleft(xright)=int limits _{a}^{x}sqrt{1+left(f’left(tright)right)^{2} } cdot dt $ будет функцией верхней границы (переменная интегрирования переобозначена, чтобы не путать её с верхней границей).
В соответствии с теоремой о производной интеграла по верхней границе производная этой функции имеет вид $l’left(xright)=sqrt{1+left(f’left(xright)right)^{2} } $.
Отсюда получаем дифференциал дуги:
$dlleft(xright)=l’left(xright)cdot dx=sqrt{1+left(f’left(xright)right)^{2} } cdot dx$, откуда $dl=sqrt{1+y’^{2} } cdot dx$ или $dl=sqrt{dx^{2} +dy^{2} } $.
При параметрическом задании функции $x=xleft(tright)$ и $y=yleft(tright)$, $alpha le tle beta $ дифференциал дуги имеет вид $dl=sqrt{left(x’left(tright)right)^{2} +left(y’left(tright)right)^{2} } cdot dt$.
При задании функции в полярных координатах $rho =rho left(phi right)$, $alpha le phi le beta $ дифференциал дуги имеет вид $dl=sqrt{rho ^{2} +rho ‘^{2} } cdot dphi $.
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме
