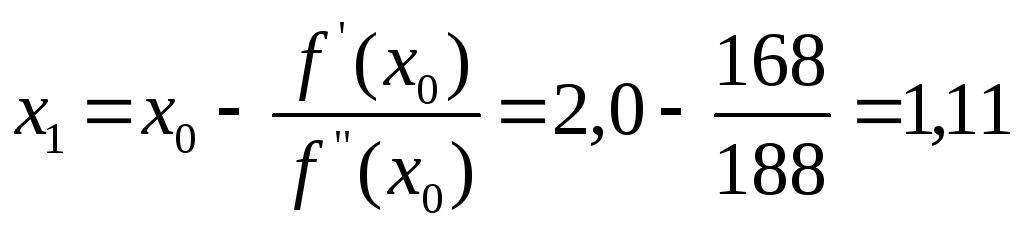Как найти второе приближение

Как найти второе приближение

Применение производной к приближенным вычислениям

  1. Определение и геометрический смысл дифференциала
  2. Алгоритм приближенных вычислений с помощью дифференциала
  3. Приближение с точностью до квадрата приращения
  4. Полезные формулы приближений для функций вблизи нуля
  5. Примеры

п.1. Определение и геометрический смысл дифференциала

Дифференциал функции (y=f(x)) – это главная, линейная часть приращения функции, равная произведению производной на приращение аргумента: $$ dy=f'(x_0)triangle x $$

Определение и геометрический смысл дифференциала
Выберем на кривой (y=f(x)) начальную точку (A(x_0,y_0)). Если мы начнем перемещаться к точке (B(x,y)), то приращению аргумента (triangle x=AC) соответствует приращение функции (triangle y=BC). Если считать, что кривая приблизительно совпадает со своей касательной при малых приращениях (triangle x), то (BCapprox MC) и (triangle yapprox dy).

Геометрический смысл дифференциала – замена приращения функции (triangle y) на линейное приращение по касательной (dy: triangle yapprox dy=f'(x_0 )triangle x)
Чем меньше (triangle x), тем ближе дифференциал к полному приращению функции: $$ triangle yrightarrow dy, triangle xrightarrow 0 $$

п.2. Алгоритм приближенных вычислений с помощью дифференциала

На входе: функция (y=f(x)), точка x*, в которой нужно посчитать значение функции
Шаг 1. Определяем ближайшую к x* начальную точку (x_0), для которой значение (y_0=f(x_0)) известно или легко находится.
Шаг 2. Находим выражение для первой производной (f'(x)).
Шаг 3. Находим значение производной в начальной точке (f'(x_0))
Шаг 4. Находим линейное приближение значения функции $$ y^*approx f(x_0)+f'(x_0)(x^*-x_0) $$ На выходе: значение y*

Например:
1) Найдем значение корня (sqrt{65})
Функция (y=sqrt{x}, x^*=65)
Начальная точка (x_0=64). Начальное значение функции (y_0=sqrt{64}=8)
Производная: (f'(x)=frac{1}{2sqrt{x}})
Производная в начальной точке: (f'(x_0)=frac{1}{2sqrt{64}}=frac{1}{16})
Подставляем: (y^*=sqrt{65}approx 8+frac{1}{16}(65-64)=8+frac{1}{16}=8,0625)
Оценим относительную ошибку для полученного результата.
Значение, полученное на калькуляторе: (sqrt{65}approx 8,062258). Откуда: $$ partial=frac{|8,062258|}{8,062258}cdot 100text{%}approx 0,003text{%} $$ Таким образом, в данном случае линейное приближение имеет высокую точность, т.к. для (x_0=64) и (x^*=65) кривая (y=sqrt{x}) очень близка к прямой, т.е. своей касательной.

2) Найдем значение корня (sqrt{5})
Пусть начальная точка (x_0=4). Начальное значение функции (y_0=sqrt{4}=2)
Производная в начальной точке: (f'(x_0)=frac{1}{2sqrt{4}}=frac14)
(y^*=sqrt{5}approx 2+frac14 (5-4)=2,25)
Значение, полученное на калькуляторе: (sqrt{5}approx 2,23607) $$ partial=frac{|2,23607-2,25|}{2,23607}cdot 100text{%}approx 0,06text{%} $$ Точность стала хуже. Однако, её можно повысить, если взять (x_0=4,84).

3) Найдем (sqrt{5}) при (x_0=4,84).
(y_0=sqrt{4,84} =2,2)
Производная в начальной точке: (f'(x_0 )=frac{1}{2cdot 2,2}=frac{1}{4,4})
(y^*=sqrt{5}approx 2,2+frac{1}{4,4}(5-4,84)=2,2+frac{0,16}{4,4}=2,2+frac{2}{55}=2,23636…)
Значение (sqrt{5}approx 2,23607) $$ partial=frac{|2,23607-2,23636|}{2,23607}cdot 100text{%}approx 0,01text{%} $$ Точность повысилась.

Вывод: точку (x_0) следует выбирать, исходя из поведения функции (y=f(x)) в окрестности (x^*). Чем ближе (x_0) к (x^*) и чем ближе кривая к касательной, тем точнее будет линейное приближение с помощью дифференциала.

п.3. Приближение с точностью до квадрата приращения

Значение функции в зависимости от приращения (triangle x=x^*-x_0) с точностью до квадратичного слагаемого определяется формулой: $$ y^*approx f(x_0)+f'(x_0)(x^*-x_0)+frac{f”(x_0)}{2}(x^*-x_0)^2 $$

Например:
1) Найдем квадратичное слагаемое для (x^*=65, x_0=64, y=sqrt{x})
Вторая производная: (f”(x)=left(frac{1}{2sqrt{x}}right)’=frac12cdotleft(-frac12right)cdotfrac{1}{xsqrt{x}}=-frac{1}{4xsqrt{x}}) $$ frac{f”(x_0)}{2}(x^*-x_0)^2=-frac{(65-64)^2}{2cdot 4cdot 64cdot 8}=-frac{1}{4096}approx -0,0002 $$ Значит, квадратичное слагаемое дает поправку в 4-м знаке.
Используя полученное выше линейное приближение, получаем: $$ y^*=sqrt{65}approx 8,0625-0,0002=8,0623approx 8,062 $$ Квадратичное слагаемое указывает, что округлить результат нужно до 3-го знака после запятой.

2) Найдем квадратичное слагаемое для (x^*=5, x_0=4, y=sqrt{x}) $$ frac{f”(x_0)}{2}(x^*-x_0)^2=-frac{(5-4)^2}{2cdot 4cdot 4cdot 2}=-frac{1}{64}approx -0,02 $$ Получаем: $$ y^*=sqrt{5}approx 2,25-0,02=2,23approx 2,2 $$ Квадратичное слагаемое указывает, что округлить результат нужно до 1-го знака после запятой.

3) Найдем квадратичное слагаемое для (x^*=5, x_0=4,84, y=sqrt{x}) $$ frac{f”(x_0)}{2}(x^*-x_0)^2=-frac{(5-4,84)^2}{2cdot 4cdot 4,84cdot 2,2}=-frac{0,0256}{85,184}approx -0,0003 $$ Получаем: $$ y^*=sqrt{5}approx 2,2367-0,0003=2,2364approx 2,236 $$ Квадратичное слагаемое указывает, что округлить результат нужно до 3-го знака после запятой.

п.4. Полезные формулы приближений для функций вблизи нуля

Рассмотрим свойства приближений некоторых функций при (x_0=0) и (triangle x=xrightarrow 0).
В разложении ограничимся слагаемым (y(0)) и линейным приближением. Только если линейное приближение равно 0, будем учитывать слагаемое квадратичного приближения.
1) (y=sinx)
(y’=cosx, y”=-sinx)
(y(0)=0, y'(0)=1, y”(0)=0)
(sinxapprox 0+1cdot x-frac02cdot x^2approx x)

2) (y=cosx)
(y’=-sinx, y”=-cosx)
(y(0)=1, y'(0)=0, y”(0)=-1)
(cosxapprox 1+0cdot x-frac12cdot x^2=1-frac{x^2}{2})

3) (y=tgx)
(y’=frac{1}{cos^2x}, y”=-frac{2cosxcdot(-sinx)}{cos^4x}=frac{2sinx}{cos^3x})
(y(0)=0, y'(0)=1, y”(0)=0)
(tgxapprox 0+1cdot x-frac02cdot x^2= x)

4) (y=e^x)
(y’=y”=e^x)
(y(0)=y'(0)=y”(0)=1)
(e^xapprox 1+1cdot x+frac12cdot x^2approx 1+x)
Пренебрегаем (frac{x^2}{2}) как очень малым слагаемым.

5) (y=ln(1+x))
(y’=frac{1}{1+x}, y”=-frac{1}{(1+x)^2})
(y(0)=0, y'(0)=1, y”(0)=-1)
(ln(1+x)approx 0+1cdot x-frac12 x^2approx x)

6) (y=sqrt{1+x})
(y’=frac{1}{2sqrt{1+x}}, y”=-frac{1}{4(1+x)^{3/2}})
(y(0)=1, y'(0)=frac12, y”(0)=-frac14)
(sqrt{1+x}approx 1+frac12cdot x-frac18 x^2approx1+frac x2)

7) (y=frac{1}{sqrt{1+x}})
(y’=-frac{1}{2(1+x)^{frac32}}, y”=frac{3}{4(1+x)^{frac52}})
(y(0)=1, y'(0)=-frac12, y”(0)=frac34)
(frac{1}{sqrt{1+x}}approx 1-frac12 x+frac38 x^2approx 1-frac x2)

8) (y=(1+x)^a, ainmathbb{R})
(y’=a(1+x)^{a-1}, y”=a(a-1)(1+x)^{a-2})
(y(0)=1, y'(0)=a, y”(0)=a(a-1))
((1+x)^aapprox 1+acdot x+frac{a(a-1)}{2}x^2approx 1+ax)

Таблица приближений для функций при (xrightarrow 0)

$$ sinxapprox x $$

$$ e^xapprox 1+x $$

$$ cosxapprox 1-frac{x^2}{2} $$

$$ ln(1+x)approx x $$

$$ tgxapprox x $$

$$ sqrt{1+x}approx 1+frac x2 $$

$$ (1+x)^aapprox 1+ax, ainmathbb{R} $$

$$ frac{1}{sqrt{1+x}}approx 1-frac x2 $$

п.5. Примеры

Пример 1. Найдите линейное приближение значения функции в заданной точке с помощью дифференциала. Ответ представьте с точностью до сотых. $$ y^*approx f(x_0)+f'(x_0)(x^*-x_0) $$ a) (sqrt[3]{28})
Функция (y=sqrt[3]{x}, x^*=28, x_0=27)
(f(x_0)=sqrt[3]{27}=3)
Производная: (f'(x)=(sqrt[3]{x})’=frac13 x^{-frac23}=frac{1}{3sqrt[3]{x^2}})
(f'(x_0)=frac{1}{3sqrt[3]{27^2}}=frac{1}{3cdot 9}=frac{1}{27}) $$ y^*=sqrt[3]{28}approx 3+frac{1}{27}(28-27)=3+frac{1}{27}approx 3,037approx 3,04 $$
б) (sin(0,03))
Функция (y=sinx, x^*=0,03, x_0=0)
(f(x_0)=sin0=0)
Производная: (f'(x)=(sinx)’=cosx)
(f'(x_0)=cos0=1) $$ y^*=sin(0,03)approx 0+1cdot(0,03-0)=0,03 $$
в) (sqrt{0,98})
Функция (y=sqrt{x}, x^*=0,98, x_0=1)
(f(x_0)=sqrt[3]{27}=3)
Производная: (f'(x)=(sqrt{x})’=frac{1}{2sqrt{x}})
(f'(x_0)=frac{1}{2sqrt{1}}=frac12) $$ y^*=sqrt{0,98}approx 1+frac12(0,98-1)=1-0,01=0,99 $$
e) (e^{0,01})
Функция (y=e^x, x^*=0,01, x_0=0)
(f(x_0)=e^0=1)
Производная: (f'(x)=(e^x)’=e^x)
(f'(x_0)=e^0=1) $$ y^*=e^{0,01}approx 1+1cdot (0,01-0)=1+0,01=1,01 $$

Пример 2. Найдите приближение значения функции в заданной точке с точностью до квадрата приращения. Ответ представьте с точностью округления последнего слагаемого. $$ y^*approx f(x_0)+f'(x_0)(x^*-x_0)+frac{f”(x_0)}{2}(x^*-x_0)^2 $$ a) (sqrt[4]{80})
Функция (y=sqrt[4]{x}, x^*=80, x_0=81)
(f(x_0)=sqrt[4]{81}=3)
Первая производная: (f'(x)=(sqrt[4]{x})’=frac14 x^{-frac34}=frac{1}{4sqrt[4]{x^3}})
(f'(x_0)=frac{1}{4sqrt[4]{81^3}}=frac{1}{4cdot 27}=frac{1}{108})
Вторая производная: (f”(x)=frac14cdot left(-frac34right)cdotfrac{1}{xsqrt[4]{x^3}}=-frac{3}{16xsqrt[4]{x^3}})
(f”(x_0)=-frac{3}{16cdot 81cdotsqrt[4]{81^3}}=-frac{3}{16cdot 81cdot 27}=-frac{1}{11664}) begin{gather*} y^*=sqrt[4]{80}approx 3+frac{1}{108}(80-81)-frac{1}{11664}cdot frac12(80-81)^2approx 3-0,00926-0,00004=\ =2,99070approx 2,9907 end{gather*}
б) (ln 1,04)
Функция (y=ln x, x^*=1,04, x_0=1)
(f(x_0)=ln 1=0)
Первая производная: (f'(x)=(ln x)’=frac1x)
(f'(x_0)=frac{1}{1}=1)
Вторая производная: (f”(x)=-frac{1}{x^2})
(f”(x_0)=-frac{1}{1^2}=-1) begin{gather*} y^*=ln 1,04approx 0+1cdot (1,04-1)-1frac12(1,04-1)^2=0,04-0,0008=0,0392approx 0,039 end{gather*}
в) (cos0,07)
Функция (y=cosx, x^*=0,07, x_0=0)
(f(x_0)=cos0=1)
Первая производная: (f'(x)=(cosx)’=-sinx)
(f'(x_0)=-sin0=0)
Вторая производная: (f”(x)=(-sinx)’=-cosx)
(f”(x_0)=-cos0=-1) begin{gather*} y^*=cos0,07approx 1+0cdot (0,07-0)-1cdotfrac12(0,07-0)^2=1-0,00245=\ =0,99755approx 0,9976 end{gather*}
г) (tg0,11)
Функция (y=tgx, x^*=0,11, x_0=0)
(f(x_0)=tg0=0)
Первая производная: (f'(x)=(tgx)’=frac{1}{cox^2x})
(f'(x_0)=frac{1}{cos^2x}=1)
Вторая производная: (f”(x)=left(frac{1}{cos^2x}right)’=-frac{2cosxcdot(-sinx)}{cos^4x}=frac{2sinx}{cos^3x})
(f”(x_0)=frac{2sin0}{cos^30}) begin{gather*} y^*=tg0,11approx 0+1cdot (0,11-0)+0cdotfrac12 (0,11-0)^2=0,11 end{gather*}

Источник

Для метода Ньютона
нужно задать начальное приближение из условия

,иначе процесс
сходимости не гарантирован.

Если ,
тои.

Если ,
тои.

Следовательно, в
качестве начального приближения следует
выбрать точку .

1) Находим первое
приближение по формуле

;

Так как
,
то требуется второе приближение.

2) Находим второе
приближение по формуле

Так как
,
то требуется третье приближение.

3) Находим третье
приближение по формуле

Так как
,
то процесс последовательных приближений
можно считать законченным и значение
принять за точку минимума.

Итак, ;число приближений.

Ниже приведены
расчеты нахождения минимума функции
методом Ньютона, выполненные с помощью
компьютерной программы.

Заметим, что в
случае выбора за начальное приближение
точки ,процесс все же
сойдется, но за большее число приближений.

Результаты всех
расчетов сведем в таблицу

№

Название метода поиска

Число приближений

Точка минимума

1

Метод дихотомии

12

(0,69; -22,04)

2

Метод «золотого сечения»

8

(0,68; -22,04)

3

Метод Ньютона

3

(0,69; -22,04)

Выводы: При поиске минимума функции на отрезке

самым быстрым
оказался метод Ньютона (4 приближения).

6 Лабораторная работа №6. Численное решение обыкновенных дифференциальных уравнений методами Эйлера, модифицированного метода Эйлера с пересчетом, Рунге-Кутты.

Задание.

Методами Эйлера,
модифицированным методом Эйлера с
пересчетом и методом Рунге-Кутты 4-го
порядка найти частное решение обыкновенного
дифференциального уравнения 1-го порядка
вида
,
с начальным условием ,на интервалес шагом.

Решение.

6.1
Найдем сначала точное решение
дифференциального уравнения .

Это уравнение
сводится к уравнению с разделяющимися
переменными с помощью подстановки .Тогдаи
уравнение примет вид Разделяя переменные,
получим

Частное решение
при начальном условии :

Итак, точное решение
имеет вид: .

Протабулируем
полученное решение на
интервалес шагоми результаты
расчетов сведем в таблицу 6.1

Таблица 6.1 Результаты
табулирования функции

6.2
Решение дифференциального уравнения
методом Эйлера.

Итерационная
формула метода Эйлера для дифференциального
уравнения имеет вид: .

У нас
;
;
;

.

Результаты расчетов
сведены в таблицу 6.2

Номер

точки
n

0

0,0

1,00

0,0+1,00=1,00

1

0,1

1,10

0,1+1,10=1,20

2

0,2

1,22

0,2+1,22=1,42

3

0,3

1,36

0,3+1,36=1,66

4

0,4

1,53

0,4+1,53=1,93

5

0,5

1,72

6.3
Решение дифференциального уравнения
модифицированным
методом Эйлера с пересчетом.

Итерационная
формула модифицированного метода Эйлера
с пересчетом для дифференциального
уравнения имеет вид:

,где

Результаты расчетов
сведены в таблицу 6.3

№

точки
n

0

0,0

1,00

0,0+1,00=1,00

1

0,1

1,11

0,1+1,11=1,21

2

0,2

1,24

0,2+1,24=1,44

3

0,3

1,40

0,3+1,40=1,70

4

0,4

1,58

0,4+1,58=1,98

5

0,5

1,79

6.4
Решение дифференциального уравнения
методом Рунге-Кутты
4-го порядка.

Итерационная
формула модифицированного метода Эйлера
с пересчетом для дифференциального
уравнения имеет вид:

       где

Результаты расчетов
сведены в таблицу 6.4

Номер

точки
n

0

0,0

1,00

0+1=1

1

0,1

1,11

0,1+1,11=1,21

2

0,2

1,24

0,2+1,24=1,44

3

0,3

1,40

0,3+1,4=1,7

4

0,4

1,58

0,4+1,58=1,98

5

0,5

1,79

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
Источник

Макеты страниц

Рис. 70

заменяют график функции на отрезке хордой, соединяющей точки Уравнение этой хорды имеет вид:

Она пересекает ось абсцисс в такой точке, где Полагая в равенстве находим, что

Это число является абсциссой точки пересечения хорды с осью Его можно принять за приближенное значение корня уравнения Чтобы получить более точное значение корня, надо вычислить значение функции в найденной точке и провести хорду, соединяющую соответствующую точку графика с тем концом графика, в котором функция имеет знак, противоположный полученному. Например, если то надо провести хорду, соединяющую точки (рис. 70). Она пересекает ось абсцисс в точке

Далее находим следующее приближение к корню:

В общем случае можно записать:

Мы получили последовательность чисел Можно доказать, что она сходится к корню уравнения Вычисления прекращают, когда в пределах заданной точности совпадают значения

Второй способ приближенного решения уравнений, называемый методом касательных, основан на замене графика функции не хордой, а касательной. Предположим, что на отрезке не только первая, но и вторая производная сохраняет один и тот же знак. Тогда график функции на всем отрезке обращен выпуклостью в одну и ту же сторону. Рисунки 71 и 72 показывают, что касательную надо проводить в точке, в которой знак функции совпадает со знаком второй производной: в точке, где функция положительна, если (т. е. график обращен выпуклостью вниз), и в точке, где функция отрицательна, в противном случае. Такая

Рис. 71

Рис. 72

точка обозначается обычно через и называется начальным при 6 лишением.

Предположим для определенности, что Тогда касательную надо проводить в точке т. е. начальное приближение Уравнение этой касательной имеет вид:

Чтобы найти точку пересечения касательной и оси абсцисс, положим Мы получим, что откуда находим абсциссу точки пересечения:

Это число можно принять за приближенное значение корня уравнения (рис. 72). Чтобы получить более точное значение корня, проведем касательную в точке с абсциссой и найдем точку ее пересечения с осью Продолжая этот процесс, получим последовательность чисел вычисляемую по формуле

Она сходится к корню I уравнения Вычисления прекращают, когда с заданной степенью точности совпадают значения

Пример 6. Найдем действительный корень уравнения с точностью до методом хорд; б) методом касательных.

Решение. Имеем:

Так как дискриминант квадратного трехчлена отрицателен, то знак трехчлена при любых совпадает со знаком старшего коэффициента. Таким образом, при любом имеем т. е. функция строго возрастает на всей числовой прямой. В таком случае заданное уравнение может иметь не более одного действительного корня.

Далее, заметим, что Значит, наше уравнение имеет единственный корень Е, лежащий в интервале

а) По методу хорд, воспользовавшись формулой (10), получим первое приближение:

Так как

Воспользовавшись формулой (11), находим второе приближение:

Так как то

Процесс сходится весьма медленно. Попробуем сузить интервал, учитывая, что значение функции в точке значительно меньше по абсолютной величине, чем Имеем Следовательно,

Применяя к интервалу метод хорд, получим новое приближение:

Дальнейшие вычисления по методу хорд дают Так как то с требуемой точностью можно считать, что

б) Для метода касательных в качестве начального приближения выбираем так как в интервале первая производная также сохраняет знак в интервале так что метод касательных применить можно.

Первое приближение:

Второе приближение:

Третье приближение:

Нужная точность достигнута уже на третьем шаге. Здесь сходимость процесса более быстрая, чем по методу хорд.

Вопросы для самопроверки

1. Опишите процесс решения уравнения методом хорд. Дайте геометрическое истолкование.

2. Опишите процесс решения уравнения методом касательных. Дайте геометрическое истолкование. Каким условиям должна удовлетворять функция , чтобы можно было применить метод касательных?

Упражнения

(см. скан)

1

Оглавление

  • ПРЕДИСЛОВИЕ
  • ГЛАВА 1. ДИФФЕРЕНЦИРУЕМЫЕ ФУНКЦИИ. ДИФФЕРЕНЦИАЛ. ПРОИЗВОДНАЯ
  • 2. Определение непрерывности функции в точке «на языке приращений».
  • § 2. ДИФФЕРЕНЦИРУЕМОСТЬ ФУНКЦИИ В ТОЧКЕ
  • 2. Связь между непрерывностью и дифференцируемостью функции в точке.
  • 3. Производная и дифференциал.
  • 4. Односторонние и бесконечные производные.
  • § 3. ПРИМЕНЕНИЯ ПРОИЗВОДНОЙ И ДИФФЕРЕНЦИАЛА ДЛЯ РЕШЕНИЯ ГЕОМЕТРИЧЕСКИХ И ФИЗИЧЕСКИХ ЗАДАЧ
  • 2. Геометрические приложения производной.
  • 3. Применения производной в физических задачах. Механический смысл производной.
  • § 4. ДИФФЕРЕНЦИРОВАНИЕ ОПЕРАЦИЙ
  • 2. Дифференцирование произведения.
  • 3. Дифференцирование частного.
  • § 5. ДИФФЕРЕНЦИРОВАНИЕ СЛОЖНОЙ ФУНКЦИИ
  • 2. Инвариантность формы записи дифференциала.
  • § 6. ДИФФЕРЕНЦИРОВАНИЕ ЭЛЕМЕНТАРНЫХ ФУНКЦИЙ
  • 2. Дифференцирование обратной функции.
  • 3. Дифференцирование обратных тригонометрических функций.
  • 4. Дифференцирование показательной и логарифмической функций.
  • 5. Дифференцирование гиперболических функций.
  • 6. Сводка правил и формул дифференцирования.
  • 7. Логарифмическое дифференцирование.
  • § 7. ПРОИЗВОДНЫЕ И ДИФФЕРЕНЦИАЛЫ ВЫСШИХ ПОРЯДКОВ
  • 2. Механический смысл второй производной.
  • 3. Натуральная степень бинома (формула Ньютона).
  • 4. Свойства производной n-го порядка.
  • 5. Дифференциалы высшего порядка.
  • ГЛАВА 2. ПРИМЕНЕНИЯ ДИФФЕРЕНЦИАЛЬНОГО ИСЧИСЛЕНИЯ
  • 1. СВЯЗЬ МЕЖДУ ХОДОМ ИЗМЕНЕНИЯ ФУНКЦИИ И ЕЕ ПРОИЗВОДНОЙ
  • 2. Экстремумы функции.
  • § 2. ТЕОРЕМА ЛАГРАНЖА И ЕЕ СЛЕДСТВИЯ
  • 2. Теорема 2 (теорема Ролля).
  • 3. Теорема Лагранжа.
  • 4. Условие постоянства функции.
  • § 3. ИССЛЕДОВАНИЕ ФУНКЦИЙ
  • 2. Исследование функций на экстремум с помощью первой производной.
  • 3. Использование второй производной для исследования функций на экстремум.
  • 4. Нахождение наибольшего и наименьшего значений функции на данном отрезке.
  • § 4. ВЫПУКЛЫЕ ФУНКЦИИ
  • 2. Достаточные условия выпуклости.
  • 3. Точки перегиба.
  • § 5. ПРИМЕНЕНИЕ ДИФФЕРЕНЦИАЛЬНОГО ИСЧИСЛЕНИЯ К ДОКАЗАТЕЛЬСТВУ НЕРАВЕНСТВ И РЕШЕНИЮ УРАВНЕНИЙ
  • 2. Приближенное решение уравнений.
  • § 6. ПРИМЕНЕНИЕ ПРОИЗВОДНЫХ ДЛЯ ВЫЧИСЛЕНИЯ ПРЕДЕЛОВ ФУНКЦИЙ
  • 2. Правило Лопиталя.
  • § 7. ПОСТРОЕНИЕ ГРАФИКОВ ФУНКЦИЙ
  • § 8. КРИВЫЕ НА ПЛОСКОСТИ
  • 2. Жордановы кривые.
  • 3. Связь между различными видами уравнений линий.
  • 4. Дифференцирование параметрически заданных функций.
  • 5. Полярное уравнение кривой.
  • 6. Производная второго порядка для параметрически заданной функции.
  • 7. Построение кривых, заданных параметрическими уравнениями.
  • 8. Построение кривых, заданных полярными уравнениями.
  • ОТВЕТЫ
Источник

Для нахождения второго приближения надо использовать вектор в первом приближении, т. е. Если ограничиться только изотропными средами или кристаллами, обладающими центом симметрии, то как было сказано, K2 = 0, и следовательно, в нужном приближении . Взяв в качестве нулевого приближения плоскую волну получим: .

Слагаемое с тройной частотой W3 = 3W приводит, очевидно, к генерации третьей гармоники. Исходное излучение частотой W создает в нелинейной среде поляризованность, осциллирующую на утроенной частоте 3W Элементарные вторичные волны третьей гармоники, испускаемые разными элементами среды, будут иметь всюду одинаковые фазовые соотношения с возбуждающей их волной поляризованности при совпадении показателей преломления на частотах W и 3W. Дисперсия среды на интервале (W, 3W) еще больше, чем в случае второй гармоники. Это ограничивает выбор кристаллов, в которых возможно выполнение условия пространственного синхронизма (N(3W) = N(W)), так как двулучепреломление должно быть настолько большим, чтобы поверхности N0(W) = Ne(3W) еще пересекались. Кроме того кубичная восприимчивость имеет малое значение, что вынуждает применять очень интенсивное исходное излучение. Мощное исходное излучение может привести к разрушению кристалла, но, несмотря на это, генерация третьей гармоники наблюдалась еще в 1962 г. группой американских ученых на кристалле исландского шпата при освещении его светом рубинового лазера.

Посмотрим теперь, какие явления связаны с первым слагаемым в выражении. Множитель есть исходная падающая волна. В рассматриваемом приближении этот множитель можно заменить . Учитывая, что , формулу (2-е уравнение Максвелла с учетом нелинейной части поляризованности) после этого можно записать так:

.

Отсюда видно, что влияние рассматриваемого слагаемого эквивалентно изменений диэлектрической проницаемости или показателя преломления среды. Учитывая малость поправки к E(W), для показателя преломления в поле интенсивной световой волны можно написать

, ,

Где — значение показателя преломления среды в линейной оптике, а N2 = 3K3/8N0 — некоторый коэффициент, зависящий от свойств среды. Этот коэффициент может быть и отрицательным, и положительным. Он особенно велик у нитробензола и имеет для него положительный знак.

Согласно, чем больше интенсивность падающей волны, тем большее изменение показателя преломления она вызывает. За счет появления нелинейной добавки к диэлектрической проницаемости (показателю преломления) световая волна изменяет собственную скорость и коэффициент поглощения в среде, т. е. волна, изменяя характеристики среды, тем самым изменяет условия для своего распространения. Это приводит к эффектам самофокусировки, самодифракции, нелинейному расширению светового пучка и т. д. Такие оптические эффекты принято называть самовоздействием световой волны.

Р и с. 8.9

Чтобы представить сущность явления самофокусировки, предположим, что в однородную среду с показателем N0 вступает плоскопараллельный пучок лучей кругового сечения с диаметром D (рис. 8.9). Допустим, что амплитуда пучка постоянна по всему сечению. Показатель преломления в пространстве, занятом пучком, станет равным , причем предположим, что N2 > 0. Из-за дифракции пучок должен расширяться, так что все направления лучей сосредоточатся в пределах конуса с углом при вершине 2QДиф, где QДиф = 1,22L/Dn0, L — длина волны в вакууме. Так как показатель преломления в пространстве, занятом пучком, больше, чем в окружающей среде, то на границе этих сред возможно полное внутреннее отражение, предельный угол скольжения для полного отражения от боковой стенки цилиндра определяется соотношением cos Q0 = N0/(N0 +N2 E02).

Ввиду малости нелинейной поправки к показателю преломления, этот угол будет мал, так что . При разложении функции cosQ0 в степенной ряд получим . Если QДиф < Q0, то часть дифрагированных лучей будет выходить из цилиндра — пучок будет ‘расширяться, при обратном соотношении QДиф < Q0 все дифрагированные лучи будут испытывать полное отражение от боковой поверхности цилиндра. Так как в реальных световых пучках интенсивность света и показатель преломления возрастают к оси пучка, то из-за искривления лучей пучок начинает сжиматься и может стянуться в тонкий шнур. Это и есть самофокусировка. В промежуточном случае когда , пучок будет проходить через нелинейную среду практически без изменения поперечных размеров. Он создаст для себя как бы волновод, в котором и распространяется без рассеяния в стороны. Такой режим распространения называется самоканализацией светового пучка. Так как условие самоканализации имеет вид , то подставив сюда значения углов и и выражение амплитуды через мощность пучка , получим так называемую пороговую мощность пучка , выше которой и начинается сжатие пучка. Заметим, что для наблюдения любого нелинейного эффекта необходимы световые пучки с определенными пороговыми мощностями.

Помимо рассмотренной, как уже отмечалось, есть и другие причины изменения показателя преломления. Это и электрострикция, и высокочастотный эффект Керра, и нагревание среды, происходящее при поглощении световой волны. Во всех этих случаях изменение показателя преломления пропорционально квадрату амплитуды волны и может быть определено формулой;.

Источник

Расчет – второе – приближение

Cтраница 1

Расчет второго приближения ( при найденном значении практически даег то же значение искомой величины.
 [1]

Производят расчет второго приближения, в котором за начальные параметры берут параметры, полученные при расчете первого приближения, за исключением параметров первой полости сжатия. Начальные параметры в первой полости второго и следующих приближений принимают следующим образом.
 [2]

Поэтому расчет второго приближения величин т, N, е, р2 и Г2 не производим.
 [3]

Результаты расчета второго приближения приведены ниже.
 [4]

Таким образом, расчет второго приближения сводится R основном к определению размеров, обеспечивающих прочность и жесткость элементов проточной части гидротормоза.
 [5]

Естественное желание избежать расчетов второго приближения заставляет очень внимательно отнестись к обобщенным данным, которыми расчетчик пользуется для первого приближения. Слишком широкое обобщение ( как, например, взятое нами выше из работы [25 ]) не гарантирует окончательных результатов по первому приближению. Такие обобщения хороши лишь для оценки исходных величин расчетов, предназначенных для более узкого применения ГТУ.
 [6]

Но часто к расчету второго приближения не прибегают, так как первое приближение дает удовлетворительные результаты.
 [7]

Как видим, расчетом второго приближения можно ограничиться и выбрать остальные размеры распылителя в соответствии с данными рекомендациями.
 [8]

Таким образом, по расчетам второго приближения давление в начале трубопровода равно 4 67 МПа, что всего на 0 17 МПа больше, чем то, которое дано в условии задачи. Следовательно, расход в точке В должен быть еще раз уменьшен.
 [9]

После первого цикла расчетов делают расчет второго приближения, при котором принимают значения параметров, полученные в нервом цикле расчетов. При определении параметров машин напольного транспорта после двух-трех циклов расчетов оптнмумы параметров стабилизируются на определенном уровне значений.
 [10]

Полученная зависимость не может использоваться в расчетах второго приближения. Величины перепадов давлений, полученных при аппроксимации зависимости 3 ступенчатой зависимостью, даются в предпоследней строке таблицы. Из рис. 57 нетрудно заметить, что до середины одиннадцатого года разработки зависимость 3 была завышенной, а затем заниженной по отношению к искомой.
 [11]

Если расхождение превышает допустимое, то выполняем расчет второго приближения.
 [12]

Далее уточняют концентрацию раствора по корпусам и выполняют расчет второго приближения. При этом рассчитывают депрессии, коэффициенты теплопередачи, скорости циркуляции, тепловые нагрузки и полезные разности температур по корпусам для режима работы, полученного в первом приближении.
 [13]

Найденное значение R3 ( t) используется в расчетах второго приближения.
 [15]

Страницы:  

   1

   2

Источник

Добавить комментарий