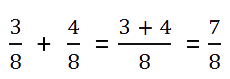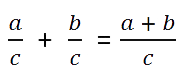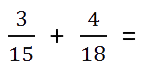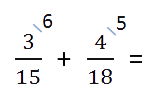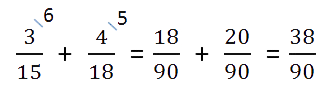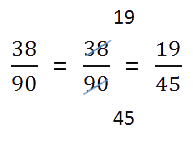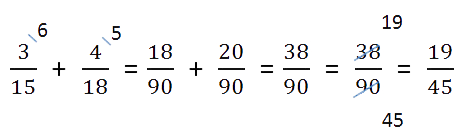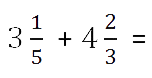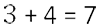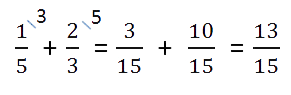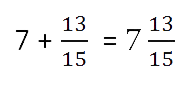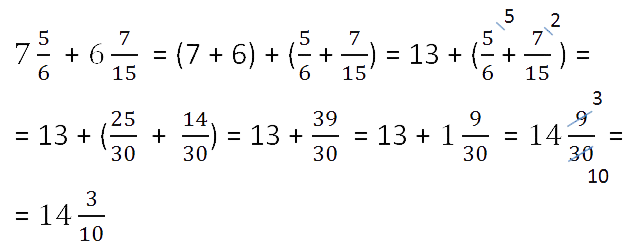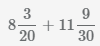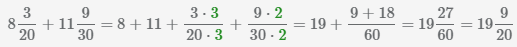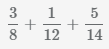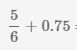Как найти второе слагаемое дроби - Сайт, где вы сможете решить свои вопросы

Похоже, вы используете блокировщик рекламы. Наш сайт существует и развивается
только за счет дохода от рекламы.

Пожалуйста, добавьте нас в исключения блокировщика.

на главную

Сложение дробей

Поддержать сайт

При сложении дробей могут встретиться разные случаи.

Сложение дробей с одинаковыми знаменателями

Такой случай наиболее простой. При сложении дробей с равными знаменателями складывают
числители, а знаменатель оставляют тот же.

Пример.

C помощью букв это правило сложения можно записать так:

Запомните!

Записывая ответ, проверьте нельзя ли полученную дробь сократить.

Сложение дробей с разными знаменателями

Чтобы сложить дроби с разными знаменателями нужно воспользоваться
следующими правилами.

Привести данные дроби к наименьшему общему знаменателю (НОЗ). Для этого найти
наименьшее общее кратное знаменателей.

Пример. Сложить дроби.

Как найти общий знаменатель

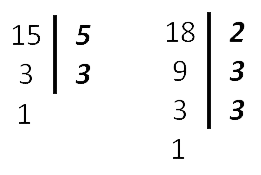
Находим НОК (15, 18).

НОК (15, 18) = 3 · 2 · 3 · 5 = 90

Найти дополнительные множители для каждой дроби. Для этого наименьший общий знаменатель (НОК из пункта 1)
делим по очереди на знаменатель каждой дроби.

Полученные числа и будут дополнительными множителями
для каждой из дробей. Множители записываем над числителем дроби справа сверху.

90 : 15 = 6 — дополнительный множитель для дроби

.

90 : 18 = 5 — дополнительный множитель для дроби

.
Числитель и знаменатель каждой дроби умножаем на свой дополнительный множитель, пользуясь
основным свойством дроби.

После умножения в знаменателях
обеих дробей должен получиться наименьший общий знаменатель.
Затем складываем дроби как дроби с одинаковыми знаменателями.
Проверяем полученную дробь.
- Eсли в результате получилась
  неправильная дробь,
  результат записываем в виде смешанного числа. Проверим нашу
  дробь.
  
  38 < 90
  
  У нас дробь правильная.
- Если в результате получилась сократимая дробь, необходимо выполнить сокращение.
Ещё раз весь пример целиком.

Сложение смешанных чисел

Сочетательное и переместитительное свойства сложения позволяют привести
сложение смешанных чисел к сложению их целых частей и к сложению их дробных частей.

Чтобы сложить смешанные числа нужно.

Отдельно сложить их целые части.
Пример.

Складываем целые части.
Отдельно сложить дробные части.
Если у дробных частей знаменатели разные, то
сначала приводим их к общему знаменателю, а затем складываем.
Сложить полученные результаты из пунктов 1 и 2.
Если при сложении дробных частей получилась неправильная дробь, то нужно
выделить целую часть из этой дроби и прибавить к полученной
в пункте 1 целой части.

Ещё один пример на сложение смешанных чисел.

Ваши комментарии

Важно!

Чтобы оставить комментарий, вам нужно войти на наш сайт при помощи

«ВКонтакте».

Оставить комментарий:

24 декабря 2018 в 11:19

Baur Nurgazinov
(^-^)
Профиль
Благодарили: 0

Сообщений: 1

(^-^)
Baur Nurgazinov
Профиль
Благодарили: 0

Сообщений: 1

0
Спасибо thanks
Ответить

2 января 2019 в 14:18
Ответ для Baur Nurgazinov

Лина Аникеева
(^-^)
Профиль
Благодарили: 0

Сообщений: 2

(^-^)
Лина Аникеева
Профиль
Благодарили: 0

Сообщений: 2

1) приводим все дроби к общему знаменателю
(2 -1 ) · х=
2) Вычислаем разность в скобках
( — ) · х=
· х=
сократим дроби на 3
· х=
3) вычисляем х
х= :
По правилу деления дробей делитель переворачиваем
x= · =
4 — сокращаем
х=3
Проверка:
(2 -1 ) · 3=( – ) · 3= · 3= · 3 = · = =

Ответ верный

0
Спасибо thanks
Ответить

24 января 2017 в 19:44

Фанис Газизов
(^-^)
Профиль
Благодарили: 0

Сообщений: 1

(^-^)
Фанис Газизов
Профиль
Благодарили: 0

Сообщений: 1

0
Спасибо thanks
Ответить

24 января 2017 в 21:12
Ответ для Фанис Газизов

Marina Kazakova
(^-^)
Профиль
Благодарили: 0

Сообщений: 1

(^-^)
Marina Kazakova
Профиль
Благодарили: 0

Сообщений: 1

0
Спасибо thanks
Ответить

1 марта 2016 в 18:39

Денис Демидов
(^-^)
Профиль
Благодарили: 0

Сообщений: 1

(^-^)
Денис Демидов
Профиль
Благодарили: 0

Сообщений: 1

спасибо сайт класс тему не понял

было очень непонятно

теперь понятно + +

+ + + + · + + + + + smile

0
Спасибо thanks
Ответить

19 сентября 2016 в 13:05
Ответ для Денис Демидов

Евгений Колосов
(^-^)
Профиль
Благодарили: 12

Сообщений: 197

(^-^)
Евгений Колосов
Профиль
Благодарили: 12

Сообщений: 197

cool

0
Спасибо thanks
Ответить

6 февраля 2016 в 18:54

Денис Бочин
(^-^)
Профиль
Благодарили: 0

Сообщений: 1

(^-^)
Денис Бочин
Профиль
Благодарили: 0

Сообщений: 1

Сложи

числа 30 и

числа 14.

0
Спасибо thanks
Ответить

10 февраля 2016 в 19:03
Ответ для Денис Бочин

Алексей Пешков
(^-^)
Профиль
Благодарили: 0

Сообщений: 2

(^-^)
Алексей Пешков
Профиль
Благодарили: 0

Сообщений: 2

1) от 30=;

от 14=

+ ===24=24

0
Спасибо thanks
Ответить

14 января 2016 в 15:31

Анжела Волк
(^-^)
Профиль
Благодарили: 0

Сообщений: 1

(^-^)
Анжела Волк
Профиль
Благодарили: 0

Сообщений: 1

2/6 или1/2 сравнение дробей smile

0
Спасибо thanks
Ответить

14 января 2016 в 18:05
Ответ для Анжела Волк

Александр Хан
(^-^)
Профиль
Благодарили: 0

Сообщений: 1

(^-^)
Александр Хан
Профиль
Благодарили: 0

Сообщений: 1

больше

0
Спасибо thanks
Ответить

19 сентября 2016 в 10:33
Ответ для Анжела Волк

Евгений Колосов
(^-^)
Профиль
Благодарили: 12

Сообщений: 197

(^-^)
Евгений Колосов
Профиль
Благодарили: 12

Сообщений: 197

Отрицательное число всегда меньше положительного =)

0
Спасибо thanks
Ответить

27 декабря 2015 в 20:00

Надежда Егина
(^-^)
Профиль
Благодарили: 0

Сообщений: 2

(^-^)
Надежда Егина
Профиль
Благодарили: 0

Сообщений: 2

0
Спасибо thanks
Ответить

19 сентября 2016 в 10:07
Ответ для Надежда Егина

Евгений Колосов
(^-^)
Профиль
Благодарили: 12

Сообщений: 197

(^-^)
Евгений Колосов
Профиль
Благодарили: 12

Сообщений: 197

· a¹²· b⁴ · · a⁸· b⁵ = · a²⁰ · b⁹=125· a²⁰ · b⁹При раскрытии скобок отбросил знак ?, т.к. степень чётная, а значит получится +.

0
Спасибо thanks
Ответить

21 апреля 2015 в 15:17

Алина Гимадеева
(^-^)
Профиль
Благодарили: 0

Сообщений: 2

(^-^)
Алина Гимадеева
Профиль
Благодарили: 0

Сообщений: 2

1) 15 — 7

4/7= 2) 20

4/5 — 1

5/6 *

1/3
3) 5

1/3 + 4

1/3 +

2/5

0
Спасибо thanks
Ответить

14 апреля 2016 в 12:32
Ответ для Алина Гимадеева

Евгений Колосов
(^-^)
Профиль
Благодарили: 12

Сообщений: 197

(^-^)
Евгений Колосов
Профиль
Благодарили: 12

Сообщений: 197

Судя по всему, не разобрались с использованием кнопки дробь. Интерпретирую задачу следующим образом:

1) 15 ? 7

2) 20

? 1 · = ? = = = =9 — похоже ошибка в примере, он гораздо сложнее двух других.

3) 5

+4 + = 9 + = + = = =10

0
Спасибо thanks
Ответить

7 апреля 2015 в 20:06

Александр Гридюшко
(^-^)
Профиль
Благодарили: 0

Сообщений: 1

(^-^)
Александр Гридюшко
Профиль
Благодарили: 0

Сообщений: 1

cry как решить?4

0
Спасибо thanks
Ответить

7 апреля 2015 в 21:13
Ответ для Александр Гридюшко

Анастасия Власова
(^-^)
Профиль
Благодарили: 0

Сообщений: 1

(^-^)
Анастасия Власова
Профиль
Благодарили: 0

Сообщений: 1

4+ =^⁺^⁼^⁺^⁼^⁼^⁼^{^{= 6}}

0
Спасибо thanks
Ответить

14 апреля 2015 в 16:55
Ответ для Александр Гридюшко

Asel Talantbekovna
(^-^)
Профиль
Благодарили: 0

Сообщений: 8

(^-^)
Asel Talantbekovna
Профиль
Благодарили: 0

Сообщений: 8

4 + = + = = =16:3=1

0
Спасибо thanks
Ответить

16 апреля 2015 в 19:06
Ответ для Александр Гридюшко

Мирон Федоров
(^-^)
Профиль
Благодарили: 0

Сообщений: 1

(^-^)
Мирон Федоров
Профиль
Благодарили: 0

Сообщений: 1

Asel не правильно

0
Спасибо thanks
Ответить

Источник

Перед тем как перейти к сложению дробей, вспомним теоретические основы. Итак, дробь — это форма записи числа:

где a — числитель, b — знаменатель.

Дробь называется правильной — если числитель меньше знаменателя (к примеру, 1/2), неправильной — если числитель больше знаменателя (например, 4/3).

Сложение обыкновенных дробей

Сложение дробей — это арифметическое действие, в результате которого получается новое число, содержащее сумму заданных чисел.

Основные свойства сложения:

От перестановки мест слагаемых сумма не меняется, т.е. a + b = b + a, где a и b — обыкновенные дроби;
Если к дроби прибавить 0 — получится тоже самое число.

Как складывать дроби с одинаковыми знаменателями?

Сложение дробей с одинаковыми знаменателями сводится к сложению их числителей. В общем виде выглядит следующим образом:

Пример 1:

3 6

2 6

Решение:

3 6

2 6

3 + 2 6

5 6

Таким образом, чтобы сложить дроби с одинаковыми знаменателями нужно сложить их числители, а знаменатель оставить без изменения.

Бывают ситуации когда в результате вычисления получается неправильная дробь, т.е. числитель больше знаменателя. В этом случае необходимо сократить дробь, т.е. привести её к смешанному виду:

Пример 2:

3 6

4 6

Решение:

3 6

4 6

3 + 4 6

7 6

1 6

Подробнее про сокращение дробей — смотрите тут.

Как складывать дроби с разными знаменателями?

В общем виде, сложение дробей с разными знаменателями, выглядит следующим образом:

a b

c d

a ∙ m1 + c ∙ m2 e

где e — наименьший общий знаменатель (НОЗ — наименьшее число, которое делится без остатка и на b и на d), m1 и m2 — дополнительные множители (m1 = e : b, m2 = e : d).

Пример 3:

3 5

1 4

Решение:

3 5

1 4

3 ∙ 4 20

1 ∙ 5 20

12 20

5 20

12 + 5 20

17 20

Подробнее про нахождение НОЗ — смотрите тут.

Как складывать смешанные дроби?

Сложение смешанных дробей сводится к переводу их к неправильному виду и дальнейшим действиям согласно вышеописанным алгоритмам. Перевод смешанного числа в неправильную дробь, в общем виде, выглядит следующим образом:

Пример 4:

3 5

1 3

Решение:

3 5

1 3

2 ∙ 5 + 3 5

1 3

13 5

1 3

13 ∙ 3 15

1 ∙ 5 15

39 15

5 15

39 + 5 15

44 15

14 15

Подробнее про сложение смешанных чисел смотрите тут

Правила сложения дробей

Резюмируя вышесказанное, выведем общий алгоритм сложения дробей:

Если дробь смешанная — приводим её к неправильному виду;
Если дроби имеют одинаковые знаменатели — складываем числители;
Если дроби имеют разные знаменатели — находим НОЗ и дополнительные множители, складываем числители;
При необходимости сокращаем.

Смотрите также:

Смотрите также
Калькуляторы
Последние примеры

Калькулятор сложения дробей

Оцените материал:

Загрузка…

Источник

Чтобы сложить смешанные числа, надо записать их в виде неправильных дробей, а затем сложить как обыкновенные дроби.
Часто удобней вначале сложить целые части, а затем дробные части, избегаю преобразования в неправильную дробь.

Пример Сложить смешанные числа

Сократим дробь 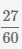с помощью нахождения наибольшего общего делителя числителя и знаменателя
и деления полученного числа на числитель и знаменатель, НОД(27,60)=3,
получим .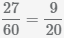

Пример Найти сумму смешанных чисел

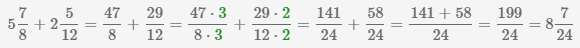
В результате сложения также получим смешанное число.

Сложение нескольких дробей

Пример Сложить 3 дроби

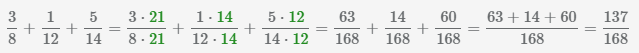
Сложение обыкновенных и десятичных дробей

Пример Найти сумму

Для сложения десятичных и обыкновенных дробей нужно преобразовать их к одному формату. В данном примере преобразуем десятичную дробь
0.75 в обыкновенную дробь .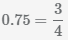

Источник

Суммой двух дробей с одинаковыми знаменателями называется дробь, числитель которой равен сумме числителей исходных дробей, а знаменатель – знаменателю дробей, то есть ab+cb=a+bcfrac{a}{b} + frac{c}{b} = frac{a+b}{c}.

Сложение дробей с одинаковыми знаменателями

Чтобы сложить две дроби с одинаковым знаменателем, надо сложить их числители и результат записать в числитель, а знаменатель оставить без изменения.

Примеры решения задач

Пример 1

Задание

Найти сумму дробей 513frac{5}{13} и 113.frac{1}{13}.

Решение

513+113=613frac{5}{13} + frac{1}{13} = frac{6}{13}

Пример 2

Задание

Найти сумму дробей 512frac{5}{12} и 112frac{1}{12}.

Решение

Складываются дроби с одинаковым знаменателем, поэтому просто складываем числитель, а знаменатель оставляем исходный:

512+112=612frac{5}{12} + frac{1}{12} = frac{6}{12}.

Полученную можно упростить – путем сокращения числителя и знаменателя на 6, то есть 512+112=612=12frac{5}{12} + frac{1}{12} = frac{6}{12} = frac {1}{2}.

Сложение дробей с разными знаменателями

Чтобы сложить дроби с разными знаменателями, вначале надо привести их к общему знаменателю, а далее складывать как дроби с общим знаменателем.

Пример решения задачи

Пример 1

Задание

Сложить дроби 13frac{1}{3} и 12frac{1}{2}.

Решение

Так как дроби с разными знаменателями, то вначале приведем их к наименьшему общему знаменателю. Для этого найдем НОК чисел 2 и 3:

НОК (3, 2) = 6

Дополнительные множители к каждой из дробей соответственно: 6:3=2, 6:2=3, то есть

13+12=26+36=2+36=56.frac{1}{3} + frac{1}{2} = frac{2}{6} + frac{3}{6} = frac{2+3}{6} = frac{5}{6}.

Сложение смешанных дробей

Чтобы сложить смешанные дроби, надо отдельно найти сумму целых частей и отдельно сумму дробных частей.

Пример решения задачи

Пример 1

Задание

Вычислить сумму дробей 2122frac{1}{2} и 3133frac{1}{3}.

Решение

В данном случае складываем отдельно целые и дробные части:

212+313=(2+3)+(12+13).2frac{1}{2} + 3frac{1}{3}=(2+3) + (frac{1}{2} +frac{1}{3}).

Так как знаменатели дробных частей разные, то приводим дроби к общему знаменателю, который равен 6. Соответственно дополнительные множители, как частные общего знаменателя и знаменателей дробей, равны 3 и 2:

212+313=(2+3)+(12+13)=2frac{1}{2} + 3frac{1}{3}=(2+3) + (frac{1}{2} +frac{1}{3}) =

=5+(36+26)=5+56=556.= 5 +(frac{3}{6} +frac{2}{6}) = 5+frac{5}{6} = 5 frac{5}{6}.

На нашем сайте вы можете заказать задачу по алгебре недорого от опытных исполнителей!

Тест по теме «Сложение дробей»

Источник

Загрузить PDF

На первый взгляд складывать дроби с разными знаменателями довольно сложно, но если привести их к общему знаменателю, все станет гораздо проще. Если вы работаете с неправильными дробями, у которых числители больше знаменателей, сделайте знаменатели одинаковыми, а затем сложите числители. Если нужно сложить смешанные числа, преобразуйте их в неправильные дроби, приведите их к общему знаменателю, а затем сложите числители.

1
Найдите наименьшее общее кратное (НОК) знаменателей. Чтобы привести дроби к общему знаменателю, необходимо найти наименьшее число, кратное обоим знаменателям.^[1]
- Например, сложите дроби 9/5 + 14/7. Кратными знаменателя 5 являются 5, 10, 15, 20, 25, 30, 35, а кратными знаменателя 7 — 7, 14, 21, 28, 35. Итак, 35 является наименьшим общим кратным.
2
Умножьте числитель и знаменатель первой дроби на соответствующее число, чтобы привести дроби к общему знаменателю. Помните, что на это число нужно умножить не только знаменатель, но и числитель.^[2]
- В нашем примере умножьте 9/5 на 7, чтобы получить знаменатель 35. Числитель также умножьте на 7; таким образом, вы получите дробь 63/35.
3
Умножьте числитель и знаменатель второй дроби на соответствующее число, чтобы привести дроби к общему знаменателю. Помните, что на это число нужно умножить не только знаменатель, но и числитель.^[3]
- В нашем примере умножьте 14/7 на 5, чтобы получить дробь 70/35. Таким образом, исходная задача 9/5 + 14/7 перепишется так: 63/35 + 70/35.
4
Сложите числители, а знаменатели оставьте без изменений. Когда вы приведете обе дроби к общему знаменателю, сложите числители. Результат запишите над знаменателем.^[4]
- В нашем примере: 63 + 70 = 133. Запишите этот результат над знаменателем, чтобы получить дробь 133/35.
5
Упростите или сократите полученную дробь (если нужно). Если получилась неправильная дробь, превратите ее в смешанное число. Для этого числитель разделите на знаменатель, чтобы получить целое число. Остаток деления запишите над знаменателем. Теперь дробь можно сократить (если она сокращается).^[5]
- Например, дробь 133/35 можно превратить в смешанное число 3 28/35. Теперь дробь 28/35 сократите до 4/5. Таким образом, окончательный ответ равен 3 4/5.
Реклама

1
Преобразуйте смешанные числа в неправильные дроби. Если даны смешанные числа (они включают целое число и дробь), превратите их в неправильные дроби, чтобы упростить сложение. Помните, что числители неправильных дробей больше знаменателей.^[6]
- Например, сложите 6 3/8 + 9 1/24. Эти смешанные числа превратятся в дроби 51/8 + 217/24.
2
Найдите наименьшее общее кратное (НОК) знаменателей. Если знаменатели разные, запишите кратные каждого из них, а затем найдите наименьшее общее кратное. В нашем примере 51/8 + 217/24 выпишите кратные знаменателей 8 и 24; вы найдете, что НОК равен 24.^[7]
- Кратными 8 являются 8, 16, 24, 32, 48, а кратными 24 — 24, 48, 72. Итак, НОК равен 24.
3
Умножьте первую дробь (числитель и знаменатель) на соответствующее число, чтобы привести ее к общему знаменателю. Общий знаменатель должен быть равен НОК.^[8]
- Например, чтобы дробь 51/8 привести к знаменателю 24, умножьте числитель и знаменатель на 3. Вы получите дробь 153/24.
4
Умножьте другие дроби (числитель и знаменатель) на соответствующее число, чтобы привести их к общему знаменателю. Если в задаче у других дробей разные знаменатели, также умножьте их на некоторое число, чтобы привести к общему знаменателю. Если знаменатель дроби уже равен НОК, такую дробь оставьте без изменений.^[9]
- В нашем примере вторая дробь 217/24, то есть ее знаменатель уже равен НОК. Таким образом, эту дробь менять не нужно.
5
Сложите числители, а знаменатель оставьте без изменений. Сложите числители, когда приведете дроби к общему знаменателю (или если знаменатели дробей были одинаковыми с самого начала). Результат сложения числителей запишите над знаменателем. Знаменатели не складывайте!^[10]
- В нашем примере: 153/24 + 217/24 = 370/24.
6
Упростите полученную дробь. Если числитель дроби больше знаменателя, разделите числитель на знаменатель, чтобы получить целое число. Остаток деления запишите над знаменателем. Теперь сократите дробь (если она сокращается).^[11]
- В нашем примере 370/24 = 15 10/24, потому что 370/24 = 15 ост. 10. Дробь 10/24 можно сократить до 5/12. Таким образом, окончательный ответ равен 15 5/12.
Реклама