Как найти второй угол вертикального угла

Вертикальные углы. Свойства вертикальных углов

Определение 1. Вертикальными углами называются два угла, у которых стороны одного угла являются продолжениями сторон другого угла.

На Рис.1 углы AOB и COD вертикальные. Вертикальные также углы AOD и BOC.

Свойства вертикальных углов

1. Вертикальные углы равны.

2. Две пересекающие прямые образуют две пары вертикальных углов.

Доказательство пункта 1. Поскольку 1, 3 и 2, 3 смежные углы, то имеем

Тогда

Следовательно 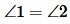. Аналогично доказывается, что .

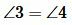Задачи и решения

Задание 1. Угол 1 равен 32°. Найти углы 2, 3, 4 (Рис.2).

Решение. Так как углы 1 и 2 вертикальны, то 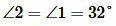. Углы 1 и 4 смежные. Следовательно 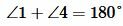. Тогда

Углы 3 и 4 вертикальные. Тогда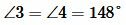

Ответ. .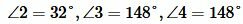

Задание 2. При пересечении двух прямых образовались четыре угла. Сумма двух углов равна 220°. Найти все углы.

Решение. Из образованных четырех углов любые две или смежные, или вертикальные. Поскольку в нашей задаче сумма двух углов равна 220°, то эти углы вертикальные (так как сумма смежных углов равна 180°). Тогда каждый из этих углов равен 220°:2=110°. Смежный по отношению угла 110° , будет угол 180°-110°=70°. Следовательно остальные два угла равны 70°. Отметим, что сумма всех четырех углов равен 360°:

Ответ. .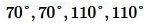

Вертикальные углы в геометрии

19 июня 2022

В двух словах: вертикальные углы возникают при пересечении двух прямых, не имеют общих сторон и всегда равны друг другу.

Содержание

1. Определение и примеры
2. Основная теорема
3. Комбинированные задачи

1. Определение и примеры

Определение. Два угла называются вертикальными, если стороны одного из них являются продолжениями сторон другого.

На рисунке ниже пересекаются две прямые: $AB$ и $MN$:

В результате образуются две пары вертикальных углов: $angle ASM$ и $angle BSN$, а также $angle ASN$ $angle BSM$.

Обратите внимание: вертикальные углы образуются только в точке пересечении прямых. Например, углы $ASM$ и $BSN$ на картинке ниже — не вертикальные, даже если они равны:

Если в одной точке пересекается более двух прямых, то вертикальных углов становится очень много:

Я не случайно пометил вертикальные углы одинаковыми дугами. Дело в том, что верна следующая теорема.

2. Основная теорема

Теорема 1. Вертикальные углы всегда равны друг другу.

Доказательство. Рассмотрим «синие» вертикальные $ASN$ и $BSM$. Каждый из них является смежным с углом $BSN$:

Но сумма смежных углов равна 180°, и если $angle BSN=color{red}{x}$, то

[begin{align}angle ASN&={180}^circ -color{red}{x} \ angle BSM&={180}^circ -color{red}{x} end{align}]

Итак, вертикальные углы равны одной и той же величине. Т.е. они равны между собой.

Эта теорема позволяет решать огромное количество задач — от самых простых до весьма нетривиальных. Начнём с простых.

Задача 1. Найдите углы 2, 3 и 4, если $angle 1={134}^circ $.

Решение.

Углы 1 и 3 вертикальные, поэтому они равны: $angle 3=angle 1={134}^circ $.

Углы 1 и 2 смежные, поэтому их сумма равна 180°:

[begin{align}angle 1+angle 2&={180}^circ \ angle 2&={180}^circ -angle 2= \ &={180}^circ -{134}^circ ={46}^circ end{align}]

Углы 2 и 4 вертикальные, поэтому они равны: $angle 4=angle 2={46}^circ $.

Из всех чертежей видно, что при пересечении двух прямых обычно возникает два острых угла и два тупых. Причём острый и тупой угол всегда будут смежными.

Если предположить, что острый угол равен $color{red}{x}$ градусов, то тупой равен $180-color{red}{x}$ градусов.

Задача 2. Найдите углы, образованные при пересечении двух прямых, если разность двух из них равна 68°.

Решение. Пусть острые углы содержат $color{red}{x}$ градусов. Тогда смежные с ними тупые углы содержат по ${180}^circ -color{red}{x}$ градусов.

По условию задачи, разность двух углов равна 68°. Очевидно, речь идёт о смежных углах. Потому что разность вертикальных углов была бы равна нулю. Вычитаем из тупого угла острый и получаем:

[begin{align}{180}^circ -color{red}{x} -color{red}{x} &={68}^circ\ 2color{red}{x}&={112}^circ\ color{red}{x}&={56}^circend{align}]

Итак, острые углы содержат по 56°. Тогда тупые углы содержат по 124°.

Единственный случай, когда все вертикальные углы равны — это когда прямые перпендикулярны, т.е. пересекаются под углом 90°.

Задача 3. На рисунке прямые $a$ и $b$ перпендикулярны, $angle color{red}{1}={36}^circ $. Найдите углы 2, 3 и 4.

Решение.

Углы 1 и 3 вертикальные, поэтому они равны: $angle color{red}{3}=angle color{red}{1}={36}^circ $.

Углы 1 и 2 смежные, поэтому их сумма равна 180°:

[begin{align}angle color{red}{1}+angle color{blue}{2}&={180}^circ \ angle color{blue}{2}&={180}^circ -angle color{red}{1}= \ &={180}^circ -{36}^circ ={144}^circ end{align}]

Углы 3 и 4 вместе образуют прямой угол, поэтому их сумма равна 90°:

[begin{align}angle color{red}{3}+angle color{green}{4}&={90}^circ \ angle color{green}{4}&={90}^circ -angle color{red}{3}= \ &={90}^circ -{36}^circ ={54}^circ end{align}]

Перед тем как переходить к более сложным задачам, рассмотрим ещё одно интересное свойство вертикальных углов.

Теорема 2. Биссектрисы вертикальных углов лежат на одной прямой.

Доказательство. В самом деле, пусть $SC$ и $SD$ — биссектрисы вертикальных углов $ASM$ и $BSN$ соответственно.

Допустим, градусные меры углов $ASM$ и $BSN$ равны $2color{red}{x}$. Тогда градусные меры всех маленьких углов $ASC$, $BSD$ и т.д. равны $color{red}{x}$. Но тогда

[begin{align}angle CSD&=angle CSA+angle ASN+angle NSD= \ &=2color{red}{x}+angle ASN end{align}]

С другой стороны, углы $ASN$ и $ASM=2color{red}{x}$ смежные, поэтому

[2color{red}{x}+angle ASN={180}^circ ]

Итак, угол $angle CSD={180}^circ $, т.е. является развёрнутым. А это как раз и означает, что лучи $SC$ и $SD$ являются дополнительными друг другу и образуют прямую.

3. Комбинированные задачи

Рассмотрим несколько более сложных задач. Тут встречаются вертикальные углы, смежные углы, а также перпендикуляры.

Задача 4. Найдите углы, образованные при пересечении двух прямых, если:

1. Сумма двух из них равна 110°.
2. Сумма трёх из них равна 308°.

Решение. Для обоих пунктов будем использовать один и тот же чертёж. Пусть острые вертикальные углы содержат по $color{red}{x}$ градусов, тогда два других угла содержат по ${180}^circ -color{red}{x}$ градусов:

1. Если сумма двух углов равна 110°, то, очевидно, речь идёт о вертикальных углах. Потому что сумма смежных углов всегда равна 180°, а не 110°.

Кроме того, это явно острые углы, иначе их сумма была бы больше 180°. Поэтому

[begin{align}color{red}{x}+color{red}{x}&={110}^circ\ 2color{red}{x}&={110}^circ\ color{red}{x}&={55}^circend{align}]

Итак, острые вертикальные углы содержат по 55°. Следовательно, смежные с ними тупые вертикальные углы содержат по 125°.

2. Сумма трёх углов всегда содержит два вертикальных и один смежный с ними. Например, так:

Зелёным пунктиром обозначены три угла, участвующие в сумме. Следовательно, эта сумма равна

[begin{align}left( {180}^circ -color{red}{x} right)+color{red}{x}+left( {180}^circ -color{red}{x} right)&={308}^circ \ {360}^circ -color{red}{x}&={308}^circ\ color{red}{x}&={52}^circend{align}]

Итак, углы равны 52° и 128°.

Эту задачу можно решить по-разному. Взгляните ещё раз на чертёж:

Мы знаем, что «большой зелёный угол» содержит 308°. А «полный оборот» содержит 360°. Но чтобы получить полный оборот, нужно добавить к зелёному сектору небольшой угол $color{red}{x}$. Поэтому

[begin{align}{308}^circ +color{red}{x}&={360}^circ\ color{red}{x}&={52}^circend{align}]

Возможно, такой подход покажется вам более простым и «очевидным».

Заметьте: благодаря введённым обозначениям нам даже не потребовались буквы для обозначения углов.:)

Задача 5. Сумма двух углов, образованных при пересечении двух прямых, равна 250°. Докажите, что эти углы вертикальные.

Решение. Пусть тупой угол $ACN$ содержит $color{blue}{x}$ градусов. Тогда смежный с ним угол $BCN$ содержит ${180}^circ -color{blue}{x}$ градусов, а вертикальный угол $BCM$ тоже равен $color{blue}{x}$ градусов:

Но тогда

[angle ACN+angle BCN={180}^circ ne {250}^circ ]

И это вполне логично, поскольку сумма смежных углов всегда равна 180°. То же самое можно сказать, например, про углы $ACN$ и $ACM$ — они тоже смежные.

Остаётся лишь вариант вертикальных углов $ACN$ и $BCM$. Но эти углы вертикальные, что и требовалось доказать.

В последнем задании мы построили чертёж исходя из следующих соображений. Если искомые углы вертикальные (а именно это мы и пытаемся доказать), то они равны, и каждый из них будет равен 125°. Следовательно, речь идёт о тупых углах, поэтому именно тупые углы мы обозначили за $x$.

Помните: в геометрии важно построить правильный чертёж. И чем сложнее задачи, тем выше требования к качеству чертежей. Иначе на можно просто «не увидеть» алгоритм решения задачи.

Кроме того, в следующих уроках мы будем всё чаще отождествлять углы и их градусные меры. Абсолютно нормально писать и говорить «угол $ABC$ равен $x$» вместо «угол $ABC$ содержит $x$ градусов» — все прекрасно поймут, о чём речь.

Смотрите также:

1. Перпендикулярные прямые — определение и свойства
2. Что такое смежные углы
3. Тест к уроку «Площади многоугольников без координатной сетки» (средний)
4. Метод координат в пространстве
5. Интегрирование по частям
6. Как формулы приведения работают в задаче B11

Вертикальные углы. Свойства вертикальных углов

Определение 1. Вертикальными углами называются два угла, у которых стороны одного угла являются продолжениями сторон другого угла.

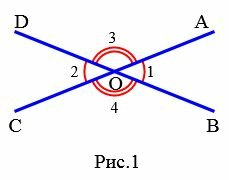
На Рис.1 углы AOB и COD вертикальные. Вертикальные также углы AOD и BOC.

Свойства вертикальных углов

1. Вертикальные углы равны.

2. Две пересекающие прямые образуют две пары вертикальных углов.

Доказательство пункта 1. Поскольку 1, 3 и 2, 3 смежные углы, то имеем

Следовательно 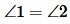. Аналогично доказывается, что .

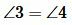Задачи и решения

Задание 1. Угол 1 равен 32°. Найти углы 2, 3, 4 (Рис.2).

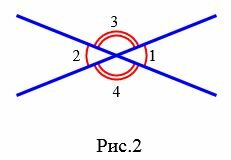
Решение. Так как углы 1 и 2 вертикальны, то 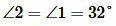. Углы 1 и 4 смежные. Следовательно 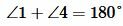. Тогда

Углы 3 и 4 вертикальные. Тогда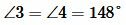

Ответ. .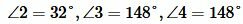

Задание 2. При пересечении двух прямых образовались четыре угла. Сумма двух углов равна 220°. Найти все углы.

Решение. Из образованных четырех углов любые две или смежные, или вертикальные. Поскольку в нашей задаче сумма двух углов равна 220°, то эти углы вертикальные (так как сумма смежных углов равна 180°). Тогда каждый из этих углов равен 220°:2=110°. Смежный по отношению угла 110° , будет угол 180°-110°=70°. Следовательно остальные два угла равны 70°. Отметим, что сумма всех четырех углов равен 360°:

.

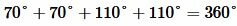Ответ. .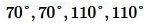

Треугольник. Формулы определения и свойства треугольников.

В данной статье мы расскажем о классификаци и свойствах основной геометрической фигуры – треугольника. А также разберем некоторе примеры решения задач на треугольники.

Содержание:

Определение треугольника

Треугольник – это фигура, которая состоит из трёх точек, не лежащих на одной прямой, и трёх отрезков, попарно соединяющих эти точки. Точки называются вершинами треугольника, а отрезки – его сторонами. В геометрических задачах треугольник обычно изображают специальным симовлом – △, после которго пишут названия вершин треугольника напр. △ABC.

Треугольник ABC (△ABC)

• Точки A, B и C – вершины треугольника. Принято писать их большими буквами.
• Отрезки AB, BC и СА – стороны треугольника. Обычно сторонам присваивают свои названия маленькими буквами. Имя выбирают по первой вершине каждой стороны. Напр. у стороны AB первая вершина А поэтому эта сторона называется а. Тоесть AB = a, BC = b, CА = c.
• Стороны треугольника в местах соединения образуют три угла, которым обычно дают названия буквами греческого алфавита α, β, γ. Причем напротив стороны a лежит угол α, b – β, с – γ.

Углы треугольника, также, можно обозначать специальным символом – ∠. После которого пишут вершины треугольника в таком порядке чтобы вершина обозначающегося угла была в серединке. Например:

Классификация треугольников

Все треугольники можно разделить на несколько видов, различающихся между собой величиной углов или длинами сторон. Такая классификация позволяет выделить особенности каждого из них.

1.Разносторонний – треугольник, у которого все стороны имеют разную длину.

2. Равнобедренный – треугольник, у которого длины двух сторон равны. Они называются боковыми сторонами AB и BC. Третья сторона называется основание СА. В данном треугольнике углы при основании равны ∠ α = ∠ β

3.Равносторонний (или правильный) – треугольник, у которого все стороны имеют одинаковую длину. Также все его углы равны 60°.

4.Остроугольный – треугольник, у которого все три угла острые, т.е. меньше 90°

5.Тупоугольный – треугольник, в котором один из углов больше 90°. Два остальных угла – острые.

6. Прямоугольный – треугольник, в котором один из углов является прямым, т.е. равен 90°. В такой фигуре две стороны, которые образуют прямой угол, называются катетами (AB и BC). Третья сторона, расположенная напротив прямого угла – это гипотенуза (CА).

Свойства треугольника

1.Свойства углов и сторон треугольника.

• Сумма всех углов треугольника равна 180°:

• Сумма длин двух любых сторон треугольника больше длины оставшейся стороны:

• В треугольнике против большей стороны лежит больший угол, и обратно. Против равных сторон лежат равные углы:

2.Теорема синусов.

Стороны треугольника пропорциональны синусам противолежащих углов.

a	=	b	=	c
sin α	sin β	sin γ

3. Теорема косинусов.

Квадрат любой стороны треугольника равен сумме квадратов двух других сторон треугольника минус удвоенное произведение этих сторон на косинус угла между ними.

4. Теорема о проекциях

Для остроугольного треугольника:

Медианы треугольника

Медиана треугольника ― отрезок внутри треугольника, который соединяет вершину треугольника с серединой противоположной стороны.

Свойства медиан треугольника:

1. Медианы треугольника пересекаются в одной точке O. (Точка пересечения медиан называется центроидом)

2. В точке пересечения медианы треугольника делятся в отношении два к одному (2:1)

AO	=	BO	=	CO	=	2
OD	OE	OF	1

3. Медиана треугольника делит треугольник на две равновеликие по площади части

4. Треугольник делится тремя медианами на шесть равновеликих треугольников.

5. Из векторов, образующих медианы, можно составить треугольник.

Формулы медиан треугольника

Формулы медиан треугольника через стороны:

Вертикальные треугольники в геометрии

Ключевые слова конспекта: углы, биссектриса, виды углов, измерение углов, смежные и вертикальные углы, свойства смежных и вертикальных углов, углы при пересечении двух прямых секущей.

Угол — фигура, образованная двумя лучами, которые выходят из одной точки (вершины).
Биссектриса — луч, который выходит из вершины угла и делит его пополам.

Виды углов. Измерение углов

• Развернутый угол — угoл, стороны которого лежат на одной прямой.
• Прямой угoл — угoл, который равен половине развернутого угла.
• Острый угол — угoл меньше прямого угла.
• Тупой угoл — угoл больше прямого, но меньше развернутого.

Единицы измерения углов:
Градус — величина (градусная мера) угла, равная части развернутого угла.
Минута — часть градуса.
Секунда — часть минуты.

Смежные и вертикальные углы

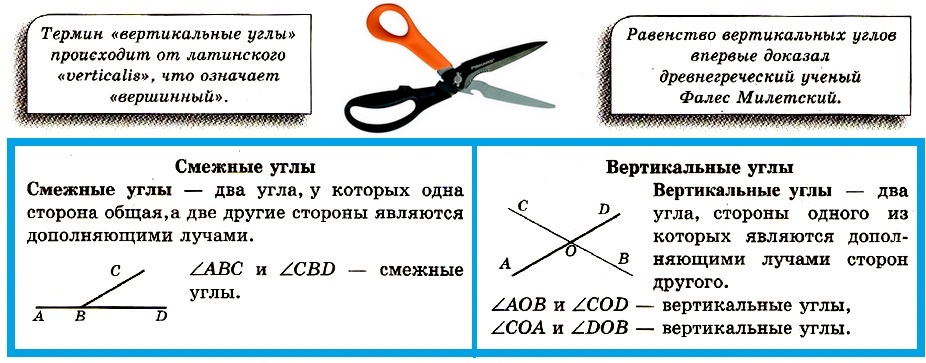
Смежные углы — два угла, у которых одна сторона общая,а две другие стороны являются дополняющими лучами.
Вертикальные углы — два угла, стороны одного из которых являются дополняющими лучами сторон другого.

Теорема. Сумма смежных углов равна 180°.

Теорема. Вертикальные углы равны.

Свойства смежных и вертикальных углов

Углы при пересечении двух прямых секущей

Вы смотрели конспект по геометрии «Угол. Смежные и вертикальные углы». Использованы цитаты из учебных пособий:

Цитирование указанных пособий произведено в учебных целях (часть 1 статьи 1274 Гражданского кодекса РФ) с указанием авторства, источника заимствования и ссылки на покупку учебного пособия в крупнейшем книжном Интернет-магазине. Выберите дальнейшие действия:

[spoiler title=”источники:”]

http://binary2hex.ru/triangle.html

[/spoiler]

        Добрый день!
Сегодня мы для закрепления темы ещё порешаем задачи на вертикальные углы.
Вспомним свойство вертикальных углов — они равны.
А теперь, имея ввиду это свойство, начнём решать задачи.

Задача 1.  Сумма двух вертикальных углов равна 90°. Чему равен каждый из углов?
        Решение. Поскольку вертикальные углы равны, а их сумма составляет 90°, то решение будет такое:
Пусть угол 1 равен α, тогда второй угол тоже равен α.
Составляем уравнение:  α + α = 90   2α = 90   α = 45.  Каждый угол равен 45º.

Задача 2. При пересечении двух прямых образовались 4 угла. Сумма двух из них равна 270º. Чему равен каждый из этих четырёх углов?
        Решение. Поскольку сумма двух углов равна 270º, то это углы не смежные. Так как сумма смежных углов равна 180º.
Значит, это углы вертикальные, и каждый из них равен (см. задачу 1)
270:2 = 135º.
А смежные с ними углы равны 180º — 135º = 45º.
Итак, у нас получились углы: 135º, 135º, 45º, 45º.

Задача 3. При пересечении двух прямых образовались четыре угла. Сумма трёх из них равна 220º. Чему равен каждый из этих четырёх углов?
        Решение: Сумма всех четырёх углов равна 360º.
Отсюда, четвёртый угол равен 360 — 220 = 140º.
Вертикальный с ним угол равен тоже 140º.
А смежные с ними углы будут равны 180 — 140 = 40º.
Ответ углы равны 140º, 140º, 40º, 40º.

Задача 4. При пересечении двух прямых образовались четыре угла меньше 180º. Найти эти углы, если один из них на 75 градусов больше половины второго.
        Решение: Пусть первый угол равен Х, тогда его половина равна Х/2, а другой угол равен Х/2 + 75.
Поскольку это не равные углы, значит они — смежные.
А сумма смежных углов равна 180º.
Имеем Х + Х/2 + 75 = 180  3Х/2 = 180 — 75   3Х/2 = 105.
Один угол равен 70º. Вертикальный ему тоже будет 70º.
А смежные с ними равны 180 — 70 = 110.
Ответ: углы равны 110º, 110º, 70º, 70º.

Задача 5.  Доказать, что сумма каждых трёх углов, не прилежащих один к другому. которые образуются тремя прямыми, проходящими. через одну точку, равна 180º.
Решение: Из рисунка видно, что углы 1 и 4 — вертикальные.  А сумма углов 2, 4 и 3 равна 180º.
Заменяя в равенстве угол 4 на угол 1,
получим: 2 + 1 + 3 = 180º.
Точно так же доказывается  равенство 180º  суммы углов 4, О и пустого.

Вот мы и закончили решение задач на  вертикальные углы.  В следующем посте мы начнём разбираться, что такое треугольник и всё, что с ним связано.