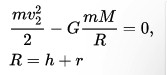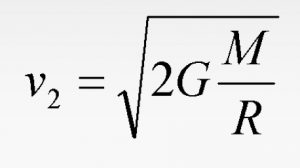Содержание
- Как определить вторую космическую скорость для Луны
- Понимание второй космической скорости
- Как определить вторую космическую скорость для Луны
- Пример расчета второй космической скорости для Луны
- Итог
- Как определить вторую космическую скорость для луны
- Определение второй космической скорости
- Формула для расчета второй космической скорости
- Определение параметров для расчета второй космической скорости для луны
- Расчет второй космической скорости для луны
- Общий итог
- Как определить вторую космическую скорость для Луны
- Что такое вторая космическая скорость
- Как определить вторую космическую скорость для Луны
- Заключение
Как определить вторую космическую скорость для Луны
Вторая космическая скорость — это минимальная скорость, необходимая для поддержания спутника на орбите вокруг планеты или другого космического тела. Так как Луна является естественным спутником Земли, для нее также может быть определена вторая космическая скорость. В этой статье мы рассмотрим, как это можно сделать.
Понимание второй космической скорости
Прежде чем погружаться в детали того, как найти вторую космическую скорость для Луны, давайте кратко рассмотрим, что это такое и как она связана с орбитой.
Вторая космическая скорость — это минимальная скорость, необходимая для поддержания спутника на орбите вокруг планеты или другого космического тела. Это связано с тем, что радиус орбиты спутника должен быть равен радиусу Земли плюс высота орбиты спутника. Чтобы оставаться на такой орбите, спутник должен двигаться со скоростью, которая позволяет ему уравновесить гравитацию Земли.
Как определить вторую космическую скорость для Луны
Для того, чтобы определить вторую космическую скорость для Луны, необходимо знать ее радиус, массу и расстояние до Земли. Затем можно использовать следующее уравнение:
v=√(GM/r)
где v — вторая космическая скорость (м/с), G — гравитационная постоянная (6,67430 × 10^-11 м^3⋅кг^-1⋅с^-2), M — масса Земли (5,972 × 10^24 кг), r — радиус Луны (м).
Чтобы получить точный результат, необходимо использовать значения в системе СИ (Система единиц Международной системы единиц). Для удобства можно использовать онлайн-калькуляторы.
Пример расчета второй космической скорости для Луны
Для примера рассчитаем вторую космическую скорость для Луны, используя ее средний радиус, который составляет 1737100 м, и расстояние до Земли в среднем значении, равном 384 400 км.
- Переводим радиус Луны в метры: 1737100 * 1000 = 1737100000 м.
- Переводим расстояние до Земли в метры: 384400 * 1000 = 384400000 м.
- Подставляем значения в формулу: v=√(6,67430 × 10^-11 × 5,972 × 10^24 / 1737100000)
- Вычисляем: v=1,022 км/с.
Таким образом, вторая космическая скорость для Луны составляет около 1,022 км/с.
Итог
Определение второй космической скорости для Луны может показаться сложной задачей, но на самом деле она не требует специальных знаний или навыков. Для этого нужно всего лишь знать радиус, массу и расстояние до Земли Луны, а затем использовать соответствующую формулу. Теперь, когда вы знаете, как это сделать, вы можете приготовиться к любопытным исследованиям Луны и ее орбиты!
Как определить вторую космическую скорость для луны
Вторая космическая скорость (V2) — это скорость, которую должно иметь тело для того, чтобы выйти на орбиту вокруг небесного тела. В данной статье мы рассмотрим, как определить вторую космическую скорость для луны.
Определение второй космической скорости
Определение второй космической скорости для луны основывается на том факте, что она вращается вокруг Земли. Для того, чтобы выйти на лунную орбиту, необходимо, чтобы скорость ракеты была таким, чтобы победить гравитационное притяжение Земли и следовать траектории лунной орбиты.
Формула для расчета второй космической скорости
Согласно законам Ньютона, для выхода на орбиту скорость тела должна быть равна корню из произведения гравитационной постоянной G на массу планеты и разность между радиусом орбиты и радиусом планеты, разделенными на радиус орбиты:
V2 =√[GM /(R+h)]
- V2 – вторая космическая скорость;
- G – гравитационная постоянная;
- M – масса планеты, вокруг которой происходит вращение на орбите;
- R – радиус планеты;
- h – высота орбиты над поверхностью планеты.
Определение параметров для расчета второй космической скорости для луны
Параметры для расчета второй космической скорости для луны следует брать из данной таблицы:
| Параметр | Значение |
|---|---|
| Масса луны (M) | 7,34 · 1022 кг |
| Радиус луны (R) | 1738 км |
| Расстояние от поверхности луны до центра Земли (r) | 384 400 км |
| Гравитационная постоянная (G) | 6,67408(31) × 10 -11 м3·кг-1·с-2 |
Расчет второй космической скорости для луны
Используя формулу, данную выше, и данные из таблицы, мы можем рассчитать вторую космическую скорость для луны.
V2 =√[(6,67408(31) × 10 -11 м3·кг-1·с-2 × 7,34 · 1022 кг) / (1738 км + 384400 км)]
После выполнения вычислений мы получаем следующее значение второй космической скорости для луны:
V2 = 2,37 км / с
Общий итог
Определение второй космической скорости для луны основывается на корректном расчете гравитационной постоянной G, массы луны M, ее радиуса R и её высоты орбиты h. Данные параметры легко найдутся в сети Интернет, а знание формулы подскажут, как произвести вычисления.
Как определить вторую космическую скорость для Луны
Луна, естественный спутник Земли, всегда вызывала глубокий интерес у ученых и любителей космоса. Одним из ключевых понятий, связанных с Луной, является вторая космическая скорость. Эта скорость определяет минимальную скорость, необходимую для того, чтобы летательное средство покинуло земную орбиту и достигло Луны. В этой статье мы рассмотрим, как определить вторую космическую скорость для Луны.
Что такое вторая космическая скорость
Вторая космическая скорость, также известная как скорость околоземной орбиты, является минимальной скоростью, при которой летательное средство сможет покинуть Землю и достичь космического пространства. Для Луны минимальная скорость для выхода на орбиту составляет около 11,2 км/с. Именно эта скорость определяет границу между атмосферой Земли и космосом.
Как определить вторую космическую скорость для Луны
Определить вторую космическую скорость для Луны можно с помощью формулы:
V = √(GM/R)
Где:
- V — вторая космическая скорость
- G — гравитационная постоянная (6,67×10^-11 m^3/kg s^2)
- M — масса Земли (5,97×10^24 кг)
- R — среднее расстояние от центра Земли до центра Луны (384 400 км)
Подставив значения в формулу, получим:
V = √((6,67×10^-11*5,97×10^24)/384400000) = 11082 м/с
Таким образом, вторая космическая скорость для Луны составляет около 11,2 км/с.
Заключение
Определение второй космической скорости для Луны — важный этап при планировании космических миссий на ее поверхность. Зная эту скорость, можно рассчитать траекторию полета и необходимые параметры летательного средства. Определить вторую космическую скорость для Луны можно с помощью формулы, которая учитывает массу Земли, гравитационную постоянную и расстояние от центра Земли до центра Луны. Вторая космическая скорость для Луны составляет около 11,2 км/с.
Анализ первой и второй космической скорости по Исааку Ньютону. Снаряды A и B падают на Землю. Снаряд C выходит на круговую орбиту, D — на эллиптическую. Снаряд E улетает в открытый космос.
Втора́я косми́ческая ско́рость (параболи́ческая ско́рость, ско́рость освобожде́ния, ско́рость убега́ния) — наименьшая скорость, которую необходимо придать стартующему с поверхности небесного тела объекту (например, космическому аппарату), масса которого пренебрежимо мала по сравнению с массой небесного тела (например, планеты), для преодоления гравитационного притяжения этого небесного тела и покидания замкнутой орбиты вокруг него. Предполагается, что после приобретения телом этой скорости оно более не получает негравитационного ускорения (двигатель выключен, атмосфера отсутствует).
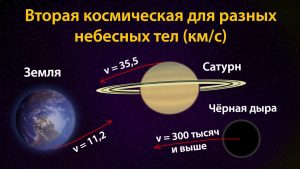
Вторая космическая скорость определяется радиусом и массой небесного тела, поэтому она своя для каждого небесного тела (для каждой планеты) и является его характеристикой. Для Земли вторая космическая скорость равна 11,2 км/с. Тело, имеющее около Земли такую скорость, покидает окрестности Земли и становится спутником Солнца. Для тела на поверхности Солнца вторая космическая скорость составляет 617,7 км/с.
Параболической вторая космическая скорость называется потому, что тела, имеющие при старте скорость, в точности равную второй космической, движутся по параболе относительно небесного тела. Однако, если энергии телу придано чуть больше, его траектория перестает быть параболой и становится гиперболой. Если чуть меньше, то она превращается в эллипс. В общем случае все они являются коническими сечениями.
Если тело запущено вертикально вверх со второй космической и более высокой скоростью, оно никогда не остановится и не начнёт падать обратно.
Эту же скорость приобретает у поверхности небесного тела любое космическое тело, которое на бесконечно большом расстоянии покоилось, а затем стало падать.
Впервые вторая космическая скорость была достигнута коcмическим аппаратом Луна-1 (СССР) 2 января 1959 года.
Вычисление[править | править код]
Для получения формулы второй космической скорости удобно обратить задачу — спросить, какую скорость получит тело на поверхности планеты, если будет падать на неё из бесконечности. Очевидно, что это именно та скорость, которую надо придать телу на поверхности планеты, чтобы вывести его за пределы её гравитационного влияния.
Запишем затем закон сохранения энергии[1][2]
где слева стоят кинетическая и потенциальная энергии на поверхности планеты (потенциальная энергия отрицательна, так как точка отсчета взята на бесконечности), справа то же, но на бесконечности (покоящееся тело на границе гравитационного влияния — энергия равна нулю). Здесь m — масса пробного тела, M — масса планеты, r — радиус планеты, h — высота тела над поверхностью планеты, R = h + r — расстояние от центра планеты до тела, G — гравитационная постоянная, v2 — вторая космическая скорость.
Решая это уравнение относительно v2, получим
Между первой и второй космическими скоростями существует простое соотношение:
Квадрат скорости убегания в данной точке (например, на поверхности небесного тела) равен с точностью до знака удвоенному ньютоновскому гравитационному потенциалу в этой точке:
Вторая космическая скорость для различных объектов[править | править код]
| Небесное тело | Масса (в единицах массы Земли, M⊕) | 2-я космическая скорость v, км/с | v/vЗемли |
|---|---|---|---|
| Плутон | 0,002 | 1,2 | 0,11 |
| Луна | 0,0123 | 2,4 | 0,21 |
| Меркурий | 0,055 | 4,3 | 0,38 |
| Марс | 0,107 | 5,0 | 0,45 |
| Венера | 0,815 | 10,22 | 0,91 |
| Земля | 1 | 11,2 | 1 |
| Уран | 14,5 | 22,0 | 1,96 |
| Нептун | 17,5 | 24,0 | 2,14 |
| Сатурн | 95,3 | 36,0 | 3,21 |
| Юпитер | 318,35 | 61,0 | 5,45 |
| Солнце | 333 000 | 617,7 | 55,2 |
| Млечный Путь* | (4,3 ± 1,0) × 1017 [3] | 551+32 −22 [4] |
49,2+2,9 −2,0 [4] |
* Для неподвижного тела на галактоцентрической орбите Солнца, на расстоянии 8,20 ± 0,09 килопарсек от центра Галактики. В отличие других примеров в таблице, здесь точка, для которой указана скорость убегания, находится не на поверхности тела, а в глубине диска Галактики.
См. также[править | править код]
- Космическая скорость
- Первая космическая скорость
- Третья космическая скорость
- Четвёртая космическая скорость
Примечания[править | править код]
- ↑ Кабардин О. Ф., Орлов В. А., Пономарева А. В. Факультативный курс физики. 8 класс. — М. : Просвещение, 1985. — С. 176. — 143 500 экз.
- ↑ Савельев И. В. Курс общей физики. — М. : Наука, 1987. — Т. 1 : Механика. Молекулярная физика. — С. 179.
- ↑ McMillan P. J. The mass distribution and gravitational potential of the Milky Way (англ.) // Monthly Notices of the Royal Astronomical Society. — 2017. — Vol. 465, iss. 1. — P. 76—94. — doi:10.1093/mnras/stw2759. — Bibcode: 2017MNRAS.465…76M. — arXiv:1608.00971.
- ↑ 1 2 Kafle P.R., Sharma S., Lewis G.F., Bland-Hawthorn J. On the Shoulders of Giants: Properties of the Stellar Halo and the Milky Way Mass Distribution (англ.) // The Astrophysical Journal. — 2014. — Vol. 794, iss. 1. — P. 59. — doi:10.1088/0004-637X/794/1/59. — Bibcode: 2014ApJ…794…59K. — arXiv:1408.1787.
поделиться знаниями или
запомнить страничку
- Все категории
-
экономические
43,655 -
гуманитарные
33,653 -
юридические
17,917 -
школьный раздел
611,939 -
разное
16,901
Популярное на сайте:
Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах.
Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте.
Как быстро и эффективно исправить почерк? Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.
Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью.
Голосование за лучший ответ
Hadja Pilygrimus
Мудрец
(13591)
8 лет назад
возьми калькулятор, – есть в любом телефоне, и считай. исходные данные в БСЭ, или британике
Джедай
Мастер
(1657)
8 лет назад
для Земли ~10км/с
Александр ДаниловГуру (3750)
8 лет назад
11,2
marat aminov
Просветленный
(32951)
8 лет назад
V=√(2GM/R) масса луны М=73477*10^18кг, средний радиус луны R=1737100м, гравитационная постоянная G=6.67384*10^(-11)м^3/кг*с^2. подставляем, считаем, получаем V=2,38км/с.
Рустам Искендеров
Искусственный Интеллект
(133392)
8 лет назад
Орбитальная скорость у поверхности Луны, умноженная не корень (2).
Из школьного курса физики мы помним, что первая космическая скорость Земли – это показатель, которого необходимо достичь, чтобы объект мог выйти на эллиптическую орбиту вращения вокруг планеты. Это же, собственно, касается и любого массивного космического тела. В свою очередь, вторая космическая скорость – это предел, необходимый для того, чтобы полностью покинуть гравитационное поле планеты.
Вторая космическая скорость зависит от ряда параметров и для каждого космического объекта – отличается. Давайте рассмотрим, по какому принципу она вычисляется, и разберем примеры для крупных планет Солнечной Системы, Солнца и Луны.
Как рассчитать вторую космическую скорость
Вторая космическая скорость зависит от массы и радиуса небесного тела. Условно можно себе представить, что для ее расчета можно пойти от обратного решения задачи. То есть, вычислить скорость с какой объект будет падать на планету из космоса. По модулю это и будет вторая космическая скорость.
Итак, учитывая закон сохранение кинетической и потенциальной энергий при движении тел, можно вывести такую формулу в падающем объекте на небесное тело:
Где m – масса стартующего объекта, М – масса небесного тела, R – сумма радиуса планеты и высоты расположение объекта над поверхностью, G – гравитационная постоянная, V – искомая вторая космическая скорость. Таким образом, из формулы можно вычислить V:
Это и будет решение нашей задачи со знанием всего двух параметров – радиуса небесного тела и его массы.
Вторая скорость для разных небесных тел
Итак, попробуем на основании выведенной формулы рассчитать вторую космическую скорость для разных небесных тел Солнечной Системы, учитывая что их радиус и массу мы знаем.
Начнем с самого простого – Земли. Радиус нашей планеты равен 6,37 тысяч километров, а масса – 5,97 х 10²³ кг. Подставляем в нашу формулу и получаем – вторая космическая скорость Земли равна 11,2 километра в секунду. Именно до таких цифр нужно разогнать гипотетический объект, чтобы он покинул зону гравитационного притяжения нашей планеты.
Теперь можно перейти к нашей звезде и посчитать вторую космическую скорость для Солнца. Радиус его равен 696 тысяч километров, а масса 1,989 х 10³⁰ кг. Расчеты по формуле дают результат в 617,7 километров в секунду! До такой скорости нужно разогнать предмет, чтобы он смог покинуть нашу Солнечную Систему и попасть в межзвездное пространство.
Теперь попробуем вычислить показатель для остальных планет системы. Итак, радиус и масса Меркурия составляют соответственно 2,438 тысяч километров и 330 х 10²¹ кг. Подставив в формулу цифры, получаем вторую космическую скорость Меркурия 4,3 км/с.
Идем далее и получаем такие цифры – вторая космическая скорость Венеры – 11,2 километров в секунду, Марса – 5,0 км/с, Юпитера – 61 км/с, Сатурна – 36 км/с, Нептуна – 24 км/с, Урана – 22 км/с, Луна – 2,4 км/с.
Таким образом, мы видим, что преимущественно чем массивнее планета (а вернее, чем плотнее, потому что радиус тоже важен) – тем больше нужна скорость, чтобы объект мог вырваться за пределы гравитационного влияния.
Показательными и интересными также являются примеры третей и четвертой космических скоростей. Что это за параметры? Если говорить грубо – то третья космическая скорость, это вторая космическая для Солнца, но высчитываемая вблизи Земли. Простыми словами – какую скорость нужно развить с Земли, чтобы покинуть Солнечную Систему? Посчитав по формуле, получим 16,65 километров в секунду.