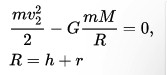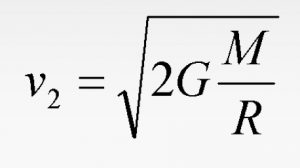Как найти вторую космическую скорость меркурия

Из школьного курса физики мы помним, что первая космическая скорость Земли – это показатель, которого необходимо достичь, чтобы объект мог выйти на эллиптическую орбиту вращения вокруг планеты. Это же, собственно, касается и любого массивного космического тела. В свою очередь, вторая космическая скорость – это предел, необходимый для того, чтобы полностью покинуть гравитационное поле планеты.

Вторая космическая скорость зависит от ряда параметров и для каждого космического объекта – отличается. Давайте рассмотрим, по какому принципу она вычисляется, и разберем примеры для крупных планет Солнечной Системы, Солнца и Луны. 

Как рассчитать вторую космическую скорость

Вторая космическая скорость зависит от массы и радиуса небесного тела. Условно можно себе представить, что для ее расчета можно пойти от обратного решения задачи. То есть, вычислить скорость с какой объект будет падать на планету из космоса. По модулю это и будет вторая космическая скорость.

Итак, учитывая закон сохранение кинетической и потенциальной энергий при движении тел, можно вывести такую формулу в падающем объекте на небесное тело:

Где m – масса стартующего объекта, М – масса небесного тела, R – сумма радиуса планеты и высоты расположение объекта над поверхностью, G – гравитационная постоянная, V – искомая вторая космическая скорость. Таким образом, из формулы можно вычислить V:

 Это и будет решение нашей задачи со знанием всего двух параметров – радиуса небесного тела и его массы.

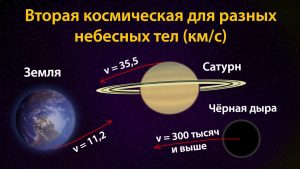
Вторая скорость для разных небесных тел

Итак, попробуем на основании выведенной формулы рассчитать вторую космическую скорость для разных небесных тел Солнечной Системы, учитывая что их радиус и массу мы знаем.

Начнем с самого простого – Земли. Радиус нашей планеты равен 6,37 тысяч километров, а масса – 5,97 х 10²³ кг. Подставляем в нашу формулу и получаем – вторая космическая скорость Земли равна 11,2 километра в секунду. Именно до таких цифр нужно разогнать гипотетический объект, чтобы он покинул зону гравитационного притяжения нашей планеты.

Теперь можно перейти к нашей звезде и посчитать вторую космическую скорость для Солнца. Радиус его равен 696 тысяч километров, а масса 1,989 х 10³⁰ кг. Расчеты по формуле дают результат в 617,7 километров в секунду! До такой скорости нужно разогнать предмет, чтобы он смог покинуть нашу Солнечную Систему и попасть в межзвездное пространство.

Теперь попробуем вычислить показатель для остальных планет системы. Итак, радиус и масса Меркурия составляют соответственно 2,438 тысяч километров и 330 х 10²¹ кг. Подставив в формулу цифры, получаем вторую космическую скорость Меркурия 4,3 км/с. 

Идем далее и получаем такие цифры – вторая космическая скорость Венеры – 11,2 километров в секунду, Марса – 5,0 км/с, Юпитера – 61 км/с, Сатурна – 36 км/с, Нептуна – 24 км/с, Урана – 22 км/с, Луна – 2,4 км/с.

Таким образом, мы видим, что преимущественно чем массивнее планета (а вернее, чем плотнее, потому что радиус тоже важен) – тем больше нужна скорость, чтобы объект мог вырваться за пределы гравитационного влияния.

Показательными и интересными также являются примеры третей и четвертой космических скоростей. Что это за параметры? Если говорить грубо – то третья космическая скорость, это вторая космическая для Солнца, но высчитываемая вблизи Земли. Простыми словами – какую скорость нужно развить с Земли, чтобы покинуть Солнечную Систему? Посчитав по формуле, получим 16,65 километров в секунду.

Четвертая космическая скорость показывает, до какой цифры нужно разогнаться чтобы покинуть галактику из заданной точки. Для Млечного пути этот показатель будет разным в зависимости от выбранной координаты. Ближе к центральной сверхмассивной черной дыре он будет гигантским, ближе к периферии галактики – меньше. Примерно в области нашей Солнечной Системы четвертая космическая скорость равна 550 километрам в секунду!

Ответ:  1) Период обращения астероида  ≈ 11,18 лет.

2) Первая космическая скорость U1 ≈ 3,018 км/с

   Вторая космическая скорость U2 ≈ 4,268 км/с

Объяснение:   1)  Дано:

Большая полуось орбиты Земли (среднее расстояние до Солнца) Аз=1а.е.

Период обращение Земли вокруг Солнца Тз = 1 год

Большая полуось орбиты астероида Аа = 5 а.е.

Найти период обращения астероида Та-?

По третьему закону Кеплера Тз²/Та² = Аз³/Аа³.    Из этого закона

Та = √(Тз²*Аа³/Аз³) = √(1²*5³/1³) = √5³ ≈ 11,18 лет

2) Дано:

Масса Меркурия Мм = 3,33*10^23 кг

Радиус Меркурия Rм = 2439,7 км = 2,4397*10^6 м

Гравитационная постоянная G = 6,674*10^-11 м³/кг*с²

Найти первую и вторую космические скорости для Меркурия U1-? U2-?

Первую космическую скорость найдем по формуле U1 = √(G*Mм/Rм) =

= √(6,674*10^-11 * 3,33*10^23/2,4397*10^6) = 3018,193 м/с ≈ 3,018 км/с.

Вторая космическая скорость U2 = √(2G*Mм/Rм) = U1√2 = 3018,193*1,4121 = 4268,369 м/с ≈ 4,268 км/с