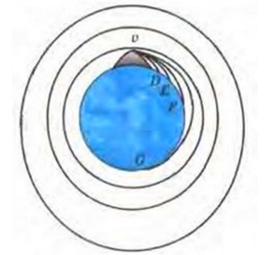
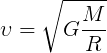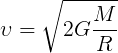Анализ первой и второй космической скорости по Исааку Ньютону. Снаряды A и B падают на Землю. Снаряд C выходит на круговую орбиту, D — на эллиптическую. Снаряд E улетает в открытый космос.
Втора́я косми́ческая ско́рость (параболи́ческая ско́рость, ско́рость освобожде́ния, ско́рость убега́ния) — наименьшая скорость, которую необходимо придать стартующему с поверхности небесного тела объекту (например, космическому аппарату), масса которого пренебрежимо мала по сравнению с массой небесного тела (например, планеты), для преодоления гравитационного притяжения этого небесного тела и покидания замкнутой орбиты вокруг него. Предполагается, что после приобретения телом этой скорости оно более не получает негравитационного ускорения (двигатель выключен, атмосфера отсутствует).
Вторая космическая скорость определяется радиусом и массой небесного тела, поэтому она своя для каждого небесного тела (для каждой планеты) и является его характеристикой. Для Земли вторая космическая скорость равна 11,2 км/с. Тело, имеющее около Земли такую скорость, покидает окрестности Земли и становится спутником Солнца. Для тела на поверхности Солнца вторая космическая скорость составляет 617,7 км/с.
Параболической вторая космическая скорость называется потому, что тела, имеющие при старте скорость, в точности равную второй космической, движутся по параболе относительно небесного тела. Однако, если энергии телу придано чуть больше, его траектория перестает быть параболой и становится гиперболой. Если чуть меньше, то она превращается в эллипс. В общем случае все они являются коническими сечениями.
Если тело запущено вертикально вверх со второй космической и более высокой скоростью, оно никогда не остановится и не начнёт падать обратно.
Эту же скорость приобретает у поверхности небесного тела любое космическое тело, которое на бесконечно большом расстоянии покоилось, а затем стало падать.
Впервые вторая космическая скорость была достигнута коcмическим аппаратом Луна-1 (СССР) 2 января 1959 года.
Вычисление[править | править код]
Для получения формулы второй космической скорости удобно обратить задачу — спросить, какую скорость получит тело на поверхности планеты, если будет падать на неё из бесконечности. Очевидно, что это именно та скорость, которую надо придать телу на поверхности планеты, чтобы вывести его за пределы её гравитационного влияния.
Запишем затем закон сохранения энергии[1][2]
где слева стоят кинетическая и потенциальная энергии на поверхности планеты (потенциальная энергия отрицательна, так как точка отсчета взята на бесконечности), справа то же, но на бесконечности (покоящееся тело на границе гравитационного влияния — энергия равна нулю). Здесь m — масса пробного тела, M — масса планеты, r — радиус планеты, h — высота тела над поверхностью планеты, R = h + r — расстояние от центра планеты до тела, G — гравитационная постоянная, v2 — вторая космическая скорость.
Решая это уравнение относительно v2, получим
Между первой и второй космическими скоростями существует простое соотношение:
Квадрат скорости убегания в данной точке (например, на поверхности небесного тела) равен с точностью до знака удвоенному ньютоновскому гравитационному потенциалу в этой точке:
Вторая космическая скорость для различных объектов[править | править код]
| Небесное тело | Масса (в единицах массы Земли, M⊕) | 2-я космическая скорость v, км/с | v/vЗемли |
|---|---|---|---|
| Плутон | 0,002 | 1,2 | 0,11 |
| Луна | 0,0123 | 2,4 | 0,21 |
| Меркурий | 0,055 | 4,3 | 0,38 |
| Марс | 0,107 | 5,0 | 0,45 |
| Венера | 0,815 | 10,22 | 0,91 |
| Земля | 1 | 11,2 | 1 |
| Уран | 14,5 | 22,0 | 1,96 |
| Нептун | 17,5 | 24,0 | 2,14 |
| Сатурн | 95,3 | 36,0 | 3,21 |
| Юпитер | 318,35 | 61,0 | 5,45 |
| Солнце | 333 000 | 617,7 | 55,2 |
| Млечный Путь* | (4,3 ± 1,0) × 1017 [3] | 551+32 −22 [4] |
49,2+2,9 −2,0 [4] |
* Для неподвижного тела на галактоцентрической орбите Солнца, на расстоянии 8,20 ± 0,09 килопарсек от центра Галактики. В отличие других примеров в таблице, здесь точка, для которой указана скорость убегания, находится не на поверхности тела, а в глубине диска Галактики.
См. также[править | править код]
- Космическая скорость
- Первая космическая скорость
- Третья космическая скорость
- Четвёртая космическая скорость
Примечания[править | править код]
- ↑ Кабардин О. Ф., Орлов В. А., Пономарева А. В. Факультативный курс физики. 8 класс. — М. : Просвещение, 1985. — С. 176. — 143 500 экз.
- ↑ Савельев И. В. Курс общей физики. — М. : Наука, 1987. — Т. 1 : Механика. Молекулярная физика. — С. 179.
- ↑ McMillan P. J. The mass distribution and gravitational potential of the Milky Way (англ.) // Monthly Notices of the Royal Astronomical Society. — 2017. — Vol. 465, iss. 1. — P. 76—94. — doi:10.1093/mnras/stw2759. — Bibcode: 2017MNRAS.465…76M. — arXiv:1608.00971.
- ↑ 1 2 Kafle P.R., Sharma S., Lewis G.F., Bland-Hawthorn J. On the Shoulders of Giants: Properties of the Stellar Halo and the Milky Way Mass Distribution (англ.) // The Astrophysical Journal. — 2014. — Vol. 794, iss. 1. — P. 59. — doi:10.1088/0004-637X/794/1/59. — Bibcode: 2014ApJ…794…59K. — arXiv:1408.1787.
Если мы подбросим камень в воздух – он упадет на Землю. Если у самолета на высоте 10 километром отключаться двигатели – он тоже упадет на Землю. Но спутники и космические корабли, что мы запускаем в космос, не падают. Почему?
Все дело в том, с какой скоростью тот или иной объект удаляется от планеты. Хватит ли этому объекту энергии преодолеть притяжение планеты.
Оглавление
- 1 Первая космическая скорость
- 1.1 Расчет
- 2 Вторая космическая скорость
- 2.1 Расчет
- 3
- 4 Третья космическая скорость
- 4.1 Расчет
- 5 Четвертая космическая скорость
- 6 Пятая космическая скорость
- 7 Почему спутники не падают на Землю
Первая космическая скорость
Это та самая минимальная скорость для выхода корабля или спутника на круговую орбиту, равную радиуса планеты, без учета вращения планеты и сопротивления ее атмосферы.
Если скорость будет превышать первую, но не достигнет второй космической скорости, то траектория тела из круговой начнет переходить в эллиптическую.
Впервые такую скорость смог достичь первый искусственный спутник Земли «Спутник-1» СССР 4 октября 1957 года.
Расчет
Вторая космическая скорость
Это минимальная скорость, которую следует придать телу для того, чтобы оно покинуло замкнутую орбиту и смогло улететь от небесного тела за пределы его гравитационного поля.
Иными словами, для Земли, это та скорость, с которой должны двигаться космические аппараты (КА) для полетов к другим объектам Солнечной системы: Луны, Марса и т.д.
Движение тела на второй космической скорости происходит по параболической траектории.
Впервые такую скорость развил Советский космический аппарат Луна-1 2 января 1959 года, чтобы преодолеть расстояние от Земли до Луны и изучить наш естественный спутник.
Расчет
Третья космическая скорость
Такую скорость необходимо придать телу, чтобы оно смогло покинуть Солнечную систему. Так как 99,8% массы Солнечной системы приходится на Солнце, то можно сказать, что КА надо преодолеть гравитационное притяжение Солнца.
Расчет
Для Солнечной системы это величина равна 16,650 км/с.
Самое выгодное расположение космодрома для подобного запуска – максимально близко к экватору, так как на экваторе самая большая скорость собственного вращения Земли вокруг своей оси и направление движения в сторону вращения Земли и в сторону орбитального движения Земли по орбите.
КА «Новые горизонты» покинул атмосферу Земли со скоростью близкой к третьей космической – 16,26 км /с. Относительно Солнца он имел скорость 45 км/с. Такой скорости недостаточно, чтобы покинуть Солнечную систему. Но благодаря гравитационному маневру у Юпитера, «Новые горизонты» добавил еще 4 км/с, что позволило ему покинуть Солнечную системы, предварительно показав нам карликовую планету Плутон.
Четвертая космическая скорость
Эта та скорость, которая позволит покинуть галактику в данной точке.
Четвертая космическая в основном не зависит от месторасположения Земли в Млечном пути. Она зависит от расположения и плотности звездного вещества в окрестностях Солнечной системы. А эти данные пока мало изучены.
Для нашей части галактики четвертая космическая скорость примерно равна 550 км/с.
Пятая космическая скорость
Эта скорость редко применима и является больше «фантазией», так как такую скорость необходимо развить для путешествия на другую планету в другую звездную систему, независимо от их взаимного расположения, с траекторией перпендикулярно плоскости эклиптики.
Для Земли эта скорость будет равна 43,6 км/с.
Почему спутники не падают на Землю
Этот вопрос поднимался в самом начале статьи. Теперь давайте на него ответим.
На спутник на орбите действует сила тяжести со стороны Земли. И под действием этой силы спутнику логичнее упасть.
Но, он летит вокруг Земли с первой космической скоростью – 7,9 км/с. Вспомните, чем больше скорость – тем сложнее затормозить. Вот и здесь, спутник и хотел бы упасть, но он не может затормозить и просто пролетает мимо Земли по инерции, тем самым продолжая бесконечное падение.
То есть, спутники падают, но промахиваются и не попадают в Землю.
Еще больше космоса и интересных фактов в телеграмм-канале.
Здесь приведены формулы и примеры расчета первой и второй космической скорости для небесных тел произвольной массы и радиуса.
Для быстрого расчета можно воспользоваться онлайн-калькулятором.
Первая космическая скорость
Первая космическая скорость – это скорость, которую нужно придать телу, масса которого пренебрежительно мала по сравнению с массой планеты,
чтобы это тело стало спутником планеты и вращалось вокруг нее по круговой траектории. Примечание: если скорость будет выше заданной (но меньше второй космической), то траектория орбиты будет
не круговой, а эллипсоидной.
Формула первой космической скорости:
где
G – гравитационная постоянная (постоянная Ньютона), равная 6,6743015·10-11 м3/(кг*с2), или Н*м2/кг2
R – радиус небесного тела
M – масса небесного тела
Вторая космическая скорость
Вторая космическая скорость – это минимальная скорость, которой должно обладать тело, чтобы преодолеть гравитационное притяжение планеты и покинуть замкнутую орбиту вокруг нее.
Формула второй космической скорости:
где
G – гравитационная постоянная
R – радиус небесного тела
M – масса небесного тела
Пример:
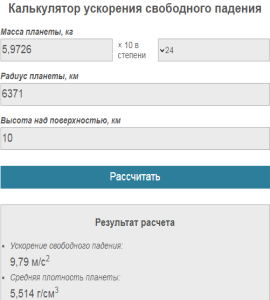
Масса планеты Земля составляет 5,9726*1024 кг, средний радиус – 6371 км (или 6371000 м). Подставив эти значения в формулы первой и второй
космических скоростей, мы получим значение соответственно 7 910 м/с и 11 187 м/с.
Теперь рассчитаем значение космических скоростей для планеты Нептун. Масса Нептуна – 1,0243*1026 кг. средний радиус – 24 622 км (24 622 000 м).
В итоге получим значения – 16 663 м/с и 23 565 м/с.
Значения для Марса (6,4171*1023 кг и 3389,5 км) будет 3 555 м/с и 5 027 м/с.
Для Венеры (4,8675*1024 кг и 6051,8 км) – 7 327 м/с и 10 362 м/с соответственно.
Калькулятор космических скоростей
Другие формулы
Содержание
- Как найти вторую космическую скорость планеты
- Как определить вторую космическую скорость
- Примеры расчета второй космической скорости
- Заключение
- Как найти вторую космическую скорость планеты
- Что такое вторая космическая скорость
- Как найти вторую космическую скорость планеты
- Заключение
- Как найти вторую космическую скорость планеты
- Шаг 1: Найти массу планеты
- Шаг 2: Найти радиус планеты
- Шаг 3: Используйте формулу для вычисления второй космической скорости
- Пример
- Итог
Как найти вторую космическую скорость планеты
Вторая космическая скорость — это скорость, которой планета должна двигаться, чтобы оставаться в орбите вокруг звезды. Это ключевой параметр, необходимый для понимания орбитальной механики планет. В этой статье мы рассмотрим, как найти вторую космическую скорость планеты.
Как определить вторую космическую скорость
Вторая космическая скорость зависит только от массы звезды и расстояния до нее. Другими словами, для двух планет, движущихся вокруг одной звезды на одном расстоянии, их вторые космические скорости будут одинаковыми.
Формула для определения второй космической скорости:
v = sqrt(GM/r)
- v — вторая космическая скорость
- G — гравитационная постоянная, равная 6,67 x 10^-11 Н x м^2 / кг^2
- M — масса звезды в килограммах
- r — расстояние от центра звезды до центра планеты в метрах
Как можно видеть из формулы, вторая космическая скорость пропорциональна корню из массы звезды и обратно пропорциональна корню расстояния до нее. Если масса звезды увеличивается, то вторая космическая скорость увеличивается, а если расстояние уменьшается, то скорость увеличивается.
Примеры расчета второй космической скорости
Рассмотрим несколько примеров расчета второй космической скорости:
- Земля: Масса Солнца — 1,989 x 10^30 кг, расстояние от центра Солнца до центра Земли — 149,6 x 10^9 м
- v = sqrt((6,67 x 10^-11) x (1,989 x 10^30) / (149,6 x 10^9)) = 29,8 км/с
- Меркурий: Масса Солнца — 1,989 x 10^30 кг, расстояние от центра Солнца до центра Меркурия — 57,91 x 10^9 м
- v = sqrt((6,67 x 10^-11) x (1,989 x 10^30) / (57,91 x 10^9)) = 47,9 км/с
- Нептун: Масса Солнца — 1,989 x 10^30 кг, расстояние от центра Солнца до центра Нептуна — 4497 x 10^9 м
- v = sqrt((6,67 x 10^-11) x (1,989 x 10^30) / (4497 x 10^9)) = 5,4 км/с
Как можно видеть из расчетов, вторая космическая скорость различается для разных планет, и зависит от их массы и расстояния до звезды.
Заключение
Вторая космическая скорость — это важный параметр, позволяющий понимать орбитальную механику планет. Она зависит только от массы звезды и расстояния до нее и может быть рассчитана с помощью формулы v = sqrt(GM/r). Расчет второй космической скорости позволяет понимать, какие планеты могут оставаться в орбите вокруг звезды и какая скорость им для этого нужна.
Как найти вторую космическую скорость планеты
Исследование космической среды является одной из главных задач современной астрономии. Космические объекты обладают многими свойствами, которые невозможно описать в условиях земной атмосферы. Один из таких параметров – вторая космическая скорость планеты.
Что такое вторая космическая скорость
Вторая космическая скорость – это минимальная скорость, при которой тело может покинуть поверхность планеты и уйти в космос. Эта скорость зависит от массы планеты и ее радиуса.
Для представления этогo в математической форме используется следующее уравнение:
V2 = (2GM / r)^0.5
Здесь V2 – вторая космическая скорость, G – гравитационная постоянная, M – масса планеты, а r – ее радиус.
Как найти вторую космическую скорость планеты
Вторая космическая скорость планеты может быть найдена с помощью следующих шагов:
- Определите гравитационную постоянную G.
- Определите массу планеты M и ее радиус r.
- Подставьте значения в формулу V2 = (2GM / r)^0.5 и рассчитайте вторую космическую скорость.
Изучение второй космической скорости планеты является важным частью изучения ее атмосферы и поверхности. Этот параметр позволяет определить, какие типы космических миссий могут быть осуществлены на данной планете. Например, для запуска с космического аппарата на Марс необходимо достичь второй космической скорости планеты.
Заключение
Вторая космическая скорость – это важный параметр при изучении космических объектов. Рассчитать ее можно с помощью простой формулы, используя данные о массе и радиусе планеты. Обладая знаниями об этом параметре, можно более эффективно планировать космические миссии и изучать космическое пространство.
Как найти вторую космическую скорость планеты
Вторая космическая скорость — это минимальная скорость, которую необходимо иметь объекту на поверхности планеты, чтобы преодолеть гравитационное поле планеты и остаться в космосе без дополнительной тяги. Эта скорость является важным фактором при разработке многих космических миссий и вычисляется на основе массы и радиуса планеты. В этой статье мы расскажем о том, как найти вторую космическую скорость планеты.
Шаг 1: Найти массу планеты
Первым шагом необходимо найти массу планеты. В Интернете можно найти информацию о массе планеты на сайтах NASA и других космических организаций. Масса планеты измеряется в килограммах и обычно указывается в научных единицах.
Шаг 2: Найти радиус планеты
Вторым шагом необходимо найти радиус планеты. Радиус планеты измеряется в километрах и также можно найти на сайтах NASA и других космических организаций.
Шаг 3: Используйте формулу для вычисления второй космической скорости
После того, как вы найдете массу и радиус планеты, используйте следующую формулу для вычисления второй космической скорости:
В2 = (Г * M / R) ^ 1/2
Где:
- V2 — вторая космическая скорость в м/с
- Г — гравитационная постоянная (6,67 х 10^-11 Нм^2/кг^2)
- M — масса планеты в кг
- R — радиус планеты в м
Пример
Предположим, что мы ищем вторую космическую скорость Земли. По информации NASA, масса Земли составляет 5,97 х 10^24 кг, а ее радиус равен 6 371 км.
Используя формулу, вычисляем вторую космическую скорость:
В2 = (6,67 х 10^-11 * 5,97 х 10^24 / (6 371 000)) ^ 1/2 = 11 186 м/с
Таким образом, вторая космическая скорость Земли составляет 11 186 м/с.
Итог
Вычисление второй космической скорости планеты может показаться сложным процессом, но с использованием правильной формулы и научных данных эта задача становится простой и понятной. Вторая космическая скорость является важным параметром при планировании космических миссий и может быть использована для достижения многих научных целей, связанных с исследованием космоса.
Чтобы внести ясность в то, какие необходимы условия для того, чтобы тело стало искусственным спутником Земли, предложен рисунок 1. Это копия ньютоновского чертежа. Изображение земного шара дополнено высокой горой, с вершины которой производят бросание камней, придавая им различные по модулю и горизонтально направленные скорости. Действие силы тяжести способствует отклонению движущихся камней от прямолинейного пути. После описания кривой траектории он падает на Землю.
Рисунок 1
Если прилагать больше сил при бросании, то он упадет дальше. Отсюда следует, что при отсутствии сопротивления воздуха и при наличии большой скорости тело может даже не приземляться на поверхность. Это говорит о его дальнейшем описывании круговых траекторий, не изменяя высоты относительно земной поверхности.
Первая космическая скорость
Чтобы движение вокруг Земли проходило по круговой орбите с радиусом, схожим с земным Rз, тело должно обладать определенной скоростью υ1, которую можно определить из условия равенства произведения массы тела на ускорение силы тяжести, действующей на тело.
Для того, чтобы какое-либо тело могло стать спутником Земли, ему должна быть сообщена скорость υ1, называемая первой космической. При подстановке значений g и Rз в формулу, получаем, что
υ1=gRз=8 км/с.
Вторая космическая скорость
Если тело обладает скоростью υ1, то впоследствии при движении не упадет. Но значения
υ1 недостаточно для выхода из сферы земного притяжения, то есть удалиться от Земли на расстояние, при котором оно теряет свою силу. Для этого нужна скорость υx, которая получила название второй космической или скорость убегания.
Для ее нахождения следует произвести вычисление работы, потраченную против сил земного притяжения для соударения с поверхности Земли на бесконечность. При удалении такого тела получаем:
mυ222-GmMR=0,R=h+r
где m – масса брошенного тела, М – масса планеты, r – радиус планеты, h – длина от основания до его центра масс, G – гравитационная постоянная, υ2 – вторая космическая скорость.
Решив уравнение относительно υ2, получим:
υ2=2GMR.
Существует связь между первой и второй скоростями
υ2=2υ1.
Квадрат скорости убегания равняется ньютоновскому потенциалу в заданной точке, то есть:
υ22=-2Φ=2GMR.
Скорость υ2 считается за вторую космическую. Из сравнений видно, что она в 2 раза больше первой. Если умножить 8 км/с на 2, то получим значение для υ2, приблизительно равняющееся 11 км/с.
Нужная величина скорости не зависит от направления движения тела. На это влияет вид траектории, по которой происходит удаление от земной поверхности.
Чтобы тело смогло стартовать с поверхности планеты, оно должно обладать второй космической скоростью при малом значении h и большом значении гравитационной силы. Как только ракета начнет удаляться от Земли, гравитационная постоянная будет уменьшаться вместе со значением, необходимым для убегания кинетической энергии.
Третья космическая скорость
Для выхода за пределы Солнечной системы телу следует преодолеть как силу притяжения к Земле, так и к Солнцу. Для этого применяется третья космическая скорость υ3, позволяющая запускать тело с земной поверхности.
Значение υ3 зависит от направления. Если запуск производится в направлении орбитального движения Земли, тогда ее значение минимально и составит около 17 км/с. Когда тело запущено противоположно направлению движения Земли, тогда значение скорости υ3≈73.
Еще в СССР были достигнуты космические скорости.
- Первый запуск искусственного спутника был осуществлен 4 октября 1957 года.
- Уже 2 января 1959 ученым удалось найти решения для преодоления сферы земного притяжения. Поэтому запущенная ракета стала первой космической планетой Солнечной системы.
- Дата 12 апреля 1961 года известна, так как был осуществлен полет человека в космическое пространство. Юрий Алексеевич Гагарин был первым советским космонавтом, совершившим один оборот вокруг Земли, после чего благополучно приземлился.
Определить первую космическую скорость для спутника Юпитера, летающего на небольшой высоте, если дана масса планеты, равная 1,9·1027 кг, а ее радиус R=7,13·107 м.
Дано:
B=1,9·1027 кг,
R=7,13·107 м.
Найти: υ1 – ?
Решение
Для начала запишем формулу для нахождения первой космической скорости: υ1=gR3 (1).
Значение g принимает ускорение свободного падения на Юпитере.
Из закона всемирного тяготения получаем, что mg=GMmr2 (2).
Значение m определено как масса спутника, а М – масса самой планеты.
Если высота спутника над поверхностью Юпитера сравнительно мала относительно его радиуса, тогда ею разрешено пренебречь: r=R.
Получаем, что из уравнения (2) найдем ускорение свободного падения для планеты из
g=GMR2.
После подстановки в уравнение (1), сможем найти первую космическую скорость.
υ1=GMR=42159,45 м/с.
Ответ: υ1=42159,45 м/с.