Как найти вторую производную функции в точке

Вторая производная

Всё
очень просто. Вторая производная –
это производная
от первой производной: 

Стандартные
обозначения второй производной: 
, 
 или 
 (дробь
читается так: «дэ два игрек по дэ икс
квадрат»). Чаще всего вторую производную
обозначают первыми двумя вариантами.
Но третий вариант тоже встречается,
причем, его очень любят включать в
условия контрольных заданий, например:
«Найдите 
 функции…».
А студент сидит и битый час чешет репу,
что это вообще такое.

Рассмотрим
простейший пример. Найдем вторую
производную от функции 
.

Для того чтобы
найти вторую производную, как многие
догадались, нужно сначала найти первую
производную:

Теперь находим
вторую производную:

Готово.

Рассмотрим более
содержательные примеры.

Пример 11

Найти
вторую производную функции 

Найдем
первую производную:

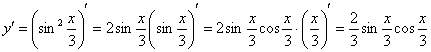
На
каждом шаге всегда смотрим, нельзя ли
что-нибудь упростить? Сейчас нам предстоит
дифференцировать произведение двух
функций, и мы избавимся от этой
неприятности, применив
известную тригонометрическую
формулу 
.
Точнее говоря, использовать формулу
будем в обратном направлении: 
:

Находим
вторую производную:

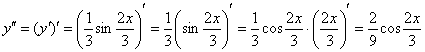
Готово.

Можно
было пойти другим путём – понизить
степень функции еще перед дифференцированием,
используя формулу 
:

Если интересно,
возьмите первую и вторую производные
снова. Результаты, естественно, совпадут.

Отмечу,
что понижение степени бывает очень
выгодно при нахождении частных
производных функции.
Здесь же оба способа решения будут
примерно одинаковой длины и сложности.

Как и
для первой производной, можно
рассмотреть задачу
нахождения второй производной в точке.

Например:
Вычислим значение найденной второй
производной в точке 
:

Необходимость
находить вторую производную и вторую
производную в точке возникает при
исследовании графика функции на
выпуклость/вогнутость и перегибы.

Пример 12

Найти
вторую производную функции 
.
Найти 

Это пример для
самостоятельного решения.

Аналогично можно
найти третью производную, а также
производные более высоких порядков.
Такие задания встречаются, но встречаются
значительно реже.

Решения
и ответы:

Пример
2: Найдем производную:

Вычислим
значение функции в точке 
:

Пример
4: Найдем производную:

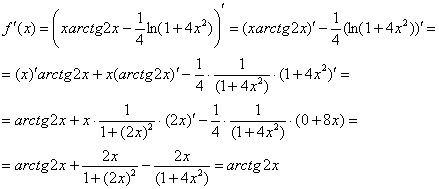
Вычислим
производную в заданной точке:

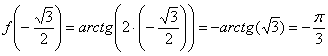
Пример
6: Уравнение касательной составим по
формуле 

1)
Вычислим значение функции в точке 
:

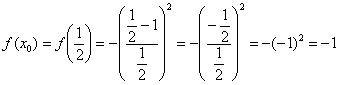
2)
Найдем производную. Перед дифференцированием
функцию выгодно упростить:

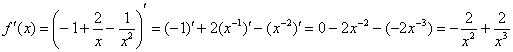
3)
Вычислим значение производной в
точке 
:

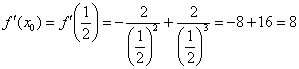
4)
Подставим значения 
, 
 и 
 в
формулу 
:

Пример
8: Преобразуем функцию:

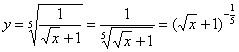
Найдем
производную:

Запишем
дифференциал:

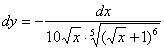
Пример
10: Найдем производную:

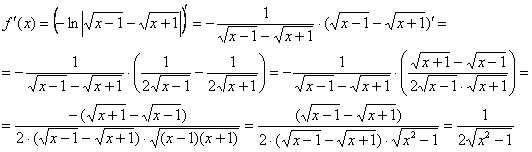
Запишем
дифференциал:

Вычислим
дифференциал в точке 
:

Пример
12: Найдем первую производную:

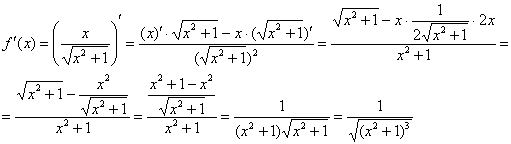
Найдем
вторую производную:

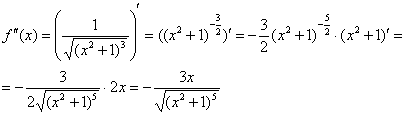
Вычислим: 

4. 2.Частные производные. Примеры решений

На
данном уроке мы познакомимся с понятием
функции двух переменных, а также подробно
рассмотрим наиболее распространенное
задание – нахождение частных
производныхпервого
и второго порядка, полного дифференциала
функции. Студенты-заочники, как правило,
сталкиваются с частными производными
на 1 курсе во 2 семестре. Причем, по моим
наблюдениям, задание на нахождение
частных производных практически всегда
встречается на экзамене.

Для
эффективного изучения нижеизложенного
материала Вам необходимо уметь
более или менее уверенно находить
«обычные» производные функции одной
переменной. Научиться правильно
обращаться с производными можно на
уроках Как
найти производную? иПроизводная
сложной функции.
Также нам потребуется таблица производных
элементарных функций и правил
дифференцирования, удобнее всего, если
она будет под рукой в распечатанном
виде. Раздобыть справочный материал
можно на страницеМатематические
формулы и таблицы.

Начнем
с самого понятия функции двух переменных,
я постараюсь ограничиться минимумом
теории, так как сайт имеет практическую
направленность. Функция двух переменных
обычно записывается как 
,
при этом переменные 
, 
 называются независимыми
переменными или аргументами.

Пример: 
 –
функция двух переменных.

Иногда
используют запись 
.
Также встречаются задания, где вместо
буквы 
 используется
буква 
.

Полезно
знать геометрический смысл функций.
Функции одной переменной 
 соответствует
определенная линия на плоскости,
например, 
  –
всем знакомая школьная парабола. Любая
функция двух переменных 
 с
геометрической точки зрения представляет
собой поверхность в трехмерном
пространстве (плоскости, цилиндры, шары,
параболоиды и т.д.). Но, собственно, это
уже аналитическая геометрия, а у нас на
повестке дня математический анализ.

Переходим
к вопросу нахождения частных производных
первого и второго порядков. Должен
сообщить хорошую новость для тех, кто
выпил несколько чашек кофе и настроился
на невообразимо трудный материал: частные
производные – это почти то же самое,
что и «обычные» производные функции
одной переменной. 

Для
частных производных справедливы все
правила дифференцирования и таблица
производных элементарных функций. Есть
только пара небольших отличий, с которыми
мы познакомимся прямо сейчас.

Пример 1

Найти
частные производные первого и второго
порядка функции 

Сначала найдем
частные производные первого порядка.
Их две.

Обозначения:

 или 
 –
частная производная по «икс»

 или 
 –
частная производная по «игрек»

Начнем
с 
. Когда
мы находим частную производную по «икс»,
то переменная 
 считается
константой (постоянным числом).

Решаем. На данном
уроке я буду приводить полное решение
сразу, а комментарии давать ниже.

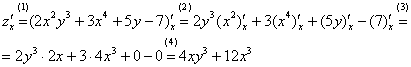
Комментарии к
выполненным действиям:

(1)
Первое, что мы делаем при нахождении
частной производной – заключаем всю функцию
в скобки под штрих с
подстрочным индексом.

Внимание,
важно! Подстрочные
индексы НЕ ТЕРЯЕМ по ходу решения. В
данном случае, если Вы где-нибудь
нарисуете «штрих» без 
,
то преподаватель, как минимум, может
поставить рядом с заданием 
 (сразу
откусить часть балла за невнимательность).

Далее данный шаг
комментироваться не будет, все сделанные
замечания справедливы для любого примера
по рассматриваемой теме.

(2)
Используем правила дифференцирования 
, 
.
Для простого примера, как этот, оба
правила вполне можно применить на одном
шаге. Обратите внимание на первое
слагаемое: так как 
 считается
константой, а любую константу можно
вынести за знак производной,
то 
 мы
выносим за скобки. То есть в данной
ситуации
 ничем
не лучше обычного числа. Теперь посмотрим
на третье слагаемое 
:
здесь, наоборот, выносить нечего. Так
как 
 константа,
то 
 –
тоже константа, и в этом смысле она ничем
не лучше последнего слагаемого –
«семерки».

(3)
Используем табличные производные 
 и 
.

(4) Упрощаем, или,
как я люблю говорить, «причесываем»
ответ.

Теперь 
. Когда
мы находим частную производную по
«игрек», то переменная 
 считается
константой (постоянным числом).

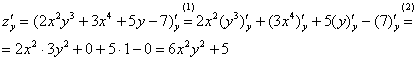
(1)
Используем те же правила дифференцирования 
, 
.
В первом слагаемом выносим константу 
 за
знак производной, во втором слагаемом
ничего вынести нельзя поскольку 
 –
уже константа.

(2)
Используем таблицу производным
элементарных функций. Мысленно
поменяем в таблице все «иксы» на «игреки».
То есть данная таблица рАвно справедлива
и для
 (да
и вообще почти для любой буквы). В
частности, используемые нами формулы
выглядят так: 
 и 
.

Итак, частные
производные первого порядка найдены

Подведем итог, чем
же отличается нахождение частных
производных от нахождения «обычных»
производных функции одной переменной:

1)
Когда мы находим частную
производную 
, переменная 
 считается
константой.

2)
Когда мы находим частную
производную 
, переменная 
 считается
константой.

3)
Правила и таблица производных элементарных
функций справедливы и применимы для
любой переменной (
, 
 либо
какой-нибудь другой), по которой ведется
дифференцирование.

Шаг второй. Находим
частные производные второго порядка.
Их четыре.

Обозначения:

 или 
 –
вторая производная по «икс»

 или 
 –
вторая производная по
«игрек»

 или 
 – смешанная производная
«икс по игрек»

 или 
 – смешанная производная
«игрек по икс»

В
понятии второй производной нет ничего
сложного. Говоря простым языком, вторая
производная – это производная от первой
производной.

Для
наглядности я перепишу уже найденные
частные производные первого порядка:

Сначала
найдем смешанные производные:

Как
видите, всё просто: берем частную
производную 
 и
дифференцируем ее еще раз, но в данном
случае – уже по «игрек».

Аналогично:

Для
практических примеров справедливо
следующее равенство: 

Таким образом,
через смешанные производные второго
порядка очень удобно проверить, а
правильно ли мы нашли частные производные
первого порядка.

Находим
вторую производную по «икс».

Никаких
изобретений, берем 
 и
дифференцируем её по «икс» еще раз:

Аналогично:

Следует
отметить, что при нахождении 
, 
 нужно
проявить повышенное
внимание, так как
никаких чудесных равенств для проверки
не существует.

Пример 2

Найти
частные производные первого и второго
порядка функции 

Это
пример для самостоятельного решения
(ответ в конце урока). Если возникли
трудности с дифференцированием корней,
рекомендую ознакомиться уроком Как
найти производную?

При определенном
опыте частные производные из примеров
№№1,2 будут решаться Вами устно.

Переходим к более
сложным примерам.

Пример 3

Найти
частные производные первого порядка
функции 
.
Проверить, что 
.
Записать полный дифференциал первого
порядка 
.

Решение:
Находим частные производные первого
порядка:

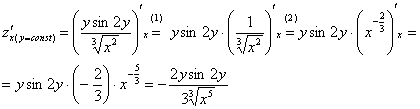
Обратите
внимание на подстрочный индекс: 
,
рядом с «иксом» не возбраняется в скобках
записывать, что 
 –
константа. Данная пометка может быть
очень полезна для начинающих, чтобы
легче было ориентироваться в решении.

Дальнейшие
комментарии:

(1)
Выносим все константы за знак производной.
В данном случае 
 и 
,
а, значит, и их произведение 
 считается
постоянным числом.

(2) Не забываем, как
правильно дифференцировать корни.

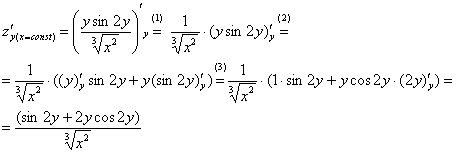
(1)
Выносим все константы за знак производной,
в данной случае константой является

.

(2) Под
штрихом у нас осталось произведение
двух функций, следовательно, нужно
использовать правило дифференцирования
произведения 
.

(3) Не
забываем, что

– это сложная функция (хотя и простейшая
из сложных). Используем соответствующее
правило:

.

Теперь находим
смешанные производные второго порядка:

,
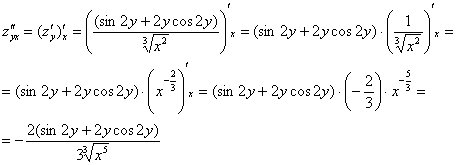
значит, все вычисления выполнены верно.

Запишем
полный дифференциал 
.
В контексте рассматриваемого задания
не имеет смысла рассказывать, что такое
полный дифференциал функции двух
переменных. Важно, что этот самый
дифференциал очень часто требуется
записать в практических задачах.

Полный
дифференциал первого порядка функции
двух переменных имеет вид:

В данном случае:

То
есть, в формулу нужно просто подставить
уже найденные частные производные
первого порядка. Значки дифференциалов 
 и 
 в
этой и похожих ситуациях по возможности
лучше записывать в числителях:

Пример 4

Найти
частные производные первого порядка
функции 
.
Проверить, что 
.
Записать полный дифференциал первого
порядка 
.

Это пример для
самостоятельного решения. Полное решение
и образец оформления задачи – в конце
урока.

Рассмотрим серию
примеров, включающих в себя сложные
функции.

Пример 5

Найти
частные производные первого порядка
функции

.

Записать
полный дифференциал 
.

Решение:

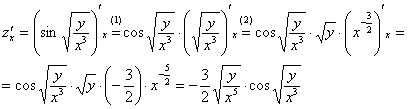
(1)
Применяем правило дифференцирования
сложной функции 
.
С урока Производная
сложной функции
следует помнить
очень важный момент: когда мы по таблице
превращаем синус (внешнюю функцию) в
косинус, то вложение

 (внутренняя
функция) у нас не
меняется.

(2)
Здесь используем свойство корней:

,
выносим константу

за знак производной, а корень

представляем в нужном для дифференцирования
виде.

Аналогично:

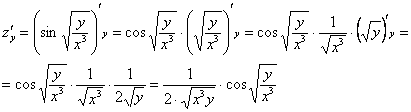
Запишем
полный дифференциал первого порядка:

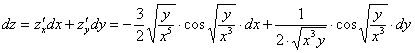
Пример 6

Найти
частные производные первого порядка
функции 
.

Записать
полный дифференциал 
.

Это пример для
самостоятельного решения (ответ в конце
урока). Полное решение не привожу, так
как оно достаточно простое

Довольно часто
все вышерассмотренные правила применяются
в комбинации.

Пример 7

Найти
частные производные первого порядка
функции 
.

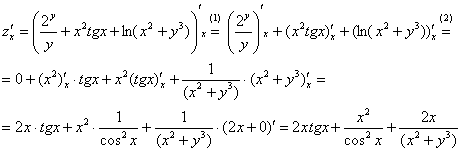
(1) Используем
правило дифференцирования суммы

(2)
Первое слагаемое  в данном случае
считается константой, поскольку в
выражении

нет ничего, зависящего от «икс» – только
«игреки».

(Знаете,
всегда приятно, когда дробь удается
превратить в ноль).

Для
второго слагаемого применяем правило
дифференцирования произведения. Кстати,
в этом смысле ничего бы не изменилось,
если бы вместо

была дана функция

– важно, что здесь произведение
двух функций, КАЖДАЯ
из которых зависит от
«икс»,
а поэтому, нужно использовать правило
дифференцирования произведения. Для
третьего слагаемого применяем правило
дифференцирования сложной функции.

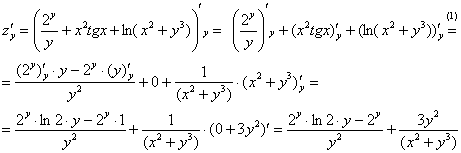
(1) В
первом слагаемом и в числителе и в
знаменателе содержится «игрек»,
следовательно, нужно использовать
правило дифференцирования частного: 
. 
Второе слагаемое зависит ТОЛЬКО от
«икс», значит, 
 считается
константой и превращается в ноль. Для
третьего слагаемого используем правило
дифференцирования сложной функции.

Для тех читателей,
которые мужественно добрались почти
до конца урока, расскажу старый
мехматовский анекдот для разрядки:

Однажды
в пространстве функций появилась злобная
производная и как пошла всех
дифференцировать. Все функции разбегаются
кто куда, никому не хочется превращаться!
И только одна функция никуда не убегает.
Подходит к ней производная и спрашивает:

– А
почему это ты от меня никуда не убегаешь?

– Ха.
А мне всё равно, ведь я «е в степени икс»,
и ты со мной ничего не сделаешь!

На
что злобная производная с коварной
улыбкой отвечает:

– Вот
здесь ты ошибаешься, я тебя продифференцирую
по «игрек», так что быть тебе нулем.

(Кто
понял анекдот, тот освоил производные,
минимум, на «тройку»).

Пример 8

Найти
частные производные первого порядка
функции

.

Это пример для
самостоятельного решения. Полное решение
и образец оформления задачи – в конце
урока.

Ну вот почти и всё.
Напоследок не могу не обрадовать
любителей математики еще одним примером.
Дело даже не в любителях, у всех разный
уровень математической подготовки –
встречаются люди (и не так уж редко),
которые любят потягаться с заданиями
посложнее. Хотя, последний на данном
уроке пример не столько сложный, сколько
громоздкий с точки зрения вычислений.

Пример 9

Дана
функция двух переменных 
.
Найти все частные производные первого
и второго порядков.

Это пример для
самостоятельного решения. Полное решение
и образец оформления где-то рядом.

Ответы:

Пример
2:

,


,


,

Пример
4: Ссылка для просмотра ниже.

Пример
6:

,


,

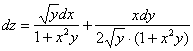
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #

  08.02.20157.31 Mб91.rtf

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Производная функции, заданной параметрически

4 января 2022

Сегодня мы научимся считать производную параметрической функции. Для этого разберём основную формулу, несколько примеров, но главное — одну из самых частых и глупых ошибок, которые допускают начинающие студенты.

План такой:

1. Параметрическое задание функции — основные понятия
2. Производная функции, заданной параметрически
3. Типичные ошибки на примере второй производной
4. Третья производная — разминка для мозгов

Начнём с ключевых определений и соображений.

1. Функция, заданная параметрически

Считая производные, мы привыкли работать с функциями, заданными аналитически, т.е. формулой $y=fleft( x right)$. Подставляя в эту формулу разные значения $x$, мы легко находим значение $y$.

Несколько примеров таких функций:

• Квадратичная функция: $y={{x}^{2}}$. График — парабола.
• Показательная функция: $y={{text{e}}^{x}}$. Она же «экспонента».
• Тригонометрическая функция: $y=sin x$. График — синусоида.

Но что если величины $y$ и $x$ зависят не друг от друга, а от некой третьей переменной? Скажем, от параметра $t$?

Пример 1. Функция, заданная параметрически:

[left{ begin{align} & x=cos t \ & y=sin t \ end{align} right.]

Перебирая разные $tin mathbb{R}$, мы будем получать точки с координатами $left( x;y right)$, которые в итоге превратятся в график:

Да это же тригонометрическая окружность! Она задаётся уравнением ${{x}^{2}}+{{y}^{2}}=1$.

График такого уравнения не является функцией (если забыли почему, гляньте урок про графики уравнений с двумя переменными). Но его можно «составить» из графиков двух функций:

[begin{align} & {{y}_{1}}=sqrt{1-{{x}^{2}}} \ & {{y}_{2}}=-sqrt{1-{{x}^{2}}} \ end{align}]

А вот это уже привычные нам аналитические функции, и для них можно посчитать производную!

К сожалению, далеко не всегда параметрическое уравнение вида

[left{ begin{align} & x=varphi left( t right) \ & y=psi left( t right) \ end{align} right.]

можно свести к привычными выражениям вида $y=fleft( x right)$. Но это ни в коем случае не означает, что для таких параметрических функций нельзя посчитать производную. Можно и даже нужно. И поможет нам в этом следующая формула.

2. Производная функции, заданной параметрически

Итак, основная теорема.

Теорема 1. Пусть функция $y=fleft( x right)$ задана параметрически:

[left{ begin{align} & x=varphi left( t right) \ & y=psi left( t right) \ end{align} right.]

Тогда производная этой функции считается по формуле

[{{{y}’}_{x}}left( x right)=frac{{{{{y}’}}_{t}}left( t right)}{{{{{x}’}}_{t}}left( t right)}]

Эту теорему очень легко доказать. В самом деле, если функция $x=varphi left( t right)$ рассматривается на интервале $tin left( a;b right)$ таком, что существует обратная функция $t={{varphi }^{-1}}left( x right)$, то можно определить сложную функцию

[yleft( x right)=psi left( {{varphi }^{-1}}left( x right) right)]

По теореме о производной сложной функции:

[{{{y}’}_{x}}left( x right)={{{psi }’}_{x}}left( {{varphi }^{-1}}left( x right) right)={{{psi }’}_{x}}left( t right)={{{psi }’}_{t}}left( t right)cdot {{{t}’}_{x}}left( x right)]

[begin{align} {{{{y}’}}_{x}}left( x right) & ={{{{psi }’}}_{x}}left( {{varphi }^{-1}}left( x right) right)= \ & ={{{{psi }’}}_{x}}left( t right)= \ & ={{{{psi }’}}_{t}}left( t right)cdot {{{{t}’}}_{x}}left( x right) end{align}]

Но по теореме об обратной функции ${{{t}’}_{x}}={1}/{{{{{x}’}}_{t}}};$, поэтому

[{{{y}’}_{x}}left( x right)=frac{{{{{psi }’}}_{t}}left( t right)}{{{{{x}’}}_{t}}left( t right)}]

Что и требовалось доказать.

Замечание. Когда выражение дифференцируется по разным переменным, целесообразно указывать в нижним индексе ту переменную, по которой выполняется дифференцирование: ${{{y}’}_{x}}$, ${{{y}’}_{t}}$, ${{{x}’}_{t}}$ и т.д.

Это поможет избежать недоразумений и глупых вычислительных ошибок. Кроме того, подобные обозначения активно используются в дифференциальном исчислении функций нескольких переменных.

Детальное руководство по работе с нижними индексами и переменными дифференцирования — см. урок «Производная сложной функции». Сейчас просто отметим, что мы привыкли считать производную по переменной $x$. Но с тем же успехом можно считать производную и по $t$, и по какому-нибудь $varphi $, и вообще по любой переменной, которую мы увидим в функции.

2.1. Примеры

Приведённые выше формулы могут показаться сложными и страшными. Но на деле это одна из самых лёгких тем в производных. Взгляните:

Пример 1. Найдите ${{{y}’}_{x}}$, если

[left{ begin{align} & x=2t \ & y=3{{t}^{2}}-5t \ end{align} right.]

Считаем производные ${{{x}’}_{t}}$ и ${{{y}’}_{t}}$:

[begin{align} & {{{{x}’}}_{t}}={{left( 2t right)}^{prime }}_{t}=2 \ & {{{{y}’}}_{t}}={{left( 3{{t}^{2}}-5t right)}^{prime }}_{t}=6t-5 end{align}]

Теперь считаем ${{{y}’}_{x}}$ по формуле производной параметрической функции:

[{{{y}’}_{x}}=frac{{{{{y}’}}_{t}}}{{{{{x}’}}_{t}}}=frac{6t-5}{2}]

Вот и всё! Готовое выражение можно разбить на две дроби, а можно оставить и так.

Пример 2. Найдите ${{{y}’}_{x}}$, если

[left{ begin{align} & x={{2}^{-t}} \ & y={{2}^{2t}} \ end{align} right.]

Вместо многочленов видим показательные функции. Это ничего не меняет, снова считаем ${{{x}’}_{t}}$ и ${{{y}’}_{t}}$:

[begin{align} & {{{{x}’}}_{t}}={{left( {{2}^{-t}} right)}^{prime }}_{t}={{2}^{-t}}cdot left( -ln 2 right) \ & {{{{y}’}}_{t}}={{left( {{2}^{2t}} right)}^{prime }}_{t}={{2}^{2t}}cdot 2ln 2 end{align}]

Теперь находим ${{{y}’}_{x}}$ по формуле:

[{{{y}’}_{x}}=frac{{{{{y}’}}_{t}}}{{{{{x}’}}_{t}}}=frac{{{2}^{2t}}cdot 2ln 2}{{{2}^{-t}}cdot left( -ln 2 right)}=-{{2}^{3t+1}}]

Для решения этого задания пришлось вспомнить производную показательной функции и некоторые свойства степеней.:)

Пример 3. Найдите ${{{y}’}_{x}}$, если

[left{ begin{align} & x=acos varphi \ & y=bsin varphi \ end{align} right.]

Здесь переменной-параметром является $varphi $, а буквы $a$ и $b$ — просто числа, которые будут частью ответа. Считаем ${{{x}’}_{varphi }}$ и ${{{y}’}_{varphi }}$ — производные тригонометрических функций:

[begin{align} & {{{{x}’}}_{varphi }}={{left( acos varphi right)}^{prime }}_{varphi }=-asin varphi\ & {{{{y}’}}_{varphi }}={{left( bsin varphi right)}^{prime }}_{varphi }=bcos varphiend{align}]

Находим ${{{y}’}_{x}}$:

[{{{y}’}_{x}}=frac{{{{{y}’}}_{varphi }}}{{{{{x}’}}_{varphi }}}=frac{bcos varphi }{-asin varphi }=-frac{b}{a}operatorname{ctg}varphi ]

2.2. Производная в точке

Понятно, что это были совсем простые задачи. Буквально через минуту мы рассмотрим примеры посерьёзнее, но сначала важное дополнение.

Часто нам требуется посчитать не производную функции вообще, а лишь в конкретной точке. Например, чтобы провести касательную или нормаль к кривой, заданной параметрически, в некой точке ${{M}_{0}}left( {{x}_{0}};{{y}_{0}} right)$, лежащей на этой кривой.

В этом случае задача ещё более упрощается.

Пример 4. Найдите ${{{y}’}_{x}}$ при $t={pi }/{4};$, если

[begin{align} & xleft( t right)=tcdot left( tcos t-2sin t right) \ & yleft( t right)=tcdot left( tsin t+2cos t right) \ end{align}]

Задача явно серьёзнее, чем все предыдущие. Считаем ${{{x}’}_{t}}$ и ${{{y}’}_{t}}$:

[begin{align} & {{{{x}’}}_{t}}={{left( tcdot left( tcos t-2sin t right) right)}^{prime }}_{t}=-left( {{t}^{2}}+2 right)cdot sin t \ & {{{{y}’}}_{t}}={{left( tcdot left( tsin t+2cos t right) right)}^{prime }}_{t}=left( {{t}^{2}}+2 right)cdot cos t end{align}]

[begin{align} {{{{x}’}}_{t}} & ={{left( tcdot left( tcos t-2sin t right) right)}^{prime }}_{t}= \ & =-left( {{t}^{2}}+2 right)cdot sin t \ {{{{y}’}}_{t}} & ={{left( tcdot left( tsin t+2cos t right) right)}^{prime }}_{t}= \ & =left( {{t}^{2}}+2 right)cdot cos tend{align}]

И сразу подставляем $t={pi }/{4};$:

[begin{align} & {{{{x}’}}_{t}}left( frac{pi }{4} right)=-left( frac{{{pi }^{2}}}{16}+2 right)cdot frac{sqrt{2}}{2} \ & {{{{y}’}}_{t}}left( frac{pi }{4} right)=left( frac{{{pi }^{2}}}{16}+2 right)cdot frac{sqrt{2}}{2} end{align}]

Осталось найти ${{{y}’}_{x}}$:

[{{{y}’}_{x}}=frac{{{{{y}’}}_{t}}}{{{{{x}’}}_{t}}}=-frac{32+{{pi }^{2}}}{32+{{pi }^{2}}}=-1]

Разумеется, можно было сначала найти общую формулу для ${{{y}’}_{x}}$, а уже затем подставить в неё $t={pi }/{4};$ — результат получится точно такой же.

3. Типичные ошибки при вычислении производных

А теперь, пожалуй, ключевой момент, связанный с дифференцированием параметрических функций. Ошибка, которую я сам допустил много лет назад.

Давайте ещё раз взглянем на функцию, заданную параметрически:

[left{ begin{align} & x=varphi left( t right) \ & y=psi left( t right) \ end{align} right.]

И на производную этой функции:

[{{{y}’}_{x}}left( x right)=frac{{{{{y}’}}_{t}}left( t right)}{{{{{x}’}}_{t}}left( t right)}]

А теперь представьте, что надо посчитать вторую производную: ${{{y}”}_{xx}}$. И тут у многих проскакивает мысль: а что если взять формулу для первой производной и просто увеличить в ней количество «штрихов»?

Получится что-то типа вот этого:

[{{{y}”}_{xx}}left( x right)=frac{{{{{y}”}}_{tt}}left( t right)}{{{{{x}”}}_{tt}}left( t right)}]

Так вот: эта формула не верна!

Чтобы правильно найти вторую производную функции, заданной параметрически, достаточно вспомнить, что вторая производная — это просто производная от производной:

[{{{y}”}_{xx}}={{left( {{{{y}’}}_{x}} right)}^{prime }}_{x}]

Проще говоря, сначала мы находим ${{{y}’}_{x}}$ — это будет какая-то функция от $t$. Затем уже от этой функции вновь считаем производную — всё по той же формуле, которую мы сегодня уже много раз использовали. Получится так:

[{{{y}”}_{xx}}={{left( {{{{y}’}}_{x}} right)}^{prime }}_{x}=frac{{{left( {{{{y}’}}_{x}} right)}^{prime }}_{t}}{{{{{x}’}}_{t}}}]

Тут нас ждёт две новости:

• Хорошая: мы уже знаем ${{{x}’}_{t}}$. Это значит, что каждая последующая производная будет считаться чуть проще и быстрее;
• Плохая: можно легко запутаться во всех этих штрихах и переменных.

Чтобы разобраться с плохой новостью, достаточно просто небольшой практики. Поэтому сейчас мы разберём три примера. А точнее, три задачи из контрольных работ МГТУ им. Баумана. А там знают толк в производных.:)

Пример 5. Найдите ${{{y}”}_{xx}}$, если

[left{ begin{align} & x=cos 2t \ & y=sin t \ end{align} right.]

1. Сначала находим первую производную. Для этого считаем ${{{x}’}_{t}}$ и ${{{y}’}_{t}}$:

[begin{align} & {{{{x}’}}_{t}}=-2sin 2t=-4sin tcos t \ & {{{{y}’}}_{t}}=cos t end{align}]

Откуда находим саму производную ${{{y}’}_{x}}$:

[{{{y}’}_{x}}=frac{{{{{y}’}}_{t}}}{{{{{x}’}}_{t}}}=frac{cos t}{-4sin tcos t}=-frac{1}{4sin t}]

2. Теперь находим вторую производную. Для этого считаем ${{left( {{{{y}’}}_{x}} right)}^{prime }}_{t}$:

[{{left( {{{{y}’}}_{x}} right)}^{prime }}_{t}={{left( -frac{1}{4sin t} right)}^{prime }}_{t}=frac{cos t}{4{{sin }^{2}}t}]

Кроме того, мы уже знаем ${{{x}’}_{t}}$. Поэтому находим вторую производную ${{{y}”}_{xx}}$:

[{{{y}”}_{xx}}={{left( {{{{y}’}}_{x}} right)}^{prime }}_{x}=frac{{{left( {{{{y}’}}_{x}} right)}^{prime }}_{t}}{{{{{x}’}}_{t}}}=frac{cos t}{4{{sin }^{2}}t}cdot frac{1}{-4sin tcos t}=-frac{1}{16}cdot frac{1}{{{sin }^{3}}t}]

[begin{align} {{{{y}”}}_{xx}} & ={{left( {{{{y}’}}_{x}} right)}^{prime }}_{x}=frac{{{left( {{{{y}’}}_{x}} right)}^{prime }}_{t}}{{{{{x}’}}_{t}}}= \ & =frac{cos t}{4{{sin }^{2}}t}cdot frac{1}{-4sin tcos t}= \ & =-frac{1}{16}cdot frac{1}{{{sin }^{3}}t} end{align}]

Вторая производная найдена.

Для сравнения посчитаем «производную» по неправильной формуле:

[frac{{{{{y}”}}_{tt}}}{{{{{x}”}}_{tt}}}=frac{{{left( {{{{y}’}}_{t}} right)}^{prime }}_{t}}{{{left( {{{{x}’}}_{t}} right)}^{prime }}_{t}}=frac{{{left( cos t right)}^{prime }}_{t}}{{{left( -2sin 2t right)}^{prime }}_{t}}=frac{-sin t}{-4cos 2t}=frac{1}{4}cdot frac{sin t}{cos 2t}]

[begin{align} frac{{{{{y}”}}_{tt}}}{{{{{x}”}}_{tt}}} & =frac{{{left( {{{{y}’}}_{t}} right)}^{prime }}_{t}}{{{left( {{{{x}’}}_{t}} right)}^{prime }}_{t}}=frac{{{left( cos t right)}^{prime }}_{t}}{{{left( -2sin 2t right)}^{prime }}_{t}}= \ & =frac{-sin t}{-4cos 2t}=frac{1}{4}cdot frac{sin t}{cos 2t} end{align}]

Получили совершенно другое выражение, которое не является второй производной.

Итак, вторая производная считается из первой ровно по той же формуле, по какой первая производная считается из исходной функции.

Пример 6. Найдите ${{{y}”}_{xx}}$, если

[left{ begin{align} & x={{text{e}}^{t}}+1 \ & y=left( {{t}^{2}}-2t+2 right)cdot {{text{e}}^{t}} \ end{align} right.]

Первая производная ${{{y}’}_{x}}$ через ${{{x}’}_{t}}$ и ${{{y}’}_{t}}$:

[begin{align} & {{{{x}’}}_{t}}={{text{e}}^{t}} \ & {{{{y}’}}_{t}}={{t}^{2}}cdot {{text{e}}^{t}} \ & {{{{y}’}}_{x}}=frac{{{{{y}’}}_{t}}}{{{{{x}’}}_{t}}}=frac{{{t}^{2}}cdot {{text{e}}^{t}}}{{{text{e}}^{t}}}={{t}^{2}} \ end{align}]

Вторая производная ${{{y}”}_{xx}}$ через ${{{x}’}_{t}}$ и ${{left( {{{{y}’}}_{x}} right)}^{prime }}_{t}$:

[begin{align} & {{left( {{{{y}’}}_{x}} right)}^{prime }}_{t}=2t \ & {{{{y}”}}_{xx}}={{left( {{{{y}’}}_{x}} right)}^{prime }}_{x}=frac{{{left( {{{{y}’}}_{x}} right)}^{prime }}_{t}}{{{{{x}’}}_{t}}}=frac{2t}{{{text{e}}^{t}}} \ end{align}]

Замечание. Когда освоитесь с основной формулой, выкладки можно сократить буквально до двух строк:

[begin{align} & {{{{y}’}}_{x}}=frac{{{{{y}’}}_{t}}}{{{{{x}’}}_{t}}}=frac{{{t}^{2}}cdot {{text{e}}^{t}}}{{{text{e}}^{t}}}={{t}^{2}} \ & {{{{y}”}}_{xx}}={{left( {{{{y}’}}_{x}} right)}^{prime }}_{x}=frac{{{left( {{{{y}’}}_{x}} right)}^{prime }}_{t}}{{{{{x}’}}_{t}}}=frac{2t}{{{text{e}}^{t}}} \ end{align}]

Впрочем, не стоит увлекаться сокращением выкладок, если у вас есть хоть малейшее сомнение или недопонимание на любом этапе вычислений.

Пара дополнительных минут — сомнительная экономия по сравнению с парой баллов на контрольной. И уж тем более по сравнению с недопониманием материала.

Пример 7. Найдите ${{{y}”}_{xx}}$, если

[left{ begin{align} & x={1}/{left( 1+{{t}^{2}} right)}; \ & y=2operatorname{arctg}t \ end{align} right.]

Дифференцирование арктангенса дробно-рациональной функции — довольно громоздкие действия. Тут в пару строк не уложиться.

1. Считаем ${{{x}’}_{t}}$ и ${{{y}’}_{t}}$:

[begin{align} & {{{{x}’}}_{t}}={{left( frac{1}{1+{{t}^{2}}} right)}^{prime }}_{t}=frac{-2t}{{{left( 1+{{t}^{2}} right)}^{2}}} \ & {{{{y}’}}_{t}}={{left( 2operatorname{arctg}t right)}^{prime }}_{t}=frac{2}{1+{{t}^{2}}} \ end{align}]

Первая производная ${{{y}’}_{x}}$:

[{{{y}’}_{x}}=frac{{{{{y}’}}_{t}}}{{{{{x}’}}_{t}}}=frac{2}{1+{{t}^{2}}}cdot frac{{{left( 1+{{t}^{2}} right)}^{2}}}{-2t}=-frac{1+{{t}^{2}}}{t}]

2. Считаем ${{left( {{{{y}’}}_{x}} right)}^{prime }}_{t}$:

[{{left( {{{{y}’}}_{x}} right)}^{prime }}_{t}=-frac{2tcdot t-left( 1+{{t}^{2}} right)}{{{t}^{2}}}=frac{1-{{t}^{2}}}{{{t}^{2}}}]

Вторая производная ${{{y}”}_{xx}}$:

[{{{y}”}_{xx}}={{left( {{{{y}’}}_{x}} right)}^{prime }}_{x}=frac{{{left( {{{{y}’}}_{x}} right)}^{prime }}_{t}}{{{{{x}’}}_{t}}}=frac{1-{{t}^{2}}}{{{t}^{2}}}cdot frac{{{left( 1+{{t}^{2}} right)}^{2}}}{-2t}=frac{{{left( 1+{{t}^{2}} right)}^{2}}left( {{t}^{2}}-1 right)}{2{{t}^{3}}}]

[begin{align} {{{{y}”}}_{xx}} & ={{left( {{{{y}’}}_{x}} right)}^{prime }}_{x}=frac{{{left( {{{{y}’}}_{x}} right)}^{prime }}_{t}}{{{{{x}’}}_{t}}}= \ & =frac{1-{{t}^{2}}}{{{t}^{2}}}cdot frac{{{left( 1+{{t}^{2}} right)}^{2}}}{-2t}= \ & =frac{{{left( 1+{{t}^{2}} right)}^{2}}left( {{t}^{2}}-1 right)}{2{{t}^{3}}} end{align}]

Замечание. При делении дробных выражений полезно заменять их умножением на обратное:

[frac{Aleft( x right)}{Bleft( x right)}:frac{Pleft( x right)}{Qleft( x right)}=frac{Aleft( x right)}{Bleft( x right)}cdot frac{Qleft( x right)}{Pleft( x right)}]

Именно так мы и поступили при вычислении ${{{y}’}_{x}}$ и ${{{y}”}_{xx}}$ в последнем примере. И не только в последнем.:)

4. Третья производная

Пример 8. Найдите производную третьего порядка ${{{y}”’}_{xxx}}$ для функции, заданной параметрически:

[left{ begin{align} & xleft( t right)={{text{e}}^{t}}left( cos t+sin t right) \ & yleft( t right)={{text{e}}^{t}}left( cos t-sin t right) \ end{align} right.]

Решение будет состоять из трёх шагов.

1. Найдём первую производную ${{{y}’}_{x}}$. Для этого считаем ${{{x}’}_{t}}$ и ${{{y}’}_{t}}$:

[begin{align} {{{{x}’}}_{t}} & =2cos tcdot {{text{e}}^{t}} \ {{{{y}’}}_{t}} & =-2sin tcdot {{text{e}}^{t}} \ end{align}]

Первая производная ${{{y}’}_{t}}$ равна

[{{{y}’}_{x}}=frac{{{{{y}’}}_{t}}}{{{{{x}’}}_{t}}}=frac{-2sin tcdot {{text{e}}^{t}}}{2cos tcdot {{text{e}}^{t}}}=-operatorname{tg}t]

2. Считаем вторую производную. При этом ${{{x}’}_{t}}$ уже посчитано, осталось найти ${{left( {{{{y}’}}_{x}} right)}^{prime }}_{t}$:

[{{left( {{{{y}’}}_{x}} right)}^{prime }}_{t}={{left( -operatorname{tg}t right)}^{prime }}_{t}=-frac{1}{{{cos }^{2}}t}]

Находим вторую производную по всё той же формуле:

[{{{y}”}_{xx}}={{left( {{{{y}’}}_{x}} right)}^{prime }}_{x}=frac{{{left( {{{{y}’}}_{x}} right)}^{prime }}_{t}}{{{{{x}’}}_{t}}}=-frac{1}{{{cos }^{2}}t}cdot frac{1}{2cos tcdot {{text{e}}^{t}}}=-frac{1}{2{{text{e}}^{t}}{{cos }^{3}}t}]

[begin{align} {{{{y}”}}_{xx}} & ={{left( {{{{y}’}}_{x}} right)}^{prime }}_{x}=frac{{{left( {{{{y}’}}_{x}} right)}^{prime }}_{t}}{{{{{x}’}}_{t}}}= \ & =-frac{1}{{{cos }^{2}}t}cdot frac{1}{2cos tcdot {{text{e}}^{t}}}= \ & =-frac{1}{2{{text{e}}^{t}}{{cos }^{3}}t} end{align}]

3. Считаем третью производную. Вновь нужно лишь найти ${{left( {{{{y}”}}_{xx}} right)}^{prime }}_{t}$:

[{{left( {{{{y}”}}_{xx}} right)}^{prime }}_{t}={{left( -frac{1}{2{{text{e}}^{t}}{{cos }^{3}}t} right)}^{prime }}_{t}=frac{cos t-3sin t}{2{{text{e}}^{t}}{{cos }^{4}}t}]

[begin{align} {{left( {{{{y}”}}_{xx}} right)}^{prime }}_{t} & ={{left( -frac{1}{2{{text{e}}^{t}}{{cos }^{3}}t} right)}^{prime }}_{t}= \ & =frac{cos t-3sin t}{2{{text{e}}^{t}}{{cos }^{4}}t} end{align}]

Для сокращения вычислений я сразу записал готовую формулу ${{left( {{{{y}”}}_{xx}} right)}^{prime }}_{t}$ — проверьте её самостоятельно. А дальше вновь используем формулу производной для параметрической функции:

[{{{y}”’}_{xxx}}=frac{{{left( {{{{y}”}}_{xx}} right)}^{prime }}_{t}}{{{{{x}’}}_{t}}}=frac{cos t-3sin t}{4{{text{e}}^{2t}}cdot {{cos }^{5}}t}]

Задача решена. Хотя вычислений получилось довольно много.

В любом случае помните главную формулу:

[{{{y}’}_{x}}left( x right)=frac{{{{{psi }’}}_{t}}left( t right)}{{{{{x}’}}_{t}}left( t right)}]

И помните, что вторая производная не равна частному вторых производных:

[{{{y}”}_{xx}}left( x right)ne frac{{{{{psi }”}}_{tt}}left( t right)}{{{{{x}”}}_{tt}}left( t right)}]

Попытка использовать эту формулу для нахождения производных высших порядков будет считаться грубой ошибкой.

Вот и вся теория. Теперь — за практику!:)

Смотрите также:

1. Частные производные для функции нескольких переменных
2. Формула полной вероятности
3. Тест по теории вероятностей (1 вариант)
4. Видеоурок по задачам C2: уравнение плоскости через определитель
5. Процент: неизвестно начальное значение (метод пропорции)
6. Производительность совместного труда

Лекция 6. Вторая производная, её геометрический и
физический смысл. Применение производной к исследованию функций и построению
графиков. Нахождение скорости для процесса, заданного формулой и графиком.

План

1. Производная
второго порядка.

2. Физический смысл
второй производной.

3. Геометрический
смысл второй производной. Точки перегиба.

4. Исследование функции на экстремум с помощью
второй производной.

5. Решение задач

(Учебник: Ш.А.
Алимов Алгебра и начала математического анализа 10-11 класс глава IX §53 стр. 283-286)

1. Производная
второго порядка.

Пусть функция y = f(x) определена на
интервале (a; b), и пусть в каждой
точке этого интервала она имеет производную ,   тогда  можно назвать первой
производной (или производной первого порядка) данной функции.

Рассмотрим функцию . Если   имеет производную в точке , то эту производную
называют второй производной (или производной второго порядка) данной
функции f(x) в точке  и обозначают .

Короче, вторая производная – это
производная от первой производной, т.е. .

Производная от , т.е. , называется третьей
производной (или производной третьего порядка) данной функции f(x) и т.д.

Определение. Вообще
n-й производной (или производного n-го
порядка) функции y = f(x) в точке x (или
на некотором интервале (a;b))
называется производная от производной (n-1)-го порядка в
этой точке x (или на этом интервале (a;b)). Она обозначается

Или .

Примеры

а) Если , то
 

 

 

 

б) если , то
 

 

 

 

 

 

и вообще

 если .

2. Физический
смысл второй производной.

Пусть
материальная точка движется прямолинейно и
 , – закон движения. Тогда
скорость  в данный момент времени  есть производная от пути  по времени , вычисленная для
момента .

 (1)

Ускорение  в данный момент времени есть производная от
скорости  по времени, вычисленная для момента .

. (2)

С другой стороны: .

. (3)

Физический смысл второй производной:

Ускорение  движения в данный
момент времени  есть вторая
производная от пути по времени.

Пример 1

Точка движется прямолинейно по закону . Найти величину скорости и
ускорения в момент времени .

Решение

Ответ:  м/с, .

3.
Геометрический смысл второй производной. Точки перегиба.

Условия выпуклости
и точки перегиба графика функции

График функции  имеет на интервале  выпуклость, направленную вниз, если он расположен не ниже любых
касательных, проведенных к графику функции (рис. 2.14а).

Выпуклость,
направленная вверх, будет, если график функции  на этом интервале расположен не выше любых касательных (рис. 2.14б).

Теорема. Если функция  имеет на интервале   вторую производную и она положительна , то функция выпукла вниз на этом интервале.

Если же , на интервале , то она выпукла вверх на этом интервале.

Точка
перегиба графика непрерывной функции  – это точка, при переходе через которую функция меняет направление
выпуклости.

Геометрическая
интерпретация: в точке перегиба касательная пересекает
график функции, так как он переходит с одной стороны касательной на другую,
«перегибаясь» через неё (рис. 2.15).

Точка x = 0 – точка перегиба кубической параболы

Теорема (необходимое
условие существования точки перегиба). Если  является точкой перегиба функции , то вторая производная, если она существует, должна обратиться в нуль:
.

Критические
точки – это точки графика, для которых .

Теорема
(достаточное условие существования точки перегиба).
Пусть функция  имеет вторую производную в окрестности точки . Эта точка  является точкой перегиба функции, если при переходе через неё вторая
производная  меняет знак.

Пример 2

Найти интервалы
выпуклости и точки перегиба функции .

Решение

Найдём ,

.

На интервале  , следовательно, функция  выпукла вниз на этом интервале.

На интервале   , следовательно, и на этом интервале функция  выпукла вниз.

На интервале   и, следовательно, функция  выпукла вверх.

Рассмотрим точку x = -1. При переходе через неё  меняет знак. Следовательно, x = -1 – это точка
перегиба данной функции.

Рассмотрим точку x = 1. Вторая производная   так же меняет знак. Точка x = 1 – точка перегиба
данной функции.

4. Исследование функции на экстремум с
помощью второй производной.

Часто бывает
рациональнее исследовать функцию на экстремум с помощью второй производной.

Правило
исследования функции на экстремум с помощью второй производной:

1. Находят первую
производную .

2. Приравняв к нулю
первую производную, находят действительные корни полученного уравнения (т.е.
критические значения).

3. Находят вторую
производную .

4. Во вторую
производную подставляют поочередно все критические значения; если при этой
подстановке вторая производная окажется положительной, то в этой точке функция
имеет минимум; если же вторая производная окажется отрицательной, то функция
имеет максимум.

5. Вычисляют
значения функции в точках максимума и минимума.

Замечание. Если при подстановке критического значения во вторую производную она
обратится в нуль, то ничего определенного относительно существования экстремума
сказать нельзя, а исследование нужно продолжить с помощью первой производной.

Пример 3

Исследовать на
экстремум с помощью второй производной функцию
 .

Решение

1. Находим
производную .

2. Из уравнения  находим критические значения.

.

3. Находим вторую
производную .

4. Знаки второй
производной в критических точках:

;

.

5. Вычислим
значения функции в точках минимума и максимума:

,

.

Ответ: функция имеет максимум в точке  и минимум в точке .

5. Задания для
самостоятельного решения

Задача 1. (1 балл) Найти производную третьего порядка функции  .      

Задача 2. (2 балла) Найдите точки перегиба кривой .

Задача 3. (2 балла) Найдите интервалы выпуклости вверх и интервалы выпуклости
вниз функции .

Задача 4. (3 балла) Исследовать на экстремум с помощью второй производной
функцию
 .

Задача 5. (2 балла) В момент времени t тело находится на
расстоянии  км от места отправления. Найти его ускорение через 2ч.

Вторая производная или производная второго порядка функции является производной от производной от . Грубо говоря, вторая производная измеряет, как изменяется скорость изменения самой величины; например, вторая производная положения объекта по времени — это мгновенное ускорение объекта или скорость изменения скорости объекта по времени. В нотации Лейбница:

где  — ускорение,  — скорость,  — время,  — положение объекта, d — мгновенная «дельта» или изменение. Последнее выражение является второй производной положения по времени.

На графике функции вторая производная соответствует кривизне или выпуклости графика. График функции с положительной второй производной на некотором участке является выпуклым вниз на этом участке, в то время как график функции с отрицательной второй производной на некотором участке изгибается в противоположную сторону на этом участке.

Обозначение[править | править код]

Вторая производная функции обычно обозначается ^[1][2]. То есть:

.

При использовании нотации Лейбница, частная вторая производная зависимой переменной по независимой переменной записывается как:

Данное обозначение получено из следующей формулы:

Вторая производная степенной функции[править | править код]

Взяв два раза производную, получается формула второй производной:

Пример[править | править код]

Дана функция

производная от  — функция

Вторая производная от является производной от , а именно

Вторая производная на графике[править | править код]

Выпуклость[править | править код]

Вторая производная функции может использоваться для определения выпуклости/вогнутости графика ^[2]. Функция, вторая производная которой положительна, будет выпуклой вниз (также называется вогнутой вверх), что означает, что касательная будет лежать ниже графика функции. Точно так же функция, у которой вторая производная отрицательна, будет выпукла вверх (также называется просто вогнутой вниз), а её касательные линии будут лежать над графиком функции.

Точки перегиба[править | править код]

Если вторая производная функции меняет знак, то график функции меняется с выпуклого вверх на выпуклый вниз или наоборот. Точка, в которой график уже не выпуклый вверх, но еще не выпуклый вниз, называется точкой перегиба. Если вторая производная непрерывна, она принимает нулевое значение в любой точке перегиба, однако стоит учитывать, что не каждая точка, в которой вторая производная равна нулю, обязательно является точкой перегиба.

Исследование стационарных точек[править | править код]

Связь второй производной и графика можно использовать для проверки того, является ли стационарная точка функции (то есть точка, где ) локальным максимумом или локальным минимумом. Более подробно:

Причину, по которой вторая производная дает такие результаты, можно понять с помощью аналогии с реальным миром. Рассмотрим транспортное средство, которое вначале движется вперед с большой скоростью, но с отрицательным ускорением. Ясно, что положение автомобиля в точке, где скорость достигает нуля, будет наибольшим расстоянием от начального положения — следующим шагом скорость станет отрицательной, и автомобиль начнет ехать в противоположную сторону. То же самое верно и для минимума, когда транспортное средство сначала имеет отрицательную скорость, но положительное ускорение.

Предел[править | править код]

Можно записать вторую производную при помощи всего одного предела:

Данный предел можно называть второй симметричной производной^[3][4]. Стоит обратить внимание, что вторая симметричная производная может существовать, даже если (обычная) вторая производная не существует.

Правую часть выражения можно записать в виде разностного отношения разностных отношений:

Этот предел можно рассматривать как непрерывную версию второй конечной разности^[en] для последовательностей.

Однако существование указанного выше предела не означает, что функция имеет вторую производную. Приведенный выше предел просто дает возможность вычислить вторую производную, но не дает представления о ее существовании. Контрпримером является функция , которая определяется как:

Функция разрывна в нуле, поэтому вторая производная для не существует. Но вышеуказанный предел существует для :

Квадратичная аппроксимация[править | править код]

Так же, как первая производная связана с линейной аппроксимацией, вторая производная связана с квадратичной аппроксимацией для функции . Эта квадратичная функция, первые и вторые производные которой такие же, как у в данной точке. Формула квадратичного приближения функции вокруг точки имеет вид

Эта квадратичная аппроксимация представляет собой ряд Тейлора второго порядка для функции с центром в точке x = a.

Собственные значения и собственные векторы второй производной[править | править код]

Для многих краевых задач можно получить явные формулы для собственных значений и собственных векторов оператора второй производной. Например, если предположить, что и заданы однородные граничные условия Дирихле (то есть ), то собственные значения и соответствующие собственные векторы (также называемые собственными функциями) равны . Здесь

Для других известных случаев см. собственные значения и собственные векторы второй производной^[en].

Обобщение на более высокие измерения[править | править код]

Гессиан[править | править код]

Вторая производная обобщается на более высокие измерения с помощью понятия вторых частных производных. Для функции есть три частные производные второго порядка:

,

и смешанные частные производные:

Если все эти производные непрерывны, то можно составить из них симметричную матрицу, известную как матрица Гессе. Собственные значения этой матрицы можно использовать для реализации многомерного аналога проверки второй производной.

Другим распространенным обобщением второй производной является лапласиан. Это дифференциальный оператор (или же ), определяется как:

Лапласиан функции равен дивергенции градиента и следу матрицы Гессе.

См. также[править | править код]

• Конечная разность, используемая для аппроксимации второй производной
• Проверка на точку перегиба^[en]
• Равенство смешанных производных

Примечания[править | править код]

Литература[править | править код]

Печатные ресурсы[править | править код]

• Anton, Howard; Bivens, Irl & Davis, Stephen (February 2, 2005), Calculus: Early Transcendentals Single and Multivariable (8th ed.), New York: Wiley, ISBN 978-0-471-47244-5
• Apostol, Tom M. (June 1967), Calculus, Vol. 1: One-Variable Calculus with an Introduction to Linear Algebra (2nd ed.), Wiley, ISBN 978-0-471-00005-1, <https://archive.org/details/calculus01apos>
• Apostol, Tom M. (June 1969), Calculus, Vol. 2: Multi-Variable Calculus and Linear Algebra with Applications (2nd ed.), Wiley, ISBN 978-0-471-00007-5, <https://archive.org/details/calculus01apos>
• Eves, Howard (January 2, 1990), An Introduction to the History of Mathematics (6th ed.), Brooks Cole, ISBN 978-0-03-029558-4
• Larson, Ron; Hostetler, Robert P. & Edwards, Bruce H. (February 28, 2006), Calculus: Early Transcendental Functions (4th ed.), Houghton Mifflin Company, ISBN 978-0-618-60624-5
• Spivak, Michael (September 1994), Calculus (3rd ed.), Publish or Perish, ISBN 978-0-914098-89-8
• Stewart, James (December 24, 2002), Calculus (5th ed.), Brooks Cole, ISBN 978-0-534-39339-7, <https://archive.org/details/calculus0000stew>
• Thompson, Silvanus P. (September 8, 1998), Calculus Made Easy^[en] (Revised, Updated, Expanded ed.), New York: St. Martin’s Press, ISBN 978-0-312-18548-0

Книги, доступные в интернете[править | править код]

• Crowell, Benjamin (2003), Calculus, <http://www.lightandmatter.com/calc/>
• Garrett, Paul (2004), Notes on First-Year Calculus, <http://www.math.umn.edu/~garrett/calculus/>
• Hussain, Faraz (2006), Understanding Calculus, <http://www.understandingcalculus.com/>
• Keisler, H. Jerome (2000), Elementary Calculus: An Approach Using Infinitesimals, <http://www.math.wisc.edu/~keisler/calc.html>
• Mauch, Sean (2004), Unabridged Version of Sean’s Applied Math Book, <http://www.its.caltech.edu/~sean/book/unabridged.html>
• Sloughter, Dan (2000), Difference Equations to Differential Equations, <http://synechism.org/drupal/de2de/>
• Strang, Gilbert (1991), Calculus, <http://ocw.mit.edu/ans7870/resources/Strang/strangtext.htm>
• Stroyan, Keith D. (1997), A Brief Introduction to Infinitesimal Calculus, <http://www.math.uiowa.edu/~stroyan/InfsmlCalculus/InfsmlCalc.htm>
• Wikibooks, Calculus, <http://en.wikibooks.org/wiki/Calculus>

Ссылки[править | править код]

• Дискретная вторая производная от неравномерно расположенных точек