Как найти вторую производную от числа

Решать физические задачи или примеры по математике совершенно невозможно без знаний о производной и методах ее вычисления. Производная – одно из важнейших понятий математического анализа. Этой фундаментальной теме мы и решили посвятить сегодняшнюю статью. Что такое производная, каков ее физический и геометрический смысл, как посчитать производную функции? Все эти вопросы можно объединить в один: как понять производную?

Ежедневная рассылка с полезной информацией для студентов всех направлений – на нашем телеграм-канале.

Геометрический и физический смысл производной

Пусть есть функция f(x), заданная в некотором интервале (a, b). Точки х и х0 принадлежат этому интервалу. При изменении х меняется и сама функция. Изменение аргумента – разность его значений х-х0. Эта разность записывается как дельта икс и называется приращением аргумента. Изменением или приращением функции называется разность значений функции в двух точках. Определение производной:

Производная функции в точке – предел отношения приращения функции в данной точке к приращению аргумента, когда последнее стремится к нулю.

Иначе это можно записать так:

Какой смысл в нахождении такого предела? А вот какой:

Геометрический смысл производной: производная от функции в точке равна тангенсу угла между осью OX и касательной к графику функции в данной точке.

Физический смысл производной: производная пути по времени равна скорости прямолинейного движения.

Действительно, еще со школьных времен всем известно, что скорость – это частное пути x=f(t) и времени t. Средняя скорость за некоторый промежуток времени:

Чтобы узнать скорость движения в момент времени t0 нужно вычислить предел:

Кстати, о том, что такое пределы и как их решать, читайте в нашей отдельной статье.

Приведем пример, иллюстрирующий практическое применение производной. Пусть тело движется то закону:

Нам нужно найти скорость в момент времени t=2c. Вычислим производную:

Правила нахождения производных

Сам процесс нахождения производной называется дифференцированием. Функция, которая имеет производную в данной точке, называется дифференцируемой.

Как найти производную? Согласно определению, нужно составить отношение приращения функции и аргумента, а затем вычислить предел при стремящемся к нулю приращении аргумента. Конечно, можно вычислять все производные так, но на практике это слишком долгий путь. Все уже давно посчитано до нас. Ниже приведем таблицу с производными элементарных функций, а затем рассмотрим правила вычисления производных, в том числе и производных сложных функций с подробными примерами.

Кстати! Для наших читателей сейчас действует скидка 10% на любой вид работы

Правило первое: выносим константу

Константу можно вынести за знак производной. Более того – это нужно делать. При решении примеров по математике возьмите за правило – если можете упростить выражение, обязательно упрощайте.

Пример. Вычислим производную:

Правило второе: производная суммы функций

Производная суммы двух функций равна сумме производных этих функций. То же самое справедливо и для производной разности функций.

Не будем приводить доказательство этой теоремы, а лучше рассмотрим практический пример.

Найти производную функции:

Решение:

Правило третье: производная произведения функций

Производная произведения двух дифференцируемых функций вычисляется по формуле:

Пример: найти производную функции:

Решение:

Здесь важно сказать о вычислении производных сложных функций. Производная сложной функции равна произведению производной этой функции по промежуточному аргументу на производную промежуточного аргумента по независимой переменной.

В вышеуказанном примере мы встречаем выражение:

В данном случае промежуточный аргумент – 8х в пятой степени. Для того, чтобы вычислить производную такого выражения сначала считаем производную внешней функции по промежуточному аргументу, а потом умножаем на производную непосредственно самого промежуточного аргумента по независимой переменной.

Правило четвертое: производная частного двух функций

Формула для определения производной от частного двух функций:

Пример:

Решение:

Мы постарались рассказать о производных для чайников с нуля. Эта тема не так проста, как кажется, поэтому предупреждаем: в примерах часто встречаются ловушки, так что будьте внимательны при вычислении производных.

С любым вопросом по этой и другим темам вы можете обратиться в студенческий сервис. За короткий срок мы поможем решить самую сложную контрольную и разобраться с заданиями, даже если вы никогда раньше не занимались вычислением производных.

Вторая производная

Всё
очень просто. Вторая производная –
это производная
от первой производной: 

Стандартные
обозначения второй производной: 
, 
 или 
 (дробь
читается так: «дэ два игрек по дэ икс
квадрат»). Чаще всего вторую производную
обозначают первыми двумя вариантами.
Но третий вариант тоже встречается,
причем, его очень любят включать в
условия контрольных заданий, например:
«Найдите 
 функции…».
А студент сидит и битый час чешет репу,
что это вообще такое.

Рассмотрим
простейший пример. Найдем вторую
производную от функции 
.

Для того чтобы
найти вторую производную, как многие
догадались, нужно сначала найти первую
производную:

Теперь находим
вторую производную:

Готово.

Рассмотрим более
содержательные примеры.

Пример 11

Найти
вторую производную функции 

Найдем
первую производную:

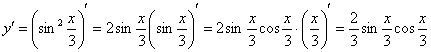
На
каждом шаге всегда смотрим, нельзя ли
что-нибудь упростить? Сейчас нам предстоит
дифференцировать произведение двух
функций, и мы избавимся от этой
неприятности, применив
известную тригонометрическую
формулу 
.
Точнее говоря, использовать формулу
будем в обратном направлении: 
:

Находим
вторую производную:

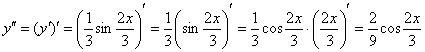
Готово.

Можно
было пойти другим путём – понизить
степень функции еще перед дифференцированием,
используя формулу 
:

Если интересно,
возьмите первую и вторую производные
снова. Результаты, естественно, совпадут.

Отмечу,
что понижение степени бывает очень
выгодно при нахождении частных
производных функции.
Здесь же оба способа решения будут
примерно одинаковой длины и сложности.

Как и
для первой производной, можно
рассмотреть задачу
нахождения второй производной в точке.

Например:
Вычислим значение найденной второй
производной в точке 
:

Необходимость
находить вторую производную и вторую
производную в точке возникает при
исследовании графика функции на
выпуклость/вогнутость и перегибы.

Пример 12

Найти
вторую производную функции 
.
Найти 

Это пример для
самостоятельного решения.

Аналогично можно
найти третью производную, а также
производные более высоких порядков.
Такие задания встречаются, но встречаются
значительно реже.

Решения
и ответы:

Пример
2: Найдем производную:

Вычислим
значение функции в точке 
:

Пример
4: Найдем производную:

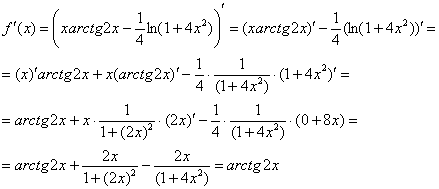
Вычислим
производную в заданной точке:

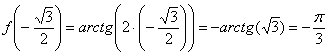
Пример
6: Уравнение касательной составим по
формуле 

1)
Вычислим значение функции в точке 
:

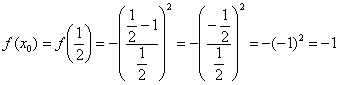
2)
Найдем производную. Перед дифференцированием
функцию выгодно упростить:

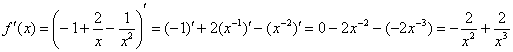
3)
Вычислим значение производной в
точке 
:

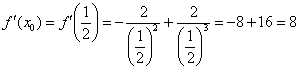
4)
Подставим значения 
, 
 и 
 в
формулу 
:

Пример
8: Преобразуем функцию:

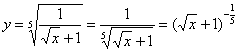
Найдем
производную:

Запишем
дифференциал:

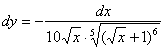
Пример
10: Найдем производную:

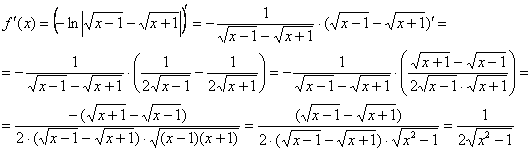
Запишем
дифференциал:

Вычислим
дифференциал в точке 
:

Пример
12: Найдем первую производную:

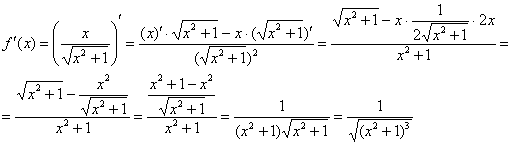
Найдем
вторую производную:

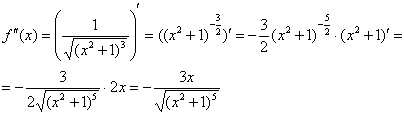
Вычислим: 

4. 2.Частные производные. Примеры решений

На
данном уроке мы познакомимся с понятием
функции двух переменных, а также подробно
рассмотрим наиболее распространенное
задание – нахождение частных
производныхпервого
и второго порядка, полного дифференциала
функции. Студенты-заочники, как правило,
сталкиваются с частными производными
на 1 курсе во 2 семестре. Причем, по моим
наблюдениям, задание на нахождение
частных производных практически всегда
встречается на экзамене.

Для
эффективного изучения нижеизложенного
материала Вам необходимо уметь
более или менее уверенно находить
«обычные» производные функции одной
переменной. Научиться правильно
обращаться с производными можно на
уроках Как
найти производную? иПроизводная
сложной функции.
Также нам потребуется таблица производных
элементарных функций и правил
дифференцирования, удобнее всего, если
она будет под рукой в распечатанном
виде. Раздобыть справочный материал
можно на страницеМатематические
формулы и таблицы.

Начнем
с самого понятия функции двух переменных,
я постараюсь ограничиться минимумом
теории, так как сайт имеет практическую
направленность. Функция двух переменных
обычно записывается как 
,
при этом переменные 
, 
 называются независимыми
переменными или аргументами.

Пример: 
 –
функция двух переменных.

Иногда
используют запись 
.
Также встречаются задания, где вместо
буквы 
 используется
буква 
.

Полезно
знать геометрический смысл функций.
Функции одной переменной 
 соответствует
определенная линия на плоскости,
например, 
  –
всем знакомая школьная парабола. Любая
функция двух переменных 
 с
геометрической точки зрения представляет
собой поверхность в трехмерном
пространстве (плоскости, цилиндры, шары,
параболоиды и т.д.). Но, собственно, это
уже аналитическая геометрия, а у нас на
повестке дня математический анализ.

Переходим
к вопросу нахождения частных производных
первого и второго порядков. Должен
сообщить хорошую новость для тех, кто
выпил несколько чашек кофе и настроился
на невообразимо трудный материал: частные
производные – это почти то же самое,
что и «обычные» производные функции
одной переменной. 

Для
частных производных справедливы все
правила дифференцирования и таблица
производных элементарных функций. Есть
только пара небольших отличий, с которыми
мы познакомимся прямо сейчас.

Пример 1

Найти
частные производные первого и второго
порядка функции 

Сначала найдем
частные производные первого порядка.
Их две.

Обозначения:

 или 
 –
частная производная по «икс»

 или 
 –
частная производная по «игрек»

Начнем
с 
. Когда
мы находим частную производную по «икс»,
то переменная 
 считается
константой (постоянным числом).

Решаем. На данном
уроке я буду приводить полное решение
сразу, а комментарии давать ниже.

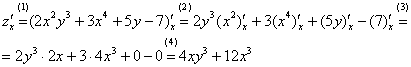
Комментарии к
выполненным действиям:

(1)
Первое, что мы делаем при нахождении
частной производной – заключаем всю функцию
в скобки под штрих с
подстрочным индексом.

Внимание,
важно! Подстрочные
индексы НЕ ТЕРЯЕМ по ходу решения. В
данном случае, если Вы где-нибудь
нарисуете «штрих» без 
,
то преподаватель, как минимум, может
поставить рядом с заданием 
 (сразу
откусить часть балла за невнимательность).

Далее данный шаг
комментироваться не будет, все сделанные
замечания справедливы для любого примера
по рассматриваемой теме.

(2)
Используем правила дифференцирования 
, 
.
Для простого примера, как этот, оба
правила вполне можно применить на одном
шаге. Обратите внимание на первое
слагаемое: так как 
 считается
константой, а любую константу можно
вынести за знак производной,
то 
 мы
выносим за скобки. То есть в данной
ситуации
 ничем
не лучше обычного числа. Теперь посмотрим
на третье слагаемое 
:
здесь, наоборот, выносить нечего. Так
как 
 константа,
то 
 –
тоже константа, и в этом смысле она ничем
не лучше последнего слагаемого –
«семерки».

(3)
Используем табличные производные 
 и 
.

(4) Упрощаем, или,
как я люблю говорить, «причесываем»
ответ.

Теперь 
. Когда
мы находим частную производную по
«игрек», то переменная 
 считается
константой (постоянным числом).

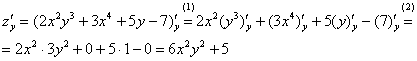
(1)
Используем те же правила дифференцирования 
, 
.
В первом слагаемом выносим константу 
 за
знак производной, во втором слагаемом
ничего вынести нельзя поскольку 
 –
уже константа.

(2)
Используем таблицу производным
элементарных функций. Мысленно
поменяем в таблице все «иксы» на «игреки».
То есть данная таблица рАвно справедлива
и для
 (да
и вообще почти для любой буквы). В
частности, используемые нами формулы
выглядят так: 
 и 
.

Итак, частные
производные первого порядка найдены

Подведем итог, чем
же отличается нахождение частных
производных от нахождения «обычных»
производных функции одной переменной:

1)
Когда мы находим частную
производную 
, переменная 
 считается
константой.

2)
Когда мы находим частную
производную 
, переменная 
 считается
константой.

3)
Правила и таблица производных элементарных
функций справедливы и применимы для
любой переменной (
, 
 либо
какой-нибудь другой), по которой ведется
дифференцирование.

Шаг второй. Находим
частные производные второго порядка.
Их четыре.

Обозначения:

 или 
 –
вторая производная по «икс»

 или 
 –
вторая производная по
«игрек»

 или 
 – смешанная производная
«икс по игрек»

 или 
 – смешанная производная
«игрек по икс»

В
понятии второй производной нет ничего
сложного. Говоря простым языком, вторая
производная – это производная от первой
производной.

Для
наглядности я перепишу уже найденные
частные производные первого порядка:

Сначала
найдем смешанные производные:

Как
видите, всё просто: берем частную
производную 
 и
дифференцируем ее еще раз, но в данном
случае – уже по «игрек».

Аналогично:

Для
практических примеров справедливо
следующее равенство: 

Таким образом,
через смешанные производные второго
порядка очень удобно проверить, а
правильно ли мы нашли частные производные
первого порядка.

Находим
вторую производную по «икс».

Никаких
изобретений, берем 
 и
дифференцируем её по «икс» еще раз:

Аналогично:

Следует
отметить, что при нахождении 
, 
 нужно
проявить повышенное
внимание, так как
никаких чудесных равенств для проверки
не существует.

Пример 2

Найти
частные производные первого и второго
порядка функции 

Это
пример для самостоятельного решения
(ответ в конце урока). Если возникли
трудности с дифференцированием корней,
рекомендую ознакомиться уроком Как
найти производную?

При определенном
опыте частные производные из примеров
№№1,2 будут решаться Вами устно.

Переходим к более
сложным примерам.

Пример 3

Найти
частные производные первого порядка
функции 
.
Проверить, что 
.
Записать полный дифференциал первого
порядка 
.

Решение:
Находим частные производные первого
порядка:

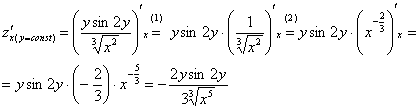
Обратите
внимание на подстрочный индекс: 
,
рядом с «иксом» не возбраняется в скобках
записывать, что 
 –
константа. Данная пометка может быть
очень полезна для начинающих, чтобы
легче было ориентироваться в решении.

Дальнейшие
комментарии:

(1)
Выносим все константы за знак производной.
В данном случае 
 и 
,
а, значит, и их произведение 
 считается
постоянным числом.

(2) Не забываем, как
правильно дифференцировать корни.

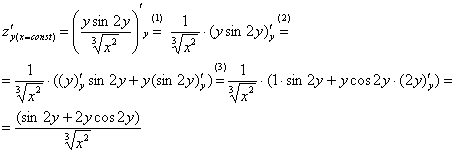
(1)
Выносим все константы за знак производной,
в данной случае константой является

.

(2) Под
штрихом у нас осталось произведение
двух функций, следовательно, нужно
использовать правило дифференцирования
произведения 
.

(3) Не
забываем, что

– это сложная функция (хотя и простейшая
из сложных). Используем соответствующее
правило:

.

Теперь находим
смешанные производные второго порядка:

,
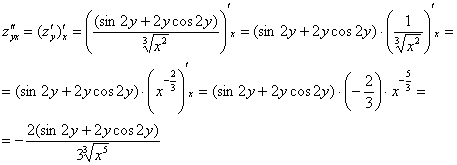
значит, все вычисления выполнены верно.

Запишем
полный дифференциал 
.
В контексте рассматриваемого задания
не имеет смысла рассказывать, что такое
полный дифференциал функции двух
переменных. Важно, что этот самый
дифференциал очень часто требуется
записать в практических задачах.

Полный
дифференциал первого порядка функции
двух переменных имеет вид:

В данном случае:

То
есть, в формулу нужно просто подставить
уже найденные частные производные
первого порядка. Значки дифференциалов 
 и 
 в
этой и похожих ситуациях по возможности
лучше записывать в числителях:

Пример 4

Найти
частные производные первого порядка
функции 
.
Проверить, что 
.
Записать полный дифференциал первого
порядка 
.

Это пример для
самостоятельного решения. Полное решение
и образец оформления задачи – в конце
урока.

Рассмотрим серию
примеров, включающих в себя сложные
функции.

Пример 5

Найти
частные производные первого порядка
функции

.

Записать
полный дифференциал 
.

Решение:

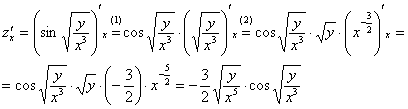
(1)
Применяем правило дифференцирования
сложной функции 
.
С урока Производная
сложной функции
следует помнить
очень важный момент: когда мы по таблице
превращаем синус (внешнюю функцию) в
косинус, то вложение

 (внутренняя
функция) у нас не
меняется.

(2)
Здесь используем свойство корней:

,
выносим константу

за знак производной, а корень

представляем в нужном для дифференцирования
виде.

Аналогично:

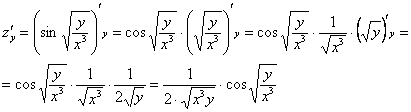
Запишем
полный дифференциал первого порядка:

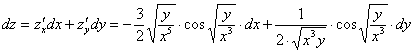
Пример 6

Найти
частные производные первого порядка
функции 
.

Записать
полный дифференциал 
.

Это пример для
самостоятельного решения (ответ в конце
урока). Полное решение не привожу, так
как оно достаточно простое

Довольно часто
все вышерассмотренные правила применяются
в комбинации.

Пример 7

Найти
частные производные первого порядка
функции 
.

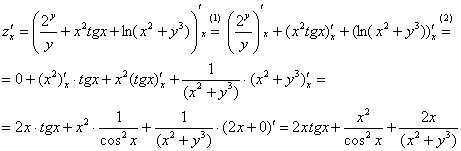
(1) Используем
правило дифференцирования суммы

(2)
Первое слагаемое  в данном случае
считается константой, поскольку в
выражении

нет ничего, зависящего от «икс» – только
«игреки».

(Знаете,
всегда приятно, когда дробь удается
превратить в ноль).

Для
второго слагаемого применяем правило
дифференцирования произведения. Кстати,
в этом смысле ничего бы не изменилось,
если бы вместо

была дана функция

– важно, что здесь произведение
двух функций, КАЖДАЯ
из которых зависит от
«икс»,
а поэтому, нужно использовать правило
дифференцирования произведения. Для
третьего слагаемого применяем правило
дифференцирования сложной функции.

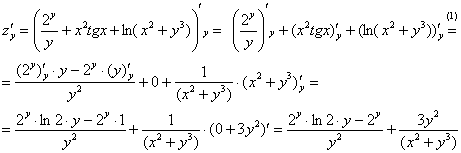
(1) В
первом слагаемом и в числителе и в
знаменателе содержится «игрек»,
следовательно, нужно использовать
правило дифференцирования частного: 
. 
Второе слагаемое зависит ТОЛЬКО от
«икс», значит, 
 считается
константой и превращается в ноль. Для
третьего слагаемого используем правило
дифференцирования сложной функции.

Для тех читателей,
которые мужественно добрались почти
до конца урока, расскажу старый
мехматовский анекдот для разрядки:

Однажды
в пространстве функций появилась злобная
производная и как пошла всех
дифференцировать. Все функции разбегаются
кто куда, никому не хочется превращаться!
И только одна функция никуда не убегает.
Подходит к ней производная и спрашивает:

– А
почему это ты от меня никуда не убегаешь?

– Ха.
А мне всё равно, ведь я «е в степени икс»,
и ты со мной ничего не сделаешь!

На
что злобная производная с коварной
улыбкой отвечает:

– Вот
здесь ты ошибаешься, я тебя продифференцирую
по «игрек», так что быть тебе нулем.

(Кто
понял анекдот, тот освоил производные,
минимум, на «тройку»).

Пример 8

Найти
частные производные первого порядка
функции

.

Это пример для
самостоятельного решения. Полное решение
и образец оформления задачи – в конце
урока.

Ну вот почти и всё.
Напоследок не могу не обрадовать
любителей математики еще одним примером.
Дело даже не в любителях, у всех разный
уровень математической подготовки –
встречаются люди (и не так уж редко),
которые любят потягаться с заданиями
посложнее. Хотя, последний на данном
уроке пример не столько сложный, сколько
громоздкий с точки зрения вычислений.

Пример 9

Дана
функция двух переменных 
.
Найти все частные производные первого
и второго порядков.

Это пример для
самостоятельного решения. Полное решение
и образец оформления где-то рядом.

Ответы:

Пример
2:

,


,


,

Пример
4: Ссылка для просмотра ниже.

Пример
6:

,


,

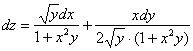
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #

  08.02.20157.31 Mб91.rtf

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Как находить производную от числа

Задача нахождения производной стоит как перед учениками старших классов школ, так и перед студентами. Для успешного дифференцирования требуется внимательно и аккуратно следовать определенным правилам и алгоритмам.

Вам понадобится

• – таблица производных;
• – правила дифференцирования.

Инструкция

Проанализируйте производную. Если она представляет собой произведение или сумму, разложите по известным правилам. В случае, если одно из слагаемых — число, воспользуйтесь формулами из пунктов 2-5 и 7.

Помните, что производная числа (константы) равна нулю. Производная по определению есть скорость изменения функции, а скорость изменения постоянной величины — нуль. При необходимости это доказывается с помощью определения производной, через пределы — приращение функции равно нулю, а нуль делить на приращение аргумента есть нуль. Следовательно, предел нуля тоже есть нуль.

Не забывайте, что, имея произведение постоянного множителя и переменной, можно вынести константу за знак производной и дифференцировать только оставшуюся функцию: (cU)’=cU’, где «c» – константа; «U» — любая функция.

Имея один из частных случаев производной дроби, когда в числителе вместо функции стоит число, воспользуйтесь формулой: производная равна минус произведению константы на производную знаменателя, деленное на стоящую в знаменателе функцию в квадрате: (c/U)’=(-c·U’)/U2.

Возьмите производную по второму следствию производной дроби: если константа стоит в знаменателе, а в числителе функция, то единица, деленная на константу, всё равно число, потому следует выносить число из-под знака производной и изменять только функцию: (U/c)’=(1/c)·U’.

Отличайте коэффициент перед аргументом («х») и перед функцией (f(x)). Если число стоит перед аргументом, то функция — сложная, и ее необходимо дифференцировать по правилам сложных функций.

Если имеете показательную функцию ах, в этом случае число возводится в степень переменной, и значит, нужно брать производную по формуле: (ах)’=lna·ах. Будьте осторожны и помните, что основанием показательной функции может быть любое положительное число отличное от единицы. Если основание показательной функции — число е, то формула примет вид: (ех)’=ех.

Видео по теме

Источники:

• Таблица производных
• производная числа

Войти на сайт

или

Забыли пароль?
Еще не зарегистрированы?

Основные функции

• : x^a

модуль x: abs(x)

Производные

Для того, чтобы найти производную функции
нужно написать в строке: f[x], x. Если Вам требуется
найти производную n-го порядка, то следует написать: f[x], {x, n}. В
том случае, если Вам требуется найти частную производную функции напишите в окне гаджета: f[x, y, z,…,t], j, где
— интересующая Вас переменная. Если нужно найти частную производную по
некоторой переменной порядка n, то следует ввести: f[x, y, z,…,t], {j,
n}, где означает тоже, что и Выше.

Важно подчеркнуть, что калькулятор выдает пошаговое нахождение
производной при нажатии на «Show Steps» в правом верхнем углу
выдаваемого ей ответа.

Примеры

• x*E^x, x;
• x^3*E^x, {x,17};
• x^3*y^2*Sin[x+y], x;
• x^3*y^2*Sin[x+y], y,
• x/(x+y^4), {x,6}.