Вторая производная или производная второго порядка функции 

где 





На графике функции вторая производная соответствует кривизне или выпуклости графика. График функции с положительной второй производной на некотором участке является выпуклым вниз на этом участке, в то время как график функции с отрицательной второй производной на некотором участке изгибается в противоположную сторону на этом участке.
Обозначение[править | править код]
Вторая производная функции 

.
При использовании нотации Лейбница, частная вторая производная зависимой переменной 

Данное обозначение получено из следующей формулы:
Вторая производная степенной функции[править | править код]
Взяв два раза производную, получается формула второй производной:
Пример[править | править код]
Дана функция
производная от 
Вторая производная от 

Вторая производная на графике[править | править код]
Выпуклость[править | править код]
Вторая производная функции 

Точки перегиба[править | править код]
Если вторая производная функции меняет знак, то график функции меняется с выпуклого вверх на выпуклый вниз или наоборот. Точка, в которой график уже не выпуклый вверх, но еще не выпуклый вниз, называется точкой перегиба. Если вторая производная непрерывна, она принимает нулевое значение в любой точке перегиба, однако стоит учитывать, что не каждая точка, в которой вторая производная равна нулю, обязательно является точкой перегиба.
Исследование стационарных точек[править | править код]
Связь второй производной и графика можно использовать для проверки того, является ли стационарная точка функции (то есть точка, где 
Причину, по которой вторая производная дает такие результаты, можно понять с помощью аналогии с реальным миром. Рассмотрим транспортное средство, которое вначале движется вперед с большой скоростью, но с отрицательным ускорением. Ясно, что положение автомобиля в точке, где скорость достигает нуля, будет наибольшим расстоянием от начального положения — следующим шагом скорость станет отрицательной, и автомобиль начнет ехать в противоположную сторону. То же самое верно и для минимума, когда транспортное средство сначала имеет отрицательную скорость, но положительное ускорение.
Предел[править | править код]
Можно записать вторую производную при помощи всего одного предела:
Данный предел можно называть второй симметричной производной[3][4]. Стоит обратить внимание, что вторая симметричная производная может существовать, даже если (обычная) вторая производная не существует.
Правую часть выражения можно записать в виде разностного отношения разностных отношений:
Этот предел можно рассматривать как непрерывную версию второй конечной разности[en] для последовательностей.
Однако существование указанного выше предела не означает, что функция 

Функция 


Квадратичная аппроксимация[править | править код]
Так же, как первая производная связана с линейной аппроксимацией, вторая производная связана с квадратичной аппроксимацией для функции 



Эта квадратичная аппроксимация представляет собой ряд Тейлора второго порядка для функции с центром в точке x = a.
Собственные значения и собственные векторы второй производной[править | править код]
Для многих краевых задач можно получить явные формулы для собственных значений и собственных векторов оператора второй производной. Например, если предположить, что ![{displaystyle xin [0,L]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d35e3fa30fa9d0e9f57923fb0101848d4fea625a)




Для других известных случаев см. собственные значения и собственные векторы второй производной[en].
Обобщение на более высокие измерения[править | править код]
Гессиан[править | править код]
Вторая производная обобщается на более высокие измерения с помощью понятия вторых частных производных. Для функции 
,
и смешанные частные производные:
Если все эти производные непрерывны, то можно составить из них симметричную матрицу, известную как матрица Гессе. Собственные значения этой матрицы можно использовать для реализации многомерного аналога проверки второй производной.
Другим распространенным обобщением второй производной является лапласиан. Это дифференциальный оператор 

Лапласиан функции равен дивергенции градиента и следу матрицы Гессе.
См. также[править | править код]
- Конечная разность, используемая для аппроксимации второй производной
- Проверка на точку перегиба[en]
- Равенство смешанных производных
Примечания[править | править код]
- ↑ Content – The second derivative. amsi.org.au. Дата обращения: 16 сентября 2020. Архивировано 24 марта 2022 года.
- ↑ 1 2 Second Derivatives (амер. англ.) (недоступная ссылка — история). Math24. Дата обращения: 16 сентября 2020.
- ↑ A. Zygmund. Trigonometric Series. — Cambridge University Press, 2002. — P. 22–23. — ISBN 978-0-521-89053-3.
- ↑ Thomson. Symmetric Properties of Real Functions. — Marcel Dekker, 1994. — ISBN 0-8247-9230-0.
Литература[править | править код]
Печатные ресурсы[править | править код]
- Anton, Howard; Bivens, Irl & Davis, Stephen (February 2, 2005), Calculus: Early Transcendentals Single and Multivariable (8th ed.), New York: Wiley, ISBN 978-0-471-47244-5
- Apostol, Tom M. (June 1967), Calculus, Vol. 1: One-Variable Calculus with an Introduction to Linear Algebra (2nd ed.), Wiley, ISBN 978-0-471-00005-1, <https://archive.org/details/calculus01apos>
- Apostol, Tom M. (June 1969), Calculus, Vol. 2: Multi-Variable Calculus and Linear Algebra with Applications (2nd ed.), Wiley, ISBN 978-0-471-00007-5, <https://archive.org/details/calculus01apos>
- Eves, Howard (January 2, 1990), An Introduction to the History of Mathematics (6th ed.), Brooks Cole, ISBN 978-0-03-029558-4
- Larson, Ron; Hostetler, Robert P. & Edwards, Bruce H. (February 28, 2006), Calculus: Early Transcendental Functions (4th ed.), Houghton Mifflin Company, ISBN 978-0-618-60624-5
- Spivak, Michael (September 1994), Calculus (3rd ed.), Publish or Perish, ISBN 978-0-914098-89-8
- Stewart, James (December 24, 2002), Calculus (5th ed.), Brooks Cole, ISBN 978-0-534-39339-7, <https://archive.org/details/calculus0000stew>
- Thompson, Silvanus P. (September 8, 1998), Calculus Made Easy[en] (Revised, Updated, Expanded ed.), New York: St. Martin’s Press, ISBN 978-0-312-18548-0
Книги, доступные в интернете[править | править код]
- Crowell, Benjamin (2003), Calculus, <http://www.lightandmatter.com/calc/>
- Garrett, Paul (2004), Notes on First-Year Calculus, <http://www.math.umn.edu/~garrett/calculus/>
- Hussain, Faraz (2006), Understanding Calculus, <http://www.understandingcalculus.com/>
- Keisler, H. Jerome (2000), Elementary Calculus: An Approach Using Infinitesimals, <http://www.math.wisc.edu/~keisler/calc.html>
- Mauch, Sean (2004), Unabridged Version of Sean’s Applied Math Book, <http://www.its.caltech.edu/~sean/book/unabridged.html>
- Sloughter, Dan (2000), Difference Equations to Differential Equations, <http://synechism.org/drupal/de2de/>
- Strang, Gilbert (1991), Calculus, <http://ocw.mit.edu/ans7870/resources/Strang/strangtext.htm>
- Stroyan, Keith D. (1997), A Brief Introduction to Infinitesimal Calculus, <http://www.math.uiowa.edu/~stroyan/InfsmlCalculus/InfsmlCalc.htm>
- Wikibooks, Calculus, <http://en.wikibooks.org/wiki/Calculus>
Ссылки[править | править код]
- Дискретная вторая производная от неравномерно расположенных точек
Лекция 6. Вторая производная, её геометрический и
физический смысл. Применение производной к исследованию функций и построению
графиков. Нахождение скорости для процесса, заданного формулой и графиком.
План
1. Производная
второго порядка.
2. Физический смысл
второй производной.
3. Геометрический
смысл второй производной. Точки перегиба.
4. Исследование функции на экстремум с помощью
второй производной.
5. Решение задач
(Учебник: Ш.А.
Алимов Алгебра и начала математического анализа 10-11 класс глава IX §53 стр. 283-286)
1. Производная
второго порядка.
Пусть функция y = f(x) определена на
интервале (a; b), и пусть в каждой
точке этого интервала она имеет производную , тогда
можно назвать первой
производной (или производной первого порядка) данной функции.
Рассмотрим функцию . Если
имеет производную в точке
, то эту производную
называют второй производной (или производной второго порядка) данной
функции f(x) в точке и обозначают
.
Короче, вторая производная – это
производная от первой производной, т.е. .
Производная от , т.е.
, называется третьей
производной (или производной третьего порядка) данной функции f(x) и т.д.
Определение. Вообще
n-й производной (или производного n-го
порядка) функции y = f(x) в точке x (или
на некотором интервале (a;b))
называется производная от производной (n-1)-го порядка в
этой точке x (или на этом интервале (a;b)). Она обозначается
Или .
Примеры
а) Если , то
б) если , то
и вообще
если
.
2. Физический
смысл второй производной.
Пусть
материальная точка движется прямолинейно и
, – закон движения. Тогда
скорость в данный момент времени
есть производная от пути
по времени
, вычисленная для
момента .
(1)
Ускорение в данный момент времени
есть производная от
скорости по времени
, вычисленная для момента
.
. (2)
С другой стороны: .
. (3)
Физический смысл второй производной:
Ускорение движения в данный
момент времени есть вторая
производная от пути по времени.
Пример 1
Точка движется прямолинейно по закону . Найти величину скорости и
ускорения в момент времени .
Решение
Ответ: м/с,
.
3.
Геометрический смысл второй производной. Точки перегиба.
Условия выпуклости
и точки перегиба графика функции
 |
График функции имеет на интервале
выпуклость, направленную вниз, если он расположен не ниже любых
касательных, проведенных к графику функции (рис. 2.14а).
Выпуклость,
направленная вверх, будет, если график функции на этом интервале расположен не выше любых касательных (рис. 2.14б).
Теорема. Если функция имеет на интервале
вторую производную и она положительна
, то функция выпукла вниз на этом интервале.
Если же , на интервале
, то она выпукла вверх на этом интервале.
Точка
перегиба графика непрерывной функции – это точка, при переходе через которую функция меняет направление
выпуклости.
Геометрическая
интерпретация: в точке перегиба касательная пересекает
график функции, так как он переходит с одной стороны касательной на другую,
«перегибаясь» через неё (рис. 2.15).

Теорема (необходимое
условие существования точки перегиба). Если является точкой перегиба функции
, то вторая производная, если она существует, должна обратиться в нуль:
.
Критические
точки – это точки графика, для которых .
Теорема
(достаточное условие существования точки перегиба).
Пусть функция имеет вторую производную в окрестности точки
. Эта точка
является точкой перегиба функции, если при переходе через неё вторая
производная меняет знак.
Пример 2
Найти интервалы
выпуклости и точки перегиба функции .
Решение
Найдём ,
.
На интервале
, следовательно, функция
выпукла вниз на этом интервале.
На интервале
, следовательно, и на этом интервале функция
выпукла вниз.
На интервале
и, следовательно, функция
выпукла вверх.
Рассмотрим точку x = -1. При переходе через неё меняет знак. Следовательно, x = -1 – это точка
перегиба данной функции.
Рассмотрим точку x = 1. Вторая производная так же меняет знак. Точка x = 1 – точка перегиба
данной функции.
4. Исследование функции на экстремум с
помощью второй производной.
Часто бывает
рациональнее исследовать функцию на экстремум с помощью второй производной.
Правило
исследования функции на экстремум с помощью второй производной:
1. Находят первую
производную .
2. Приравняв к нулю
первую производную, находят действительные корни полученного уравнения (т.е.
критические значения).
3. Находят вторую
производную .
4. Во вторую
производную подставляют поочередно все критические значения; если при этой
подстановке вторая производная окажется положительной, то в этой точке функция
имеет минимум; если же вторая производная окажется отрицательной, то функция
имеет максимум.
5. Вычисляют
значения функции в точках максимума и минимума.
Замечание. Если при подстановке критического значения во вторую производную она
обратится в нуль, то ничего определенного относительно существования экстремума
сказать нельзя, а исследование нужно продолжить с помощью первой производной.
Пример 3
Исследовать на
экстремум с помощью второй производной функцию
.
Решение
1. Находим
производную .
2. Из уравнения находим критические значения.
.
3. Находим вторую
производную .
4. Знаки второй
производной в критических точках:
;
.
5. Вычислим
значения функции в точках минимума и максимума:
,
.
Ответ: функция имеет максимум в точке и минимум в точке
.
5. Задания для
самостоятельного решения
Задача 1. (1 балл) Найти производную третьего порядка функции .
Задача 2. (2 балла) Найдите точки перегиба кривой .
Задача 3. (2 балла) Найдите интервалы выпуклости вверх и интервалы выпуклости
вниз функции .
Задача 4. (3 балла) Исследовать на экстремум с помощью второй производной
функцию
.
Задача 5. (2 балла) В момент времени t тело находится на
расстоянии км от места отправления. Найти его ускорение через 2ч.
Производная второго порядка
Содержание:
- Производная второго порядка
- Производная второго порядка. Пройденный путь, скорость, ускорение
- Задача пример №101
- Задача пример №102
Производная второго порядка
Производная второго порядка. Пройденный путь, скорость, ускорение
Пусть для функции 




Известно, что производная показывает мгновенное изменение. Мгновенное изменение пройденного пути в зависимости от времени является скоростью. Отсюда становится ясным физический смысл производной. При прямолинейном движении по закону 

Скорость также изменяется в зависимости от времени. Изменение скорости выражается новой величиной, называемой ускорением. Вообще, находя производную функции зависимости пройденного пути от времени, находят функцию скорости. Находя производную от функции скорости получаем ускорение. Т.е. получая два раза подряд производную от функции пройденного пути можно найти ускорение:
Из физики известно, что и скорость, и ускорение являются векторными величинами. Если скорость и ускорение имеют одинаковые знаки, то движение ускоренное, если знаки разные, то движение замедленное. Производная второго порядка используется для решения ряда экономических задач, в том числе задач, моделирующих реальные жизненные ситуации. Умение приблизительно определить является ли скорость изменения положительной или отрицательной имеет важное практическое значение.
Задача пример №101
Найдите производную второго порядка у.
а) 
Решение: a) 

b)


Задача пример №102
Для функции пройденного пути 




Решение:
Из графика 


В интервалах (0; 2) и (6; 8) угловой коэффициент касательной к графику функции 




Из графика функции 

На интервале [0; 4) угловой коэффициент касательной к графику функции v(t) отрицателен, а на интервале (4; 8) угловой коэффициент положителен и функция 
Эта лекция взята из раздела решения задач по математике, там вы найдёте другие лекци по всем темам математики:
Другие темы которые вам помогут понять математику:
|
|
|
|
Лекции:
- Метод Жордана Гаусса
- Некоторые простые неявные функции
- Рациональные числа
- Предел числовой последовательности
- Пересекающиеся прямые
- Метод интервалов
- Обратная матрица примеры решения
- Дифференцирование функций, заданных неявно и параметрически
- Полярная система координат: примеры решения
- Сходимость функционального ряда
Решать физические задачи или примеры по математике совершенно невозможно без знаний о производной и методах ее вычисления. Производная – одно из важнейших понятий математического анализа. Этой фундаментальной теме мы и решили посвятить сегодняшнюю статью. Что такое производная, каков ее физический и геометрический смысл, как посчитать производную функции? Все эти вопросы можно объединить в один: как понять производную?
Ежедневная рассылка с полезной информацией для студентов всех направлений – на нашем телеграм-канале.
Геометрический и физический смысл производной
Пусть есть функция f(x), заданная в некотором интервале (a, b). Точки х и х0 принадлежат этому интервалу. При изменении х меняется и сама функция. Изменение аргумента – разность его значений х-х0. Эта разность записывается как дельта икс и называется приращением аргумента. Изменением или приращением функции называется разность значений функции в двух точках. Определение производной:
Производная функции в точке – предел отношения приращения функции в данной точке к приращению аргумента, когда последнее стремится к нулю.
Иначе это можно записать так:
Какой смысл в нахождении такого предела? А вот какой:
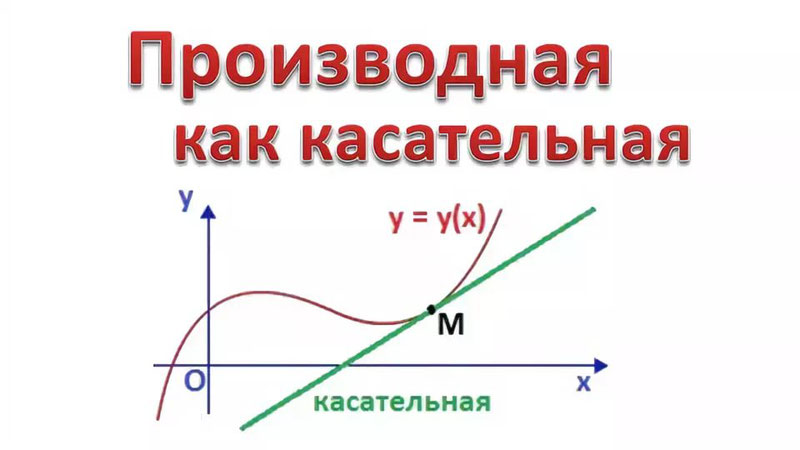
Геометрический смысл производной: производная от функции в точке равна тангенсу угла между осью OX и касательной к графику функции в данной точке.
Физический смысл производной: производная пути по времени равна скорости прямолинейного движения.
Действительно, еще со школьных времен всем известно, что скорость – это частное пути x=f(t) и времени t. Средняя скорость за некоторый промежуток времени:
Чтобы узнать скорость движения в момент времени t0 нужно вычислить предел:
Кстати, о том, что такое пределы и как их решать, читайте в нашей отдельной статье.
Приведем пример, иллюстрирующий практическое применение производной. Пусть тело движется то закону:
Нам нужно найти скорость в момент времени t=2c. Вычислим производную:
Правила нахождения производных
Сам процесс нахождения производной называется дифференцированием. Функция, которая имеет производную в данной точке, называется дифференцируемой.
Как найти производную? Согласно определению, нужно составить отношение приращения функции и аргумента, а затем вычислить предел при стремящемся к нулю приращении аргумента. Конечно, можно вычислять все производные так, но на практике это слишком долгий путь. Все уже давно посчитано до нас. Ниже приведем таблицу с производными элементарных функций, а затем рассмотрим правила вычисления производных, в том числе и производных сложных функций с подробными примерами.
Кстати! Для наших читателей сейчас действует скидка 10% на любой вид работы
Правило первое: выносим константу
Константу можно вынести за знак производной. Более того – это нужно делать. При решении примеров по математике возьмите за правило – если можете упростить выражение, обязательно упрощайте.
Пример. Вычислим производную:
Правило второе: производная суммы функций
Производная суммы двух функций равна сумме производных этих функций. То же самое справедливо и для производной разности функций.
Не будем приводить доказательство этой теоремы, а лучше рассмотрим практический пример.
Найти производную функции:
Решение:
Правило третье: производная произведения функций
Производная произведения двух дифференцируемых функций вычисляется по формуле:
Пример: найти производную функции:
Решение:
Здесь важно сказать о вычислении производных сложных функций. Производная сложной функции равна произведению производной этой функции по промежуточному аргументу на производную промежуточного аргумента по независимой переменной.
В вышеуказанном примере мы встречаем выражение:
В данном случае промежуточный аргумент – 8х в пятой степени. Для того, чтобы вычислить производную такого выражения сначала считаем производную внешней функции по промежуточному аргументу, а потом умножаем на производную непосредственно самого промежуточного аргумента по независимой переменной.
Правило четвертое: производная частного двух функций
Формула для определения производной от частного двух функций:
Пример:
Решение:
Мы постарались рассказать о производных для чайников с нуля. Эта тема не так проста, как кажется, поэтому предупреждаем: в примерах часто встречаются ловушки, так что будьте внимательны при вычислении производных.
С любым вопросом по этой и другим темам вы можете обратиться в студенческий сервис. За короткий срок мы поможем решить самую сложную контрольную и разобраться с заданиями, даже если вы никогда раньше не занимались вычислением производных.
From Wikipedia, the free encyclopedia
A time derivative is a derivative of a function with respect to time, usually interpreted as the rate of change of the value of the function.[1] The variable denoting time is usually written as 
Notation[edit]
A variety of notations are used to denote the time derivative. In addition to the normal (Leibniz’s) notation,
A very common short-hand notation used, especially in physics, is the ‘over-dot’. I.E.
(This is called Newton’s notation)
Higher time derivatives are also used: the second derivative with respect to time is written as
with the corresponding shorthand of 
As a generalization, the time derivative of a vector, say:
is defined as the vector whose components are the derivatives of the components of the original vector. That is,
Use in physics[edit]
Time derivatives are a key concept in physics. For example, for a changing position 


A large number of fundamental equations in physics involve first or second time derivatives of quantities. Many other fundamental quantities in science are time derivatives of one another:
- force is the time derivative of momentum
- power is the time derivative of energy
- electric current is the time derivative of electric charge
and so on.
A common occurrence in physics is the time derivative of a vector, such as velocity or displacement. In dealing with such a derivative, both magnitude and orientation may depend upon time.
Example: circular motion[edit]
For example, consider a particle moving in a circular path. Its position is given by the displacement vector 
For this example, we assume that θ = t. Hence, the displacement (position) at any time t is given by
This form shows the motion described by r(t) is in a circle of radius r because the magnitude of r(t) is given by
using the trigonometric identity sin2(t) + cos2(t) = 1 and where 
With this form for the displacement, the velocity now is found. The time derivative of the displacement vector is the velocity vector. In general, the derivative of a vector is a vector made up of components each of which is the derivative of the corresponding component of the original vector. Thus, in this case, the velocity vector is:
Thus the velocity of the particle is nonzero even though the magnitude of the position (that is, the radius of the path) is constant. The velocity is directed perpendicular to the displacement, as can be established using the dot product:
Acceleration is then the time-derivative of velocity:
The acceleration is directed inward, toward the axis of rotation. It points opposite to the position vector and perpendicular to the velocity vector. This inward-directed acceleration is called centripetal acceleration.
In differential geometry[edit]
In differential geometry, quantities are often expressed with respect to the local covariant basis, 




where 


as well as:
In terms of the covariant derivative, 
Use in economics[edit]
In economics, many theoretical models of the evolution of various economic variables are constructed in continuous time and therefore employ time derivatives.[3]: ch. 1-3 One situation involves a stock variable and its time derivative, a flow variable. Examples include:
- The flow of net fixed investment is the time derivative of the capital stock.
- The flow of inventory investment is the time derivative of the stock of inventories.
- The growth rate of the money supply is the time derivative of the money supply divided by the money supply itself.
Sometimes the time derivative of a flow variable can appear in a model:
- The growth rate of output is the time derivative of the flow of output divided by output itself.
- The growth rate of the labor force is the time derivative of the labor force divided by the labor force itself.
And sometimes there appears a time derivative of a variable which, unlike the examples above, is not measured in units of currency:
- The time derivative of a key interest rate can appear.
- The inflation rate is the growth rate of the price level—that is, the time derivative of the price level divided by the price level itself.
See also[edit]
- Differential calculus
- Notation for differentiation
- Circular motion
- Centripetal force
- Spatial derivative
- Temporal rate
References[edit]
- ^ Chiang, Alpha C., Fundamental Methods of Mathematical Economics, McGraw-Hill, third edition, 1984, ch. 14, 15, 18.
- ^ Grinfeld, Pavel. “Tensor Calculus 6d: Velocity, Acceleration, Jolt and the New δ/δt-derivative”. YouTube. Archived from the original on 2021-12-13.
- ^ See for example Romer, David (1996). Advanced Macroeconomics. McGraw-Hill. ISBN 0-07-053667-8.





![{displaystyle {frac {d^{2}}{dx^{2}}}left[x^{n}right]={frac {d}{dx}}{frac {d}{dx}}left[x^{n}right]={frac {d}{dx}}left[nx^{n-1}right]=n{frac {d}{dx}}left[x^{n-1}right]=n(n-1)x^{n-2}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8337b61f3135c31b26a72a371265dc1197e6315a)


















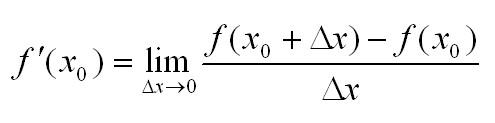
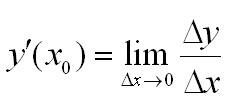
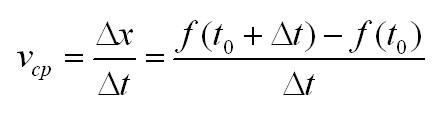
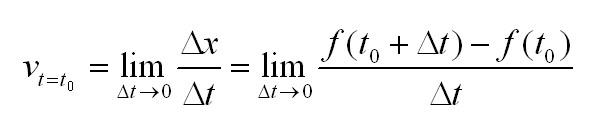
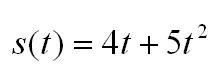
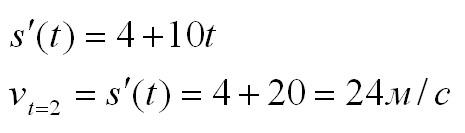
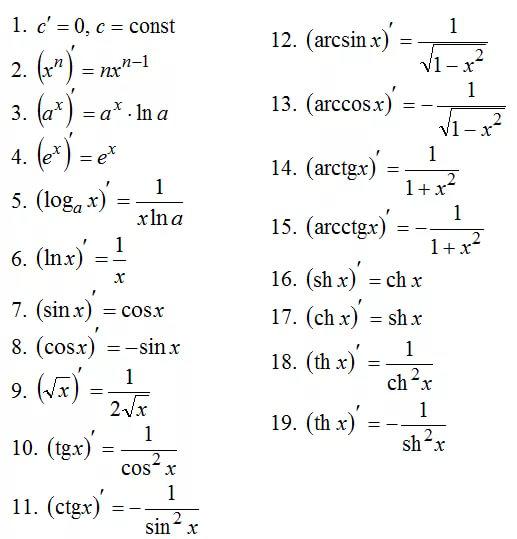
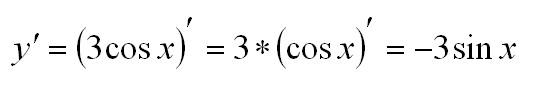
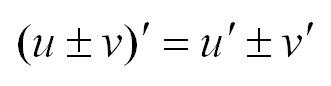
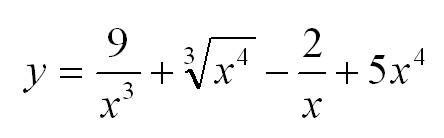
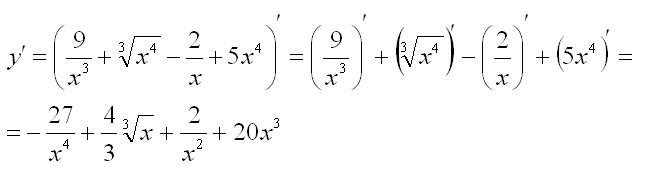
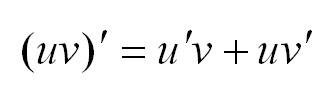
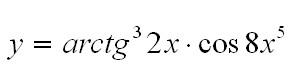
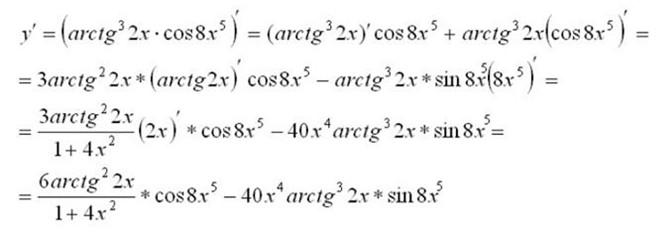
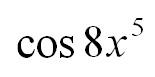
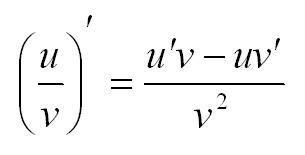
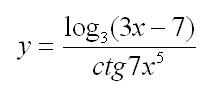
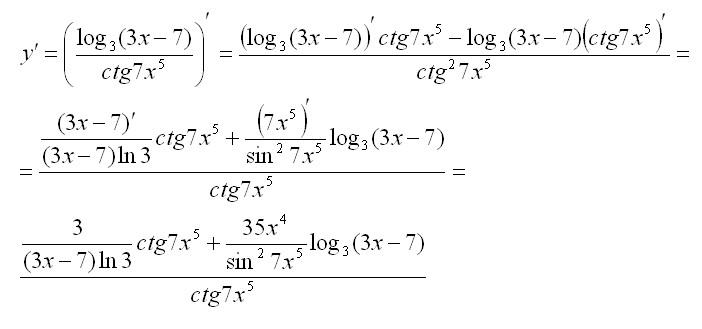


![{displaystyle mathbf {v} =left[v_{1}, v_{2}, v_{3},ldots right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/68dfa5814b9db087a469264531cd6a72a34305a5)
![{displaystyle {frac {dmathbf {v} }{dt}}=left[{frac {dv_{1}}{dt}},{frac {dv_{2}}{dt}},{frac {dv_{3}}{dt}},ldots right].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/920d22bf6c5750867769364cf644a2fbe7245905)




![begin{align}
mathbf{v}(t) = frac {d,mathbf{r}(t) }{dt} &= r left[frac{d, cos(t)}{dt}, frac{d, sin(t)}{dt} right] \
&= r [ -sin(t), cos(t)] \
&= [-y (t), x(t)].
end{align}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2430c683f9ec15ff667b1689397d12fb54568fca)
![mathbf{v} cdot mathbf{r} = [-y, x] cdot [x, y] = -yx + xy = 0, .](https://wikimedia.org/api/rest_v1/media/math/render/svg/fb7ed48b27b1ee26f840146fcc93fc1e6f08186e)
![mathbf{a}(t) = frac {d, mathbf{v}(t)}{dt} = [-x(t), -y(t)] = -mathbf{r}(t), .](https://wikimedia.org/api/rest_v1/media/math/render/svg/d393d537ee16a061158073b64746fcc022b4a1b6)




