Как найти вторую смешанную производную функции - Сайт, где вы сможете решить свои вопросы

Смешанная частная производная

Как найти?

Постановка задачи

Найти смешанную частную производную второго порядка функции $ z = f(x_1,x_2) $

План решения

Смешанная частная производная второго порядка функции $ z = f(x_1,x_2) $ по переменным $ x_1 $ и $ x_2 $ обозначается: $ frac{partial^2 z}{partial x_1 partial x_2} $ или $ z”_{x_1 x_2} $

Порядок дифференцирования не имеет значения, то есть выполняется свойство:

$$ frac{partial^2 z}{partial x_1 partial x_2} = frac{partial^2 z}{partial x_1 partial x_2} $$

$$ z”_{xy} = z”_{yx} $$

Фиксируем $ x_2 $. Считая функцию $ z = f(x_1,x_2) $ одной переменной от $ x_1 $ находим её производную $ z’_{x_1} $
Фиксируем $ x_1 $ и по правилу дифференцирования функции одной переменной находим производную функции $ z = f(x_1,x_2) $ по $ x_2 $ и получаем $ z”_{x_1 x_2} $

Примеры решений

Пример 1

Найти смешанную частную производную функции $ z(x,y) = ln (x+y) $

Решение

Фиксируем переменную $ x $ и находим производную по $ y $:

$$ z’_y = frac{1}{x+y} cdot (x+y)’_y = frac{1}{x+y} $$

Считая переменную $ y $ постоянной дифференцируем функцию $ z’_y $ по $ x $:

$$ z”_{yx} = -frac{1}{(x+y)^2} cdot (x+y)’_x = -frac{1}{(x+y)^2} $$

Если не получается решить свою задачу, то присылайте её к нам. Мы предоставим подробное решение онлайн. Вы сможете ознакомиться с ходом вычисления и почерпнуть информацию. Это поможет своевременно получить зачёт у преподавателя!

Ответ

$$ z”_{xy} = z”_{yx} = -frac{1}{(x+y)^2} $$

Пример 2

Найти смешанную производную функции $ z(x,y) = sin x cos y $

Решение

Фиксируем переменную $ y $ и выполняем дифференцирование по $ x $:

$$ z’_x (y = const) = cos x cos y $$

Считаем постоянной $ x $ и находим производную по $ y $:

$$ z’_{xy} (x = const) = -cos x sin y $$

Ответ

$$ z’_{xy} = z’_{yx} = -cos x sin y $$

Источник

Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 19 февраля 2016 года; проверки требуют 4 правки.

Определение[править | править код]

Пусть функция , и её частные производные

${displaystyle {frac {partial f}{partial x}},;{frac {partial f}{partial y}}}$

определены в некоторой окрестности точки $(x_{0},;y_{0})$ .
Тогда предел

${displaystyle lim _{Delta yto 0}{frac {displaystyle {{frac {partial f(x_{0},y_{0}+Delta y)}{partial x}}-{frac {partial f(x_{0},;y_{0})}{partial x}}}}{Delta y}},}$

если он существует, называется смешанной (смежной) производной функции f(x,;y) в точке $(x_{0},;y_{0})$ и обозначается ${displaystyle {frac {partial ^{2}f(x_{0},;y_{0})}{partial ypartial x}}}$ .

Аналогично определяется ${displaystyle {frac {partial ^{2}f(x_{0},;y_{0})}{partial xpartial y}}}$ как

${displaystyle lim _{Delta xto 0}{frac {displaystyle {{frac {partial f(x_{0}+Delta x,;y_{0})}{partial y}}-{frac {partial f(x_{0},;y_{0})}{partial y}}}}{Delta x}},}$

если он существует.

Смешанные частные производные порядка большего двух определяются индуктивно.^{[уточнить]}

Обозначение[править | править код]

${displaystyle {frac {partial ^{2}f}{partial ypartial x}}={frac {partial ^{2}z}{partial ypartial x}}=f''_{yx}=z''_{yx}}$
${displaystyle {frac {partial ^{2}f}{partial xpartial y}}={frac {partial ^{2}z}{partial xpartial y}}=f''_{xy}=z''_{xy}}$

Свойства[править | править код]

Если смешанные производные непрерывны в точке, то имеет место равенство ${displaystyle {frac {partial ^{2}f}{partial xpartial y}}={frac {partial ^{2}f}{partial ypartial x}}}$ .

Пример Шварца[править | править код]

${displaystyle f(x,;y)={begin{cases}displaystyle {xy{frac {x^{2}-y^{2}}{x^{2}+y^{2}}}},quad x^{2}+y^{2}>0\0,quad x=y=0end{cases}}Rightarrow {frac {partial ^{2}f(0,;0)}{partial xpartial y}}=-1neq 1={frac {partial ^{2}f(0,;0)}{partial ypartial x}}}$

То есть смешанные производные в примере Шварца не равны.

Имеет место теорема о равенстве смешанных производных

Теорема Шварца[править | править код]

Пусть выполнены условия:

функции ${displaystyle z=f(x,;y),;{frac {partial f}{partial x}},;{frac {partial f}{partial y}},;{frac {partial ^{2}f}{partial xpartial y}},;{frac {partial ^{2}f}{partial ypartial x}}}$ определены в некоторой окрестности точки $(x_{0},;y_{0})$ .
${displaystyle {frac {partial ^{2}f}{partial xpartial y}},;{frac {partial ^{2}f}{partial ypartial x}}}$ непрерывны в точке $(x_{0},;y_{0})$ .

Тогда ${displaystyle {frac {partial ^{2}f(x_{0},;y_{0})}{partial xpartial y}}={frac {partial ^{2}f(x_{0},;y_{0})}{partial ypartial x}}}$ , то есть смешанные производные второго порядка равны в каждой точке, где они непрерывны.

Теорема Шварца о равенстве смешанных частных производных индуктивно распространяется на смешанные частные производные высших порядков, при условии, что они непрерывны.

Тем не менее, условие непрерывности смешанных производных отнюдь не является необходимым в теореме Шварца.

Пример[править | править код]

${displaystyle f(x,;y)={begin{cases}displaystyle {frac {x^{2}y^{2}}{x^{2}+y^{2}}},quad x^{2}+y^{2}>0\0,quad x=y=0end{cases}}Rightarrow }$ смешанные производные второго порядка равны всюду (в том числе и в точке ), однако частные производные второго порядка не являются непрерывными в точке

Доказательство

Так как ,
то ${displaystyle {frac {partial f}{partial x}}(0,;0)={frac {partial f}{partial y}}(0,;0)=0}$

В остальных точках

${displaystyle {frac {partial f}{partial x}}(x,;y)={frac {2xy^{4}}{(x^{2}+y^{2})^{2}}}}$

${displaystyle {frac {partial f}{partial y}}(x,;y)={frac {2x^{4}y}{(x^{2}+y^{2})^{2}}}}$

Таким образом,

${displaystyle {frac {partial f}{partial x}}(x,;0)=0;forall xin mathbb {R} }$

${displaystyle {frac {partial f}{partial x}}(0,;y)=0;forall yin mathbb {R} }$

Следовательно,

${displaystyle {frac {partial ^{2}f(x_{0},;y_{0})}{partial xpartial y}}={frac {partial ^{2}f(x_{0},;y_{0})}{partial ypartial x}}=0}$

При

${displaystyle {frac {partial ^{2}f(x_{0},;y_{0})}{partial xpartial y}}={frac {partial ^{2}f(x_{0},;y_{0})}{partial ypartial x}}={frac {8x^{3}y^{3}}{(x^{2}+y^{2})^{3}}}}$

Легко видеть, что вторая смешанная производная имеет разрыв в точке , так как

${displaystyle lim _{xto 0}{frac {partial ^{2}f}{partial xpartial y}}(x,;x)=1}$ , а, например,

${displaystyle lim _{xto 0}{frac {partial ^{2}f}{partial xpartial y}}(x,;-x)=-1}$

^[1].

Примечания[править | править код]

↑ Тер-Крикоров А. М., Шабунин М. И. Глава 5. Функции многих переменных // Курс математического анализа. — 2-е изд. — М.: МФТИ, 1997. — С. 283. — 716 с. — ISBN 5-89155-006-7.

Источник

Вторая производная

Всё
очень просто. Вторая производная –
это производная
от первой производной:

Стандартные
обозначения второй производной:
,
или
(дробь
читается так: «дэ два игрек по дэ икс
квадрат»). Чаще всего вторую производную
обозначают первыми двумя вариантами.
Но третий вариант тоже встречается,
причем, его очень любят включать в
условия контрольных заданий, например:
«Найдите
функции…».
А студент сидит и битый час чешет репу,
что это вообще такое.

Рассмотрим
простейший пример. Найдем вторую
производную от функции
.

Для того чтобы
найти вторую производную, как многие
догадались, нужно сначала найти первую
производную:

Теперь находим
вторую производную:

Готово.

Рассмотрим более
содержательные примеры.

Пример 11

Найти
вторую производную функции

Найдем
первую производную:

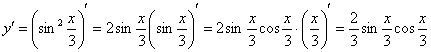
На
каждом шаге всегда смотрим, нельзя ли
что-нибудь упростить? Сейчас нам предстоит
дифференцировать произведение двух
функций, и мы избавимся от этой
неприятности, применив
известную тригонометрическую
формулу
.
Точнее говоря, использовать формулу
будем в обратном направлении:
:

Находим
вторую производную:

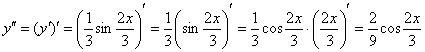
Готово.

Можно
было пойти другим путём – понизить
степень функции еще перед дифференцированием,
используя формулу
:

Если интересно,
возьмите первую и вторую производные
снова. Результаты, естественно, совпадут.

Отмечу,
что понижение степени бывает очень
выгодно при нахождении частных
производных функции.
Здесь же оба способа решения будут
примерно одинаковой длины и сложности.

Как и
для первой производной, можно
рассмотреть задачу
нахождения второй производной в точке.

Например:
Вычислим значение найденной второй
производной в точке
:

Необходимость
находить вторую производную и вторую
производную в точке возникает при
исследовании графика функции на
выпуклость/вогнутость и перегибы.

Пример 12

Найти
вторую производную функции
.
Найти

Это пример для
самостоятельного решения.

Аналогично можно
найти третью производную, а также
производные более высоких порядков.
Такие задания встречаются, но встречаются
значительно реже.

Решения
и ответы:

Пример
2: Найдем производную:

Вычислим
значение функции в точке
:

Пример
4: Найдем производную:

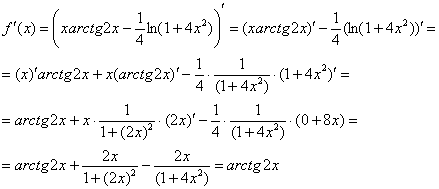
Вычислим
производную в заданной точке:

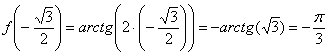
Пример
6: Уравнение касательной составим по
формуле

1)
Вычислим значение функции в точке
:

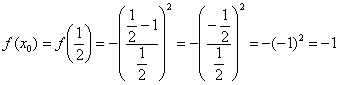
2)
Найдем производную. Перед дифференцированием
функцию выгодно упростить:

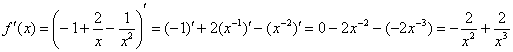
3)
Вычислим значение производной в
точке
:

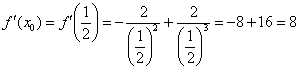
4)
Подставим значения
,
и
в
формулу
:

Пример
8: Преобразуем функцию:

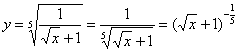
Найдем
производную:

Запишем
дифференциал:

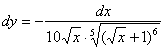
Пример
10: Найдем производную:

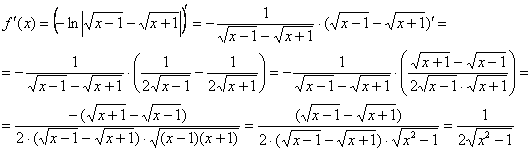
Запишем
дифференциал:

Вычислим
дифференциал в точке
:

Пример
12: Найдем первую производную:

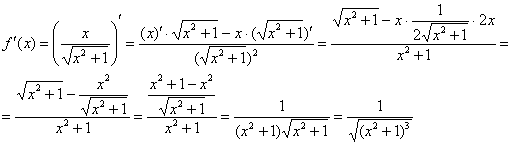
Найдем
вторую производную:

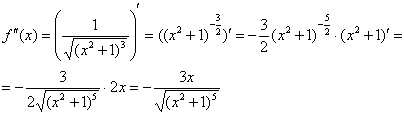
Вычислим:

4. 2.Частные производные. Примеры решений

На
данном уроке мы познакомимся с понятием
функции двух переменных, а также подробно
рассмотрим наиболее распространенное
задание – нахождение частных
производныхпервого
и второго порядка, полного дифференциала
функции. Студенты-заочники, как правило,
сталкиваются с частными производными
на 1 курсе во 2 семестре. Причем, по моим
наблюдениям, задание на нахождение
частных производных практически всегда
встречается на экзамене.

Для
эффективного изучения нижеизложенного
материала Вам необходимо уметь
более или менее уверенно находить
«обычные» производные функции одной
переменной. Научиться правильно
обращаться с производными можно на
уроках Как
найти производную? иПроизводная
сложной функции.
Также нам потребуется таблица производных
элементарных функций и правил
дифференцирования, удобнее всего, если
она будет под рукой в распечатанном
виде. Раздобыть справочный материал
можно на страницеМатематические
формулы и таблицы.

Начнем
с самого понятия функции двух переменных,
я постараюсь ограничиться минимумом
теории, так как сайт имеет практическую
направленность. Функция двух переменных
обычно записывается как
,
при этом переменные
,
называются независимыми
переменными или аргументами.

Пример:
–
функция двух переменных.

Иногда
используют запись
.
Также встречаются задания, где вместо
буквы
используется
буква
.

Полезно
знать геометрический смысл функций.
Функции одной переменной
соответствует
определенная линия на плоскости,
например,
–
всем знакомая школьная парабола. Любая
функция двух переменных
с
геометрической точки зрения представляет
собой поверхность в трехмерном
пространстве (плоскости, цилиндры, шары,
параболоиды и т.д.). Но, собственно, это
уже аналитическая геометрия, а у нас на
повестке дня математический анализ.

Переходим
к вопросу нахождения частных производных
первого и второго порядков. Должен
сообщить хорошую новость для тех, кто
выпил несколько чашек кофе и настроился
на невообразимо трудный материал: частные
производные – это почти то же самое,
что и «обычные» производные функции
одной переменной.

Для
частных производных справедливы все
правила дифференцирования и таблица
производных элементарных функций. Есть
только пара небольших отличий, с которыми
мы познакомимся прямо сейчас.

Пример 1

Найти
частные производные первого и второго
порядка функции

Сначала найдем
частные производные первого порядка.
Их две.

Обозначения:

или
–
частная производная по «икс»

или
–
частная производная по «игрек»

Начнем
с
. Когда
мы находим частную производную по «икс»,
то переменная
считается
константой (постоянным числом).

Решаем. На данном
уроке я буду приводить полное решение
сразу, а комментарии давать ниже.

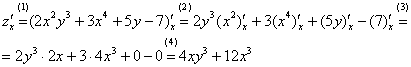
Комментарии к
выполненным действиям:

(1)
Первое, что мы делаем при нахождении
частной производной – заключаем всю функцию
в скобки под штрих с
подстрочным индексом.

Внимание,
важно! Подстрочные
индексы НЕ ТЕРЯЕМ по ходу решения. В
данном случае, если Вы где-нибудь
нарисуете «штрих» без
,
то преподаватель, как минимум, может
поставить рядом с заданием
(сразу
откусить часть балла за невнимательность).

Далее данный шаг
комментироваться не будет, все сделанные
замечания справедливы для любого примера
по рассматриваемой теме.

(2)
Используем правила дифференцирования
,
.
Для простого примера, как этот, оба
правила вполне можно применить на одном
шаге. Обратите внимание на первое
слагаемое: так как
считается
константой, а любую константу можно
вынести за знак производной,
то
мы
выносим за скобки. То есть в данной
ситуации
ничем
не лучше обычного числа. Теперь посмотрим
на третье слагаемое
:
здесь, наоборот, выносить нечего. Так
как
константа,
то
–
тоже константа, и в этом смысле она ничем
не лучше последнего слагаемого –
«семерки».

(3)
Используем табличные производные
и
.

(4) Упрощаем, или,
как я люблю говорить, «причесываем»
ответ.

Теперь
. Когда
мы находим частную производную по
«игрек», то переменная
считается
константой (постоянным числом).

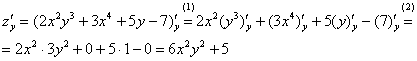
(1)
Используем те же правила дифференцирования
,
.
В первом слагаемом выносим константу
за
знак производной, во втором слагаемом
ничего вынести нельзя поскольку
–
уже константа.

(2)
Используем таблицу производным
элементарных функций. Мысленно
поменяем в таблице все «иксы» на «игреки».
То есть данная таблица рАвно справедлива
и для
(да
и вообще почти для любой буквы). В
частности, используемые нами формулы
выглядят так:
и
.

Итак, частные
производные первого порядка найдены

Подведем итог, чем
же отличается нахождение частных
производных от нахождения «обычных»
производных функции одной переменной:

1)
Когда мы находим частную
производную
, переменная
считается
константой.

2)
Когда мы находим частную
производную
, переменная
считается
константой.

3)
Правила и таблица производных элементарных
функций справедливы и применимы для
любой переменной (
,
либо
какой-нибудь другой), по которой ведется
дифференцирование.

Шаг второй. Находим
частные производные второго порядка.
Их четыре.

Обозначения:

или
–
вторая производная по «икс»

или
–
вторая производная по
«игрек»

или
– смешанная производная
«икс по игрек»

или
– смешанная производная
«игрек по икс»

В
понятии второй производной нет ничего
сложного. Говоря простым языком, вторая
производная – это производная от первой
производной.

Для
наглядности я перепишу уже найденные
частные производные первого порядка:

Сначала
найдем смешанные производные:

Как
видите, всё просто: берем частную
производную
и
дифференцируем ее еще раз, но в данном
случае – уже по «игрек».

Аналогично:

Для
практических примеров справедливо
следующее равенство:

Таким образом,
через смешанные производные второго
порядка очень удобно проверить, а
правильно ли мы нашли частные производные
первого порядка.

Находим
вторую производную по «икс».

Никаких
изобретений, берем
и
дифференцируем её по «икс» еще раз:

Аналогично:

Следует
отметить, что при нахождении
,
нужно
проявить повышенное
внимание, так как
никаких чудесных равенств для проверки
не существует.

Пример 2

Найти
частные производные первого и второго
порядка функции

Это
пример для самостоятельного решения
(ответ в конце урока). Если возникли
трудности с дифференцированием корней,
рекомендую ознакомиться уроком Как
найти производную?

При определенном
опыте частные производные из примеров
№№1,2 будут решаться Вами устно.

Переходим к более
сложным примерам.

Пример 3

Найти
частные производные первого порядка
функции
.
Проверить, что
.
Записать полный дифференциал первого
порядка
.

Решение:
Находим частные производные первого
порядка:

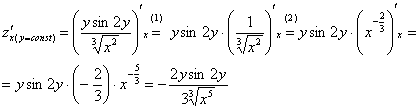
Обратите
внимание на подстрочный индекс:
,
рядом с «иксом» не возбраняется в скобках
записывать, что
–
константа. Данная пометка может быть
очень полезна для начинающих, чтобы
легче было ориентироваться в решении.

Дальнейшие
комментарии:

(1)
Выносим все константы за знак производной.
В данном случае
и
,
а, значит, и их произведение
считается
постоянным числом.

(2) Не забываем, как
правильно дифференцировать корни.

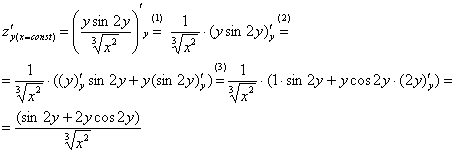
(1)
Выносим все константы за знак производной,
в данной случае константой является

(2) Под
штрихом у нас осталось произведение
двух функций, следовательно, нужно
использовать правило дифференцирования
произведения
.

(3) Не
забываем, что

– это сложная функция (хотя и простейшая
из сложных). Используем соответствующее
правило:

Теперь находим
смешанные производные второго порядка:

,
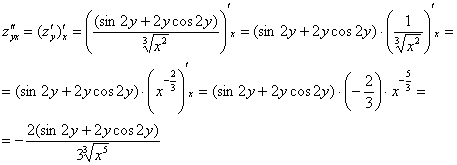
значит, все вычисления выполнены верно.

Запишем
полный дифференциал
.
В контексте рассматриваемого задания
не имеет смысла рассказывать, что такое
полный дифференциал функции двух
переменных. Важно, что этот самый
дифференциал очень часто требуется
записать в практических задачах.

Полный
дифференциал первого порядка функции
двух переменных имеет вид:

В данном случае:

То
есть, в формулу нужно просто подставить
уже найденные частные производные
первого порядка. Значки дифференциалов
и
в
этой и похожих ситуациях по возможности
лучше записывать в числителях:

Пример 4

Это пример для
самостоятельного решения. Полное решение
и образец оформления задачи – в конце
урока.

Рассмотрим серию
примеров, включающих в себя сложные
функции.

Пример 5

Найти
частные производные первого порядка
функции

.

Записать
полный дифференциал
.

Решение:

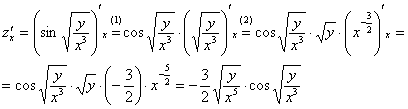
(1)
Применяем правило дифференцирования
сложной функции
.
С урока Производная
сложной функции
следует помнить
очень важный момент: когда мы по таблице
превращаем синус (внешнюю функцию) в
косинус, то вложение

(внутренняя
функция) у нас не
меняется.

(2)
Здесь используем свойство корней:

,
выносим константу

за знак производной, а корень

представляем в нужном для дифференцирования
виде.

Аналогично:

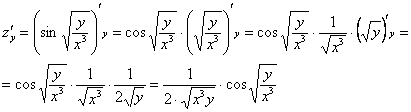
Запишем
полный дифференциал первого порядка:

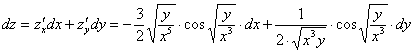
Пример 6

Найти
частные производные первого порядка
функции
.

Записать
полный дифференциал
.

Это пример для
самостоятельного решения (ответ в конце
урока). Полное решение не привожу, так
как оно достаточно простое

Довольно часто
все вышерассмотренные правила применяются
в комбинации.

Пример 7

Найти
частные производные первого порядка
функции
.

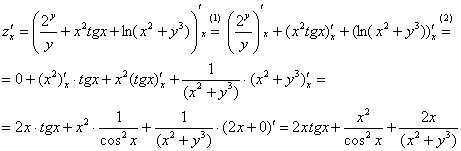
(1) Используем
правило дифференцирования суммы

(2)
Первое слагаемое в данном случае
считается константой, поскольку в
выражении

нет ничего, зависящего от «икс» – только
«игреки».

(Знаете,
всегда приятно, когда дробь удается
превратить в ноль).

Для
второго слагаемого применяем правило
дифференцирования произведения. Кстати,
в этом смысле ничего бы не изменилось,
если бы вместо

была дана функция

– важно, что здесь произведение
двух функций, КАЖДАЯ
из которых зависит от
«икс»,
а поэтому, нужно использовать правило
дифференцирования произведения. Для
третьего слагаемого применяем правило
дифференцирования сложной функции.

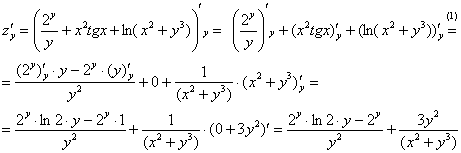
(1) В
первом слагаемом и в числителе и в
знаменателе содержится «игрек»,
следовательно, нужно использовать
правило дифференцирования частного:
.
Второе слагаемое зависит ТОЛЬКО от
«икс», значит,
считается
константой и превращается в ноль. Для
третьего слагаемого используем правило
дифференцирования сложной функции.

Для тех читателей,
которые мужественно добрались почти
до конца урока, расскажу старый
мехматовский анекдот для разрядки:

Однажды
в пространстве функций появилась злобная
производная и как пошла всех
дифференцировать. Все функции разбегаются
кто куда, никому не хочется превращаться!
И только одна функция никуда не убегает.
Подходит к ней производная и спрашивает:

– А
почему это ты от меня никуда не убегаешь?

– Ха.
А мне всё равно, ведь я «е в степени икс»,
и ты со мной ничего не сделаешь!

На
что злобная производная с коварной
улыбкой отвечает:

– Вот
здесь ты ошибаешься, я тебя продифференцирую
по «игрек», так что быть тебе нулем.

(Кто
понял анекдот, тот освоил производные,
минимум, на «тройку»).

Пример 8

Найти
частные производные первого порядка
функции

.

Это пример для
самостоятельного решения. Полное решение
и образец оформления задачи – в конце
урока.

Ну вот почти и всё.
Напоследок не могу не обрадовать
любителей математики еще одним примером.
Дело даже не в любителях, у всех разный
уровень математической подготовки –
встречаются люди (и не так уж редко),
которые любят потягаться с заданиями
посложнее. Хотя, последний на данном
уроке пример не столько сложный, сколько
громоздкий с точки зрения вычислений.

Пример 9

Дана
функция двух переменных
.
Найти все частные производные первого
и второго порядков.

Это пример для
самостоятельного решения. Полное решение
и образец оформления где-то рядом.

Ответы:

Пример
2:

,

,

,

Пример
4: Ссылка для просмотра ниже.

Пример
6:

,

,

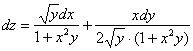
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
08.02.20157.31 Mб91.rtf
#
#
#
#
#
#
#
#
#
#

Источник

Смешанная производная

Содержание:

Теорема 10.4 (о равенстве смешанных производных):
Доказательство:

Пусть функция определена и имеет частные производные и во всех точках множества . Тогда и сами являются функциями двух переменных, и, стало быть, можно определить их частные производные:

Они называются частными производными второго порядка функции .

Точно таким же образом можно определить частные производные -го порядка для произвольного натурального . Они называются частными производными высших порядков. — примеры частных производных высших порядков. Здесь возникает естественный вопрос: равны ли между собой частные производные второго порядка и , которые называются смешанными производными?

Ответ на этот вопрос в общем случае отрицательный. Однако справедлива следующая теорема.

По этой ссылке вы найдёте полный курс лекций по высшей математике:

Теорема 10.4 (о равенстве смешанных производных):

Пусть функция и ее частные производные

определены в некоторой окрестности точки , причем и непрерывны в точке . Тогда в точке .

Доказательство:

Составим смешанные частные приращения функции :

(109)

Учитывая последнее равенство и применяя теорему Лагранжа по переменной к функции на промежутке , получим , (10.10)

где .

Применение теоремы Лагранжа правомерно, поскольку по предположению теоремы существует частная производная в достаточно малой окрестности точки . Так как такое же предположение верно и для частной смешанной производной то, снова применяя теорему Лагранжа на промежутке , из (10.10) получим , (10.11) где . Поскольку по условию теоремы функция непрерывна в точке , то последнее равенство можно записать в следующей форме: , (10.12) где при и . Из (10.12) следует, что . (10.13) Совершенно аналогично можно доказать, что

. (10.14) Из последних двух равенств в силу (10.9) следует утверждение теоремы.

Возможно вам будут полезны данные страницы:

Замечание 10.2.

В последней теореме условие непрерывности смешанных производных является существенным. То есть при отсутствии этого условия смешанные производные могут быть различными в данной точке .

Действительно, рассмотрим функцию и докажем, что ее смешанные частные производные в точке (0,0) не равны друг другу. Действительно,

Теперь вычислим вторые производные: Осталось заметить, что смешанные частные производные разрывны в точке (0,0). В самом деле, например, при . Следовательно, . А это значит, что не является непрерывной в точке (0,0).