Как найти вторую степень множества - Сайт, где вы сможете решить свои вопросы

Рассмотрим
декартово произведение

,
в котором декартовы сомножители
совпадают:

.
Обозначим каждое из этих множеств через

.
Тогда декартово произведение

представляет собой декартову

степень множества

Декартова
степень множества

с показателем степени

представляет собой множество упорядоченных

.
Высказывательная форма множества

имеет вид:

Пример 2.9

Рассмотрим
множество

.
Найдём для него вторую декартову степень:

Аналогично
можно задать множество, представляющее
слбой третью декартову степень множества

Если
число элементов множества

обозначить как

,
то

.

2.8. Сечение и проекция

Сначала
разберём понятие проекции. Рассмотрим
некоторое множество

и

.
В соответствии с определением элемент

представляет собой упорядоченную пару

,
первый элемент которой принадлежит
множеству

,
а второй – множеству

,

.
Элемент

является проекцией множества

на множество

и обозначается

,
а

проекцией множества

на множество

и обозначается

.

Рассмотрим
множество Е, которое представляет
собой подмножество множества

:

.

Можно
говорить о проекции подмножества E
на множества

Проекцией
множества

на множество

называется множество тех элементов,
которые являются проекциями всех
элементов множества

на множество

.
Высказывательная форма проекций
множества

на множества

записывается в виде:

,

.

Пример 2.10

Рассмотрим
множества

и

.
Множество

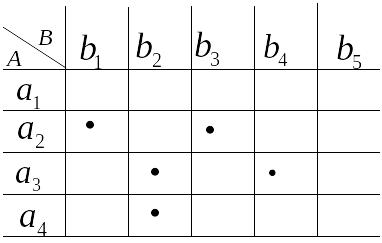
зададим таблицей 2.1.

Зададим
множество

методом перечисления его элементов:

Тогда
если

,
то

,

,

Таблица 2.1

Декартово произведение

Пример 2.11

Декартово
произведение

.
Если

представляют собой множества действительных
чисел, то геометрической интерпретацией
множества

является множество точек плоскости

(рис 2.10.).

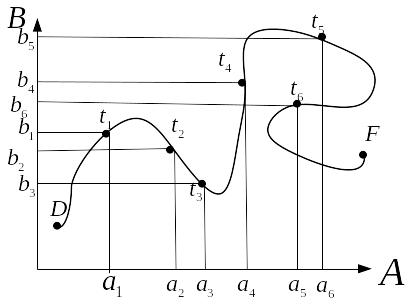
Рис. 2.10. Множество

для примера 1

Рассмотрим
подмножество

,
представляющее собой некоторую кривую

и множество

,
в свою очередь являющееся подмножеством

,

.
Проекциями множества

на множества

являются следующие множества:

,

.

Множество

может представлять собой декартово
произведение множеств, число которых
больше двух:

Если
рассмотреть некоторое подмножество
этого множества

,
то можно говорить о проекции этого
множества на множество

Разберём
понятие сечения. Рассмотрим некоторый
элемент

из множества

.
Тогда сечение множества

элементом

называется множество элементов из

,
которые составляют упорядоченную пару
из множества

Аналогично
можно рассматривать сечение множества

элементом

:

.

Пример 2.12

Рассмотрим
множества

и множество

,
заданное таблицей 2.1. Тогда сечением
множества

элементом

является множество

,
а сечением множества

элементом

является множество

.

Рассмотрим
понятие сечения, когда множество

является подмножеством множества

Тогда
сечение множества

элементом

представляет собой множество, задаваемое
высказывательной формой:

Можно
говорить о сечении множества

более сложным элементом, представляющим
собой упорядоченное множество

:

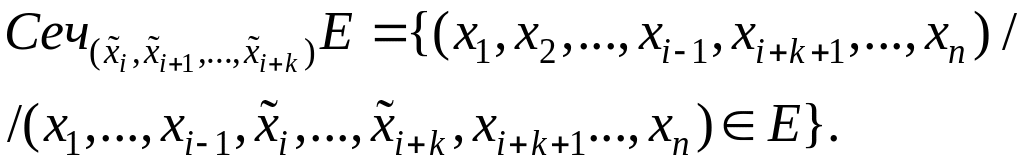
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Онлайн калькулятор для вычисления булеана (степень множества, показательное множество, множество частей) – множество всех подмножеств некоего множества A называют булеаном или степенью множества A. Обозначается булеан как P(A) или 2A .

Скачать калькулятор

Рейтинг: 2.7 (Голосов 38)

Пожалуйста напишите с чем связна такая низкая оценка:

Для установки калькулятора на iPhone – просто добавьте страницу
«На главный экран»

Для установки калькулятора на Android – просто добавьте страницу
«На главный экран»

Сообщить об ошибке

Смотрите также

Теория множеств	Комбинаторика	Операции над множествами	Объединение множеств	Пересечение множеств
Разность множеств	Подмножество из множества	Число подмножеств	Математический анализ	Элементы комбинаторики

Источник

Сообщения без ответов | Активные темы

Автор

Сообщение

Заголовок сообщения: Множество в степени множество?

Добавлено: 11 дек 2016, 15:28

Начинающий

Зарегистрирован:
11 дек 2016, 15:21
Сообщений: 4
Cпасибо сказано: 1
Спасибо получено:
0 раз в 0 сообщении
Очков репутации: 1

Добрый день!

Решаю задачи по дискретной математике, нужно упросить выражение.

Честно говоря, не понимаю запись:

[math]2^{A}[/math] и [math]C^{B}[/math]

где А, В и С- конечные множества

Например, A={1}, B={2,3}, C={4,5}

Как с этим работать? Подскажите, пожалуйста! или где почитать? Когда ищу в интернете, везде выдается стандартные пересечения и т.д.

Вернуться к началу

Nataly-Mak	Заголовок сообщения: Re: Множество в степени множество? Добавлено: 11 дек 2016, 16:37
	Eumi писал(а): Добрый день! Честно говоря, не понимаю запись: [math]2^{A}[/math] и [math]C^{B}[/math] где А, В и С- конечные множества Там, где вы встретили такую запись, наверное, объясняют, что она значит. Если бы мне такое задание дали, я решила бы его так: [math]2^{A}[/math] – это множество, которое получается возведением числа 2 в степень, где показателем степени служат все элементы множества А. Аналогично в другом примере.
Вернуться к началу

searcher	Заголовок сообщения: Re: Множество в степени множество? Добавлено: 11 дек 2016, 16:43
	Eumi писал(а): Решаю задачи по дискретной математике Eumi писал(а): Когда ищу в интернете Тут есть нетрадиционный по нынешним временам подход – перед тем как решать задачи. почитать учебник. Ныне этот подход устарел. Вам всё разжуют в интернете.
Вернуться к началу

Eumi	Заголовок сообщения: Re: Множество в степени множество? Добавлено: 11 дек 2016, 16:50
	Eumi писал(а): Если бы мне такое задание дали, я решила бы его так: 2A 2A – это множество, которое получается возведением числа 2 в степень, где показателем степени служат все элементы множества А. Аналогично в другом примере. Я правда подумала что 2^A булиан. Теперь сомневаюсь правильно ли =) searcher писал(а): Eumi писал(а): Решаю задачи по дискретной математике Eumi писал(а): Когда ищу в интернете Тут есть нетрадиционный по нынешним временам подход – перед тем как решать задачи. почитать учебник. Ныне этот подход устарел. Вам всё разжуют в интернете. Если бы нам его дали. я бы посмотрела. Я заочница, дали задания и книгу в которой, почти одна только комбинаторика.
Вернуться к началу

Eumi	Заголовок сообщения: Re: Множество в степени множество? Добавлено: 11 дек 2016, 17:24
	searcher писал(а): Eumi писал(а): правда подумала что 2^A булиан. Теперь сомневаюсь правильно ли =) Насчёт булИана я не в курсе. Степень [math]A^B[/math]– это множество функций из [math]B[/math] в [math]A[/math]. Если множество [math]A[/math] состоит из двух элементов, то мы получаем множество всех подмножеств [math]B[/math]. О! Спасибо огромное! Сделала!
Вернуться к началу

Eumi	Заголовок сообщения: Re: Множество в степени множество? Добавлено: 11 дек 2016, 20:57
	А можно еще вопрос? Не в тему, но чтобы не плодить новые темы. Есть система уравнений: AX = B B [math]lnot X[/math] = [math]lnot C[/math] Как я понимаю: Необходимым условием будет: [math]lnot C[/math] = [math]varnothing[/math] Но что же будет решением? Сломала уже всю голову.
Вернуться к началу

Похожие темы	Автор	Ответы	Просмотры	Последнее сообщение
Множество в форуме Дискретная математика, Теория множеств и Логика	Roman99999	3	137	05 апр 2020, 19:14
Множество в форуме Дискретная математика, Теория множеств и Логика	AGN	0	176	04 окт 2019, 19:54
Множество в форуме Дискретная математика, Теория множеств и Логика	Eva Vostrikova+	1	83	26 сен 2022, 12:28
Множество в форуме Дискретная математика, Теория множеств и Логика	Eva Vostrikova+	1	74	26 сен 2022, 12:41
Множество в форуме Дискретная математика, Теория множеств и Логика	kicultanya	1	322	09 май 2017, 17:57
Множество К2 в форуме Дискретная математика, Теория множеств и Логика	MichailC++	0	314	17 май 2017, 15:54
Множество в R в форуме Дискретная математика, Теория множеств и Логика	protor	8	361	20 май 2017, 17:23
Множество в форуме Дискретная математика, Теория множеств и Логика	Eva Vostrikova+	8	156	25 сен 2022, 17:30
Описать множество в форуме Дискретная математика, Теория множеств и Логика	photographer	4	651	14 июл 2015, 10:24
Универсальное множество в форуме Дискретная математика, Теория множеств и Логика	zawdarkin	2	135	16 дек 2020, 17:43

Кто сейчас на конференции

Сейчас этот форум просматривают: нет зарегистрированных пользователей и гости: 1

Вы не можете начинать темы
Вы не можете отвечать на сообщения
Вы не можете редактировать свои сообщения
Вы не можете удалять свои сообщения
Вы не можете добавлять вложения

Источник

Прямое или декартово произведение множеств — множество, элементами которого являются всевозможные упорядоченные пары элементов исходных двух множеств. Данное понятие употребляется не только в теории множеств, но также в алгебре, топологии и прочих разделах математики благодаря тому, что прямое произведение часто наследует структуры (алгебраические, топологические и т. д.), существующие на перемножаемых множествах.

Содержание

1 Прямое произведение в теории множеств
- 1.1 Произведение двух множеств
- 1.2 Декартова степень
- 1.3 Прямое произведение семейства множеств
2 Прямое произведение отображений
3 Воздействие на математические структуры
- 3.1 Прямое произведение групп
- 3.2 Прямое произведение других алгебраических структур
- 3.3 Прямое произведение топологических пространств
- 3.4 Прямое произведение графов
4 Вариации и обобщения
5 См. также

Прямое произведение в теории множеств

Произведение двух множеств

Произведение множества {в, и, к} на множество цветов радуги

в	в	в	в	в	в	в	в
и	и	и	и	и	и	и	и
к	к	к	к	к	к	к	к

Пусть дано два множества X и Y. Прямое произведение 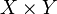множества X и множества Y есть такое множество 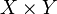, элементами которого являются упорядоченные пары (x,y) для всевозможных xin X и yin Y .

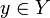Отображения произведения множеств в его множител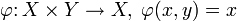и ( и 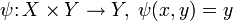) называют координатными функциями.

Аналогично строятся произведения нескольких множеств.

Декартова степень

{0, 1, 2}³, 3³ = 27 элементов
000	001	002	010	011	012	020	021	022
100	101	102	110	111	112	120	121	122
200	201	202	210	211	212	220	221	222

n-я Декартова степень множества X определяется для целых неотрицательных n, как n-кратное Декартово произведение X на себя:

$begin{matrix} X^n = &amp; underbrace{Xtimes Xtimes ldots times X}. \ &amp; n end{matrix}$

При положительных n Декартова степень Xⁿ состоит из всех упорядоченных наборов (кортежей) элементов из X длины n.

При n = 0, Декартова степень X⁰ по определению содержит единственный элемент — пустой кортеж.

Прямое произведение семейства множеств

Дальнейшее обобщение понятия прямого произведения приводит к произведениям по индексному множеству I (возможно, бесконечному): X = ΠX_i, элементы которого сопоставляют каждому индексу i из I элемент множества X_i.

Прямое произведение отображений

Пусть f — отображение из A в B, а g — отображение из X в Y. Их прямым произведением 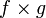называется отображение из в : .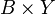

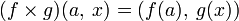Аналогично вышеизложенному, данное определение обобщается на многократные и бесконечные произведения.

Воздействие на математические структуры

Прямое произведение групп

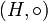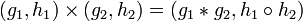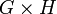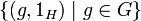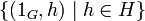Прямое (декартово) произведение двух групп (G, * ) и — это группа из всех пар элементов (g,h) с операцией поэлементного умножения: . Эта группа обозначается как . Сомножители G и H изоморфны двум нормальным подгруппам своего произведения, ${(g,1_H)mid gin G}$ и ${(1_G,h)mid hin H}$ соответственно. Пересечение этих подгрупп состоит из одного элемента (1_G,1_H), который является единицей группы-произведения. Координатные функции произведения групп являются гомоморфизмами.

Это определение распространяется на произвольное конечное число перемножаемых групп; ассоциативность декартова произведения следует из ассоциативности операций перемножаемых групп.

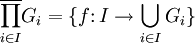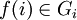Однако, для бесконечного числа перемножаемых групп понятия декартового и прямого произведения принято различать. В общем случае, $overline{prod_{iin I}} G_i={fcolon Itobigcup_{iin I} G_i}$ , где и 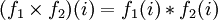. (Операция в правой части — это операция группы G_i.) Единицей группы-произведения будет последовательность, составленная из единиц всех перемножаемых групп: 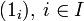. Например, для счётного числа групп: 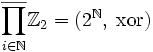$overline{prod_{iinmathbb{N}}} mathbb{Z}_2=(2^mathbb{N},; operatorname{xor})$ , где в правой части стоит множество всех бесконечных двоичных последовательностей.

Подгруппа на множестве всех f, носитель которых (то есть множество 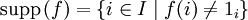$mathrm{supp},(f) = {iin Imid f(i)ne 1_i}$ ) конечен, называется прямым произведением. Например, прямое произведение того же самого набора множеств $prod_{iinmathbb{N}} mathbb{Z}_2 = (mathbb{N},; operatorname{xor})$ содержит все двоичные последовательности с конечным числом единиц, а их можно трактовать как двоичные представления натуральных чисел.

Прямое произведение других алгебраических структур

Аналогично произведению групп, можно определить произведения колец, алгебр, модулей и линейных пространств, причём в определении прямого произведения 1_i (см. выше) следует заменить нулём. Однако, как правило, произведения этих структур называют прямой суммой.

Прямое произведение топологических пространств

Пусть X и Y — два топологических пространства. Топология произведения 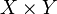задаётся базой, состоящей из всевозможных произведений 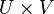, где U — открытое подмножество X и V — открытое подмножество Y.

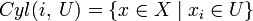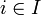Определение легко обобщается на случай произведения нескольких пространств. Для бесконечного произведения X = ΠX_i определение усложняется. Определим открытый цилиндр $Cyl(i,;U) = {xin Xmid x_iin U}$ , где iin I и U — открытое подмножество X_i.

Топология бесконечного произведения будет задаваться базой, составленной из всевозможных пересечений конечного числа открытых цилиндров (такая топология аналогична компактно-открытой топологии пространств отображений если считать индексное множество I имеющим дискретную топологию).

Теорема Тихонова утверждает компактность произведений любого количества компактных пространств; однако для бесконечных произведений её не удаётся доказать без использования аксиомы выбора (или равносильных ей утверждений теории множеств).

Также, теорема Александрова показывает, что любое топологическое пространство можно вложить в (бесконечное) произведение связных двоеточий, если только выполнена аксиома Колмогорова (а иные пространства и не рассматриваются).

Прямое произведение графов

	—	
	—	
		
	—	

Множество вершин прямого произведения двух графов G и H задаётся как произведение вершин графов сомножителей. Рёбрами будут соединены следующие па́ры вершин:

Иначе говоря, множество рёбер произведения графов является объединением двух произведений: рёбер первого на вершины второго, и вершин первого на рёбра второго.

Вариации и обобщения

Дальнейшее развитие идея прямого произведения получила в теории категорий, где она послужила основой для понятия произведения объектов. Неформально, произведение двух объектов A и B — это наиболее общий объект в данной категории, для которого существуют проекции на A и B. Во многих категориях (множеств, групп, графов, …) произведением объектов является именно их прямое произведение. Важно, что в большинстве случаев важно не столько конкретное определение прямого произведения, сколько указанное выше свойство универсальности. Различные определения будут давать при этом изоморфные объекты.

См. также

Дизъюнктное объединение
Полупрямое произведение
Прямая сумма
Тензорное произведение
Декартовы координаты
Операции над множествами
Комбинаторика

Wikimedia Foundation.
2010.

Источник

Булеан (степень множества^{[источник не указан 87 дней]}, показательное множество, множество частей^{[источник не указан 87 дней]}) — множество всех подмножеств данного множества (включая пустое множество и само множество ); обозначается или 2^A (так как оно соответствует множеству отображений из в ).

Если два множества равномощны, то равномощны и соответствующие множества подмножеств. Обратное утверждение (то есть инъективность операции $kappa mapsto 2^{kappa }$ для кардиналов) является независимым от ZFC.

В категории множеств можно снабдить функцию структурой ковариантного или контравариантного функтора следующим образом:

Мощность конечного множества подмножеств[править | править код]

Справедливо следующее утверждение: число подмножеств конечного множества, состоящего из элементов, равно $2^{n}$ . Результат доказывается методом математической индукции. В базе, у пустого множества ( n=0 ) только одно подмножество — оно само, и $2^{0}=1$ . На шаге индукции утверждение считается установленным для множеств мощности и рассматривается произвольное множество с кардинальным числом n+1 ; зафиксировав некоторый элемент $a_{0}in M$ , подмножества множества разделяются на два семейства:

$M_{1}$ , содержащие $a_{0}$ ,
$M_{2}$ , не содержащие $a_{0}$ , то есть являющиеся подмножествами множества $Msetminus {a_{0}}$ .

Подмножеств второго типа по предположению индукции $2^{n}$ , подмножеств первого типа ровно столько же, так как подмножество такого типа получается из некоторого и притом единственного подмножества второго типа добавлением элемента $a_{0}$ и, следовательно:

$2^{M}=M_{1}bigcup M_{2}$

и $M_{1}bigcap M_{2}=varnothing$

По индукционному предположению $left|M_{1}right|=2^{n}$ и $left|M_{2}right|=2^{n}$ , то есть:

$left|2^{M}right|=left|M_{1}right|+left|M_{2}right|=2^{n}+2^{n}=2^{{n+1}}=2^{left|Mright|}$

См. также[править | править код]

Аксиома множества подмножеств
Теорема Кантора
Континуум-гипотеза

Примечания[править | править код]

Литература[править | править код]

Брудно А. Л. Теория функций действительного переменного. — М.: Наука, 1971. — 119 с.

Источник

2.8. Сечение и проекция

Декартово произведение

Смотрите также

Кто сейчас на конференции

Содержание

Прямое произведение в теории множеств

Произведение двух множеств

Декартова степень

Прямое произведение семейства множеств

Прямое произведение отображений

Воздействие на математические структуры

Прямое произведение групп

Прямое произведение других алгебраических структур

Прямое произведение топологических пространств

Прямое произведение графов

Вариации и обобщения

См. также

Мощность конечного множества подмножеств[править | править код]

См. также[править | править код]

Примечания[править | править код]

Литература[править | править код]

Вам также может понравиться

Как найти страну в hoi 4

Как найти папку localappdata

Обливион как найти эктоплазму

Добавить комментарий Отменить ответ