Как найти вторые частные производные функции онлайн - Сайт, где вы сможете решить свои вопросы

Данный онлайн калькулятор предназначен для решения частных производных первого и второго порядков.
Частная производная – это производная функции одной переменной, когда значение другой переменной фиксировано. Следовательно, частные производные находятся так же, как и производные функций одной переменной. Частная производная это обобщенное понятие производной, когда в функции содержится несколько переменных.

Калькулятор поможет найти частные производные функции онлайн.
Для получения полного хода решения нажимаем в ответе Step-by-step.

Основные функции

$x^{a}$ : x^a

модуль x: abs(x)

Производные

Для того, чтобы найти производную функции f(x)
нужно написать в строке: f[x], x. Если Вам требуется
найти производную n-го порядка, то следует написать: f[x], {x, n}. В
том случае, если Вам требуется найти частную производную функции напишите в окне гаджета: f[x, y, z,…,t], j, где
— интересующая Вас переменная. Если нужно найти частную производную по
некоторой переменной порядка n, то следует ввести: f[x, y, z,…,t], {j,
n}, где означает тоже, что и Выше.

Важно подчеркнуть, что калькулятор выдает пошаговое нахождение
производной при нажатии на «Show Steps» в правом верхнем углу
выдаваемого ей ответа.

Примеры

x*E^x, x;
x^3*E^x, {x,17};
x^3*y^2*Sin[x+y], x;
x^3*y^2*Sin[x+y], y,
x/(x+y^4), {x,6}.

Источник

Частные производные

Частной производной по x функции z = f(x,y) в точке A(x₀,y₀) называется предел отношения частного приращения по x функции в точке A к приращению ∆x при стремлении ∆x к нулю.

Частные производные функции z(x,y) находятся по следующим формулам:

Вторые частные производные функции z(x,y) находятся по формулам:

Смешанные частные производные функции z(x,y) находятся по формулам:

Назначение сервиса. Сервис используется для нахождения частных производных функции (см. пример). Решение производится в онлайн режиме и оформляется в формате Word.

Решение онлайн
Видеоинструкция
Также решают

Правила ввода функции, заданной в явном виде

Примеры

x²+xy ≡ x^2+x*y.

cos²(2x+y) ≡ (cos(2*x+y))^2

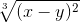≡ (x-y)^(2/3)

Правила ввода функции, заданной в неявном виде

Все переменные выражаются через x,y,z

Примеры

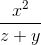≡ x^2/(z+y)

cos²(2x+zy) ≡ (cos(2*x+z*y))^2

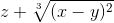≡ z+(x-y)^(2/3)

Частные производные используются, например, при нахождении полного дифференциала и экстремумов функции.

Частные производные функции нескольких переменных

Ели одному из аргументов функции z = f(x,y) придать приращение, а другой аргумент не изменять, то функция получит частное приращение по одному из аргументов: Δ_xz=f(x+Δ_x,y)-f(x,y) – это частное приращение функции z по аргументу x; Δ_yz=f(x,y+Δ_y)-f(x,y) – это частное приращение функции z по аргументу у.

Частной производной функции нескольких переменных по одному из её аргументов называется предел отношения частного приращения функции по этому аргументу к соответствующему приращению аргумента при условии, что приращение аргумента стремится к нулю:

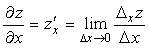– это частная производная функции z по аргументу x;

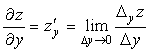– это частная производная функции z по аргументу у.

Чтобы вычислить частную производную ФНП по одному из её аргументов, нужно все другие её аргументы считать постоянными и проводить дифференцирование по правилам дифференцирования функции одного аргумента.

Пример 1. z=2x⁵+3x²y+y²–4x+5y-1

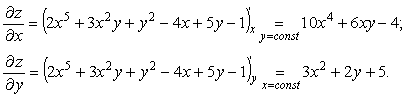
Пример 2. Найти частные производные функции z = f(x;y) в точке A(x₀;y₀).

Находим частные производные:

Найдем частные производные в точке А(1;1)

Находим вторые частные производные:

Найдем смешанные частные производные:

Задать свои вопросы или оставить замечания можно внизу страницы в разделе Disqus.
Можно также оставить заявку на помощь в решении своих задач у наших проверенных партнеров (здесь или здесь).

Источник

bold{mathrm{Basic}}

bold{alphabetagamma}

bold{mathrm{ABGamma}}

bold{sincos}

bold{gedivrightarrow}

bold{overline{x}spacemathbb{C}forall}

bold{sumspaceintspaceproduct}

bold{begin{pmatrix}square&square\square&squareend{pmatrix}}

bold{H_{2}O}

square^{2}

x^{square}

sqrt{square}

nthroot[msquare]{square}

frac{msquare}{msquare}

log_{msquare}

theta

infty

int

frac{d}{dx}

ge	le	cdot	div	x^{circ}	(square)	\|square\|	(f:circ:g)	f(x)	ln	e^{square}
left(squareright)^{‘}	frac{partial}{partial x}	int_{msquare}^{msquare}	lim	sum	sin	cos	tan	cot	csc	sec

alpha	beta	gamma	delta	zeta	eta	theta	iota	kappa	lambda	mu
nu	xi	pi	rho	sigma	tau	upsilon	phi	chi	psi	omega

A	B	Gamma	Delta	E	Z	H	Theta	K	Lambda	M
N	Xi	Pi	P	Sigma	T	Upsilon	Phi	X	Psi	Omega

sin	cos	tan	cot	sec	csc	sinh	cosh	tanh	coth	sech
arcsin	arccos	arctan	arccot	arcsec	arccsc	arcsinh	arccosh	arctanh	arccoth	arcsech

begin{cases}square\squareend{cases}	begin{cases}square\square\squareend{cases}	=	ne	div	cdot	times	<	>	le	ge
(square)	[square]	▭:longdivision{▭}	times twostack{▭}{▭}	+ twostack{▭}{▭}	– twostack{▭}{▭}	square!	x^{circ}	rightarrow	lfloorsquarerfloor	lceilsquarerceil

overline{square}	vec{square}	in	forall	notin	exist	mathbb{R}	mathbb{C}	mathbb{N}	mathbb{Z}	emptyset
vee	wedge	neg	oplus	cap	cup	square^{c}	subset	subsete	superset	supersete

int	intint	intintint	int_{square}^{square}	int_{square}^{square}int_{square}^{square}	int_{square}^{square}int_{square}^{square}int_{square}^{square}	sum	prod
lim	lim _{xto infty }	lim _{xto 0+}	lim _{xto 0-}	frac{d}{dx}	frac{d^2}{dx^2}	left(squareright)^{‘}	left(squareright)^{”}	frac{partial}{partial x}

(2times2)	(2times3)	(3times3)	(3times2)	(4times2)	(4times3)	(4times4)	(3times4)	(2times4)	(5times5)
(1times2)	(1times3)	(1times4)	(1times5)	(1times6)	(2times1)	(3times1)	(4times1)	(5times1)	(6times1)	(7times1)

mathrm{Радианы}	mathrm{Степени}	square!	(	)	%	mathrm{очистить}
arcsin	sin	sqrt{square}	7	8	9	div
arccos	cos	ln	4	5	6	times
arctan	tan	log	1	2	3	–
pi	e	x^{square}	0	.	bold{=}	+

Подпишитесь, чтобы подтвердить свой ответ

Войдите, чтобы сохранять заметки

Войти

Номер Строки

Примеры

frac{partial}{partial x}(sin (x^2y^2))
frac{partial}{partial y}(sin (x^2y^2))
frac{partial}{partial ypartial x}(sin (x^2y^2))
frac{partial}{partial w}(te^{(frac{w}{t})})
frac{partial}{partial t}(te^{(frac{w}{t})})
frac{partial}{partial v}(sqrt{u^2+v^2})
Показать больше

Описание

Поэтапное дифференцирование частной производной функций

partial-derivative-calculator

Блог-сообщения, имеющие отношение к Symbolab

High School Math Solutions – Derivative Calculator, the Basics

Differentiation is a method to calculate the rate of change (or the slope at a point on the graph); we will not…

Введите Задачу

Сохранить в блокнот!

Войти

Источник

Частная производная функции

Примеры частных производных

С дробью
```
x^2*y + x/y
```
```
(x-y)/(x+y)
```
С экспонентой
```
exp(x^2 + y^2)
```
Со степенью и показательные
```
x^(2*y)
```
```
u=(x*y)^z
```
С квадратным и кубическим корнем
```
sqrt(x^2 - y^2)
```
```
cbrt(x^2)/(cbrt(y) - 1)
```
С квадратом и кубом
```
z=x^3*y^2
```
С натуральным логарифмом
```
z=ln(x + sqrt(x^2 + y^2))
```
С тригонометрическими функциями
```
z=arctg(y/x)
```
```
y*sin(2y)/cbrt(x^2)
```
С параметром
```
z=x^3 - 5axy + y^3
```

Указанные выше примеры содержат также:

модуль или абсолютное значение: absolute(x) или |x|
квадратные корни sqrt(x),
кубические корни cbrt(x)
тригонометрические функции:
синус sin(x), косинус cos(x), тангенс tan(x), котангенс ctan(x)
показательные функции и экспоненты exp(x)
обратные тригонометрические функции:
арксинус asin(x), арккосинус acos(x), арктангенс atan(x),
арккотангенс acot(x)
натуральные логарифмы ln(x),
десятичные логарифмы log(x)
гиперболические функции:
гиперболический синус sh(x), гиперболический косинус ch(x),
гиперболический тангенс и котангенс tanh(x), ctanh(x)
обратные гиперболические функции:
гиперболический арксинус asinh(x), гиперболический арккосинус acosh(x),
гиперболический арктангенс atanh(x), гиперболический арккотангенс acoth(x)
другие тригонометрические и гиперболические функции:
секанс sec(x), косеканс csc(x), арксеканс asec(x),
арккосеканс acsc(x), гиперболический секанс sech(x),
гиперболический косеканс csch(x), гиперболический арксеканс asech(x),
гиперболический арккосеканс acsch(x)
функции округления:
в меньшую сторону floor(x), в большую сторону ceiling(x)
знак числа:
sign(x)
для теории вероятности:
функция ошибок erf(x) (интеграл вероятности),
функция Лапласа laplace(x)
Факториал от x:
x! или factorial(x)
Гамма-функция gamma(x)
Функция Ламберта LambertW(x)
Тригонометрические интегралы: Si(x),
Ci(x),
Shi(x),
Chi(x)

Правила ввода

Можно делать следующие операции

2*x: – умножение
3/x: – деление
x^2: – возведение в квадрат
x^3: – возведение в куб
x^5: – возведение в степень
x + 7: – сложение
x – 6: – вычитание
Действительные числа: вводить в виде 7.5, не 7,5

Постоянные

pi: – число Пи
e: – основание натурального логарифма
i: – комплексное число
oo: – символ бесконечности

Источник

Понятие частной производной применимо только к функциям многих переменных. Рассмотрим функцию двух переменных
z=f(x,y).
Частные производные по переменным

и

записываются в виде
∂z∂x

и
∂z∂y

соответственно. Сами частные производные
∂z∂x

и
∂z∂y

также являются функциями двух переменных:
∂z∂xpx,y

и
∂z∂yqx,y

, поэтому от них тоже можно взять производные:

∂p∂x∂∂x∂z∂x∂2z∂x2

∂q∂y∂∂y∂z∂y∂2z∂y2

∂p∂y∂∂y∂z∂x∂2z∂x∂y

∂q∂x∂∂x∂z∂y∂2z∂y∂x

Производные
∂2z∂x2

и
∂2z∂y2

– являются вторыми частными производными функции

по переменным

и

соответственно. Производные
∂2z∂x∂y

и
∂2z∂y∂x

– называются смешанными производными функции

по переменным
,

и
,

соответственно. При условии, что функция

и её смешанные производные
∂2z∂x∂y

и
∂2z∂y∂x

определены в некоторой окрестности точки
M(x₀,y₀)
и непрерывны в этой точке, выполняется равенство:

∂2z∂x∂y∂2z∂y∂x

По аналогии, можно ввести производные более высоких порядков, например, запись
∂5z∂x2∂y3

означает, что мы должны продифференцировать функцию

по переменной

два раза, а затем по переменной

три раза, т.е. фактически:

∂5z∂x2∂y3∂3∂y3∂2z∂x2∂∂y∂∂y∂∂y∂∂x∂z∂x

Иногда, для обозначения частных производных некоторой функции
z=f(x,y)
используют запись вида:
f_x‘(x,y)
и
f_y‘(x,y),
указывая переменную по которой происходит дифференцирование. Таким образом можно обозначать и смешанные производные:
f_xy”(x,y)
и
f_yx”(x,y)
а также вторые производные и производные более высокого порядка:
f_xx”(x,y)
и
f_xxy”’(x,y)
соответственно. Следующие обозначения эквиваленты:

В нашем онлайн калькуляторе для обозначения частных производных используются символы:

∂z∂x

;

∂z∂y

;

∂5z∂x2∂y3

.
Пример подробного решения, выдаваемого нашим онлайн сервисом, можно посмотреть
здесь.

Источник

Частные производные

Правила ввода функции, заданной в явном виде

Правила ввода функции, заданной в неявном виде

Частные производные функции нескольких переменных

Номер Строки

Частная производная функции

Примеры частных производных

Правила ввода

Постоянные

Вам также может понравиться

Как составить план сказки девочка снегурочка

Блины в дырочку как исправить

Гугл как найти в роблокс

Добавить комментарий Отменить ответ