Вязкость
– это внутреннее трение жидкости, которое
испытывает один слой жидкости относительно
другого при истечении. Сила трения f
пропорциональна поверхности S
и градиенту скорости
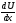 ,
,
т.е.
 ,
,
(закон
Ньютона)
где
(«этта») – коэффициент внутреннего
трения, который называют вязкостью
(динамической вязкостью). Отсюда:

В
системе СИ единицей измерения вязкости
является [Па×с], часто применяют и
несистемную единицу – [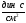 ],
],
получившую название пуаз
[П]; 1 П = 0,1 Па с.
Добавление
коллоидных частиц к растворителю с
вязкостью Ƞ0
приводит
к увеличению вязкости раствора Ƞ.
Повышение вязкости есть результат
увелечения трения между прилегающими
мономолекулярными слоями жидкости,
вызванного тем, что частицы крупнее
молекул растворителя. Изменение выражают
как отношение Ƞ/ Ƞ0,
называемое
относительной вязкостью Ƞотн.
Вязкость
гидрофобного
золя зависит от концентрации золя и не
зависит от способа его приготовления.
Вязкость гидрофобного золя всегда выше
вязкости дисперсионной среды.
Относительная
вязкость гидрофобных коллоидов
описывается уравнением Эйнштейна

где
и 0
–
вязкость
золя и дисперсионной среды соответственно,
–
объемная концентрация дисперсной фазы,
– коэффициент, учитывающий форму частиц
дисперсионной фазы.
Гидрофильные
коллоиды, частицы которых значительно
сольватированы (гидратированы), имеют
большую вязкость, чем гидрофобные
коллоиды равной концентрации. Их вязкость
резко возрастает с увеличением
концентрации золя. Уравнение Эйнштейна
для лиофильных систем принимает вид:
 ,
,
где
V-
объем сольватных оболочек частиц
дисперсной фазы.
Суммарный
заряд белковой макромолекулы определяется
соотношением числа кислотных групп
(СОО–)
и основных (NH3+).
Изменяя рН раствора, можно создать такие
условия, при которых суммарный заряд
белковых молекул будет равен 0. Такое
состояние белков называется
изоэлектрическим,
а рН, при котором оно осуществляется,
изоэлектрической
точкой
(ИЭТ).
Изменяя
рН среды, можно влиять на вязкость
раствора ВМС. Например, увеличение
вязкости желатина при уменьшении
рН среды (переход в более кислую
область от изоэлектрической точки)
объясняется увеличением положительного
заряда белковой молекулы за счет
протонирования нейтральных аминных
групп (-NH3+),
что сопровождается увеличением
гидратации и, следовательно, вязкости.

При
дальнейшем уменьшении рН, когда
прореагируют все нейтральные аминогруппы,
ионизация (заряд) молекулы начинает
уменьшаться за счет присоединения ионов
водорода к карбоксильным анионам. Этот
процесс сопровождается уменьшением
гидратации, а, следовательно, и вязкости.

При
дальнейшем уменьшении рН в сильнокислой
среде начинается деструкция белка
(кислотный гидролиз), белок начинает
распадаться на отдельные аминокислоты.
При
увеличении рН от изоэлектрической точки
(переход в более щелочную область)
происходит увеличение суммарного
отрицательного заряда за счет диссоциации
карбоксильных групп, что приводит к
увеличению отрицательных зарядов на
поверхности макромолекулы. Следствием
этого, опять-таки, является увеличение
гидратации макромолекул и вязкости
растворов ВМС. При максимальной вязкости
в щелочной области белковая молекула
схематически представляется так:

Дальнейшее
увеличение рН вызывает уменьшение
ионизации макромолекулы за счет
отщепления иона водорода от заряженной
аминогруппы, что сопровождается
уменьшением гидратации и вязкости.

При
дальнейшем увеличении рН в сильнощелочной
среде начинается деструкция белка
(щелочной гидролиз), белок начинает
распадаться на отдельные аминокислоты,
что сопровождается уменьшением
гидратации.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
Вязкость – золе
Cтраница 2
Для того чтобы определить структурную вязкость, находят опытным лутем зависимость вязкости золя от давления. Чем сильнее выражена эта структурирован золь.
[16]
Полученные результаты записывают в таблицу и делают выводы о влиянии анионов на вязкость золя.
[17]
Поскольку в уравнение ( X, 5) не входит радиус частицы, вязкость золя должна находиться в прямой зависимости от его концентрации.
[18]
Поскольку в уравнение ( IX, 2) не входит радиус частицы, вязкость золя должна находиться в прямой зависимости от его концентрации.
[19]
Надежные экспериментальные данные по поводу показателя s в соотношении ( 7.4 J) для вязкости золя в настоящее время отсутствуют, однако для выяснения этого вопроса готовятся новые эксперименты.
[20]
Вычислить коэффициент диффузии для шарообразных коллоидных частиц, диаметр которых D 20 мц, если температура 20, вязкость золя не отличается от вязкости воды.
[21]
Если к золю гидроксида железа прибавить какой-нибудь коагулятор ( NaCl) в количестве, недостаточном для полной коагуляции, вязкость золя начнет заметно увеличиваться. При сильном встряхивании гель вновь приобретает прежнюю легкоподвижность, вязкость его уменьшается до первоначального исходного значения. Однако стоит золь на некоторое время оставить в покое, он вновь превращается в студень. Это явление изотермического обратимого перехода золь – П; гель получило название тиксотропии ( от греч.
[22]
Если к золю гидроксида железа прибавить какой-нибудь коагулятор ( NaCl) в количестве, недостаточном для полной коагуляции, вязкость золя начнет заметно увеличиваться. При сильном встряхивании гель вновь приобретает прежнюю легкоподвижность, вязкость его уменьшается до первоначального исходного значения. Однако стоит золь на некоторое время оставить в покое, он вновь превращается в студень.
[23]
Чтобы подсчитать объемную долю микрогеля в ходе превращения золя в гель, необходимо учитывать отношение вязкости в момент измерения к вязкости золя до начала гелеобразования, а не к вязкости только лишь водной среды.
[25]
На той стадии, когда большая часть мономера уже превратилась в частицы, но последние еще не начали агрегировать, можно подсчитать вязкость золя из объемной доли дисперсной фазы. Такая фаза представляет собой кремнеземные частицы с водой, удерживаемой на их поверхности водородной связью.
[26]
Типичные значения вязкости, полученные расчетным путем, показаны на рис. 3.35. Видно, что существует интервал значений, в котором при различных концентрациях кремнезема на вязкость золя при рН 1 5 – 3 может оказывать влияние размер частиц.
[28]
Переработка пластизолей в различные изделия происходит при нагревании с большой скоростью повышения температуры. При этом вязкость золя сначала снижается, затем, пройдя минимум, повышается до потери текучести. Температура, при которой золь теряет текучесть и превращается в гель, называется температурой желатинизации. При дальнейшем нагревании гель сначала становится хрупким, потом при повышении температуры его прочность постепенно повышается, а поверхность становится глянцевой.
[30]
Страницы:
1
2
3
4
Лекция №13.
План лекции:
ПРОЧНОСТЬ И ВЯЗКОСТЬ ДИСПЕРСНЫХ СИСТЕМ
Вязкие тела текут при любом напряжении сдвига t ( R t ) :
F — сила вязкого сопротивления, В — площадь, на которую распространяется действие этой силы.
Течение вязких тел определяется законом Ньютона:
Р t = h ( d g / d P t ) , F = h В( d g / d P t ) (13.2)
где h — коэффициент вязкости, d g / d P t -изменение деформации сдвига во времени (скорость деформации).
Если обозначить скорость деформации через g . , то вязкость системы:
Вязкость свободнодисперсных систем растет по мере увеличения концентрации дисперсной фазы. Присутствие частиц дисперсной фазы приводит к искажению потока жидкости вблизи этих частиц, что влияет на вязкость. Если концентрация незначительна и столкновения исключаются, то характер движения жидкости около одной частицы не влияет на характер движения жидкости около другой частицы. В этих условиях для определения вязкости свободнодисперсных систем можно воспользоваться уравнением Эйнштейна:
h , h 0 — вязкость свободнодисперсной системы и дисперсионной среды, u об — объемная концентрация дисперсной фазы, к — коэффициент, зависящий от формы частиц (для сферической формы к = 2,5).
Формула Эйнштейна справедлива при отсутствии деформации частиц, если концентрация дисперсной фазы не превышает 6%.
При увеличении объемной концентрации до 30% можно пользоваться формулой:
При сопоставлении формул 13.4 и 13.5 видно, что по мере увеличения концентрации частиц линейная зависимость между вязкостью и
концентрацией нарушается. Тем не менее, вязкость подобных систем при данной концентрации остается постоянной. Подобные системы называются ньютоновскими.
Течение и вязкость неньютоновских жидкостей, которые называют еще аномальными жидкостями, зависят от внешнего воздействия (напряжения сдвига). Вязкость является величиной переменной для данной концентрации и уже не определяется соотношениями 13.2 и 13.3.
Рассмотрим особенности движения структурированных систем (рис.13.1).

Рис.13.1.Зависимость скорости течения (а) и коэффициента вязкости (б) от внешнего усилия Р.
Р r — предел прочности, Рх1 — предел упругости, Рх2 -условный предел прочности, Р m — напряжение полного разрушения структуры, h макс — вязкость неразрушенной структуры, h мин — наименьшая вязкость предельно разрушенной структуры.
Кривые h = f (Р) — полные реологические кривые течения структурированных дисперсных систем. Каждое значение вязкости на этих кривых соответствует равновесному состоянию систем в стационарном ламинарном потоке.
Четыре состояния структурированных систем:
1. 0 P Р x1 (Р x1 — предел упругости). В этом состоянии течение отсутствует, и внешнее воздействие не может нарушить прочность системы.
2. Р > Р x 1 — система начинает течь. Скорость перемещения незначительна, связи между частицами после их разрушения успевают восстановиться. Структура не разрушается. Подобное перемещение называют ползучестью. Вязкость системы в данной зоне наибольшая. Скорость движения в данной зоне:
к — коэффициент, характеризующий структурные особенности дисперсной системы.
Необратимое разрушение системы начинается на границе зон 2 и 3, а на границе участков 3 и 4 оно заканчивается. В этом состоянии дисперсной системы связи между частицами не восстанавливаются, вязкость снижается, скорость движения системы увеличивается. Для этого случая скорость системы:
На участке 4 структура разрушается полностью, минимальная вязкость — полное разрушение системы. На рисунке приведены реологические кривые для твердообразных тел, для жидкообразных систем — пунктирная линия 1а.
Изменение вязкости структурированных жидкостей широко используется на практике.
ВИДЫ ДИСПЕРСНЫХ СИСТЕМ. ЗОЛИ И СУСПЕНЗИИ
Золи и суспензии, а также их производные — гели и пасты — разновидности одного и того же типа дисперсных систем — Т/Ж, различаются они размером частиц дисперсной фазы.
Золи — высокодисперсные системы, их называют еще коллоидными растворами. В зависимости от дисперсионной среды делятся на гидрозоли (вода) и органозоли (органическая среда).
Помимо твердых частиц, дисперсная фаза золей может формироваться из мицелл — электрически нейтральных агрегатов ионов дисперсной среды.
Суспензии — средне- и грубодисперсные системы.
Золи — седиментационно-устойчивые системы, суспензии — седиментационно-неустойчивы.
Особенно резко различаются оптические свойства золей и суспензий. Золи способны рассеиваться по закону Рэлея, а действие света на суспензии происходит по законам геометрической оптики.
Общие свойства золей и суспензий определяются границей раздела фаз Т/Ж, на которой происходят адсорбционные процессы и образуется ДЭС. Больший размер частиц у суспензий приводит к тому, что электроосмос, потенциал седиментации и течения у них выражен слабо, а электрофорез — отсутствует.
ПАСТЫ, ГЕЛИ И ОСАДКИ
При увеличении концентрации частиц дисперсной фазы системы из свободнодисперсных превращаются в связанодисперсные. Связнодисперсные системы, в которые переходят суспензии, называются пастами. Золи переходят в гели. Пасты и гели образуют структуры, для них характерны структурно-механические свойства.
Пасты — концентрированные суспензии или осадок, который образуется при потере суспензией седиментационной устойчивости. Кроме того, пасты могут быть приготовлены искусственно путем растирания твердых тел в жидкой среде.
Осадки золей могут переходить обратно в коллоидный раствор — пептизация (процесс, обратный коагуляции — распад агрегатов до первичных частиц).
Пептизация может протекать под действием электролитов, при этом восстанавливается ДЭС, повышается дзета-потенциал, а силы электростатического отталкивания преобладают над силами межмолекулярного взаимодействия. Пептизация может также происходить под действием растворов ПАВ, молекулы которых адсорбируются на границе раздела фаз и образуют адсорбционные слоя, которые противодействуют сближению частиц.
Пептизация протекает с определенной скоростью и зависит от концентрации электролита-пептизатора (рис.13.2)
SHAPE * MERGEFORMAT

Рис.13.2.Изменение массы перешедшего в раствор осадка в зависимости от концентрации пептизатора.
В начале процесса при незначительной концентрации пептизатора перехода осадка в раствор не т (участок 1) — происходит адсорбция пептизатора на поверхности частиц. По мере увеличения концентрации пептизатора (участок 2) количество осадка, перешедшего в коллоидный раствор, возрастает. При дальнейшем увеличении концентрации пептизатора весь осадок переходит в коллоидный раствор (участок 3).
Вязкость коллоидных растворов
Вязкостью (η) называют внутреннее трение между слоями данного вещества, движущимися относительно друг друга (сопротивление жидкости или газа течению под действием внешних сил).
Вязкость является результатом межмолекулярного взаимодействия, и она тем выше, чем больше силы межмолекулярного притяжения. Вязкость жидкостей может сильно изменяться в присутствии растворенных или диспергированных веществ. Вязкость большинства гидрофобных золей и суспензий при малых концентрациях почти не отличается от вязкости чистого растворителя. По мере увеличения концентрации дисперсной фазы вязкость коллоидного раствора увеличивается. Это объясняется тем, что частицы ДФ взаимодействуют между собой и образуют пространственные сетки (структуры), а с молекулами дисперсионной среды – сольватные оболочки и тем самым преграждают путь слоям движущейся жидкости. В результате обтекания частиц, траектория течения жидкости искривляется, удлиняется и в единицу времени вытекает меньший объем жидкости. Этот эффект усиливается, если частицы имеют удлиненную форму, т.к. они могут вращаться вокруг своей поперечной оси (как пропеллер) под действием движущейся жидкости.
Эйнштейном установлена зависимость вязкости коллоидного раствора от концентрации взвешенных частиц. При этом были допущены, что:
─ частицы ДФ удалены друг от друга
─ частицы ДФ имеют одинаковый размер и форму
─ между частицами ДФ отсутствуют взаимодействия
─ размер частиц больше размера молекул растворителя.
η = ηо(1+ αj), где α – коэффициент, зависящий от формы частиц. Для частиц круглой формы α = 2,5; для удлиненных частиц α > 2,5. j — объемная доля дисперсной фазы. ηо – вязкость дисперсионной среды.
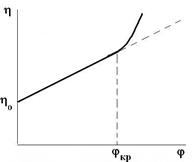 Рис. Рис. |
Графически уравнение Эйнштейна должно выражаться прямой. Однако при повышении некоторой критической концентрации, вязкость не подчиняется уравнению Эйнштейна. Это объясняется 2-мя факторами: 1) частицы имеют больший размер и сольватную оболочку, т.е. большую поверхность поперечного сечения; 2) частицы взаимодействуют между собой образуя агрегаты, структуры, ограничивающие подвижность жидкости. |
Поэтому уравнение Эйнштейна применимо для золей и разбавленных
суспензий, у которых частицы ДФ не взаимодействуют с дисперсионной средой (т.е. для лиофобных систем).
Лако-красочные материалы — производство
Технологии и оборудование для изготовления красок, ЛКМ
ЗАВИСИМОСТЬ ВЯЗКОСТИ КОЛЛОИДНЫХ СИСТЕМ ОТ КОНЦЕНТРАЦИИ ДИСПЕРСНОЙ ФАЗЫ
Вязкость коллоидных систем всегда выше вязкости чистой дисперсионной среды. Эйнштейн в 1906 г., исходя из чисто гидродинамических представлений, вывел уравнение, устанавливающее связь между вязкостью системы rj. и концентрацией дисперсной фазы:
11 = т1о(1 +2,5Ф) (X, 17)
Где Т]0 — вязкость дисперсионной среды; ф — объемная концентрация дисперсной фазы.
Уравнение (X,17) пригодно только при условии, что взвешенные в жидкости частицы являются твердыми шарообразными телами, концентрация дисперсной^ фазы сравнительно невелика и между частицами отсутствуют взаимодействия. Кроме того, для
Соблюдения уравнения Эйнштейна необходимо, чтобы система была несжимаема, течение жидкости носило ламинарный характер, между частицами и жидкостью отсутствовало скольжение и, наконец, чтобы частицы были велики по сравнению со свободным пробегом молекул среды, но малы по сравнению с пространством, в котором происходит течение.
Значение численного коэффициента в уравнении (X, 17) зависит от формы частиц. Поэтому в общем виде уравнение Эйнштейна можно записать так:
Где а — множитель, зависящий от формы частиц.
Уравнение Эйнштейна часто пишут также следующим образом:
(тіЛіо) — 1 = (ті — чіо)/тіо = a
Где ti/tjo — отношение вязкости системы к вязкости среды (относительная вязкость) ; п — общее число частиц в системе; о — объем одной частицы дисперсной фазы; V — объем системы, мл. ‘
Величину (т] — Ло)/»По. характеризующую относительное увеличение вязкости дисперсионной среды при введении в нее определенного количества дисперсной фазы, не совсем правильно называют удельной вязкостью. Ее обычно обозначают символом т]уд. Из предыдущего следует, ЧТО
Из всего сказанного следует, что, по Эйнштейну, между вязкостью системы и содержанием в ней дисперсной фазы должна су-» ществовать прямолинейная зависимость. Весьма существенно также, что, согласно Эйнштейну, вязкость не зависит от дисперсности суспензии.
Экспериментальную проверку уравнения Эйнштейна проводили Банселен на суспензиях гуммигута, Оден на золях серы и наиболее обстоятельно Эйрих на суспензиях мельчайших стеклянных шариков, шарообразных спор грибов и дрожжевых клеток. Во всех этих исследованиях при сферической форме частиц и малых концентрациях дисперсной фазы численный коэффициент при (р имел значение, близкое к 2,5. Отклонения наблюдались, когда частицы не были шарообразны, концентрация дисперсной фазы в суспензии была значительной и между частицами существовали электрические или другие силы взаимодействия.
Влияние анизодиаметричности частиц. При палочкообразной, эллипсоидной или пластинчатой форме частиц суспензии вязкость системы всегда больше, чем должна быть согласно уравнению Эйнштейна. Причина этого заключается в том, что жидкость, попадающая в объем (эллипсоид вращения), образующийся вокруг нешарообразных частиц, находящихся в интенсивном броуновском движении, становится как бы связанной с частицей. В результате
Этого возникает кажущееся увеличение объемной доли дириерсной фазы в системе, что и приводит к повышению вязкости.
Экспериментально показано, что вязкость суспензии С малыми анизодиамет — рическими частицами, находящимися обычно в интенсивном броуновском движении, повышается пропорционально квадрату отношения большой и малой осей эллипсоида вращения, а вязкость суспензии с достаточно большими нешарообразными частицами, совершающими медленное броуновское движение, возрастает лишь прямо пропорционально отношению осей.
Теоретические вычисления, проведенные Куном, Симха и другими исследователями с использованием в качестве моделей частиц самой разнообразной формы, весьма сложны и не всегда убедительны. Поэтому до сих пор еще иет общей теории зависимости вязкости коллоидных систем от формы частиц.
Вязкость систем, содержащих анизодиаметрические частицы, как мы видели, зависит от скорости течения. Вытянуты^ частицы ориентируются в потоке, вращательное движение их затрудняется и в результате этого вязкость системы с увеличением скорости течения снижается. Подобное явление можно наблюдать, например, при измерении вязкости золя V2O5, частицы которого сильно ани- зодиаметричны.
Влияние истинной концентрации дисперсной фазы и сольватации. Отличие вязкости концентрированной дисперсной системы от значений вязкости, вычисленной по уравнению Эйнштейна, объясняется тем, что в жидкости около частиц возникают взаимовозму — щающие микропотоки, затрудняющие движение системы. Дебройн считает, что при этом, помимо гидродинамических взаимодействий, необходимо учитывать также и механические (столкновения частиц, образование пар и т. д.).
При очень малых концентрациях суспензии поток, возникающий вокруг одной частицы, очень мало влияет на потоки, возникающие около других частиц, и на скорость движения всего потока жидкости в целом. Однако с увеличением концентрации дисперсной фазы это влияние все увеличивается и приводит к отклонению от закона Эйнштейна.
Другое объяснение отклрнения вязкости дисперсных систем от значений, найденных с помощью уравнения Эйнштейна, заключается в сольватации частиц. Явление сольватации может объяснить и часто наблюдающуюся зависимость вязкости от дисперсности системы при одинаковой объемной концентрации дисперсной фазы.
Влияние сольватации можно представить следующим образом. Если к поверхности шарообразной частицы радиусом г прилип слой дисперсионной среды толщиной H, то влияющий на вязкость эффективный объем частицы (объем самой частицы вместе с объемом сольватного слоя) составляет 4/зя(г + /г)3. Для значений H, малых по сравнению с г, будем иметь 4/зЯ(г3 + 3/»2/г). Соответственно этому при вычислении эффективной объемной концентрации дисперсной фазы ф за объем дисперсной фазы следует принять не величину 4/3 nr3v, а 4/зя(г3+3r2ft)v (где v — численная концентрация). Если принять истинный объем дисперсной фазы ф0 = 4/злг, то для ф получаем:
Следовательно, .величина ф окажется больше объема дисперсной фазы фо, и эта величина будет тем больше, чем меньше частицы. Иными словами, вязкость возрастает с уменьшением размера частиц зеля. Подобное возрастание иязкости при повышении степени дисперсности золя серы наблюдал Свен Оден.
Фикенчер и Марк для учета влияния сольватации предложили модифицировать уравнение Эйнштейна, введя в него соответствующую поправку. Согласно этим авторам, в уравнении Эйнштейна, так же как и в уравнении Ван-дер-Ваальса, вместо общего объема системы следует ввести эффективный объем, т. е. объем системы за вычетом объема частиц. Так как частицы в системе находятся в сольватированном состоянии и, кроме того, совершают броуновское движение, описывая некие тела вращения, то объем дисперсионной среды, энергетически и стерически связанной с частицами, также следует причислить к объему дисперсной фазы. Тогда уравнение (X, 18) примет вид:
Где о’ — объем частицы имеете с энергетически и стерически связанной с ней средой.
Уравнение Фикенчера и Марка хорошо объясняет, почему в некоторых случаях вязкость возрастает с увеличением концентрации дисперсной фазы быстрее, чем это должно быть в соответствии с прямолинейной зависимостью. Действительно, с увеличением концентрации дисперсной фазы в растворе возрастает пропорциональная ей величина п в числителе и одновременно уменьшается величина (V — Nv‘) в знаменателе, что и приводит к более быстрому возрастанию вязкости, чем концентрации.
Влияние взаимодействия между частицами. Причина неприменимости в некоторых случаях уравнения Эйнштейна к дисперсным системам может заключаться в проявлении сил притяжения между коллоидными частицами. При этом в системе образуются более или менее рыхлые структуры, которые включают значительные объемы дисперсионной среды. Подобная иммобилизация, т. е. уменьшение подвижности растворителя, приводит к тому, что вязкость системы оказывается гораздо больше той, которая может быть вычислена по уравнению Эйнштейна. Вязкость в таких системах сильно зависит от скорости течения, так как представляет собой структурную вязкость, обусловленную наличием в системе рыхлых пространственных сеток.
. С другой стороны, непрйменимость уравнения Эйнштейна к коллоидным системам может быть связана и с проявлением сил отталкивания между частицами, несущими одноименный электрический заряд. Согласно Смолуховскому, вязкость золей с заряженными частицами выше вязкости золей с незаряженными частицами. Повышение вязкости в результате наличия на поверхности частиц двойного электрического слоя называется электровязкостным Эф* Фектом.
Смолуховский вывел следующее уравнение, связывающее удельную вязкость золя с электрокинетическим ^-потенциалом двойного электрического слоя частиц:
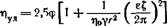
Где т]о — вязкость дисперсионной среды; у — удельная электропроводность; г — радиус частиц; е — диэлектрическая проницаемость
Поправочный член в уравнении (X, 22) может иметь весьма большое значение. Подсчеты показывают, что для золей, радиус частиц которых равен 10_6 см, а электропроводность у = — Ю-4 Ом-1-см-1, поправочный член может быть в 10 раз больше основного.
Согласно уравнению Смолуховского, вязкость коллоидных систем при введении электролитов должна уменьшаться как вследствие снижения ^-потенциала, так и в результате увеличения электропроводности межмицеллярной жидкости. В изоэлектрическом состоянии золя (при % = 0) уравнение Смолуховского переходит в уравнение Эйнштейна. Следует, однако, отметить, что при астабилизации коллоидной системы введением в нее электролита (вследствие уменьшения сил отталкивания между частицами в золе) возможны явления агрегации частиц, приводящие к образованию структур и появлению структурной вязкости, что не предусмотрено уравнением Смолуховского. В результате этого понижение ^-потенциала частиц золя в определенных условиях может не только не вызывать понижения вязкости золя, но и обусловить ее повышение.
Буутс в 1948 г. вывел уравнение для электровязкостного эффекта, существенно отличающееся от уравнения Смолуховского. Согласно Буутсу, величина электровязкостного эффекта значительно меньше, чем об этом можно судить по уравнению Смолуховского, и независимо от значения ^-потенциала становится ничтожной, когда толіЦииа двойного электрического слоя очень мала по сравнению с радиусом частиц.
источники:
http://helpiks.org/6-45799.html
http://kraska.biz/kurs-kolloidnoj-ximii/zavisimost-vyazkosti-kolloidnyx-sistem-ot-koncentracii-dispersnoj-fazy/
ХИМИЯ КРЕМНЕЗЕМА
Вязкость
Как отмечал Круит [207], вязкость золя зависит от объемной доли «дисперсной фазы» согласно уравнению Эйнштейна
1пты=1 +2,5^
Где Цгеї — относительная вязкость или отношение вязкости дисперсной системы к вязкости дисперсной среды; Ф — доля объема, занимаемая дипергированными, однородными по размеру сферическими частицами. Муни [208] распространил уравнение Эйнштейна на суспензии с ограниченным значением концентрации:
Был выведен целый ряд других уравнений, по которым можно предсказывать даже с большей точностью вязкость более высоко концентрированных суспензий, состоящих из сферических частиц, но эти уравнения в основном не были применены к золям. Симха [209], Вэнд [210] и Форд [211] использовали такие уравнения в своих исследованиях.
В 1965 г. Томас [212] опубликовал обзор, в котором рассмотрел большой объем экспериментальных данных по значениям относительной вязкости суспензии с однородными по размеру сферическими частицами и связал эти данные с уравнениями, полученными из предварительного теоретического анализа. Он пришел к заключению, что к указанным экспериментальным данным в пределах всей области концентраций лучше всего подходит следующее уравнение (при значениях концентраций <0,25 экспоненциальный член в уравнении можно опустить):
Тгеі = 1 + 2,5ф + 10,05ф2 + 0,002 73 ехр (16,6ф)
Льюис и Нильсен [213] распространили эту теорию на вязкость непрерывно образующихся агрегатов из сферических частиц, начиная от агрегатов, состоящих из двух или трех частиц, и вплоть до кластеров, в которых удерживается вместе большое число таких сферических частиц. Можно ожидать, что эта теория более правильно описывает не те золи кремнезема, в которых все частицы представляют собой индивидуальные сферы, а те, в которых уже начинает формироваться фаза геля, стабилизирующаяся впоследствии. Теорию можно также было бы применить к золям, содержащим агрегаты, подобные тем, которые образуются в кремнеземах пирогенного типа.
Федоре [214] принял во внимание максимальную плотность упаковки сферических частиц в суспензии, что позволило ему получить уравнение для очень высоких концентраций золей. Объемная доля упакованных произвольным образом, но плотно, сферических частиц составляет 0,63.
Другие исследования вязкости сферических частиц, находящихся в суспензии, были выполнены Менли и Мейсоном [215] и Хеппелом [216], а реология суспензий кремнезема (неколлоидного типа) описана Пивинским [217].
Как показано на рис. 4.11, при заданной массовой концентрации кремнезема в золе объемная доля дисперсной фазы изменяется в зависимости от объема ионной оболочки, окружающей каждую частицу кремнезема в виде двойного слоя, и от пористости или степени гидратации частиц. Если вязкость измеряется при рН 2, когда отсутствует заряд на поверхности частиц, то величина объемной доли может быть использована для установления того, сколько воды связано с поверхностью твердых частиц или удерживается внутри частиц с губчатой структурой и агрегатов, поскольку эта вода может рассматриваться как часть дисперсной фазы.
В серии измерений вязкости, выполненных при рН 2 Айле – ром и Дальтоном [64] на ряде образцов золей, состоящих из плотных частиц с диаметром менее 8 нм, было показано, что такая связанная вода соответствует слою толщиной в одну молекулу воды. Если диаметр частиц свыше 20 нм, подобный фиксированный гидратный слой воды толщиной всего лишь около 0,3 нм оказывает небольшое воздействие на вязкость, но, когда частицы кремнезема имеют размер только 5 нм, различие в 0,6 нм повышает эффективный диаметр частиц до 5,6 нм и, следовательно, увеличивает эффективный объем «дисперсной фазы» на 40 %.
Что же касается пористых частиц, которые рассматривались выше, то вязкость оказывается не очень чувствительным показателем для оценки пористости, особенно если объем пор составляет менее 10—20%. С другой стороны, как упоминалось в гл. 3, при рН 2 вязкость представляет собой чувствительный критерий агрегирования частиц или присутствия в системе микрогеля. Для частиц, в диаметре меньших -~20 нм, необходимо принимать во внимание влияние гидратного слоя. Из известной величины удельной поверхности, которая не сильно изменяется по мере формирования микрогеля, можно оценить средний размер частиц. В таком случае оказывается возможным подсчитать из размера частиц вязкость золя, со-

Стоящего из неагрегированных частиц, и его концентрацию. Окончательно величина относительной вязкости вследствие присутствия в системе микрогеля берется как отношение фактической вязкости золя к ее значению, подсчитанному для золя, состоящего из неагрегированных частиц.
Зависимость вязкости концентрированных золей от толщины двойного ионного слоя следует рассматривать с точки зрения наибольших достижимых на практике концентраций, до которых могут быть сконцентрированы золи с различающимися по размеру частицами. Для того чтобы охарактеризовать
концентрированные коммерческие золи, представляется полезным ввести такую величину, как «выраженная в масс. % доля, занимаемая кремнеземом в дисперсной фазе». Если такая дисперсная фаза состоит из больших твердых сферических частиц кремнезема, когда связанная с поверхностью вода составляет незначительную часть по сравнению с массой самой частицы, то масс. % Si02 близок к 100%. Для меньших по размеру частиц, когда связанная с поверхностью вода и сила – нольные группы на поверхности частицы составляют значительную долю от ее массы, масс. % Si02 оказывается менее 100%. Однако, когда частицы кремнезема агрегируют и образуют суспендированную в системе массу микрогеля, подобные агрегаты составляют дисперсную фазу, которая также включает в себя и воду. В последнем примере масс. °/о Si02 значительно понижен. (Для обозначения концентрации кремнезема в дисперсной фазе Александер использовал символ S, но в данной монографии такая концентрация будет обозначаться символом Сй.) Величина вязкости дает возможность измерять содержание геля кремнезема, полученного из золя, при условии, что измерение выполняется при рН 2. Александер [9] подробно описал этот способ измерений. Золь кремнезема деионизируют и значение рН доводят до 2 добавлением сильной кислоты. Наиболее удобна для проведения эксперимента концентрация ~4% Si02, которая должна быть в точности известна. Измерения вязкости выполняют с образцами объемом в 10 мл при 30°С в пипетках Оствальда № 100. Величина — объемная доля дисперсной фазы — высчитывается из уравнения Муни [208], a Cd — доля (в масс. %), занимаемая в дисперсной фазе кремнеземом,— определяется по уравнению
Г________________ Ct____________
D O, OO566C, + 0 (1 -0.00566Q)
Где Сt — суммарное содержание кремнезема в золе, масс. %• Плотность аморфного кремнезема при этом принимается равной 2,2 г/см3. Золи, не содержащие сколько-нибудь заметного количества фазы геля, имеют Са менее 100 %, обычно 70—80 %, благодаря наличию воды, связанной с поверхностью частиц [64]. Если золь подвергается старению при низком значении рН, а вязкость повышается вследствие начинающегося процесса гелеобразования, то доля Са падает ниже 50 %.
В области значений рН*3—4, когда поверхность кремнезема заряжается очень слабо, в коммерческих кремнеземных золях на поверхности может обнаруживаться заметно больший отрицательный заряд, определяемый присутствием немногочисленных алюмосиликатных центров, так как алюминий почти всегда имеется на поверхности в качестве загрязнения. При рН 2 такие центры подавляются. Авторы работы [218] считают, что данные по вязкости дают основание предполагать существование на поверхности частиц кремнеземных золей при рН 2,8 гидратной оболочки толщиной 15 А, приблизительно соответствующей пяти мономолекулярным слоям воды. Толщина слоя представляет собой среднее расстояние от поверхности кремнезема до граничной поверхности скольжения при условии, что подобная поверхность частично заряжена. При высоких значениях рН гидратный слой вокруг частицы, содержащий проти – воионы, становится во много раз толще, чем это имеет место в разбавленных золях. Но в концентрированных, стабилизированных щелочью золях окружающая частицу оболочка из противоионов может быть сжата до такой степени, что ее толщина подсчитанная из вязкости, не составляет более 20—30 А. Как уже обсуждалось выше в связи с вопросом о получаемых практически наиболее высоких концентрациях коммерческих золей, содержащих различные по размеру частицы, было сделано заключение о том, что среднее значение минимальной толщины двойного слоя составляет примерно 2,4 нм, или 24 А.
Можно отметить, что для достижения наиболее высокой возможной концентрации коллоидного кремнезема с целью определенного его применения необходимо понижать значение рН до 2 для исключения электрического двойного слоя, а также использовать смесь, состоящую из двух или трех разновидностей золей, в значительной степени различающихся по размерам частиц [219]. Высушенный гель, полученный в виде смеси, состоящей из 10 массовых частей частиц размером 100 нм и 6,24 массовых частей частиц размером 7 нм, имел пористость, составляющую только 20 объемн. %.
Высокие значения удельной поверхности и скорости растворения аморфного кремнезема позволяют проводить необходимые реакции при значительно более низких температурах, чем это требуется для измельченного в порошок кристаллического кремнезема. Повышенная химическая реакционная …
Для некоторых применений желательно, чтобы поверхность кремнезема или стекла смачивалась водой. Но в то же время должны отсутствовать различные характерные ионные, гидрофобные или водородные связи, которые возникают при адсорбции органических …
Несомненно, что наиболее древними ископаемыми остатками живых организмов являются сине-зеленые водоросли, обнаруженные в виде включений в шерте (микрокристаллическом кремнеземе), открытые Баргхорном и Тайлером [12] и в дальнейшем изученные многими исследователями …
