Перестановки
- Выборки
- Перестановка без повторений
- Перестановка с повторениями
- Примеры
п.1. Выборки
Рассмотрим некоторое непустое конечное множество A мощностью |A| = n (т.е. состоящее из n элементов). Из этого множества всегда можно выбрать k элементов.
Выборка (кортеж) – набор из k элементов из некоторого множества n элементов. Назовём её ⟨n,k⟩ – выборка.
Важной характеристикой выборки является её упорядоченность.
Выборка называется упорядоченной, если в ней задан порядок следования элементов. Две упорядоченные выборки с одинаковым набором элементов, но разными порядками следования, являются различными.
Если порядок следования не задан (не важен), выборка называется неупорядоченной.
Второй важной характеристикой выборки является повторение элементов.
Если элементы в выборке не повторяются, она называется выборкой без повторений.
В отличие от множества, элементы в выборке могут повторяться; в этом случае она называется выборкой с повторениями. При этом может оказаться, что k > n – количество элекментов выборки больше мощности исходного множества.
Например:
Пусть задано множество A={a,b,c,d,e,f,g}. Его мощность |A|=7.
(a,c,d) – это ⟨7,3⟩– выборка без повторений
Если мы работаем с неупорядоченными выборками, то
(a,c,d) = (c,d,a) = (d,a,c) = …
Если мы определяем наши выборки как упорядоченные, то
(a,c,d) ≠ (c,d,a) ≠ (d,a,c) ≠ …
(a,a,a,g,c,d,e,e,g) – это ⟨7,9⟩– выборка с повторениями. Она также может быть упорядоченной или неупорядоченной, в зависимости от задачи.
п.2. Перестановка без повторений
Перестановка без повторений – это упорядоченная ⟨n,n⟩– выборка без повторений.
Общее количество перестановок без повторений:
$P_n=n!$
Лексикографический порядок – способ упорядочения перестановок, основанный на сравнении. Меньшей считается та перестановка, у которой на первом месте стоит меньший элемент. Если оба первых элементов равны, сравниваются вторые элементы; и т.д. Отношение лексикографического «меньше» обозначается ≺
Читается «меньше» или «предшествует».
Например:
1) Пусть задано множество A={a,b}, n=2
Его перестановки без повторений: (a,b) и (b,a) – итого два варианта (2!=2)
2) Для A={a,b,c}, n=3
Все перестановки без повторений:
(a,b,c),(b,c,a),(c,a,b),(b,a,c),(a,c,b),(c,b,a) – итого шесть вариантов (3!=6)
В лексикографическом порядке:
(a,b,c)≺(a,c,b)≺(b,a,c)≺(b,c,a)≺(c,a,b)≺(c,b,a)
п.3. Перестановка с повторениями
Перестановка с повторениями – это упорядоченная⟨n,k⟩ – выборка с повторениями, в которой элемент a1 повторяется k1 раз, элемент a2 повторяется k2 раз, и так далее, до последнего элемента as, который повторяется ks раз (s ≤ n). При этом
k = k1 + k2 + … + ks.
Общее количество перестановок с повторениями: $$ mathrm{ P_k(k_1,k_2,…,k_s)=frac{k!}{k_1!k_2!…k_s!} } $$
Например:
Сколько различных 6-тибуквенных слов можно написать из 3 букв {a,b,c}, если буква a должна повторяться 3 раза, буква b – 2 раза, буква c – 1 раз.
Пример такого слова: (a,b,a,a,b,c) – это ⟨3,6⟩ – выборка с повторениями.
По условию k1=3, k2=2, k3=1, k=3+2+1=6 $$ mathrm{ P_6(3,2,1)=frac{6!}{3! 2! 1!}=frac{720}{6cdot 2cdot 1}=60 } $$ Всего – 60 слов.
п.4. Примеры
Пример 1. Сколько 4-значных чисел можно составить из 4-х карточек с цифрами 0,1,3,5?
У нас только 4 карточки – значит, исследуем перестановки без повторений для ⟨4,4⟩-выборки. Таких перестановок P4 = 4! = 24.
Кроме того, нужно учесть, что число не может начинаться с 0. Отложим карточку «0» в сторону, и посчитаем, сколько перестановок без повторений у выборки (1,3,5), т.е. у ⟨3,3⟩- выборки: P3 = 3! = 6.
Получаем искомое число вариантов: N = P4 – P3 = 24 – 6 = 18
Ответ: 18.
Пример 2. У Маши четыре вазы. Сколькими способами Маша может расставить их по углам комнаты, если вазы разноцветные: белая, голубая, розовая и красная? Сколько способов останется, если все вазы – совершенно одинаковые?
1) Для разноцветных ваз рассматриваем ⟨4,4⟩-выборку вида (a,b,c,d). Количество перестановок без повторений P4 = 4! = 24.
2) Для одинаковых ваз рассматриваем ⟨4,4⟩-выборку вида (a,a,a,a). В выборке один элемент, который повторяется 4 раза. Количество перестановок с повторениями: (mathrm{P_4(4)=frac{4!}{4!}}). Для одинаковых ваз есть только 1 вариант.
Ответ: 24; 1.
Пример 3. Сколькими способами можно разместить на полке 7 книг? Если среди книг – один трёхтомник, тома которого нужно ставить рядом (в любом порядке), сколько способов размещения останется?
1) Для 7 книг рассматриваем ⟨7,7⟩-выборку. Количество перестановок без повторений P7 = 7! = 5040.
2) Для трёхтомника рассматриваем ⟨3,3⟩-выборку. Расставить 3 тома можно P3 = 3! = 6 способами. Теперь рассматриваем трёхтомник как одно целое: получатся, что нужно расставить 5 книг, т.е. посчитать перестановки без повторений для ⟨5,5⟩-выборки: P5 = 5! = 120 вариантов. Общее количество расстановок ищем по правилу произведения: N = P3 · P5 = 720.
Ответ: 5040; 720.
Пример 4. Сколько различных слов можно составить, переставляя буквы слова «МАТЕМАТИКА»? Сколько слов останется, если потребовать, чтобы три буквы «А» не стояли рядом?
1) По условию рассматриваем перестановки с повторениями.
a1=M, k1=2, a2=A, k2=3, a3=T, k3=2,
a4=E, k4=1, a5=И, k5=1, a6=K, k6=1,
k = k1 + k2 + … + k6 = 2+3+2+1+1+1 = 10
$$ mathrm{ P_{10}(2;3;2;1;1;1)=frac{10!}{2! cdot 3! cdot 2!}=frac{3628800}{2 cdot 6 cdot 2}=151200 } $$ 2) Найдем количество слов с тремя «А» подряд. Условие для перестановок с повторениями изменится так:
a1=M, k1=2, a2=”AAA”, k2=1, a3=T, k3=2,
a4=E, k4=1, a5=И, k5=1, a6=K, k6=1,
k = k1 + k2 + … + k6 = 2+1+2+1+1+1 = 8
$$ mathrm{ P_{8}(2;1;2;1;1;1)=frac{8!}{2! cdot 2!}=frac{40320}{2 cdot 2}=10080 } $$ Исключим слова с тремя «А» подряд из общего набора.
Останется N = 151200 – 10080 = 141120 слов.
Ответ: 151200 слов; 141120 слов.
Разработка урока по математике в 9 классе на тему: «Выборочные исследования. Выборки».
Урок «Выборочные исследования. Выборки».
Цель урока: конкретизировать представления учащихся о статистических исследованиях, обработке данных, интерпретации результатов; развивать способность к применению приемов обработки результатов статистических исследований к составлению таблиц, диаграмм и графиков; формировать навыки саморегуляции и самоорганизации, оценки и самооценки при работе в группах. Слайд №1
Задачи урока:
обучающая – формирование у учащихся представления о статистических понятиях – выборочные исследования, выборки, мода, среднеарифметическая ряда, медиана, репрезентативность исследования, генеральная совокупность, объем выборки, полигоны.
развивающая – развитие навыков аналитического мышления; развитие умений работать с различными источниками знаний, мыслить, анализировать, сравнивать, обобщать информацию.
воспитательная – развитие навыков работы в группе, формирование навыков самоконтроля, самооценки
Оборудование: Интерактивная доска, «Алгебра», учебник для 9 класса под редакцией Г.В. Дорофеева, раздаточный материал, мультимедиа – презентация.
Тип урока: урок закрепление
План урока
1. Организационный момент
2. Повторение ранее изученного материала
3. Изучение нового материала
4. Закрепление нового материала. Рефлексия.
5. Итоги урока
Ход урока
1.Организационный момент.
2. Повторение ранее изученного материала. Самостоятельная работа на 5-7 минут по подготовке к ОГЭ (по одному заданию из номеров 16,17,18 из пробных вариантов ОГЭ)
3. Изучение нового материала. Слайд №2.
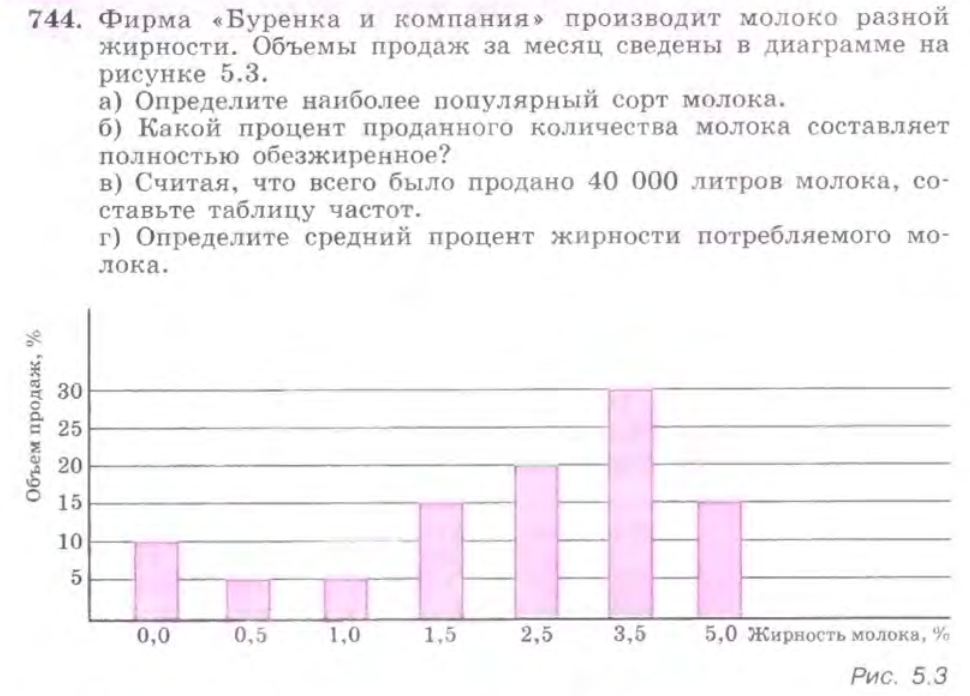
Совместно с классом, на примере ситуации, описанной в номере 744 учебника, еще раз обосновать необходимость статистических данных, вспомнить процесс сбора, обработки информации, и подвести учеников к самостоятельному выводу о методах представления полученных данных, и необходимости их анализа. Повторить и оперировать в решении задач такими понятиями как «генеральная совокупность», «репрезентативная выборка», «объем выборки», «таблица частот», «мода», «среднеарифметическая ряда», «медиана ряда», «ранжирование ряда данных». Ввести такие понятия как «полигоны частот», «гистограмма». Обосновать необходимость проведения правильной выборки.

4.Закрепление пройденного материала.
Для закрепления пройденной темы класс разбивается на 2 группы, одинаковых способностей. Каждая группа решает свой вариант и оформляют ее в 2 тетрадях, одна остается в группе для самопроверки, вторая передается второй команде для проверки и последующего оценивания.


Через указанное время, на интерактивной выводятся верные ответы для сверки (Слайд 3-4). Разбираются возможные ошибки, отмечаются лучшие результаты. Учитель при необходимости, корректирует выставленные оценки, при этом объясняя свою позицию, и прислушиваясь к мнению групп.
5.Подведение итогов урока. Рефлексия.
Вспомнить этапы работы со статистическими данными. Повторить новые понятия, введенные на уроке, их определения и записать их в опоры.
В конце урока раздать результаты самостоятельной работы, проведенной в начале урока, указать на наиболее часто встречаемые ошибки. Озвучить оценки, полученные в течении урока.
Домашнее задание. п.5.1., №745,743. Повторение: номера ОГЭ №15-19 (на самостоятельную работу)
Разработка урока по математике в 9 классе
на тему: «Выборочные исследования. Выборки».
Урок «Выборочные
исследования. Выборки».
Цель урока:
конкретизировать представления учащихся о статистических исследованиях,
обработке данных, интерпретации результатов; развивать способность к применению
приемов обработки результатов статистических исследований к составлению таблиц,
диаграмм и графиков; формировать навыки саморегуляции и самоорганизации, оценки
и самооценки при работе в группах. Слайд №1
Задачи урока:
обучающая
– формирование у учащихся представления о статистических понятиях – выборочные
исследования, выборки, мода, среднеарифметическая ряда, медиана,
репрезентативность исследования, генеральная совокупность, объем выборки,
полигоны.
развивающая
– развитие навыков аналитического мышления; развитие умений работать с
различными источниками знаний, мыслить, анализировать, сравнивать, обобщать
информацию.
воспитательная
– развитие навыков работы в группе, формирование навыков самоконтроля,
самооценки
Оборудование:
Интерактивная доска, «Алгебра», учебник для 9 класса под редакцией Г.В. Дорофеева,
раздаточный материал, мультимедиа – презентация.
Тип урока:
урок закрепление
План урока
1. Организационный момент
2. Повторение ранее изученного
материала
3. Изучение нового материала
4. Закрепление нового материала.
Рефлексия.
5. Итоги урока
Ход урока
1.Организационный момент.
2. Повторение
ранее изученного материала. Самостоятельная
работа на 5-7 минут по подготовке к ОГЭ (по одному заданию из номеров 16,17,18
из пробных вариантов ОГЭ)
3. Изучение нового материала. Слайд №2.
Совместно с
классом, на примере ситуации, описанной в номере 744 учебника, еще раз
обосновать необходимость статистических данных, вспомнить процесс сбора,
обработки информации, и подвести учеников к самостоятельному выводу о методах
представления полученных данных, и необходимости их анализа. Повторить и оперировать
в решении задач такими понятиями как «генеральная совокупность»,
«репрезентативная выборка», «объем выборки», «таблица частот», «мода», «среднеарифметическая
ряда», «медиана ряда», «ранжирование ряда данных». Ввести такие понятия как
«полигоны частот», «гистограмма». Обосновать необходимость проведения
правильной выборки.

4.Закрепление пройденного
материала.
Для закрепления пройденной темы класс
разбивается на 2 группы, одинаковых способностей. Каждая группа решает свой
вариант и оформляют ее в 2 тетрадях, одна остается в группе для самопроверки,
вторая передается второй команде для проверки и последующего оценивания.


Через указанное время, на интерактивной
выводятся верные ответы для сверки (Слайд 3-4). Разбираются возможные ошибки,
отмечаются лучшие результаты. Учитель при необходимости, корректирует
выставленные оценки, при этом объясняя свою позицию, и прислушиваясь к мнению
групп.
5.Подведение итогов урока. Рефлексия.
Вспомнить
этапы работы со статистическими данными. Повторить новые понятия, введенные на
уроке, их определения и записать их в опоры.
В конце урока
раздать результаты самостоятельной работы, проведенной в начале урока, указать
на наиболее часто встречаемые ошибки. Озвучить оценки, полученные в течении
урока.
Домашнее задание. п.5.1., №745,743. Повторение:
номера ОГЭ №15-19 (на самостоятельную работу)
Разработка урока по математике в 9 классе на тему: «Выборочные исследования. Выборки».
Урок «Выборочные исследования. Выборки».
Цель урока: конкретизировать представления учащихся о статистических исследованиях, обработке данных, интерпретации результатов; развивать способность к применению приемов обработки результатов статистических исследований к составлению таблиц, диаграмм и графиков; формировать навыки саморегуляции и самоорганизации, оценки и самооценки при работе в группах. Слайд №1
Задачи урока:
обучающая – формирование у учащихся представления о статистических понятиях – выборочные исследования, выборки, мода, среднеарифметическая ряда, медиана, репрезентативность исследования, генеральная совокупность, объем выборки, полигоны.
развивающая – развитие навыков аналитического мышления; развитие умений работать с различными источниками знаний, мыслить, анализировать, сравнивать, обобщать информацию.
воспитательная – развитие навыков работы в группе, формирование навыков самоконтроля, самооценки
Оборудование: Интерактивная доска, «Алгебра», учебник для 9 класса под редакцией Г.В. Дорофеева, раздаточный материал, мультимедиа – презентация.
Тип урока: урок закрепление
План урока
1. Организационный момент
2. Повторение ранее изученного материала
3. Изучение нового материала
4. Закрепление нового материала. Рефлексия.
5. Итоги урока
Ход урока
1.Организационный момент.
2. Повторение ранее изученного материала. Самостоятельная работа на 5-7 минут по подготовке к ОГЭ (по одному заданию из номеров 16,17,18 из пробных вариантов ОГЭ)
3. Изучение нового материала. Слайд №2.
Совместно с классом, на примере ситуации, описанной в номере 744 учебника, еще раз обосновать необходимость статистических данных, вспомнить процесс сбора, обработки информации, и подвести учеников к самостоятельному выводу о методах представления полученных данных, и необходимости их анализа. Повторить и оперировать в решении задач такими понятиями как «генеральная совокупность», «репрезентативная выборка», «объем выборки», «таблица частот», «мода», «среднеарифметическая ряда», «медиана ряда», «ранжирование ряда данных». Ввести такие понятия как «полигоны частот», «гистограмма». Обосновать необходимость проведения правильной выборки.
4.Закрепление пройденного материала.
Для закрепления пройденной темы класс разбивается на 2 группы, одинаковых способностей. Каждая группа решает свой вариант и оформляют ее в 2 тетрадях, одна остается в группе для самопроверки, вторая передается второй команде для проверки и последующего оценивания.
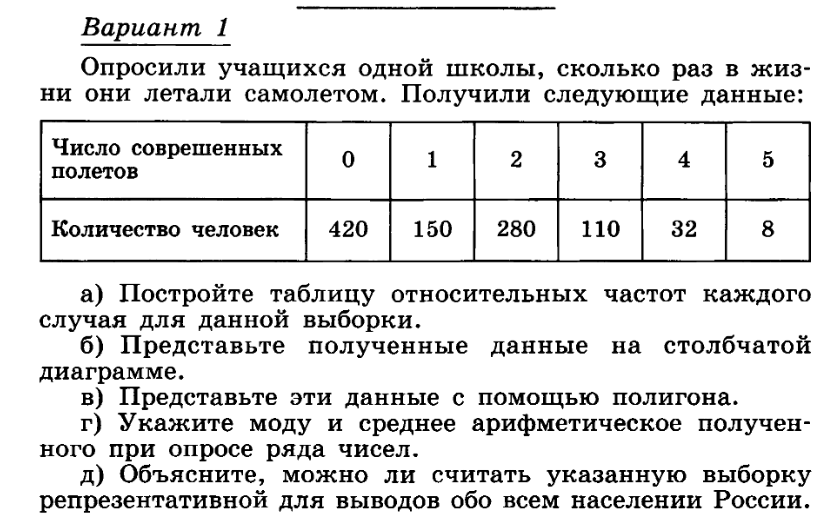
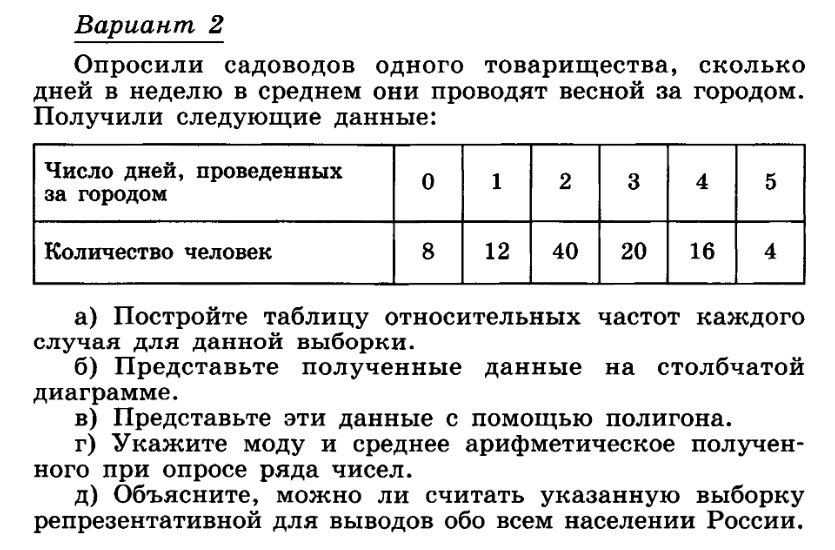
Через указанное время, на интерактивной выводятся верные ответы для сверки (Слайд 3-4). Разбираются возможные ошибки, отмечаются лучшие результаты. Учитель при необходимости, корректирует выставленные оценки, при этом объясняя свою позицию, и прислушиваясь к мнению групп.
5.Подведение итогов урока. Рефлексия.
Вспомнить этапы работы со статистическими данными. Повторить новые понятия, введенные на уроке, их определения и записать их в опоры.
В конце урока раздать результаты самостоятельной работы, проведенной в начале урока, указать на наиболее часто встречаемые ошибки. Озвучить оценки, полученные в течении урока.
Домашнее задание. п.5.1., №745,743. Повторение: номера ОГЭ №15-19 (на самостоятельную работу)
Слайд 1Генеральная совокупность и выборка.
Размах и центральные тенденции
Презентация
учителя математики
ГБОУ СОШ
№ 458
ГРИГОРЕНКО С. В.
9 класс

Слайд 2Генеральная совокупность и выборка
В реальной жизни схожие элементы некоторой совокупности
сравнивают по различным признакам
Например,
учащихся IX классов можно сравнивать по росту
или размеру одежды, или успеваемости и т. д.
болты можно сравнивать по длине, весу, материалу и т. д.
Практически любой признак либо поддается непосредственному измерению, либо может получить условную числовую характеристику.
Таким образом, некоторый признак совокупности можно рассматривать как случайную величину, принимающую те или иные числовые значения.

Слайд 3Генеральная совокупность и выборка
При изучении реальных явлений часто бывает невозможно
обследовать все элементы совокупности
Например,
практически невозможно выявить размеры обуви у всех
людей планеты
В подобных случаях вместо изучения всех элементов совокупности, которую называют генеральной совокупностью,
обследуют ее значительную часть, выбранную случайным образом. Эту часть называют выборкой

Слайд 4Генеральная совокупность и выборка
Если в выборке присутствуют все значения случайной
величины примерно в тех же пропорциях, что и в генеральной
совокупности, то эту выборку называют репрезентативной
Например,
если менеджер швейной фабрики города хочет выяснить, в каком количестве нужно шить одежду тех или иных размеров, он должен составить репрезентативную выборку людей этого города. При этом объем ее может быть не очень большим.
В качестве такой выборки нельзя брать только детей детского сада или только рабочих одного завода.
Микромоделью города могут послужить, например, жильцы многоквартирного дома или нескольких домов, в которых проживают люди разных возрастов и разных комплекции

Слайд 5Размах и центральные тенденции
Генеральные совокупности и выборки иногда приходится характеризовать
одним числом. Это бывает необходимо, например, для быстрого сравнения двух
или нескольких совокупностей по общему признаку.
Рассмотрим конкретный пример
Распределение случайной величины Х – числа прочитанных за каникулы книг десятью девочками по частотам М
Х 3 4 5 8 12
М 3 2 3 1 1
2) Распределение случайной величины У – числа прочитанных за каникулы книг девятью мальчиками того же класса
У 3 4 5 6 7
М 2 4 1 1 1

Слайд 6Размах и центральные тенденции
Сравним интерес к чтению девочек и мальчиков
этого класса
Для наглядности выпишем в виде упорядоченного ряда чисел –
последовательности значений случайной величины в порядке их возрастания.
При этом каждое значение выпишем столько раз, какова его частота в совокупности.
3 3 3 4 4 5 5 5 8 12
Получим следующие ряды
3 3 4 4 4 4 5 6 7

Слайд 7Размах и центральные тенденции
Для сравнения предложенных совокупностей могут быть использованы
следующие характеристики
1) Размах (обозначение R) – разница между наибольшим
и наименьшим значениями случайной величины
3 3 3 4 4 5 5 5 8 12
1. R1 = 12 – 3 = 9
3 3 4 4 4 4 5 6 7
2. R2 = 7 – 3 = 4

Слайд 8Размах и центральные тенденции
2) Мода (обозначение Мо) – наиболее
часто встречающееся значение случайной величины
3 3
3 4 4 5 5 5 8 12
В совокупности 1 Мо1 = 3 и Мо2 = 5
3 3 4 4 4 4 5 6 7
В совокупности 2 Мо = 4

Слайд 9Размах и центральные тенденции
3) Медиана (обозначение Ме) – это
так называемое серединное значение упорядоченного ряда значений случайной величины
3 3 3 4 4 5 5 5 8 12
В совокупности 1 (N = 10) – четное. Для него медиана равна среднему арифметическому двух центральных значений (пятого и шестого)
3 3 4 4 4 4 5 6 7
Ме = (4 + 5) : 2 = 4,5
В совокупности 2 (N = 9) – нечетное. Для него медиана равна значению центрального (пятого) члена ряда
Ме = 4

Слайд 10Размах и центральные тенденции
4) Среднее значение (обозначение Х) –
среднее арифметическое всех значений случайной величины
3
3 3 4 4 5 5 5 8 12
3 3 4 4 4 4 5 6 7
Хд = (3·3 + 4·2 + 5·3 + 8 + 12) : (3 + 2 + 3 + 1 +1) = 52 : 10 = 5,2
Хм = (3·2 + 4·4 + 5 + 6 + 7) : (2 + 4+ 1 + 1 +1) = 40 : 9 ≈ 4,4

Слайд 11Задача
Найти размах, моду и медиану следующей совокупности значений случайной величины
-2 3 4
-3 0 1 3 -2 -1 2 -2 1
Записываем значения в виде упорядоченного ряда
-3 -2 -2 -2 -1 0 1 1 2 3 3 4
1. R = 4 – (-3) = 7
2. Me = (0 + 1) : 2 = 0,5
3. Мо = -2

