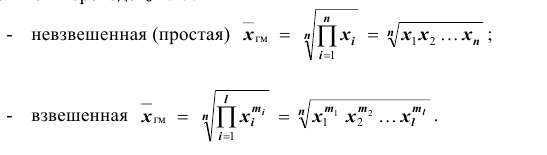Содержание курса лекций “Статистика”
Выборочное наблюдение как источник статистической информации в изучении социально-экономических явлений и процессов

Статистическая методология исследования массовых явлений различает, как известно, два способа наблюдения в зависимости от полноты охвата объекта: сплошное и несплошное. Разновидностью несплошного наблюдения является выборочное, которое в условиях рыночных отношений в России находит все более широкое применение. Переход статистики РФ на международные стандарты системы национального счетоводства требует более широкого применения выборки для получения и анализа показателей СНС не только в промышленности, но и в других секторах экономики.
Под выборочным наблюдением понимается несплошное наблюдение, при котором статистическому обследованию (наблюдению) подвергаются единицы изучаемой совокупности, отобранные случайным способом. Выборочное наблюдение ставит перед собой задачу ‑ по обследуемой части дать характеристику всей совокупности единиц при условии соблюдения всех правил и принципов проведения статистического наблюдения и научно организованной работы по отбору единиц.
К выборочному наблюдению статистика прибегает по различным причинам. На современном этапе появилось множество субъектов хозяйственной деятельности, которые характерны для рыночной экономики. Речь идет об акционерных обществах, малых и совместных предприятиях, фермерских хозяйствах и т.д. Сплошное обследование этих статистических совокупностей, состоящих из десятков и сотен тысяч единиц, потребовало бы огромных материальных, финансовых и иных затрат. Использование же выборочного обследования позволяет значительно сэкономить силы и средства, что имеет немаловажное значение.
Наряду с экономией ресурсов одной из причин превращения выборочного наблюдения в важнейший источник статистической информации является возможность значительно ускорить получение необходимых данных. Ведь при обследовании, скажем, 10% единиц совокупности будет затрачено гораздо меньше времени, а результаты могут быть представлены быстрее, и будут более актуальными. Фактор времени важен для статистического исследования особенно в условиях изменяющейся социально-экономической ситуации.
Реализация выборочного метода базируется на понятиях генеральной и выборочной совокупностей.
Генеральной совокупностью называется вся исходная изучаемая статистическая совокупность, из которой на основе отбора единиц или групп единиц формируется совокупность выборочная. Поэтому генеральную совокупность также называют основой выборки.
Отбор единиц в выборочную совокупность может быть повторным или бесповторным.
При повторном отборе попавшая в выборку единица подвергается обследованию, т.е. регистрации значений ее признаков, возвращается в генеральную совокупность и наравне с другими единицами участвует в дальнейшей процедуре отбора. Таким образом, некоторые единицы могут попадать в выборку дважды, трижды или даже большее число раз. И при изучении выборочной совокупности они будут рассматриваться как отдельные независимые наблюдения.
Отметим, что число единиц генеральной совокупности, участвующих в отборе, при таком подходе остается постоянным. Поэтому вероятность попадания в выборку для всех единиц совокупности на протяжении всего процесса отбора также не меняется.
На практике методология повторного отбора обычно используется в тех случаях, когда объем генеральной совокупности не известен и теоретически возможно повторение единиц с уже встречавшимися значениями всех регистрируемых признаков.
Например, при проведении маркетинговых исследований мы не можем сколько-нибудь точно оценить, какое число потребителей предпочитают стиральный порошок конкретной торговой марки, сколько покупателей предпочитают делать покупки именно в данном супермаркете и т.д. Поэтому возможно повторение совершенно идентичных единиц как по причине практически неограниченных объемов совокупности, так и вследствие возможной повторной регистрации. Предположим, при проведении обследования один и тот же покупатель может дважды прийти в магазин и дважды подвергнуться обследованию.
При выборочном контроле качества продукции объем генеральной совокупности также часто не определен, так как процесс производства может осуществляться постоянно, каждый день дополняя генеральную совокупность новыми единицами-изделиями. Поэтому в выборочную совокупность могут попасть два и более изделий с абсолютно одинаковыми характеристиками. Следовательно, и в этом случае при обработке результатов выборки необходимо ориентироваться на методологию, используемую при повторном отборе.
При бесповоротном отборе попавшая в выборку единица подвергается обследованию и в дальнейшей процедуре отбора не участвует. Такой отбор целесообразен и практически возможен в тех случаях, когда объем генеральной совокупности четко определен. Получаемые при этом результаты, как правило, являются более точными по сравнению с результатами, основанными на повторной выборке.
Как уже отмечалось выше, выборочное наблюдение всегда связано с определенными ошибками получаемых характеристик. Эти ошибки называются ошибками репрезентативности (представительности).
Ошибки репрезентативности обусловлены тем обстоятельством, что выборочная совокупность не может по всем параметрам в точности воспроизвести совокупность генеральную. Получаемые расхождения или ошибки репрезентативности позволяют заключить, в какой степени попавшие в выборку единицы могут представлять всю генеральную совокупность. При этом следует различать систематические и случайные ошибки репрезентативности.
Систематические ошибки репрезентативности связаны с нарушением принципов формирования выборочной совокупности. Например, вследствие каких-либо причин, связанных с организацией отбора, в выборку попали единицы, характеризующиеся несколько большими или, наоборот, несколько меньшими по сравнению с другими единицами значениями наблюдаемых признаков. В этом случае и рассчитанные выборочные характеристики будут завышенными или заниженными.
Случайные ошибки репрезентативности обусловлены действием случайных факторов, не содержащих каких-либо элементов системности в направлении воздействия на рассчитываемые выборочные характеристики. Но даже при строгом соблюдении всех принципов формирования выборочной совокупности выборочные и генеральные характеристики будут несколько различаться. Получаемые случайные ошибки могут быть статистически оценены и учтены при распространении результатов выборочного наблюдения на всю генеральную совокупность. Оценка ошибок выборочного наблюдения основана на теоремах теории вероятностей.
При дальнейшем рассмотрении теории и методов выборочного наблюдения используются следующие общепринятые условные обозначения:
N ‑ объем (число единиц) генеральной совокупности;
n ‑ объем (число единиц) выборочной совокупности;
![]()
‑ генеральная средняя, т.е. среднее значение изучаемого признака по генеральной совокупности (средняя прибыль, средняя величина активов, средняя численность работников предприятия и т.п.);
![]()
‑ выборочная средняя,
т.е. среднее значение изучаемого признака по выборочной совокупности;
М ‑ численность единиц генеральной совокупности, обладающих определенным вариантом или вариантами изучаемого признака (численность городского населения, численность сельского населения, количество бракованных изделий, число нерентабельных предприятий и т.п.);
р ‑ генеральная доля, т.е. доля единиц, обладающих определенным вариантом или вариантами изучаемого признака, во всей генеральной совокупности (доля городского населения в общей численности населения, доля бракованной продукции в общем выпуске, доля нерентабельных предприятий в общей численности предприятий и т.п.); определяетcя как
m ‑ численность единиц выборочной совокупности, обладающих определенным вариантом или вариантами изучаемого признака;
w ‑ выборочная доля, т.е. доля единиц, обладающих определенным вариантом или вариантами изучаемого признака, в выборочной совокупности,
определяется как ;
![]()
‑ средняя ошибка выборки;
![]()
‑ предельная ошибка выборки;
![]()
‑ коэффициент доверия, определяемый в зависимости от уровня вероятности.
Ошибка выборки или отклонение выборочной средней от средней генеральной находится в прямой зависимости от дисперсии изучаемого признака в генеральной совокупности, и в обратной зависимости ‑ от объема выборки.
Таким образом среднюю ошибку выборки можно представить как

(10.1)
При проведении выборочного наблюдения дисперсия изучаемого признака в генеральной совокупности, как правило, не известна. В то же время, между генеральной дисперсией и средней из всех возможных выборочных дисперсий существует следующее соотношение:

(10.2)
В связи с тем, что на практике в большинстве случаев из генеральной совокупности в определенный момент времени производится только одна выборка, дисперсия изучаемого признака по этой выборке и используется при расчете ошибки.
Учитывая, что при достаточно большом объеме выборки отношение  близко к 1, формула средней ошибки повторной выборки принимает следующий вид:
близко к 1, формула средней ошибки повторной выборки принимает следующий вид:

(10.3)
Где ‑ ![]() дисперсия изучаемого признака по выборочной совокупности.
дисперсия изучаемого признака по выборочной совокупности.
При определении возможных границ значений характеристик генеральной совокупности рассчитывается предельная ошибка выборки, которая зависит от величины ее средней ошибки и уровня вероятности, с которым гарантируется, что генеральная средняя не выйдет за указанные границы.
Согласно теореме А.М. Ляпунова, вероятность той или иной величины предельной ошибки, при достаточно большом объеме выборочной совокупности, подчиняется нормальному закону распределения и может быть определена на основе интеграла Лапласа.
Значения интеграла Лапласа при различных величинах t табулированы и представлены в статистических справочниках.
При обобщении результатов выборочного наблюдения наиболее часто используются следующие уровни вероятности и соответствующие им значения t:
Таблица 10.1 ‑ !!!Некоторые значения t
| Вероятность, рi. | 0,683 | 0,866 | 0,954 | 0,988 | 0,997 | 0,999 |
| Значение t | 1,0 | 1,5 | 2,0 | 2,5 | 3,0 | 3,5 |
Например, если при расчете предельной ошибки выборки мы используем значение t=2, то с вероятностью 0,954 можно утверждать, что расхождение между выборочной средней и генеральной средней не превысит двукратной величины средней ошибки выборки.
Теоретической основой для определения границ генеральной доли, т.е. доли единиц, обладающих тем или иным вариантом признака, является теорема Вернули. Согласно данной теореме вероятность получения сколь угодно малого расхождения между выборочной долей и генеральной долей при достаточно большом объеме выборки будет стремиться к единице. С учетом того, что вероятность расхождения между выборочной и генеральной долями подчиняется нормальному закону распределения, эта вероятность также определяется по функции F(t) при заданном значении t.
Процесс подготовки и проведения выборочного наблюдения включает ряд последовательных этапов:
- Определение цели обследования.
- Установление границ генеральной совокупности.
- Составление программы наблюдения и программы разработки данных
- Определение вида выборки, процента отбора и метода отбора
- Отбор и регистрация наблюдаемых признаков у отобранных единиц.
- Насчет выборочных характеристик и их ошибок.
- Распространение полученных результатов на генеральную совокупность.
В зависимости от состава и структуры генеральной совокупности выбирается вид выборки или способ отбора.
К наиболее распространенным на практике видам относятся:
- собственно-случайная (простая случайная) выборка;
- механическая (систематическая) выборка;
- типическая (стратифицированная, расслоенная) выборка;
- серийная (гнездовая) выборка.
Отбор единиц из генеральной совокупности может быть комбинированным, многоступенчатым и многофазным.
Комбинированный отбор предполагает объединение нескольких видов выборки. Так, например, можно комбинировать типическую и серийную, серийную и собственно-случайную выборки. Ошибка такой выборки определяется ступенчатостью отбора.
Многоступенчатым называется отбор, при котором из генеральной совокупности сначала извлекаются укрупненные группы, потом ‑ более мелкие и так до тех пор, пока не будут отобраны те единицы, которые подвергаются обследованию.
Многофазная выборка, в отличие от многоступенчатой, предполагает сохранение одной и той же единицы отбора на всех этапах его проведения; при этом отобранные на каждой стадии единицы подвергаются обследованию, каждый раз – по более расширенной программе.
Собственно-случайная (простая случайная) выборка заключается в отборе единиц из генеральной совокупности наугад или наудачу без каких-либо элементов системности.
Однако прежде чем производить собственно-случайный отбор, необходимо убедиться, что все без исключения единицы генеральной совокупности имеют абсолютно равные шансы попадания в выборку, в списках или перечне отсутствуют пропуски, игнорирования отдельных единиц и т.п. Следует также установить четкие границы генеральной совокупности таким образом, чтобы включение или не включение в нее отдельных единиц не вызывало сомнений. Так, например, при обследовании студентов необходимо указать, будут ли приниматься во внимание лица, находящиеся в академическом отпуске, студенты негосударственных вузов, военных училищ и т.п.; при обследовании торговых предприятий важно определиться, включит ли генеральная совокупность торговые павильоны, коммерческие палатки и прочие подобные объекты.
Технически собственно-случайный отбор проводят методом жеребьевки или по таблице случайных чисел.
Расчет ошибок позволяет решить одну из главных проблем организации выборочного наблюдения – оценить репрезентативность (представительность) выборочной совокупности.
Различают среднюю и предельную ошибки выборки. Эти два вида связаны следующим соотношением:

(10.4)
Величина средней ошибки выборки рассчитывается дифференцированно в зависимости от способа отбора и процедуры выборки.
Так, при собственно-случайном повторном отборе средняя ошибка определяется по формуле:

(10.5)
а при расчете средней ошибки собственно-случайной бесповторной выборки:

(10.6)
Расчет средней и предельной ошибок выборки позволяет определить возможные пределы, в которых будут находиться характеристики генеральной совокупности.
Например, для выборочной средней такие пределы устанавливаются на основе следующих соотношений:

(10.7)
где ![]() и
и ![]() ‑ генеральная и выборочная средняя соответственно;
‑ генеральная и выборочная средняя соответственно;
![]() ‑ предельная ошибка выборочной средней.
‑ предельная ошибка выборочной средней.
Пример.
При проверке веса импортируемого груза на таможне методом случайной повторной выборки было отобрано 200 изделий. В результате был установлен средний вес изделия 30 г. при среднем квадратическом отклонении 4 г. С вероятностью 0,997 определите пределы, в которых находится средний вес изделия в генеральной совокупности.
Решение. Рассчитаем сначала предельную ошибку выборки. Так как при р = 0,997, t = 3, она равна:
Определим пределы генеральной средней:
 или
или

Вывод: Следовательно, с вероятностью 0,997 можно утверждать, что средний вес изделий в генеральной совокупности находится в пределах от 29,16 г. до 30,84 г.
Пример 2.
В городе проживает 250 тыс. семей. Для определения среднего числа детей в семье была организована 2%-ная случайная бесповторная выборка семей. По ее результатам было получено следующее распределение семей по числу детей:
Таблица 10.2 ‑ Распределение семей по числу детей в городе N
| Число детей в семье | 0 | 1 | 2 | 3 | 4 | 5 |
| Количество
семей |
1000 | 2000 | 1200 | 400 | 200 | 200 |
С вероятностью 0,954 определите пределы, в которых будет находиться среднее число детей в генеральной совокупности.
Решение. В начале на основе имеющегося распределения семей определим выборочные среднюю и дисперсию:
Таблица 10.3 ‑ Вспомогательная таблица для расчета среднего числа детей
|
Число детей в семье, х; |
Количество семей, f | ||||
|
0 1 2 3 4 5 |
1000 2000 1200 400 200 200 |
0
2000 2400 1200 800 1000 |
-1,5
-0,5 0,5 1,5 2,5 3,5 |
2,25
0,25 0,25 2,25 6,25 12,25 |
2250 500 300 900 1250 2450 |
|
Итого |
5000 | 7400 | – | – | 7650 |


Вычислим теперь предельную ошибку выборки (с учетом того, что при р = 0,954 t = 2).

Следовательно, пределы генеральной средней:

Таким образом, с вероятностью 0,954 можно утверждать, что среднее число детей в семьях города практически не отличается от 1,5, т.е. в среднем на каждые две семьи приходится три ребенка.
Наряду с определением ошибок выборки и пределов для генеральной средней эти же показатели могут быть определены для доли признака.
В этом случае особенности расчета связаны с определением дисперсии доли, которая вычисляется так:

(10.8)
где ![]() ‑ доля единиц, обладающих данным признаком в выборочной совокупности, определяемая как отношение количества соответствующих единиц к объему выборки.
‑ доля единиц, обладающих данным признаком в выборочной совокупности, определяемая как отношение количества соответствующих единиц к объему выборки.
Тогда, например, при собственно-случайном повторном отборе для определения предельной ошибки выборки используется следующая формула:

(10.9)
Соответственно, при бесповторном отборе:

(10.10)
Пределы доли признака в генеральной совокупности p выглядят следующим образом:

(10.11)
Рассмотрим пример.
С целью определения средней фактической продолжительности рабочего дня в государственном учреждении с численностью служащих 480 человек, в январе 2009 г. было проведена 25%-ная случайная бесповторная выборка. По результатам наблюдения оказалось, что у 10% обследованных потери времени достигали более 45 мин. в день. С вероятностью 0,683 установите пределы, в которых находится генеральная доля служащих с потерями рабочего времени более 45 мин. в день.
Решение. Определим объем выборочной совокупности:
n= 480 х 0,25 = 120 чел.
Выборочная доля w равна по условию 10%.
Учитывая, что при р = 0,683 t=1, вычислим предельную ошибку выборочной доли:

Пределы доли признака в генеральной совокупности:

Таким образом, с вероятностью 0,683 можно утверждать, что доля работников учреждения с потерями рабочего времени более 45 мин. в день находится в пределах от 7,6% до 12,4%.
Мы рассмотрели определение границ генеральной средней и генеральной доли по результатам уже проведенного выборочного наблюдения, при известном объеме выборки или проценте отбора. На этапе же проектирования выборочного наблюдения именно объем выборочной совокупности и требует определения.
Для определения необходимого объема собственно-случайной повторной выборки применяют следующую формулу:

(10.12)
Полученный на основе использования данной формулы результат всегда округляется в большую сторону. Например, если мы получили, что необходимый объем выборки составляет 493,1 единицы, то обследовав 493 единицы мы не достигнем требуемой точности. Поэтому, для достижения желаемого результата обследованием должны быть охвачены 494 единицы.
С другой стороны, рассчитанное значение необходимого объема выборки свободно может быть увеличено в большую сторону на несколько единиц. Если мы располагаем необходимыми ресурсами, если по причинам организационного порядка (компактность расположения единиц, фиксированная нагрузка на каждого регистратора и т.п.) мы вполне можем охватить больший объем, то включение в выборочную совокупность 500 или, например, 550 единиц только уменьшит значения полученных случайной и предельной ошибок.
При определении необходимого объема выборки для определения границ генеральной доли задача оценки вариации решается значительно проще. Если дисперсия изучаемого альтернативного признака неизвестна, то можно использовать ее максимальное возможное значение:

Например, предприятию связи с вероятностью 0,954 необходимо определить удельный вес телефонный разговоров продолжительностью менее 1 минуты с предельной ошибкой 2%. Сколько разговоров нужно обследовать в порядке собственно-случайного повторного отбора для решения этой задачи?
Для получения ответа на поставленный вопрос воспользуемся формулой (10.12) и будем ориентироваться на максимальную возможную дисперсию доли телефонных разговоров такой продолжительности. Расчет приводит к следующему результату:

Таким образом, обследованием должны быть охвачены не менее 2500 разговоров на предмет их продолжительности.
Необходимый объем собственно-случайной бесповторной выборки может быть определен по следующей формуле:

(10.13)
Укажем на одну особенность формулы (10.13). При проведении вычислений объем генеральной совокупности должен быть выражен только в единицах, а не в тысячах или в миллионах единиц.
Например, подставив в данную формулу общую численность населения региона, выраженную в тысячах человек, мы не получим правильное значение необходимой численности выборки, также выраженное в тысячах человек, как это иногда бывает в других расчетах. Результат вычислений будет неверен.
Механическая выборка может быть применена в тех случаях, когда генеральная совокупность каким-либо образом упорядочена, т.е. имеется определенная последовательность в расположении единиц (табельные номера работников, списки избирателей, телефонные номера респондентов, номера домов и квартир и т.п.). Для проведения отбора желательно, чтобы все единицы также имели порядковые номера от 1 до N.
Для проведения механической выборки устанавливается пропорция отбора, которая определяется соотнесением объемов выборочной и генеральной совокупностей.
Так, если из совокупности в 500000 единиц предполагается отобрать 10000 единиц, то пропорция отбора составит

Отбор единиц осуществляется в соответствии с установленной пропорцией через равные интервалы.
Например, при пропорции 1:50 (2%-ная выборка) отбирается каждая 50-я единица, при пропорции 1:20 (5%-ная выборка) – каждая 20-я единица и т.д.
Интервал отбора также можно определить как частное от деления 100% на установленный процент отбора.
Так, например при 2%-ном отборе интервал составит 50 (100%:2%), при 4%-ном отборе ‑ 25 (100%:4%). В тех случаях, когда результат деления получается дробным, сформировать выборку механическим способом при строгом соблюдении процента отбора не представляется возможным.
Например, по этой причине нельзя сформировать 3%-ную или 6%-ную выборки.
Генеральную совокупность при механическом отборе можно ранжировать или упорядочить по величине изучаемого или коррелирующего с ним признака, что позволит повысить репрезентативность выборки. Однако в этом случае возрастает опасность систематической ошибки, связанной с занижением значений изучаемого признака (если из каждого интервала регистрируется первое значение) или его завышением (если из каждого интервала регистрируется последнее значение). Поэтому целесообразно из каждого интервала отбирать центральную или одну из двух центральных единиц.
Например, при 5%-ной выборке интервал отбора составит 20 единиц, тогда отбор целесообразно начинать с 10-й или с 11-й единицы. В первом случае в выборку попадут 10, 30, 50, 70 и с таким же интервалом последующие единицы; во втором случае – единицы с номерами 11,31,51,71 и т.д.
При механической выборке также может появиться опасность систематической ошибки, обусловленной случайным совпадением выбранного интервала и циклических закономерностей в расположении единиц генеральной совокупности. Так, при переписи населения 1989 г. в ходе 25%-го выборочного обследования семей имела место опасность попадания в выборку квартир только одного типа (например, только однокомнатных или только трехкомнатных), так как на лестничных площадках многих типовых домов располагаются именно по 4 квартиры. Чтобы избежать систематической ошибки, в каждом новом подъезде счетчик менял начало отбора.
Для определения средней ошибки механической выборки, а также необходимой ее численности, используются соответствующие формулы, применяемые при собственно-случайном бесповторном отборе(10.6 и 10.13). При этом, определив необходимую численность выборки и сопоставив ее с объемом генеральной совокупности, как правило, приходится производить соответствующее округление для получения целочисленного интервала отбора.
Например, в области зарегистрировано 12000 фермерских хозяйств. Определим, сколько из них нужно отобрать в порядке механического отбора для определения средней площади сельхозугодий с ошибкой ± 2 га. (Р=0,997). По результатам ранее проведенного обследования известно, что среднее квадратическое отклонение площади сельхозугодий составляет 8 га. Произведем расчет, воспользовавшись формулой (10.13).

С учетом полученного необходимого объема выборки (143 фермерских хозяйства) определим интервал отбора: 12000:143=83,9.
Определенный таким способом интервал всегда округляется в меньшую сторону, так как при округлении в большую сторону произведенная выборка не достигнет рассчитанного по формуле необходимого объема.
Следовательно, в нашем примере, из общего списка фермерских хозяйств необходимо отобрать для обследования каждое 83-е хозяйство. При этом процент отбора составит 1,2% (100% : 83).
Типический отбор целесообразно использовать в тех случаях, когда все единицы генеральной совокупности объединены в несколько крупных типических групп.. Такие группы также называют стартами или слоями, в связи с чем типический отбор также называют стратифицированным или расслоенным. При обследованиях населения в качестве типических групп могут быть выбраны области, районы, социальные, возрастные или образовательные группы, при обследовании предприятий – отрасли или подотрасли, формы собственности и т.п.
Рассматривать генеральную совокупность в разрезе нескольких крупных групп единиц имеет смысл только в том случае, если средние значения изучаемых признаков по группам существенно различаются. Например, с большой уверенностью можно предположить, что доходы населения крупного города будут в среднем выше доходов населения, проживающего в сельской местности; численность работников промышленного предприятия в среднем будет выше численности работников торгового или сельскохозяйственного предприятия; средний возраст студентов будет значительно меньше среднего возраста занятого населения и, тем более, пенсионеров. В то же время, нет никакого смысла при выделении типических групп ориентироваться на признак, не связанный или очень слабо связанный с изучаемым.
Отбор единиц в выборочную совокупность из каждой типической группы осуществляется собственно-случайным или механическим способом. Поскольку в выборочную совокупность в той или иной пропорции обязательно попадают представители всех групп, типизация генеральной совокупности позволяет исключить влияние межгрупповой дисперсии на среднюю ошибку выборки. В то же время, в выделенных типических группах обследуются далеко не все единицы, а только включенные в выборку. Следовательно, на величине полученной ошибки будет сказываться различие между единицами внутри этих групп, т.е. внутригрупповая вариация. Поэтому, ошибка типической выборки будет определяться величиной не общей дисперсии, а только ее части – средней из внутригрупповых дисперсий.
При типической выборке, пропорциональной объему типических групп, число единиц, подлежащих отбору из каждой группы, определяется следующим образом:

(10.14)
Где Ni – объем i-ой группы. а ni ‑ объем выборки из i-ой группы.
Пример. Предположим, общая численность населения области составляет 1,5 млн. чел., в том числе городское – 900 тыс. чел. и сельское – 600 тыс. чел. Если в ходе выборочного наблюдения планируется обследовать 100 тыс. жителей, то эта численность должна быть поделена пропорционально объему типических групп следующим образом:

Средняя ошибка типической выборки определяется по формулам:

(10.15)
 (10.16)
(10.16)
где ![]() – средняя из внутригрупповых дисперсий.
– средняя из внутригрупповых дисперсий.
При выборке, пропорциональной дифференциации признака, число наблюдений по каждой группе рассчитывается по формуле:

(10.17)
Где ![]() ‑ среднее отклонение признака в i-ой группе.
‑ среднее отклонение признака в i-ой группе.
Cредняя ошибка такого отбора определяется следующим образом:

(10.18)

(10.19)
Отбор, пропорциональный дифференциации признака, дает лучшие результаты, однако на практике его применение затруднено вследствие трудности получения сведений о вариации до проведения выборочного наблюдения.
Таблица 10.4 ‑ Результаты обследования рабочих предприятия
| Цех | Всего рабочих, человек | Обследовано, человек | Число дней временной нетрудоспособности за год | |
| средняя | дисперсия | |||
| I
II III |
1000
1400 800 |
100
140 80 |
18
12 15 |
49
25 16 |
Рассмотрим оба варианта типической выборки на условном примере. Предположим, 10% бесповторный типический отбор рабочих предприятия, пропорциональный размерам цехов, проведенный с целью оценки потерь из-за временной нетрудоспособности, привел к следующим результатам (табл. 10.4)
Рассчитаем среднюю из внутригрупповых дисперсий:

Определим среднюю и предельную ошибки выборки (с вероятностью 0,954):

Рассчитаем выборочную среднюю:

С вероятностью 0,954 можно сделать вывод, что среднее число дней временной нетрудоспособности одного рабочего в целом по предприятию находится в пределах:

Воспользуемся полученными внутригрупповыми дисперсиями для проведения отбора пропорционального дифференциации признака. Определим необходимый объем выборки по каждому цеху:


С учетом полученных значений рассчитаем среднюю ошибку выборки:

В данном случае средняя, а следовательно, и предельная ошибки будут несколько меньше, что отразится и на границах генеральной средней.
Серийный отбор. Данный способ отбора удобен в тех случаях, когда единицы совокупности объединены в небольшие группы или серии. В качестве таких серий могут рассматриваться упаковки с определенным количеством готовой продукции, партии товара, студенческие группы, бригады и другие объединения. Сущность серийной выборки заключается в собственно-случайном или механическом отборе серий, внутри которых производится сплошное обследование единиц.
Поскольку внутри групп (серий) обследуются все без исключения единицы, средняя ошибка серийной выборки (при отборе равновеликих серий) зависит от величины только межгрупповой (межсерийной) дисперсии и определяется по следующим формулам:

(10.20)

(10.21)
Где r ‑ число отобранных серий; R ‑ общее число серий.
Межгрупповую дисперсию вычисляют следующим образом:
 (10.22)
(10.22)
где ![]() ‑ средняя i-й серии;
‑ средняя i-й серии;
![]() ‑ общая средняя по всей выборочной совокупности.
‑ общая средняя по всей выборочной совокупности.
Пример.
В области, состоящей из 20 районов, проводилось выборочное обследование урожайности на основе отбора серий (районов). Выборочные средние по районам составили соответственно 14,5 ц/га; 16 ц/га; 15,5 ц/га; 15 ц/га и 14 ц/га. С вероятностью 0,954 определите пределы урожайности во всей области.
Решение. Рассчитаем общую среднюю:

Межгрупповая (межсерийная) дисперсия равна:

Определим теперь предельную ошибку серийной бесповторной выборки (t = 2 при р = 0,954):

Вывод: Следовательно, урожайность будет с вероятностью 0,954 находиться в пределах:

Определение необходимого объема выборки
При проектировании выборочного наблюдения возникает вопрос о необходимой численности выборки. Эта численность может быть определена на базе допустимой ошибки при выборочном наблюдении, исходя из вероятности, на основе которой можно гарантировать величину устанавливаемой ошибки, и, наконец, на базе способа отбора.
Формулы необходимого объема выборки для различных способов формирования выборочной совокупности могут быть выведены из соответствующих соотношений, используемых при расчете предельных ошибок выборки. Приведем наиболее часто применяемые на практике выражения необходимого объема выборки:
– собственно-случайная и механическая выборка:

(10.23)

(10.24)
– типическая выборка:

(10.25)

(10.26)
– серийная выборка:

(10.27)

(10.28)
При этом в зависимости от целей исследования дисперсии и ошибки выборки могут быть рассчитаны для средней величины или доли признака.
Рассмотрим примеры определения необходимого объема выборки при различных способах формирования выборочной совокупности.
Пример.
В 100 туристических агентствах города предполагается провести обследование среднемесячного количества реализованных путевок методом механического отбора. Какова должна быть численность выборки, чтобы с вероятностью 0,683 ошибка не превышала 3 путевок, если по данным пробного обследования дисперсия составляет 225.
Решение. Рассчитаем необходимый объем выборки:

Пример.
С целью определения доли сотрудников коммерческих банков области в возрасте старше 40 лет предполагается организовать типическую выборку пропорциональную численности сотрудников мужского и женского пола с механическим отбором внутри групп. Общее число сотрудников банков составляет 12 тыс. чел., в том числе 7 тыс. мужчин и 5 тыс. женщин.
На основании предыдущих обследований известно, что средняя из внутригрупповых дисперсий составляет 1600. Определите необходимый объем выборки при вероятности 0,997 и ошибке 5%.
Решение. Рассчитаем общую численность типической выборки:

Вычислим теперь объем отдельных типических групп:

Вывод: Таким образом, необходимый объем выборочной совокупности сотрудников банков составляет 550 чел., в т.ч. 319 мужчин и 231 женщина.
Пример.
В акционерном обществе 200 бригад рабочих. Планируется проведение выборочного обследования с целью определения удельного веса рабочих, имеющих профессиональные заболевания. Известно, что межсерийная дисперсия доли равна 225. С вероятностью 0,954 рассчитайте необходимое количество бригад для обследования рабочих, если ошибка выборки не должна превышать 5%.
Решение. Необходимое количество бригад рассчитаем на основе формулы объема серийной бесповторной выборки:

Содержание курса лекций “Статистика”
Контрольные задания
Самостоятельно проведите выборочное наблюдение и произведите соответствующие расчеты.
Содержание:
Математическая статистика возникла (XVII в.) и создавалась параллельно с теорией вероятностей. Дальнейшее развитие математической статистики (вторая половина ХІХ и начало ХХ вв.) обязано, в первую очередь, П.Л.Чебышеву, А.А.Маркову, А.М.Ляпунову, а также К.Гауссу, А.Кетле, К.Пирсону и др. В ХХ в. наиболее существенный вклад в математическую статистику был сделан советскими математиками (В.И.Романовский, А.Н.Колмогоров и др.), а также английскими (Стьюдент, Р.Фишер, Э.Пирсон) и американскими (Ю.Нейман,
А.Вальд) учёными.
Установление закономерностей, которым подчинены массовые случайные явления, основано на изучении статистических данных – результатах наблюдений, то есть основу исследований в математической статистике составляют данные наблюдений или опытов над случайными величинами.
Первая задача математической статистики – указать способы сбора и группировки (если данных
очень много) статистических сведений, в том числе определение объёма необходимых экспериментов до начала и в ходе исследования. Вторая задача математической статистики – разработать методы анализа статистических данных, в зависимости от целей исследования.
Изучение тех или иных явлений методами математической статистики служит средством решения многих вопросов, выдвигаемых наукой и практикой (правильная организация технологического процесса, наиболее целесообразное планирование и др.). Итак, задача математической статистики состоит в создании методов сбора и обработки статистических данных для получения научных и практических выводов.
Генеральная и выборочная совокупности
Пусть требуется изучить совокупность однородных объектов относительно некоторого качественного или количественного признака, характеризующего эти объекты. Например, если имеется партия деталей, то качественным признаком может служить стандартность детали, а количественным – контролируемый размер детали. Иногда проводят сплошное обследование, то есть обследуют каждый из
объектов совокупности относительно признака, которым интересуются. На практике, однако, сплошное обследование применяется сравнительно редко. Например, если совокупность содержит очень большое число объектов, то провести сплошное обследование физически невозможно. Если обследование объекта связано с его уничтожением или требует больших материальных затрат, то проводить сплошное обследование практически не имеет смысла. В таких случаях случайно отбирают из всей совокупности ограниченное число объектов и
подвергают их изучению.
Выборочной совокупностью, или просто выборкой, называют совокупность случайно отобранных объектов.
Генеральной совокупностью называют совокупность объектов, из которых производится выборка.
Объёмом совокупности (выборочной или генеральной) называют число объектов этой совокупности.

Например, если из 1000 деталей отобрано для обследования 100 деталей, то объём генеральной совокупности N = 1 000, а объём выборки n = 100. Часто генеральная совокупность содержит конечное число объектов. Однако, если это число достаточно велико, то иногда в целях упрощения
вычислений, или для облегчения теоретических выводов, допускают, что генеральная совокупность состоит из бесчисленного множества объектов. Такое допущение оправдывается тем, что увеличение объёма генеральной совокупности (достаточно большого объёма) практически не сказывается на результатах обработки данных выборки. При этом, что важно, для того чтобы по данным выборки можно было достаточно уверенно судить об интересующем нас признаке генеральной совокупности, необходимо, чтобы объекты выборки правильно его представляли. Это требование коротко формулируют так: выборка должна быть репрезентативной (представительной). В силу закона больших чисел можно утверждать, что выборка будет репрезентативной, если её осуществить случайно: каждый объект выборки отобран случайно из генеральной совокупности, при этом все объекты имеют одинаковую вероятность попасть в выборку.
При составлении выборки можно поступать двояко: после того, как объект отобран и над ним произведено наблюдение, он может быть возвращён, либо не возвращён в генеральную совокупность. В соответствии с этим, выборки подразделяют на повторные и бесповторные. Повторной называют выборку, при которой отобранный объект (перед отбором следующего) возвращается в генеральную совокупность. Бесповторной называют выборку, при которой отобранный объект в генеральную совокупность не возвращается. Если объём генеральной совокупности достаточно велик, а выборка составляет лишь незначительную часть этой совокупности, то различие между повторной и бесповторной выборкам стирается; в предельном случае, когда рассматривается бесконечная генеральная совокупность, а выборка имеет конечный объём, это различие исчезает.
На практике применяются различные способы отбора. Принципиально эти способы можно подразделить на два вида:
1. Отбор, не требующий расчленения генеральной совокупности на части. Сюда относится, так называемый, простой случайный отбор (как повторный, так и бесповторный), то есть отбор, при котором объекты извлекают по одному из всей генеральной совокупности.
2. Отбор, при котором генеральная совокупность разбивается на части. Сюда относятся:
- – типический отбор – отбор, при котором объекты отбираются не из всей генеральной совокупности, а из каждой её «типической» части (например, если детали изготавливают на нескольких станках, то отбор производят не из всей совокупности деталей, произведённых всеми станками, а из продукции каждого станка в отдельности);
- – механический отбор – отбор, при котором генеральная совокупность «механически» делится на столько групп, сколько объектов должно войти в выборку, и затем из каждой группы отбирается один объект (например, если нужно отобрать 20% изготовленных станком деталей, то отбирают каждую пятую деталь; если требуется отобрать 5% деталей, то отбирают каждую двадцатую деталь и т. д.);
- – серийный отбор – отбор, при котором объекты отбирают из генеральной совокупности не по одному, а «сериями», которые подвергаются сплошному обследованию. Например, если изделия изготавливаются большой группой станков-автоматов, то подвергают сплошному обследованию продукцию только нескольких станков.
Заметим, что серийным отбором пользуются тогда, когда обследуемый признак колеблется в различных сериях незначительно.
Статистическое распределение выборки
В результате статистической обработки материалов можно подсчитать число единиц, обладающих конкретным значением того или иного признака. Каждое отдельное значение признака будем обозначать 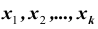
Если при изучении результатов выборки отдельные значения признака (варианты) расположим в возрастающем или убывающем порядке и относительно каждой варианты укажем, как часто она встречается в данной совокупности, тополучим статистическое распределение признака, или вариационный ряд. Он характеризует изменение (варьирование) какого-нибудь количественного признака. Следовательно, вариационный ряд представляет собой две строки (или колонки). В одной из них приводятся варианты, в другой – частоты.
Вариация признака может быть дискретной и непрерывной:
- Дискретной называется вариация, при которой отдельные значения признака (варианты) отличаются друг от друга на некоторую конечную величину (обычно целое число). Например: количество детей в семье; оценки, полученные студентами на экзамене; размеры обуви, проданной магазином за день. Если число элементов вариационного ряда велико, то для удобства его изучения образуют интервальный ряд, группируя значения в интервалы. Для интервального ряда частота i m равна числу значений, наблюдавшихся в i -ом интервале. Длина интервала чаще всего берётся одинаковой.
- Непрерывной называется вариация, при которой значения признака могут отличаться одно от другого на сколь угодно малую величину. Например: уровень рентабельности предприятия; процент занятости трудоспособного населения; депозитная ставка коммерческих банков. При непрерывной вариации распределение признака называется интервальным. Частоты относятся не к отдельному значению признака, а ко всему интервалу. Часто значением интервала принимают его середину, то есть центральное значение.
Нередко вместо абсолютных значений частот используют относительные. Для этого можно использовать долю частоты того или иного варианта (а также интервала) в сумме всех частот. Такая величина называется относительной частотой и обозначается w . Для получения относительных частот необходимо соответствующую частоту разделить на сумму всех частот:
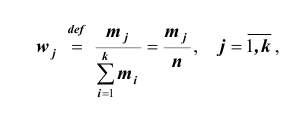 где
где 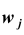 – относительная частота j -ой варианты или интервала
– относительная частота j -ой варианты или интервала 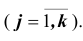 . Сумма
. Сумма
всех относительных частот равна единице: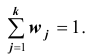 Относительные частоты можно выражать и в процентах, тогда их сумма равна 100%.
Относительные частоты можно выражать и в процентах, тогда их сумма равна 100%.
В интервальном вариационном ряду в каждом интервале различают нижнюю и верхнюю границы интервала: нижняя граница интервала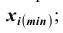 ; верхняя граница интервала
; верхняя граница интервала 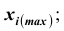 ; величина интервала
; величина интервала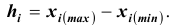 . Как правило, при построении интервальных вариационных рядов в каждый интервал включаются варианты, числовые значения которых больше нижней границы и меньше или равны верхней границе. Интервальные вариационные ряды бывают с одинаковыми и неодинаковыми интервалами. В последнем случае чаще всего встречаются
. Как правило, при построении интервальных вариационных рядов в каждый интервал включаются варианты, числовые значения которых больше нижней границы и меньше или равны верхней границе. Интервальные вариационные ряды бывают с одинаковыми и неодинаковыми интервалами. В последнем случае чаще всего встречаются
последовательно увеличивающиеся интервалы. Для выбора оптимальной величины интервала, то есть такой величины, при которой вариационный ряд не будет громоздким и, при этом, будут сохранены все особенности данного явления, можно рекомендовать формулу:
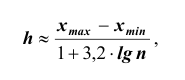 где n – число единиц в совокупности. Так, если в совокупности 200 единиц, наибольший вариант равен 49,961,
где n – число единиц в совокупности. Так, если в совокупности 200 единиц, наибольший вариант равен 49,961,
а наименьший – 49,918, то 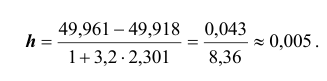
Другими словами, в данном случае оптимальной величиной интервала может служить 0,005.
Гистограмма и полигон статистических распределений
Для наглядности представления вариационного ряда большое значение имеют его графические изображения. Графически вариационный ряд может быть изображён в виде полигона, гистограммы и кумуляты. Полигон распределения (дословно – многоугольник распределения) называют ломанную, которая строится в прямоугольной системе координат. Величина признака 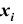 откладывается на оси абсцисс, соответствующие частоты
откладывается на оси абсцисс, соответствующие частоты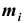 (или относительные частоты
(или относительные частоты 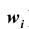 ) – по оси ординат. Точки
) – по оси ординат. Точки 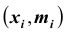
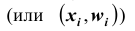 соединяют отрезками прямых и получают полигон распределения. Чаще всего полигоны применяются для изображения дискретных вариационных рядов, но их
соединяют отрезками прямых и получают полигон распределения. Чаще всего полигоны применяются для изображения дискретных вариационных рядов, но их
можно применять также и для интервальных рядов. В этом случае на оси абсцисс откладываются точки, соответствующие серединам данных интервалов. Гистограммой распределения называют ступенчатую фигуру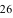 , состоящую из прямоугольников, основанием которых служат частичные интервалы длиною h, а высоты пропорциональны частотам (или относительным частотам) и равны
, состоящую из прямоугольников, основанием которых служат частичные интервалы длиною h, а высоты пропорциональны частотам (или относительным частотам) и равны 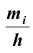 плотность частоты (или
плотность частоты (или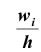 – плотность относительной частоты). Для построения гистограммы на оси абсцисс откладывают частичные интервалы, а над ними проводят отрезки, параллельные оси абсцисс на расстоянии
– плотность относительной частоты). Для построения гистограммы на оси абсцисс откладывают частичные интервалы, а над ними проводят отрезки, параллельные оси абсцисс на расстоянии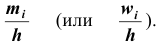 Заметим, что площадь гистограммы частот (относительных частот) равна сумме всех частот (относительных частот), то есть, равна объему выборки (то есть – единице).
Заметим, что площадь гистограммы частот (относительных частот) равна сумме всех частот (относительных частот), то есть, равна объему выборки (то есть – единице).
Пример №1
Уровень рентабельности предприятий лёгкой промышленности характеризуется следующими данными:
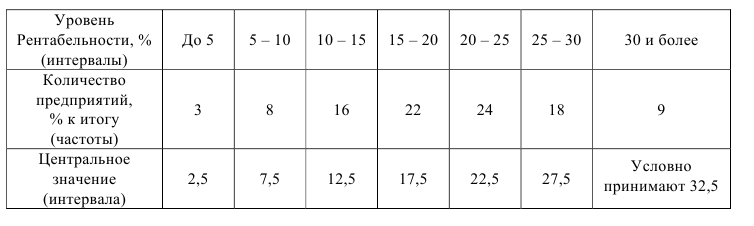
По приведённым данным построить полигон распределения и гистограмму.
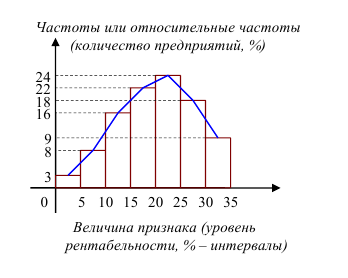
Решение. Воспользовавшись определениями, нетрудно построить полигон распределения и гистограмму (см. рис.)
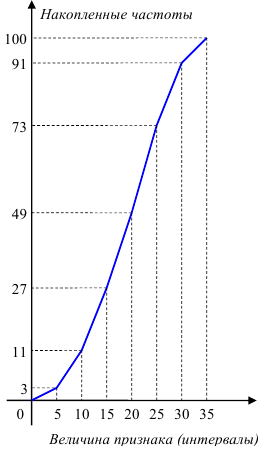
Кумулятивная кривая (кривая сумм – кумулята) получается при изображении вариационного ряда с накопленными частотами (или относительными частотами) в прямоугольной системе координат. Накопленная частота (или относительная частота) определённой варианты получается суммированием всех частот (относительных частот) вариант, предшествующих данной, с частотой (относительной частотой) этой варианты. При построении кумуляты дискретного признака по оси абсцисс откладывают значения признака (варианты). Ординатами
служат вертикальные отрезки, длина которых пропорциональна накопленной частоте (или относительной частоте) той или иной варианты. Соединением вершин ординат прямыми линиями получаем ломанную (кривую) кумуляту. При построении кумуляты интервального вариационного ряда нижней границе первого интервала соответствует частота (относительная частота), равная нулю, а верхней – вся частота (относительная частота) интервала. Верхней границе второго интервала соответствует накопленная частота (относительная частота) первых двух интервалов (то есть сумма частот (относительных частот) этих интервалов) и т. д.
Пример №2
По данным примера 1 построить кумуляту распределения.
Решение. Воспользовавшись определением и правилом построения кумуляты интервального вариационного ряда, нетрудно построить кумулятивную кривую данного распределения (см. рисунок).
Пример №3
В результате эксперимента получены следующие значения случайной величины X:
3; 6; 8; 11; 6; 10; 7; 9; 7; 3; 4; 8;
7; 9; 4; 9; 11; 7; 8; 4; 10; 5; 6; 7; 2.
Требуется:
а) составить статистический ряд;
б) построить статистическое распределение;
в) изобразить полигон распределения.
Решение. а) Объем выборки n = 25.
Построим статистический ряд данной выборки: в первой строке таблицы укажем все различные значения, принимаемые случайной величиной X; во второй строке укажем, сколько раз она приняла эти значения.

б) Найдем статистическое распределение случайной величины X, для чего в табл. 7.2 заменим вторую строку строкой, содержащей относительные частоты 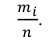

Контроль:
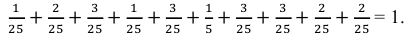
в) На плоскости  построим точки:
построим точки:
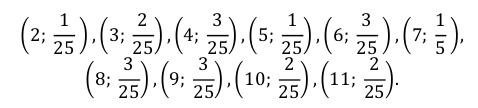
Соединим их (рис. 7.3). Полученная ломаная – полигон данного распределения.
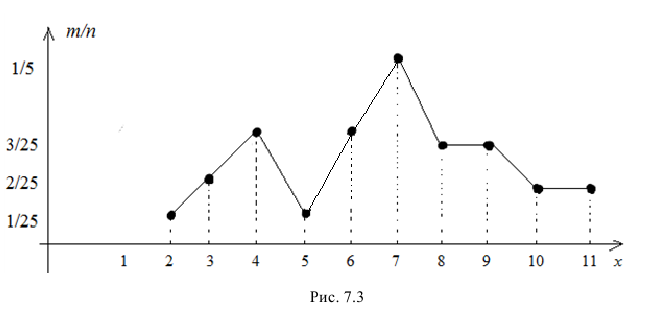
Ответ: а) табл. 7.2, б) табл. 7.3, в) рис. 7.3.
Пример №4
В результате эксперимента получены следующие значения случайной величины X:
16; 17; 9; 13; 21; 11; 7; 7; 19; 5; 17; 5; 20;
18; 11; 4; 6; 22; 21; 15; 15; 23; 19; 25; 1.
Требуется:
а) построить интервальный статистический ряд, разбив промежуток [0; 25] на 5 промежутков равной длины;
б) построить гистограмму относительных частот.
Решение.
а) Объем выборки n = 25. По экспериментальным данным составим таблицу (табл. 7.4). В её первой строке укажем промежутки разбиения: [0; 5), [5; 10), [10; 15), [15; 20) [20; 25].
Во второй строке укажем соответствующие числа 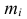 − сколько раз случайная величина X приняла значение из этого промежутка.
− сколько раз случайная величина X приняла значение из этого промежутка.

Контроль: 2 + 6 + 3 + 8 + 6 = 25.
По табл. 7.4 составим интервальный статистический ряд, где во второй строке указаны относительные частоты (табл. 7.5).

б) На оси Ox отложим промежутки:
[0; 5), [5; 10), [10; 15), [15; 20) [20; 25]
интервального статистического ряда, а на оси  – относительные частоты. Построив по этим данным прямоугольники с основаниями
– относительные частоты. Построив по этим данным прямоугольники с основаниями 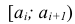 и высотами
и высотами 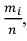 получим ступенчатую фигуру – гистограмму (рис.7.4)
получим ступенчатую фигуру – гистограмму (рис.7.4)
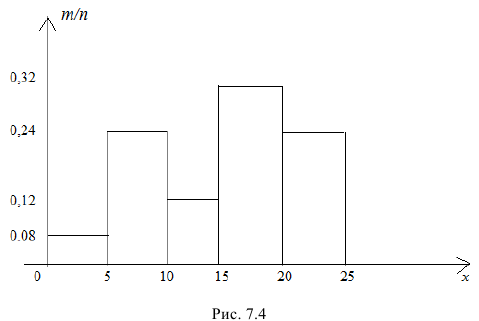
Ответ: а) табл. 7.4; б) рис. 7.5.
Пример №5
Дан статистический ряд

Найти статистическую функцию распределения и построить её график.
Решение. Воспользовавшись формулой
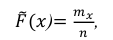
где n – объем выборки; 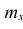 – число выборочных значений, меньших x, вычисляем:
– число выборочных значений, меньших x, вычисляем:
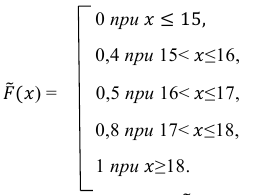 (1)
(1)
Построим график функции 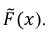
Ответ: а) формула (1); б) рис. 7.5.
Числовые характеристики выборки
В качестве одной из важнейших характеристик вариационного ряда применяют среднюю величину. Математическая статистика различает несколько типов средних величин: арифметическую, геометрическую, гармоническую, квадратическую, кубическую и др. Все перечисленные типы средних могут быть рассчитаны для случаев, когда каждая из вариант вариационного ряда встречается только один раз (тогда средняя называется простой, или невзвешенной) и когда варианты или интервалы повторяются. При этом число повторений вариант или интервалов называют частотой, или статистическим весом, а среднюю, вычисленную с учётом статистического веса, – взвешенной средней.
Для характеристики вариационного ряда один из перечисленных типов средних выбирается не произвольно, а в зависимости от особенностей изучаемого явления и цели, для которой среднее вычисляется.
Практически при выборе того или иного типа средней следует исходить из принципа осмысленности результата при суммировании или при взвешивании. Только тогда средняя применена правильно, когда в результате взвешивания или суммирования получаются величины, имеющие реальный смысл.
Обычно затруднения при выборе типа средней возникают лишь в использовании средней арифметической, или гармонической. Что же касается геометрической и квадратической средних, то их применение обусловлено особыми случаями (см. далее).
Следует иметь в виду, что средняя только в том случае является обобщающей характеристикой, если она применяется к однородной совокупности. В случае использования средней для неоднородных совокупностей можно прийти к неверным выводам. Научной основой статистического анализа является метод статистических группировок, то есть расчленения совокупности на качественно однородные группы.
Все указанные типы средних величин можно получить из формул степенной средней. Если имеются варианты 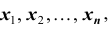 , то среднюю из данных вариант можно рассчитать по формуле простой невзвешенной степенной средней порядка
, то среднюю из данных вариант можно рассчитать по формуле простой невзвешенной степенной средней порядка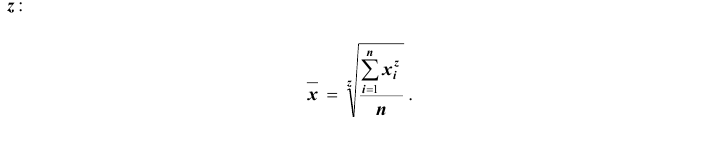
При наличии соответствующих частот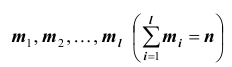 средняя рассчитывается по формуле взвешенной степенной средней:
средняя рассчитывается по формуле взвешенной степенной средней:
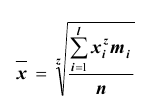 Здесь
Здесь 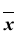 – степенная средняя;
– степенная средняя; 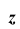 – показатель степени, определяющий тип средней;
– показатель степени, определяющий тип средней;
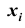 – варианты;
– варианты; 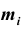 – частоты или статистические веса вариантов.
– частоты или статистические веса вариантов.
Средняя арифметическая получается из формулы степенной средней при
подстановке значения 
- – невзвешенная (простая)
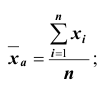
- – взвешенная
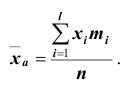
Средняя гармоническая получается при подстановке в формулу степенной средней значения 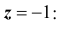
- – невзвешенная (простая)
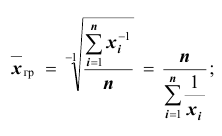
- – взвешенная
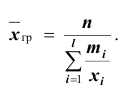
Средняя гармоническая вычисляется тогда, когда средняя предназначается для расчёта сумм слагаемых, обратно пропорциональных величине данного признака, то есть, когда суммированию подлежат не сами варианты, а обратные им величины 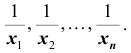
Средняя квадратическая получается из формулы степенной средней при подстановке
- – невзвешенная (простая)
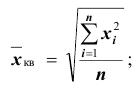
- – взвешенная
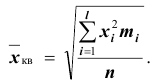
Средняя квадратическая используется только тогда, когда варианты представляют собой отклонения фактических величин от их средней
арифметической или от заданной нормы.
Средняя геометрическая получается из формулы степенной средней при предельном переходе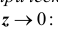
Вычисления средней геометрической в значительной мере упрощаются, если воспользоваться логарифмированием. В этом случае получаем:
- – для невзвешенной (простой) средней геометрической
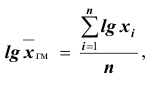
- – для взвешенной
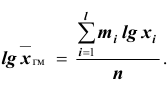
Таким образом, логарифм средней геометрической есть средняя арифметическая из логарифмов вариант. Средняя геометрическая используется главным образом при изучении динамики. Средние коэффициенты и темпы роста также рассчитывают по формулам средней геометрической. Если вычислить различные типы средних для одного и того же вариационного ряда, то числовые их значения будут различаться. При этом средние по своей величине расположатся в определённом порядке. Наименьшей из перечисленных средних окажется средняя гармоническая, затем геометрическая и т. д., наибольшей будет средняя квадратическая. При этом порядок возрастания средних определяется показателем степени z в формуле степенной средней. Так, при z =1 получаем среднюю гармоническую, при z =0 – геометрическую, при z =1 – арифметическую, при z = 2 – квадратическую:
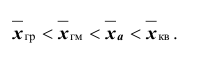
В качестве характеристики вариационного ряда используют медиану , то есть такое значение варьирующего признака, которое приходится на середину упорядоченного вариационного ряда. Если в вариационном ряду 2m +1 случаев, то значение признака у случая m +1 будет медианным. Если в ряду чётное число 2m случаев, то медиана равна средней арифметической из двух серединных значений.
, то есть такое значение варьирующего признака, которое приходится на середину упорядоченного вариационного ряда. Если в вариационном ряду 2m +1 случаев, то значение признака у случая m +1 будет медианным. Если в ряду чётное число 2m случаев, то медиана равна средней арифметической из двух серединных значений.
Таким образом, медиана рассчитывается по формуле
- – при нечётном количестве вариантов:
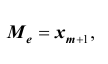
- – при чётном:
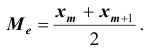
При расчёте медианы интервального вариационного ряда сначала находят интервал, содержащий медиану, путём использования накопленных частот (или относительных частот). Медианному интервалу соответствует первая из накопленных частот (или относительных частот), превышающая половину всего объёма совокупности. Для нахождения медианы при постоянстве плотности внутри интервала, содержащего медиану, используют формулу:
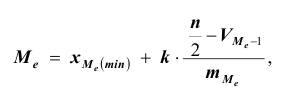 где
где 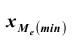 нижняя граница медианного интервала; k – величина медианного интервала;
нижняя граница медианного интервала; k – величина медианного интервала; 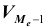 – накопленная частота интервала, предшествующая медианному;
– накопленная частота интервала, предшествующая медианному; 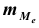 – частота медианного интервала.
– частота медианного интервала.
Медиану можно также определить графически – по кумуляте. Для этого последнюю ординату, пропорциональную суме всех частот (или относительных частот), делят пополам. Из полученной точки восстанавливают перпендикуляр до пересечения с кумулятой. Абсцисса точки пересечения – значение медианы.
Медиана обладает таким свойством: сумма абсолютных величин отклонений вариантов от медианы меньше, чем от любой другой величины (в том числе и от средней арифметической). Другими словами:
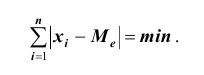
Это свойство медианы можно использовать при проектировании расположения трамвайных и троллейбусных остановок, бензоколонок и т. д.
Пример №6
На шоссе 100км имеется 10 гаражей. Для проектирования строительства бензоколонки были собраны данные о числе предполагаемых поездок на заправку с каждого гаража. Результаты обследования приведены в следующей таблице:

Бензоколонку нужно поставить так, чтобы общий пробег машин на заправку был наименьшим.
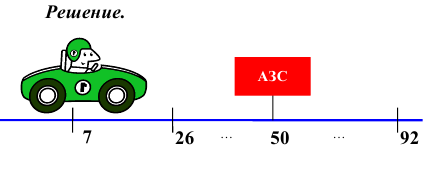
1-й способ:
Если бензоколонку поставить на середине шоссе, то есть на 50-м километре (средняя арифметическая), то пробеги с учётом числа поездок составят
– в одном направлении:
(50-7)-10 +(50-26)-15+ (50-28)-5+ (50-37)-20 +(50-40)-5 +(50-46)-25 = 1310 км;
– в противоположном:
(60 – 50)-15 + (78 – 50)- 30 + (86 – 50)-10 + (92-50)- 65 = 4080 км .
Общий пробег в оба направления окажется равным 5390 км.
2-й способ:
Уменьшения пробега можно достичь, если бензоколонку поставить на 63,85-м километре, то есть на среднем участке шоссе с учётом числа поездок (средняя арифметическая взвешенная). В этом случае пробеги составят по 2475,75 км в оба направления. Таким образом, общий пробег составит 4951,5 км и окажется меньше, чем в первом способе решения, на 438,5 км.
3-й способ:
Наилучший результат, то есть минимальный общий пробег, получим, если поставить бензоколонку на 78-м километре, что будет соответствовать медиане. Заметим, что медиана вычислена по формуле: 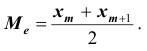 При этом вариационный ряд записываем в виде
При этом вариационный ряд записываем в виде
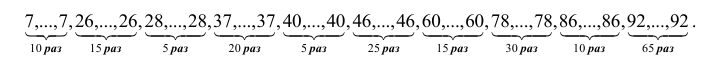
Следовательно 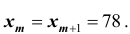 Тогда пробеги составят 3820 км и 990 км
Тогда пробеги составят 3820 км и 990 км
соответственно. Общий пробег, в этом случае, равен 4810 км, то есть он оказался меньше общих пробегов, рассчитанных в предыдущих способах. Модой  называется варианта, наиболее часто встречающаяся в данном вариационном ряду. Для дискретного ряда мода, являющаяся характеристикой вариационного ряда, определяется по частотам вариант и соответствует варианте с наибольшей частотой. В случае интервального распределения с равными интервалами, модальный интервал (то есть интервал, содержащий моду) определяется по наибольшей частоте, а при неравных интервалах – по наибольшей плотности. Мода рассчитывается по формуле:
называется варианта, наиболее часто встречающаяся в данном вариационном ряду. Для дискретного ряда мода, являющаяся характеристикой вариационного ряда, определяется по частотам вариант и соответствует варианте с наибольшей частотой. В случае интервального распределения с равными интервалами, модальный интервал (то есть интервал, содержащий моду) определяется по наибольшей частоте, а при неравных интервалах – по наибольшей плотности. Мода рассчитывается по формуле:

где 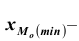 – нижняя граница модального интервала; k – величина модального интервала;
– нижняя граница модального интервала; k – величина модального интервала; 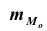 – частота модального интервала;
– частота модального интервала; 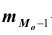 – частота интервала, предшествующего модальному;
– частота интервала, предшествующего модальному;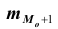 – частота интервала, следующего за модальным.
– частота интервала, следующего за модальным.
Вариационные ряды, в которых частоты вариант, равноотстоящих от средней, равны между собой, называются симметричными. Особенность симметричны вариационных рядов состоит в равенстве трёх характеристик – средней арифметической, моды и медианы, то есть:
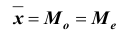
(это необходимое, но не достаточное, условие симметричности вариационного ряда). Вариационные ряды, в которых расположение вариант вокруг средней не одинаково, то есть частоты по обе стороны от средней изменяются по-разному, называются асимметричными, или скошенными. Различают асимметрию – левостороннюю и правостороннюю. Средние величины, характеризую вариационный ряд одним числом, не учитывают вариацию признака, между тем эта вариация существует. Для измерения вариации признака в математической статистике применяют ряд способов.
Вариационный размах ( R), или широта распределения, есть разность между наибольшим и наименьшим значениями вариационного ряда:
Вариационный размах представляет собой величину неустойчивую, чрезвычайно зависящую от случайных обстоятельств; применяется для приблизительной оценки вариации.
Среднее линейное отклонение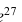 (обозначается d ) представляет собой среднюю арифметическую из абсолютных значений отклонений вариант от средней. В зависимости от отсутствия или наличия частот вычисляют среднее линейное отклонение невзвешенное или взвешенное:
(обозначается d ) представляет собой среднюю арифметическую из абсолютных значений отклонений вариант от средней. В зависимости от отсутствия или наличия частот вычисляют среднее линейное отклонение невзвешенное или взвешенное: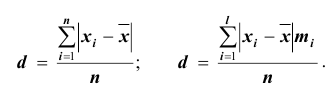
Средний квадрат отклонения, или дисперсия (обозначается D) наиболее часто применяется как мера колеблемости признака. Дисперсии невзвешенную и взвешенную вычисляют по формулам: 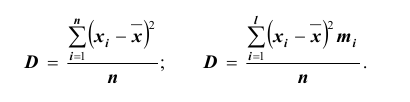 Таким образом, дисперсия есть средняя арифметическая из квадратов отклонений вариант от их средней арифметической. Квадратный корень из дисперсии
Таким образом, дисперсия есть средняя арифметическая из квадратов отклонений вариант от их средней арифметической. Квадратный корень из дисперсии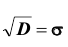 называется среднеквадратическим отклонением. Обобщающими характеристиками вариационных рядов являются моменты
называется среднеквадратическим отклонением. Обобщающими характеристиками вариационных рядов являются моменты
распределения. Характер распределения можно определить с помощью небольшого количества моментов. Средняя из k – х степеней отклонений вариант x от некоторой постоянной величины A (ложный ноль) называется моментом k -го порядка: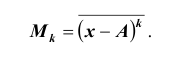
При расчёте средних в качестве весов можно использовать частоты, относительные частоты или вероятности. При использовании в качестве весов частот или относительных частот моменты называются эмпирическими, а при использовании вероятностей – теоретическими. Порядок момента определяется величиной k . Эмпирический момент k -го порядка находится как отношение суммы произведений k -х степеней отклонений вариант 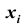 от постоянной величины A на соответствующие частоты
от постоянной величины A на соответствующие частоты 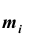 к сумме частот
к сумме частот 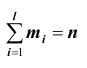 (объём
(объём
выборки), то есть 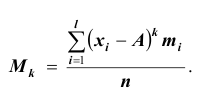
В зависимости от выбора постоянной величины A различают следующее моменты:
1. Если A= 0, то моменты называются начальными. Будем обозначать их через  и вычислять по формуле:
и вычислять по формуле:
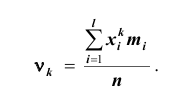
Тогда:
- – при k = 0 получаем начальный момент нулевого порядка
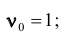 ;
; - – при k =1 получаем начальный момент первого порядка
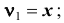
- – при k =2 получаем начальный момент второго порядка
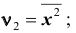 ;
; - – при k = 3 получаем начальный момент третьего порядка
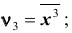
- – при k = 4 получаем начальный момент четвёртого порядка
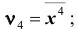
и так далее. На практике чаще всего используют моменты первых четырёх порядков.
2. Если 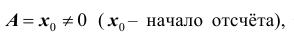 то моменты называются начальными относительно
то моменты называются начальными относительно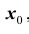 , обозначаются
, обозначаются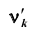 и рассчитываются по формуле:
и рассчитываются по формуле:
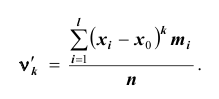
3. Если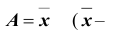 средняя), то моменты называются центральными, обозначаются
средняя), то моменты называются центральными, обозначаются 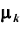 и вычисляются так:
и вычисляются так:
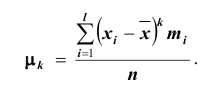
Тогда
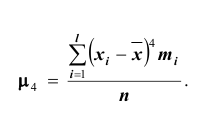
Коэффициентом асимметрии 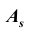 называется отношение центрального момента третьего порядка к кубу среднеквадратического отклонения:
называется отношение центрального момента третьего порядка к кубу среднеквадратического отклонения:
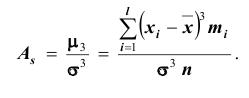
Если полигон вариационного ряда скошен, то есть одна из его ветвей, начиная от вершины, зримо короче другой, то такой ряд называют асимметричным.
Эксцессом называют уменьшенное на три единицы отношение центрального момента четвёртого порядка к четвёртой степени среднеквадратического отклонения:
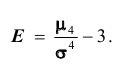 Кривые распределения, у которых
Кривые распределения, у которых 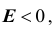 , менее крутые, имеют более плоскую вершину и называются плосковершинными. Кривые распределения, у которых
, менее крутые, имеют более плоскую вершину и называются плосковершинными. Кривые распределения, у которых 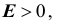 более крутые, имеют более острую вершину и называются островершинными.
более крутые, имеют более острую вершину и называются островершинными.
Выборки и доверительные интервалы
Пусть у нас имеется большое количество предметов, с нормальным распределением некоторых характеристик (например, полный склад однотипных овощей, размер и вес которых варьируется). Вы хотите знать средние характеристики всей партии товара, но у Вас нет ни времени, ни желания измерять и взвешивать каждый овощ. Вы понимаете, что в этом нет необходимости. Но сколько штук надо было бы взять на выборочную проверку?
Прежде, чем дать несколько полезных для этой ситуации формул напомним некоторые обозначения.
Во-первых, если бы мы все-таки промерили весь склад овощей (это множество элементов называется генеральной совокупностью), то мы узнали бы со всей доступной нам точностью среднее значение веса всей партии. Назовем это среднее значение Х ср.ген. – генеральным средним. Мы уже знаем, что нормальное распределение определяется полностью, если известно его среднее значение и отклонение s. Правда, пока мы ни 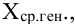 ни s генеральной совокупности не знаем. Мы можем только взять некоторую выборку, замерить нужные нам значения и посчитать для этой выборки как среднее значение
ни s генеральной совокупности не знаем. Мы можем только взять некоторую выборку, замерить нужные нам значения и посчитать для этой выборки как среднее значение 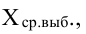 так и среднее квадратическое отклонение
так и среднее квадратическое отклонение 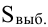
Известно, что если наша выборочная проверка содержит большое количество элементов (обычно n больше 30), и они взяты действительно случайным образом, то s генеральной совокупности почти не будет отличаться от 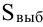
Кроме того, для случая нормального распределения мы можем пользоваться следующими формулами:
С вероятностью 95% 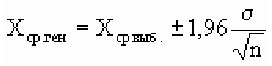
С вероятностью 99% 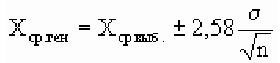
В общем виде с вероятностью P(t)
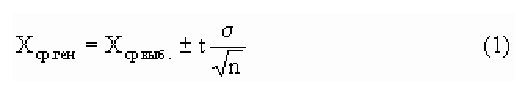
Связь значения t со значением вероятности P(t), с которой мы хотим знать доверительный интервал, можно взять из следующей таблицы: 
Таким образом, мы определили, в каком диапазоне находится среднее значение для генеральной совокупности (с данной вероятностью). Если у нас нет достаточно большой выборки, мы не можем утверждать, что генеральная совокупность имеет 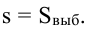 Кроме того, в этом случае проблематична близость выборки к нормальному распределению. В этом случае также пользуются
Кроме того, в этом случае проблематична близость выборки к нормальному распределению. В этом случае также пользуются 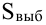 вместо s в формуле:
вместо s в формуле: 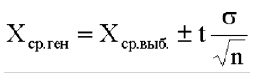
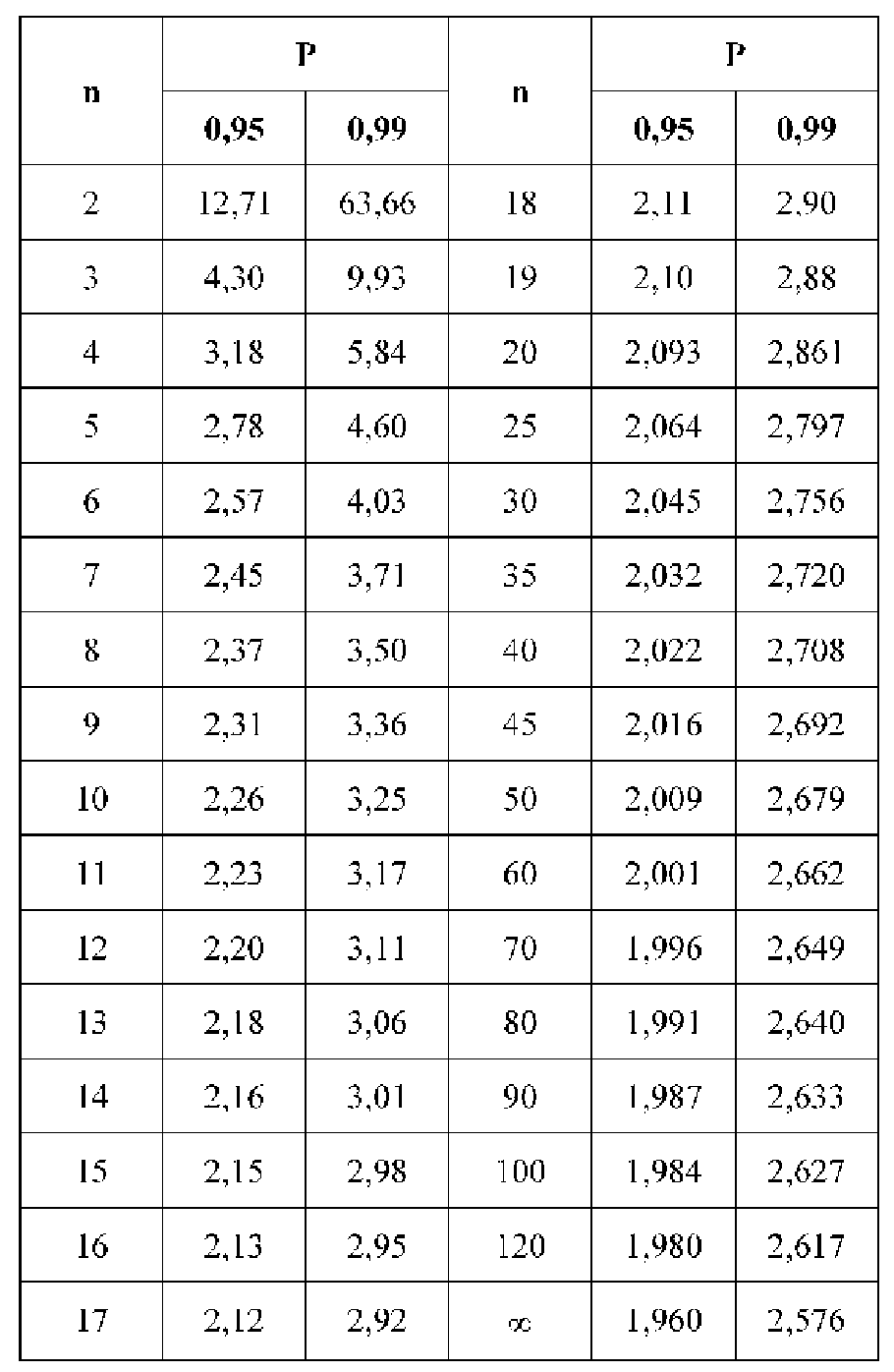
но значение t для фиксированной вероятности P(t) будет зависеть от количества элементов в выборке n. Чем больше n, тем ближе будет полученный доверительный интервал к значению, даваемому формулой (1). Значения t в этом случае берутся из другой таблицы (t-критерий Стьюдента), которую мы приводим ниже:
Значения t-критерия Стьюдента для вероятности 0,95 и 0,99
Пример №7
Из работников фирмы случайным образом отобрано 30 человек. По выборке оказалось, что средняя зарплата (в месяц) составляет 10 тыс. рублей при среднем квадратическом отклонении 3 тыс. рублей. С вероятностью 0,99 определить среднюю зарплату в фирме.
Решение:
По условию имеем 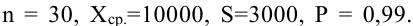 Для нахождения доверительного интервала воспользуемся формулой, соответствующей критерию Стьюдента. По таблице для n = 30 и Р = 0,99 находим t = 2,756, следовательно,
Для нахождения доверительного интервала воспользуемся формулой, соответствующей критерию Стьюдента. По таблице для n = 30 и Р = 0,99 находим t = 2,756, следовательно,
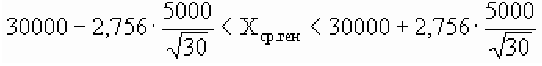
т.е. искомый доверительный интервал 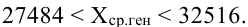 Итак, вероятностью 0,99 можно утверждать, что интервал (27484; 32516) содержит внутри себя среднюю зарплату в фирме. Мы надеемся, что Вы будете пользоваться этим методом, при этом не обязательно, чтобы при Вас каждый раз была таблица. Подсчеты можно проводить в Excel автоматически. Находясь в файле Excel, нажмите в верхнем меню кнопку
Итак, вероятностью 0,99 можно утверждать, что интервал (27484; 32516) содержит внутри себя среднюю зарплату в фирме. Мы надеемся, что Вы будете пользоваться этим методом, при этом не обязательно, чтобы при Вас каждый раз была таблица. Подсчеты можно проводить в Excel автоматически. Находясь в файле Excel, нажмите в верхнем меню кнопку  Затем, выберите среди функций тип “статистические”, и из предложенного перечня в окошке – СТЬЮДРАСПОБР. Затем, по подсказке, поставив курсор в поле “вероятность” наберите значение обратной вероятности (т.е. в нашем случае вместо вероятности 0,95 надо набирать вероятность 0,05). Видимо, электронная таблица составлена так, что результат отвечает на вопрос, с какой вероятностью мы можем ошибиться. Аналогично в поле “степень свободы” введите значение (n-1) для своей выборки.
Затем, выберите среди функций тип “статистические”, и из предложенного перечня в окошке – СТЬЮДРАСПОБР. Затем, по подсказке, поставив курсор в поле “вероятность” наберите значение обратной вероятности (т.е. в нашем случае вместо вероятности 0,95 надо набирать вероятность 0,05). Видимо, электронная таблица составлена так, что результат отвечает на вопрос, с какой вероятностью мы можем ошибиться. Аналогично в поле “степень свободы” введите значение (n-1) для своей выборки.
Понятие о статистике
«Статистика знает все», — утверждали И. Ильф и Е. Петров в своем знаменитом романе «Двенадцать стульев» и продолжали: «Известно, сколько какой пищи съедает в год средний гражданин республики… Известно, сколько в стране охотников, балерин, станков, собак всех пород, велосипедов, памятников, девушек, маяков и швейных машинок… Как много жизни, полной пыла, страстей и мысли, глядит на нас из статистических таблиц!»
Это ироничное описание дает достаточно точное представление о статистике (от латинского status — состояние) — науке, изучающей, обрабатывающей и анализирующей количественные данные о разнообразнейших массовых явлениях в жизни. Экономическая статистика изучает изменение цен, спроса и предложения товаров, прогнозирует рост и падение производства и потребления. Медицинская статистика изучает эффективность разных лекарств и методов лечения, вероятность возникновения некоторых заболеваний в зависимости от возраста, пола, наследственности, условий жизни, вредных привычек, прогнозирует распространение эпидемий. Демографическая статистика изучает рождаемость, численность населения, его состав (возрастной, национальный, профессиональный). А есть еще статистика финансовая, налоговая, биологическая, метеорологическая…
Статистика имеет многовековую историю. Уже в Древнем мире вели статистический учет населения. Однако случайное толкование статистических данных, отсутствие строгой научной базы статистических прогнозов даже в середине XIX в. еще не позволяли говорить о статистике как науке. Только в XX в. появилась математическая статистика — наука, опирающаяся на законы теории вероятностей. Выяснилось, что статистические методы обработки данных из самых разных областей жизни имеют много общего. Это позволило создать универсальные научно обоснованные методы статистических исследований и проверки статистических гипотез.
Таким образом:
Математическая статистика — это раздел математики, изучающий математические методы обработки и использования статистических данных для научных и практических выводов.
В математической статистике рассматриваются методы, которые дают возможность по результатам экспериментов (статистическим данным) делать определенные выводы вероятностного характера.
Математическая статистика подразделяется на две обширные области: 1) описательная статистика, которая рассматривает методы описания статистических данных, их табличное и графическое представление и пр.; 2) аналитическая статистика (теория статистических выводов), которая рассматривает обработку данных, полученных в ходе эксперимента, и формулировку выводов, имеющих прикладное значение для конкретной области человеческой деятельности. Теория статистических выводов тесно связана с теорией вероятностей и базируется на ее математическом аппарате. Среди основных задач математической статистики можно отметить следующие. 1. Оценка вероятности. Пусть некоторое случайное событие имеет вероятность p > 0, но ее значение нам неизвестно. Требуется оценить эту вероятность по результатам экспериментов, то есть решить задачу об оценке вероятности через частоту.
Оценка закона распределения:
Исследуется некоторая случайная величина, точное выражение для закона распределения которой нам неизвестно. Необходимо по результатам экспериментов найти приближенное выражение для функции, задающей закон распределения.
Оценка числовых характеристик случайной величины (например, математического ожидания ).
Проверка статистических гипотез (предположений).
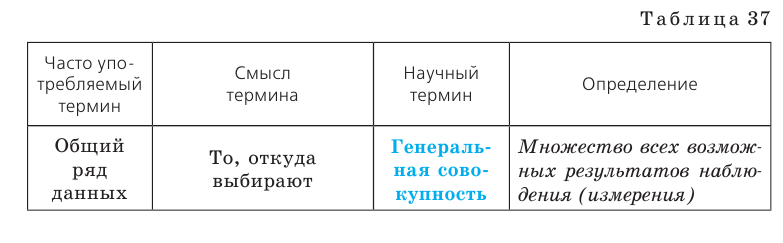
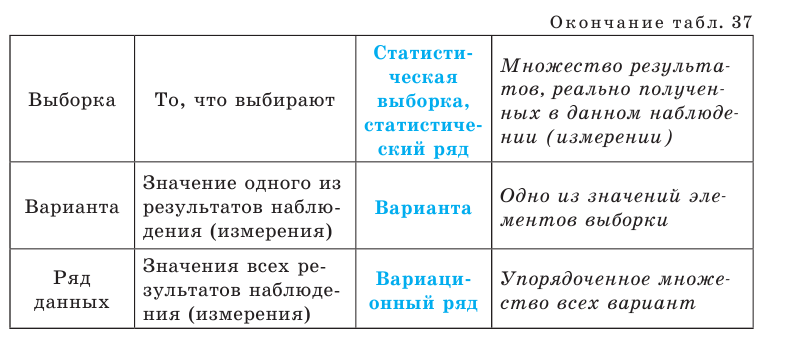
Исследуется некоторая случайная величина. Исходя из определенных рассуждений, выдвигается, например, гипотеза о распределении этой случайной величины. Необходимо по результатам экспериментов принять или отвергнуть эту гипотезу. Результаты исследований, проводимых методами математической статистики, применяются для принятия решений. В частности, при планировании и организации производства, при контроле качества продукции, при выборе оптимального времени наладки или замены действующей аппаратуры (например, при определении времени замены двигателя самолета, отдельных частей станков и т. д.). Как и в каждой науке, в статистике используются свои специфические термины и понятия. Некоторые из них приведены в табл. 37. Запоминать их определения необязательно, достаточно понимать их смысл.
Генеральная совокупность и выборка
Для изучения различных массовых явлений проводятся специальные статистические исследования. Любое статистическое исследование начинается с целенаправленного сбора информации об изучаемом явлении или процессе. Этот этап называют этапом статистических наблюдений.
Для получения статистических данных в результате наблюдений похожие элементы некоторой совокупности сравнивают по разным признакам. Например, учащихся 11 классов можно сравнивать по росту, размеру одежды, успеваемости и пр. Болты можно сравнивать по длине, диаметру, массе, материалу и другим характеристикам. Практически любой признак или непосредственно измеряется, или может получить условную числовую характеристику (см. пример с выпадением «герба» или «числа» при подбрасывании монеты).
Таким образом, некоторый признак элементов совокупности можно рассматривать как величину, принимающую те или иные числовые значения. При изучении реальных явлений часто бывает невозможно обследовать все элементы совокупности.
Например, практически невозможно выяснить размеры обуви у всех людей планеты. А проверить, например, наличие листов некачественной фотобумаги в большой партии хотя и реально, но бессмысленно, потому что полная проверка приведет к уничтожению всей партии бумаги. В подобных случаях вместо изучения всех элементов совокупности, называемой генеральной совокупностью, обследуют ее значительную часть, выбранную случайным образом. Эту часть называют выборкой, а число элементов в выборке называется объемом выборки. Eсли в выборке все основные признаки генеральной совокупности представлены в той же пропорции и с той же относительной частотой, с которой данный признак выступает в данной генеральной совокупности, то эту выборку называют репрезентативной (от французского représentatif — показательный).
Иными словами, репрезентативная выборка представляет собой меньшую по размеру, но точную модель той генеральной совокупности, которую она должна отражать. В той степени, в какой выборка является репрезентативной, выводы, основанные на изучении этой выборки, можно с большой долей уверенности считать применимыми ко всей генеральной совокупности.
Понятие репрезентативности отобранной выборки не означает ее полного представительства по всем признакам генеральной совокупности, поскольку это практически обеспечить невозможно. Отобранная из всей совокупности часть должна быть репрезентативной относительно тех признаков, которые изучаются.
Чтобы выборка была репрезентативной, она должна быть выделена из генеральной совокупности случайным образом. Этого можно достичь различными способами.
Чаще всего используют следующие виды выборок:
- собственно-случайную;
- механическую;
- типическую;
- серийную.
Кратко охарактеризуем каждую из них.
1) Члены генеральной совокупности можно предварительно занумеровать и каждый номер записать на отдельной карточке. После тщательного перемешивания будем отбирать наугад из пачки таких карточек по одной и таким образом получим выборочную совокупность любого нужного объема, которая называется собственно-случайной выборкой. Номера на отобранных карточках укажут, какие члены генеральной совокупности попали в выборку. (Заметим, что при этом возможны два принципиально различных способа отбора карточек в зависимости от того, возвращается или не возвращается обратно вынутая карточка после записи ее номера.) Собственно-случайную выборку заданного объема п можно образовать и с помощью так называемых таблиц случайных чисел или генератора случайных чисел на компьютере. При образовании собственно-случайной выборки каждый член генеральной совокупности с одинаковой вероятностью может попасть в выборку.
2) Выборка, в которую члены из генеральной совокупности отбираются через определенный интервал, называется механической. Например, если объем выборки должен составлять 5% объема генеральной совокупности (5%-ная выборка), то отбирается ее каждый 20-й член, при 10%-ной выборке — каждый 10-й член генеральной совокупности и т. д. Механическую выборку можно образовать, если имеется определенный порядок следования членов генеральной совокупности, например, если они следуют друг за другом в определенной последовательности во времени. Именно так появляются изготовленные на станке детали, приборы, сошедшие с конвейера, и т. п. При этом необходимо убедиться, что в следующих один за другим членах генеральной совокупности значения признака не изменяются с той же (или кратной ей) периодичностью, что и периодичность отбора элементов в выборку. Например, пусть из продукции металлообрабатывающего станка в выборку попадает каждая пятая деталь, а после каждой десятой детали рабочий производит смену (или заточку) режущего инструмента и наладку станка. Эти операции рабочего направлены на улучшение качества деталей (износ режущего инструмента происходит более или менее равномерно). Следовательно, в выборочную совокупность попадут детали, на качество которых работа станка влияет в одну и ту же сторону, и значения признака выборочной совокупности могут неправильно отразить соответствующие значения признака генеральной совокупности.
3) Если из предварительно разбитой на непересекающиеся группы генеральной совокупности образовать собственно-случайные выборки из каждой группы (с повторным или бесповторным отбором членов), то отобранные элементы составят выборочную совокупность, которая называется типической.
4) Если генеральную совокупность предварительно разбить на непересекающиеся серии (группы), а затем, рассматривая серии как элементы, образовать собственно-случайную выборку (с повторным или бесповторным отбором серий), то все члены отобранных серий составят выборочную совокупность, которая называется серийной. Например, пусть на заводе 150 станков (10 цехов по 15 станков) производят одинаковые изделия. Если в выборку отбирать изделия из тщательно перемешанной продукции всех 150 станков, то образуется собственно-случайная выборка. Но можно отбирать изделия отдельно из продукции первого, второго и т. д. станков. Тогда будет образована типическая выборка. Если же членами генеральной совокупности считать цеха и сначала образовать собственно-случайную выборку цехов, а потом в каждом из отобранных цехов взять все произведенные изделия, то все отобранные изделия (из всех отобранных цехов) составят серийную выборку. Как уже отмечалось, практически любой изучаемый признак X может быть непосредственно измерен или получить числовую характеристику. Поэтому первичные экспериментальные данные, характеризующие выделенную выборку, обычно представлены в виде набора чисел, записанных исследователем в порядке их поступления. Количество (n) чисел в этом наборе – объем выборки, а численность (m) варианты (одного из значений элементов выборки) называют частотой варианты. Отношение m n называют относительной частотой (W) варианты.
Используя эти понятия, запишем соотношение между ними в репрезентативной выборке.
Пусть S — объем генеральной совокупности, n — объем репрезентативной выборки, в которой k значений исследуемых признаков распределены по частотам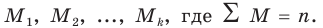 . Тогда в генеральной совокупности частотам
. Тогда в генеральной совокупности частотам 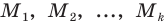 будут соответствовать частоты
будут соответствовать частоты 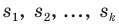 тех же значений признака, что и в выборке
тех же значений признака, что и в выборке 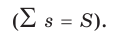 По определению репрезентативной выборки получаем:
По определению репрезентативной выборки получаем: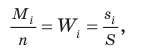 , где і — порядковый номер значения признака
, где і — порядковый номер значения признака 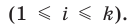 Из этого соотношения находим:
Из этого соотношения находим:
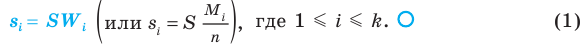
Пример №8
Обувной цех должен выпустить 1000 пар кроссовок молодежного фасона. Для того чтобы определить, сколько кроссовок и какого размера необходимо выпустить, были выявлены размеры обуви у 50 случайным образом выбранных подростков. Распределение размеров обуви по частотам представлено в таблице:

Сколько кроссовок разного размера будет изготавливать фабрика?
Решение:
 Будем считать рассмотренную выборку объемом n = 50 подростков репрезентативной. Тогда в генеральной совокупности (объемом S = 1000) количество кроссовок каждого размера пропорционально количеству кроссовок соответствующего размера в выборке (и для каждого размера находится по формуле (1)). Результаты расчетов будем записывать в таблицу:
Будем считать рассмотренную выборку объемом n = 50 подростков репрезентативной. Тогда в генеральной совокупности (объемом S = 1000) количество кроссовок каждого размера пропорционально количеству кроссовок соответствующего размера в выборке (и для каждого размера находится по формуле (1)). Результаты расчетов будем записывать в таблицу:
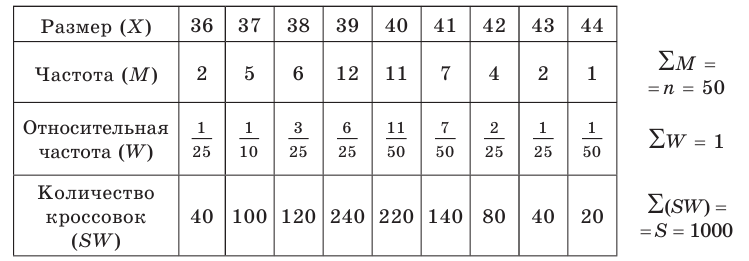
Ответ:

В сельском хозяйстве для определения количественного соотношения продукции разного сорта пользуются так называемым выборочным
методом. Суть этого метода будет ясна из описания следующего опыта, теоретическую основу которого составляет закон больших чисел. В коробке тщательно перемешан горох двух сортов: зеленый и желтый. Небольшой емкостью, например ложкой, вынимают из разных мест коробки порции гороха. В каждой порции подсчитывают число М желтых горошин и число n всех горошин. Для каждой порции находят относительную частоту появления желтой горошины 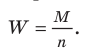 Так делают k раз (на практике обычно берут 5 < k < 10) и каждый раз вычисляют относительную частоту. За статистическую вероятность извлечения желтой горошины из коробки принимают среднее арифметическое полученных относительных частот
Так делают k раз (на практике обычно берут 5 < k < 10) и каждый раз вычисляют относительную частоту. За статистическую вероятность извлечения желтой горошины из коробки принимают среднее арифметическое полученных относительных частот 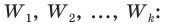
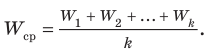
Табличное и графическое представление данных. Числовые характеристики рядов данных
Ранжирование ряда данных:
Под ранжированием ряда данных понимают расположение элементов этого ряда в порядке возрастания (имеется в виду, что каждое следующее число или больше, или не меньше предыдущего).
Пример:
Если ряд данных выборки имеет вид 5, 3, 7, 4, 6, 4, 6, 9, 4, то после ранжирования он превращается в ряд 3, 4, 4, 4, 5, 6, 6, 7, 9. (*)
Размах выборки (R)
Размах выборки — это разность между наибольшим и наименьшим значениями величины в выборке.
Для ряда (*) размах выборки: R = 9 – 3 = 6.
Мода (Mo)
Мода — это значение элемента выборки, встречающееся чаще остальных.
В ряду (*) значение 4 встречается чаще всего, итак, Mo = 4.
Медиана (Me)
Медиана — это так называемое серединное значение упорядоченного ряда значений: — если количество чисел в ряду нечетное, то медиана — это число, записанное посередине; — если количество чисел в ряду четное, то медиана — это среднее арифметическое двух чисел, стоящих посередине.
Для ряда (*), в котором 9 членов, медиана — это среднее (то есть пятое) число 5: Me = 5. Если рассмотреть ряд 3, 3, 4, 4, 4, 5, 6, 6, 7, 9, в котором 10 членов, то медиана — это среднее арифметическое пятого и шестого членов: 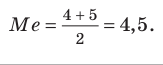
Среднее значение 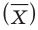 выборки
выборки
Средним значением выборки называется среднее арифметическое всех чисел ряда данных выборки. Если в ряду данных записаны значения 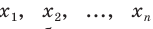 (среди которых могут быть и одинаковые), то
(среди которых могут быть и одинаковые), то 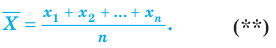
Если известно, что в ряду данных различные значения 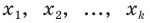 встречаются соответственно с частотами
встречаются соответственно с частотами 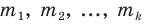 (тогда
(тогда 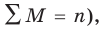 то среднее арифметическое можно вычислить по формуле
то среднее арифметическое можно вычислить по формуле 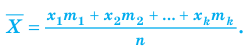
Пусть ряд данных задан таблицей распределения его различных значений по частотам M:
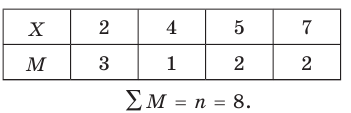
Тогда по формуле (**) 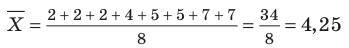 или по другой формуле
или по другой формуле
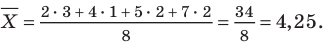
Табличное и графическое представление данных. Полигоны частот
Как уже отмечалось, практически любой изучаемый признак X может быть непосредственно измерен или получить числовую характеристику. Поэтому первичные экспериментальные данные, характеризующие выделенную выборку, обычно представлены в виде набора чисел, записанных исследователем в порядке их поступления.
Если данных много, то полученный набор чисел трудно обозрим и сделать по нему какие-то выводы очень сложно. Поэтому первичные данные нуждаются в обработке, которая обычно начинается с их группировки. Группировка выполняется различными методами в зависимости от целей исследования, вида изучаемого признака и количества экспериментальных данных (объема выборки). Наиболее часто группировка сводится к представлению данных в виде таблиц, в которых различные значения элементов выборки упорядочены по возрастанию и указаны их частоты (то есть количество каждого элемента в выборке).
При необходимости в этой таблице указывают также относительные частоты для каждого элемента, записанного в первой строке. Такую таблицу часто называют рядом распределения (или вариационным рядом). Например, пусть при изучении размера обуви 30 мальчиков 11 класса получили набор чисел (результаты записаны в порядке опроса): 39; 44; 41; 39; 40; 41; 45; 42; 44; 41; 41; 43; 42; 43; 41; 44; 42; 38; 40; 38; 41; 40; 42; 43; 42; 41; 43; 40; 40; 42. Чтобы удобнее было анализировать информацию, в подобных ситуациях числовые данные сначала ранжируют, располагая их в порядке возрастания (когда каждое следующее число или больше, или не меньше предыдущего). В результате ранжирования получаем следующий ряд: 38; 38; 39; 39; 40; 40; 40; 40; 40; 41; 41; 41; 41; 41; 41; 41; 42; 42; 42; 42; 42; 42; 43; 43; 43; 43; 44; 44; 44; 45. Затем составляем таблицу, в первой строке которой указаны все различные значения полученного ряда данных (X размер обуви выбранных 30 мальчиков 11 класса), а во второй строке – их частоты М:

Получаем ряд распределения рассматриваемого признака X по частотам. Иногда удобно проводить анализ ряда распределения на основе его графического изображения. Отметим на координатной плоскости точки с координатами
 и соединим их последовательно отрезками (рис. 23.1). Полученную ломаную линию называют полигоном частот.
и соединим их последовательно отрезками (рис. 23.1). Полученную ломаную линию называют полигоном частот.
Итак, полигоном частот называют ломаную, отрезки которой последовательно соединяют точки с координатами 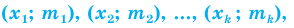 , где
, где 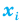 — значения различных элементов ряда данных, а
— значения различных элементов ряда данных, а 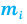 — соответствующие им частоты. Аналогично определяется и строится полигон относительных частот для рассматриваемого признака X (строятся точки с координатами
— соответствующие им частоты. Аналогично определяется и строится полигон относительных частот для рассматриваемого признака X (строятся точки с координатами — значения различных элементов ряда данных, а
— значения различных элементов ряда данных, а 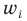 — соответствующие им относительные частоты.
— соответствующие им относительные частоты.
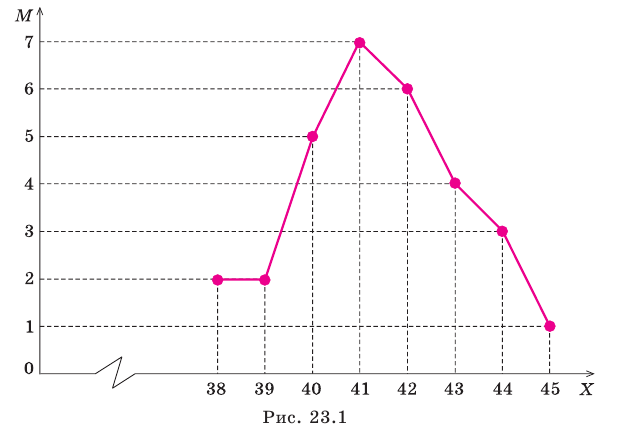
Если вычислить относительные частоты для каждого из различных значений ряда данных, рассмотренного в начале этого пункта, то распределение значений рассматриваемого признака X по относительным частотам можно задать таблицей:

Распределение значений рассматриваемого признака X по относительным частотам можно представить также в виде полигона относительных частот (рис. 23.2), в виде линейной диаграммы (рис. 23.3) или в виде круговой диаграммы, предварительно записав значения относительной частоты в процентах (рис. 23.4).
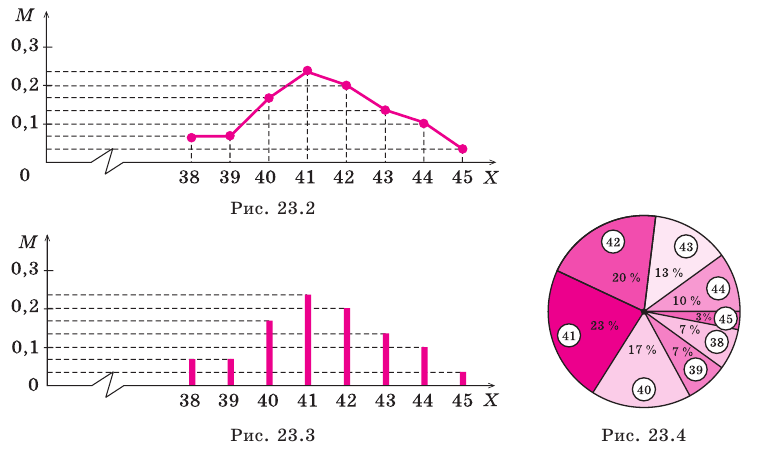
Напомним, что для построения круговой диаграммы круг разбивается на секторы, центральные углы которых пропорциональны относительным частотам, вычисленным для каждого из различных значений ряда данных. Обратим внимание, что круговая диаграмма сохраняет свою наглядность и выразительность только при небольшом количестве полученных секторов. В противном случае ее применение малоэффективно. Если рассматриваемый признак принимает много различных значений, то его распределение можно лучше себе представить после разбиения всех значений ряда данных на классы.
Количество классов может быть любым, удобным для исследования (обычно от 4 до 12). При этом величины (объемы) классов должны быть одинаковыми. Например, в следующей таблице представлены сведения о заработной плате 100 рабочих одного предприятия (в некоторых условных единицах). При этом значения зарплаты (округлены до целого числа условных единиц) сгруппированы в 7 классов, каждый объемом в 100 условных единиц.
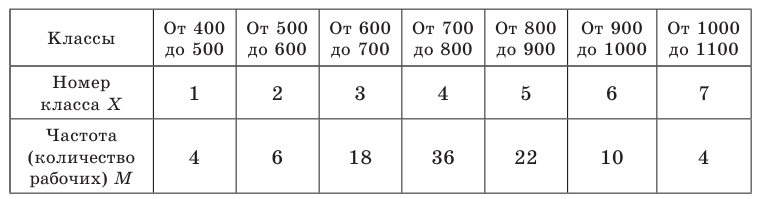
(проверка: 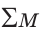 = 100) Наглядно частотное распределение зарплат по классам можно представить с помощью полигона частот (рис. 23.5) или столбчатой диаграммы (рис. 23.6).
= 100) Наглядно частотное распределение зарплат по классам можно представить с помощью полигона частот (рис. 23.5) или столбчатой диаграммы (рис. 23.6).
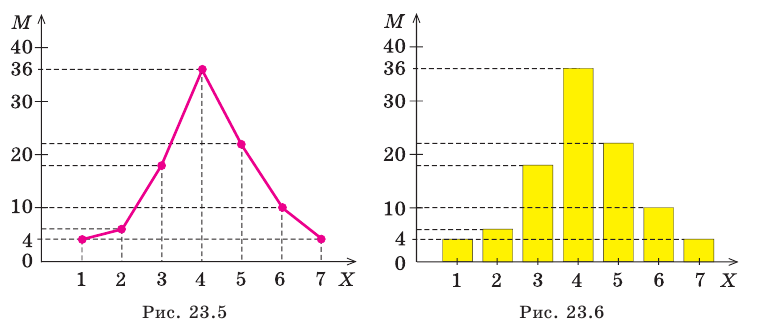
Числовые характеристики рядов данных. Размах, мода и медиана ряда данных
Иногда выборку случайных величин или всю генеральную совокупность этих величин приходится характеризовать одним числом. На практике это необходимо, например, для быстрого сравнения двух или больше совокупностей по общему признаку. Рассмотрим конкретный пример. Пусть после летних каникул провели опрос 10 девочек и 9 мальчиков одного класса о количестве книг, прочитанных ими за каникулы. Результаты были записаны в порядке опроса. Получили следующие ряды чисел:
- для девочек: 4, 3, 5, 3, 8, 3, 12, 4, 5, 5;
- для мальчиков: 5, 3, 3, 4, 6, 4, 4, 7, 4.
Как уже отмечалось, чтобы удобнее было анализировать информацию, в подобных случаях числовые данные ранжируют, располагая их в порядке возрастания (когда каждое следующее число или больше, или не меньше предыдущего). В результате ранжирования получили следующие ряды:
- для девочек: 3, 3, 3, 4, 4, 5, 5, 5, 8, 12; (1)
- для мальчиков: 3, 3, 4, 4, 4, 4, 5, 6, 7. (2)
Тогда распределение по частотам M величин: X — число книг, прочитанных за каникулы девочками, и Y — число книг, прочитанных за каникулы мальчиками, можно задать таблицами:

Эти распределения можно проиллюстрировать также графически с помощью полигона частот (рис. 23.7, а, б).
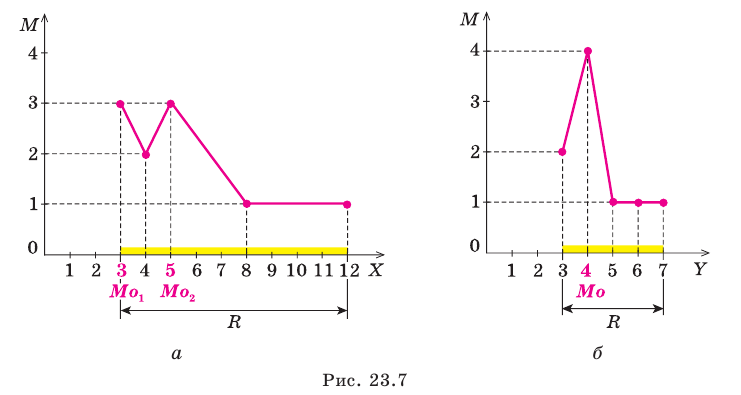
Для сравнения рядов (1) и (2) используют различные характеристики. Приведем некоторые из них. Размахом ряда чисел (обозначается R) называют разность между наибольшим и наименьшим из этих чисел. Поскольку мы анализируем выборку некоторых величин, то размах выборки — это разность между наибольшим и наименьшим значениями величины в выборке.
Для ряда (1) размах R = 12 – 3 = 9, а для ряда (2) размах R = 7 – 3 = 4. На графике размах — это длина области определения полигона частот (рис. 23.7). Одной из статистических характеристик ряда данных является его мода (обозначается Mo, от латинского слова modus — мера, правило).
Мода — это значение элемента выборки, встречающееся чаще остальных.
Так, в ряду (1) две моды — числа 3 и 5: 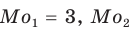 = 5, а в ряду (2) одна мода — число 4: Mo = 4. На графике мода — это значение абциссы точки, в которой достигается максимум полигона частот (см. рис. 23.7). Отметим, что моды может и не быть, если все значения рассматриваемого признака встречаются одинаково часто. Моду ряда данных обычно находят тогда, когда хотят выяснить некоторый типовой показатель. Например, когда изучают данные о моделях мужских рубашек, проданных в определенный день в универмаге, то удобно использовать такой показатель, как мода, который характеризует модель, пользующуюся наибольшим спросом (собственно, этим и объясняется название «мода»). Еще одной статистической характеристикой ряда данных является его медиана. Медиана — это так называемое серединное значение упорядоченного ряда значений (обозначается Me). Медиана делит упорядоченный ряд данных на две равные по количеству элементов части.
= 5, а в ряду (2) одна мода — число 4: Mo = 4. На графике мода — это значение абциссы точки, в которой достигается максимум полигона частот (см. рис. 23.7). Отметим, что моды может и не быть, если все значения рассматриваемого признака встречаются одинаково часто. Моду ряда данных обычно находят тогда, когда хотят выяснить некоторый типовой показатель. Например, когда изучают данные о моделях мужских рубашек, проданных в определенный день в универмаге, то удобно использовать такой показатель, как мода, который характеризует модель, пользующуюся наибольшим спросом (собственно, этим и объясняется название «мода»). Еще одной статистической характеристикой ряда данных является его медиана. Медиана — это так называемое серединное значение упорядоченного ряда значений (обозначается Me). Медиана делит упорядоченный ряд данных на две равные по количеству элементов части.
Если количество чисел в ряду нечетное, то медиана — это число, записанное посередине. Например, в ряду (2) нечетное количество элементов (n = 9). Тогда его медианой является число, стоящее посередине, то есть на пятом месте: Me =4

Следовательно, о мальчиках можно сказать, что одна половина из них прочитала не больше 4 книг, а вторая — не меньше 4 книг. (Отметим, что в случае нечетного n номер среднего члена ряда равен 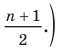
Если количество чисел в ряду четное, то медиана — это среднее арифметическое двух чисел, стоящих посередине. Например, в ряду (1) четное количество элементов (n = 10). Тогда его медианой является число, равное среднему арифметическому чисел, стоящих посередине, то есть на пятом и шестом местах: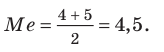
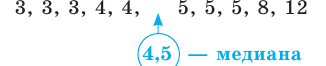
Следовательно, о девочках можно сказать, что одна половина из них прочитала меньше 4,5 книги, а вторая — больше 4,5 книги. (Отметим, что в случае четного n номера средних членов ряда равны 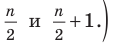
Среднее значение выборки
Средним значением выборки (обозначается 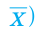 называется среднее арифметическое всех чисел ряда данных выборки. Если в ряду данных записаны значения
называется среднее арифметическое всех чисел ряда данных выборки. Если в ряду данных записаны значения 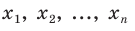 (среди которых могут быть и одинаковые), то
(среди которых могут быть и одинаковые), то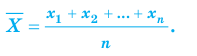
Если известно, что в ряду данных различные значения  встречаются соответственно с частотами
встречаются соответственно с частотами 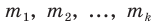 (тогда ∑M = n ), то, заменяя одинаковые слагаемые в числителе на соответствующие произведения, получаем, что среднее арифметическое можно вычислять по формуле
(тогда ∑M = n ), то, заменяя одинаковые слагаемые в числителе на соответствующие произведения, получаем, что среднее арифметическое можно вычислять по формуле
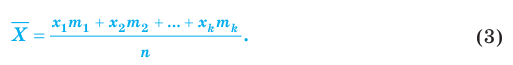
Последнюю формулу удобно использовать в тех случаях, когда в выборке распределение величины по частотам задано в виде таблицы. Напомним, что распределение по частотам M величин: X — число книг, прочитанных за каникулы девочками, и Y — число книг, прочитанных за каникулы мальчиками, было задано такими таблицами:

Тогда средние значения заданных выборок равны:
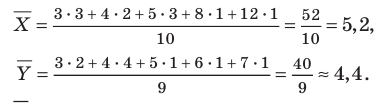
Поскольку 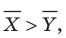 то можно сказать, что за один и тот же промежуток времени девочки в классе читают книг больше, чем мальчики. Обратим внимание, что в пособиях по статистике моду, медиану и среднее значение выборки объединяют одним термином — меры центральной тенденции, подчеркивая тем самым возможность охарактеризовать ряд выборки одним числом. Не для каждого ряда данных имеет смысл формально находить центральные тенденции.
то можно сказать, что за один и тот же промежуток времени девочки в классе читают книг больше, чем мальчики. Обратим внимание, что в пособиях по статистике моду, медиану и среднее значение выборки объединяют одним термином — меры центральной тенденции, подчеркивая тем самым возможность охарактеризовать ряд выборки одним числом. Не для каждого ряда данных имеет смысл формально находить центральные тенденции.
Например, если исследуется ряд 5, 5, 8, 110 (5) годовых доходов четырех людей (в тыс. у. е.), то очевидно, что ни мода (5), ни медиана (6,5), ни среднее значение (32) не могут выступать в роли единой характеристики всех значений ряда данных. Это объясняется тем, что размах ряда (105) является соизмеримым с наибольшим из его значений. В данном случае можно искать центральные тенденции, например, для части ряда (5): 5, 5, 8, условно назвав его выборкой годового дохода низкооплачиваемой части населения. Если в выборке среднее значение существенно отличается от моды, то его нецелесообразно выбирать в качестве типичной характеристики рассматриваемой совокупности данных (чем больше значение моды отличается от среднего значения, тем «более несимметричным» является полигон частот совокупности).
Сведения из истории:
Элементарные задачи, которые позднее были отнесены к стохастике, то есть к комбинаторике, теории вероятностей и математической статистике, ставились и решались еще во времена Древних Египта, Греции и Рима. Этот период так называемой предыстории теории вероятностей заканчивается в XVI в. работами итальянских математиков Д. Кардано (1501–1576) «Книга об игре в кости», Н. Тартальи (1499–1557) «Общий трактат о числе и мере», Г. Г а л и л е я (1564–1642) «О выпадении очков при игре в кости» и др. В этих работах уже фигурирует понятие вероятности, используется теорема о вероятности произведения независимых событий, высказываются некоторые соображения относительно так называемого закона больших чисел. В XVII–XVIII вв. вопросами теории вероятностей заинтересовались французские математики П. Ферма (1601–1665) и Б. Паскаль (1623–1662), нидерландский математик X. Гюйгенс (1629– 1695), швейцарские математики Я. Бернулли (1654–1705), И. Бернулли (1687–1759), Д. Бернулли (1700–1782) и российский математик Л. Эйлер (1707–1783). В своих работах они уже использовали теоремы сложения и умножения вероятностей, понятия зависимых и независимых событий, математического ожидания. Большую роль в распространении идей теории вероятностей и математической статистики в России сыграли выдающиеся российские математики В. Я. Буняковский (1804–1889) и М. В. Остроградский (1801–1862). Дальнейшее развитие теории вероятностей потребовало уточнения основных ее положений. Большую работу в этом направлении провел выдающийся российский математик П. Л. Чебышёв (1821–1894). Его ученик А. А. Марков (1856– 1922) стал выдающимся математиком именно благодаря своим исследованиям в теории вероятностей.
Книга А. А. Маркова «Исчисление вероятностей», первое издание которой вышло в 1900 г., а четвертое — в 1924 г., в течение многих лет была лучшей из тех, по которым учились российские математики. В этой книге, в частности, раскрывается, в каком понимании статистическая вероятность 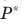 (А) близка к вероятности Р (А) при больших п: вероятность значительного отклонения
(А) близка к вероятности Р (А) при больших п: вероятность значительного отклонения 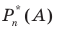 от Р (А) близка к нулю, но это не означает, что значительные отклонения невозможны при больших п. В XX в. теория вероятностей постепенно превращается в строгую аксиоматическую теорию. Это произошло благодаря работам многих математиков. Но действительно решающим этапом в развитии теории вероятностей стала работа А. Н. Колмогорова (1903–1987) «Основные понятия теории вероятностей» (изданная в 1937 г.), в которой он изложил свою аксиоматику теории вероятностей и после которой теория вероятностей заняла равноправное место среди других математических дисциплин. Большие достижения в теории вероятностей и математической статистике имели также российские математики А. Я. Хинчин (1894–1959), Е. Е. Слуцкий (1880–1948), Б. В. Генеденко (1911–1995), математики И. И. Гихман (1918–1985), В. С. Михалевич (1930–1994), и другие.
от Р (А) близка к нулю, но это не означает, что значительные отклонения невозможны при больших п. В XX в. теория вероятностей постепенно превращается в строгую аксиоматическую теорию. Это произошло благодаря работам многих математиков. Но действительно решающим этапом в развитии теории вероятностей стала работа А. Н. Колмогорова (1903–1987) «Основные понятия теории вероятностей» (изданная в 1937 г.), в которой он изложил свою аксиоматику теории вероятностей и после которой теория вероятностей заняла равноправное место среди других математических дисциплин. Большие достижения в теории вероятностей и математической статистике имели также российские математики А. Я. Хинчин (1894–1959), Е. Е. Слуцкий (1880–1948), Б. В. Генеденко (1911–1995), математики И. И. Гихман (1918–1985), В. С. Михалевич (1930–1994), и другие.
Выборка, вариационный ряд и гистограмма
Если теория вероятностей оперирует с известными законами распределения и их параметрами (числовыми характеристиками), то математическая статистика по результатам экспериментов проверяет, правильно ли подобрано распределение (нормальное, биномиальное, экспоненциальное и т. д.), оценивает параметры этого распределения, проверяет гипотезы о параметрах принятого распределения. Это позволяет заменить большое число экспериментальных данных небольшим числом параметров распределения, которые в сжатом виде характеризуют случайную величину и позволяют прогнозировать результаты эксперимента при известном комплексе условий.
Пусть проводится 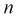 измерений. В результате измерений получено
измерений. В результате измерений получено 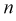 чисел
чисел 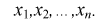 . Если повторить еще раз
. Если повторить еще раз 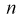 измерений, то получатся другие
измерений, то получатся другие 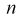 чисел, отличные от первого набора. Процесс из
чисел, отличные от первого набора. Процесс из 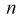 измерений можно описать как и независимых случайных величин.
измерений можно описать как и независимых случайных величин.
Результат и наблюдений 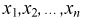 случайной величины X называется выборкой,
случайной величины X называется выборкой, 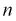 – объем выборки, а сама случайная величина X – называется генеральной случайной величиной.
– объем выборки, а сама случайная величина X – называется генеральной случайной величиной.
Результат эксперимента 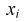 может быть интерпретирован либо апостериорной величиной, либо априорной. В первом случае это результат опыта. Во втором случае является случайной величиной (т. к. до опыта неизвестна), которая получит свое конкретное значение в результате какого-то
может быть интерпретирован либо апостериорной величиной, либо априорной. В первом случае это результат опыта. Во втором случае является случайной величиной (т. к. до опыта неизвестна), которая получит свое конкретное значение в результате какого-то 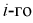 опыта. В этом случае можно предполагать, что закон распределения
опыта. В этом случае можно предполагать, что закон распределения 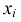 , совпадает с законом распределения генеральной случайной величиной X и
, совпадает с законом распределения генеральной случайной величиной X и 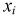 , можно рассматривать как экземпляр генеральной случайной величины X.
, можно рассматривать как экземпляр генеральной случайной величины X.
Далее мы будем считать выборки априорными. При этом будем полагать, что элементы выборки – независимые случайные величины с одинаковым законом распределения, т. е. мы можем широко использовать теоремы независимых случайных величинах.
Упорядоченная в порядке возрастания последовательность выборочных значений образует вариационный ряд:
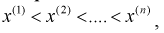
члены вариационного ряда 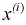 называются порядковыми статистиками. Если объем выборки
называются порядковыми статистиками. Если объем выборки  – велик, то выборка позволяет приблизительно оценить закон распределения случайной величиной X. Для этого необходимо построить гистограмму. Есть два способа построения гистограммы – равноинтервальный и равновероятностный.
– велик, то выборка позволяет приблизительно оценить закон распределения случайной величиной X. Для этого необходимо построить гистограмму. Есть два способа построения гистограммы – равноинтервальный и равновероятностный.
Рассмотрим равноинтервалъный способ.
- Разобьем весь диапазон выборочных значений от
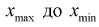 на
на 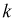 равных частей. Величину
равных частей. Величину 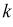 выбирают достаточно произвольно, можно так:
выбирают достаточно произвольно, можно так: 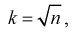 где
где 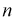 – объем выборки.
– объем выборки. - Определяем длину каждого интервала:
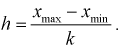
- Находим границы каждого интервала: для первого:
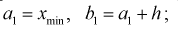 для второго:
для второго: 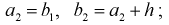 для
для 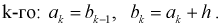
Определим середины каждого интервала: 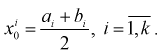
4. Подсчитываем (используя вариационный ряд) количество выборочных значений, попадающих в  интервал –
интервал – 
5. Находим относительную частоту 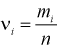 попадания случайной величиной X в
попадания случайной величиной X в 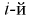 интервал.
интервал.
Полученные данные заносим в таблицу.

Эта таблица называется статистическим рядом.
Графическое изображение статистического ряда – это гистограмма.
Рисуем оси координат, делаем разметку осей, наносим на ось X границы интервалов и их середины. После этого строим на каждом отрезке прямоугольники высотой 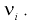 . Аппроксимируем фигуру из прямоугольников пунктирной линией (рис. 8.1). По виду этой кривой можно выдвинуть предположение (гипотезу) о виде закона распределения генеральной случайной величиной X (на рис. 8.1. видно, что пунктирная линия похожа на кривую Гаусса, которая относится к нормальному закону).
. Аппроксимируем фигуру из прямоугольников пунктирной линией (рис. 8.1). По виду этой кривой можно выдвинуть предположение (гипотезу) о виде закона распределения генеральной случайной величиной X (на рис. 8.1. видно, что пунктирная линия похожа на кривую Гаусса, которая относится к нормальному закону).
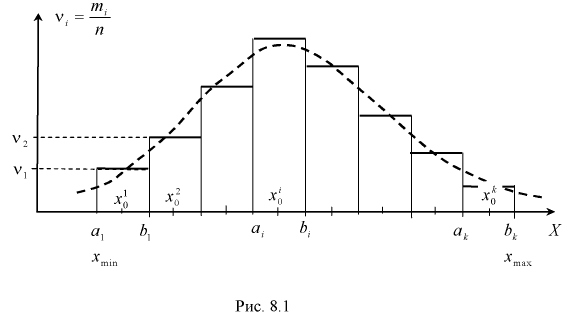
Имея статистический ряд можно оценить числовые характеристики генеральной случайной величиной X :
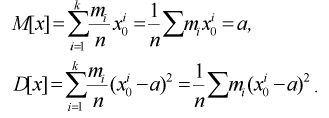
Выборочный метод
Группа предметов или явлений, объединенных каким-либо общим признаком или свойством качественного или количественного характера, называется совокупностью. Предметы или явления, образующие совокупность, называются единицами совокупности. Если совокупность содержит ограниченное число единиц, то она называется конечной. Если число единиц совокупности безгранично, то ее называют бесконечной совокупностью.
Теоретические основы выборочного метода содержатся в теоремах Чебышева и Ляпунова.
Основной предпосылкой применения выборочного метода является возможность судить о характеристиках генеральной (общей) совокупности по отобранной, так называемой выборочной совокупности. Наиболее важным принципом в применении выборочного метода является обеспечение равной возможности всем единицам, входящим в состав генеральной совокупности, быть избранными. При таком объективном подходе к отбору единиц, при котором ни одна единица не обладает преимуществом попасть в отбираемую совокупность по сравнению с другими единицами, характеристики выборочной совокупности при увеличении объема выборки стремятся к характеристикам генеральной совокупности.
Теорема Чебышева (применительно к выборочному методу) может быть записана в следующем виде:
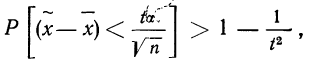
где 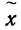 —средняя по совокупности выбранных единиц;
—средняя по совокупности выбранных единиц;
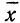 — средняя по генеральной совокупности;
— средняя по генеральной совокупности;
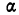 — среднее квадратическое отклонение в генеральной совокупности.
— среднее квадратическое отклонение в генеральной совокупности.
Теорема формулируется так: с вероятностью, сколь угодно близкой к единице (достоверности), можно утверждать, что при достаточно большом объеме выборки, и ограниченной дисперсии генеральной совокупности разность между выборочной средней 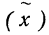 и генеральной средней
и генеральной средней 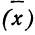 будет сколь угодно мала.
будет сколь угодно мала.
Примечания. 1. Выражение 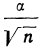 часто обозначают
часто обозначают 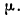
2. При практическом использовании теоремы Чебышева генеральную-дисперсию 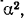 которая неизвестна, заменяют выборочной дисперсией
которая неизвестна, заменяют выборочной дисперсией 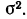
Теорема Ляпунова
Ляпунов с помощью разработанного им метода характеристических функций доказал в 1900 г. центральную предельную теорему, носящую его имя. Эта теорема выясняет общие условия, при осуществлении которых распределение суммы независимых случайных величин стремится к нормальному распределению вероятностей. В частности, эта теорема дает возможность оценить погрешность приближенных равенств: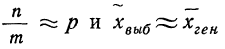
при достаточно больших n (modo Bernulliano). Если 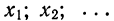
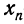 —независимые случайные величины и
—независимые случайные величины и  то вероятность их средней
то вероятность их средней 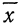 находится в пределе от а до b и может быть определена равенством:
находится в пределе от а до b и может быть определена равенством:
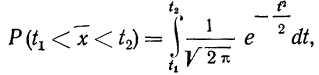
где
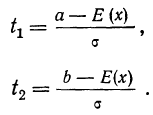
Ограничительные условия теоремы Ляпунова сводятся в основном к тому, чтобы среди слагаемых случайных величин не было сильно выделяющихся (таких, колеблемость которых значительно превосходила бы большинство остальных). В приложении к выборочному методу данная теорема может быть сформулирована следующим образом:
При достаточно большом объеме выборки и ограниченной дисперсии генеральной совокупности вероятность того, что разность между выборочной средней и генеральной средней будет в пределах 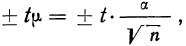 равна
равна 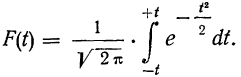
Формулировка Ляпунова придает теореме Чебышева полную определенность и записывается так:
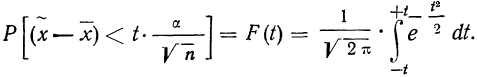
Замечание о практическом использовании ее то же, что и для формулы на стр. 125.
Теорема Я. Бернулли, опубликованная в 1713 г., послужила началом возникновения большой группы теорем, именуемых в общем законом больших чисел. Она представляет собой частный случай теоремы Чебышева и может быть из нее получена
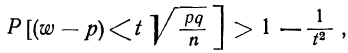
где 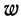 — доля признака среди отобранных единиц (частость);
— доля признака среди отобранных единиц (частость);
р — доля признака в генеральной совокупности.
Теорема Бернулли применяется в тех случаях, когда из генеральной совокупности производится отбор единиц и доля признака не меняется от испытания к испытанию. Формулировка теоремы Бернулли применительно к выборке: с вероятностью, сколь угодно близкой к единице, можно утверждать, что разность между частостью и долей в генеральной совокупности при достаточно большом объеме выборки будет сколь угодно мала. При практическом использовании данной теоремы величина 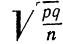 рассчитывается путем замены р на
рассчитывается путем замены р на 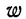 и q на
и q на 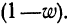
Теорема Пуассона также является частным случаем теоремы Чебышева, когда доля признака в генеральной совокупности (р) с ходом выборки все время меняется. В этом случае
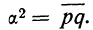
Тогда:
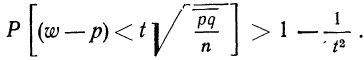
Ошибка репрезентативности (представительства 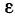 представляет собой разность между характеристиками выборочной и генеральной совокупности. Генеральная средняя
представляет собой разность между характеристиками выборочной и генеральной совокупности. Генеральная средняя 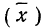 вычитается из выборочной средней
вычитается из выборочной средней 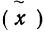 или доля признака в генеральной совокупности (р) вычитается из доли признака в выборочной совокупности, т. е. частости
или доля признака в генеральной совокупности (р) вычитается из доли признака в выборочной совокупности, т. е. частости 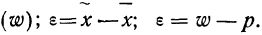
Если  представляет собой предел,которого не превосходит абсолютная величина
представляет собой предел,которого не превосходит абсолютная величина 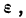 то
то
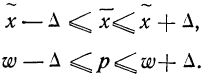
В формулах выборочного метода фигурирует дисперсия генеральной совокупности (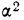 ). Но при производстве выборки характеристики генеральной совокупности неизвестны. Однако обычно (за исключением очень малочисленных выборок) без большой погрешности можно заменить дисперсию генеральной совокупности дисперсией выборочной совокупности (
). Но при производстве выборки характеристики генеральной совокупности неизвестны. Однако обычно (за исключением очень малочисленных выборок) без большой погрешности можно заменить дисперсию генеральной совокупности дисперсией выборочной совокупности (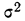 ), которая вычисляется по формулам:
), которая вычисляется по формулам:

Предельная и средние ошибки выборки
Теория устанавливает соотношение между пределом ошибки выборки (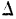 ), гарантируемым с некоторой вероятностью (P), величиной t, связанной с этой вероятностью (см. приложение III), и так называемой средней ошибкой выборки (
), гарантируемым с некоторой вероятностью (P), величиной t, связанной с этой вероятностью (см. приложение III), и так называемой средней ошибкой выборки (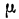 ):
):
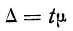
или
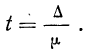
Предельная ошибка выборки равна t-кратному числу средних ошибок выборки.
По способу организации выборки различают:
- собственно случайный отбор;
- типический отбор;
- механический отбор;
- серийный отбор;
- комбинированный отбор.
Собственно случайный отбор ориентирован на выборку единиц из генеральной совокупности без всякого расчленения ее на части или группы. При этом теоретически возможно применение собственно случайного повторного отбора и собственно случайного бесповторного отбора.
Формулы средней ошибки выборки при собственно случайном методе отбора: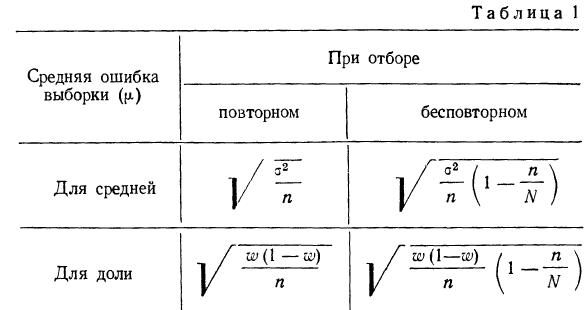
Для большей точности вместо множителя 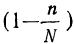 следует брать множитель
следует брать множитель 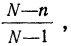 но при большой численности N различие между этими выражениями практически значения не имеет.
но при большой численности N различие между этими выражениями практически значения не имеет.
Пример №9
Из совокупности 10 000 деталей отобрано собственно случайным бесповторным методом 1000 деталей, для которых средний вес детали оказался равным 50 г, дисперсия 49. Бракованных деталей было обнаружено 20 штук. Вычислить средние ошибки выборки для средней и доли.
Дано:
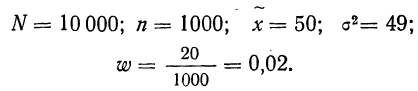
По формулам табл. 1 находим средние ошибки выборки: для среднего веса детали при бесповторном отборе:
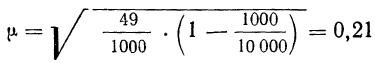
и для доли брака:
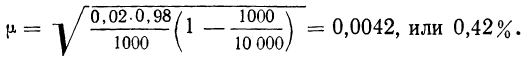
Случайные числа и таблицы случайных чисел
Однозначные числа, расположенные в случайном порядке, называются случайными числами. Случайность расположения чисел состоит в отсутствии закона, определяющего их расположение, и вместе с тем в приближенно равной частоте каждой из десяти цифр.
При организации собственно случайной выборки для соблюдения основного принципа выборки — равной возможности каждой единице генеральной совокупности быть отобранной — используются таблицы случайных чисел, позволяющие производить случайный отбор единиц наудачу, т. е. без привнесения элементов субъективности.
Таблицы случайных чисел составляются различными методами. Так, например, М. Кодыров выписывал 50 000 однозначных чисел из результатов переписи населения 1926 г. Брались срединные цифры одна за другой, в том порядке, в каком они встречались в сводках по городам и губерниям. Для избежания неслучайности крайние цифры из сводок вследствие тенденций к округлениям отбрасывались. А. К. Митропольский для получения таблиц случайных чисел брал 16—19-е знаки двадцатизначной таблицы логарифмов чисел от 90 000 до 100 000. Случайные цифры объединяются в четырехзначные числа.
Таблицы случайных чисел используются путем нумерации всех единиц генеральной совокупности и выписки из таблиц стольких чисел, сколько требуется для выборки. Из генеральной совокупности отбираются те единицы, порядковый номер которых соответствует выписанным из таблицы случайных чисел. Если число единиц в генеральной совокупности не более 999, то последнюю или первую цифру четырехзначного числа отбрасывают. Выборка с помощью таблицы случайных чисел может быть произведена по схеме возвращенного шара (повторная) и по схеме невозвращенного шара (бесповторная). В последнем случае одинаковые числа опускаются.
Пример №10
Генеральная совокупность состоит из 500 единиц. Производится 10-процентный бесповторный отбор. Пронумеруем все 500 единиц генеральной совокупности и возьмем из таблицы случайных чисел (приложение XI) 50 различных трехзначных чисел, начиная с первого числа 3-й колонки. Числа большие, чем 500, отбрасываем.
Получаем: 315, 255, 337, 179, 210, 455, 235-, 364, 489, 80, 117, 118, 174, 476, 111, 341, 296, 332, 4, 307, 22, 430, 52, 22, 83, 248, 319, 262, 36, 101, 27, 342, 470, 330, 170, 443, 499, 109, 42, 70, 490, 422, 336, 67, 121, 225, 57, 319, 499, 362, 198, 50, 286.
Эти числа означают номера тех единиц из 500, которые попали в случайную бесповторную выборку (в данном случае совпадают только три числа: 22, 319, 499; поэтому заменяем их другими).
Для случая, когда частость даже приблизительно неизвестна, можно произвести «грубый» расчет средней ошибки выборки для доли, вводя в расчет максимальную величину произведения 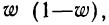 равную 0,25. Тогда для повторного отбора получим:
равную 0,25. Тогда для повторного отбора получим:
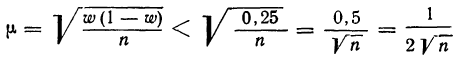
и для бесконечного отбора:
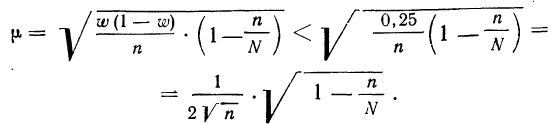
Пример №11
Из совокупности численностью в 900 деталей взята на выборку 81 деталь. Никаких данных, даже предположительных, об удельном весе деталей I сорта в генеральной совокупности нет.
Определить среднюю ошибку выборки для доли продукции I сорта.
Дано: N = 900; n = 81; допускаем, что 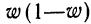 =0,25, тогда получаем:
=0,25, тогда получаем:
Как было показано в § 7, 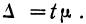 Из приложения III возьмем три значения t, тогда
Из приложения III возьмем три значения t, тогда
при t=1 F(t) = 0,683;
t=2 F(t) = 0,954;
t=3 F(t) = 0,997.
Это показывает, что 0,683 измеряет вероятность того, что ошибка выборки не превысит предела, равного одной средней ошибке. Значительно больше вероятность того, что ошибка не превысит двойной средней ошибки, и т. д.
Вероятность 0,997 практически принимают за достоверность, т. е. считают, что предельная ошибка выборки равна трехкратной средней ошибке.
Иногда для определения размеров предельной ошибки связывают величину t с объемом выборки, применяя эмпирическую формулу:
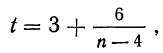
тогда
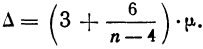
Чем больше объем выборки, тем ближе предельная ошибка к утроенным средним ошибкам.
Численность выборки
При проектировке выборочного наблюдения предполагают заранее заданными величину допустимой ошибки выборки и вероятность ответа. Неизвестным, следовательно, остается тот минимальный объем выборки, который должен обеспечить требуемую точность. Из формулы 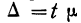 и формул средних ошибок выборки устанавливаем необходимую численность выборки (называемую иногда достаточно большим числом).
и формул средних ошибок выборки устанавливаем необходимую численность выборки (называемую иногда достаточно большим числом).
Формулы для определения численности выборки (n) при собственно случайном способе отбора:
Примечание. При проектировании объема необходимой выборки величины  и
и  неизвестны, поэтому вместо точного их значения берут приближенные, установленные на основании уже проведенного другого наблюдения или нескольких пробных наблюдений, избирая из найденных результатов наибольшие значения
неизвестны, поэтому вместо точного их значения берут приближенные, установленные на основании уже проведенного другого наблюдения или нескольких пробных наблюдений, избирая из найденных результатов наибольшие значения 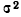 и
и 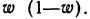
Пример №12
Проектируется выборочное наблюдение, целью которого является установление среднего размера деталей в совокупности, состоящей из 10 000 деталей. Требуемая точность 1 см. Произведенные пробные выборки дали наибольшую дисперсию, равную 49. Нужно определить необходимую численность случайной бесповторной выборки, обеспечивающей с вероятностью 0,95 заданную точность.
Дано: N= 10 000; 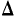 =1; F(y)=0,95;
=1; F(y)=0,95; 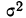 =49.
=49.
По приложению III находим по F(t) значение t= 1,96 и по формуле для бесповторной выборки, взятой из табл. 2, получаем:
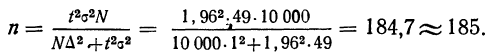
Типический отбор дает более точные результаты. Генеральная совокупность делится по некоторому признаку на типические группы. Количество отбираемых единиц из каждой типической группы устанавливается в следующих размерах (см. табл. 3).

При отборе, не пропорциональном объему типических групп, общее число отбираемых единиц делится на число типических групп и полученная величина дает численность отбора из каждой типической группы.
При отборе, пропорциональном объему типических групп, число наблюдений по каждой группе определяется по формуле:
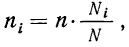
где 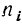 —объем выборки из i-й типической группы;
—объем выборки из i-й типической группы;
n— общий объем выборки;
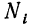 — объем i-й типической группы;
— объем i-й типической группы;
N—объем генеральной совокупности.
При отборе с учетом колеблемости признака, дающем наименьшую величину ошибки выборки, процент выборки из каждой типической группы должен быть пропорционален среднему квадратическому отклонению в этой группе 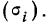 Расчет численности
Расчет численности 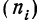 производится по формулам:
производится по формулам:
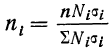 – для средней;
– для средней;
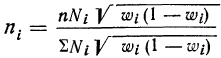 – для доли.
– для доли.
Для вычисления средних ошибок выборки используют формулы табл. 3.
Пример №13
Для определения средней из совокупности 10 000 единиц производится выборка типическим методом. Вся совокупность делится на 5 типических групп. Отбор единиц внутри типических групп производится случайным бесповторным методом пропорционально объему каждой группы. Отбирается 2000 единиц. При отборе получены следующие результаты:
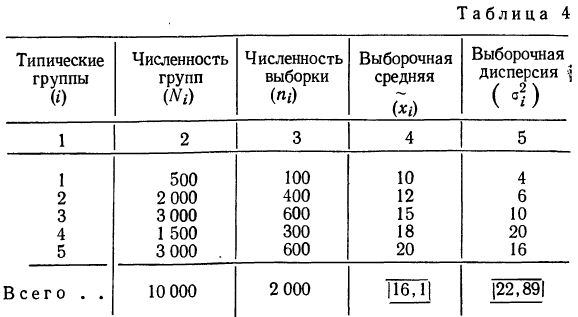
Вычислить: а) среднюю ошибку для каждой группы и для всей выборочной совокупности (при собственно случайном и типическом способах отбора); б) границы, в которых с вероятностью 0,997 находится генеральная средняя по группам и по всей совокупности (при собственно случайном и типическом методах отбора).
Прежде всего рассчитывают численность отбираемых единиц из каждой типической группы пропорционально ее объему (см. колонку 3 табл. 4). Так, для первой типической группы имеем при заданном объеме всей выборки, равном 2000 единиц:
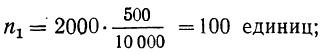
для второй типической группы:
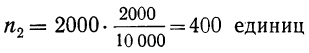
и т. д.
Для определения средней ошибки выборки по группам и общей средней ошибки выборки при собственно случайном способе отбора (бесповторном) используем формулы из табл. 1, Получаем среднюю ошибку выборки:
для первой типической группы
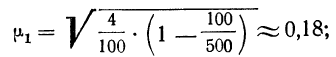
для второй типической группы
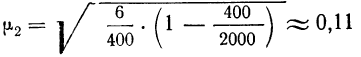
и т. д. по всем группам (см. колонку 2 табл. 5).
Для удобства располагаем все получаемые результаты в таблицу (см. табл. 5).
Для расчета средней ошибки выборки всей совокупности при собственно случайном методе отбора и границ генеральной средней при этом же методе отбора нужно знать общую выборочную среднюю и общую дисперсию выборочной совокупности. Производим расчет общей выборочной средней из групповых выборочных средних путем взвешивания последних по численности отобранных групп
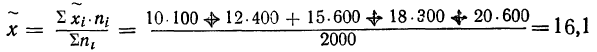
(см. итог колонки 4 табл. 4).
Для определения общей выборочной дисперсии используют теорему сложения вариации.
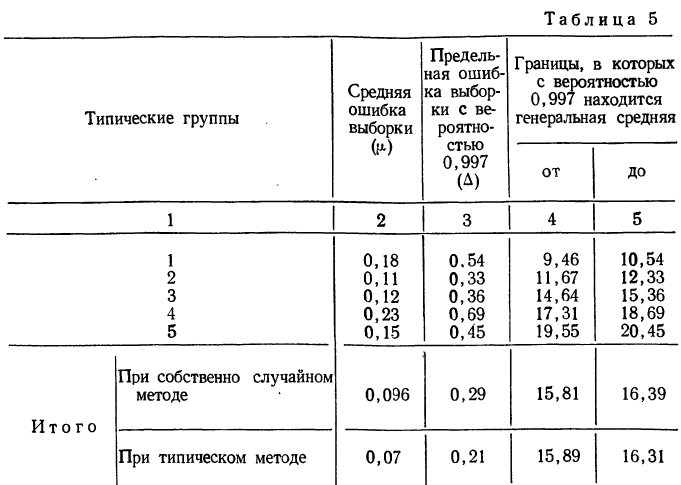
Находим сначала среднюю взвешенную из выборочных дисперсий:
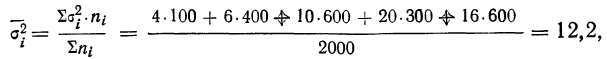
а затем межгрупповую дисперсию:
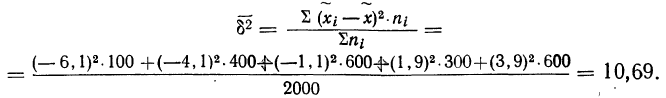
Получаем общую дисперсию выборочной совокупности:
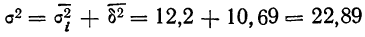
(см. итог колонки 5 табл. 4).
Находим среднюю ошибку выборки всей совокупности при собственно случайном методе отбора
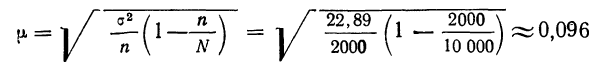
(см. первую строку итога колонки 2 табл. 5).
Предельная ошибка собственно случайной выборки:
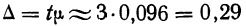
(см. первую строку итога колонки 3 табл. 5).
Соответственно находим границы генеральной средней при собственно случайном методе отбора:
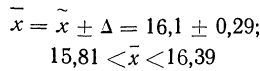
(см. первую строку итога колонок 4 и 5 табл. 5).
Рассчитываем среднюю ошибку типической выборки, пропорциональной объему типических групп, по формуле из табл. 3. Получим:
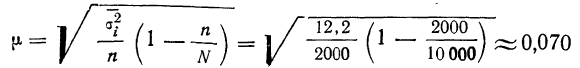
(см. вторую строку итога колонки 2 табл. 5).
Далее определяем ошибку типической выборки 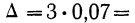
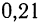 и границы генеральной средней
и границы генеральной средней 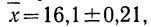 т. е.
т. е. 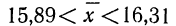 (см. вторую строку итога колонок 4 и 5 табл. 5).
(см. вторую строку итога колонок 4 и 5 табл. 5).
Пример №14
Для определения доли признака производится типическая выборка 400 единиц из совокупности 10 500 единиц, разбитых на 3 типические группы численностью в 5000, 2500 и 3000 единиц. Имеются основания (прошлое обследование) считать, что искомая доля по типическим группам составляет около 10, 20 и 50%.
В каком объеме произвести выборку из типических групп, чтобы пропорции отбора были наивыгоднейшими?
Определяем численность первой типической группы по соответствующей формуле при объеме всей выборки, равной 400 единицам:
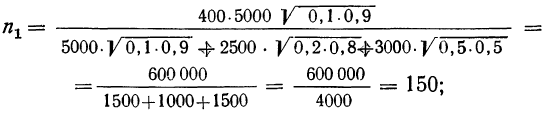
для второй типической группы:
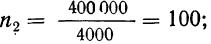
для третьей типической группы:
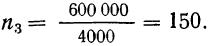
При механической выборке совокупность делится на столько групп, сколько единиц должно войти в выборку, и из 1 каждой группы отбирается одна единица.
Средняя ошибка выборки подсчитывается по формулам ( собственно случайной выборки (табл. 1).
При серийном отборе с равновеликими сериями генеральную совокупность делят на одинаковые по объему группы — серии и производят выборку не единиц совокупности, а серий. Попавшие в выборку серии обследуются сплошь. Серии могут отбираться повторным и бесповторным методами.
Средние ошибки выборки при таком отборе рассчитывают по формулам:

где К — число серий в генеральной совокупности;
r — число отобранных серий;
 — межсерийная (межгрупповая) дисперсия средних;
— межсерийная (межгрупповая) дисперсия средних;
 — межсерийная (межгрупповая) дисперсия доли.
— межсерийная (межгрупповая) дисперсия доли.
Пример №15
Генеральная совокупность состоит из 5000 единиц, разбитых на 50 равных по величине серий (по 100 единиц). Бесповторным методом отобрано 10 серий. Результаты выборки представлены в следующей таблице:

Исчислить среднюю ошибку серийной бесповторной выборки. Вычисляем: а) общую среднюю всей выборочной совокупности по серийным средним: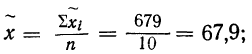
б) межсерийную (межгрупповую) дисперсию средних:
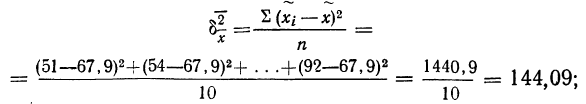
в) среднюю ошибку серийной выборки:
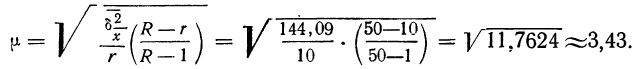
Необходимая численность отбираемых серий при серийном отборе получается из формул табл. 2, в которых вместо N, n и 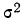 подставляют R, r и
подставляют R, r и 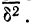
Пример №16
Совокупность разбита на 50 серий. Имеются основания предполагать, что межсерийная дисперсия равна 16. Сколько серий нужно отобрать бесповторным методом, чтобы с вероятностью 0,954 утверждать, что ошибка выборочной средней не превысит 2,3.
Дано:
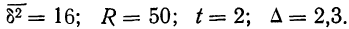
Находим необходимое число серий, отбор которых обеспечит требуемую точность:
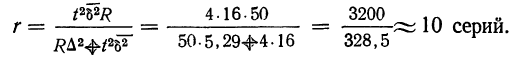
Комбинированная выборка (равновеликие серии) предполагает комбинацию серийного отбора с индивидуальным отбором.
Генеральная совокупность разбивается на одинаковые по объему серии. Сначала отбираются серии, а затем из отобранных серий производится индивидуальная выборка единиц.
Квадрат средних ошибок выборки  рассчитывают по следующим формулам (см. табл. 8),
рассчитывают по следующим формулам (см. табл. 8),
где  — общее число единиц, попавших в выборку при отборе серий, определяется по формуле:
— общее число единиц, попавших в выборку при отборе серий, определяется по формуле:
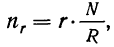
n — число единиц, попавших в выборку из серий.

Пример №17
Генеральная совокупность состоит из 100 000 единиц, разбитых на 200 равных по объему серий. Произведена бесповторная выборка 50% серий и из каждой серии по 20% единиц. Средняя из серийных дисперсий оказалась равной 12, а межсерийная дисперсия — 5. Определить среднюю ошибку выборки. Дано:
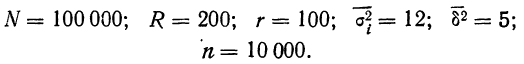
Определяем общее число единиц, попавших в выборку:
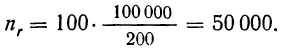
Определяем среднюю ошибку выборки:
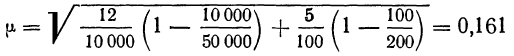
(по формуле из табл. 8 для бесповторного отбора).
Мы получили среднюю ошибку комбинированной выборки при отборе из генеральной совокупности 10 000 единиц. Можно было бы произвести выборку такого же объема, но отобрав 20% серий и 50% единиц из каждой серии.
При тех же значениях — средней из серийных дисперсий и межсерийной дисперсии — средняя ошибка выборки была бы равна:
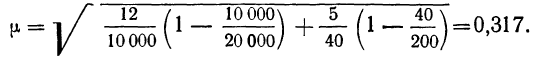
Таким образом, величина ошибки увеличилась бы больше чем в два раза.
В иных случаях большая точность достигается большим числом наблюдений в пределах отобранных серий за счет сокращения числа последних.
Средняя ошибка разности выборочных средних
Выборочная средняя отличается от генеральной средней на t-кратное число средних ошибок  Если в результате выборок получены две выборочные средние
Если в результате выборок получены две выборочные средние  для каждой из которых найдена средняя ошибка выборки
для каждой из которых найдена средняя ошибка выборки  то среднюю ошибку разности этих двух выборочных средних
то среднюю ошибку разности этих двух выборочных средних 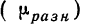 можно определить по средним ошибкам этих выборочных средних
можно определить по средним ошибкам этих выборочных средних
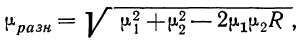
где R—коэффициент корреляции между вариантами двух выборочных совокупностей (см. раздел VII).
В случае некоррелированности признаков, т. е. равенства коэффициента корреляции нулю, формула примет следующий вид:
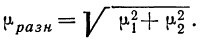
Пример №18
Из генеральной совокупности произведены две выборки. При этом средние ошибки выборочных средних оказались равными 0,48 и 0,43. Признаки некоррелированы. Найти среднюю ошибку разности двух выборочных средних. Она равна
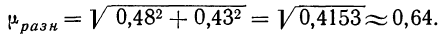
Распределение выборочных средних
Имеется случайная величина х, распределенная в генеральной совокупности по закону нормального распределения со средней 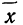 и дисперсией
и дисперсией 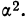 Если произвести достаточно много выборок из указанной совокупности собственно случайным методом и для каждой из выборок вычислить выборочную среднюю, то их распределение будет также подчинено закону нормального распределения со средней
Если произвести достаточно много выборок из указанной совокупности собственно случайным методом и для каждой из выборок вычислить выборочную среднюю, то их распределение будет также подчинено закону нормального распределения со средней 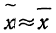 и дисперсией
и дисперсией 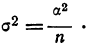
Такое распределение выборочных средних не будет зависеть от объема выборок.
Доверительная вероятность
Для суждения о том, являются ли достоверными характеристики, полученные с помощью выборочных наблюдений, применяют доверительную вероятность, т. е. такую вероятность, которую исследователь признает достаточной при установлении границ случайного колебания изучаемого явления.
В качестве доверительной вероятности принимают Р(t), равное 0,95 или 0,99. Последняя наиболее достаточна.
Достоверность существенного различия
Сравнивая несколько статистических характеристик, например средние или коэффициенты вариации, исчисленные по результатам случайных выборок из генеральной совокупности, хотят установить, существенна ли разность между ними.
Существенным различием называют различие между средними или коэффициентами вариации, превосходящее по величине то, которое можно было бы объяснить случайными колебаниями.
Для признания достоверности существенного различия, приведшего к резкому качественному сдвигу величины изучаемого признака, сравнивают разность между характеристиками с доверительной границей, выражающей пределы случайной вариации. Если эта разность больше доверительной границы, то различие называют существенным, и оно выражает систематическое различие сравниваемых характеристик.
Нулевая гипотеза
При проверке статистической гипотезы об отсутствии существенных различий между несколькими выборочными совокупностями используют так называемую нулевую гипотезу, состоящую в признании того, что они взяты наудачу из одной генеральной совокупности.
Проверка нулевой гипотезы производится с помощью различных критериев согласия, позволяющих с помощью доверительных вероятностей сделать вывод об ее опровержении или неопровержении. При этом следует иметь в виду, что неопро-вержение нулевой гипотезы не означает ее подтверждения, а свидетельствует лишь о необходимости проведения дальнейшей проверки, в частности путем увеличения числа наблюдений. При проверке нулевой гипотезы наибольшее значение придается практической неосуществимости маловероятных событий. Так, если вероятность критерия согласия, выражающего вероятность случайного расхождения, очень мала (<0,05), то это свидетельствует о существенном различии, и нулевая гипотеза опровергается; если же она достаточна велика (>0,05), то вопрос о существенности различия остается без ответа.
В качестве критерия согласия, т. е. оценки существенности расхождения или различия двух выборочных средних, в случае,.если число отобранных единиц в каждой выборке больше 25, принимается неравенство:
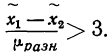
При этом нулевая гипотеза состоит в отрицании существенности различия средних.
Пример №19
Произведем проверку нулевой гипотезы по следующим данным.
Выделено 5 участков лесонасаждений и с каждого участка взяты пробные площадки. В среднем на 1 га по пяти участкам получилось следующее распределение деревьев по толщине: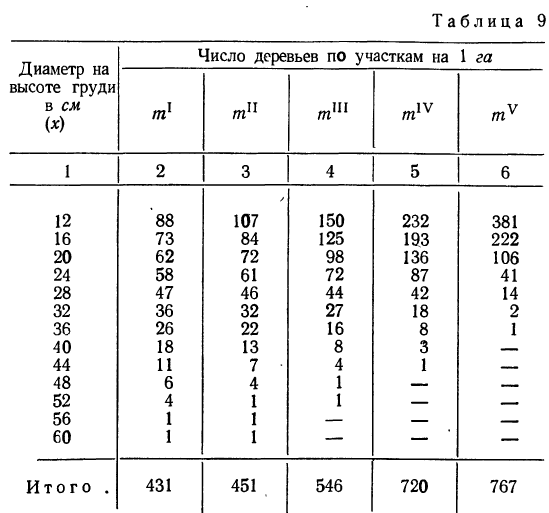
Определить существенность расхождения средних диаметров деревьев по участкам:
а) Находим средние диаметры деревьев по участкам:
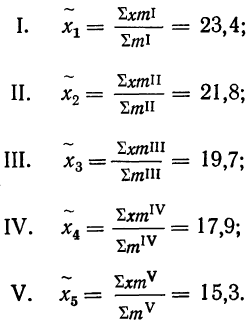
б) Вычисляем средние квадратические отклонения по участкам:

в) Вычисляем средние ошибки выборочных средних:
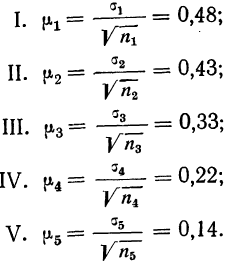
г) Находим, например, следующие разности выборочных средних по участкам:
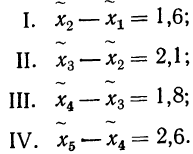
д) Находим средние ошибки разности соответствующих пар выборочных средних:
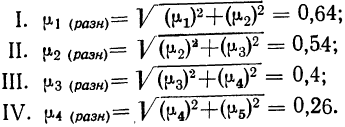
е) Находим критерий оценки существенности расхождения соответствующих выборочных средних:
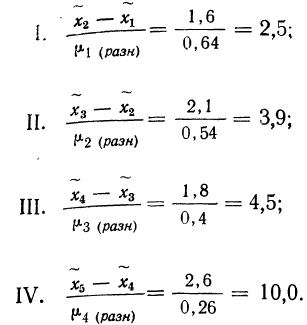
Вывод. Из критериев оценки существенности заключаем, что выделения II, III, IV и V участков произведены правильно, так как критерии оценки существенности больше трех. И следовательно, мы имеем разные насаждения.
При сравнении I и II участков вопрос остается открытым.
Смещенные и несмещенные оценки
Если из генеральной совокупности производится выборка и по ее результатам вычисляются характеристики:
1) выборочная средняя 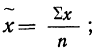
2) выборочная дисперсия 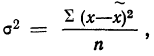 то при большом
то при большом
числе отобранных единиц (n) эти характеристики будут приближаться к соответствующим математическим ожиданиям: Е(х)
и 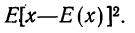
При малом,числе отобранных единиц эти две характеристики могут значительно отличаться от соответствующих математических ожиданий. Поэтому, принимая эти выборочные характеристики в качестве оценок генеральных характеристик, мы допускаем определенную ошибку. Эта ошибка может быть несистематической, когда при неограниченном повторении выборок средняя из выборочных характеристик совпадет с генеральной; при этом систематической ошибки, т. е. регулярного завышения или занижения, не будет. В случае, если среднее значение принятых в качестве оценок выборочных характеристик совпадает с генеральной характеристикой, эти оценки называются несмещенными.
Можно доказать, что 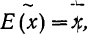 поэтому величина
поэтому величина  является несмещенной оценкой генеральной средней. Что же касается выборочной дисперсии, то ее математическое ожидание не равно генеральной дисперсии.
является несмещенной оценкой генеральной средней. Что же касается выборочной дисперсии, то ее математическое ожидание не равно генеральной дисперсии. 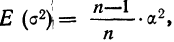 и поэтому
и поэтому 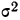 является смещенной оценкой. Для устранения систематической ошибки и получения несмещенной оценки нужно
является смещенной оценкой. Для устранения систематической ошибки и получения несмещенной оценки нужно 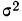 умножить на
умножить на 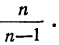
Тогда дисперсию при малом числе наблюдений следует вычислять по формуле:
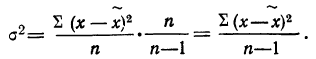
Малая выборка
При необходимости оценки генеральной совокупности по результатам малого числа наблюдений, т. е. при n меньше 20, формулы для обычной (большой) выборки, основанные на нормальном распределении вероятностей, дают значительные неточности.
Оценка результатов малой выборки производится путем «исправления» выборочного среднего квадратического отклонения и использования закона распределения вероятностей Стюдента.
Выборочное среднее квадратическое отклонение малой выборки исчисляется по формуле:
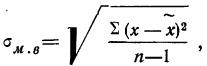
где n—1 представляет собой «Число степеней свободы», т. е. количество вариантов, могущих принимать произвольные значения, не меняющие величины средней.
Таким образом, выборочное среднее квадратическое отклонение малой выборки отличается от выборочного среднего квадратического отклонения (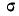 ) тем, что сумму квадратов отклонений от выборочной средней делят не на n, а на n—1. Зная выборочное среднее квадратическое отклонение
) тем, что сумму квадратов отклонений от выборочной средней делят не на n, а на n—1. Зная выборочное среднее квадратическое отклонение 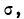 можно путем его «исправления» вычислить выборочное среднее квадратическое отклонение малой выборки
можно путем его «исправления» вычислить выборочное среднее квадратическое отклонение малой выборки 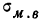 по формуле:
по формуле:
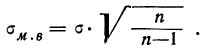
Пример №20
Произведена выборка 16 единиц. Выборочное среднее квадратическое отклонение ( ) оказалось равным 100.
) оказалось равным 100.
Вычислить выборочное среднее квадратическое отклонение малой выборки 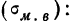
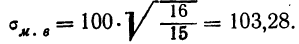
Средняя ошибка малой выборки исчисляется по формуле:
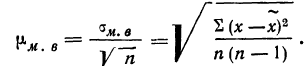
Пример №21
На основе данных примера 12 можно вычислить среднюю ошибку малой выборки:
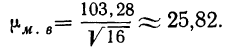
Среднюю ошибку малой выборки можно получить и путем использования «неисправленного» выборочного среднего квадратического отклонения
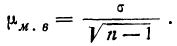
Среднюю ошибку разности двух выборочных средних исчисляют по формуле:
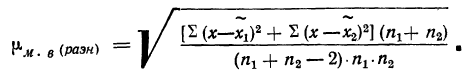
Нормированное отклонение или стандартизованная разность малой выборки (t) получается аналогично тому, как это получалось в обычной выборке:
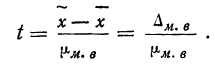
Предельная ошибка малой выборки:
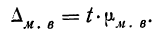
Опираясь на предположение о нормальном распределении признака в генеральной совокупности, Стюдент в 1908 г. нашел закон распределения t, который называется распределением Стюдента:
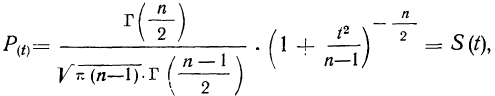
где P(t) =S(t) — вероятности того, что стандартизованная разность между выборочной и генеральной средней имеет величину t;
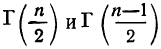 – гаммы-функции, которые можно рассматривать как обобщение факториала натурального числа.
– гаммы-функции, которые можно рассматривать как обобщение факториала натурального числа.
Для любого положительного числа n гамма-функция определяется следующим равенством:
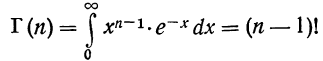
Частные случаи:
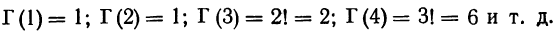
Свойства гаммы-функции:
1)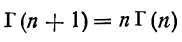 и 2)
и 2)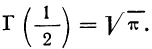
Первый частный случай гаммы-функции и первое указанное ее свойство дают:
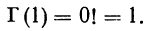
Свойство гаммы-функции позволяет находить Г(n) при n, кратном 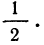 Например:
Например:
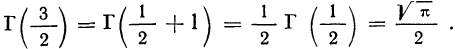
Особенностью распределения Стюдента является то, что вероятность того или иного значения t зависит только от двух величин: объема выборки (n) и величины t. При возрастании объема выборки распределение Стюдента приближается к нормальному:
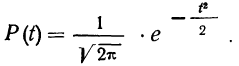
Если сделать определенные допущения о величине Генеральной средней, то можно вычислить фактическое нормированное отношение 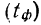 при помощи интеграла Стюдента:
при помощи интеграла Стюдента:
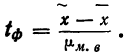
Тогда
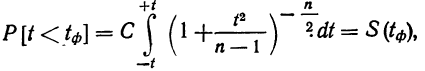
где
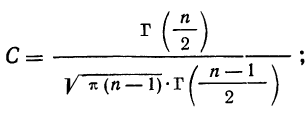
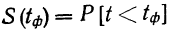 —вероятность того, что стандартизованная разность (t) между действительной генеральной средней и выборочной средней будет меньше стандартизованной разности, вычисленной по результатам малой выборки
—вероятность того, что стандартизованная разность (t) между действительной генеральной средней и выборочной средней будет меньше стандартизованной разности, вычисленной по результатам малой выборки 
 —определяется из приложения IV. При этом значение n определяется вычитанием единицы из числа наблюдений.
—определяется из приложения IV. При этом значение n определяется вычитанием единицы из числа наблюдений.
Интеграл Стюдента используют для решения ряда обычных задач малой выборки как для случаев, когда генеральная совокупность обладает нормальным распределением, так и для случаев, когда распределение признака в генеральной совокупности не совсем совпадает с нормальным.
Функция 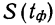 используется для определения также вероятностей того, что: 1)
используется для определения также вероятностей того, что: 1) 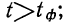 2)
2)  и 3)
и 3) 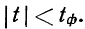
Так, вероятность того, что 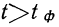 будет:
будет:
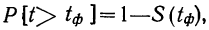
где 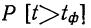 — вероятность значений t, больших, чем
— вероятность значений t, больших, чем 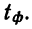 И далее:
И далее:

где 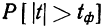 — вероятность значений t, абсолютная величина которых больше, чем
— вероятность значений t, абсолютная величина которых больше, чем 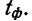
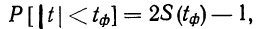
где 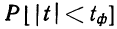 — вероятность значений t, абсолютная величина которых меньше, чем
— вероятность значений t, абсолютная величина которых меньше, чем 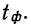
Пример №22
Первая типовая задача малой выборки. Оценка выборочной средней.
Произведена малая выборка урожая пшеницы. Срок уборки урожая своевременный. На выборку собственно случайным повторным методом взято 8 участков. Результаты выборки по отдельным участкам следующие:
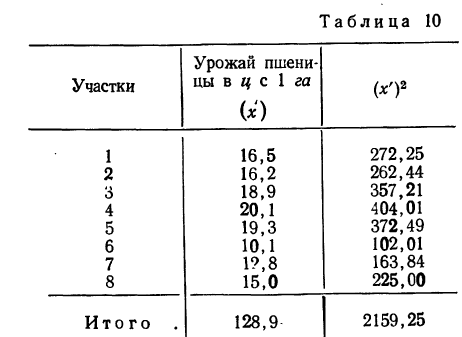
Определить вероятность того, что разность между выборочным и генеральным средним урожаем не больше 0,5 ц с 1 га.
Дано:
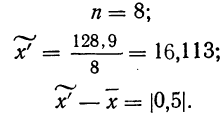
Находим 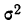 по формуле (см. раздел I, стр. 58):
по формуле (см. раздел I, стр. 58): 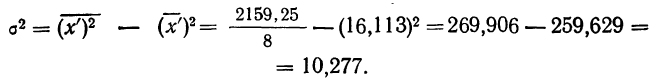
Определяем:

«Исправляем» 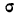 и получаем:
и получаем:
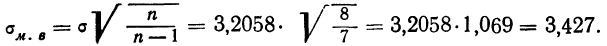
Вычисляем среднюю ошибку малой выборки 
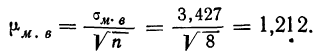
Определяем величину нормированного отклонения по выборочным данным и предполагаемым границам генеральной средней 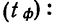
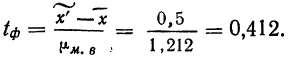
Находим: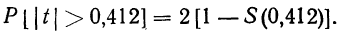
Так как число наблюдений равно 8, то берем n=7; тогда по приложению IV находим: 
Следовательно:
Р[ |/| >0,412] = 2 (1—0,649) = 2 • 0,351 = 0,702« 0,7.
Таким образом видно, что вероятность нормированных отклонений, по абсолютной величине превышающих 0,412, или, иными словами, вероятность отклонений генеральной средней от выборочной средней на абсолютную величину, превышающую 0,5 ц с 1 га, не мала (0,7). Поэтому разность между генеральной и выборочной средними легко могла превысить 0,5 ц с 1 га.
Можно было воспользоваться другой формулой и определить вероятность нормированных отклонений, абсолютная величина которых меньше 0,412, и прийти к тому же заключению:
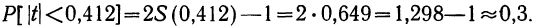
Вероятность того, что генеральная средняя находится в определенных границах, определяется по формуле:
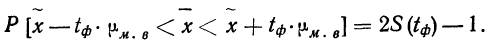
Пример №23
Вторая типовая задача малой выборки: определение границ интервала, в которых находится генеральная средняя.
Из данных предыдущего примера 14 найти с вероятностью 0,954 границы интервала, в которых содержится генеральная средняя урожая.
Дано:
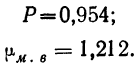
Находим 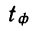 по соответствующей формуле:
по соответствующей формуле:
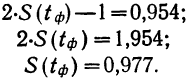
По приложению IV находим 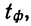 равное 2,5.
равное 2,5.
Следовательно, границы генеральной средней 
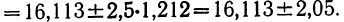
С вероятностью 0,954 можно утверждать, что 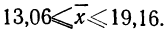
Теория малой выборки дает возможность оценить существенность различия между двумя .выборочными средними. Вероятность значений разностей между двумя выборочными средними, по абсолютной величине не меньших, чем разность, полученная в результате опыта, т. е. фактическая, определяется по формуле:
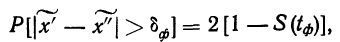
где 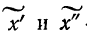 — выборочные средние;
— выборочные средние;
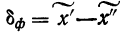 — фактическая разность между двумя выборочными средними;
— фактическая разность между двумя выборочными средними;
а величина 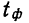 определяется по формуле:
определяется по формуле:
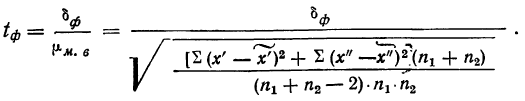
Примечания: 1. При определении вероятности, равной  по приложению IV в качестве n следует брать
по приложению IV в качестве n следует брать 
2. Если вероятность (Р) получается большой, то это свидетельствует о том, что следовало ожидать разностей, превышающих ту, которую мы получили фактически. И следовательно, фактическая разность, будучи меньше тех, которых следовало ожидать с большой вероятностью, не дает основания считать, что различия между средними существенны.
При полученной малой вероятности (Р) различие между средними не случайно, а существенно.
3. При вычислении 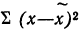 можно использовать равенство
можно использовать равенство 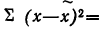
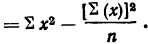
Пример №24
Третья типовая задача малой выборки. Оценка разности двух выборочных средних. Произведена малая выборка девяти участков аналогично тому, как это сделано в примере 14. Урожай убрали с большим опозданием.
Результат сбора урожая по участкам представлен в табл. 11 (в колонках 1 и 2).
Оценить расхождение между средним урожаем, полученным при своевременной уборке урожая (пример 14) и уборке его с большим опозданием.
Дано:
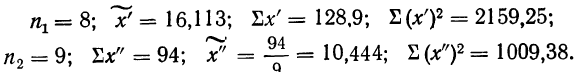
Вычисляем:
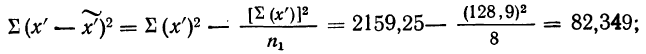

По соответствующей формуле получаем:
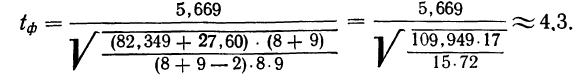
Из приложения IV для n = 8+9—2=15 находим:
S (4,3) =0,999.
Тогда:
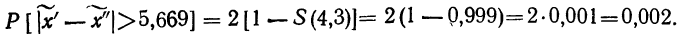
Так как вероятность (Р) очень мала, то следует считать, что средние урожаи существенно отличаются друг от друга, т. е. что опоздание в сроках уборки существенно снижает урожай.
При оценке существенности расхождения между двумя выборочными средними часто применяют правило трех сигм:
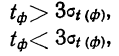
где 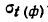 —среднее квадратическое отклонение, вычисляемое по формуле:
—среднее квадратическое отклонение, вычисляемое по формуле:
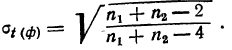
В первом случае, т. е. если 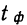 больше трех сигм, расхождение между средними двух выборок полагают не случайным.
больше трех сигм, расхождение между средними двух выборок полагают не случайным.
Пример №25
По данным примеров 14 и 16 оценить расхождение между двумя выборочными средними по указанным формулам:
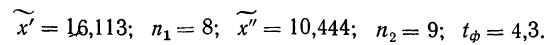
Находим:
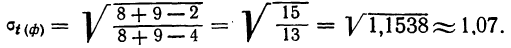
Получаем:
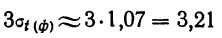
и, следовательно,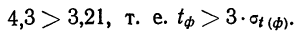
Поэтому расхождение между двумя выборочными средними следует считать существенным, что согласуется с выводом примера 16.
Оценка существенности различия двух выборочных средних может быть произведена также путем использования критерия, основанного на подсчете инверсий. В данном случае нулевой гипотезой является предположение, что две выборочные средние отличаются друг от друга несущественно. Подсчет инверсий производится путем расположения ранжированных результатов двух полученных выборок последовательно. Инверсия образуется в том случае, если какому-нибудь варианту из первой выборки (х) предшествует вариант из второй выборки (у). Например, соединенные в одну последовательность ранжированные варианты двух выборок расположились следующим образом:
Тогда подсчет инверсий для 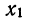 дает 1, для
дает 1, для 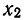 и
и 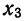 — тоже единицу, для
— тоже единицу, для 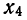 инверсий —4, для
инверсий —4, для 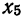 — 5 и т. д.
— 5 и т. д.
После подсчета числа инверсий находят математическое ожидание инверсии по формуле:
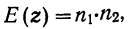
где 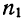 и
и 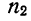 — объемы выборок.
— объемы выборок.
Далее находят дисперсию: 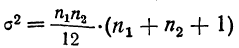
и 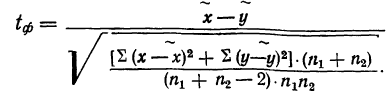
Путем вычитания и прибавления к E(z) произведения 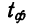 на
на  находят ожидаемые границы г. Если z находится в найденных границах, то нулевая гипотеза не опровергается. При выходе z за найденные границы нулевая гипотеза опровергается и делается вывод о существенности различий средних.
находят ожидаемые границы г. Если z находится в найденных границах, то нулевая гипотеза не опровергается. При выходе z за найденные границы нулевая гипотеза опровергается и делается вывод о существенности различий средних.
Данный метод обоснован в случаях, когда объем выборок больше 10, но может быть использован и при n, близком к 10.
Пример №26
Используя данные примеров 14 и 16, найдем существенность различия двух средних урожаев, полученных в результате сбора урожая своевременно и с большим опозданием.
Располагаем результаты обеих выборок в ранжированном порядке.

Имеем: 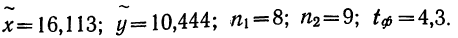 Подсчитываем:
Подсчитываем: 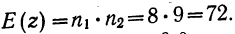
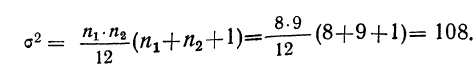

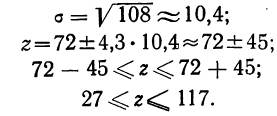
Подсчитываем фактическое число инверсий: z=1 +1 + 1 + + 2 = 5.
В данном случае нулевая гипотеза опровергается и результат свидетельствует о существенном расхождении двух средних урожаев, что согласуется с выводами, полученными ранее другими способами.
При проверке гипотезы случайности выборки можно использовать метод последовательных разностей.
Пусть выборка n единиц из генеральной совокупности со средней 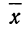 и дисперсией
и дисперсией 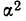 расположились по значению признака в следующем порядке:
расположились по значению признака в следующем порядке: 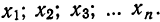 Находим сначала разности между значениями признака в последовательности их отбора.
Находим сначала разности между значениями признака в последовательности их отбора.
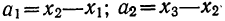 и т. д. до
и т. д. до 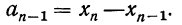 Определяем среднюю из квадратов разностей по формуле:
Определяем среднюю из квадратов разностей по формуле:
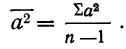
Находим:
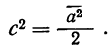
Вычисляем выборочную дисперсию:
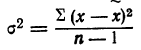
и для получения критерия 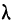 делим
делим 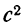 на
на 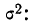
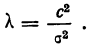
Сравнение найденного критерия с теоретическим (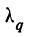 ) в зависимости от объема выборки производится так.
) в зависимости от объема выборки производится так.
Если n<20, то используют следующую таблицу (см. табл. 13):

Из таблицы находят 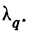 При этом если найденная
При этом если найденная 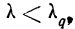 то это указывает на неверность рассматриваемой гипотезы. Если
то это указывает на неверность рассматриваемой гипотезы. Если 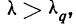 то гипотеза верна.
то гипотеза верна.
При большом числе отобранных единиц (n>20) 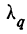 определяется по формуле:
определяется по формуле:
где находится по табличному значению 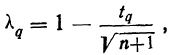
где 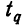 находится по табличному значению
находится по табличному значению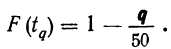
При q = 5% имеем 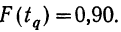 Из приложения III находим, что
Из приложения III находим, что 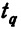 = 1,65, значит
= 1,65, значит
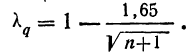
Пример №27
Используя данные примера 16 о результатах сбора урожая по участкам с большим опозданием, оценим гипотезу случайности выборки.
1) Находим разности:
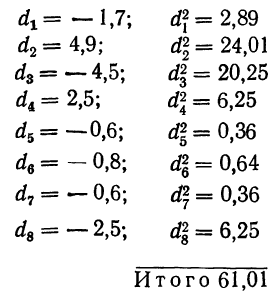
и вычисляем 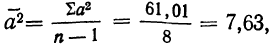 а затем
а затем 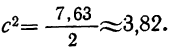
2) Определяем сначала среднюю:
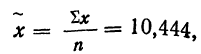 а затем дисперсию:
а затем дисперсию:
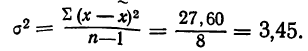
3) Находим критерий:
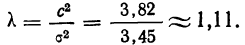
4) По табл. 13 определяем верхнюю допустимую границу  При n = 9
При n = 9  = 0,512.
= 0,512.
5) Делаем вывод о том, что найденная 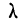 превосходит допустимую верхнюю границу
превосходит допустимую верхнюю границу 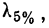 и поэтому наша гипотеза о случайности выборки верна.
и поэтому наша гипотеза о случайности выборки верна.
Пример №28
Пусть отобрано 35 единиц. При q = 5% получаем:
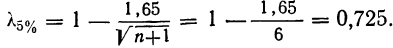
Следовательно, если при выборке 35 единиц 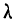 будет меньше 0,725, то это укажет на неверность нашей гипотезы; если же больше, то гипотеза верна.
будет меньше 0,725, то это укажет на неверность нашей гипотезы; если же больше, то гипотеза верна.
Оценка существенности различия коэффициентов вариации устанавливается аналогично тому, как это делается при оценке существенности различия выборочных средних по критерию согласия. Если принять:
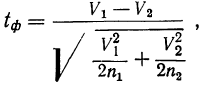
то при  >3 различие коэффициентов вариации полагают неслучайным.
>3 различие коэффициентов вариации полагают неслучайным.
Во всех случаях  <3 делают вывод, что при данном числе наблюдений нулевая гипотеза не подтверждается и тем самым существенность различия не доказана.
<3 делают вывод, что при данном числе наблюдений нулевая гипотеза не подтверждается и тем самым существенность различия не доказана.
Пример №29
Используя данные примера 11 о выделении участков лесонасаждений, оценим существенность различия коэффициентов вариации по двум участкам — IV и V.
Имеем: 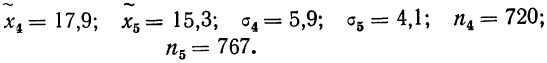
Определяем коэффициенты вариации:
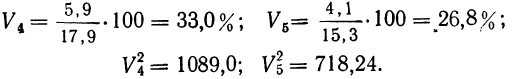
Находим
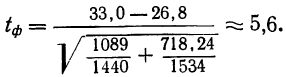
Так как  > 3, делаем вывод, что рассматриваемые коэффициенты вариации отличаются существенно, т. е. неслучайно.
> 3, делаем вывод, что рассматриваемые коэффициенты вариации отличаются существенно, т. е. неслучайно.
- Статистическая проверка гипотез
- Статистические оценки
- Теория статистической проверки гипотез
- Линейный регрессионный анализ
- Регрессионный анализ
- Корреляционный анализ
- Статистические решающие функции
- Случайные процессы
Приступим к изучению элементов математической статистики, в которой разрабатываются научно обоснованные методы сбора статистических данных и их обработки.
Пусть требуется изучить множество однородных объектов (это множество называют статистической совокупностью) относительно некоторого качественного или количественного признака, характеризующего эти объекты. Например, если имеется партия деталей, то качественным признаком может служить соответствие детали стандартам, а количественным — контролируемый размер детали.
Лучше всего осуществить сплошное обследование, т. е. изучить каждый объект. Однако в большинстве случаев по разным причинам это сделать невозможно. Препятствовать сплошному обследованию может большое число объектов, их недоступность и т. п. Если, например, нужно знать среднюю глубину воронки при взрыве снаряда из опытной партии, то, проводя сплошное обследование, мы должны будем уничтожить всю партию.
Если сплошное обследование невозможно, то из всей совокупности выбирают для изучения часть объектов.
Статистическая совокупность, из которой отбирают часть объектов, называется генеральной совокупностью. Множество объектов, случайно отобранных из генеральной совокупности, называется выборкой.
Число объектов генеральной совокупности и выборки называется соответственно объемом генеральной совокупности и объемом выборки.
Пример. Плоды одного дерева (200 шт.) обследуют на наличие специфического для данного сорта вкуса. Для этого отбирают 10 шт. Здесь 200 —объем генеральной совокупности, а 10 —объем выборки.
Если выборку отбирают по одному объекту, который обследуют и снова возвращают в генеральную совокупность, то выборка называется повторной. Если объекты выборки уже не возвращаются в генеральную совокупность, то выборка называется бесповторной. На практике чаще используется бесповторная выборка. Если объем выборки составляет небольшую долю объема генеральной совокупности, то разница между повторной и бесповторной выборками незначительна
Свойства объектов выборки должны правильно отражать свойства объектов генеральной совокупности, или, как говорят, выборка должна быть репрезентативной (представительной). Считается, что выборка репрезентативна, если все объекты генеральной совокупности имеют одинаковую вероятность попасть в выборку, т. е. выбор осуществляется случайно. Например, для того чтобы оценить будущий урожай, можно сделать выборку из генеральной совокупности еще не созревших плодов и исследовать их характеристики (массу, качество и пр.). Если вся выборка будет взята с одного дерева, то она не будет репрезентативной. Репрезентативная выборка должна состоять из случайно выбранных плодов со случайно выбранных деревьев.

Статистическое распределение выборки. Полигон. Гистограмма
Пусть из генеральной совокупности извлечена выборка, причем 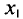 , наблюдалось
, наблюдалось 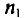 раз,
раз, 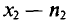 раз,
раз, 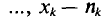 раз и
раз и 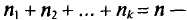 объем выборки. Наблюдаемые значения
объем выборки. Наблюдаемые значения 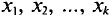 называются вариантами, а последовательность вариант, записанная в возрастающем порядке,— вариационным рядом. Числа наблюдений
называются вариантами, а последовательность вариант, записанная в возрастающем порядке,— вариационным рядом. Числа наблюдений 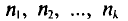 называют частотами, а их отношения к объему выборки
называют частотами, а их отношения к объему выборки 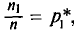
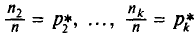 — относительными частотами. Отметим, что сумма относительных частот равна единице:
— относительными частотами. Отметим, что сумма относительных частот равна единице:
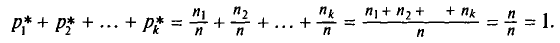
Статистическим распределением выборки называют перечень вариант и соответствующих им частот или относительных частот. Статистическое распределение можно задать также в виде последовательности интервалов и соответствующих им частот (непрерывное распределение). В качестве частоты, соответствующей интервалу, принимают сумму частот вариант, попавших в этот интервал.
Заметим, что в теории вероятностей под распределением понимают соответствие между возможными значениями случайной величины и их вероятностями, а в математической статистике — соответствие между наблюдаемыми вариантами и их частотами или относительными частотами.
Пример:
Перейдем от частот к относительным частотам в следующем распределении выборки объема n = 20:

Найдем относительные частоты:
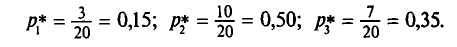
Поэтому получаем следующее распределение:

Для графического изображения статистического распределения используются полигоны и гистограммы.
Для построения полигона в декартовых координатах на оси Ох откладывают значения вариант 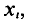 на оси Оу— значения частот
на оси Оу— значения частот 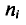 (относительных частот
(относительных частот 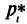 ).
).
Пример:
Рис. 14 представляет собой полигон следующего распределения:

Полигоном обычно пользуются в случае небольшого количества вариант. В случае большого количества вариант и в случае непрерывного распределения признака чаще строят гистограммы. Для этого интервал, в котором заключены все наблюдаемые значения признака, разбивают на несколько частичных интервалов шириной h и находят для каждого частичного интервала 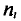 — сумму частот вариант, попавших в і-й интервал. Затем на этих интервалах как на основаниях строят прямоугольники с высотами
— сумму частот вариант, попавших в і-й интервал. Затем на этих интервалах как на основаниях строят прямоугольники с высотами 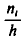 (или
(или 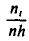 , где n —объем выборки). Площадь i-го частичного прямоугольника равна
, где n —объем выборки). Площадь i-го частичного прямоугольника равна 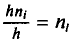
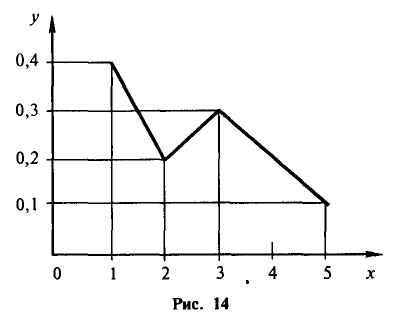
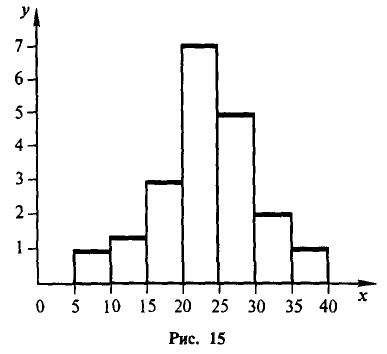
(или 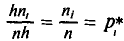 ). Следовательно, площадь гистограммы равна сумме всех частот (или относительных частот), т. е. объему выборки (или единице).
). Следовательно, площадь гистограммы равна сумме всех частот (или относительных частот), т. е. объему выборки (или единице).
Пример:
Рис. 15 показывает гистограмму непрерывного распределения объема n =100, заданного следующей таблицей:

Оценки параметров генеральной совокупности по ее выборке
Выборка как набор случайных величин
Пусть имеется некоторая генеральная совокупность, каждый объект которой наделен количественным признаком X. При случайном извлечении объекта из генеральной совокупности становится известным значение х признака X этого объекта. Таким образом, мы можем рассматривать извлечение объекта из генеральной совокупности как испытание, X—как случайную величину, а х —как одно из возможных значений X.
Допустим, что из теоретических соображений удалось установить, к какому типу распределений относится признак X. Естественно, возникает задача оценки (приближенного определения) параметров, которыми описывается это распределение. Например, если известно, что изучаемый признак распределен в генеральной совокупности нормально, то необходимо оценить, т. е. приближенно найти математическое ожидание и среднее квадратическое отклонение, так как эти два параметра полностью определяют нормальное распределение.
Обычно в распоряжении исследователя имеются лишь данные выборки генеральной совокупности, например значения количественного признака 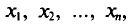 полученные в результате n наблюдений (здесь и далее наблюдения предполагаются независимыми). Через эти данные и выражают оцениваемый параметр.
полученные в результате n наблюдений (здесь и далее наблюдения предполагаются независимыми). Через эти данные и выражают оцениваемый параметр.
Опытные значения признака X можно рассматривать и как значения разных случайных величин 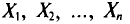 с тем же распределением, что и X, и, следовательно, с теми же числовыми характеристиками, которые имеет X. Значит,
с тем же распределением, что и X, и, следовательно, с теми же числовыми характеристиками, которые имеет X. Значит, 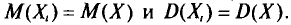 Величины
Величины 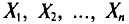 можно считать независимыми в силу независимости наблюдений. Значения
можно считать независимыми в силу независимости наблюдений. Значения 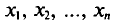 в этом случае называются реализациями случайных величин
в этом случае называются реализациями случайных величин 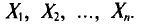 Отсюда и из предыдущего следует, что найти оценку неизвестного параметра — это значит найти функцию от наблюдаемых случайных величин
Отсюда и из предыдущего следует, что найти оценку неизвестного параметра — это значит найти функцию от наблюдаемых случайных величин 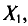
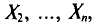 которая и дает приближенное значение оцениваемого параметра.
которая и дает приближенное значение оцениваемого параметра.
Генеральная и выборочная средние. Методы их расчета
Пусть изучается дискретная генеральная совокупность объема N относительно количественного признака X.
Определение:
Генеральной средней 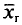 (или а) называется среднее арифметическое значений признака генеральной совокупности.
(или а) называется среднее арифметическое значений признака генеральной совокупности.
Если все значения 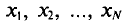 признака генеральной совокупности объема N различны, то
признака генеральной совокупности объема N различны, то
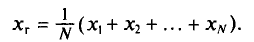
Если же значения признака 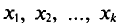 имеют соответственно частоты
имеют соответственно частоты 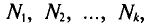 причем
причем  то
то
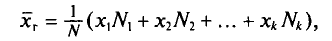
или

Как уже отмечалось (п. 1), извлечение объекта из генеральной совокупности есть наблюдение случайной величины X.
Пусть все значения  различны. Так как каждый объект может быть извлечен с одной и той же вероятностью 1/N, то
различны. Так как каждый объект может быть извлечен с одной и той же вероятностью 1/N, то
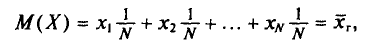
т. е.

Такой же итог следует, если значения 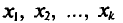 имеют соответственно частоты
имеют соответственно частоты 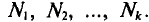
В случае непрерывного распределения признака X по определению полагают 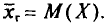
Пусть для изучения генеральной совокупности относительно количественного признака X произведена выборка объема n.
Определение:
Выборочной средней 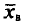 , называется среднее арифметическое значений признака выборочной совокупности.
, называется среднее арифметическое значений признака выборочной совокупности.
Если все значения 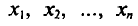 признака выборки объема n различны, то
признака выборки объема n различны, то
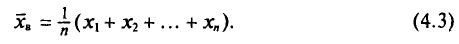
Если же значения признака  имеют соответственно частоты
имеют соответственно частоты 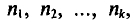 причем
причем  , то
, то
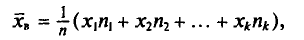
или

Пример:
Выборочным путем были получены следующие данные о массе 20 морских свинок при рождении (в г): 30, 30, 25, 32, 30, 25, 33, 32, 29, 28^27, 36, 31, 34, 30, 23, 28, 31, 36, 30. Найдем выборочную среднюю 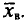
Согласно формуле (4.4), имеем:
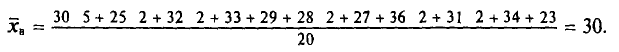
Итак, 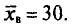
Далее, не уменьшая общности рассуждений, будем считать значения 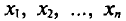 признака различными.
признака различными.
Разумеется, выборочная средняя для различных выборок того же объема n из той же генеральной совокупности будет получаться, вообще говоря, различной. И это не удивительно — ведь извлечение і-го по счету объекта есть наблюдение случайной величины 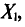 а их среднее арифметическое
а их среднее арифметическое
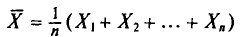
есть тоже случайная величина.
Таким образом, всевозможные получающиеся выборочные средние есть возможные значения случайной величины 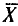 , которая называется выборочной средней случайной величиной.
, которая называется выборочной средней случайной величиной.
Найдем 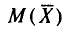 , пользуясь тем, что
, пользуясь тем, что 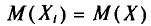 (см. п. 1).
(см. п. 1).
С учетом свойств математического ожидания (см. гл. II) получаем:
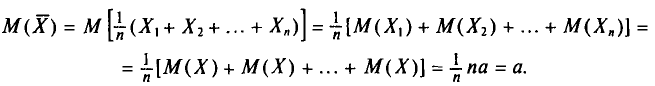
Итак, 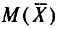 (математическое ожидание выборочной средней) совпадает с а (генеральной средней).
(математическое ожидание выборочной средней) совпадает с а (генеральной средней).
Теперь найдем 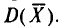 Так как
Так как 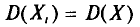 (п. 1) и
(п. 1) и 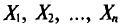 независимы, то, согласно свойствам дисперсии (см. гл. II), получаем
независимы, то, согласно свойствам дисперсии (см. гл. II), получаем
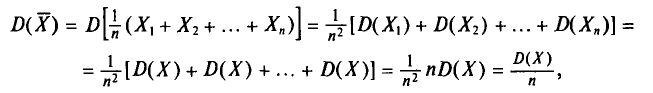
T. e.

Наконец, отметим, что если варианты 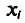 —большие числа, то для облегчения вычисления выборочной средней применяют следующий прием. Пусть С — константа.
—большие числа, то для облегчения вычисления выборочной средней применяют следующий прием. Пусть С — константа.
Так как
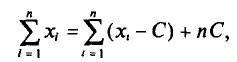
то формулу (4.3) можно преобразовать к виду
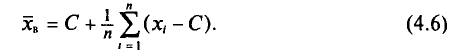
За константу С (так называемый ложный нуль) берут некоторое среднее значение между наименьшим и наибольшим значениями х, (і- 1, 2, …, n).
Пример:
Имеется выборка:
Требуется найти 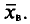
Возьмем С =72,00 и вычислим разности 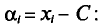
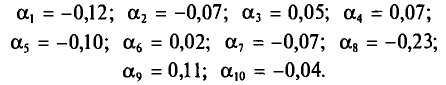
Их сумма: 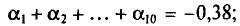 их среднее арифметическое
их среднее арифметическое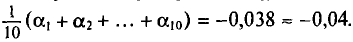 Выборочная средняя
Выборочная средняя
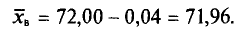
Генеральная и выборочная дисперсии
Для того чтобы охарактеризовать рассеяние значений количественного признака X генеральной совокупности вокруг своего среднего значения, вводят следующую характеристику — генеральную дисперсию.
Определение:
Генеральной дисперсией D, называется среднее арифметическое квадратов отклонений значений признака X генеральной совокупности от генеральной средней 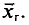
Если все значения 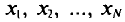 признака генеральной совокупности объема N различны, то
признака генеральной совокупности объема N различны, то
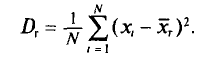
Если же значения признака 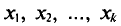 имеют соответственно
имеют соответственно
частоты 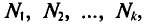 причем
причем  то
то
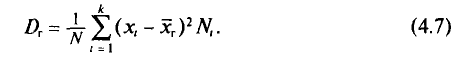
Пример:
Генеральная совокупность задана таблицей распределения:

Найдем генеральную дисперсию.
Согласно формулам (4.1) и (4.7), имеем:
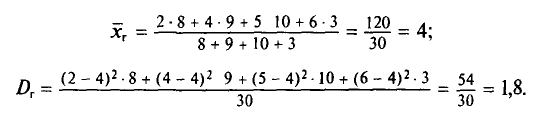
Генеральным средним квадратическим отклонением (стандартом) называется 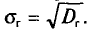
Пусть все значения 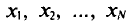 различны.
различны.
Найдем дисперсию признака X, рассматриваемого как случайная величина:
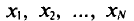
Так как 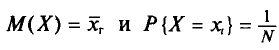 (см. п. 2), то
(см. п. 2), то
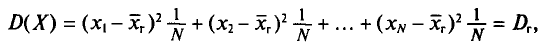
т. е.
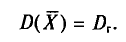
Таким образом, дисперсия D(X) равна 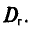
Такой же итог можно получить, если значения 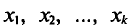 имеют соотвественно частоты
имеют соотвественно частоты 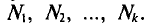
В случае непрерывного распределения признака X по определению полагают

С учетом формулы (4.8) формула (4.5) (п. 2) перепишется в виде
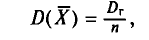
откуда 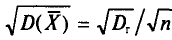 или
или 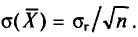 Величина
Величина 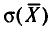 называется средней квадратической ошибкой.
называется средней квадратической ошибкой.
Для того чтобы охарактеризовать рассеяние наблюдаемых значений количественного признака выборки вокруг своего среднего значения 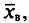 вводят выборочную дисперсию.
вводят выборочную дисперсию.
Определение:
Выборочной дисперсией 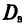 , называется среднее арифметическое квадратов отклонений наблюдаемых значений признака X от выборочной средней
, называется среднее арифметическое квадратов отклонений наблюдаемых значений признака X от выборочной средней 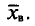
Если все значения 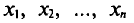 признака выборки объема n различны, то
признака выборки объема n различны, то
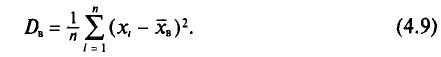
Если же значения признака 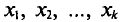 имеют соответственно частоты
имеют соответственно частоты 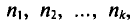 причем
причем 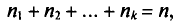 то
то
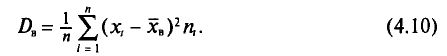
Пример:
Пусть выборочная совокупность задана таблицей распределения:

Найдем выборочную дисперсию. Согласно формулам (4.4) и (4.10), имеем:
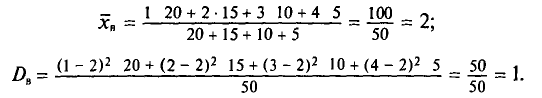
Выборочным средним квадратическим отклонением (стандартом) называется квадратный корень из выборочной дисперсии:
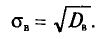
В условиях примера 2 получаем, что 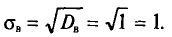
Далее, не уменьшая общности рассуждений, будем считать значения 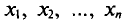 признака различными.
признака различными.
Выборочную дисперсию, рассматриваемую нами как случайная величина, будем обозначать 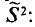
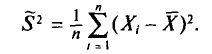
Теорема:
Математическое ожидание выборочной дисперсии равно 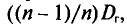 т.е.
т.е.
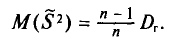
Доказательство:
С учетом свойств математического ожидания (см. гл. II) получаем
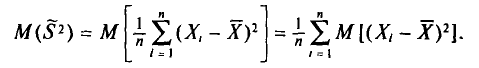
Вычислим одно слагаемое 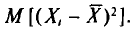 Имеем
Имеем
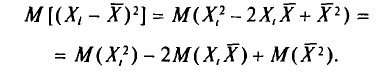
Вычислим по отдельности эти математические ожидания.
Согласно свойству I дисперсии (см. гл. И) и формулам (4.2), (4.8) имеем
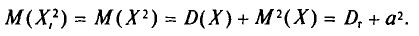
Далее, с учетом свойства 4 математического ожидания (см. гл. II)
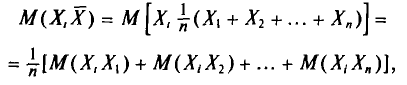
но слагаемое этой суммы, у которого второй индекс равен і, т.е. 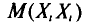 , равно
, равно 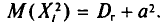 У всех остальных слагаемых
У всех остальных слагаемых 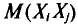 индексы разные. Поэтому в силу независимости
индексы разные. Поэтому в силу независимости  (см. гл. II)
(см. гл. II)
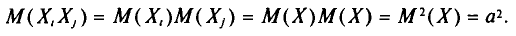
Так как имеется n-1 таких слагаемых, то
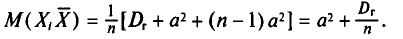
В силу свойства 1 дисперсии (см. гл. П) получаем
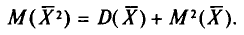
Нами уже найден (см. пп. 2 и 3):
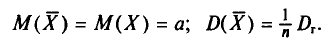
Поэтому
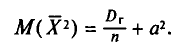
Таким образом,
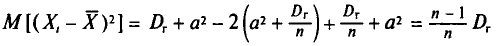
и не зависит от индекса суммирования і. Поэтому
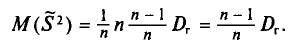
Что и требовалось доказать.
В заключение этого пункта отметим, что если варианты 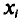 — большие числа, то для облегчения вычисления выборочной дисперсии
— большие числа, то для облегчения вычисления выборочной дисперсии 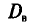 , формулу (4.9) преобразуют к следующему виду:
, формулу (4.9) преобразуют к следующему виду:
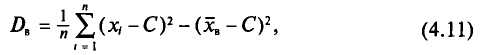
где С—ложный нуль.
Действительно, с учетом формулы (4.3) имеем
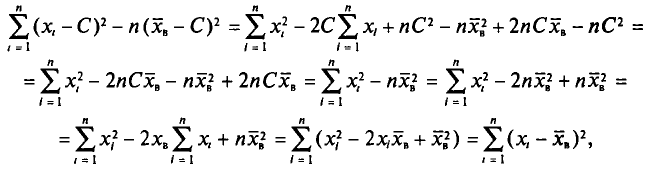
откуда
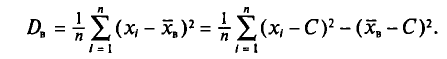
Пример:
Для выборки, указанной в примере 2 из п. 2, найдем 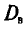 (ложный нуль остается прежним С= 72,00)
(ложный нуль остается прежним С= 72,00)
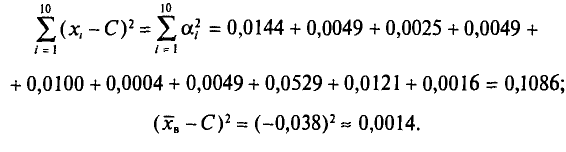
Наконец, согласно формуле (4.11)
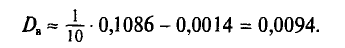
Оценки параметров распределения
Одной из задач статистики является оценка параметров распределения случайной величины X по данным выборки. При этом в теоретических рассуждениях считают, что генеральная совокупность бесконечна. Это делается для того, чтобы можно было переходить к пределу при 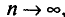 где n — объем выборки. Для оценки параметров распределения X из данных выборки составляют выражения, которые должны служить оценками неизвестных параметров. Например,
где n — объем выборки. Для оценки параметров распределения X из данных выборки составляют выражения, которые должны служить оценками неизвестных параметров. Например,  (см. п. 2) является оценкой генеральной средней, а
(см. п. 2) является оценкой генеральной средней, а 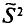 (см. п. 3) — оценкой генеральной дисперсии
(см. п. 3) — оценкой генеральной дисперсии 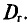 Обозначим через
Обозначим через 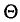 оцениваемый параметр, через
оцениваемый параметр, через 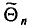 — оценку этого параметра
— оценку этого параметра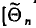 является выражением^ составленным из
является выражением^ составленным из 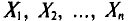 (см. п. 1)]. Для того чтобы оценка
(см. п. 1)]. Для того чтобы оценка 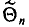 давала хорошее приближение, она должна удовлетворять определенным требованиям. Укажем эти требования.
давала хорошее приближение, она должна удовлетворять определенным требованиям. Укажем эти требования.
Несмещенной называют оценку 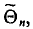 математическое ожидание которой равно оцениваемому параметру
математическое ожидание которой равно оцениваемому параметру 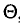 , т. е.
, т. е. 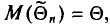 в противном случае оценка называется смещенной.
в противном случае оценка называется смещенной.
Пример:
Оценка 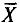 является несмещенной оценкой генеральной средней а, так как
является несмещенной оценкой генеральной средней а, так как 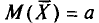 (см. п. 2).
(см. п. 2).
Пример:
Оценка 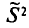 является смещенной оценкой генеральной дисперсии
является смещенной оценкой генеральной дисперсии 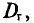 так как, согласно установленной выше теореме (см. п. 3),
так как, согласно установленной выше теореме (см. п. 3),
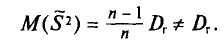
Пример:
Наряду с выборочной дисперсией 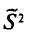 рассматривают еще так называемую исправленную дисперсию
рассматривают еще так называемую исправленную дисперсию 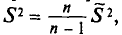 которая является также оценкой генеральной дисперсии. Для
которая является также оценкой генеральной дисперсии. Для 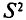 с учетом установленной выше теоремы (см. п. 3) имеем
с учетом установленной выше теоремы (см. п. 3) имеем
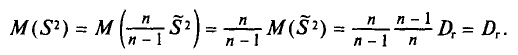
Таким образом, оценка 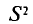 в отличие от оценки
в отличие от оценки 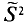 является несмещенной оценкой генеральной дисперсии. Явное выражение для
является несмещенной оценкой генеральной дисперсии. Явное выражение для 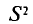 имеет вид
имеет вид
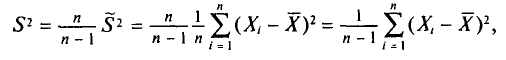
T. e.
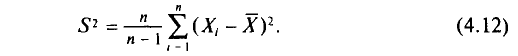
Естественно в качестве приближенного неизвестного параметра брать несмещенные оценки для того, чтобы не делать систематической ошибки в сторону завышения или занижения.
Состоятельной называют такую оценку 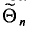 параметра
параметра 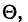 , что для любого наперед заданного числа
, что для любого наперед заданного числа  вероятность
вероятность 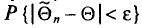 при
при 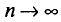 стремится к единице*. Это значит, что при достаточно больших n можно с вероятностью, близкой к единице, т. е. почти наверное, утверждать, что оценка
стремится к единице*. Это значит, что при достаточно больших n можно с вероятностью, близкой к единице, т. е. почти наверное, утверждать, что оценка 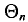 отличается от оцениваемого параметра
отличается от оцениваемого параметра 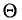 меньше, чем на
меньше, чем на 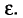
Очевидно, такому требованию должна удовлетворять всякая оценка, пригодная для практического использования.
Заметим, что несмещенная оценка 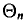 будет состоятельной, если при
будет состоятельной, если при 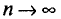 дисперсия стремится к нулю:
дисперсия стремится к нулю: 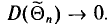 Это следует из неравенства Чебышева ((2.33) см. § 2.8, п. 1).
Это следует из неравенства Чебышева ((2.33) см. § 2.8, п. 1).
Пример:
Как было установлено (см. п. 3), 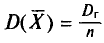 . Отсюда следует, что несмещенная оценка
. Отсюда следует, что несмещенная оценка 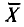 является и состоятельной, так как
является и состоятельной, так как
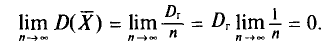
Можно показать, что несмещенная оценка 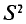 является также состоятельной. Поэтому в качестве оценки генеральной дисперсии принимают исправленную дисперсию. Заметим, что оценки
является также состоятельной. Поэтому в качестве оценки генеральной дисперсии принимают исправленную дисперсию. Заметим, что оценки  отличаются множителем
отличаются множителем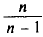 , который стремится к 1 при
, который стремится к 1 при 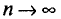 . На практике
. На практике  не различают при n > 30.
не различают при n > 30.
Для оценки генерального среднего квадратического отклонения используют исправленное среднее квадратическое отклонение, которое равно квадратному корню из исправленной дисперсии:
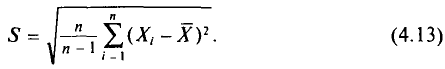
Левые части формул (4.12), (4.13), в которых случайные величины 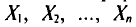 заменены их реализациями
заменены их реализациями 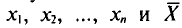 выборочной средней
выборочной средней 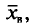 будем обозначать соответственно через
будем обозначать соответственно через 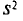 и s
и s
Отметим, что если варианты 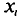 — большие числа, то для облегчения вычисления
— большие числа, то для облегчения вычисления 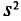 формулу для
формулу для 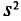 аналогично формуле (4.9) преобразуют к виду
аналогично формуле (4.9) преобразуют к виду
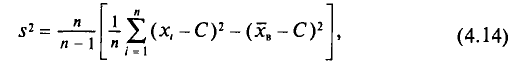
где С—ложный нуль.
Оценки, обладающие свойствами несмещенности и состоятельности, при ограниченном числе опытов могут отличаться дисперсиями.
Ясно, что чем меньше дисперсия оценки, тем меньше вероятность грубой ошибки при определении приближенного значения параметра. Поэтому необходимо, чтобы дисперсия оценки была минимальной. Оценка, обладающая таким свойством, называется эффективной.
Из отмеченных требований, предъявляемых к оценке, наиболее важными являются требования несмещенности и состоятельности.
Пример:
С плодового дерева случайным образом отобрано 10 плодов. Их массы 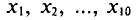 (в граммах) записаны в первой колонке приведенной ниже таблицы. Обработаем статистические данные выборки. Для вычисления
(в граммах) записаны в первой колонке приведенной ниже таблицы. Обработаем статистические данные выборки. Для вычисления 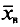 и s пo формулам (4.6) и (4.14) введем ложный нуль С=250 и все необходимые при этом вычисления сведем в указанную таблицу:
и s пo формулам (4.6) и (4.14) введем ложный нуль С=250 и все необходимые при этом вычисления сведем в указанную таблицу:
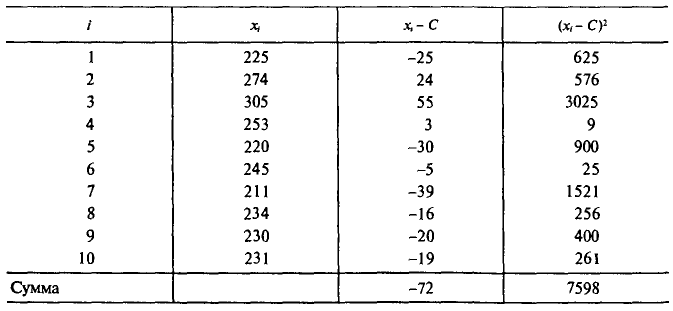
Следовательно,
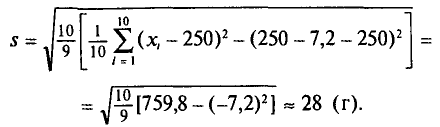
Отсюда 
Итак, оценка генеральной средней массы плода равна 243 г со средней квадратической ошибкой 9 г.
Оценка генерального среднего квадратического отклонения массы плода равна 28 г.
Пример:
Через каждый час измерялось напряжение в электросети. Результаты измерений (в вольтах) представлены в следующей таблице:
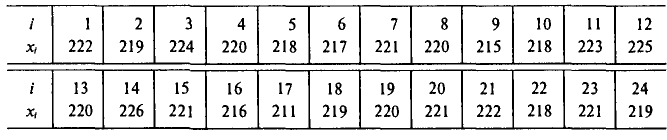
Найти оценки для математического ожидания и дисперсии результатов измерений. Оценки для математического ожидания и дисперсии найдем по формулам (6) и (14), положив С=220. Все необходимые вычисления приведены в нижеследующей таблице:
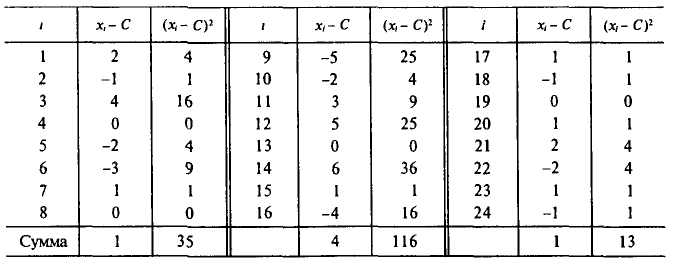
Следовательно,
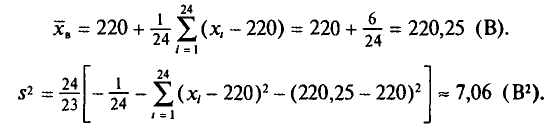
Доверительные интервалы для параметров нормального распределения
Пусть  — оцениваемый параметр,
— оцениваемый параметр,  — его оценка, составленная из
— его оценка, составленная из 
Если известно, что оценка  является несмещенной и состоятельной, то по данным выборки вычисляют значение
является несмещенной и состоятельной, то по данным выборки вычисляют значение  и считают его приближением истинного значения
и считают его приближением истинного значения  . При этом среднее квадратическое отклонение (если его вообще вычисляют) оценивает порядок ошибки. Такие оценки называются точечными. Например, в предыдущем параграфе речь шла о точечных оценках генеральной средней и генеральной дисперсии. В общем случае, когда о распределении признака X ничего неизвестно, это уже немало.
. При этом среднее квадратическое отклонение (если его вообще вычисляют) оценивает порядок ошибки. Такие оценки называются точечными. Например, в предыдущем параграфе речь шла о точечных оценках генеральной средней и генеральной дисперсии. В общем случае, когда о распределении признака X ничего неизвестно, это уже немало.
Если же о распределении имеется какая-либо информация, то можно сделать больше.
Здесь речь будет идти об оценке параметров а и  случайной величины, имеющей нормальное распределение. Это очень важный случай. Например (см. § 2.7), результат измерения имеет нормальное распределение. В этом случае становится возможным применять так называемое интервальное оценивание, к изложению которого мы и переходим.
случайной величины, имеющей нормальное распределение. Это очень важный случай. Например (см. § 2.7), результат измерения имеет нормальное распределение. В этом случае становится возможным применять так называемое интервальное оценивание, к изложению которого мы и переходим.
Пусть  — некоторое число. Если выполняется неравенство
— некоторое число. Если выполняется неравенство 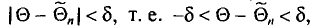 что можно записать в виде
что можно записать в виде 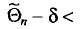
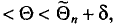 то говорят, что интервал
то говорят, что интервал 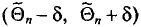 покрывает параметр
покрывает параметр  . Однако невозможно указать оценку
. Однако невозможно указать оценку  такую, чтобы событие
такую, чтобы событие 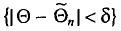 было достоверным, поэтому мы будем говорить о вероятности этого события. Число
было достоверным, поэтому мы будем говорить о вероятности этого события. Число 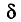 называется точностью оценки
называется точностью оценки 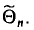
Определение:
Надежностью (доверительной вероятностью) оценки  параметра
параметра  0 для заданного
0 для заданного 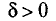 называется вероятность
называется вероятность  того, что интервал
того, что интервал 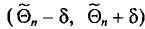 покроет параметр
покроет параметр  , т. е.
, т. е.
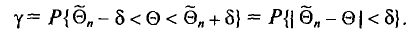
Заметим, что после того, как по данным выборки вычислена оценка  , событие
, событие 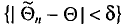 становится или достоверным, или невозможным, так как интервал
становится или достоверным, или невозможным, так как интервал 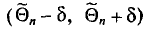 или покрывает
или покрывает  , или нет. Но дело в том, что параметр
, или нет. Но дело в том, что параметр  нам неизвестен. Поэтому мы называем надежностью
нам неизвестен. Поэтому мы называем надежностью  уже вычисленной оценки
уже вычисленной оценки  вероятность того, что интервал
вероятность того, что интервал 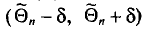 , найденный для произвольной выборки, покроет
, найденный для произвольной выборки, покроет  . Если мы сделаем много выборок объема n и для каждой из них построим интервал
. Если мы сделаем много выборок объема n и для каждой из них построим интервал 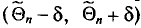 , то доля тех выборок, чьи интервалы покроют
, то доля тех выборок, чьи интервалы покроют  , равна
, равна  .
.
Иными словами,  есть мера нашего доверия вычисленной оценке
есть мера нашего доверия вычисленной оценке 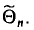
Ясно, что, чем меньше число 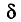 , тем меньше надежность
, тем меньше надежность  .
.
Определение:
Доверительным интервалом называется найденный по данным выборки интервал 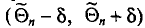 , который покрывает параметр
, который покрывает параметр  с заданной надежностью
с заданной надежностью  .
.
Надежность  обычно принимают равной 0,95 или 0,99, или 0,999.
обычно принимают равной 0,95 или 0,99, или 0,999.
Конечно, нельзя категорически утверждать, что найденный доверительный интервал покрывает параметр  . Но в этом можно быть уверенным на 95% при
. Но в этом можно быть уверенным на 95% при  = 0,95, на 99% при
= 0,95, на 99% при  =0,99 и т. д. Это значит, что если сделать много выборок, то для 95% из них (если, например,
=0,99 и т. д. Это значит, что если сделать много выборок, то для 95% из них (если, например,  = 0,95) вычисленные доверительные интервалы действительно покроют
= 0,95) вычисленные доверительные интервалы действительно покроют  .
.
Доверительный интервал для математического ожидания при известном
Доверительный интервал для математического ожидания при известном 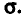
В некоторых случаях среднее квадратическое отклонение о ошибки измерения (а вместе с нею и самого измерения) бывает известно. Например, если измерения осуществляются одним и тем же прибором при одних и тех же условиях.
Итак, пусть случайная величина X распределена нормально с параметрами а и  , причем
, причем  известно. Построим доверительный интервал, покрывающий неизвестный параметр а с заданной надежностью
известно. Построим доверительный интервал, покрывающий неизвестный параметр а с заданной надежностью  . Данные выборки есть реализации случайных величин
. Данные выборки есть реализации случайных величин 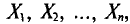 имеющих нормальное распределение с параметрами а и
имеющих нормальное распределение с параметрами а и  (§ 4.2, п. 1). Оказывается, что и выборочная средняя случайная величина
(§ 4.2, п. 1). Оказывается, что и выборочная средняя случайная величина 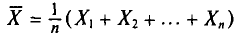 тоже имеет нормальное распределение (это мы примем без доказательства). При этом (см. § 4.2, пп. 2, 3)
тоже имеет нормальное распределение (это мы примем без доказательства). При этом (см. § 4.2, пп. 2, 3)
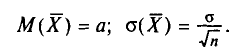
Потребуем, чтобы выполнялось соотношение 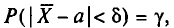 где
где  —заданная надежность. Пользуясь формулой (2.27) (§ 2.7, п. 2), получим
—заданная надежность. Пользуясь формулой (2.27) (§ 2.7, п. 2), получим
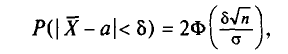
или
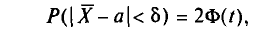
где

Найдя из равенства (4.15) 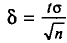 можем написать
можем написать
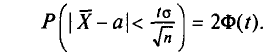
Так как Р задана и равна  , то окончательно имеем (для получения рабочей формулы выборочную среднюю заменяем на
, то окончательно имеем (для получения рабочей формулы выборочную среднюю заменяем на 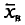 ):
):
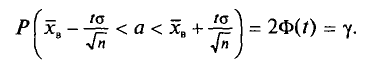
Смысл полученного соотношения таков: с надежностью у можно утверждать, что доверительный интервал 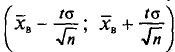 покрывает неизвестный параметр а; точность оценки
покрывает неизвестный параметр а; точность оценки 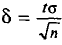 . Здесь число t определяется из равенства
. Здесь число t определяется из равенства 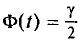 (оно следует из
(оно следует из 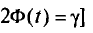 по таблице приложения 3.
по таблице приложения 3.
Как уже упоминалось, надежность  обычно принимают равной или 0,95 или 0,99, или 0,999.
обычно принимают равной или 0,95 или 0,99, или 0,999.
Пример:
Признак X распределен в генеральной совокупности нормально с известным  = 0,40. Найдем по данным выборки доверительный интервал для а с надежностью
= 0,40. Найдем по данным выборки доверительный интервал для а с надежностью  = 0,99, если n = 20,
= 0,99, если n = 20, 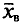 = 6,34.
= 6,34.
Для 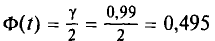 находим по таблице приложения 3
находим по таблице приложения 3
t=2,58. Следовательно, 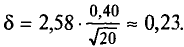 . Границы доверительного интервала 6,34 — 0,23 = 6,11 и 6,34 + 0,23 = 6,57. Итак, доверительный интервал (6,11; 6,57) покрывает а с надежностью 0,99.
. Границы доверительного интервала 6,34 — 0,23 = 6,11 и 6,34 + 0,23 = 6,57. Итак, доверительный интервал (6,11; 6,57) покрывает а с надежностью 0,99.
Доверительный интервал для математического ожидания при неизвестном
Доверительный интервал для математического ожидания при неизвестном  .
.
Пусть случайная величина X имеет нормальное распределение с неизвестными нам параметрами а и  . Оказывается, что случайная величина (ее возможные значения будем обозначать через t)
. Оказывается, что случайная величина (ее возможные значения будем обозначать через t)
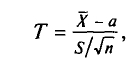
где n —объем выборки; 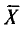 — выборочная средняя; S—исправленное среднее квадратическое отклонение, имеет распределение, не зависящее от а и
— выборочная средняя; S—исправленное среднее квадратическое отклонение, имеет распределение, не зависящее от а и  . Оно называется распределением Стьюдента*.
. Оно называется распределением Стьюдента*.
Плотность вероятности распределения Стьюдента дается формулой
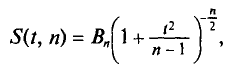
где коэффициент  зависит от объема выборки.
зависит от объема выборки.
Потребуем, чтобы выполнялось соотношение
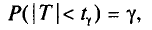
где  —заданная надежность.
—заданная надежность.
Так как S(t, n) — четная функция от t, то, пользуясь формулой
(2.15) (см. § 2.5), получим
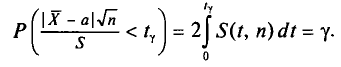
Отсюда
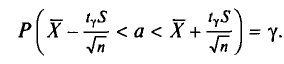
Следовательно, приходим к утверждению: с надежностью  можно утверждать, что доверительный интервал
можно утверждать, что доверительный интервал 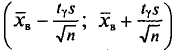 покрывает неизвестный параметр а, точность оценки
покрывает неизвестный параметр а, точность оценки 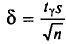 -. Здесь случайные величины
-. Здесь случайные величины 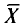 и S заменены неслучайными величинами
и S заменены неслучайными величинами 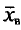 и s, найденными по выборке.
и s, найденными по выборке.
В приложении 4 приведена таблица значений 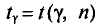 для различных значений n и обычно задаваемых значений надежности.
для различных значений n и обычно задаваемых значений надежности.
Заметим, что при 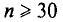 распределение Стьюдента практически не отличается от нормированного нормального распределения
распределение Стьюдента практически не отличается от нормированного нормального распределения
(см. § 2.7, п. 2). Это связано с тем, что 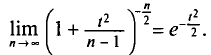
Пример. Признак X распределен в генеральной совокупности нормально. Найдем доверительный интервал для 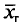 с надежностью
с надежностью  =0,99, если
=0,99, если 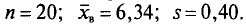 Для надежности
Для надежности  =0,99 и n = 20 находим по таблице приложения 4
=0,99 и n = 20 находим по таблице приложения 4 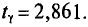 Следовательно,
Следовательно, 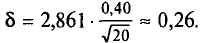 . Концы доверительного интервала 6,34-0,26 =
. Концы доверительного интервала 6,34-0,26 =
= 6,08 и 6,34 + 0,26 = 6,60. Итак, доверительный интервал (6,08; 6,60) покрывает 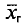 с надежностью 0,99.
с надежностью 0,99.
Доверительный интервал для среднего квадратического отклонения
Для нахождения доверительного интервала для среднего квадратического отклонения  будем использовать следующее предложение, устанавливаемое аналогично двум предыдущим (пп. 2 и 3).
будем использовать следующее предложение, устанавливаемое аналогично двум предыдущим (пп. 2 и 3).
С надежностью  можно утверждать, что доверительный интервал
можно утверждать, что доверительный интервал 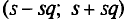 покрывает неизвестный параметр
покрывает неизвестный параметр  ; точность оценки
; точность оценки 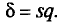
В приложении 5 приведена таблица значений 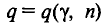 для различных значений n и обычно задаваемых значений надежности
для различных значений n и обычно задаваемых значений надежности  .
.
Пример:
Признак X распределен в генеральной совокупности нормально. Найдем доверительный интервал для  с надежностью
с надежностью  =0,95, если n = 20, s = 0,40.
=0,95, если n = 20, s = 0,40.
Для надежности  =0,95 и n = 20 находим в таблице приложения 5 q = 0,37. Далее, sq = 0,40 0,37 = 0,15. Границы доверительного интервала 0,40-0,15 = 0,25 и 0,40 + 0,15 = 0,55. Итак, доверительный интервал (0,25; 0,55) покрывает
=0,95 и n = 20 находим в таблице приложения 5 q = 0,37. Далее, sq = 0,40 0,37 = 0,15. Границы доверительного интервала 0,40-0,15 = 0,25 и 0,40 + 0,15 = 0,55. Итак, доверительный интервал (0,25; 0,55) покрывает  с надежностью 0,95.
с надежностью 0,95.
Пример:
На ферме испытывалось влияние витаминов на прибавку в массе телят. С этой целью было осмотрено 20 телят одного возраста. Средняя масса их оказалась равной 340 кг, а «исправленное» среднее квадратическое отклонение — 20 кг.
Определим: 1) доверительный интервал для математического ожидания а с надежностью 0,95; 2) доверительный интервал для среднего квадратического отклонения с той же надежностью.
При решении задачи будем исходить из предположения, что данные пробы взяты из нормальной генеральной совокупности.
Решение:
1) Согласно условиям задачи, 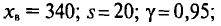 n = 20.
n = 20.
Пользуясь распределением Стьюдента, для надежности у=0,95 и n = 20 находим в таблице приложения 4 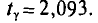 Следовательно,
Следовательно, 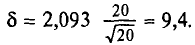 Границы доверительного интервала 340-9,4 =
Границы доверительного интервала 340-9,4 =
= 330,6 и 340 + 9,4 = 349,4. Итак, доверительный интервал (330,6; 349,4) покрывает а с надежностью 0,95.
Можно считать, что в данном случае истинная масса измерена 9 4 достаточно точно (отклонение порядка 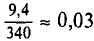 ).
).
2) Для надежности у =0,95 и n = 20 находим в таблице приложения 5 q = 0,37. Далее, sq = 20 * 0,37 = 7,4. Границы доверительного интервала 20 — 7,4 = 12,6 и 20 + 7,4 = 27,4. Таким образом, 12,6 <  < 27,4, откуда можно заключить, что
< 27,4, откуда можно заключить, что  определено неудовлетворительно (отклонение порядка
определено неудовлетворительно (отклонение порядка 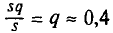 — почти половина!). Чтобы сузить доверительный интервал при той же надежности, необходимо увеличить число проб n.
— почти половина!). Чтобы сузить доверительный интервал при той же надежности, необходимо увеличить число проб n.
Примечание. Выше предполагалось, что q<1. Если q> 1, то, учитывая, что  >0, получаем 0<
>0, получаем 0< <s + sq. Значения q и в этом случае определяются по таблице приложения 5.
<s + sq. Значения q и в этом случае определяются по таблице приложения 5.
Пример:
Признак X генеральной совокупности распределен нормально. По выборке объема n = 10 найдено «исправленное» среднее квадратическое отклонение s = 0,16. Найдем доверительный интервал для  с надежностью 0,999.
с надежностью 0,999.
Для надежности у = 0,999 и n= 10 по таблице приложения 5 находим q=1,80.
Следовательно, искомый доверительный интервал таков’
или
Оценка истинного значения измеряемой величины
Пусть проводится n независимых равноточных измерений* некоторой физической величины, истинное значение а которой неизвестно. Будем рассматривать результаты отдельных измерений как случайные величины 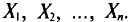 Эти величины независимы (измерения независимы), имеют одно и то же математическое ожидание а (истинное значение измеряемой величины), одинаковые дисперсии
Эти величины независимы (измерения независимы), имеют одно и то же математическое ожидание а (истинное значение измеряемой величины), одинаковые дисперсии 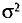 (измерения равноточны) и распределены нормально (такое допущение подтверждается опытом). Таким образом, все предположения, которые были сделаны при выводе доверительных интервалов в пп. 2 и 3 настоящего параграфа, выполняются, следовательно, мы вправе использовать полученные в них предложения. Так как обычно
(измерения равноточны) и распределены нормально (такое допущение подтверждается опытом). Таким образом, все предположения, которые были сделаны при выводе доверительных интервалов в пп. 2 и 3 настоящего параграфа, выполняются, следовательно, мы вправе использовать полученные в них предложения. Так как обычно  неизвестно, следует пользоваться предложением, найденным в п. 3 данного параграфа.
неизвестно, следует пользоваться предложением, найденным в п. 3 данного параграфа.
Пример:
По данным девяти независимых равноточных измерений физической величины найдены среднее арифметическое результатов отдельных измерений 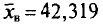 и «исправленное» среднее квадратическое отклонение s = 5,0. Требуется оценить истинное значение а измеряемой величины с надежностью у = 0,99.
и «исправленное» среднее квадратическое отклонение s = 5,0. Требуется оценить истинное значение а измеряемой величины с надежностью у = 0,99.
Истинное значение измеряемой величины равно ее математическому ожиданию. Поэтому задача сводится к оценке математического ожидания (при неизвестном  ) при помощи доверительного интервала
) при помощи доверительного интервала
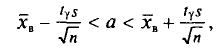
покрывающего а с заданной надежностью у=0,99.
Пользуясь таблицей приложения 4 по у=0,99 и n = 9, находим 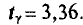
Найдем точность оценки:
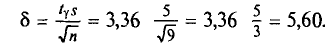
Границы доверительного интервала
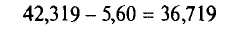
и
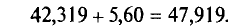
Итак, с надежностью у=0,99 истинное значение измеренной величины а заключено в доверительном интервале 36,719<а< 47,919.
Оценка точности измерений
В теории ошибок принято точность измерений (точность прибора) характеризовать с помощью среднего квадратического отклонения  случайных ошибок измерений. Для оценки
случайных ошибок измерений. Для оценки  используют «исправленное» среднее квадратическое отклонение s. Поскольку обычно результаты измерений независимы, имеют одно и то же математическое ожидание (истинное значение измеряемой величины) и одинаковую дисперсию (в случае равноточных измерений), то утверждение, приведенное в п. 4, применимо для оценки точности измерений.
используют «исправленное» среднее квадратическое отклонение s. Поскольку обычно результаты измерений независимы, имеют одно и то же математическое ожидание (истинное значение измеряемой величины) и одинаковую дисперсию (в случае равноточных измерений), то утверждение, приведенное в п. 4, применимо для оценки точности измерений.
Пример:
По 16 независимым равноточным измерениям найдено «исправленное» среднее квадратическое отклонение s=0,4. Найдем точность измерений с надежностью у = 0,99.
Как отмечено выше, точность измерений характеризуется средним квадратическим отклонением о случайных ошибок измерений. Поэтому задача сводится к отысканию доверительного интервала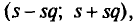 покрывающего
покрывающего  с заданной надежностью у=0,99 (см. п. 4). По таблице приложения 5 по у = 0,99 и n=16 найдем q = 0,70. Следовательно, искомый доверительный интервал таков:
с заданной надежностью у=0,99 (см. п. 4). По таблице приложения 5 по у = 0,99 и n=16 найдем q = 0,70. Следовательно, искомый доверительный интервал таков:
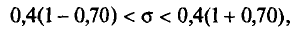
или
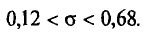
Решение заданий и задач по предметам:
- Теория вероятностей
- Математическая статистика
Дополнительные лекции по теории вероятностей:
- Случайные события и их вероятности
- Случайные величины
- Функции случайных величин
- Числовые характеристики случайных величин
- Законы больших чисел
- Статистические оценки
- Статистическая проверка гипотез
- Статистическое исследование зависимостей
- Теории игр
- Вероятность события
- Теорема умножения вероятностей
- Формула полной вероятности
- Теорема о повторении опытов
- Нормальный закон распределения
- Определение законов распределения случайных величин на основе опытных данных
- Системы случайных величин
- Нормальный закон распределения для системы случайных величин
- Вероятностное пространство
- Классическое определение вероятности
- Геометрическая вероятность
- Условная вероятность
- Схема Бернулли
- Многомерные случайные величины
- Предельные теоремы теории вероятностей
- Оценки неизвестных параметров

План урока:
Понятие выборки и генеральной совокупности
Среднее арифметическое выборки
Упорядоченный ряд и таблица частот
Размах выборки
Мода выборки
Медиана выборки
Ошибки в статистике
Понятие выборки и генеральной совокупности
Слово статистика, образованное от латинского status(состояние дел), появилось только в 1746 году, когда его употребил немец Готфрид Ахенвалль. Однако ещё в Древнем Китае проводились переписи населения, в ходе которых правители собирали информацию о своих владениях и жителях, проживающих в них.
В основе любого статистического исследования лежит массив информации, который называют выборкой данных. Покажем это на примере. Пусть в классе, где учится 20 учеников, проводился тест по математике, содержавший 25 вопросов. В результате учащиеся показали следующие результаты:

Ряд чисел, приведенный во второй строке таблицы (12, 19, 19, 14, 17, 16, 18, 20, 15, 25, 13, 20, 25, 16, 17, 12, 24, 13, 21, 13), будет выборкой. Также ее могут называть рядом данных или выборочной совокупностью.

В примере с классом выборка состоит из 20 чисел. Эту величину (количество чисел в ряду) называют объемом выборки. Каждое отдельное число в ряду именуют вариантой выборки.
В примере со школьным классом в выборку попали все его ученики. Это позволяет точно определить, насколько хорошо учащиеся написали математический тест. Однако иногда необходимо проанализировать очень большие группы населения, состоящие из десятков и даже сотен миллионов человек. Например, необходимо узнать, какая часть населения страны курит. Опросить каждого жителя государства невозможно, поэтому в ходе исследования опрашивают лишь его малую часть. В этом случае статистики выделяют понятие генеральная совокупность.

Так, если с помощью опроса 10 тысяч человек ученые делают выводы о распространении курения в России, то все российское население будет составлять генеральную совокупность исследования, а опрошенные 10 тысяч людей вместе образуют выборку.
Среднее арифметическое выборки
Сбор информации о выборке является лишь первой стадией статистического исследования. Далее ее необходимо обобщить, то есть получить некоторые цифры, характеризующие выборку. Самой часто используемой статистической характеристикой является среднее арифметическое.

Другими словами, для подсчета среднего арифметического необходимо просто сложить все числа в ряде данных, а потом поделить получившееся значение на количество чисел в ряде. Так, в примере с тестом по математике (таблица 1) средний балл учащихся составит: (12+19+19+14+17+16+18+20+15+25+13+20+25+16+17+12+24+13+21+13):20=
= 349:20 = 17,45.
Среднее арифметическое позволяет одним числом характеризовать какое-либо качество всех объектов группы. Чем больше средний балл учащихся в классе, тем выше их успеваемость. Чем меньше среднее количество голов, пропускаемых футбольной командой за один матч, тем лучше она играет в обороне. Если средняя зарплата программистов в городе составляет 90 тысяч рублей, а дворников – 25 тысяч рублей, то это значит, что программисты значительно более востребованы на рынке труда, а потому при выборе будущей профессии лучше предпочесть именно эту специальность.
Упорядоченный ряд и таблица частот
В ряде данных в таблице 1 числа приведены в произвольном порядке. Перепишем ряд так, чтобы все числа шли в неубывающем порядке, то есть от самого маленького к самому большому:
12, 12, 13, 13, 13, 14, 15, 16, 16, 17, 17, 18, 19, 19, 20, 20, 21, 24, 25, 25.
Такую запись называют упорядоченным рядом данных.

Его характеристики ничем не отличаются от изначальной выборки, однако с ним удобнее работать. С его помощью можно видеть, что ни одному ученику не удалось набрать 22 или 23 балла на тесте, но сразу двое учащихся дали 25 правильных ответов. На основе упорядоченного ряда данных несложно составить таблицу частот, в которой будет указано, как часто та или иная варианта выборки встречается в ряде. Выглядеть она будет так:

При составлении этой таблицы мы исключили из нее те варианты количества набранных баллов, частота которых равна нулю (от 0 до 12, 22 и 23).Заметим, что сумма чисел в нижней строке таблицы частот должна равняться объему выборки. Действительно,
2+3+1+1+2+2+1+2+2+1+1+2 = 20.
С помощью таблицы частот можно быстрее посчитать среднее арифметическое выборки. Для этого каждую варианту надо умножить на ее частоту, после чего сложить полученные результаты и поделить их на объем выборки:
(12•2+13•3+14•1+15•1+16•2+17•2+18•1+19•2+20•2+21•1+24•1+25•2):20 =
(24+39+14+15+32+34+18+38+40+42+24+50):20 = 349:20 = 17,45.
Размах выборки
Следующий важная характеристика ряда данных – это размах выборки.

Если выборка представлена в виде упорядоченного ряда данных, то достаточно вычесть из последнего числа ряда первое число. Так, размах выборки результатов теста в классе равен:
25 – 12 = 13,
так как самые лучшие ученики смогли решить все 25 заданий, а наихудший учащийся ответил правильно только на 13 вопросов.
Размах выборки характеризует стабильность, однородность исследуемых свойств. Например, пусть два спортсмена-стрелка в ходе соревнований производят по 5 выстрелов по круговой мишени, где за попадание начисляют от 0 до 10 очков. Первый стрелок показал результаты 8, 9, 9, 8, 9 очков. Второй же спортсмен в своих попытках показал результаты 7, 10, 10, 6, 10. Средние арифметические этих рядов равны:
(8+9+9+8+9):5 = 43:5 = 8,6;
(7+10+10+6+10):5 = 43:5 = 8,6.
Получается, что в среднем оба стрелка стреляют одинаково точно, однако первый спортсмен демонстрирует более стабильные результаты. У его выборки размах равен
9 – 8 = 1,
в то время как размах выборки второго спортсмена равен
10 – 6 = 4.
Размах выборки может быть очень важен в метеорологии. Например, в Алма-Ате и Амстердаме средняя температура в течение года почти одинакова и составляет 10°С. Однако в Алма-Ате в январе и феврале иногда фиксируются температуры ниже -30°С, в то время как в Амстердаме за всю историю наблюдений она никогда не падала ниже -20°С.
Мода выборки
Иногда важно знать не среднее арифметическое выборки, а то, какая из ее вариант встречается наиболее часто. Так, при управлении магазином одежды менеджеру не важен средний размер продаваемых футболок, а необходима информация о том, какие размеры наиболее популярны. Для этого используется такой показатель, как мода выборки.

В примере с математическим тестом сразу 3 ученика набрали по 13 баллов, а частота всех других вариант не превысила 2, поэтому мода выборки равна 13. Возможна ситуация, когда в ряде есть сразу две или более вариант, которые встречаются одинаково часто и чаще остальных вариант. Например, в ряде
1, 2, 3, 3, 3, 4, 5, 5, 5
варианты 3 и 5 встречаются по три раза. В таком случае ряд имеет сразу две моды – 3 и 5, а всю выборку именуют мультимодальной. Особо выделяется случай, когда в выборке все варианты встречаются с одинаковой частотой:
6, 6, 7, 7, 8, 8.
Здесь числа 6, 7 и 8 встречаются одинаково часто (по два раза), а другие варианты отсутствуют. В таких случаях говорят, что ряд не имеет моды.
Медиана выборки
Иногда, например, при расчете средней зарплаты, среднее арифметическое не вполне адекватно отражает ситуацию. Это происходит из-за наличия в выборке чисел, очень сильно отличающихся от среднего. Так, из-за огромных зарплат некоторых начальников большинство рядовых сотрудников компаний обнаруживают, что их зарплата ниже средней. В таких случаях целесообразно использовать такую характеристику, как медиану ряда. Это такое значение, которое делит ряд данных пополам. В упорядоченном ряде 2, 3, 6, 8, 8, 12, 15, 15, 18, 19, 25 медианой будет равна 12, так как именно она находится в середине ряда:

Однако таким образом можно найти только медиану ряда, в котором находится нечетное количество чисел. Если же их количество четное, то за медиану условно принимают среднее арифметическое двух средних чисел. Так, для ряда 2, 3, 6, 8, 8, 12, 15, 15, 18, 19, 25, 30, содержащего 12 чисел, медиана будет равна среднему значению 12 и 15, которые занимают 6-ое и 7-ое место в ряду:


Вернемся к примеру с математическим тестом в школе. Так как его сдавали 20 учеников, а 20 – четное число, то для расчета медианы следует найти среднее арифметическое 10-ого и 11-ого числа в упорядоченном ряде
12, 12, 13, 13, 13, 14, 15, 16, 16, 17, 17, 18, 19, 19, 20, 20, 21, 24, 25, 25.
Эти места занимают числа 17 и 17 (выделены жирным шрифтом). Медиана ряда будет равна
(17+17):2 = 34:2 = 17.
Три приведенные основные статистические характеристики выборки, а именно среднее арифметическое, мода и медиана, называются мерами центральной тенденции. Они позволяют одним числом указать значение, относительно которого группируются все числа ряда.
Рассмотрим для наглядности ещё один пример. Врач в ходе диспансеризации измерил вес мальчиков в классе. В результате он получил 10 значений (в кг):
39, 41, 67, 36, 60, 58, 46, 44, 39, 69.
Найдем среднее арифметическое, размах, моду и медиану для этого ряда.
Решение. Сначала перепишем ряд в упорядоченном виде:
36, 39, 39, 41, 44, 46, 58, 60, 67, 69.
Так как в ряде 10 чисел, то объем выборки равен 10. Найдем среднее арифметическое. Для этого сложим все числа в ряде и поделим их на объем выборки (то есть на 10):
(36+39+39+41+44+46+58+60+67+69):10 =
= 499:10 = 49,9 кг.
Размах выборки равен разнице между наибольшей и наименьшей вариантой в ней. Самый тяжелый мальчик весит 69 кг, а самый легкий – 36 кг, а потому размах ряда равен
69 – 36 = 33 кг.
В упорядоченном ряде только одно число, 39, встречается дважды, а все остальные числа встречаются по одному разу. Поэтому мода ряда будет равна 39 кг.
В выборке 10 чисел, а это четное число. Поэтому для нахождения медианы надо найти два средних по счету значение найти их среднее. На 5-ом и 6-ом месте в ряде находятся числа 44 и 46. Их среднее арифметическое равно
(44+46):2 = 90:2 = 45 кг.
Поэтому и медиана ряда будет равна 45 кг.
Ошибки в статистике
Статистика является очень мощным инструментом для исследований во всех областях человеческой деятельности. Однако иногда ее иронично называют самой точной из лженаук. Известно и ещё одно высказывание, приписываемое политику Дизраэли, согласно которому существует просто ложь, наглая ложь и статистика. С чем же связана такая репутация этой дисциплины?
Дело в том, что некоторые люди и организации часто манипулируют данными статистики, чтобы убедить других в своей правоте или преимуществах товара, которые они продают. Требуются определенные навыки, чтобы правильно пользоваться статистикой. Одна из самых распространенных ошибок – это неправильный выбор выборки.
В 1936 году перед президентскими выборами в США был проведен телефонный опрос, который показал, что с большим преимуществом победу должен одержать Альфред Лендон. Однако на выборах Франклин Рузвельт набрал почти вдвое больше голосов. Ошибка была связана с тем, что в те годы телефон могли позволить себе только богатые люди, которые в большинстве своем поддерживали Лендона. Однако бедные люди (а их, конечно же, больше, чем богатых) голосовали за Рузвельта.
Ещё один пример – это агитация в конце XIX века в США к службе на флоте. Пропагандисты в своей рекламе указывали, что, согласно статистике, смертность на флоте во время войны (испано-американской) составляет 0,09%, в то время как среди населения Нью-Йорка она равнялась 0,16%. Получалось, что служить на флоте в военное время безопаснее, чем жить мирной жизнью. Однако на самом деле причина таких цифр заключается в том, что во флот всегда отбирали молодых мужчин с хорошим здоровьем, которые не могли умереть от «старческих» болезней, в то время как в население Нью-Йорка входят больные и старые люди.
При указании среднего значения исследователь может использовать разные характеристики – среднее арифметическое, медиана, мода. При этом почти всегда среднее арифметическое несколько больше медианы. Именно поэтому большинство людей, узнающих о средней зарплате в стране, удивляются, так как они столько не зарабатывают. Правильнее ориентироваться на медианную зарплату.
Ну и наконец, нельзя забывать, что любая статистика может показать только корреляцию между двумя величинами, но это не всегда означает причинно-следственную связь. Так, известно, что чем больше в городе продается мороженого, тем больше в это же время людей тонет на пляжах. Означает ли это, что поедание мороженого увеличивает риск во время плавания? Нет. Дело в том, что оба этих показателя, продажи мороженого и количество утонувших, зависят от третьей величины – температуры в городе. Чем жарче на улице, тем большее количество людей ходят на пляж и тем больше мороженого продается в магазинах.
План:
1. Задачи математической статистики.
2. Виды выборок.
3. Способы отбора.
4. Статистическое распределение выборки.
5. Эмпирическая функция распределения.
6. Полигон и гистограмма.
7. Числовые характеристики вариационного ряда.
8. Статистические оценки параметров
распределения.
9. Интервальные оценки параметров распределения.
1.
Задачи и методы математической статистики
Математическая статистика– это раздел математики, посвященный методам
сбора, анализа и обработки результатов статистических данных наблюдений для
научных и практических целей.
Пусть требуется
изучить совокупность однородных объектов относительно некоторого качественного
или количественного признака, характеризующего эти объекты. Например, если
имеется партия деталей, то качественным признаком может служить стандартность детали,
а количественным- контролируемый размер детали.
Иногда проводят
сплошное исследование, т.е. обследуют каждый объект относительно нужного
признака. На практике сплошное обследование применяется редко. Например, если
совокупность содержит очень большое число объектов, то провести сплошное
обследование физически невозможно. Если обследование объекта связано с его
уничтожением или требует больших материальных затрат, то проводить сплошное
обследование не имеет смысла. В таких случаях случайно отбирают из всей
совокупности ограниченное число объектов (выборочную совокупность) и подвергают
их изучению.
Основная задача
математической статистики заключается в исследовании всей совокупности по
выборочным данным в зависимости от поставленной цели, т.е. изучение
вероятностных свойств совокупности: закона распределения, числовых
характеристик и т.д. для принятия управленческих решений в условиях
неопределенности.
2.
Виды выборок
Генеральная совокупность – это совокупность объектов, из которой производится выборка.
Выборочная совокупность (выборка) – это совокупность случайно отобранных
объектов.
Объем совокупности –
это число объектов этой совокупности. Объем генеральной совокупности
обозначается N,
выборочной – n.
Пример:
Если из 1000
деталей отобрано для обследования 100 деталей, то объем генеральной
совокупности N =
1000, а объем выборки n =
100.
При составлении выборки можно поступить двумя
способами: после того, как объект отобран и над ним произведено наблюдение, он
может быть возвращен либо не возвращен в генеральную совокупность. Т.о. выборки
делятся на повторные и бесповторные.
Повторной называют выборку, при которой
отобранный объект (перед отбором следующего) возвращается в генеральную
совокупность.
Бесповторной называют выборку, при которой отобранный
объект в генеральную совокупность не возвращается.
На практике обычно
пользуются бесповторным случайным отбором.
Для того, чтобы по
данным выборки можно было достаточно уверенно судить об интересующем признаке
генеральной совокупности, необходимо, чтобы объекты выборки правильно его
представляли. Выборка должна правильно представлять пропорции генеральной
совокупности. Выборка должна быть репрезентативной (представительной).
В силу закона больших чисел можно утверждать,
что выборка будет репрезентативной, если ее осуществлять случайно.
Если объем
генеральной совокупности достаточно велик, а выборка составляет лишь
незначительную часть этой совокупности, то различие между повторной и
бесповторной выборками стирается; в предельном случае, когда рассматривается
бесконечная генеральная совокупность, а выборка имеет конечный объем, это
различие исчезает.
Пример:
В американском журнале
«Литературное обозрение» с помощью статистических методов было проведено исследование прогнозов
относительно исхода предстоящих выборов президента США в 1936 году.
Претендентами на этот пост были Ф.Д. Рузвельт и А. М. Ландон. В качестве
источника для генеральной совокупности исследуемых американцев были взяты
справочники телефонных абонентов. Из них случайным образом были выбраны 4
миллиона адресов., по которым редакция журнала разослала открытки с просьбой
высказать свое отношение к кандидатам на пост президента. Обработав результаты
опроса, журнал опубликовал социологический прогноз о том, что на предстоящих
выборах с большим перевесом победит Ландон. И … ошибся: победу одержал
Рузвельт.
Этот пример можно рассматривать, как пример нерепрезентативной выборки. Дело в
том, что в США в первой половине двадцатого века телефоны имела лишь зажиточная
часть населения, которые поддерживали взгляды Ландона.
3.
Способы отбора
На практике
применяются различные способы отбора, которые можно разделить на 2 вида:
1. Отбор не требует
расчленения генеральной совокупности на части (а) простой случайный
бесповторный; б) простой случайный повторный).
2. Отбор, при
котором генеральная совокупность разбивается на части. (а) типичный отбор;
б) механический отбор; в) серийный отбор).
Простым случайным
называют такой отбор, при котором объекты извлекаются по одному из всей
генеральной совокупности (случайно).
Типичным называют отбор, при котором объекты
отбираются не из всей генеральной совокупности, а из каждой ее «типичной»
части. Например, если деталь изготавливают на нескольких станках, то отбор
производят не из всей совокупности деталей, произведенных всеми станками, а из
продукции каждого станка в отдельности. Таким отбором пользуются тогда, когда
обследуемый признак заметно колеблется в различных «типичных» частях
генеральной совокупности.
Механическим называют отбор, при котором
генеральную совокупность «механически» делят на столько групп, сколько объектов
должно войти в выборку, а из каждой группы отбирают один объект. Например, если
нужно отобрать 20 % изготовленных станком деталей, то отбирают каждую 5-ую
деталь; если требуется отобрать 5 % деталей- каждую 20-ую и т.д. Иногда такой
отбор может не обеспечивать репрезентативность выборки (если отбирают каждый
20-ый обтачиваемый валик, причем сразу же после отбора производится замена
резца, то отобранными окажутся все валики, обточенные затупленными резцами).
Серийным называют отбор, при котором объекты
отбирают из генеральной совокупности не по одному, а «сериями», которые
подвергают сплошному обследованию. Например, если изделия изготавливаются
большой группой станков-автоматов, то подвергают сплошному обследованию
продукцию только нескольких станков.
На практике часто
применяют комбинированный отбор, при котором сочетаются указанные выше способы.
4.
Статистическое распределение выборки
Пусть из генеральной совокупности извлечена выборка, причем значение x1–наблюдалось
раз,
x2-n2
раз,… xk – nk
раз. n =
n1+n2+…+nk– объем
выборки. Наблюдаемые значения
называются вариантами, а
последовательность вариант, записанных в возрастающем порядке- вариационным
рядом. Числа наблюдений
называются
частотами (абсолютными частотами), а их отношения к объему выборки
– относительными частотами или статистическими вероятностями.
Если количество
вариант велико или выборка производится из непрерывной генеральной
совокупности, то вариационный ряд составляется не по отдельным точечным
значениям, а по интервалам значений генеральной совокупности. Такой
вариационный ряд называется интервальным.
Длины интервалов при этом должны быть равны.
Статистическим
распределением выборки
называется перечень вариант и соответствующих им частот или относительных
частот.
Статистическое
распределение можно задать также в виде последовательности интервалов и
соответствующих им частот (суммы частот, попавших в этот интервал значений)
Точечный
вариационный ряд частот может быть представлен таблицей:
|
xi |
x1 |
x2 |
… |
xk |
|
ni |
n1 |
n2 |
… |
nk |
Аналогично можно
представить точечный вариационный ряд относительных частот.
Причем:
Пример:
Число букв в
некотором тексте Х оказалось равным 1000. Первой встретилась буква «я», второй- буква «и», третьей- буква
«а», четвертой- «ю». Затем шли буквы
«о», «е», «у», «э», «ы».
Выпишем места,
которые они занимают в алфавите, соответственно имеем: 33, 10, 1, 32, 16, 6,
21, 31, 29.
После упорядочения
этих чисел по возрастанию получаем вариационный ряд: 1, 6, 10, 16, 21, 29, 31,
32, 33.
Частоты появления
букв в тексте: «а» – 75, «е» -87, «и»- 75, «о»- 110, «у»- 25, «ы»- 8, «э»- 3,
«ю»- 7, «я»- 22.
Составим точечный
вариационный ряд частот:

Пример:
Задано
распределение частот выборки объема n
= 20.
Составьте точечный
вариационный ряд относительных частот.
Решение:
Найдем
относительные частоты:
|
xi |
2 |
6 |
12 |
|
wi |
0,15 |
0,5 |
0,35 |
При построении интервального
распределения существуют правила выбора
числа интервалов или величины каждого интервала. Критерием здесь служит
оптимальное соотношение: при увеличении числа интервалов улучшается репрезентативность,
но увеличивается объем данных и время на их обработку. Разность
xmax – xmin между наибольшим и наименьшим значениями
вариант называют размахом выборки.
Для подсчета числа
интервалов k
обычно применяют эмпирическую формулу Стреджесса (подразумевая округление до
ближайшего удобного целого): k
= 1 + 3.322 lg n.
Соответственно,
величину каждого интервала h
можно вычислить по формуле
:
5.
Эмпирическая
функция распределения
Рассмотрим некоторую
выборку из генеральной совокупности. Пусть известно статистическое
распределение частот количественного признака Х. Введем обозначения: nx
– число наблюдений, при которых
наблюдалось значение признака, меньшее х; n – общее число наблюдений (объем
выборки). Относительная частота события Х<х равна
nx/n. Если х изменяется, то изменяется и относительная частота, т.е.
относительная частота nx/n–
есть функция от х. Т.к. она находится эмпирическим путем, то она называется
эмпирической.
Эмпирической функцией распределения
(функцией распределения выборки) называют функцию
,
определяющую для каждого х относительную частоту события Х<х.
где
число вариант, меньших х,
n– объем выборки.
В отличие от эмпирической функции
распределения выборки, функцию распределения F(x)
генеральной совокупности называют теоретической функцией распределения.
Различие между эмпирической и
теоретической функциями распределения состоит в том, что теоретическая функция F(x) определяет вероятность события Х<x , а эмпирическая
функция
F*(x) -относительную
частоту этого же события. Из теоремы Бернулли следует, что относительная
частота события Х<х , т.е
F*(x) стремится
по вероятности к вероятности F(x) этого события. Т.е.при
большом n F*(x)
и
F(x) мало отличаются друг от друга.
Т.о. целесообразно использовать
эмпирическую функцию распределения выборки для приближенного представления
теоретической (интегральной) функции распределения генеральной совокупности.
F*(x) обладает всеми свойствами F(x).
1. Значения
F*(x)
принадлежат
интервалу [0; 1].
2.
F*(x)
– неубывающая
функция.
3. Если
– наименьшая варианта, то
F*(x)= 0, при х
< x1
; если xk
– наибольшая варианта, то
F*(x)= 1, при х
> xk
.
Т.е.
F*(x) служит для
оценки F(x).
Если выборка задана вариационным рядом, то эмпирическая
функция имеет вид:
График эмпирической функции называется кумулятой.
Пример:
Постройте эмпирическую функцию по данному распределению
выборки.
Решение:
Объем выборки n = 12 + 18 +30 = 60. Наименьшая
варианта 2, т.е.
при х <
2. Событие X<6,
( x1= 2) наблюдалось 12 раз, т.е.
F*(x)=12/60=0,2 при 2 < x <
6. Событие Х<10, (
x1=2,
x2= 6) наблюдалось 12 + 18 = 30 раз, т.е. F*(x)=30/60=0,5
при 6 < x <
10. Т.к. х=10 наибольшая варианта, то F*(x) = 1
при х>10. Искомая эмпирическая функция имеет вид:
Кумулята:
Кумулята дает возможность
понимать графически представленную информацию, например, ответить на вопросы:
«Определите число наблюдений, при которых значение признака было меньше 6 или
не меньше 6. F*(6)=0,2
» Тогда число наблюдений, при которых
значение наблюдаемого признака было меньше 6 равно 0,2*n = 0,2*60 = 12. Число наблюдений, при
которых значение наблюдаемого признака было не меньше 6 равно (1-0,2)*n = 0,8*60 = 48.
Если задан интервальный вариационный
ряд, то для составления эмпирической функции распределения находят середины
интервалов и по ним получают эмпирическую функцию распределения аналогично
точечному вариационному ряду.
6. Полигон и гистограмма
Для наглядности строят различные графики
статистического распределения: полином и гистограммы
Полигон
частот- это ломаная, отрезки которой соединяют точки (
x1
;n1
), (
x2
;n2
),…, (
xk
; nk
), где
– варианты,
–
соответствующие им частоты.
Полигон
относительных частот- это ломаная, отрезки которой соединяют точки (
x1
;w1
), (x2
;w2
),…, (
xk
;wk
), где
xi–варианты,
wi –
соответствующие им относительные частоты.
Пример:
Постройте полином относительных
частот по данному распределению выборки:
Решение:
В случае
непрерывного признака целесообразно строить гистограмму, для чего интервал, в
котором заключены все наблюдаемые значения признака, разбивают на несколько
частичных интервалов длиной h
и находят для каждого частичного интервала ni – сумму частот вариант,
попавших в i-ый
интервал. (Например, при измерении роста человека или веса, мы имеем дело с
непрерывным признаком).
Гистограмма
частот- это ступенчатая фигура, состоящая из прямоугольников, основаниями
которых служат частичные интервалы длиною h, а высоты равны отношению
(плотность
частот).
Площадь i-го частичного
прямоугольника равна– сумме частот вариант i– го интервала, т.е. площадь
гистограммы частот равна сумме всех частот, т.е. объему выборки.
Пример:
Даны результаты изменения напряжения
(в вольтах) в электросети. Составьте вариационный ряд, постройте полигон и
гистограмму частот, если значения напряжения следующие: 227, 215, 230, 232,
223, 220, 228, 222, 221, 226, 226, 215, 218, 220, 216, 220, 225, 212, 217, 220.
Решение:
Составим вариационный ряд. Имеем n = 20, xmin=212
, xmax=232
.
Применим формулу
Стреджесса для подсчета числа интервалов.
.
Интервальный вариационный ряд
частот имеет вид:
|
|
|
Плотность частот |
|
212-216 |
3 |
0,75 |
|
216-220 |
3 |
0,75 |
|
220-224 |
7 |
1,75 |
|
224-228 |
4 |
1 |
|
228-232 |
3 |
0,75 |
Построим гистограмму частот:
Построим полигон частот, найдя предварительно середины
интервалов:
Гистограммой относительных
частот называют ступенчатую фигуру, состоящую из прямоугольников ,
основаниями которых служат частичные
интервалы длиною h, а
высоты равны отношению wi/h
(плотность
относительной частоты).
Площадь i-го частичного прямоугольника равна
– относительной частоте вариант, попавших в i– ый интервал. Т.е. площадь
гистограммы относительных частот равна сумме всех относительных частот, т.е.
единице.
7.
Числовые
характеристики вариационного ряда
Рассмотрим основные характеристики генеральной и выборочной
совокупностей.
Генеральным средним
называется среднее
арифметическое значений признака генеральной совокупности.
Для различных значений x1, x2
, x3
, …, xn.
признака
генеральной совокупности объема N
имеем:
Если
значения признака имеют соответствующие частоты N1
+N2
+…+Nk
=N,
то
Выборочным средним называется среднее арифметическое значений
признака выборочной совокупности.
Для различных значений x1, x2
, x3, …, xn
признака выборочной
совокупности объема n
имеем:
Если
значения признака имеют соответствующие частоты n1+n2+…+nk
= n,
то
Пример:
Вычислите выборочное среднее для выборки :
x1= 51,12;
x2= 51,07;
x3= 52,95; x4
=52,93;
x5= 51,1;x6
= 52,98; x7
= 52,29; x8
= 51,23; x9
= 51,07; x10
= 51,04.
Решение:
Генеральной дисперсией называется среднее арифметическое квадратов отклонений
значений признака Х генеральной совокупности от генерального среднего .
Для различных значений x1, x2, x3, …, xN
признака
генеральной совокупности объема N
имеем:
Если
значения признака имеют соответствующие частоты
N1+N2+…+Nk
=N,
то
Генеральным среднеквадратическим отклонением (стандартом)
называют квадратный корень из генеральной дисперсии
Выборочной дисперсией называется среднее
арифметическое квадратов отклонений наблюдаемых значений признака от среднего
значения.
Для различных значений
x1, x2, x3, …, xn
признака выборочной
совокупности объема n
имеем:
Если
значения признака имеют соответствующие частоты n1+n2+…+nk
= n,
то
Выборочным среднеквадратическим
отклонением (стандартом) называется квадратный корень из выборочной
дисперсии.
Пример:
Выборочная совокупность задана таблицей распределения. Найдите
выборочную дисперсию.
Решение:
Теорема: Дисперсия
равна разности среднего квадратов значений признака и квадрата общего среднего.
Пример:
Найдите дисперсию по данному распределению.
Решение:
8. Статистические оценки параметров распределения
Пусть генеральная совокупность исследуется по некоторой
выборке. При этом можно получить лишь приближенное значение неизвестного
параметра Q, который
служит его оценкой. Очевидно, что оценки могут изменяться от одной выборки к
другой.
Статистической
оценкой Q* неизвестного параметра
теоретического распределения называется функция f, зависящая от наблюдаемых значений
выборки. Задачей статистического оценивания неизвестных параметров по выборке
заключается в построении такой функции от имеющихся данных статистических
наблюдений, которая давала бы наиболее точные приближенные значения реальных,
не известных исследователю, значений этих параметров.
Статистические оценки делятся на
точечные и интервальные, в зависимости от способа их предоставления (числом или
интервалом).
Точечной
называют статистическую оценку параметра Q теоретического распределения определяемую одним значением
параметра Q*=f(x1, x2, …, xn), где x1, x2, …, xn – результаты эмпирических наблюдений над
количественным признаком Х некоторой выборки.
Такие оценки параметров, полученные по
разным выборкам, чаще всего отличаются друг от друга. Абсолютная разность /Q*-Q/ называют ошибкой выборки (оценивания).
Для того, чтобы статистические оценки
давали достоверные результаты об оцениваемых параметрах, необходимо, чтобы они
были несмещенными, эффективными и состоятельными.
Точечная
оценка, математическое ожидание которой равно (не равно) оцениваемому
параметру, называется несмещенной
(смещенной). М(Q*)=Q.
Разность М(Q*)-Q называют смещением или
систематической ошибкой. Для несмещенных оценок систематическая ошибка
равна 0.
Эффективной
называют такую статистическую оценку
Q*, которая при
заданном объеме выборки n
имеет наименьшую возможную дисперсию: D[Q*]min
(n=const). Эффективная оценка
имеет наименьший разброс по сравнению с другими несмещенными и состоятельными
оценками.
Состоятельной
называют такую статистическую оценку
Q*,
которая при n стремится по вероятности к оцениваемому
параметру Q,
т.е. при увеличении объема выборки n
оценка стремится по вероятности к истинному значению параметра Q.
Требование состоятельности
согласуется с законом больших числе: чем больше исходной информации об
исследуемом объекте, тем точнее результат. Если объем выборки мал, то точечная
оценка параметра может привести к серьезным ошибкам.
Любую выборку (объема n) можно рассматривать
как упорядоченный набор
x1, x2, …, xn независимых
одинаково распределенных случайных величин.
Выборочные средние для
различных выборок объема n из одной и той же генеральной
совокупности будут различны. Т. е. выборочное среднее можно рассматривать как
случайную величину, а значит, можно говорить о распределении выборочного
среднего и его числовых характеристиках.
Выборочное среднее
удовлетворяет всем накладываемым к статистическим оценкам требованиям, т.е.
дает несмещенную, эффективную и состоятельную оценку генерального среднего.
Можно доказать, что. Таким образом, выборочная дисперсия
является смещенной оценкой генеральной дисперсии, давая ее заниженное значение.
Т. е. при небольшом объеме выборки она будет давать систематическую ошибку. Для
несмещенной, состоятельной оценки достаточно взять величину
, которую называют исправленной
дисперсией. Т. е.
На практике для оценки генеральной дисперсии применяют исправленную
дисперсию при n
< 30. В остальных случаях (n>30) отклонение
от
малозаметно. Поэтому при больших значениях n
ошибкой смещения можно пренебречь.
Можно
так же доказать, что относительная
частота
ni / n является
несмещенной и состоятельной оценкой вероятности P(X=xi). Эмпирическая функция распределения F*(x) является несмещенной
и состоятельной оценкой теоретической функции распределения F(x)=P(X<x).
Пример:
Найдите
несмещенные оценки математического ожидания
и дисперсии по таблице выборки.
Решение:
Объем выборки n=20.
Несмещенной оценкой математического
ожидания является выборочное среднее.
Для вычисления несмещенной оценки
дисперсии сначала найдем выборочную дисперсию:
Теперь найдем
несмещенную оценку:
9.
Интервальные
оценки параметров распределения
Интервальной называется статистическая
оценка, определяемая двумя числовыми значениями- концами исследуемого
интервала.
Число> 0, при котором |Q–Q*|<
, характеризует точность интервальной
оценки.
Доверительным
называется интервал
, который с заданной вероятностью
покрывает неизвестное значение параметра Q. Дополнение
доверительного интервала до множества всех возможных значений параметра Q называется критической областью. Если критическая
область расположена только с одной стороны от доверительного интервала, то
доверительный интервал называется односторонним:
левосторонним, если критическая область существует только слева, и правосторонним- если только справа. В
противном случае, доверительный интервал называется двусторонним.
Надежностью,
или доверительной вероятностью, оценки Q (с помощью Q*) называют вероятность,
с которой выполняется следующее неравенство: |Q–Q*|<
.
Чаще всего доверительную вероятность
задают заранее (0,95; 0,99; 0,999) и на нее накладывают требование быть близкой
к единице.
Вероятность
называют вероятностью
ошибки, или уровнем значимости.
Пусть |Q–Q*|<
, тогда
. Это означает, что с вероятностью
можно утверждать, что истинное значение
параметра Q
принадлежит интервалу. Чем меньше величина отклонения
, тем точнее оценка.
Границы (концы) доверительного интервала
называют доверительными границами, или
критическими границами.
Значения границ доверительного интервала
зависят от закона распределения параметра Q*.
Величину отклонения
равную половине ширины доверительного
интервала, называют точностью оценки.
Методы построения доверительных
интервалов впервые были разработаны американским статистом Ю. Нейманом.
Точность оценки
, доверительная вероятность
и
объем выборки n связаны между собой. Поэтому, зная
конкретные значения двух величин, всегда можно вычислить третью.
Нахождение
доверительного интервала для оценки математического ожидания нормального
распределения, если известно среднеквадратическое отклонение.
Пусть произведена выборка из генеральной
совокупности, подчиненной закону нормального распределения. Пусть известно
генеральное среднеквадратическое отклонение
, но неизвестно математическое ожидание
теоретического распределения a
().
Справедлива следующая формула:
Т.е.
по заданному значению отклонения
можно найти, с какой вероятностью неизвестное
генеральное среднее принадлежит интервалу. И наоборот. Из формулы видно, что при
возрастании объема выборки и фиксированной величине доверительной вероятности
величина
–
уменьшается, т.е. точность оценки увеличивается. С увеличением надежности
(доверительной вероятности), величина
-увеличивается,
т.е. точность оценки уменьшается.
Пример:
В результате испытаний
были получены следующие значения -25, 34, -20, 10, 21. Известно, что они
подчиняются закону нормального распределения с среднеквадратическим отклонением
2. Найдите оценку а* для математического ожидания а. Постройте для него 90%-ый
доверительный интервал.
Решение:
Найдем несмещенную
оценку
Тогда
Доверительный интервал
для а имеет вид: 4 – 1,47< a
< 4+ 1,47 или 2,53 < a
< 5, 47
Нахождение
доверительного интервала для оценки математического ожидания нормального
распределения, если неизвестно среднеквадратическое отклонение.
Пусть известно, что генеральная
совокупность подчинена закону нормального распределения, где неизвестны а и
. Точность доверительного интервала,
покрывающего с надежностью
истинное значение параметра а, в данном случае вычисляется по формуле:
, где n– объем выборки,
,
– коэффициент Стьюдента (его следует
находить по заданным значениям n и
из
таблицы «Критические точки распределения Стьюдента»).
Пример:
В результате испытаний были получены
следующие значения -35, -32, -26, -35, -30, -17. Известно, что они подчиняются
закону нормального распределения. Найдите доверительный интервал для
математического ожидания а генеральной совокупности с доверительной вероятностью
0,9.
Решение:
Найдем несмещенную оценку
.
Найдем
.
Далее найдем
.
Тогда
Доверительный интервал примет вида (-29,2
– 5,62; -29,2 + 5,62) или (-34,82; -23,58).
Нахождение
доверительного интерла для дисперсии и среднеквадратического отклонения
нормального распределения
Пусть из некоторой генеральной
совокупности значений, распределенной по нормальному закону, взята случайная
выборка объема n <
30, для которой вычислены выборочные
дисперсии: смещенная
и
исправленная s2
. Тогда для нахождения интервальных
оценок с заданной надежностью
для генеральной дисперсии D генерального
среднеквадратического отклонения
используются следующие формулы.
или
,
Значения
– находят с помощью таблицы значений
критических точек распределения
Пирсона.
Доверительный интервал для дисперсии
находится из этих неравенств путем возведения всех частей неравенства в
квадрат.
Пример:
Было проверено качество 15 болтов.
Предполагая, что ошибка при их изготовлении подчинена нормальному закону
распределения, причем выборочное среднеквадратическое отклонение
равно 5 мм, определить с надежностью
доверительный интервал для неизвестного
параметра
.
Решение:
Т. к. n = 15 <30, то воспользуемся формулой
.
Найдем пограничные значения вероятности
для .
Тогда:
Границы интервала представим в виде двойного неравенства:
Концы двустороннего доверительного
интервала для дисперсии можно определить и без выполнения арифметических
действий по заданному уровню доверия и объему выборки с помощью соответствующей
таблицы (Границы доверительных интервалов для дисперсии в зависимости от числа
степеней свободы и надежности). Для этого полученные из таблицы концы интервала
умножают на исправленную дисперсию s2
.
Пример:
Решим предыдущую задачу другим способом.
Решение:
Найдем исправленную
дисперсию:
По таблице «Границы
доверительных интервалов для дисперсии в зависимости от числа степеней свободы
и надежности» найдем границы доверительного интервала для дисперсии при k=14 и
: нижняя граница 0,513 и верхняя 2,354.
Умножим полученные
границы на
s2 и
извлечем корень (т.к. нам нужен доверительный интервал не для дисперсии, а для
среднеквадратического отклонения).
Как видно из примеров,
величина доверительного интервала зависит от способа его построения и дает
близкие между собой, но неодинаковые результаты.
При выборках достаточно
большого объема (n>30)
границы доверительного интервала для генерального среднеквадратического
отклонения можно определить по формуле:
Существует и другой
способ определения границы доверительного интервала для дисперсии, в основе
которого лежит выбор интервала, симметричного относительно
:
Причем
–
некоторое число, которое табулировано и приводится в соответствующей справочной
таблице.
Если 1- q<1, то формула имеет
вид:
Пример:
Решим предыдущую задачу третьим способом.
Решение:
Ранее было найдено s
= 5,17. q(0,95;
15) = 0,46 – находим по таблице.
Тогда: