Как найти выборочное среднее для случайной величины - Сайт, где вы сможете решить свои вопросы

Выборочные среднее и дисперсия

Пусть
для изучения генеральной совокупности
относительно количественного признака
Xизвлечена выборка объемаn.

Выборочным
средним
называют среднее арифметическое значение
признака выборочной совокупности. Если
все значенияпризнака
выборки объемаnразличны,
то.

Если
значения признака
имеют
частотысоответственно, причем,
то.

Выборочное
среднее, найденное по данным одной
выборки, равно определенному числу. При
извлечении других выборок того же объема
выборочное среднее будет меняться от
выборки к выборке. То есть выборочное
среднее можно рассматривать как случайную
величину и говорить о его распределениях
(теоретическом и эмпирическом) и о
числовых характеристиках этого
распределения (например, о математическом
ожидании и дисперсии).

Для
охарактеризования рассеяния наблюдаемых
значений количественного признака
выборки вокруг среднего значения
вводитсявыборочная дисперсия.Выборочной дисперсией называют среднее арифметическое
квадратов отклонения наблюдаемых
значений признака от их среднего значения.
Если все значенияпризнака
выборки объемаnразличны,
то
.

Если
значения признака
имеют
частотысоответственно, причем,
то.

Аналогично
выборочным среднему и дисперсии
определяются генеральные среднее
и дисперсия, характеризующие
генеральную совокупность в целом. Для
расчета этих характеристик достаточно
в вышеприведенных соотношениях заменить
объем выборкиnна объем
генеральной совокупностиN.

Фундаментальное
значение для практики имеет нахождение
среднего и дисперсии признака генеральной
совокупностипо соответствующим
известнымвыборочнымпараметрам.
Можно показать, чтовыборочное
среднееявляется несмещенной
состоятельной оценкой генерального
среднего. В то же время, несмещенной
состоятельной оценкой генеральной
дисперсии оказывается не выборочная
дисперсия,
а так называемая “исправленная”
выборочная дисперсия, равная.

Таким
образом, в качестве оценок генерального
среднего и дисперсии в математической
статистике принимают выборочнее среднее
и исправленную выборочную дисперсию.

Надежность и
доверительный интервал.

До
сих пор мы рассматривали точечные
оценки, т.е. такие оценки, которые
определяются одним числом. При выборке
малого
объема
точечная оценка может значительно
отличаться от оцениваемого параметра,
что приводит к грубым ошибкам. В связи
с этим при небольшом объеме выборки
пользуются интервальными оценками.

Интервальнойназывают оценку, определяющуюся двумя
числами – концами интервала. Пусть
найденная по данным выборки статистическая
характеристикаслужит оценкой неизвестного параметра.
Очевидно,тем точнее определяет параметр,
чем меньше абсолютная величина разности.
Другими словами, еслии,
то чем меньшеd, тем
точнее оценка. Таким образом, положительное
числоdхарактеризуетточность оценки.

Статистические
методы не позволяютутверждать,
что оценкаудовлетворяет неравенству;
можно говорить лишь о вероятности, с
которой это неравенство осуществляется.

Надежностью
(доверительной вероятностью)оценкипоназывают вероятностьg,
с которой осуществляется неравенство.
Обычно надежность оценки задается
заранее, причем в качествеgберут число, близкое к единице – как
правило 0,95; 0,99 или 0,999.

Пусть
вероятность того, что
равнаg:.

Заменим
неравенство
равносильным ему двойным неравенством

Это
соотношение следует понимать так:
вероятность того, что интервал
заключает в себе (покрывает) неизвестный
параметрQ, равна.

Таким
образом, доверительнымназывают
интервал,
который покрывает неизвестный параметр
с заданной надежностью.

Величину
1 – g=aназывают уровнем значимости или
вероятностью ошибки.

Для
построения интервальной оценки параметра
необходимо знать закон его распределения
как случайной величины

Лекция
14. Доверительные интервалы для
математического ожидания и дисперсии

Доверительный
интервал для математического ожидания
нормального распределения при известной
дисперсии.

Пусть
количественный признак Xгенеральной совокупности распределен
нормально, причем среднее квадратическое
отклонениеsэтого
распределенияизвестно. Требуется
оценить неизвестное математическое
ожиданиепо выборочному среднему.
Найдем доверительные интервалы,
покрывающие параметрaс
надежностью.

Будем
рассматривать выборочное среднее
как случайную величину(т.к.меняется
от выборки к выборке) и выборочные
значения– как одинаково распределенные независимые
случайные величины(эти числа также меняются от выборки к
выборке). Другими словами, математическое
ожидание каждой из этих величин равнои среднее квадратическое отклонение -s. Так как случайная
величинаXраспределена
нормально, то и выборочное среднеетакже распределено нормально. Параметры
распределенияравны.

Потребуем,
чтобы выполнялось соотношение
,

где
– заданная надежность. Используем формулу.

Заменим
Xнаиsнаи получим

где
.
Выразив из последнего равенства,
получим

Так
как вероятность Pзадана
и равна,
окончательно имеем

Таким
образом, с надежностью
можно утверждать, что доверительный
интервалпокрывает
неизвестный параметрa,
причем точность оценки равна.

Число
определяется из равенства;
по таблице функции Лапласа находят
аргумент,
которому соответствует значение функции
Лапласа, равное.

Отметим
два момента: 1) при возрастании объемавыборкиnчислоубывает и, следовательно, точность
оценки увеличивается, 2) увеличениенадежностиоценкиприводит к увеличению(так как функция Лапласа возрастающая
функция) и, следовательно, к возрастанию,
то естьувеличение надежностиоценки влечет за собойуменьшение
ее точности.

Если
требуется оценить математическое
ожидание с наперед заданной точностью
и надежностью,
то минимальный объем выборки, который
обеспечит эту точность, находят по
формуле

следующей
из равенства
.

Доверительный
интервал для математического ожидания
нормального распределения при неизвестной
дисперсии

Пусть
количественный признак Xгенеральной совокупности распределен
нормально, причем среднее квадратическое
отклонениеsэтого
распределениянеизвестно.
Требуется оценить неизвестное
математическое ожидание с помощью
доверительных интервалов.

Оказывается,
что по данным выборки можно построить
случайную величину
,

которая
имеет распределение Стьюдента с
степенями свободы. В последнем выражении
––
выборочное среднее,– исправленное среднее квадратическое
отклонение,– объем выборки; возможные значения
случайной величиныTмы
будем обозначать черезt.
Плотность распределения Стьюдента
имеет вид

,
где
некоторая постоянная, выражающаяся
через гамма – функции.

Несколько
слов о распределении Стьюдента. Пусть
– независимые стандартные нормальные
величины. Тогда случайная величина

имеет
распределение Стьюдента (В.
Госсет) сстепенями свободы. При росте числа
степеней свободы распределение Стьюдента
стремится к нормальному распределению
и уже прииспользование нормального распределения
дает хорошие результаты.

Как
видно, распределение Стьюдента
определяется параметром n– объемом выборки (или, что то же самое
– числом степеней свободы)
и не зависит от неизвестных параметров.
Поскольку– четная функция отt, то
вероятность выполнения неравенства

определяется
следующим образом:.

Заменив
неравенство в круглых скобках двойным
неравенством, получим выражение для
искомого доверительного интервала

Итак,
с помощью распределения Стьюдента
найден доверительный интервал
,
покрывающий неизвестный параметрaс надежностью.
По таблице распределения Стьюдента и
заданнымnиможно найтии
используя найденные по выборкеи,
, можно определить доверительный
интервал.

Пример.
Количественный признакXгенеральной совокупности распределен
нормально. По выборке объемаn= 16 найдены генеральное среднееи исправленное среднее квадратическое
отклонение.
Требуется оценить неизвестное
математическое ожидание при помощи
доверительного интервала с надежностью
0,95.

Решение.
Найдемпо таблице распределения Стьюдента,
используя значения.
Этот параметр оказывается равным 2,13.
Найдем границы доверительного интервала:

То
есть с надежностью 0,95 неизвестный
параметр aзаключен в
доверительном интервале

Можно показать,
что при возрастании объема выборки nраспределение Стьюдента стремится к
нормальному. Поэтому практически приn> 30 можно вместо него
пользоваться нормальным распределением.
Прималыхnэто
приводит к значительным ошибкам.

3.
Доверительный интервал для оценки
среднего квадратического отклонения
s
нормального распределения

Пусть
количественный признак Xгенеральной совокупности распределен
нормально и требуется оценить неизвестное
генеральное среднее квадратическое
отклонениеsпо
исправленному выборочному среднему
квадратическому отклонениюs.
Найдем доверительные интервалы,
покрывающие параметрsс заданной надежностью.

Потребуем,
чтобы выполнялось соотношение

или

Преобразуем
двойное неравенство
в равносильное неравенствои обозначимd/s=q. Имеем(A)

и
необходимо найти q. С этой
целью введем в рассмотрение случайную
величину

Оказывается,
величина
распределена по законусn– 1 степенями свободы.

Несколько
слов о распределении хи-квадрат. Если
– независимые стандартные нормальные
величины, то говорят, что случайная
величина

имеет
распределение хи-квадратсстепенями свободы.

Плотность
распределения cимеет
вид

Это
распределение не зависит от оцениваемого
параметра s, а зависит
только от объема выборкиn.

Преобразуем
неравенство (A) так, чтобы
оно приняло вид.
Вероятность этого неравенства равна
заданной вероятности,
т.е..

Предполагая,
что q< 1, перепишем (A)
в виде

далее, умножим все
члены неравенства на
:

или.

Вероятность того,
что это неравенство, а также равносильное
ему неравенство (A) будет
справедливо, равна

Из этого уравнения
можно по заданным
найти,
используя имеющиеся расчетные таблицы.
Вычислив по выборкеи найдя по таблице,
получим искомый интервал (A1),
покрывающийsс
заданной надежностью.

Пример.
Количественный признакXгенеральной совокупности распределен
нормально. По выборке объемаn= 25 найдено исправленное среднее
квадратическое отклонениеs= 0.8. Найти доверительный интервал,
покрывающий генеральное среднее
квадратическое отклонениеsс надежностью 0,95.

Решение.
По заданнымпо таблице находим значениеq= 0.32. Искомый доверительный интервал
есть

Мы предполагали,
что q< 1. Если это не так,
то мы придем к соотношениям

и значение q>1 может быть найдено из уравнения

Лекция
14. Доверительные интервалы для
математического ожидания и дисперсии

Доверительный
интервал для математического ожидания
нормального распределения при известной
дисперсии.

Потребуем,
чтобы выполнялось соотношение
,

где
– заданная надежность. Используем формулу.

Заменим
Xнаиsнаи получим

где
.
Выразив из последнего равенства,
получим

Так
как вероятность Pзадана
и равна,
окончательно имеем

следующей
из равенства
.

Доверительный
интервал для математического ожидания
нормального распределения при неизвестной
дисперсии

Оказывается,
что по данным выборки можно построить
случайную величину
,

,
где
некоторая постоянная, выражающаяся
через гамма – функции.

определяется
следующим образом:.

То
есть с надежностью 0,95 неизвестный
параметр aзаключен в
доверительном интервале

3.
Доверительный интервал для оценки
среднего квадратического отклонения
s
нормального распределения

Потребуем,
чтобы выполнялось соотношение

или

Преобразуем
двойное неравенство
в равносильное неравенствои обозначимd/s=q. Имеем(A)

и
необходимо найти q. С этой
целью введем в рассмотрение случайную
величину

Оказывается,
величина
распределена по законусn– 1 степенями свободы.

имеет
распределение хи-квадратсстепенями свободы.

Плотность
распределения cимеет
вид

Это
распределение не зависит от оцениваемого
параметра s, а зависит
только от объема выборкиn.

Предполагая,
что q< 1, перепишем (A)
в виде

далее, умножим все
члены неравенства на
:

или.

Вероятность того,
что это неравенство, а также равносильное
ему неравенство (A) будет
справедливо, равна

Решение.
По заданнымпо таблице находим значениеq= 0.32. Искомый доверительный интервал
есть

Мы предполагали,
что q< 1. Если это не так,
то мы придем к соотношениям

и значение q>1 может быть найдено из уравнения

Лекция
15. Проверка статистических гипотез.
Нулевая и альтернативная гипотезы,
статистический критерий. Ошибки первого
и второго рода. Этапы проверки
статистической гипотезы. Критерий
согласия Пирсона о виде распределения.

На прошлой
лекции мы рассматривали задачу построения
доверительных интервалов для неизвестных
параметров генеральной совокупности.
Сегодня мы продолжим изучение основных
задач математической статистики и
перейдем к вопросупроверки
статистических гипотез.

Проверка
статистических гипотез представляет
собой важнейший этап процесса принятия
решения в управленческой деятельности,
позволяя проводить подготовительный
этап предстоящих действий с учетом
реальных характеристик процесса
производства, контроля качества
продукции, коммерческой деятельности,
и т.п.

Как известно,
закон распределенияопределяет
количественные характеристики генеральной
совокупности.

Если закон
распределения неизвестен, но есть
основания предположить, что он имеет
определенный вид (например, А), то
выдвигают гипотезу: генеральная
совокупность распределена по закону
А. В этой гипотезе речь идето виде
предполагаемого распределения.

Часто закон
распределения известен, но неизвестны
его параметры. Если есть основания
предположить, что неизвестный параметрравен определенному значению,
то может выдвигаться гипотеза.
В этой гипотезе речь идет опредполагаемой
величине параметраизвестного
распределения.

Возможны и другие
гипотезы: о равенстве параметров двух
или нескольких распределений, о
независимости выборок и т. д.

Приведем несколько
задач, которые могут быть решены с
помощью проверки статистических гипотез.

1. Используется
два метода измерения одной и той же
величины. Первый метод дает оценки
этой величины, второй –.
Требуется определить, обеспечивают ли
оба методаодинаковую точность
измерений.

2. Контроль точности
работы некоторой производственной
системы. Получаемые характеристики
выпускаемой продукции характеризуются
некоторым разбросом (дисперсией). Обычно
величина этого разброса не должна
превышать некоторого заранее заданного
уровня. Требуется определить, обеспечивает
ли система (например, линия сборки или
отдельный станок) заданную точность.

Итак, статистической
называют гипотезу о виде неизвестного
распределения или о параметрах известных
распределений. Примеры статистических
гипотез: генеральная совокупность
распределена по закону Пуассона;
дисперсии двух нормальных распределений
равны между собой.

Наряду с выдвинутой
гипотезой всегда рассматривают и
противоречащую ей гипотезу. Если
выдвинутая гипотеза будет отвергнута,
то принимается противоречащая гипотеза.

Нулевой (основной)
называют выдвинутую гипотезу.

Альтернативной
(конкурирующей) называют
гипотезу,
которая противоречит нулевой. Например,
если нулевая гипотеза состоит в
предположении, что математическое
ожидание нормального распределения
равно 5, то альтернативная гипотеза,
например, может состоять в предположении,
что.
Кратко это записывают так:.

Простойназывают гипотезу, содержащую только
одно предположение. Например, если– параметр показательного распределения,
то гипотеза– простая.Сложной называют
гипотезу, состоящую из конечного или
бесконечного числа простых гипотез.
Например, сложная гипотезасостоит из бесконечного множества
простых гипотез вида,
где– любое число, большее 3.

Выдвинутая гипотеза
может быть правильной или неправильной,
поэтому возникает необходимость ее
проверки. Так как проверку производят
статистическими методами, то ее называют
статистической. В итогестатистической проверки гипотезыв двух случаях может быть принято
неправильное решение, т.е. могут быть
допущены ошибки двух родов.

Ошибка первого
рода состоит в том, что будетотвергнута правильнаягипотеза.
Ошибка второго рода состоит
в том, что будетпринята неправильнаягипотеза. Следует отметить, что последствия
ошибок могут оказаться различными. Если
отвергнуто правильное решение “продолжать
строительство жилого дома”, то эта
ошибка первого рода повлечет материальный
ущерб; если же принято неправильное
решение “продолжать строительство”
несмотря на опасность обвала дома, то
эта ошибка второго рода может привести
к многочисленным жертвам. Иногда,
наоборот, ошибка первого рода влечет
более тяжелые последствия.

Естественно,
правильное решение может быть принято
также в двух случаях, когда принимается
правильнаягипотеза илиотвергается
невернаягипотеза.

Вероятность
совершения ошибки первого роданазываютуровнем значимостии
обозначают.
Чаще всего уровень значимости принимают
равным 0,05 или 0,01. Если, например, принят
уровень значимости 0,05, то это означает,
что в пяти случаях из ста имеется риск
допустить ошибку первого рода (отвергнуть
правильную гипотезу).

Источник

Сейчас Вы научитесь находить числовые характеристики статистического распределения выборки. Примеры подобраны на основании индивидуальных заданий по теории вероятностей, которые задавали студентам ЛНУ им. И. Франка. Ответы послужат для студентов математических дисциплин хорошей инструкцией на экзаменах и тестах. Подобные решения точно используют в обучении экономисты , поскольку именно им задавали все что приведено ниже. ВУЗы Киева, Одессы, Харькова и других городов Украины имеют подобную систему обучения поэтому много полезного для себя должен взять каждый студент. Задачи различной тематики связаны между собой линками в конце статьи, поэтому можете найти то, что Вам нужно.

Индивидуальное задание 1
Вариант 11

Задача 1. Построить статистическое распределение выборки, записать эмпирическую функцию распределения и вычислить такие числовые характеристики:

выборочное среднее;
выборочную дисперсию;;
подправленную дисперсию;
выборочное среднее квадратичное отклонение;
подправленное среднее квадратичное отклонение;
размах выборки;
медиану;
моду;
квантильное отклонение;
коэффициент вариации;
коэффициент асимметрии;
эксцесс для выборки:

Выборка задана рядом 11, 9, 8, 7, 8, 11, 10, 9, 12, 7, 6, 11, 8, 7, 10, 9, 11, 8, 13, 8.

Решение:
Запишем выборку в виде вариационного ряда (в порядке возрастания):
6; 7; 7; 7; 8; 8; 8; 8; 8; 9; 9; 9; 10; 10; 11; 11; 11; 11; 12; 13.
Далее записываем статистическое распределение выборки в виде дискретного статистического распределения частот:

Эмпирическую функцию распределения определим по формуле

Здесь n_x – количество элементов выборки которые меньше х. Используя таблицу и учитывая что объем выборки равен n = 20, запишем эмпирическую функцию распределения:

Далее вычислим числовые характеристики статистического распределения выборки.
Выборочное среднее вычисляем по формуле

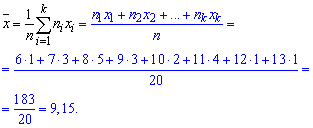
Выборочную дисперсию находим по формуле

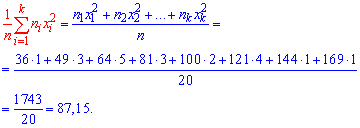
Выборочное среднее, что фигурирует в формуле дисперсии в квадрате найдено выше. Остается все подставить в формулу

Подправленную дисперсию вычисляем согласно формулы

Выборочное среднее квадратичное отклонение вычисляем по формуле

Подправленное среднее квадратичное отклонение вычисляем как корень из подправленной дисперсии

Размах выборки вычисляем как разность между наибольшим и наименьшим значениями вариант, то есть:

Медиану находим по 2 формулам:
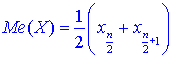если число n – четное;
если число n – нечетное.
Здесь берем индексы в x_i согласно нумерации варианта в вариационном ряду.
В нашем случае n = 20, поэтому

Мода – это варианта которая в вариационном ряду случается чаще всего, то есть

Квантильное отклонение находят по формуле

где – первый квантиль, – третий квантиль.
Квантили получаем при разбивке вариационного ряда на 4 равные части.
Для заданного статистического распределения квантильное отклонения примет значение

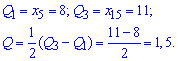
Коэффициент вариации равный процентному отношению подправленного среднего квадратичного к выборочному среднему

Коэффициент асимметрии находим по формуле

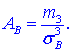
Здесь 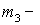центральный эмпирический момент 3-го порядка,

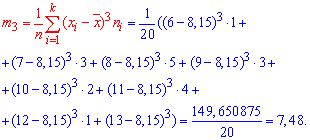
Подставляем в формулу коэффициента асимметрии

Эксцессом статистического распределения выборки называется число, которое вычисляют по формуле:

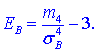
Здесь m₄ центральный эмпирический момент 4-го порядка. Находим момент

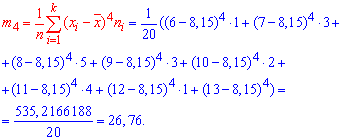
а далее эксцесс
Теперь Вы имеете все необходимые формулы чтобы найти числовые характеристики статистического распределения. Как найти моду, медиану и дисперсию должен знать каждый студент, который изучает теорию вероятностей.

Готовые решения по теории вероятностей

Следующая статья – Построение уравнения прямой регрессии Y на X

Источник

Эксперт по предмету «Математика»

Задать вопрос автору статьи

Генеральная средняя

Пусть нам дана генеральная совокупность относительно случайной величины $X$. Для начала напомним следующее определение:

Определение 1

Генеральная совокупность — совокупность случайно отобранных объектов данного вида, над которыми проводят наблюдения с целью получения конкретных значений случайной величины, проводимых в неизменных условиях при изучении одной случайной величины данного вида.

Определение 2

Генеральная средняя — среднее арифметическое значений вариант генеральной совокупности.

Пусть значения вариант $x_1, x_2,dots ,x_k$ имеют, соответственно, частоты $n_1, n_2,dots ,n_k$. Тогда генеральная средняя вычисляется по формуле:

Сделаем домашку
с вашим ребенком за 380 ₽

Уделите время себе, а мы сделаем всю домашку с вашим ребенком в режиме online

Бесплатное пробное занятие

*количество мест ограничено

Рассмотрим частный случай. Пусть все варианты $x_1, x_2,dots ,x_k$ различны. В этом случае $n_1, n_2,dots ,n_k=1$. Получаем, что в этом случае генеральная средняя вычисляется по формуле:

Выборочная средняя

Пусть нам дана выборочная совокупность относительно случайной величины $X$. Для начала напомним следующее определение:

Определение 3

Выборочная совокупность — часть отобранных объектов из генеральной совокупности.

Определение 4

Выборочная средняя — среднее арифметическое значений вариант выборочной совокупности.

Пусть значения вариант $x_1, x_2,dots ,x_k$ имеют, соответственно, частоты $n_1, n_2,dots ,n_k$. Тогда выборочная средняя вычисляется по формуле:

Рассмотрим частный случай. Пусть все варианты $x_1, x_2,dots ,x_k$ различны. В этом случае $n_1, n_2,dots ,n_k=1$. Получаем, что в этом случае выборочная средняя вычисляется по формуле:

«Средняя выборки: генеральная, выборочная» 👇

!!! В случае, когда значение вариант не являются дискретными, а представляют из себя интервалы, то в формулах для вычисления генеральной или выборочной средних значений за значение $x_i$ принимается значение середины интервала, которому принадлежит $x_i.$

Примеры задач на нахождение средней выборки

Пример 1

В магазин завезли 10 видов шоколадных конфет. По ним проведена следующая выборка по цене за килограмм: 70, 65, 97, 83, 120, 107, 77, 88, 100, 86. Построить ряд распределения данной генеральной совокупности и найти её генеральное среднее.

Решение.

Видим, что все значения вариант различны, поэтому частоты равны единице. Ряд распределения можно записать следующим образом, перечислив значения вариант в порядке возрастания:

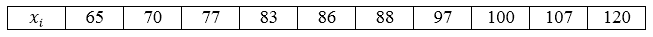
Рисунок 1.

Так как наша совокупность является генеральной и все варианты различны, то мы будем пользоваться следующей формулой:

[overline{x_г}=frac{sumlimits^k_{i=1}{x_i}}{n}]

Получим:

[overline{x_г}=frac{65+70+77+83+86+88+97+100+107+120}{10}=89,3]

Ответ: 89,3.

Пример 2

Выборочная совокупность задана следующей таблицей распределения:

Рисунок 2.

Найти среднее выборочное данной совокупности.

Решение.

Для нахождения значения выборочной средней будем пользоваться следующей формулой:

[overline{x_в}=frac{sumlimits^k_{i=1}{x_in_i}}{n}]

Обычно, для наглядности и удобности вычислений составляется расчетная таблица, в которую входят необходимые промежуточные вычисления. В нашем случае составим таблицу со следующей «шапкой»:

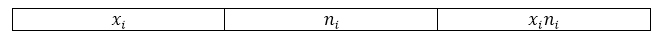
Рисунок 3.

Внизу таблицы также добавляется строка «итог», в которой подсчитывается сумма по всем значениям столбцов. Проведя необходимые вычисления, получим следующую расчетную таблицу:

Рисунок 4.

Используя формулу, получим:

[overline{x_в}=frac{sumlimits^k_{i=1}{x_in_i}}{n}=frac{305}{20}=15,25]

Ответ: 15,25.

Пример 3

Проводится социальный опрос среди 100 пенсионеров об уровне их пенсии. Получена следующая таблица распределения результатов опроса (размер пенсии указан в тысячах рублей):

Рисунок 5.

Найти среднее выборочное данной совокупности.

Данная совокупность является выборочной, поэтому будем пользоваться следующей формулой:

[overline{x_в}=frac{sumlimits^k_{i=1}{x_in_i}}{n}]

Составим, для начала, расчетную таблицу.

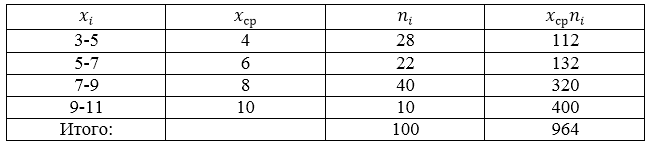
Рисунок 6.

Получаем:

[overline{x_в}=frac{sumlimits^k_{i=1}{x_in_i}}{n}=frac{964}{100}=9,64]

Ответ: 9,64.

Находи статьи и создавай свой список литературы по ГОСТу

Поиск по теме

Источник

Вы́борочное (эмпири́ческое) сре́днее — это приближение теоретического среднего распределения, основанное на выборке из него.

Определение[править | править код]

Пусть $X_{1},ldots ,X_{n}$ — выборка из распределения вероятности, определённая на некотором вероятностном пространстве . Тогда её выборочным средним называется случайная величина

${displaystyle {overline {X}}={frac {1}{n}}sum limits _{i=1}^{n}X_{i}}$

Свойства выборочного среднего[править | править код]

Пусть — выборочная функция распределения данной выборки. Тогда для любого фиксированного функция является (неслучайной) функцией дискретного распределения. Тогда математическое ожидание этого распределения равно .

Выборочное среднее — несмещённая оценка теоретического среднего:

${displaystyle mathbb {E} left[{bar {X}}right]=mathbb {E} [X_{i}],quad i=1,ldots ,n}$

Выборочное среднее — сильно состоятельная оценка теоретического среднего:

${displaystyle {overline {X}}to mathbb {E} [X_{i}]}$

почти наверное при

Выборочное среднее — асимптотически нормальная оценка. Пусть дисперсия случайных величин $X_{i}$ конечна и ненулевая, то есть ${displaystyle mathrm {D} [X_{i}]=sigma ^{2}<infty ,sigma ^{2}not =0,;i=1,ldots ,n}$ . Тогда

${displaystyle {sqrt {n}}left({overline {X}}-mathbb {E} [X_{1}]right)to mathrm {N} (0,sigma ^{2})}$

по распределению при

где ${displaystyle mathrm {N} (0,sigma ^{2})}$ — нормальное распределение со средним и дисперсией $sigma ^{2}$ .

Выборочное среднее из нормальной выборки — эффективная оценка её среднего.

См. также[править | править код]

Выборочная дисперсия
Выборочные моменты

В статье не хватает ссылок на источники (см. рекомендации по поиску).

Информация должна быть проверяема, иначе она может быть удалена. Вы можете отредактировать статью, добавив ссылки на авторитетные источники в виде сносок. (11 января 2015)

Среднее значение
Математика	Среднее степенное (взвешенное) Среднее гармоническое взвешенное Среднее геометрическое взвешенное Среднее арифметическое взвешенное Среднее квадратическое Среднее кубическое Скользящая средняя Среднее арифметико-геометрическое Среднее значение функции Среднее Колмогорова
Геометрия	Геометрический центр Барицентр
Теория вероятностей и математическая статистика	Винзоризованное среднее Выборочное среднее Математическое ожидание Медиана Мода Среднеквадратическое отклонение Среднее усечённое Условное математическое ожидание
Информационные технологии	Медоид Метод k-медиан
Теоремы	Первая теорема о среднем Вторая теорема о среднем Неравенство о среднем арифметическом, геометрическом и гармоническом
Другое	Показатели центра распределения

Источник

План:

1. Задачи математической статистики.

2. Виды выборок.

3. Способы отбора.

4. Статистическое распределение выборки.

5. Эмпирическая функция распределения.

6. Полигон и гистограмма.

7. Числовые характеристики вариационного ряда.

8. Статистические оценки параметров
распределения.

9. Интервальные оценки параметров распределения.

1.
Задачи и методы математической статистики

Математическая статистика– это раздел математики, посвященный методам
сбора, анализа и обработки результатов статистических данных наблюдений для
научных и практических целей.

Пусть требуется
изучить совокупность однородных объектов относительно некоторого качественного
или количественного признака, характеризующего эти объекты. Например, если
имеется партия деталей, то качественным признаком может служить стандартность детали,
а количественным- контролируемый размер детали.

Иногда проводят
сплошное исследование, т.е. обследуют каждый объект относительно нужного
признака. На практике сплошное обследование применяется редко. Например, если
совокупность содержит очень большое число объектов, то провести сплошное
обследование физически невозможно. Если обследование объекта связано с его
уничтожением или требует больших материальных затрат, то проводить сплошное
обследование не имеет смысла. В таких случаях случайно отбирают из всей
совокупности ограниченное число объектов (выборочную совокупность) и подвергают
их изучению.

Основная задача
математической статистики заключается в исследовании всей совокупности по
выборочным данным в зависимости от поставленной цели, т.е. изучение
вероятностных свойств совокупности: закона распределения, числовых
характеристик и т.д. для принятия управленческих решений в условиях
неопределенности.

2.
Виды выборок

Генеральная совокупность – это совокупность объектов, из которой производится выборка.

Выборочная совокупность (выборка) – это совокупность случайно отобранных
объектов.

Объем совокупности –
это число объектов этой совокупности. Объем генеральной совокупности
обозначается N,
выборочной – n.

Пример:

Если из 1000
деталей отобрано для обследования 100 деталей, то объем генеральной
совокупности N =
1000, а объем выборки n =
100.

При составлении выборки можно поступить двумя
способами: после того, как объект отобран и над ним произведено наблюдение, он
может быть возвращен либо не возвращен в генеральную совокупность. Т.о. выборки
делятся на повторные и бесповторные.

Повторной называют выборку, при которой
отобранный объект (перед отбором следующего) возвращается в генеральную
совокупность.

Бесповторной называют выборку, при которой отобранный
объект в генеральную совокупность не возвращается.

На практике обычно
пользуются бесповторным случайным отбором.

Для того, чтобы по
данным выборки можно было достаточно уверенно судить об интересующем признаке
генеральной совокупности, необходимо, чтобы объекты выборки правильно его
представляли. Выборка должна правильно представлять пропорции генеральной
совокупности. Выборка должна быть репрезентативной (представительной).

В силу закона больших чисел можно утверждать,
что выборка будет репрезентативной, если ее осуществлять случайно.

Если объем
генеральной совокупности достаточно велик, а выборка составляет лишь
незначительную часть этой совокупности, то различие между повторной и
бесповторной выборками стирается; в предельном случае, когда рассматривается
бесконечная генеральная совокупность, а выборка имеет конечный объем, это
различие исчезает.

Пример:

В американском журнале
«Литературное обозрение» с помощью статистических методов было проведено исследование прогнозов
относительно исхода предстоящих выборов президента США в 1936 году.
Претендентами на этот пост были Ф.Д. Рузвельт и А. М. Ландон. В качестве
источника для генеральной совокупности исследуемых американцев были взяты
справочники телефонных абонентов. Из них случайным образом были выбраны 4
миллиона адресов., по которым редакция журнала разослала открытки с просьбой
высказать свое отношение к кандидатам на пост президента. Обработав результаты
опроса, журнал опубликовал социологический прогноз о том, что на предстоящих
выборах с большим перевесом победит Ландон. И … ошибся: победу одержал
Рузвельт.
Этот пример можно рассматривать, как пример нерепрезентативной выборки. Дело в
том, что в США в первой половине двадцатого века телефоны имела лишь зажиточная
часть населения, которые поддерживали взгляды Ландона.

3.
Способы отбора

На практике
применяются различные способы отбора, которые можно разделить на 2 вида:

1. Отбор не требует
расчленения генеральной совокупности на части (а) простой случайный
бесповторный; б) простой случайный повторный).

2. Отбор, при
котором генеральная совокупность разбивается на части. (а) типичный отбор;
б) механический отбор; в) серийный отбор).

Простым случайным
называют такой отбор, при котором объекты извлекаются по одному из всей
генеральной совокупности (случайно).

Типичным называют отбор, при котором объекты
отбираются не из всей генеральной совокупности, а из каждой ее «типичной»
части. Например, если деталь изготавливают на нескольких станках, то отбор
производят не из всей совокупности деталей, произведенных всеми станками, а из
продукции каждого станка в отдельности. Таким отбором пользуются тогда, когда
обследуемый признак заметно колеблется в различных «типичных» частях
генеральной совокупности.

Механическим называют отбор, при котором
генеральную совокупность «механически» делят на столько групп, сколько объектов
должно войти в выборку, а из каждой группы отбирают один объект. Например, если
нужно отобрать 20 % изготовленных станком деталей, то отбирают каждую 5-ую
деталь; если требуется отобрать 5 % деталей- каждую 20-ую и т.д. Иногда такой
отбор может не обеспечивать репрезентативность выборки (если отбирают каждый
20-ый обтачиваемый валик, причем сразу же после отбора производится замена
резца, то отобранными окажутся все валики, обточенные затупленными резцами).

Серийным называют отбор, при котором объекты
отбирают из генеральной совокупности не по одному, а «сериями», которые
подвергают сплошному обследованию. Например, если изделия изготавливаются
большой группой станков-автоматов, то подвергают сплошному обследованию
продукцию только нескольких станков.

На практике часто
применяют комбинированный отбор, при котором сочетаются указанные выше способы.

4.
Статистическое распределение выборки

Пусть из генеральной совокупности извлечена выборка, причем значение x₁–наблюдалось
раз,
x₂-n₂
раз,… x_k – n_k
раз. n =
n₁+n₂+…+n_k– объем
выборки. Наблюдаемые значения
называются вариантами, а
последовательность вариант, записанных в возрастающем порядке- вариационным
рядом. Числа наблюдений
называются
частотами (абсолютными частотами), а их отношения к объему выборки
– относительными частотами или статистическими вероятностями.

Если количество
вариант велико или выборка производится из непрерывной генеральной
совокупности, то вариационный ряд составляется не по отдельным точечным
значениям, а по интервалам значений генеральной совокупности. Такой
вариационный ряд называется интервальным.
Длины интервалов при этом должны быть равны.

Статистическим
распределением выборки
называется перечень вариант и соответствующих им частот или относительных
частот.

Статистическое
распределение можно задать также в виде последовательности интервалов и
соответствующих им частот (суммы частот, попавших в этот интервал значений)

Точечный
вариационный ряд частот может быть представлен таблицей:

x_i	x₁	x₂	…	x_k
n_i	n₁	n₂	…	n_k

Аналогично можно
представить точечный вариационный ряд относительных частот.

Причем:

Пример:

Число букв в
некотором тексте Х оказалось равным 1000. Первой встретилась буква «я», второй- буква «и», третьей- буква
«а», четвертой- «ю». Затем шли буквы
«о», «е», «у», «э», «ы».

Выпишем места,
которые они занимают в алфавите, соответственно имеем: 33, 10, 1, 32, 16, 6,
21, 31, 29.

После упорядочения
этих чисел по возрастанию получаем вариационный ряд: 1, 6, 10, 16, 21, 29, 31,
32, 33.

Частоты появления
букв в тексте: «а» – 75, «е» -87, «и»- 75, «о»- 110, «у»- 25, «ы»- 8, «э»- 3,
«ю»- 7, «я»- 22.

Составим точечный
вариационный ряд частот:

Пример:

Задано
распределение частот выборки объема n
= 20.

Составьте точечный
вариационный ряд относительных частот.

Решение:

Найдем
относительные частоты:

x_i	2	6	12
w_i	0,15	0,5	0,35

При построении интервального
распределения существуют правила выбора
числа интервалов или величины каждого интервала. Критерием здесь служит
оптимальное соотношение: при увеличении числа интервалов улучшается репрезентативность,
но увеличивается объем данных и время на их обработку. Разность
x_max – x_min между наибольшим и наименьшим значениями
вариант называют размахом выборки.

Для подсчета числа
интервалов k
обычно применяют эмпирическую формулу Стреджесса (подразумевая округление до
ближайшего удобного целого): k
= 1 + 3.322 lg n.

Соответственно,
величину каждого интервала h
можно вычислить по формуле
:

5.
Эмпирическая
функция распределения

Рассмотрим некоторую
выборку из генеральной совокупности. Пусть известно статистическое
распределение частот количественного признака Х. Введем обозначения: n_x
– число наблюдений, при которых
наблюдалось значение признака, меньшее х; n – общее число наблюдений (объем
выборки). Относительная частота события Х<х равна
n_x/n. Если х изменяется, то изменяется и относительная частота, т.е.
относительная частота n_x/n–
есть функция от х. Т.к. она находится эмпирическим путем, то она называется
эмпирической.

Эмпирической функцией распределения
(функцией распределения выборки) называют функцию
,
определяющую для каждого х относительную частоту события Х<х.

где
число вариант, меньших х,

n– объем выборки.

В отличие от эмпирической функции
распределения выборки, функцию распределения F(x)
генеральной совокупности называют теоретической функцией распределения.

Различие между эмпирической и
теоретической функциями распределения состоит в том, что теоретическая функция F(x) определяет вероятность события Х<x , а эмпирическая
функция
F*(x) -относительную
частоту этого же события. Из теоремы Бернулли следует, что относительная
частота события Х<х , т.е
F*(x) стремится
по вероятности к вероятности F(x) этого события. Т.е.при
большом n F*(x)
и
F(x) мало отличаются друг от друга.

Т.о. целесообразно использовать
эмпирическую функцию распределения выборки для приближенного представления
теоретической (интегральной) функции распределения генеральной совокупности.

F*(x) обладает всеми свойствами F(x).

1. Значения
F*(x)
принадлежат
интервалу [0; 1].

2.
F*(x)

– неубывающая
функция.

3. Если
– наименьшая варианта, то

F*(x)= 0, при х
< x₁

; если x_k
– наибольшая варианта, то
F*(x)= 1, при х
> x_k
.

Т.е.
F*(x) служит для
оценки F(x).

Если выборка задана вариационным рядом, то эмпирическая
функция имеет вид:

График эмпирической функции называется кумулятой.

Пример:

Постройте эмпирическую функцию по данному распределению
выборки.

Решение:

Объем выборки n = 12 + 18 +30 = 60. Наименьшая
варианта 2, т.е.
при х <
2. Событие X<6,
( x₁= 2) наблюдалось 12 раз, т.е.
F*(x)=12/60=0,2 при 2 < x <
6. Событие Х<10, (

x₁=2,
x₂= 6) наблюдалось 12 + 18 = 30 раз, т.е. F*(x)=30/60=0,5

при 6 < x <
10. Т.к. х=10 наибольшая варианта, то F*(x) = 1
при х>10. Искомая эмпирическая функция имеет вид:

Кумулята:

Кумулята дает возможность
понимать графически представленную информацию, например, ответить на вопросы:
«Определите число наблюдений, при которых значение признака было меньше 6 или
не меньше 6. F*(6)=0,2

» Тогда число наблюдений, при которых
значение наблюдаемого признака было меньше 6 равно 0,2*n = 0,2*60 = 12. Число наблюдений, при
которых значение наблюдаемого признака было не меньше 6 равно (1-0,2)*n = 0,8*60 = 48.

Если задан интервальный вариационный
ряд, то для составления эмпирической функции распределения находят середины
интервалов и по ним получают эмпирическую функцию распределения аналогично
точечному вариационному ряду.

6. Полигон и гистограмма

Для наглядности строят различные графики
статистического распределения: полином и гистограммы

Полигон
частот- это ломаная, отрезки которой соединяют точки (
x₁
;n₁
), (
x₂
;n₂
),…, (
x_k
; n_k
), где
– варианты,
–
соответствующие им частоты.

Полигон
относительных частот- это ломаная, отрезки которой соединяют точки (
x₁
;w₁
), (x₂
;w₂
),…, (
x_k
;w_k
), где
x_i–варианты,
w_i –
соответствующие им относительные частоты.

Пример:

Постройте полином относительных
частот по данному распределению выборки:

Решение:

В случае
непрерывного признака целесообразно строить гистограмму, для чего интервал, в
котором заключены все наблюдаемые значения признака, разбивают на несколько
частичных интервалов длиной h
и находят для каждого частичного интервала n_i – сумму частот вариант,
попавших в i-ый
интервал. (Например, при измерении роста человека или веса, мы имеем дело с
непрерывным признаком).

Гистограмма
частот- это ступенчатая фигура, состоящая из прямоугольников, основаниями
которых служат частичные интервалы длиною h, а высоты равны отношению
(плотность
частот).

Площадь i-го частичного
прямоугольника равна– сумме частот вариант i– го интервала, т.е. площадь
гистограммы частот равна сумме всех частот, т.е. объему выборки.

Пример:

Даны результаты изменения напряжения
(в вольтах) в электросети. Составьте вариационный ряд, постройте полигон и
гистограмму частот, если значения напряжения следующие: 227, 215, 230, 232,
223, 220, 228, 222, 221, 226, 226, 215, 218, 220, 216, 220, 225, 212, 217, 220.

Решение:

Составим вариационный ряд. Имеем n = 20, x_min=212
, x_max=232
.

Применим формулу
Стреджесса для подсчета числа интервалов.

Интервальный вариационный ряд
частот имеет вид:

		Плотность частот
212-216	3	0,75
216-220	3	0,75
220-224	7	1,75
224-228	4	1
228-232	3	0,75

Построим гистограмму частот:

Построим полигон частот, найдя предварительно середины
интервалов:

Гистограммой относительных
частот называют ступенчатую фигуру, состоящую из прямоугольников ,
основаниями которых служат частичные
интервалы длиною h, а
высоты равны отношению w_i/h

(плотность
относительной частоты).

Площадь i-го частичного прямоугольника равна
– относительной частоте вариант, попавших в i– ый интервал. Т.е. площадь
гистограммы относительных частот равна сумме всех относительных частот, т.е.
единице.

7.
Числовые
характеристики вариационного ряда

Рассмотрим основные характеристики генеральной и выборочной
совокупностей.

Генеральным средним
называется среднее
арифметическое значений признака генеральной совокупности.

Для различных значений x₁, x₂
, x₃
, …, x_n.
признака
генеральной совокупности объема N
имеем:

Если
значения признака имеют соответствующие частоты N₁
+N₂
+…+N_k
=N,
то

Выборочным средним называется среднее арифметическое значений
признака выборочной совокупности.

Для различных значений x₁, x₂
, x₃, …, x_n
признака выборочной
совокупности объема n
имеем:

Если
значения признака имеют соответствующие частоты n₁+n₂+…+n_k
= n,
то

Пример:

Вычислите выборочное среднее для выборки :
x₁= 51,12;
x₂= 51,07;

x₃= 52,95; x₄
=52,93;

x₅= 51,1;x₆
= 52,98; x₇
= 52,29; x₈
= 51,23; x₉
= 51,07; x₁₀
= 51,04.

Решение:

Генеральной дисперсией называется среднее арифметическое квадратов отклонений
значений признака Х генеральной совокупности от генерального среднего .

Для различных значений x₁, x₂, x₃, …, x_N
признака
генеральной совокупности объема N
имеем:

Если
значения признака имеют соответствующие частоты
N₁+N₂+…+N_k
=N,
то

Генеральным среднеквадратическим отклонением (стандартом)
называют квадратный корень из генеральной дисперсии

Выборочной дисперсией называется среднее
арифметическое квадратов отклонений наблюдаемых значений признака от среднего
значения.

Для различных значений
x₁, x₂, x₃, …, x_n
признака выборочной
совокупности объема n
имеем:

Если
значения признака имеют соответствующие частоты n₁+n₂+…+n_k
= n,
то

Выборочным среднеквадратическим
отклонением (стандартом) называется квадратный корень из выборочной
дисперсии.

Пример:

Выборочная совокупность задана таблицей распределения. Найдите
выборочную дисперсию.

Решение:

Теорема: Дисперсия
равна разности среднего квадратов значений признака и квадрата общего среднего.

Пример:

Найдите дисперсию по данному распределению.

Решение:

8. Статистические оценки параметров распределения

Пусть генеральная совокупность исследуется по некоторой
выборке. При этом можно получить лишь приближенное значение неизвестного
параметра Q, который
служит его оценкой. Очевидно, что оценки могут изменяться от одной выборки к
другой.

Статистической
оценкой Q* неизвестного параметра
теоретического распределения называется функция f, зависящая от наблюдаемых значений
выборки. Задачей статистического оценивания неизвестных параметров по выборке
заключается в построении такой функции от имеющихся данных статистических
наблюдений, которая давала бы наиболее точные приближенные значения реальных,
не известных исследователю, значений этих параметров.

Статистические оценки делятся на
точечные и интервальные, в зависимости от способа их предоставления (числом или
интервалом).

Точечной
называют статистическую оценку параметра Q теоретического распределения определяемую одним значением
параметра Q*=f(x₁, x₂, …, x_n), где x₁, x₂, …, x_n– результаты эмпирических наблюдений над
количественным признаком Х некоторой выборки.

Такие оценки параметров, полученные по
разным выборкам, чаще всего отличаются друг от друга. Абсолютная разность /Q*-Q/ называют ошибкой выборки (оценивания).

Для того, чтобы статистические оценки
давали достоверные результаты об оцениваемых параметрах, необходимо, чтобы они
были несмещенными, эффективными и состоятельными.

Точечная
оценка, математическое ожидание которой равно (не равно) оцениваемому
параметру, называется несмещенной
(смещенной). М(Q*)=Q.

Разность М(Q*)-Q называют смещением или
систематической ошибкой. Для несмещенных оценок систематическая ошибка
равна 0.

Эффективной
называют такую статистическую оценку
Q*, которая при
заданном объеме выборки n
имеет наименьшую возможную дисперсию: D[Q*]min
(n=const). Эффективная оценка
имеет наименьший разброс по сравнению с другими несмещенными и состоятельными
оценками.

Состоятельной
называют такую статистическую оценку
Q*,
которая при n стремится по вероятности к оцениваемому
параметру Q,
т.е. при увеличении объема выборки n
оценка стремится по вероятности к истинному значению параметра Q.

Требование состоятельности
согласуется с законом больших числе: чем больше исходной информации об
исследуемом объекте, тем точнее результат. Если объем выборки мал, то точечная
оценка параметра может привести к серьезным ошибкам.

Любую выборку (объема n) можно рассматривать
как упорядоченный набор
x₁, x₂, …, x_n независимых
одинаково распределенных случайных величин.

Выборочные средние для
различных выборок объема n из одной и той же генеральной
совокупности будут различны. Т. е. выборочное среднее можно рассматривать как
случайную величину, а значит, можно говорить о распределении выборочного
среднего и его числовых характеристиках.

Выборочное среднее
удовлетворяет всем накладываемым к статистическим оценкам требованиям, т.е.
дает несмещенную, эффективную и состоятельную оценку генерального среднего.

Можно доказать, что. Таким образом, выборочная дисперсия
является смещенной оценкой генеральной дисперсии, давая ее заниженное значение.
Т. е. при небольшом объеме выборки она будет давать систематическую ошибку. Для
несмещенной, состоятельной оценки достаточно взять величину
, которую называют исправленной
дисперсией. Т. е.

На практике для оценки генеральной дисперсии применяют исправленную
дисперсию при n
< 30. В остальных случаях (n>30) отклонение
от

малозаметно. Поэтому при больших значениях n
ошибкой смещения можно пренебречь.

Можно
так же доказать, что относительная
частота
n_i/ n является
несмещенной и состоятельной оценкой вероятности P(X=x_i). Эмпирическая функция распределения F*(x) является несмещенной
и состоятельной оценкой теоретической функции распределения F(x)=P(X<x).

Пример:

Найдите
несмещенные оценки математического ожидания
и дисперсии по таблице выборки.

Решение:

Объем выборки n=20.

Несмещенной оценкой математического
ожидания является выборочное среднее.

Для вычисления несмещенной оценки
дисперсии сначала найдем выборочную дисперсию:

Теперь найдем
несмещенную оценку:

9.
Интервальные
оценки параметров распределения

Интервальной называется статистическая
оценка, определяемая двумя числовыми значениями- концами исследуемого
интервала.

Число> 0, при котором |Q–Q*|<
, характеризует точность интервальной
оценки.

Доверительным
называется интервал
, который с заданной вероятностью покрывает неизвестное значение параметра Q. Дополнение
доверительного интервала до множества всех возможных значений параметра Q называется критической областью. Если критическая
область расположена только с одной стороны от доверительного интервала, то
доверительный интервал называется односторонним:
левосторонним, если критическая область существует только слева, и правосторонним- если только справа. В
противном случае, доверительный интервал называется двусторонним.

Надежностью,
или доверительной вероятностью, оценки Q (с помощью Q*) называют вероятность,
с которой выполняется следующее неравенство: |Q–Q*|<
.

Чаще всего доверительную вероятность
задают заранее (0,95; 0,99; 0,999) и на нее накладывают требование быть близкой
к единице.

Вероятность
называют вероятностью
ошибки, или уровнем значимости.

Пусть |Q–Q*|<

, тогда

. Это означает, что с вероятностью
можно утверждать, что истинное значение
параметра Q
принадлежит интервалу. Чем меньше величина отклонения
, тем точнее оценка.

Границы (концы) доверительного интервала
называют доверительными границами, или
критическими границами.

Значения границ доверительного интервала
зависят от закона распределения параметра Q*.

Величину отклонения
равную половине ширины доверительного
интервала, называют точностью оценки.

Методы построения доверительных
интервалов впервые были разработаны американским статистом Ю. Нейманом.
Точность оценки
, доверительная вероятность
и
объем выборки n связаны между собой. Поэтому, зная
конкретные значения двух величин, всегда можно вычислить третью.

Нахождение
доверительного интервала для оценки математического ожидания нормального
распределения, если известно среднеквадратическое отклонение.

Пусть произведена выборка из генеральной
совокупности, подчиненной закону нормального распределения. Пусть известно
генеральное среднеквадратическое отклонение
, но неизвестно математическое ожидание
теоретического распределения a
().

Справедлива следующая формула:

Т.е.
по заданному значению отклонения
можно найти, с какой вероятностью неизвестное
генеральное среднее принадлежит интервалу. И наоборот. Из формулы видно, что при
возрастании объема выборки и фиксированной величине доверительной вероятности
величина
–
уменьшается, т.е. точность оценки увеличивается. С увеличением надежности
(доверительной вероятности), величина
-увеличивается,
т.е. точность оценки уменьшается.

Пример:

В результате испытаний
были получены следующие значения -25, 34, -20, 10, 21. Известно, что они
подчиняются закону нормального распределения с среднеквадратическим отклонением
2. Найдите оценку а* для математического ожидания а. Постройте для него 90%-ый
доверительный интервал.

Решение:

Найдем несмещенную
оценку

Тогда

Доверительный интервал
для а имеет вид: 4 – 1,47< a
< 4+ 1,47 или 2,53 < a
< 5, 47

Нахождение
доверительного интервала для оценки математического ожидания нормального
распределения, если неизвестно среднеквадратическое отклонение.

Пусть известно, что генеральная
совокупность подчинена закону нормального распределения, где неизвестны а и
. Точность доверительного интервала,
покрывающего с надежностью
истинное значение параметра а, в данном случае вычисляется по формуле:

, где n– объем выборки,
,– коэффициент Стьюдента (его следует
находить по заданным значениям n и
из
таблицы «Критические точки распределения Стьюдента»).

Пример:

В результате испытаний были получены
следующие значения -35, -32, -26, -35, -30, -17. Известно, что они подчиняются
закону нормального распределения. Найдите доверительный интервал для
математического ожидания а генеральной совокупности с доверительной вероятностью
0,9.

Решение:

Найдем несмещенную оценку
.

Найдем
.

Далее найдем
.

Тогда

Доверительный интервал примет вида (-29,2
– 5,62; -29,2 + 5,62) или (-34,82; -23,58).

Нахождение
доверительного интерла для дисперсии и среднеквадратического отклонения
нормального распределения

Пусть из некоторой генеральной
совокупности значений, распределенной по нормальному закону, взята случайная
выборка объема n <
30, для которой вычислены выборочные
дисперсии: смещенная
и
исправленная s²
. Тогда для нахождения интервальных
оценок с заданной надежностью
для генеральной дисперсии D генерального
среднеквадратического отклонения
используются следующие формулы.

или
,

Значения
– находят с помощью таблицы значений
критических точек распределения
Пирсона.

Доверительный интервал для дисперсии
находится из этих неравенств путем возведения всех частей неравенства в
квадрат.

Пример:

Было проверено качество 15 болтов.
Предполагая, что ошибка при их изготовлении подчинена нормальному закону
распределения, причем выборочное среднеквадратическое отклонение
равно 5 мм, определить с надежностью доверительный интервал для неизвестного
параметра
.

Решение:

Т. к. n = 15 <30, то воспользуемся формулой
.

Найдем пограничные значения вероятности
для .

Тогда:

Границы интервала представим в виде двойного неравенства:

Концы двустороннего доверительного
интервала для дисперсии можно определить и без выполнения арифметических
действий по заданному уровню доверия и объему выборки с помощью соответствующей
таблицы (Границы доверительных интервалов для дисперсии в зависимости от числа
степеней свободы и надежности). Для этого полученные из таблицы концы интервала
умножают на исправленную дисперсию s²
.

Пример:

Решим предыдущую задачу другим способом.

Решение:

Найдем исправленную
дисперсию:

По таблице «Границы
доверительных интервалов для дисперсии в зависимости от числа степеней свободы
и надежности» найдем границы доверительного интервала для дисперсии при k=14 и
: нижняя граница 0,513 и верхняя 2,354.

Умножим полученные
границы на
s² и
извлечем корень (т.к. нам нужен доверительный интервал не для дисперсии, а для
среднеквадратического отклонения).

Как видно из примеров,
величина доверительного интервала зависит от способа его построения и дает
близкие между собой, но неодинаковые результаты.

При выборках достаточно
большого объема (n>30)
границы доверительного интервала для генерального среднеквадратического
отклонения можно определить по формуле:

Существует и другой
способ определения границы доверительного интервала для дисперсии, в основе
которого лежит выбор интервала, симметричного относительно
: