Выборочное среднее
Выборочное
среднее
значение как статистический показатель
представляет
собой среднюю оценку изучаемого в
эксперименте психологического качества.
Эта
оценка характеризует степень его
развития
в целом у той группы испытуемых, которая
была подвергнута
психодиагностическому обследованию.
Сравнивая непосредственно средние
значения двух или нескольких выборок,
мы
можем судить об относительной степени
развития у людей, составляющих эти
выборки, оцениваемого качества.
Выборочное
среднее определяется при помощи следующей
формулы:
![]()
где
хср
—выборочная
средняя величина или среднее арифметическое
значение по выборке;
п —
количество
испытуемых в выборке
или частных психодиагностических
показателей, на основе которых
вычисляется средняя величина;
xk
— частные
значения показателей
у отдельных испытуемых. Всего таких
показателей п,
поэтому
индекс k
данной
переменной принимает значения от 1 до
п;
∑ — принятый
в математике знак суммирования величин
тех
переменных, которые находятся справа
от этого знака.
Выражение
![]()
соответственно означает сумму всех х
с индексом k
от 1 до n.
Пример.
Допустим,
что в результате применения
психодиагностической
методики для оценки некоторого
психологического
свойства у десяти испытуемых мы получили
следующие частные
показатели степени развитости данного
свойства у отдельных
испытуемых: х1=
5,
х2
=
4, х3
= 5,
х4
= 6,
х5
= 7,
х6
= 3,
х7
= 6,
х8=
2,
х9=
8,
х10
=
4. Следовательно, п
= 10,
а индекс k
меняет
свои значения от 1 до 10 в приведенной
выше формуле. Для данной выборки
среднее значение1,
вычисленное по этой формуле, будет
равно:
![]()
1
В дальнейшем, как это и принято в
математической статистике, с целью
сокращения
текста мы будем опускать слова «выборочное»
и «арифметическое» и просто говорить
о «среднем» или «среднем значении».
В
психодиагностике и в экспериментальных
психолого-педагогических исследованиях
среднее,
как правило, не вычисляется
с точностью, превышающей один, два знака
после запятой, т.е.
с большей, чем десятые или сотые доли
единицы.
В
психодиагностических обследованиях
большая точность расчетов не требуется
и не имеет смысла, если принять во
внимание приблизительность тех оценок,
которые в них получаются, и достаточность
таких оценок для производства сравнительно
точных расчетов.
Дисперсия
Дисперсия
как статистическая, величина характеризует,
насколько
частные значения отклоняются от средней
величины в данной
выборке.
Чем
больше дисперсия, тем больше отклонения
или разброс данных. Прежде чем представлять
формулу для расчетов
дисперсии, рассмотрим пример. Воспользуемся
теми первичными
данными, которые были приведены ранее
и на основе которых вычислялась в
предыдущем примере средняя величина.
Мы видим, что все они разные и отличаются
не только друг от
друга, но и от средней величины. Меру их
общего отличия от средней
величины и характеризует дисперсия. Ее
определяют для того,
чтобы можно было отличать друг от друга
величины, имеющие
одинаковую среднюю, но разный разброс.
Представим
себе другую, отличную от предыдущей
выборку первичных значений,
например такую: 5, 4, 5, 6, 5, 6, 5, 4, 5, 5. Легко
убедиться в том, что ее средняя величина
также равна 5,0. Но в данной выборке
ее отдельные частные значения отличаются
от средней гораздо
меньше, чем в первой выборке. Выразим
степень этого отличия
при помощи дисперсии, которая определяется
по
следующей
формуле:

где
![]()
— выборочная
дисперсия, или просто дисперсия;

— выражение,
означающее, что для всех xk
от
первого
до последнего в данной выборке необходимо
вычислить разности
между частными и средними значениями,
возвести эти разности
в квадрат и просуммировать;
п —
количество
испытуемых в выборке или первичных
значений,
по которым вычисляется дисперсия.
Заметим,
что во многих изданиях дисперсию принято
обозначать как D(x).
Определим
дисперсии для двух приведенных выше
выборок частных
значений, обозначив эти дисперсии
соответственно индексами
1 и 2:
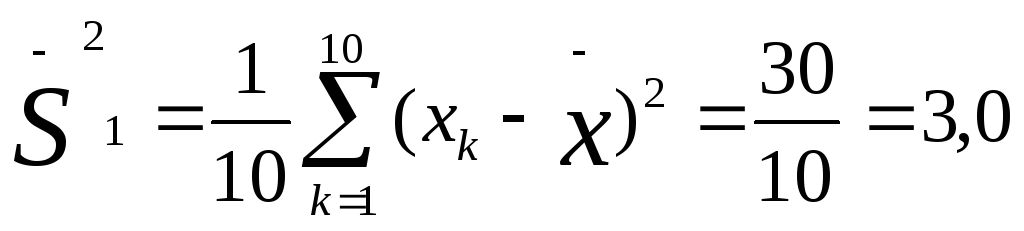

Мы
видим, что дисперсия по второй выборке
(0,4) значительно меньше дисперсии по
первой выборке (3,0). Если бы не было
дисперсии,
то мы не в состоянии были бы различить
данные выборки.
Соседние файлы в папке МатМетоды в Психологии (литература)
- #
- #
13.02.201616.87 Mб1467Наследов А.Д. IBM SPSS Statistics 20 профессиональный анализ данных.pdf
- #
Сейчас Вы научитесь находить числовые характеристики статистического распределения выборки. Примеры подобраны на основании индивидуальных заданий по теории вероятностей, которые задавали студентам ЛНУ им. И. Франка. Ответы послужат для студентов математических дисциплин хорошей инструкцией на экзаменах и тестах. Подобные решения точно используют в обучении экономисты , поскольку именно им задавали все что приведено ниже. ВУЗы Киева, Одессы, Харькова и других городов Украины имеют подобную систему обучения поэтому много полезного для себя должен взять каждый студент. Задачи различной тематики связаны между собой линками в конце статьи, поэтому можете найти то, что Вам нужно.
Индивидуальное задание 1
Вариант 11
Задача 1. Построить статистическое распределение выборки, записать эмпирическую функцию распределения и вычислить такие числовые характеристики:
- выборочное среднее;
- выборочную дисперсию;;
- подправленную дисперсию;
- выборочное среднее квадратичное отклонение;
- подправленное среднее квадратичное отклонение;
- размах выборки;
- медиану;
- моду;
- квантильное отклонение;
- коэффициент вариации;
- коэффициент асимметрии;
- эксцесс для выборки:
Выборка задана рядом 11, 9, 8, 7, 8, 11, 10, 9, 12, 7, 6, 11, 8, 7, 10, 9, 11, 8, 13, 8.
Решение:
Запишем выборку в виде вариационного ряда (в порядке возрастания):
6; 7; 7; 7; 8; 8; 8; 8; 8; 9; 9; 9; 10; 10; 11; 11; 11; 11; 12; 13.
Далее записываем статистическое распределение выборки в виде дискретного статистического распределения частот:
![]()
Эмпирическую функцию распределения определим по формуле
![]()
Здесь nx – количество элементов выборки которые меньше х. Используя таблицу и учитывая что объем выборки равен n = 20, запишем эмпирическую функцию распределения:

Далее вычислим числовые характеристики статистического распределения выборки.
Выборочное среднее вычисляем по формуле
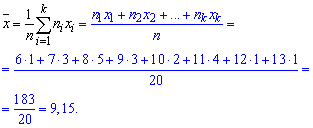
Выборочную дисперсию находим по формуле
![]()
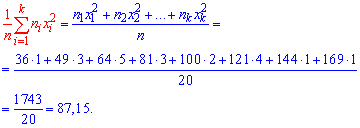
Выборочное среднее, что фигурирует в формуле дисперсии в квадрате найдено выше. Остается все подставить в формулу
![]()
Подправленную дисперсию вычисляем согласно формулы
![]()
Выборочное среднее квадратичное отклонение вычисляем по формуле
![]()
Подправленное среднее квадратичное отклонение вычисляем как корень из подправленной дисперсии
![]()
Размах выборки вычисляем как разность между наибольшим и наименьшим значениями вариант, то есть:
![]()
Медиану находим по 2 формулам:
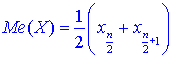 если число n – четное;
если число n – четное;
![]() если число n – нечетное.
если число n – нечетное.
Здесь берем индексы в xi согласно нумерации варианта в вариационном ряду.
В нашем случае n = 20, поэтому
![]()
Мода – это варианта которая в вариационном ряду случается чаще всего, то есть
![]()
Квантильное отклонение находят по формуле
![]()
где ![]() – первый квантиль,
– первый квантиль, ![]() – третий квантиль.
– третий квантиль.
Квантили получаем при разбивке вариационного ряда на 4 равные части.
Для заданного статистического распределения квантильное отклонения примет значение
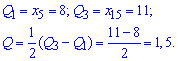
Коэффициент вариации равный процентному отношению подправленного среднего квадратичного к выборочному среднему
![]()
Коэффициент асимметрии находим по формуле
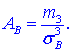
Здесь 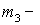 центральный эмпирический момент 3-го порядка,
центральный эмпирический момент 3-го порядка,
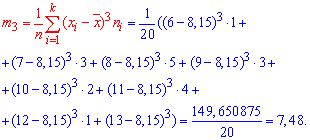
Подставляем в формулу коэффициента асимметрии
![]()
Эксцессом ![]() статистического распределения выборки называется число, которое вычисляют по формуле:
статистического распределения выборки называется число, которое вычисляют по формуле:
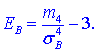
Здесь m4 центральный эмпирический момент 4-го порядка. Находим момент
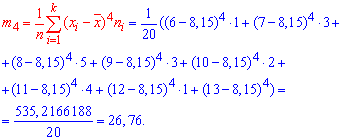
а далее эксцесс![]()
Теперь Вы имеете все необходимые формулы чтобы найти числовые характеристики статистического распределения. Как найти моду, медиану и дисперсию должен знать каждый студент, который изучает теорию вероятностей.
Готовые решения по теории вероятностей
- Следующая статья – Построение уравнения прямой регрессии Y на X
Вы́борочное (эмпири́ческое) сре́днее — это приближение теоретического среднего распределения, основанное на выборке из него.
Определение[править | править код]
Пусть 

.
Свойства выборочного среднего[править | править код]
- Пусть
— выборочная функция распределения данной выборки. Тогда для любого фиксированного
функция
является (неслучайной) функцией дискретного распределения. Тогда математическое ожидание этого распределения равно
.
- Выборочное среднее — несмещённая оценка теоретического среднего:
.
- Выборочное среднее — сильно состоятельная оценка теоретического среднего:
почти наверное при
.
- Выборочное среднее — асимптотически нормальная оценка. Пусть дисперсия случайных величин
конечна и ненулевая, то есть
. Тогда
по распределению при
,
где 


- Выборочное среднее из нормальной выборки — эффективная оценка её среднего.
См. также[править | править код]
- Выборочная дисперсия
- Выборочные моменты
|
|
В статье не хватает ссылок на источники (см. рекомендации по поиску). Информация должна быть проверяема, иначе она может быть удалена. Вы можете отредактировать статью, добавив ссылки на авторитетные источники в виде сносок. (11 января 2015) |
Среднее значение |
|
|---|---|
| Математика |
|
| Геометрия |
|
| Теория вероятностей и математическая статистика |
|
| Информационные технологии |
|
| Теоремы |
|
| Другое |
|
3.1. Показатели центральной тенденции
Простейший пример такого показателя нам уже встречался – это среднее арифметическое значение. Но средней
дело не ограничивается, впрочем, обо всём по порядку:
3.1.1. Генеральная и выборочная средняя
Пусть исследуется некоторая генеральная совокупность объёма ![]() , а именно её числовая характеристика
, а именно её числовая характеристика ![]() , не важно, дискретная или непрерывная.
, не важно, дискретная или непрерывная.
Генеральной средней называют среднее арифметическое всех значений этой совокупности:
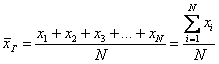
Если среди чисел ![]() есть одинаковые (что
есть одинаковые (что
характерно для дискретного ряда), то формулу можно записать в более компактном
виде:
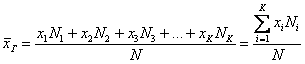 , где:
, где:
варианта ![]() повторяется
повторяется ![]() раз;
раз;
варианта ![]() –
– ![]() раз;
раз;
варианта ![]() –
– ![]() раз;
раз;
…
варианта ![]() –
– ![]() раз.
раз.
Живой пример вычисления генеральной средней встретился в Примере 2, но чтобы не занудничать, я даже не буду
напоминать его содержание. Далее.
Как мы помним, обработка всей генеральной совокупности часто затруднена либо невозможна, и поэтому из неё организуют представительную выборку объема ![]() , и на основании исследования этой выборки делают вывод обо всей совокупности.
, и на основании исследования этой выборки делают вывод обо всей совокупности.
Выборочной средней называется среднее арифметическое всех значений выборки:
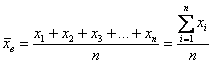
и при наличии одинаковых вариант формула запишется компактнее:
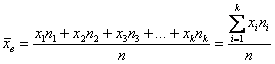 – как сумма произведений вариант
– как сумма произведений вариант ![]() на соответствующие частоты
на соответствующие частоты ![]() , делённая на объём совокупности
, делённая на объём совокупности ![]() .
.
Выборочная средняя ![]() позволяет достаточно
позволяет достаточно
точно оценить истинное значение ![]() , при этом, чем
, при этом, чем
больше выборка, тем точнее будет эта оценка.
Практику начнём с дискретного вариационного ряда и знакомого условия:
Пример 8
По результатам выборочного исследования ![]() рабочих цеха были установлены их квалификационные разряды: 4, 5, 6, 4, 4, 2, 3, 5, 4,
рабочих цеха были установлены их квалификационные разряды: 4, 5, 6, 4, 4, 2, 3, 5, 4,
4, 5, 2, 3, 3, 4, 5, 5, 2, 3, 6, 5, 4, 6, 4, 3.
Это числа из Примера 4, но теперь нам требуется: вычислить выборочную среднюю, и, не отходя от станка, найти моду
и медиану.
Как решать задачу? Если нам даны первичные данные (конкретные варианты ![]() ), то их можно тупо просуммировать и разделить результат на объём
), то их можно тупо просуммировать и разделить результат на объём
выборки:
![]() – средний квалификационный разряд рабочих
– средний квалификационный разряд рабочих
цеха.
Но здесь удобнее составить вариационный ряд:
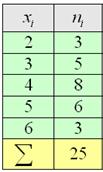
и использовать «цивилизованную» формулу:
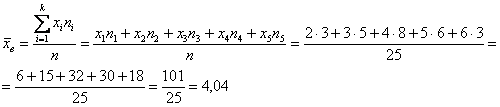
 3.1.2. Мода
3.1.2. Мода
 3. Основные показатели статистической совокупности
3. Основные показатели статистической совокупности
| Оглавление |
