Выборочная дисперсия, описание
Выборочная дисперсия является сводной характеристикой для наблюдения рассеяния количественного признака выборки вокруг среднего значения.
Определение
Выборочная дисперсия – это среднее арифметическое значений вариантов части отобранных объектов генеральной совокупности (выборки).
Связь выборочной и генеральной дисперсии
Генеральная дисперсия представляет собой среднее арифметическое квадратов отступлений значений признаков генеральной совокупности от их среднего значения.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Определение
Генеральная совокупность – это комплекс всех возможных объектов, относительно которых планируется вести наблюдение и формулировать выводы.
Выборочная совокупность или выборка является частью генеральной совокупности, выбранной для изучения и составления заключения касательной всей генеральной совокупности.
Как вычислить выборочную дисперсию
Выборочная дисперсия при различии всех значений варианта выборки находится по формуле:
({widehat D}_В=frac{displaystylesum_{i-1}^n{(x_i-{overline x}_В)}^2}n)
Для значений признаков выборочной совокупности с частотами n1, n2,…,nk формула выглядит следующим образом:
({widehat D}_В=frac{displaystylesum_{i-1}^kn_i{(x_i-{overline x}_В)}^2}n)
Квадратный корень из выборочной дисперсии характеризует рассеивание значений вариантов выборки вокруг своего среднего значения. Данная характеристика называется выборочным средним квадратическим отклонением и имеет вид:
({widehatsigma}_В=sqrt{{widehat D}_В})
Упрощенный способ вычисления выборочной или генеральной дисперсии производят по формуле:
(D=overline{x^2}-left[overline xright]^2)
Если вариационный ряд выборочной совокупности интервальный, то за xi принимается центр частичных интервалов.
Пример
Найти выборочную дисперсию выборки со значениями:
- xi: 1, 2, 3, 4;
- ni: 20, 15, 10, 5.
Решение
Для начала необходимо определить выборочную среднюю:
({overline x}_В=frac1{50}(1cdot20+2cdot15+3cdot10+4cdot5)=frac1{50}cdot100=2)
Затем найдем выборочную дисперсию:
(D_В=frac1{50}({(1-2)}^2cdot20+{(2-2)}^2cdot15+{(3-2)}^2cdot10+{(4-2)}^2cdot5)=1)
Исправленная дисперсия
Математически выборочная дисперсия не соответствует генеральной, поскольку выборочная используется для смещенного оценивания генеральной дисперсии. По этой причине математическое ожидание выборочной дисперсии вычисляется так:
(Mleft[D_Bright]=frac{n-1}nD_Г)
В данной формуле DГ – это истинное значение дисперсии генеральной совокупности.
Исправить выборочную дисперсию можно путем умножения ее на дробь:
(frac n{n-1})
Получим формулу следующего вида:
(S^2=frac n{n-1}cdot D_В=frac{displaystylesum_{i=1}^kn_i{(x_i-{overline x}_В)}^2}{n-1})
Исправленная дисперсия используется для несмещенной оценки генеральной дисперсии и обозначается S2.
Среднеквадратическая генеральная совокупность оценивается при помощи исправленного среднеквадратического отклонения, которое вычисляется по формуле:
(S=sqrt{S^2})
При нахождении выборочной и исправленной дисперсии разнятся лишь знаменатели в формулах. Различия в этих характеристиках при больших n незначительны. Применение исправленной дисперсии целесообразно при объеме выборки меньше 30.
Для чего применяют исправленную выборочную дисперсию
Исправленную выборочную используют для точечной оценки генеральной дисперсии.
Пример
Длину стержня измерили одним и тем же прибором пять раз. В результате получили следующие величины: 92 мм, 94 мм, 103 мм, 105 мм, 106 мм. Задача найти выборочную среднюю длину предмета и выборочную исправленную дисперсию ошибок измерительного прибора.
Решение
Сначала вычислим выборочную среднюю:
({overline x}_В=frac{92+94+103+105+106}5=100)
Затем найдем выборочную дисперсию:
(D_В=frac{displaystylesum_{i=1}^k{(x_i-{overline x}_В)}^2}n=frac{{(92-100)}^2+{(94-100)}^2+{(103-100)}^2+{(105-100)}^2+{(106-100)}^2}5=34)
Теперь рассчитаем исправленную дисперсию:
(S^2=frac5{5-1}cdot34=42,5)
У к а з а н и е . Перейти к условным вариантам м/ =jc/—2620.
455. По выборке объема /г = 41 найдена смещенная оценка D„ = 3 генеральной дисперсии. Найти несмещен ную оценку дисперсии генеральной совокупности.
|
Р е ш е н и е . Искомая несмещенная |
оценка равна исправленной |
|
дисперсии: |
|
|
S^ == – ^ DB = ~ |
-3 = 3,075. |
456.По выборке объема л = 51 найдена смещенная оценка DB = 5 генеральной дисперсии. Найти несмещен ную оценку дисперсии генеральной совокупности.
457.В итоге пяти измерений длины стержня одним прибором (без систематических ошибок) получены сле дующие результаты (в мм): 92; 94; 103; 105; 106. Найти: а) выборочную среднюю длину стержня; б) выборочную
иисправленную дисперсии ошибок прибора.
Р е ш е н и е , а) Найдем выборочную среднюю:
|
i ^ = 9 2 + ( 0 – b 2 + n + 13 + 14)/5-=92-h8 = 100. |
|
|
б) Найдем выборочную дисперсию: |
|
|
Оя |
.=[(92—100)* + (94-~ 100)2+(103—100)2]/5+ |
+ [(105 —100)«-!- (J06—100)2]/5 = 34. Найдем исправленную дисперсию:
п—1 D B = ^ – 3 4 = 42,5.
458.В итоге четырех измерений некоторой физической величины одним прибором (без систематических ошибок) получены следующие результаты: 8; 9; 11; 12. Найти: а) выборочную среднюю результатов измерений; б) выбо рочную и исправленную дисперсии ошибок прибора.
|
459, Ниже |
приведены результаты измерения роста |
|
(в см) случайно |
отобранных 100 студентов. |
|
Рост |
154—I58|l58—162 162—166 166—170 170—174 174—178| 178—182 |
||||||
|
Число |
|||||||
|
сту |
10 |
14 |
26 |
28 |
12 |
8 |
2 |
|
дентов |
Найти выборочную среднюю и выборочную дисперсию
|
роста обследованных |
студентов. |
|
У к а з а н и е . Найти |
середины интервала и принять их в ка |
|
честве вариант. |
160
460. Найти выборочную дисперсию по данному рас пределению выборки объема /г=10:
|
Xi |
186 |
192 |
194 |
|
Ai,. |
2 |
5 |
3 |
Р е ш е н и е . Варианты—сравнительно большие числа, поэтому перейдем к условным.вариантам Uf^^Xi—191 (мы вычли из вариант
|
число С = 191, близкое |
к выборочной |
средней). В итоге получим |
||
|
распределение условных |
вариант: |
|||
|
Ui |
—5 |
1 |
3 |
|
|
Л/ |
2 |
5 |
3 |
Найдем искомую выборочную дисперсию:
—[(2. (—5) + 51+3 – 3)/10]2 = 8,2—0,16 = 8,04.
461.Найти выборочную дисперсию по данному рас пределению выборки объема л =100:
|
Х; |
340 |
360 |
375 |
380 |
|
п,. |
20 |
50 |
18 |
12 |
У к а з а н и е . Перейти к условным вариантам а/ =д:/—360.
462. Найти выборочную дисперсию по данному рас пределению выборки объема п=100:
|
Xi |
2502 |
2804 |
2903 |
3028 |
|
rii |
8 |
30 |
60 |
2 |
У к а з а н и е . Перейти к условным вариантам Ui = Xi—2844.
463. Найти выборочную дисперсию по данному рас пределению выборки объема п = 1 0 :
|
Xi 0,01 |
0,04 |
0,08 |
|
|
п,. |
5 |
3 |
2 |
|
Р е ш е н и е . Для того |
чтобы избежать действий с дробями, |
перейдем к условным вариантам а,==100х/. В итоге получим рас
|
пределение |
1 |
4 |
8 |
|
Ui |
|||
|
л/ |
5 |
3 |
2 |
Найдем выборочную дисперсию условных вариант:
Ов (и) = (S «,«?)/л-[(2 л,«,)/«]^
Подставив в эту формулу условные варианты и их частоты, получим
D B ( « ) = 7,21.
Найдем искомую выборочную дисперсию первоначальных вариант: DB(A:) = DB(W)/1002 =7,21/10 000 = 0.0007.
161
464. Найти выборочную дисперсию по данному рас пределению выборки объема /г = 50:
|
xi |
0,1 |
0,5 |
0,6 |
0,8 |
|
rii |
5 |
15 |
20 |
10 |
У к а з а н и е . Перейти к условным вариантам U{ = Ox{.
465. Найти выборочную дисперсию по данному рас пределению выборки объема п = 50:
|
Xi |
18,4 |
18,9 |
19,3 |
19,6 |
|
Л; |
5 |
10 |
20 |
15 |
У к а з а н и е . Перейти к условным вариантам Ui^=Oxi—195.
466. Найти исправленную выборочную дисперсию по данному распределению выборки /г = 10:
|
Xi |
102 |
104 |
108 |
|||
|
/г^ |
2 |
3 |
5 |
|||
|
Р е ш е н и е . |
Перейдем к |
условным вариантам |
ut^Xi—104. |
|||
|
В итоге получим |
распределение |
|||||
|
«/ |
—2 |
О |
4 |
|||
|
/I/ |
2 |
3 |
5 |
Найдем исправленную выборочную дисперсию условных вариант:
^” 1Г^ •
Подставив в эту формулу условные варианты, их частоты и объем
выборки, получим 5^=6,93.’ Все первоначальные варианты были уменьшены на одно и то же
посюянное число С =104, поэтому дисперсия не изменилась, т. е. искомая дисперсия равна дисперсии условных вариант: ^х’^^^ ==6,93.
|
467. Найти |
исправленную |
выборочную |
дисперсию |
||
|
по данному распределению выборки объема |
п = 100: |
||||
|
Xi |
1250 |
1275 |
1280 |
1300 |
|
|
п^ |
20 |
25 |
50 |
5 |
У к а з а н и е . Перейти к условным вариантам Ui^=^Xi—1275.
4в8, Найти исправленную выборочную дисперсию по
|
данному распределению выборки объема |
п=: |
||||
|
Xi |
0,01 |
0,05 |
0,09 |
||
|
П/ |
2 |
3 |
5 |
||
|
Р е ш е н и е . Для того чтобы |
избежать действий с дробями, пе |
||||
|
рейдем к условным вариантам а/=: lOOx/. В итоге |
получим распре |
||||
|
деление |
<// |
1 |
5 |
9 |
|
|
п/ |
2 |
3 |
5 |
162
Найдем исправленную выборочную дисперсию условных вариант
^== 7Г=Г1
Подставив в згу формулу данные задачи, получим s ^ ^ 10,844.
Найдем искомую исправленную дисперсию первоначальных вариант:
4=л^ /100*» 10,844/10 000 с^ 0,0085.
469.Найти исправленную выборочную дисперсию по данному распределению выборки объема /1 — 20:
|
Xi |
0,1 |
0,5 |
0,7 |
0,9 |
|
П/ |
6 |
12 |
1 |
1 |
У к а з а н и е . Перейти к условным вариантам а/»Юдг/.
|
470. Найти исправленную |
выборочную дисперсию по |
|||
|
данному распределению выборки объема п = 10: |
||||
|
х^ |
23,5 |
26,1 |
28,2 |
30,4 |
|
п^ |
2 |
3 |
4 |
1 |
|
У к а з а н и е . Перейти к условным вариантам UisЮдг/ —268. |
||||
|
§ 2. Метод момеитов |
||||
|
Метод моментов т о ч е ч н о й о ц е н к и |
неизвестных параметров |
заданного распределения состоит в приравнивании теоретических моментов соответствующим эмпирическим моментам того же порядка.
Если распределение определяется о д н и м п а р а м е т р о м » то для его отыскания приравнивают один теоретический момент одному эмпирическому моменту того же порядка. Например, можно при
|
равнять начальный |
теоретический момент |
первого порядка началь |
|
ному эмпирическому |
моменту первого порядка: Vi=sAfx. Учитывая, |
|
|
1ITO Vi=sM(X) и Aii=XB, получим |
||
|
М ( Х ) – 1 , . |
(•) |
Математическое ожидание является функцией от неизвестного параметра заданного распределения, поэтому, решив уравнение (*) относительно неизвестного параметра, тем самым получим его точеч ную оценку.
Если распределение определяется д в у м я п а р а м е т р а м и , то приравнивают два теоретических момента двум соответствующим эм пирическим моментам того же порядка. Например, можно прирав нять начальный теоретический момент первого порядка начальному эмпирическому моменту первого порядка и центральный теорети ческий момент второго порядка центральному эмпирическому моменту второго порядка:
163
|
Учитывая, что Vi=M(X), |
Mi^x^, ^i2=Z)(X), та==Ов, имеем |
D ( X ) = DB.
Левые части этих равенств являются функциями от неизвестных параметров, поэтому, решив систему (**) относительно неизвестных параметров, тем самым получим их точечные оценки.
Разумеется, для вычисления выборочной средней дсв и выбо рочной дисперсии DB надо располагать выборкой Xi, Хг, …,л:„.
471. Случайная величина X распределена по закону Пуассона
где m—число испытаний, произведенных в одном опыте; Х/—число появлений события в t-м опыте.
Найти методом моментов по выборке х^, AT^, . . . • х„ точечную оценку неизвестного параметра Я, определяю щего распределение Пуассона.
Р е ш е н и е . Требуется оценить один параметр, поэтому доста точно иметь одно уравнение относительно этого параметра. Прирав
|
няем |
начальный теоретический момент первого порядка |
V] началь |
|
ному |
эмпирическому моменту первого порядка Afi: |
|
|
V i = M i . |
||
|
Приняв во внимание, что Vi==Al(X), Mi = x’^, получим |
Л1(Х) = дг^1. |
Учитывая, что математическое ожидание распределения Пуассона равно параметру к этого распределения (см. задачу 207), оконча тельно имеем k=Xji.
Итак, точечной оценкой параметра X распределения Пуассона служит выборочная средняя: Х*=дгв.
472. Случайная величина X (число семян сорняков в пробе зерна) распределена по закону Пуассона. Ниже приведено распределение семян сорняков в п = 1000 про бах зерна (в первой строке указано количество х^ сор няков в одной пробе; во второй строке указана частота /I/—число проб, содержащих х^ семян сорняков):
|
л:,. |
О |
1 |
2 |
3 |
4 |
5 |
6 |
|
п^ |
405 |
366 |
175 |
40 |
8 |
4 |
2 |
Найти методом моментов точечную оценку неизвест ного параметра распределения Пуассона•
У к а з а н и е . Использовать решение задачи 471.
473. Случайная величина X (число нестандартных изделий в партии изделий) распределена по закону Пу-
164
ассона. Ниже приведено распределение нестандартных изделий в п = 200 партиях (в первой строке указано количество л:,- нестандартных изделий в одной партии; во второй строке указана частота м,- — число партий, содержащих Xi нестандартных изделий):
|
АГу |
О |
1 |
2 |
3 |
4 |
|
rii |
132 |
43 |
20 |
3 |
2 |
Найти методом моментов точечную оценку неизвест ного параметра X распределения Пуассона.
474. Найти методом моментов по выборке Xj, х^, . . . , Хп точечную оценку параметра р биномиального распре деления
|
где Х( — число появлений |
события |
в /-м опыте (/ = 1, 2, |
|
. . . , /г), т — количество испытаний |
в одном опыте. |
|
|
У к а з а н и е . Приравнять |
начальный теоретический момент пер |
|
|
вого порядка начальному эмпирическому |
моменту первого порядка. |
|
|
475. Случайная величина X (число появлений собы |
тия А ъ т независимых испытаниях) подчинена биноми альному закону распределения с неизвестным парамет
|
ром р. |
Ниже приведено |
эмпирическое распределение |
|
числа |
появлений события |
в 10 опытах по 5 испытаний |
|
в каждом (в первой строке |
указано число Xi появлений |
события А в одном опыте; во второй строке указана
|
частота л,- — количество опытов, |
в |
которых наблюдалось |
|||
|
Xi появлений события Л): |
|||||
|
X,. |
О |
1 |
2 |
3 |
4 |
|
л,. |
5 |
2 |
1 |
1 |
1 |
Найти методом моментов точечную оценку параметра р биномиального распределения.
У к а з а н и е . Использовать решение задачи 474.
476. Найти методом моментов по выборке х^, Xg, . . . , Хп точечную оценку неизвестного параметра X показа тельного распределения, плотность которого f{x) = Xe-‘^^ (х>0) .
477. Случайная величина X (время работы элемента) имеет показательное распределение f{x) = Xe-^ (х^О). Ниже приведено эмпирическое распределение среднего времени работы п=200 элементов (в первой строке при-
165
ведено среднее время х^ работы элемента в часах; во вто рой строке указана частота щ—количество элементов» проработавших в среднем Х/ часов):
|
Xi |
2,5 |
7,5 |
12,5 |
17,5 |
22,5 |
27,5 |
|
л^ |
133 |
45 |
15 |
4 |
2 |
1 |
Найти методом моментов точечную оценку неизвест ного параметра показательного распределения.
У к а з а н и е . Использовать решение задачи 476.
478. Найти методом моментов точечную оценку пара метра р (вероятности) геометрического распределения P(X = Xi) = {}—pY”’^-pf где X/—число испытаний, про изведенных до появления события; р—вероятность по явления события в одном испытании.
Указание . Принять во внимание, что М(X) = 1/р (см. за дачу 222).
479.Найти методом моментов оценку параметра р геометрического распределения Р{Х = х^) = {1—ру^’^-р^ если в четырех опытах событие появилось соответственно после двух, четырех, шести и восьми испытаний.
480.Найти методом моментов по выборке х^, х,, …» Хп точечные оценки неизвестных параметров а и р гам ма-распределения, плотность которого
/(^) = ра^хга+1)^^^”^^ ( а > – 1 . Р > 0 , х>0) .
Решение. Для отыскания двух неизвестных параметров не обходимо иметь два уравнения; приравняем начальный теоретический момент первого порядка Vi начальному эмпирическому моменту пер вого порядка Ml и центральный теоретический момент второго по рядка fis центральному эмпирическому моменту второго порядка т^;
Учитывая, что Vi = Ai(X), Мг^х^^ ^ia=Z>(X), m^^D^, имеем ГЛ1(Х)=7,. *.
Математическое ожидание и дисперсия гамма-распределения со ответственно равны Л1 (Х) = (а+1)Р» D(X)=(aH-l)p* (см. зада чу 302), поэтому (^) можно записать в виде
/(а+1)р=7„
Ua+1)P*=I>B.
Решив эту систему, окончателыю^ получим искомые JFOчeчныe оценки ненэтестяых параметров: а*=(х^)^/0,^—1, ^*=0^/х^’
16в
481. Случайная величина X (уровень воды в реке по сравнению с номиналом) подчинена гамма-распределению,
|
плотность |
которого |
определяется |
параметрами а |
и Э |
|||||
|
( а > — 1 , р > 0 ) : |
|||||||||
|
Ниже приведено распределение среднего уровня |
воды по |
||||||||
|
данным |
/г = 45 паводков (в первой |
строке указан |
сред |
||||||
|
ний уровень воды х^ (см); |
во второй строке приведена |
||||||||
|
частота |
п^- — количество |
паводков со |
средним |
уровнем |
|||||
|
воды JC,): |
|||||||||
|
Xi |
37,5 |
62,5 |
87,5 |
112,5 |
137,5 |
162,5 |
187,5 |
250 |
350 |
|
п ^ 1 3 6 7 |
7 |
5 |
4 8 4 |
Найти методом моментов точечные оценки неизвестных параметров а и р рассматриваемого гамма-распределения.
|
Р е ш е н и е . |
Используем точечные оценки параметров |
гамма- |
|
распределения (см. задачу 480): |
||
|
O C * = ( 7 B ) V Z ) B – 1, Р * = ^ В М В . |
П |
|
|
По заданному |
распределению легко найдем выборочную среднюю |
|
|
и выборочную дисперсию: х^=1&6, DB = 6782. |
Подставив эти числа в формулы (*), окончательно получим искомые точечные оценки неизвестных параметров рассматриваемого гамма-распределения: а* =3,06, р* =40,86.
482. Устройство состоит из элементов, время безот казной работы которых подчинено гамма-распределению. Испытания пяти элементов дали следующие наработки (время работы элемента в часах до отказа): 50, 75, 125, 250, 300. Найти методом моментов точечные оценки неизвест ных параметров а и р , которыми определяется гаммараспределение.
У к а з а н и е . Использовать решение задачи 480. Учесть, что объем выборки п = 5 мал, поэтому в формулах для вычисления па раметров а и р вместо выборочной дисперсии подставить исправлен ную дисперсию s^ = ‘Lni(Xi—х^)^/(п — 1).
|
483. Найти |
методом моментов по выборке лг^, Xg, . . . , |
|||
|
Хп точечные оценки |
неизвестных параметров а и о нор |
|||
|
мального распределения, плотность |
которого |
|||
|
/(л:) = —i=e-<^-«>V(2a«). |
||||
|
У к а з а н и е . |
Приравнять |
начальный |
теоретический момент |
|
|
первого порядка |
и центральный |
теоретический момент второго по |
||
|
рядка соответствующим |
эмпирическим моментам. |
167
484. Случайная величина X (отклонение контролируе мого размера изделия от номинала; подчинена нормаль ному закону распределения с неизвестными параметрами а и о. Ниже приведено эмпирическое распределение от клонения от номинала п = 200 изделий (в первой строке указано отклонение х^- (мм); во второй строке приведена частота п,- — количество изделий, имеющих отклонение Xf):
|
Xi |
0,3 |
0,5 |
0,7 |
0,9 |
1,1 |
1,3 |
1,5 |
1,7 |
1,9 |
2,2 |
2,3 |
|
п^ |
6 |
9 |
26 |
25 |
30 |
26 |
21 |
24 |
20 |
8 |
5 |
Найти методом моментов точечные оценки неизвестных параметров а и о нормального распределения.
|
У к а з а н и е . |
Использовать задачу 483. |
|||
|
485. Найти |
методом моментов |
по выборке х^, дг^, |
…» |
|
|
х„ точечные |
оценки параметров а |
и b равномерного |
рас |
|
|
пределения, |
плотность которого |
/ (х) = 1/(6—а) (6 > а). |
У к а з а н и е . Использовать решения задач 313, 315.
486. Случайная величина X (ошибка измерения даль ности радиодальномером) подчинена равномерному за кону распределения с неизвестными параметрами а и Ь. Ниже приведено эмпирическое распределение средней ошибки л = 200 измерений дальности (в первой строке указана средняя ошибка л:,-; во второй строке указана частота п^—количество измерений, имеющих среднюю ошибку АГ/):
л:,. 3 5 7 9 11 13 15 17 19 21 п^ 21 16 15 26 22 14 21 22 18 25
Найти методом моментов точечные оценки неизвестных параметров а и Ь равномерного распределения.
У к а з а н и е . Использовать задачу 485.
487. Найти методом моментов по выборке х^, х^, . . . , л:„ точечные оценки неизвестных параметров Х^ и Яд «двойного распределения» Пуассона
|
1 |
Х^’е~^« |
1 |
Х^’е~^« |
|
* Х = Xf) = -оГ • |
; |
h “о* • |
i — » |
где х^ — число появлений события в п^ испытаниях Х^ и Яа—положительные числа, причем X2>^i.
Р е ш е н и е . Если случайная величина Z распределена по закону Пуассона с параметром X, то ее начальные теоретические моменты
168
первого и второго порядка соответственно равны (см. задачи 207, 227):
Vi = Af(Z)==^,
Найдем начальные теоретические моменты первого и второго порядка рассматриваемой случайной величины X, учитывая соотно шения (*):
Vi = M (X) = A,,/2 + X2/2=(Xi + X2)/2,
V2=Af(X2) = (l/2)(^i + A?)+(l/2)(X2 + ^l)=Vi+(>.?+Xi)/2.
Отсюда
/Xi + X2 = 2vb
Xf + X| = 2v2 —2vi.
Решив эту систему относительно неизвестных параметров, приняв во внимание, что Лг > Ki, получим:
^i = vi —Kv2-—Vi —V?, X2 = Vi+K Va —Vi —V?.
488. Случайная величина X распределена по «двой ному» закону Пуассона:
|
1 |
Xfe-^* |
1 Ц^e-^* |
|||||||||||
|
Р |
(2С = |
X:) == “7Г • |
i |
Ь 7Г “ |
i |
• |
|||||||
|
Ниже приведено эмпирическое распределение числа |
|||||||||||||
|
появлений |
события |
в л = 327 |
испытаниях |
(в первой |
|||||||||
|
строке указано число х,- появлений события; |
во второй |
||||||||||||
|
строке |
приведена частота |
n^• — количество |
испытаний, |
||||||||||
|
в которых появилось Х/ событий): |
|||||||||||||
|
X,. |
О |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
||
|
п^ 28 47 |
81 67 |
53 |
24 |
13 |
8 |
3 |
2 |
1 |
|||||
|
Найти методом моментов точечные оценки неизвест |
|||||||||||||
|
ных параметров |
Х^ и К^ «двойного |
распределения» Пу |
|||||||||||
|
ассона. |
|||||||||||||
|
У к а з а н и е . |
Использовать |
решение |
задачи |
487. |
Вычислить по |
||||||||
|
выборке |
начальные |
эмпирические |
моменты |
первого и второго по |
|||||||||
|
рядков: |
Ml = ( 2 niXi)/n, |
Af2 = ( 2 ^i^b/^- |
|||||||||||
§ 3. Метод наибольшего правдоподобия
Метод наибольшего правдоподобия точечной оценки неизвестных параметров заданного распределения сводится к отысканию макси мума функции одного или нескольких оцениваемых параметров.
А. Дискретные случайные величины. Пусть X—дискретная слу чайная величина, которая в результате «опытов приняла возмож ные значения Xi, х^, . . . , л:„. Допустим, что вид закона распреде ления величины X задан, но неизвестен параметр в , которым оп-
169
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Евгений Николаевич Беляев
Эксперт по предмету «Математика»
Задать вопрос автору статьи
Генеральная дисперсия
Пусть нам дана генеральная совокупность относительно случайной величины $X$. Для начала напомним следующее определение:
Определение 1
Генеральная совокупность — совокупность случайно отобранных объектов данного вида, над которыми проводят наблюдения с целью получения конкретных значений случайной величины, проводимых в неизменных условиях при изучении одной случайной величины данного вида.
Определение 2
Генеральная дисперсия — среднее арифметическое квадратов отклонений значений вариант генеральной совокупности от их среднего значения.
Пусть значения вариант $x_1, x_2,dots ,x_k$ имеют, соответственно, частоты $n_1, n_2,dots ,n_k$. Тогда генеральная дисперсия вычисляется по формуле:

Сдай на права пока
учишься в ВУЗе
Вся теория в удобном приложении. Выбери инструктора и начни заниматься!
Получить скидку 3 000 ₽
Рассмотрим частный случай. Пусть все варианты $x_1, x_2,dots ,x_k$ различны. В этом случае $n_1, n_2,dots ,n_k=1$. Получаем, что в этом случае генеральная дисперсия вычисляется по формуле:
С этим понятием также связано понятие генерального среднего квадратического отклонения.
Определение 3
Генеральное среднее квадратическое отклонение — квадратный корень из генеральной дисперсии:
[{sigma }_г=sqrt{D_г}]
Выборочная дисперсия
Пусть нам дана выборочная совокупность относительно случайной величины $X$. Для начала напомним следующее определение:
Определение 4
Выборочная совокупность — часть отобранных объектов из генеральной совокупности.
Определение 5
Выборочная дисперсия — среднее арифметическое значений вариант выборочной совокупности.
«Дисперсия: генеральная, выборочная, исправленная» 👇
Пусть значения вариант $x_1, x_2,dots ,x_k$ имеют, соответственно, частоты $n_1, n_2,dots ,n_k$. Тогда выборочная дисперсия вычисляется по формуле:
Рассмотрим частный случай. Пусть все варианты $x_1, x_2,dots ,x_k$ различны. В этом случае $n_1, n_2,dots ,n_k=1$. Получаем, что в этом случае выборочная дисперсия вычисляется по формуле:
С этим понятием также связано понятие выборочного среднего квадратического отклонения.
Определение 6
Выборочное среднее квадратическое отклонение — квадратный корень из генеральной дисперсии:
[{sigma }_в=sqrt{D_в}]
Исправленная дисперсия
Для нахождения исправленной дисперсии $S^2$ необходимо умножить выборочную дисперсию на дробь $frac{n}{n-1}$, то есть
С этим понятием также связано понятие исправленного среднего квадратического отклонения, которое находится по формуле:
!!! В случае, когда значение вариант не являются дискретными, а представляют из себя интервалы, то в формулах для вычисления генеральной или выборочной дисперсий за значение $x_i$ принимается значение середины интервала, которому принадлежит $x_i.$
Пример задачи на нахождение дисперсии и среднего квадратического отклонения
Пример 1
Выборочная совокупность задана следующей таблицей распределения:

Рисунок 1.
Найдем для нее выборочную дисперсию, выборочное среднее квадратическое отклонение, исправленную дисперсию и исправленное среднее квадратическое отклонение.
Решение:
Для решения этой задачи для начала сделаем расчетную таблицу:
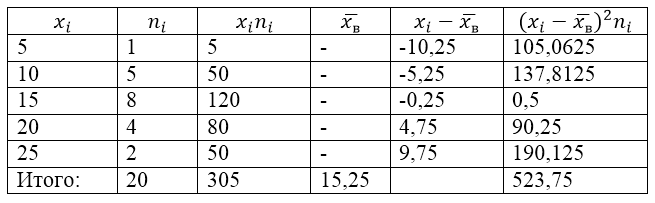
Рисунок 2.
Величина $overline{x_в}$ (среднее выборочное) в таблице находится по формуле:
[overline{x_в}=frac{sumlimits^k_{i=1}{x_in_i}}{n}]
То есть
[overline{x_в}=frac{sumlimits^k_{i=1}{x_in_i}}{n}=frac{305}{20}=15,25]
Найдем выборочную дисперсию по формуле:
[D_в=frac{sumlimits^k_{i=1}{{{(x}_i-overline{x_в})}^2n_i}}{n}=frac{523,75}{20}=26,1875]
Выборочное среднее квадратическое отклонение:
[{sigma }_в=sqrt{D_в}approx 5,12]
Исправленная дисперсия:
[{S^2=frac{n}{n-1}D}_в=frac{20}{19}cdot 26,1875approx 27,57]
Исправленное среднее квадратическое отклонение:
[S=sqrt{S^2}approx 5,25]
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме
Генеральная и выборочная дисперсия
Для анализа полученных данных в математической статистике используют различные виды показателей вариации, среди которых:
- размах вариации;
- среднее абсолютное отклонение;
- дисперсия.
Разберем понятие дисперсии, ее виды и свойства.
Дисперсия — величина, являющаяся мерой разброса полученных в ходе наблюдений данных относительно истинного значения.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Дисперсия является точечной оценкой параметра, так как имеет одно конкретное числовое значение.
Статистический анализ при исследовании некоторого объекта может быть сплошным или выборочным в зависимости от охватываемого объема данных.
В обоих вариантах результаты анализа распространяют на генеральную совокупность, однако при сплошном анализе наблюдению подвергают абсолютно все имеющиеся данные. Выборочный анализ, напротив, предполагает наблюдение только за некоторой выбранной частью данных. При этом выбранная совокупность должна сохранять структуру и закономерности генеральной.
Дисперсию также делят на два вида в зависимости от используемых данных:
- генеральная дисперсия;
- выборочная дисперсия.
Как видно из названия, дисперсии отличаются объемом выборки, на основе которой происходит расчет и анализ.
Выборочная дисперсия, определение, формулы для вычисления
Пусть имеется некоторая выборка Y из генеральной совокупности объемом n. Среднее значение выборки обозначим как ({overline y}_в).
Выборочная дисперсия (D_в) — величина, равная среднему арифметическому отклонению квадратов разности признаков выборки (y_1,;y_2,;…y_n) от ее среднего значения ({overline y}_в).
Данные в выборке могут располагаться хаотично, то есть быть несгруппированными, или же сформированы в вариационный ряд.
Выборочную дисперсию для несгруппированной выборки можно посчитать по формуле:
Формула 1
(D_в=frac{{displaystylesum_{i=1}^n}(y_i-{overline y}_в)}n)
В случае вариационного ряда используют кратные значения и частоты для дискретного представления; середины частичных интервалов и частоты для интервального представления.
Формула 2
(D_в=frac{{displaystylesum_{i=1}^k}(y’_i-{overline y}_в)cdot n_i}n)
где (y’_i )— кратное (одинаковое) значение в выборке или значение, соответствующее середине интервала;
(n_i )— частота.
Выборочная дисперсия, рассчитанная по приведенным выше формулам, дает недостоверное (заниженное) значение. Это значит, что при большом количестве экспериментов выборочная дисперсия будет давать смещенное относительно истинного значения генеральной совокупности значение.
Чтобы получить несмещенную выборочную дисперсию, используют следующую формулу:
Формула 3
(D_в=frac{{displaystylesum_{i=1}^n}{(y_i-{overline y}_в)}^2}{n-1})
Примечание 1
Как правило при использовании термина «выборочная дисперсия» имеют в виду именно несмещенную выборочную дисперсию.
Генеральная дисперсия, определение, что является оценкой, формулы для вычисления
Пусть имеется некоторая генеральная совокупность X объемом N и среднее значение признаков совокупности (X — {overline x}_г.)
Генеральная дисперсия (D_г) есть среднее арифметическое отклонение квадратов разности признаков (x_1,;x_2,;…x_n) генеральной совокупности X от их среднего значения ({overline x}_г).
Примечание 2
Иногда генеральную дисперсию называют теоретической.
Аналогично выборочной, генеральная дисперсия может быть рассчитана для несгруппированных данных генеральной совокупности:
Формула 4
(D_г=frac{{displaystylesum_{i=1}^N}{(x_i-{overline x}_г)}^2}N)
и для сформированного вариационного ряда:
Формула 5
(D_г=frac{{displaystylesum_{i=1}^K}{(x’_i-{overline x}_г)}^2cdot n_i}N)
Значение теоретической дисперсии бывает сложно вычислить из-за большого объема данных или их недостатка. Тогда для оценки используют выборочную дисперсию. Но если для оценки генеральной дисперсии применить выборочную, это приведет к возникновению ряда систематических ошибок. В результате оценка будет произведена неверно, а значение генеральной дисперсии занижено.
Чтобы устранить возникающую погрешность в качестве оценки генеральной дисперсии используют исправленную или несмещенную выборочную дисперсию, формула которой представлена выше.
Оценки параметров распределения
Оценкой параметра в статистике считают численное значение какого-либо параметра данной выборки.
Приведем оценки параметров распределения случайной величины, которые связаны с дисперсией.
Среднеквадратическое отклонение (δ) — характеристика рассеивания случайной величины относительно ее математического ожидания. Определяется как корень квадратный из дисперсии.
Формула 6
(delta=sqrt D)
Математическое ожидание случайной величины X — среднее (по весу вероятностей возможных значений) значение случайной величины. Обозначается как M(X).
Математическое ожидание и дисперсия для дискретной случайной величины связаны соотношением:
Формула 7
(D=Mleft[X-M(X)right]^2)
для непрерывной:
Формула 8
(D=int_{-infty}^infty(x-M{(x))}^2cdot f(x)dx)
где f(x) — функция распределения случайной величины.
Отметим, что указанные выше параметры могут быть определены как для генеральной совокупности, так и для некоторой выборки.
Примеры решения задач
Пример 1
Напряжение в цепи измеряют 6 раз с помощью одного и того же вольтметра. Получены следующие значения: 210 В, 200 В, 195 В, 205 В, 190 В, 200 В. Найти выборочную смещенную дисперсию и дать оценку генеральной дисперсии.
Решение.
Сначала вычислим выборочное среднее значение:
({overline x}_в=frac{210+200+195+205+190+200}6=200;B.)
Теперь найдем выборочную дисперсию:
(D_в=frac{{(210-200)}^2+{(200-200)}^2+{(195-200)}^2+{(205-200)}^2+{(190-200)}^2+{(200-200)}^2}6=frac{250}6approx42.)
Оценкой генеральной дисперсии является исправленная или выборочная несмещенная дисперсия. Чтобы вычислить исправленную дисперсию, умножим полученную ранее выборочную дисперсию на множитель (frac n{n-1} (n=6):)
(D_и=frac n{n-1}cdot D_в=frac65cdotfrac{250}6=50.)
Примечание 3
Данный пример показывает, что значение выборочной смещенной дисперсии занижено относительно генеральной.
Пример 2
Случайная величина задана следующей таблицей распределения, среднее значение выборки равно 14. Найти выборочную несмещенную дисперсию и среднеквадратическое отклонение.
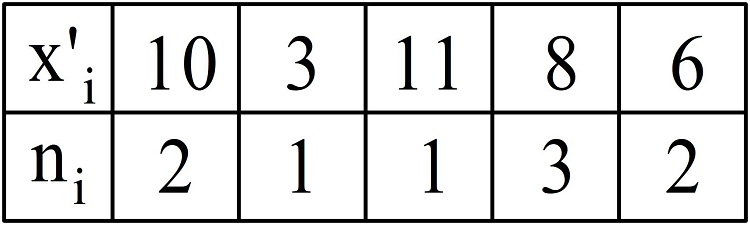
Решение.
Вычислим выборочную несмещенную дисперсию:
(D_в=frac{2{(10-14)}^2+1{(3-14)}^2+1{(11-14)}^2+3{(8-14)}^2+2{(6-14)}^2}9cdotfrac98=frac{398}8approx50.)
Теперь найдем среднеквадратическое отклонение:
(delta=sqrt{D_в}=sqrt{frac{398}8}=frac{sqrt{199}}2approx7.)
