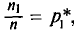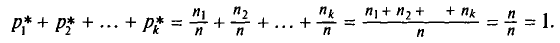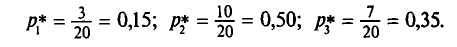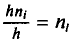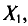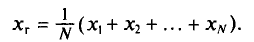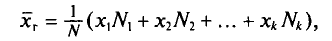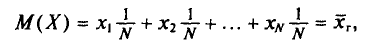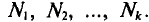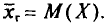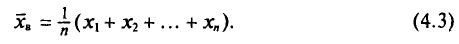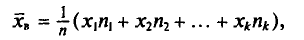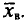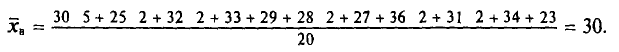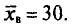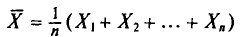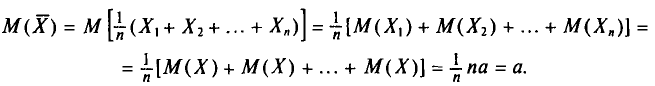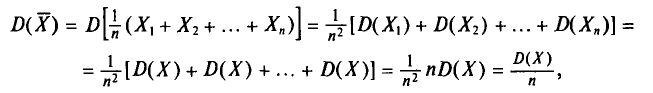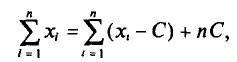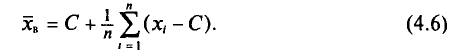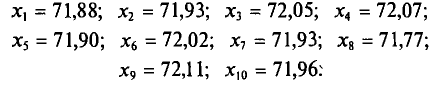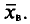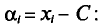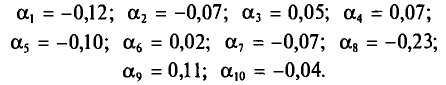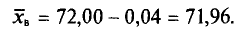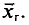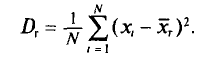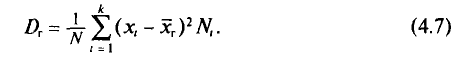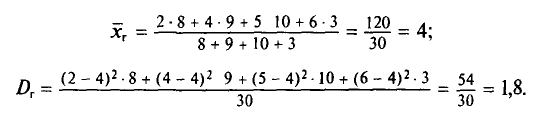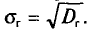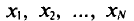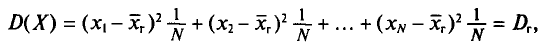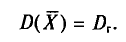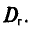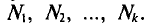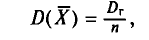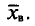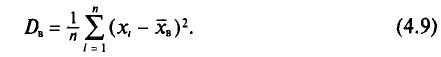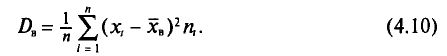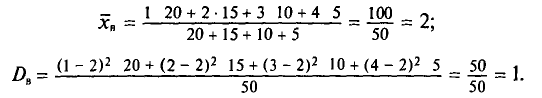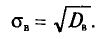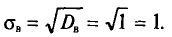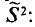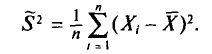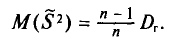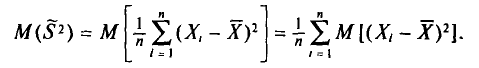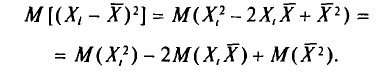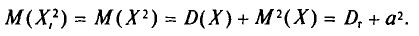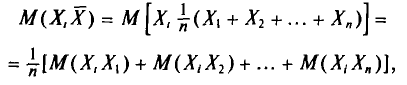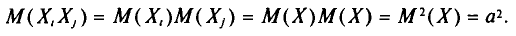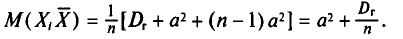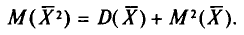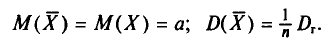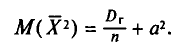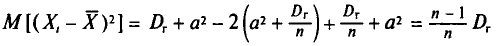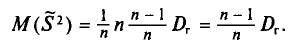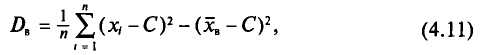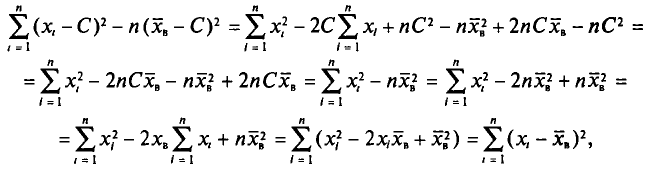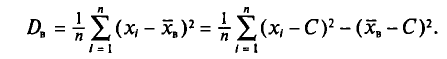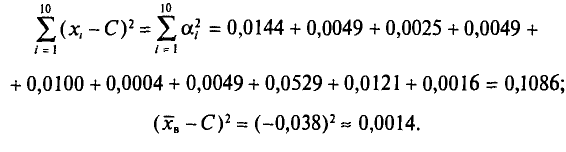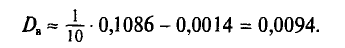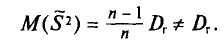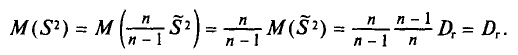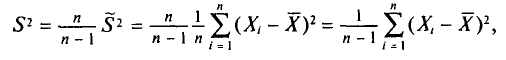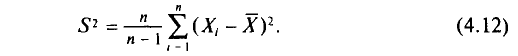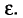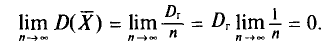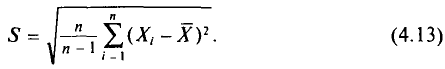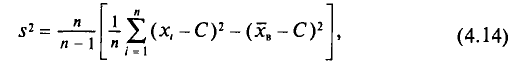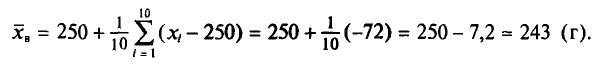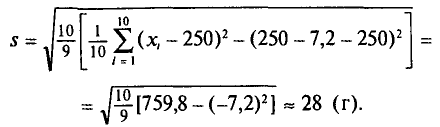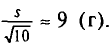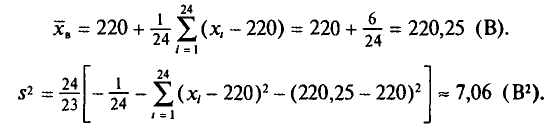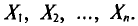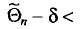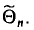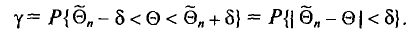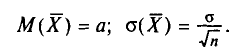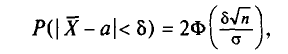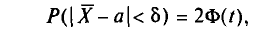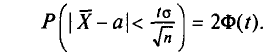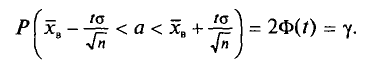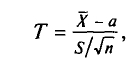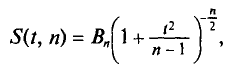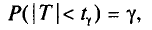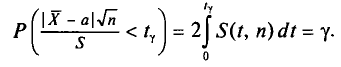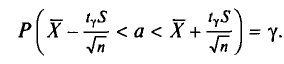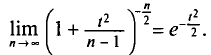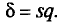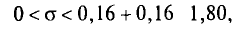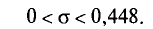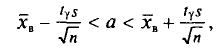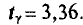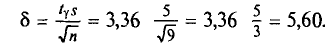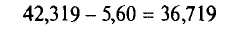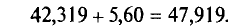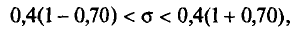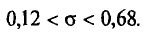Выборочная дисперсия, описание
Выборочная дисперсия является сводной характеристикой для наблюдения рассеяния количественного признака выборки вокруг среднего значения.
Определение
Выборочная дисперсия – это среднее арифметическое значений вариантов части отобранных объектов генеральной совокупности (выборки).
Связь выборочной и генеральной дисперсии
Генеральная дисперсия представляет собой среднее арифметическое квадратов отступлений значений признаков генеральной совокупности от их среднего значения.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Определение
Генеральная совокупность – это комплекс всех возможных объектов, относительно которых планируется вести наблюдение и формулировать выводы.
Выборочная совокупность или выборка является частью генеральной совокупности, выбранной для изучения и составления заключения касательной всей генеральной совокупности.
Как вычислить выборочную дисперсию
Выборочная дисперсия при различии всех значений варианта выборки находится по формуле:
({widehat D}_В=frac{displaystylesum_{i-1}^n{(x_i-{overline x}_В)}^2}n)
Для значений признаков выборочной совокупности с частотами n1, n2,…,nk формула выглядит следующим образом:
({widehat D}_В=frac{displaystylesum_{i-1}^kn_i{(x_i-{overline x}_В)}^2}n)
Квадратный корень из выборочной дисперсии характеризует рассеивание значений вариантов выборки вокруг своего среднего значения. Данная характеристика называется выборочным средним квадратическим отклонением и имеет вид:
({widehatsigma}_В=sqrt{{widehat D}_В})
Упрощенный способ вычисления выборочной или генеральной дисперсии производят по формуле:
(D=overline{x^2}-left[overline xright]^2)
Если вариационный ряд выборочной совокупности интервальный, то за xi принимается центр частичных интервалов.
Пример
Найти выборочную дисперсию выборки со значениями:
- xi: 1, 2, 3, 4;
- ni: 20, 15, 10, 5.
Решение
Для начала необходимо определить выборочную среднюю:
({overline x}_В=frac1{50}(1cdot20+2cdot15+3cdot10+4cdot5)=frac1{50}cdot100=2)
Затем найдем выборочную дисперсию:
(D_В=frac1{50}({(1-2)}^2cdot20+{(2-2)}^2cdot15+{(3-2)}^2cdot10+{(4-2)}^2cdot5)=1)
Исправленная дисперсия
Математически выборочная дисперсия не соответствует генеральной, поскольку выборочная используется для смещенного оценивания генеральной дисперсии. По этой причине математическое ожидание выборочной дисперсии вычисляется так:
(Mleft[D_Bright]=frac{n-1}nD_Г)
В данной формуле DГ – это истинное значение дисперсии генеральной совокупности.
Исправить выборочную дисперсию можно путем умножения ее на дробь:
(frac n{n-1})
Получим формулу следующего вида:
(S^2=frac n{n-1}cdot D_В=frac{displaystylesum_{i=1}^kn_i{(x_i-{overline x}_В)}^2}{n-1})
Исправленная дисперсия используется для несмещенной оценки генеральной дисперсии и обозначается S2.
Среднеквадратическая генеральная совокупность оценивается при помощи исправленного среднеквадратического отклонения, которое вычисляется по формуле:
(S=sqrt{S^2})
При нахождении выборочной и исправленной дисперсии разнятся лишь знаменатели в формулах. Различия в этих характеристиках при больших n незначительны. Применение исправленной дисперсии целесообразно при объеме выборки меньше 30.
Для чего применяют исправленную выборочную дисперсию
Исправленную выборочную используют для точечной оценки генеральной дисперсии.
Пример
Длину стержня измерили одним и тем же прибором пять раз. В результате получили следующие величины: 92 мм, 94 мм, 103 мм, 105 мм, 106 мм. Задача найти выборочную среднюю длину предмета и выборочную исправленную дисперсию ошибок измерительного прибора.
Решение
Сначала вычислим выборочную среднюю:
({overline x}_В=frac{92+94+103+105+106}5=100)
Затем найдем выборочную дисперсию:
(D_В=frac{displaystylesum_{i=1}^k{(x_i-{overline x}_В)}^2}n=frac{{(92-100)}^2+{(94-100)}^2+{(103-100)}^2+{(105-100)}^2+{(106-100)}^2}5=34)
Теперь рассчитаем исправленную дисперсию:
(S^2=frac5{5-1}cdot34=42,5)
Для того чтобы охарактеризовать
рассеяние наблюдаемых значений
количественного признака выборки вокруг
своего среднего значения ,
вводят сводную
характеристику – выборочную дисперсию.
Выборочной дисперсией
называют среднее
арифметическое квадратов отклонения
наблюдаемых значений признака от их
среднего значения .
Если все значения x1,
х2,
…, xn
признака выборки объема п
различны, то
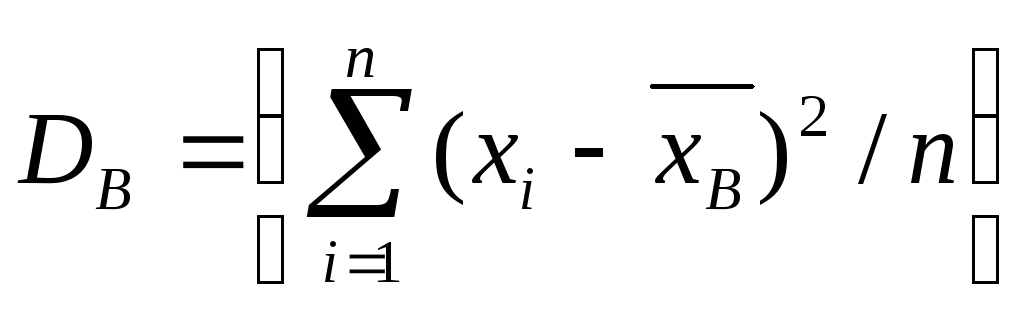
Если же значения признака
x1,
х2,
…, xk
имеют соответственно
частоты п1,
n2,…,
nk,
причем n1
+ n2+…+nk
= n, то
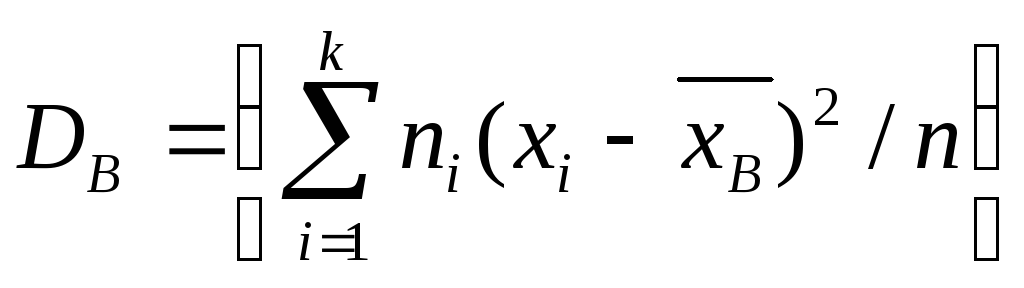
т.е. выборочная дисперсия есть средняя
взвешенная квадратов отклонений с
весами, равными соответствующим частотам.
Пример.
Выборочная
совокупность задана таблицей распределения
xi
1
2 3 4
ni
20 15
10
5
Найти выборочную
дисперсию.
Решение.
Найдем выборочную среднюю (см. § 4):
.
Найдем выборочную
дисперсию:
.
Кроме дисперсии для характеристики
рассеяния значений признака выборочной
совокупности вокруг своего среднего
значения пользуются сводной
характеристикой-средним квадратическим
отклонением.
Выборочным средним
квадратическим отклонением (стандартом)
называют квадратный
корень из выборочной дисперсии:
.
§ 10. Формула для вычисления дисперсии
Вычисление дисперсии, безразлично-выборочной
или генеральной, можно упростить,
используя следующую теорему.
Теорема. Дисперсия
равна среднему квадратов значений
признака минус квадрат общей средней:
.
Доказательство. Справедливость теоремы
вытекает из преобразований:
.
Итак,
,
где
,
.
Пример.
Найти
дисперсию по данному распределению
xi
1
2 3 4
ni
20
15
10
5
Решение.
Найдем
общую среднюю:
.
Найдем
среднюю квадратов
значений признака:
.
Искомая дисперсия
=5-22=1.
§11. Групповая, внутригрупповая, межгрупповая и общая дисперсии
Допустим, что все значения
количественного признака X
совокупности,
безразлично-генеральной или выборочной,
разбиты на k
групп. Рассматривая
каждую группу как самостоятельную
совокупность, можно найти групповую
среднюю (см. § 6) и дисперсию значений
признака, принадлежащих группе,
относительно групповой средней.
Групповой дисперсией называют
дисперсию значений признака, принадлежащих
группе, относительно групповой средней
,
где ni
–
частота значения
xi;
j –
номер группы;
– групповая средняя
группы j;
–
объем группыj.
Пример
1. Найти
групповые дисперсии совокупности,
состоящей из следующих двух групп:
|
первая группа |
вторая группа |
||||||
|
xi |
ni |
xi |
ni |
||||
|
2 |
1 |
3 |
2 |
||||
|
4 |
7 |
8 |
3 |
||||
|
5 |
2 |
||||||
|
|
|
Решение.
Найдем
групповые средние:
;
.
Найдем
искомые
групповые дисперсии:
;
.
Зная дисперсию каждой группы, можно
найти их среднюю арифметическую.
Внутригрупповой дисперсией называют
среднюю арифметическую дисперсий,
взвешенную по объемам групп:
,
где Nj
– объем группы
j;
п =–
объем всей совокупности.
Пример
2.
Найти
внутригрупповую дисперсию по данным
примера 1.
Решение.
Искомая внутригрупповая дисперсия
равна
Зная групповые средние и общую среднюю,
можно найти дисперсию групповых средних
относительно общей средней.
Межгрупповой дисперсией называют
дисперсию групповых средних относительно
общей средней:
,
где
–
групповая средняя группыj;
Nj
– объем группы j;
– общая средняя;
n
=–
объем всей совокупности.
Пример
3. Найти
межгрупповую дисперсию по
данным
примера 1.
Решение.
Найдем общую среднюю:
.
Используя
вычисленные выше величины
=
4,=
6, найдем искомую межгрупповую дисперсию:
.
Теперь целесообразно ввести специальный
термин для дисперсии всей совокупности.
Общей дисперсией называют дисперсию
значений признака всей совокупности
относительно общей средней:
,
где ni
– частота значения
xi
;
–
общая средняя; n
– объем всей совокупности.
Пример
4. Найти
общую дисперсию по данным примера 1.
Решение.
Найдем искомую общую дисперсию, учитывая,
что общая средняя равна 14/3:
Замечание.
Найденная общая дисперсия равна сумме
внутригрупповой и межгрупповой дисперсий:
Dобщ=
148/45;
Dвнгр
+ Dмежгр=
12/5 + 8/9= 148/45.
В следующем
параграфе будет доказано, что такая
закономерность справедлива для любой
совокупности.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Интервальный вариационный ряд и его характеристики
- Построение интервального вариационного ряда по данным эксперимента
- Гистограмма и полигон относительных частот, кумулята и эмпирическая функция распределения
- Выборочная средняя, мода и медиана. Симметрия ряда
- Выборочная дисперсия и СКО
- Исправленная выборочная дисперсия, стандартное отклонение выборки и коэффициент вариации
- Алгоритм исследования интервального вариационного ряда
- Примеры
п.1. Построение интервального вариационного ряда по данным эксперимента
Интервальный вариационный ряд – это ряд распределения, в котором однородные группы составлены по признаку, меняющемуся непрерывно или принимающему слишком много значений.
Общий вид интервального вариационного ряда
| Интервалы, (left.left[a_{i-1},a_iright.right)) | (left.left[a_{0},a_1right.right)) | (left.left[a_{1},a_2right.right)) | … | (left.left[a_{k-1},a_kright.right)) |
| Частоты, (f_i) | (f_1) | (f_2) | … | (f_k) |
Здесь k – число интервалов, на которые разбивается ряд.
Размах вариации – это длина интервала, в пределах которой изменяется исследуемый признак: $$ F=x_{max}-x_{min} $$
Правило Стерджеса
Эмпирическое правило определения оптимального количества интервалов k, на которые следует разбить ряд из N чисел: $$ k=1+lfloorlog_2 Nrfloor $$ или, через десятичный логарифм: $$ k=1+lfloor 3,322cdotlg Nrfloor $$
Скобка (lfloor rfloor) означает целую часть (округление вниз до целого числа).
Шаг интервального ряда – это отношение размаха вариации к количеству интервалов, округленное вверх до определенной точности: $$ h=leftlceilfrac Rkrightrceil $$
Скобка (lceil rceil) означает округление вверх, в данном случае не обязательно до целого числа.
Алгоритм построения интервального ряда
На входе: все значения признака (left{x_jright}, j=overline{1,N})
Шаг 1. Найти размах вариации (R=x_{max}-x_{min})
Шаг 2. Найти оптимальное количество интервалов (k=1+lfloorlog_2 Nrfloor)
Шаг 3. Найти шаг интервального ряда (h=leftlceilfrac{R}{k}rightrceil)
Шаг 4. Найти узлы ряда: $$ a_0=x_{min}, a_i=1_0+ih, i=overline{1,k} $$ Шаг 5. Найти частоты (f_i) – число попаданий значений признака в каждый из интервалов (left.left[a_{i-1},a_iright.right)).
На выходе: интервальный ряд с интервалами (left.left[a_{i-1},a_iright.right)) и частотами (f_i, i=overline{1,k})
Заметим, что поскольку шаг h находится с округлением вверх, последний узел (a_kgeq x_{max}).
Например:
Проведено 100 измерений роста учеников старших классов.
Минимальный рост составляет 142 см, максимальный – 197 см.
Найдем узлы для построения соответствующего интервального ряда.
По условию: (N=100, x_{min}=142 см, x_{max}=197 см).
Размах вариации: (R=197-142=55) (см)
Оптимальное число интервалов: (k=1+lfloor 3,322cdotlg 100rfloor=1+lfloor 6,644rfloor=1+6=7)
Шаг интервального ряда: (h=lceilfrac{55}{5}rceil=lceil 7,85rceil=8) (см)
Получаем узлы ряда: $$ a_0=x_{min}=142, a_i=142+icdot 8, i=overline{1,7} $$
| (left.left[a_{i-1},a_iright.right)) cм | (left.left[142;150right.right)) | (left.left[150;158right.right)) | (left.left[158;166right.right)) | (left.left[166;174right.right)) | (left.left[174;182right.right)) | (left.left[182;190right.right)) | (left[190;198right]) |
п.2. Гистограмма и полигон относительных частот, кумулята и эмпирическая функция распределения
Относительная частота интервала (left.left[a_{i-1},a_iright.right)) – это отношение частоты (f_i) к общему количеству исходов: $$ w_i=frac{f_i}{N}, i=overline{1,k} $$
Гистограмма относительных частот интервального ряда – это фигура, состоящая из прямоугольников, ширина которых равна шагу ряда, а высота – относительным частотам каждого из интервалов.
Площадь гистограммы равна 1 (с точностью до округлений), и она является эмпирическим законом распределения исследуемого признака.
Полигон относительных частот интервального ряда – это ломаная, соединяющая точки ((x_i,w_i)), где (x_i) – середины интервалов: (x_i=frac{a_{i-1}+a_i}{2}, i=overline{1,k}).
Накопленные относительные частоты – это суммы: $$ S_1=w_1, S_i=S_{i-1}+w_i, i=overline{2,k} $$ Ступенчатая кривая (F(x)), состоящая из прямоугольников, ширина которых равна шагу ряда, а высота – накопленным относительным частотам, является эмпирической функцией распределения исследуемого признака.
Кумулята – это ломаная, которая соединяет точки ((x_i,S_i)), где (x_i) – середины интервалов.
Например:
Продолжим анализ распределения учеников по росту.
Выше мы уже нашли узлы интервалов. Пусть, после распределения всех 100 измерений по этим интервалам, мы получили следующий интервальный ряд:
| i | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| (left.left[a_{i-1},a_iright.right)) cм | (left.left[142;150right.right)) | (left.left[150;158right.right)) | (left.left[158;166right.right)) | (left.left[166;174right.right)) | (left.left[174;182right.right)) | (left.left[182;190right.right)) | (left[190;198right]) |
| (f_i) | 4 | 7 | 11 | 34 | 33 | 8 | 3 |
Найдем середины интервалов, относительные частоты и накопленные относительные частоты:
| (x_i) | 146 | 154 | 162 | 170 | 178 | 186 | 194 |
| (w_i) | 0,04 | 0,07 | 0,11 | 0,34 | 0,33 | 0,08 | 0,03 |
| (S_i) | 0,04 | 0,11 | 0,22 | 0,56 | 0,89 | 0,97 | 1 |
Построим гистограмму и полигон:
Построим кумуляту и эмпирическую функцию распределения:
Эмпирическая функция распределения (относительно середин интервалов): $$ F(x)= begin{cases} 0, xleq 146\ 0,04, 146lt xleq 154\ 0,11, 154lt xleq 162\ 0,22, 162lt xleq 170\ 0,56, 170lt xleq 178\ 0,89, 178lt xleq 186\ 0,97, 186lt xleq 194\ 1, xgt 194 end{cases} $$
п.3. Выборочная средняя, мода и медиана. Симметрия ряда
Выборочная средняя интервального вариационного ряда определяется как средняя взвешенная по частотам: $$ X_{cp}=frac{x_1f_1+x_2f_2+…+x_kf_k}{N}=frac1Nsum_{i=1}^k x_if_i $$ где (x_i) – середины интервалов: (x_i=frac{a_{i-1}+a_i}{2}, i=overline{1,k}).
Или, через относительные частоты: $$ X_{cp}=sum_{i=1}^k x_iw_i $$
Модальным интервалом называют интервал с максимальной частотой: $$ f_m=max f_i $$ Мода интервального вариационного ряда определяется по формуле: $$ M_o=x_o+frac{f_m-f_{m-1}}{(f_m-f_{m-1})+(f_m+f_{m+1})}h $$ где
(h) – шаг интервального ряда;
(x_o) – нижняя граница модального интервала;
(f_m,f_{m-1},f_{m+1}) – соответственно, частоты модального интервала, интервала слева от модального и интервала справа.
Медианным интервалом называют первый интервал слева, на котором кумулята превысила значение 0,5. Медиана интервального вариационного ряда определяется по формуле: $$ M_e=x_o+frac{0,5-S_{me-1}}{w_{me}}h $$ где
(h) – шаг интервального ряда;
(x_o) – нижняя граница медианного интервала;
(S_{me-1}) накопленная относительная частота для интервала слева от медианного;
(w_{me}) относительная частота медианного интервала.
Расположение выборочной средней, моды и медианы в зависимости от симметрии ряда аналогично их расположению в дискретном ряду (см. §65 данного справочника).
Например:
Для распределения учеников по росту получаем:
| (x_i) | 146 | 154 | 162 | 170 | 178 | 186 | 194 | ∑ |
| (w_i) | 0,04 | 0,07 | 0,11 | 0,34 | 0,33 | 0,08 | 0,03 | 1 |
| (x_iw_i) | 5,84 | 10,78 | 17,82 | 57,80 | 58,74 | 14,88 | 5,82 | 171,68 |
$$ X_{cp}=sum_{i=1}^k x_iw_i=171,68approx 171,7 text{(см)} $$ На гистограмме (или полигоне) относительных частот максимальная частота приходится на 4й интервал [166;174). Это модальный интервал.
Данные для расчета моды: begin{gather*} x_o=166, f_m=34, f_{m-1}=11, f_{m+1}=33, h=8\ M_o=x_o+frac{f_m-f_{m-1}}{(f_m-f_{m-1})+(f_m+f_{m+1})}h=\ =166+frac{34-11}{(34-11)+(34-33)}cdot 8approx 173,7 text{(см)} end{gather*} На кумуляте значение 0,5 пересекается на 4м интервале. Это – медианный интервал.
Данные для расчета медианы: begin{gather*} x_o=166, w_m=0,34, S_{me-1}=0,22, h=8\ \ M_e=x_o+frac{0,5-S_{me-1}}{w_me}h=166+frac{0,5-0,22}{0,34}cdot 8approx 172,6 text{(см)} end{gather*} begin{gather*} \ X_{cp}=171,7; M_o=173,7; M_e=172,6\ X_{cp}lt M_elt M_o end{gather*} Ряд асимметричный с левосторонней асимметрией.
При этом (frac{|M_o-X_{cp}|}{|M_e-X_{cp}|}=frac{2,0}{0,9}approx 2,2lt 3), т.е. распределение умеренно асимметрично.
п.4. Выборочная дисперсия и СКО
Выборочная дисперсия интервального вариационного ряда определяется как средняя взвешенная для квадрата отклонения от средней: begin{gather*} D=frac1Nsum_{i=1}^k(x_i-X_{cp})^2 f_i=frac1Nsum_{i=1}^k x_i^2 f_i-X_{cp}^2 end{gather*} где (x_i) – середины интервалов: (x_i=frac{a_{i-1}+a_i}{2}, i=overline{1,k}).
Или, через относительные частоты: $$ D=sum_{i=1}^k(x_i-X_{cp})^2 w_i=sum_{i=1}^k x_i^2 w_i-X_{cp}^2 $$
Выборочное среднее квадратичное отклонение (СКО) определяется как корень квадратный из выборочной дисперсии: $$ sigma=sqrt{D} $$
Например:
Для распределения учеников по росту получаем:
| $x_i$ | 146 | 154 | 162 | 170 | 178 | 186 | 194 | ∑ |
| (w_i) | 0,04 | 0,07 | 0,11 | 0,34 | 0,33 | 0,08 | 0,03 | 1 |
| (x_iw_i) | 5,84 | 10,78 | 17,82 | 57,80 | 58,74 | 14,88 | 5,82 | 171,68 |
| (x_i^2w_i) – результат | 852,64 | 1660,12 | 2886,84 | 9826 | 10455,72 | 2767,68 | 1129,08 | 29578,08 |
$$ D=sum_{i=1}^k x_i^2 w_i-X_{cp}^2=29578,08-171,7^2approx 104,1 $$ $$ sigma=sqrt{D}approx 10,2 $$
п.5. Исправленная выборочная дисперсия, стандартное отклонение выборки и коэффициент вариации
Исправленная выборочная дисперсия интервального вариационного ряда определяется как: begin{gather*} S^2=frac{N}{N-1}D end{gather*}
Стандартное отклонение выборки определяется как корень квадратный из исправленной выборочной дисперсии: $$ s=sqrt{S^2} $$
Коэффициент вариации это отношение стандартного отклонения выборки к выборочной средней, выраженное в процентах: $$ V=frac{s}{X_{cp}}cdot 100text{%} $$
Подробней о том, почему и когда нужно «исправлять» дисперсию, и для чего использовать коэффициент вариации – см. §65 данного справочника.
Например:
Для распределения учеников по росту получаем: begin{gather*} S^2=frac{100}{99}cdot 104,1approx 105,1\ sapprox 10,3 end{gather*} Коэффициент вариации: $$ V=frac{10,3}{171,7}cdot 100text{%}approx 6,0text{%}lt 33text{%} $$ Выборка однородна. Найденное значение среднего роста (X_{cp})=171,7 см можно распространить на всю генеральную совокупность (старшеклассников из других школ).
п.6. Алгоритм исследования интервального вариационного ряда
На входе: все значения признака (left{x_jright}, j=overline{1,N})
Шаг 1. Построить интервальный ряд с интервалами (left.right[a_{i-1}, a_ileft.right)) и частотами (f_i, i=overline{1,k}) (см. алгоритм выше).
Шаг 2. Составить расчетную таблицу. Найти (x_i,w_i,S_i,x_iw_i,x_i^2w_i)
Шаг 3. Построить гистограмму (и/или полигон) относительных частот, эмпирическую функцию распределения (и/или кумуляту). Записать эмпирическую функцию распределения.
Шаг 4. Найти выборочную среднюю, моду и медиану. Проанализировать симметрию распределения.
Шаг 5. Найти выборочную дисперсию и СКО.
Шаг 6. Найти исправленную выборочную дисперсию, стандартное отклонение и коэффициент вариации. Сделать вывод об однородности выборки.
п.7. Примеры
Пример 1. При изучении возраста пользователей коворкинга выбрали 30 человек.
Получили следующий набор данных:
18,38,28,29,26,38,34,22,28,30,22,23,35,33,27,24,30,32,28,25,29,26,31,24,29,27,32,24,29,29
Постройте интервальный ряд и исследуйте его.
1) Построим интервальный ряд. В наборе данных: $$ x_{min}=18, x_{max}=38, N=30 $$ Размах вариации: (R=38-18=20)
Оптимальное число интервалов: (k=1+lfloorlog_2 30rfloor=1+4=5)
Шаг интервального ряда: (h=lceilfrac{20}{5}rceil=4)
Получаем узлы ряда: $$ a_0=x_{min}=18, a_i=18+icdot 4, i=overline{1,5} $$
| (left.left[a_{i-1},a_iright.right)) лет | (left.left[18;22right.right)) | (left.left[22;26right.right)) | (left.left[26;30right.right)) | (left.left[30;34right.right)) | (left.left[34;38right.right)) |
Считаем частоты для каждого интервала. Получаем интервальный ряд:
| (left.left[a_{i-1},a_iright.right)) лет | (left.left[18;22right.right)) | (left.left[22;26right.right)) | (left.left[26;30right.right)) | (left.left[30;34right.right)) | (left.left[34;38right.right)) |
| (f_i) | 1 | 7 | 12 | 6 | 4 |
2) Составляем расчетную таблицу:
| (x_i) | 20 | 24 | 28 | 32 | 36 | ∑ |
| (f_i) | 1 | 7 | 12 | 6 | 4 | 30 |
| (w_i) | 0,033 | 0,233 | 0,4 | 0,2 | 0,133 | 1 |
| (S_i) | 0,033 | 0,267 | 0,667 | 0,867 | 1 | – |
| (x_iw_i) | 0,667 | 5,6 | 11,2 | 6,4 | 4,8 | 28,67 |
| (x_i^2w_i) | 13,333 | 134,4 | 313,6 | 204,8 | 172,8 | 838,93 |
3) Строим полигон и кумуляту
Эмпирическая функция распределения: $$ F(x)= begin{cases} 0, xleq 20\ 0,033, 20lt xleq 24\ 0,267, 24lt xleq 28\ 0,667, 28lt xleq 32\ 0,867, 32lt xleq 36\ 1, xgt 36 end{cases} $$ 4) Находим выборочную среднюю, моду и медиану $$ X_{cp}=sum_{i=1}^k x_iw_iapprox 28,7 text{(лет)} $$ На полигоне модальным является 3й интервал (самая высокая точка).
Данные для расчета моды: begin{gather*} x_0=26, f_m=12, f_{m-1}=7, f_{m+1}=6, h=4\ M_o=x_o+frac{f_m-f_{m-1}}{(f_m-f_{m-1})+(f_m+f_{m+1})}h=\ =26+frac{12-7}{(12-7)+(12-6)}cdot 4approx 27,8 text{(лет)} end{gather*}
На кумуляте медианным является 3й интервал (преодолевает уровень 0,5).
Данные для расчета медианы: begin{gather*} x_0=26, w_m=0,4, S_{me-1}=0,267, h=4\ M_e=x_o+frac{0,5-S_{me-1}}{w_{me}}h=26+frac{0,5-0,4}{0,267}cdot 4approx 28,3 text{(лет)} end{gather*} Получаем: begin{gather*} X_{cp}=28,7; M_o=27,8; M_e=28,6\ X_{cp}gt M_egt M_0 end{gather*} Ряд асимметричный с правосторонней асимметрией.
При этом (frac{|M_o-X_{cp}|}{|M_e-X_{cp}|} =frac{0,9}{0,1}=9gt 3), т.е. распределение сильно асимметрично.
5) Находим выборочную дисперсию и СКО: begin{gather*} D=sum_{i=1}^k x_i^2w_i-X_{cp}^2=838,93-28,7^2approx 17,2\ sigma=sqrt{D}approx 4,1 end{gather*}
6) Исправленная выборочная дисперсия: $$ S^2=frac{N}{N-1}D=frac{30}{29}cdot 17,2approx 17,7 $$ Стандартное отклонение (s=sqrt{S^2}approx 4,2)
Коэффициент вариации: (V=frac{4,2}{28,7}cdot 100text{%}approx 14,7text{%}lt 33text{%})
Выборка однородна. Найденное значение среднего возраста (X_{cp}=28,7) лет можно распространить на всю генеральную совокупность (пользователей коворкинга).
Евгений Николаевич Беляев
Эксперт по предмету «Математика»
Задать вопрос автору статьи
Генеральная дисперсия
Пусть нам дана генеральная совокупность относительно случайной величины $X$. Для начала напомним следующее определение:
Определение 1
Генеральная совокупность — совокупность случайно отобранных объектов данного вида, над которыми проводят наблюдения с целью получения конкретных значений случайной величины, проводимых в неизменных условиях при изучении одной случайной величины данного вида.
Определение 2
Генеральная дисперсия — среднее арифметическое квадратов отклонений значений вариант генеральной совокупности от их среднего значения.
Пусть значения вариант $x_1, x_2,dots ,x_k$ имеют, соответственно, частоты $n_1, n_2,dots ,n_k$. Тогда генеральная дисперсия вычисляется по формуле:
Сдай на права пока
учишься в ВУЗе
Вся теория в удобном приложении. Выбери инструктора и начни заниматься!
Получить скидку 3 000 ₽
Рассмотрим частный случай. Пусть все варианты $x_1, x_2,dots ,x_k$ различны. В этом случае $n_1, n_2,dots ,n_k=1$. Получаем, что в этом случае генеральная дисперсия вычисляется по формуле:
С этим понятием также связано понятие генерального среднего квадратического отклонения.
Определение 3
Генеральное среднее квадратическое отклонение — квадратный корень из генеральной дисперсии:
[{sigma }_г=sqrt{D_г}]
Выборочная дисперсия
Пусть нам дана выборочная совокупность относительно случайной величины $X$. Для начала напомним следующее определение:
Определение 4
Выборочная совокупность — часть отобранных объектов из генеральной совокупности.
Определение 5
Выборочная дисперсия — среднее арифметическое значений вариант выборочной совокупности.
«Дисперсия: генеральная, выборочная, исправленная» 👇
Пусть значения вариант $x_1, x_2,dots ,x_k$ имеют, соответственно, частоты $n_1, n_2,dots ,n_k$. Тогда выборочная дисперсия вычисляется по формуле:
Рассмотрим частный случай. Пусть все варианты $x_1, x_2,dots ,x_k$ различны. В этом случае $n_1, n_2,dots ,n_k=1$. Получаем, что в этом случае выборочная дисперсия вычисляется по формуле:
С этим понятием также связано понятие выборочного среднего квадратического отклонения.
Определение 6
Выборочное среднее квадратическое отклонение — квадратный корень из генеральной дисперсии:
[{sigma }_в=sqrt{D_в}]
Исправленная дисперсия
Для нахождения исправленной дисперсии $S^2$ необходимо умножить выборочную дисперсию на дробь $frac{n}{n-1}$, то есть
С этим понятием также связано понятие исправленного среднего квадратического отклонения, которое находится по формуле:
!!! В случае, когда значение вариант не являются дискретными, а представляют из себя интервалы, то в формулах для вычисления генеральной или выборочной дисперсий за значение $x_i$ принимается значение середины интервала, которому принадлежит $x_i.$
Пример задачи на нахождение дисперсии и среднего квадратического отклонения
Пример 1
Выборочная совокупность задана следующей таблицей распределения:
Рисунок 1.
Найдем для нее выборочную дисперсию, выборочное среднее квадратическое отклонение, исправленную дисперсию и исправленное среднее квадратическое отклонение.
Решение:
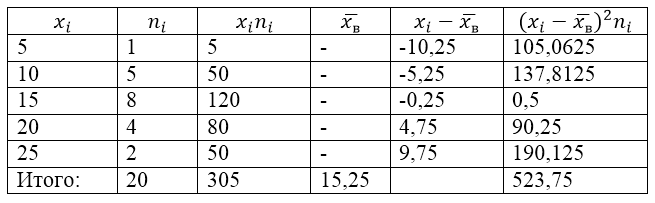
Для решения этой задачи для начала сделаем расчетную таблицу:
Рисунок 2.
Величина $overline{x_в}$ (среднее выборочное) в таблице находится по формуле:
[overline{x_в}=frac{sumlimits^k_{i=1}{x_in_i}}{n}]
То есть
[overline{x_в}=frac{sumlimits^k_{i=1}{x_in_i}}{n}=frac{305}{20}=15,25]
Найдем выборочную дисперсию по формуле:
[D_в=frac{sumlimits^k_{i=1}{{{(x}_i-overline{x_в})}^2n_i}}{n}=frac{523,75}{20}=26,1875]
Выборочное среднее квадратическое отклонение:
[{sigma }_в=sqrt{D_в}approx 5,12]
Исправленная дисперсия:
[{S^2=frac{n}{n-1}D}_в=frac{20}{19}cdot 26,1875approx 27,57]
Исправленное среднее квадратическое отклонение:
[S=sqrt{S^2}approx 5,25]
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме
Приступим к изучению элементов математической статистики, в которой разрабатываются научно обоснованные методы сбора статистических данных и их обработки.
Пусть требуется изучить множество однородных объектов (это множество называют статистической совокупностью) относительно некоторого качественного или количественного признака, характеризующего эти объекты. Например, если имеется партия деталей, то качественным признаком может служить соответствие детали стандартам, а количественным — контролируемый размер детали.
Лучше всего осуществить сплошное обследование, т. е. изучить каждый объект. Однако в большинстве случаев по разным причинам это сделать невозможно. Препятствовать сплошному обследованию может большое число объектов, их недоступность и т. п. Если, например, нужно знать среднюю глубину воронки при взрыве снаряда из опытной партии, то, проводя сплошное обследование, мы должны будем уничтожить всю партию.
Если сплошное обследование невозможно, то из всей совокупности выбирают для изучения часть объектов.
Статистическая совокупность, из которой отбирают часть объектов, называется генеральной совокупностью. Множество объектов, случайно отобранных из генеральной совокупности, называется выборкой.
Число объектов генеральной совокупности и выборки называется соответственно объемом генеральной совокупности и объемом выборки.
Пример. Плоды одного дерева (200 шт.) обследуют на наличие специфического для данного сорта вкуса. Для этого отбирают 10 шт. Здесь 200 —объем генеральной совокупности, а 10 —объем выборки.
Если выборку отбирают по одному объекту, который обследуют и снова возвращают в генеральную совокупность, то выборка называется повторной. Если объекты выборки уже не возвращаются в генеральную совокупность, то выборка называется бесповторной. На практике чаще используется бесповторная выборка. Если объем выборки составляет небольшую долю объема генеральной совокупности, то разница между повторной и бесповторной выборками незначительна
Свойства объектов выборки должны правильно отражать свойства объектов генеральной совокупности, или, как говорят, выборка должна быть репрезентативной (представительной). Считается, что выборка репрезентативна, если все объекты генеральной совокупности имеют одинаковую вероятность попасть в выборку, т. е. выбор осуществляется случайно. Например, для того чтобы оценить будущий урожай, можно сделать выборку из генеральной совокупности еще не созревших плодов и исследовать их характеристики (массу, качество и пр.). Если вся выборка будет взята с одного дерева, то она не будет репрезентативной. Репрезентативная выборка должна состоять из случайно выбранных плодов со случайно выбранных деревьев.
Статистическое распределение выборки. Полигон. Гистограмма
Пусть из генеральной совокупности извлечена выборка, причем 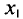
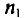
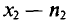
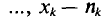
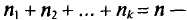
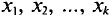
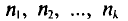
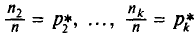
Статистическим распределением выборки называют перечень вариант и соответствующих им частот или относительных частот. Статистическое распределение можно задать также в виде последовательности интервалов и соответствующих им частот (непрерывное распределение). В качестве частоты, соответствующей интервалу, принимают сумму частот вариант, попавших в этот интервал.
Заметим, что в теории вероятностей под распределением понимают соответствие между возможными значениями случайной величины и их вероятностями, а в математической статистике — соответствие между наблюдаемыми вариантами и их частотами или относительными частотами.
Пример:
Перейдем от частот к относительным частотам в следующем распределении выборки объема n = 20:
Найдем относительные частоты:
Поэтому получаем следующее распределение:
Для графического изображения статистического распределения используются полигоны и гистограммы.
Для построения полигона в декартовых координатах на оси Ох откладывают значения вариант 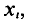
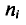
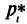
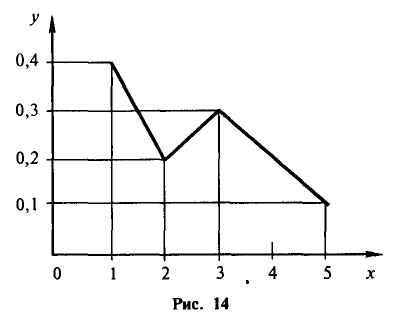
Пример:
Рис. 14 представляет собой полигон следующего распределения:
Полигоном обычно пользуются в случае небольшого количества вариант. В случае большого количества вариант и в случае непрерывного распределения признака чаще строят гистограммы. Для этого интервал, в котором заключены все наблюдаемые значения признака, разбивают на несколько частичных интервалов шириной h и находят для каждого частичного интервала 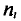
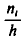
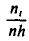
(или 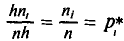
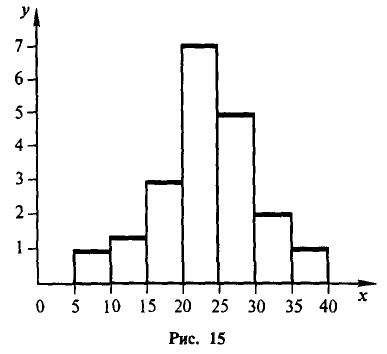
Пример:
Рис. 15 показывает гистограмму непрерывного распределения объема n =100, заданного следующей таблицей:
Оценки параметров генеральной совокупности по ее выборке
Выборка как набор случайных величин
Пусть имеется некоторая генеральная совокупность, каждый объект которой наделен количественным признаком X. При случайном извлечении объекта из генеральной совокупности становится известным значение х признака X этого объекта. Таким образом, мы можем рассматривать извлечение объекта из генеральной совокупности как испытание, X—как случайную величину, а х —как одно из возможных значений X.
Допустим, что из теоретических соображений удалось установить, к какому типу распределений относится признак X. Естественно, возникает задача оценки (приближенного определения) параметров, которыми описывается это распределение. Например, если известно, что изучаемый признак распределен в генеральной совокупности нормально, то необходимо оценить, т. е. приближенно найти математическое ожидание и среднее квадратическое отклонение, так как эти два параметра полностью определяют нормальное распределение.
Обычно в распоряжении исследователя имеются лишь данные выборки генеральной совокупности, например значения количественного признака 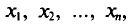
Опытные значения признака X можно рассматривать и как значения разных случайных величин 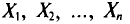
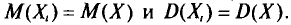
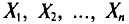
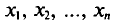
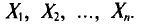
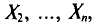
Генеральная и выборочная средние. Методы их расчета
Пусть изучается дискретная генеральная совокупность объема N относительно количественного признака X.
Определение:
Генеральной средней 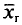
Если все значения 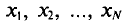
Если же значения признака 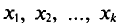
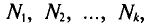

или
Как уже отмечалось (п. 1), извлечение объекта из генеральной совокупности есть наблюдение случайной величины X.
Пусть все значения 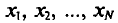
т. е.
Такой же итог следует, если значения 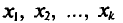
В случае непрерывного распределения признака X по определению полагают
Пусть для изучения генеральной совокупности относительно количественного признака X произведена выборка объема n.
Определение:
Выборочной средней 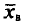
Если все значения 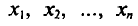
Если же значения признака 
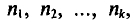

или
Пример:
Выборочным путем были получены следующие данные о массе 20 морских свинок при рождении (в г): 30, 30, 25, 32, 30, 25, 33, 32, 29, 28^27, 36, 31, 34, 30, 23, 28, 31, 36, 30. Найдем выборочную среднюю
Согласно формуле (4.4), имеем:
Итак,
Далее, не уменьшая общности рассуждений, будем считать значения 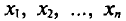
Разумеется, выборочная средняя для различных выборок того же объема n из той же генеральной совокупности будет получаться, вообще говоря, различной. И это не удивительно — ведь извлечение і-го по счету объекта есть наблюдение случайной величины 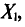
есть тоже случайная величина.
Таким образом, всевозможные получающиеся выборочные средние есть возможные значения случайной величины 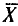
Найдем 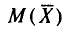
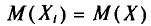
С учетом свойств математического ожидания (см. гл. II) получаем:
Итак, 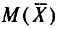
Теперь найдем 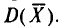
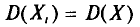
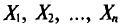
T. e.
Наконец, отметим, что если варианты 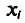
Так как
то формулу (4.3) можно преобразовать к виду
За константу С (так называемый ложный нуль) берут некоторое среднее значение между наименьшим и наибольшим значениями х, (і- 1, 2, …, n).
Пример:
Имеется выборка:
Требуется найти
Возьмем С =72,00 и вычислим разности
Их сумма: 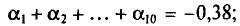
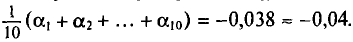
Генеральная и выборочная дисперсии
Для того чтобы охарактеризовать рассеяние значений количественного признака X генеральной совокупности вокруг своего среднего значения, вводят следующую характеристику — генеральную дисперсию.
Определение:
Генеральной дисперсией D, называется среднее арифметическое квадратов отклонений значений признака X генеральной совокупности от генеральной средней
Если все значения 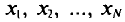
Если же значения признака 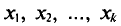
частоты 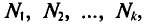

Пример:
Генеральная совокупность задана таблицей распределения:
Найдем генеральную дисперсию.
Согласно формулам (4.1) и (4.7), имеем:
Генеральным средним квадратическим отклонением (стандартом) называется
Пусть все значения 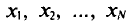
Найдем дисперсию признака X, рассматриваемого как случайная величина:
Так как 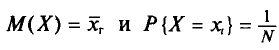
т. е.
Таким образом, дисперсия D(X) равна
Такой же итог можно получить, если значения 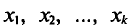
В случае непрерывного распределения признака X по определению полагают
С учетом формулы (4.8) формула (4.5) (п. 2) перепишется в виде
откуда 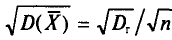
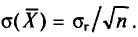
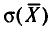
Для того чтобы охарактеризовать рассеяние наблюдаемых значений количественного признака выборки вокруг своего среднего значения 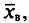
Определение:
Выборочной дисперсией 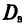
Если все значения 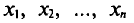
Если же значения признака 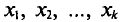
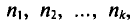
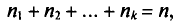
Пример:
Пусть выборочная совокупность задана таблицей распределения:
Найдем выборочную дисперсию. Согласно формулам (4.4) и (4.10), имеем:
Выборочным средним квадратическим отклонением (стандартом) называется квадратный корень из выборочной дисперсии:
В условиях примера 2 получаем, что
Далее, не уменьшая общности рассуждений, будем считать значения 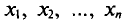
Выборочную дисперсию, рассматриваемую нами как случайная величина, будем обозначать
Теорема:
Математическое ожидание выборочной дисперсии равно 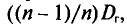
Доказательство:
С учетом свойств математического ожидания (см. гл. II) получаем
Вычислим одно слагаемое 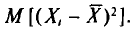
Вычислим по отдельности эти математические ожидания.
Согласно свойству I дисперсии (см. гл. И) и формулам (4.2), (4.8) имеем
Далее, с учетом свойства 4 математического ожидания (см. гл. II)
но слагаемое этой суммы, у которого второй индекс равен і, т.е. 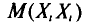
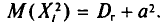
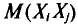
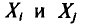
Так как имеется n-1 таких слагаемых, то
В силу свойства 1 дисперсии (см. гл. П) получаем
Нами уже найден (см. пп. 2 и 3):
Поэтому
Таким образом,
и не зависит от индекса суммирования і. Поэтому
Что и требовалось доказать.
В заключение этого пункта отметим, что если варианты 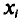
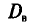
где С—ложный нуль.
Действительно, с учетом формулы (4.3) имеем
откуда
Пример:
Для выборки, указанной в примере 2 из п. 2, найдем 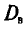
Наконец, согласно формуле (4.11)
Оценки параметров распределения
Одной из задач статистики является оценка параметров распределения случайной величины X по данным выборки. При этом в теоретических рассуждениях считают, что генеральная совокупность бесконечна. Это делается для того, чтобы можно было переходить к пределу при 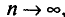
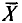
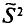
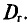
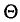
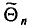
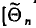
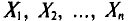
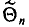
Несмещенной называют оценку 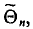
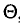
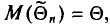
Пример:
Оценка 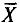
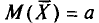
Пример:
Оценка 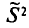
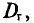
Пример:
Наряду с выборочной дисперсией 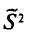
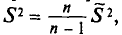
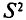
Таким образом, оценка 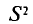
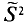
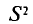
T. e.
Естественно в качестве приближенного неизвестного параметра брать несмещенные оценки для того, чтобы не делать систематической ошибки в сторону завышения или занижения.
Состоятельной называют такую оценку 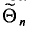
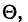
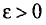
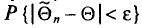
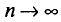
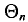
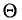
Очевидно, такому требованию должна удовлетворять всякая оценка, пригодная для практического использования.
Заметим, что несмещенная оценка 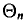
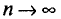
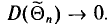
Пример:
Как было установлено (см. п. 3), 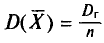
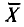
Можно показать, что несмещенная оценка 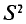
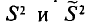
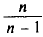
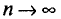
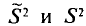
Для оценки генерального среднего квадратического отклонения используют исправленное среднее квадратическое отклонение, которое равно квадратному корню из исправленной дисперсии:
Левые части формул (4.12), (4.13), в которых случайные величины 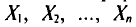
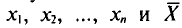
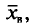
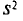
Отметим, что если варианты 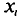
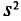
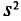
где С—ложный нуль.
Оценки, обладающие свойствами несмещенности и состоятельности, при ограниченном числе опытов могут отличаться дисперсиями.
Ясно, что чем меньше дисперсия оценки, тем меньше вероятность грубой ошибки при определении приближенного значения параметра. Поэтому необходимо, чтобы дисперсия оценки была минимальной. Оценка, обладающая таким свойством, называется эффективной.
Из отмеченных требований, предъявляемых к оценке, наиболее важными являются требования несмещенности и состоятельности.
Пример:
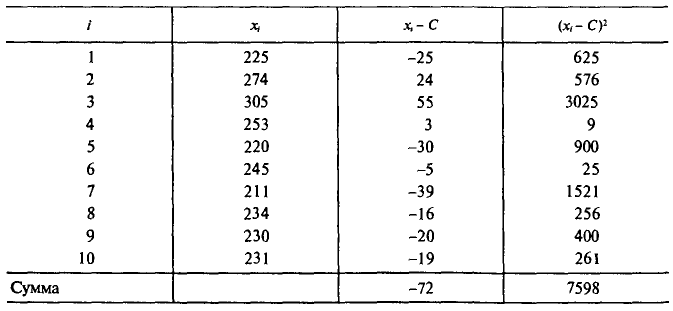
С плодового дерева случайным образом отобрано 10 плодов. Их массы 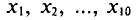
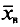
Следовательно,
Отсюда
Итак, оценка генеральной средней массы плода равна 243 г со средней квадратической ошибкой 9 г.
Оценка генерального среднего квадратического отклонения массы плода равна 28 г.
Пример:
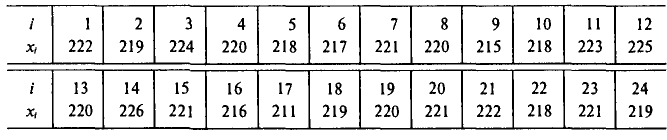
Через каждый час измерялось напряжение в электросети. Результаты измерений (в вольтах) представлены в следующей таблице:
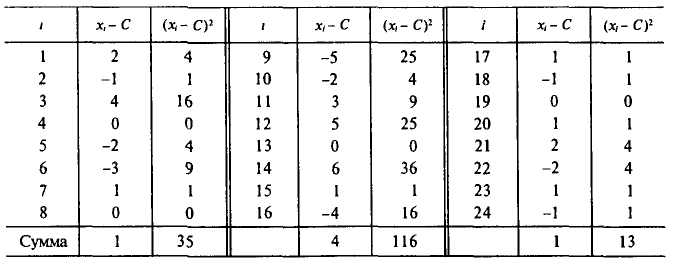
Найти оценки для математического ожидания и дисперсии результатов измерений. Оценки для математического ожидания и дисперсии найдем по формулам (6) и (14), положив С=220. Все необходимые вычисления приведены в нижеследующей таблице:
Следовательно,
Доверительные интервалы для параметров нормального распределения
Пусть 

Если известно, что оценка 


Если же о распределении имеется какая-либо информация, то можно сделать больше.
Здесь речь будет идти об оценке параметров а и 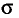
Пусть 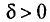
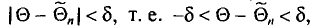
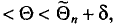
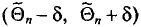


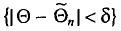
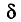
Определение:
Надежностью (доверительной вероятностью) оценки 

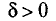

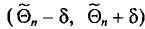

Заметим, что после того, как по данным выборки вычислена оценка 
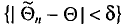
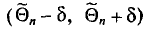




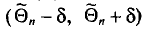

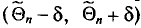


Иными словами, 
Ясно, что, чем меньше число 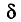

Определение:
Доверительным интервалом называется найденный по данным выборки интервал 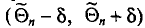


Надежность 
Конечно, нельзя категорически утверждать, что найденный доверительный интервал покрывает параметр 




Доверительный интервал для математического ожидания при известном
Доверительный интервал для математического ожидания при известном
В некоторых случаях среднее квадратическое отклонение о ошибки измерения (а вместе с нею и самого измерения) бывает известно. Например, если измерения осуществляются одним и тем же прибором при одних и тех же условиях.
Итак, пусть случайная величина X распределена нормально с параметрами а и 


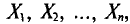

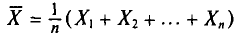
Потребуем, чтобы выполнялось соотношение 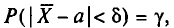

или
где
Найдя из равенства (4.15) 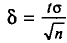
Так как Р задана и равна 
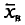
Смысл полученного соотношения таков: с надежностью у можно утверждать, что доверительный интервал 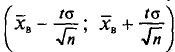
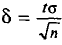
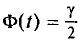
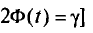
Как уже упоминалось, надежность 
Пример:
Признак X распределен в генеральной совокупности нормально с известным 

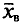
Для 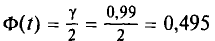
t=2,58. Следовательно, 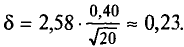
Доверительный интервал для математического ожидания при неизвестном
Доверительный интервал для математического ожидания при неизвестном 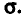
Пусть случайная величина X имеет нормальное распределение с неизвестными нам параметрами а и 
где n —объем выборки; 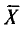

Плотность вероятности распределения Стьюдента дается формулой
где коэффициент 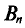
Потребуем, чтобы выполнялось соотношение
где 
Так как S(t, n) — четная функция от t, то, пользуясь формулой
(2.15) (см. § 2.5), получим
Отсюда
Следовательно, приходим к утверждению: с надежностью 
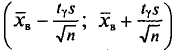
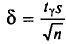
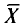
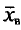
В приложении 4 приведена таблица значений 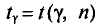
Заметим, что при 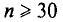
(см. § 2.7, п. 2). Это связано с тем, что
Пример. Признак X распределен в генеральной совокупности нормально. Найдем доверительный интервал для 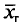

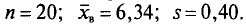

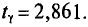
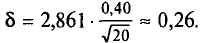
= 6,08 и 6,34 + 0,26 = 6,60. Итак, доверительный интервал (6,08; 6,60) покрывает 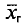
Доверительный интервал для среднего квадратического отклонения
Для нахождения доверительного интервала для среднего квадратического отклонения 
С надежностью 
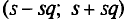

В приложении 5 приведена таблица значений 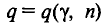

Пример:
Признак X распределен в генеральной совокупности нормально. Найдем доверительный интервал для 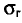

Для надежности 
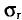
Пример:
На ферме испытывалось влияние витаминов на прибавку в массе телят. С этой целью было осмотрено 20 телят одного возраста. Средняя масса их оказалась равной 340 кг, а «исправленное» среднее квадратическое отклонение — 20 кг.
Определим: 1) доверительный интервал для математического ожидания а с надежностью 0,95; 2) доверительный интервал для среднего квадратического отклонения с той же надежностью.
При решении задачи будем исходить из предположения, что данные пробы взяты из нормальной генеральной совокупности.
Решение:
1) Согласно условиям задачи, 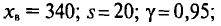
Пользуясь распределением Стьюдента, для надежности у=0,95 и n = 20 находим в таблице приложения 4 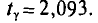
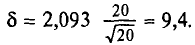
= 330,6 и 340 + 9,4 = 349,4. Итак, доверительный интервал (330,6; 349,4) покрывает а с надежностью 0,95.
Можно считать, что в данном случае истинная масса измерена 9 4 достаточно точно (отклонение порядка 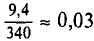
2) Для надежности у =0,95 и n = 20 находим в таблице приложения 5 q = 0,37. Далее, sq = 20 * 0,37 = 7,4. Границы доверительного интервала 20 — 7,4 = 12,6 и 20 + 7,4 = 27,4. Таким образом, 12,6 < 

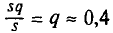
Примечание. Выше предполагалось, что q<1. Если q> 1, то, учитывая, что 

Пример:
Признак X генеральной совокупности распределен нормально. По выборке объема n = 10 найдено «исправленное» среднее квадратическое отклонение s = 0,16. Найдем доверительный интервал для 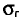
Для надежности у = 0,999 и n= 10 по таблице приложения 5 находим q=1,80.
Следовательно, искомый доверительный интервал таков’
или
Оценка истинного значения измеряемой величины
Пусть проводится n независимых равноточных измерений* некоторой физической величины, истинное значение а которой неизвестно. Будем рассматривать результаты отдельных измерений как случайные величины 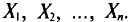
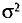

Пример:
По данным девяти независимых равноточных измерений физической величины найдены среднее арифметическое результатов отдельных измерений 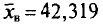
Истинное значение измеряемой величины равно ее математическому ожиданию. Поэтому задача сводится к оценке математического ожидания (при неизвестном 
покрывающего а с заданной надежностью у=0,99.
Пользуясь таблицей приложения 4 по у=0,99 и n = 9, находим
Найдем точность оценки:
Границы доверительного интервала
и
Итак, с надежностью у=0,99 истинное значение измеренной величины а заключено в доверительном интервале 36,719<а< 47,919.
Оценка точности измерений
В теории ошибок принято точность измерений (точность прибора) характеризовать с помощью среднего квадратического отклонения 

Пример:
По 16 независимым равноточным измерениям найдено «исправленное» среднее квадратическое отклонение s=0,4. Найдем точность измерений с надежностью у = 0,99.
Как отмечено выше, точность измерений характеризуется средним квадратическим отклонением о случайных ошибок измерений. Поэтому задача сводится к отысканию доверительного интервала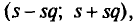

или
Решение заданий и задач по предметам:
- Теория вероятностей
- Математическая статистика
Дополнительные лекции по теории вероятностей:
- Случайные события и их вероятности
- Случайные величины
- Функции случайных величин
- Числовые характеристики случайных величин
- Законы больших чисел
- Статистические оценки
- Статистическая проверка гипотез
- Статистическое исследование зависимостей
- Теории игр
- Вероятность события
- Теорема умножения вероятностей
- Формула полной вероятности
- Теорема о повторении опытов
- Нормальный закон распределения
- Определение законов распределения случайных величин на основе опытных данных
- Системы случайных величин
- Нормальный закон распределения для системы случайных величин
- Вероятностное пространство
- Классическое определение вероятности
- Геометрическая вероятность
- Условная вероятность
- Схема Бернулли
- Многомерные случайные величины
- Предельные теоремы теории вероятностей
- Оценки неизвестных параметров