Как найти выборочную дисперсию случайной величины - Сайт, где вы сможете решить свои вопросы

Выборочная дисперсия, описание

Выборочная дисперсия является сводной характеристикой для наблюдения рассеяния количественного признака выборки вокруг среднего значения.

Определение

Выборочная дисперсия – это среднее арифметическое значений вариантов части отобранных объектов генеральной совокупности (выборки).

Связь выборочной и генеральной дисперсии

Генеральная дисперсия представляет собой среднее арифметическое квадратов отступлений значений признаков генеральной совокупности от их среднего значения.

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.

Определение

Генеральная совокупность – это комплекс всех возможных объектов, относительно которых планируется вести наблюдение и формулировать выводы.

Выборочная совокупность или выборка является частью генеральной совокупности, выбранной для изучения и составления заключения касательной всей генеральной совокупности.

Как вычислить выборочную дисперсию

Выборочная дисперсия при различии всех значений варианта выборки находится по формуле:

({widehat D}_В=frac{displaystylesum_{i-1}^n{(x_i-{overline x}_В)}^2}n)

Для значений признаков выборочной совокупности с частотами n₁, n₂,…,n_kформула выглядит следующим образом:

({widehat D}_В=frac{displaystylesum_{i-1}^kn_i{(x_i-{overline x}_В)}^2}n)

Квадратный корень из выборочной дисперсии характеризует рассеивание значений вариантов выборки вокруг своего среднего значения. Данная характеристика называется выборочным средним квадратическим отклонением и имеет вид:

({widehatsigma}_В=sqrt{{widehat D}_В})

Упрощенный способ вычисления выборочной или генеральной дисперсии производят по формуле:

(D=overline{x^2}-left[overline xright]^2)

Если вариационный ряд выборочной совокупности интервальный, то за x_i принимается центр частичных интервалов.

Пример

Найти выборочную дисперсию выборки со значениями:

x_i: 1, 2, 3, 4;
n_i: 20, 15, 10, 5.

Решение

Для начала необходимо определить выборочную среднюю:

({overline x}_В=frac1{50}(1cdot20+2cdot15+3cdot10+4cdot5)=frac1{50}cdot100=2)

Затем найдем выборочную дисперсию:

(D_В=frac1{50}({(1-2)}^2cdot20+{(2-2)}^2cdot15+{(3-2)}^2cdot10+{(4-2)}^2cdot5)=1)

Исправленная дисперсия

Математически выборочная дисперсия не соответствует генеральной, поскольку выборочная используется для смещенного оценивания генеральной дисперсии. По этой причине математическое ожидание выборочной дисперсии вычисляется так:

(Mleft[D_Bright]=frac{n-1}nD_Г)

В данной формуле D_Г – это истинное значение дисперсии генеральной совокупности.

Исправить выборочную дисперсию можно путем умножения ее на дробь:

(frac n{n-1})

Получим формулу следующего вида:

(S^2=frac n{n-1}cdot D_В=frac{displaystylesum_{i=1}^kn_i{(x_i-{overline x}_В)}^2}{n-1})

Исправленная дисперсия используется для несмещенной оценки генеральной дисперсии и обозначается S².

Среднеквадратическая генеральная совокупность оценивается при помощи исправленного среднеквадратического отклонения, которое вычисляется по формуле:

(S=sqrt{S^2})

При нахождении выборочной и исправленной дисперсии разнятся лишь знаменатели в формулах. Различия в этих характеристиках при больших n незначительны. Применение исправленной дисперсии целесообразно при объеме выборки меньше 30.

Для чего применяют исправленную выборочную дисперсию

Исправленную выборочную используют для точечной оценки генеральной дисперсии.

Пример

Длину стержня измерили одним и тем же прибором пять раз. В результате получили следующие величины: 92 мм, 94 мм, 103 мм, 105 мм, 106 мм. Задача найти выборочную среднюю длину предмета и выборочную исправленную дисперсию ошибок измерительного прибора.

Решение

Сначала вычислим выборочную среднюю:

({overline x}_В=frac{92+94+103+105+106}5=100)

Затем найдем выборочную дисперсию:

(D_В=frac{displaystylesum_{i=1}^k{(x_i-{overline x}_В)}^2}n=frac{{(92-100)}^2+{(94-100)}^2+{(103-100)}^2+{(105-100)}^2+{(106-100)}^2}5=34)

Теперь рассчитаем исправленную дисперсию:

(S^2=frac5{5-1}cdot34=42,5)

Источник

Для того чтобы охарактеризовать
рассеяние наблюдаемых значений
количественного признака выборки вокруг
своего среднего значения ,
вводят сводную
характеристику – выборочную дисперсию.

Выборочной дисперсией

называют среднее
арифметическое квадратов отклонения
наблюдаемых значений признака от их
среднего значения .

Если все значения x₁,
х₂,
…, x_n
признака выборки объема п
различны, то

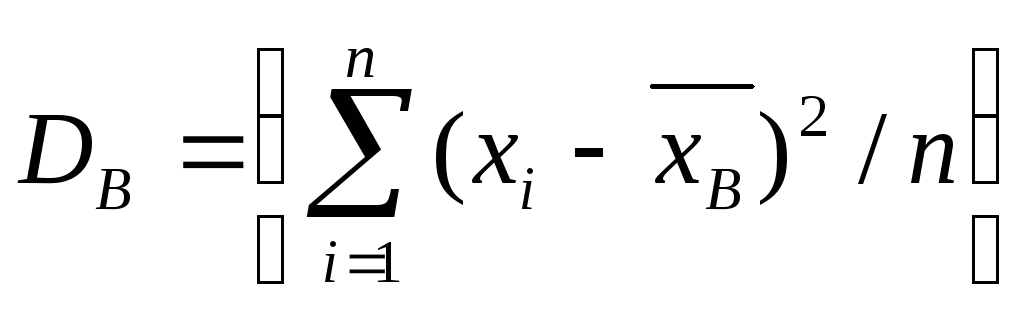
Если же значения признака
x₁,
х₂,
…, x_kимеют соответственно
частоты п₁,
n₂,…,
n_k,
причем n₁
+ n₂+…+n_k
= n, то

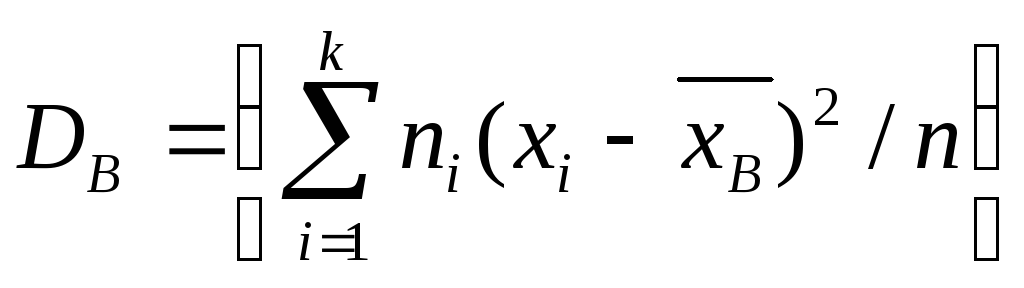
т.е. выборочная дисперсия есть средняя
взвешенная квадратов отклонений с
весами, равными соответствующим частотам.

Пример.
Выборочная
совокупность задана таблицей распределения

x_i

1
2 3 4

n_i
20 15
10
5

Найти выборочную
дисперсию.

Решение.
Найдем выборочную среднюю (см. § 4):

Найдем выборочную
дисперсию:

Кроме дисперсии для характеристики
рассеяния значений признака выборочной
совокупности вокруг своего среднего
значения пользуются сводной
характеристикой-средним квадратическим
отклонением.

Выборочным средним
квадратическим отклонением (стандартом)
называют квадратный
корень из выборочной дисперсии:

§ 10. Формула для вычисления дисперсии

Вычисление дисперсии, безразлично-выборочной
или генеральной, можно упростить,
используя следующую теорему.

Теорема. Дисперсия
равна среднему квадратов значений
признака минус квадрат общей средней:

Доказательство. Справедливость теоремы
вытекает из преобразований:

Итак,

где
,.

Пример.
Найти
дисперсию по данному распределению

x_i
1
2 3 4

n_i
20
15
10
5

Решение.
Найдем
общую среднюю:

Найдем
среднюю квадратов
значений признака:

Искомая дисперсия

=5-2²=1.

§11. Групповая, внутригрупповая, межгрупповая и общая дисперсии

Допустим, что все значения
количественного признака X
совокупности,
безразлично-генеральной или выборочной,
разбиты на k
групп. Рассматривая
каждую группу как самостоятельную
совокупность, можно найти групповую
среднюю (см. § 6) и дисперсию значений
признака, принадлежащих группе,
относительно групповой средней.

Групповой дисперсией называют
дисперсию значений признака, принадлежащих
группе, относительно групповой средней

где n_i–
частота значения
x_i;
j –
номер группы;

– групповая средняя
группы j;
–
объем группыj.

Пример
1. Найти
групповые дисперсии совокупности,
состоящей из следующих двух групп:

первая группа		вторая группа
	x_i	n_i		x_i	n_i
2	1	3	2
4	7	8	3
5	2

Решение.
Найдем
групповые средние:

;

Найдем
искомые
групповые дисперсии:

;

Зная дисперсию каждой группы, можно
найти их среднюю арифметическую.

Внутригрупповой дисперсией называют
среднюю арифметическую дисперсий,
взвешенную по объемам групп:

где N_j
– объем группы
j;
п =–
объем всей совокупности.

Пример
2.
Найти
внутригрупповую дисперсию по данным
примера 1.

Решение.
Искомая внутригрупповая дисперсия
равна

Зная групповые средние и общую среднюю,
можно найти дисперсию групповых средних
относительно общей средней.

Межгрупповой дисперсией называют
дисперсию групповых средних относительно
общей средней:

где
–
групповая средняя группыj;
N_j
– объем группы j;

– общая средняя;
n
=–
объем всей совокупности.

Пример
3. Найти
межгрупповую дисперсию по

данным
примера 1.

Решение.
Найдем общую среднюю:

Используя
вычисленные выше величины
=
4,=
6, найдем искомую межгрупповую дисперсию:

Теперь целесообразно ввести специальный
термин для дисперсии всей совокупности.

Общей дисперсией называют дисперсию
значений признака всей совокупности
относительно общей средней:

где n_i
– частота значения
x_i
;
–
общая средняя; n
– объем всей совокупности.

Пример
4. Найти
общую дисперсию по данным примера 1.

Решение.
Найдем искомую общую дисперсию, учитывая,
что общая средняя равна 14/3:

Замечание.
Найденная общая дисперсия равна сумме
внутригрупповой и межгрупповой дисперсий:

D_общ=
148/45;

D_внгр
+ D_межгр=
12/5 + 8/9= 148/45.

В следующем
параграфе будет доказано, что такая
закономерность справедлива для любой
совокупности.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Евгений Николаевич Беляев

Эксперт по предмету «Математика»

Задать вопрос автору статьи

Генеральная дисперсия

Пусть нам дана генеральная совокупность относительно случайной величины $X$. Для начала напомним следующее определение:

Определение 1

Генеральная совокупность — совокупность случайно отобранных объектов данного вида, над которыми проводят наблюдения с целью получения конкретных значений случайной величины, проводимых в неизменных условиях при изучении одной случайной величины данного вида.

Определение 2

Генеральная дисперсия — среднее арифметическое квадратов отклонений значений вариант генеральной совокупности от их среднего значения.

Пусть значения вариант $x_1, x_2,dots ,x_k$ имеют, соответственно, частоты $n_1, n_2,dots ,n_k$. Тогда генеральная дисперсия вычисляется по формуле:

Рассмотрим частный случай. Пусть все варианты $x_1, x_2,dots ,x_k$ различны. В этом случае $n_1, n_2,dots ,n_k=1$. Получаем, что в этом случае генеральная дисперсия вычисляется по формуле:

С этим понятием также связано понятие генерального среднего квадратического отклонения.

Определение 3

Генеральное среднее квадратическое отклонение — квадратный корень из генеральной дисперсии:

[{sigma }_г=sqrt{D_г}]

Выборочная дисперсия

Пусть нам дана выборочная совокупность относительно случайной величины $X$. Для начала напомним следующее определение:

Определение 4

Выборочная совокупность — часть отобранных объектов из генеральной совокупности.

Определение 5

Выборочная дисперсия — среднее арифметическое значений вариант выборочной совокупности.

«Дисперсия: генеральная, выборочная, исправленная» 👇

Пусть значения вариант $x_1, x_2,dots ,x_k$ имеют, соответственно, частоты $n_1, n_2,dots ,n_k$. Тогда выборочная дисперсия вычисляется по формуле:

Рассмотрим частный случай. Пусть все варианты $x_1, x_2,dots ,x_k$ различны. В этом случае $n_1, n_2,dots ,n_k=1$. Получаем, что в этом случае выборочная дисперсия вычисляется по формуле:

С этим понятием также связано понятие выборочного среднего квадратического отклонения.

Определение 6

Выборочное среднее квадратическое отклонение — квадратный корень из генеральной дисперсии:

[{sigma }_в=sqrt{D_в}]

Исправленная дисперсия

Для нахождения исправленной дисперсии $S^2$ необходимо умножить выборочную дисперсию на дробь $frac{n}{n-1}$, то есть

С этим понятием также связано понятие исправленного среднего квадратического отклонения, которое находится по формуле:

!!! В случае, когда значение вариант не являются дискретными, а представляют из себя интервалы, то в формулах для вычисления генеральной или выборочной дисперсий за значение $x_i$ принимается значение середины интервала, которому принадлежит $x_i.$

Пример задачи на нахождение дисперсии и среднего квадратического отклонения

Пример 1

Выборочная совокупность задана следующей таблицей распределения:

Рисунок 1.

Найдем для нее выборочную дисперсию, выборочное среднее квадратическое отклонение, исправленную дисперсию и исправленное среднее квадратическое отклонение.

Решение:

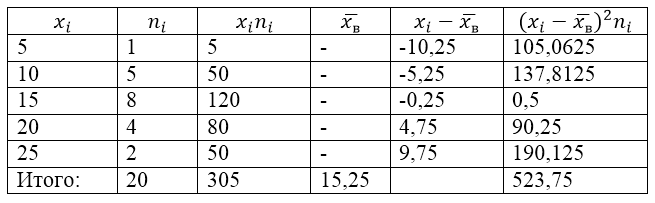
Для решения этой задачи для начала сделаем расчетную таблицу:

Рисунок 2.

Величина $overline{x_в}$ (среднее выборочное) в таблице находится по формуле:

[overline{x_в}=frac{sumlimits^k_{i=1}{x_in_i}}{n}]

То есть

[overline{x_в}=frac{sumlimits^k_{i=1}{x_in_i}}{n}=frac{305}{20}=15,25]

Найдем выборочную дисперсию по формуле:

[D_в=frac{sumlimits^k_{i=1}{{{(x}_i-overline{x_в})}^2n_i}}{n}=frac{523,75}{20}=26,1875]

Выборочное среднее квадратическое отклонение:

[{sigma }_в=sqrt{D_в}approx 5,12]

Исправленная дисперсия:

[{S^2=frac{n}{n-1}D}_в=frac{20}{19}cdot 26,1875approx 27,57]

Исправленное среднее квадратическое отклонение:

[S=sqrt{S^2}approx 5,25]

Находи статьи и создавай свой список литературы по ГОСТу

Поиск по теме

Источник

Выборочная дисперсия в математической статистике — это оценка теоретической дисперсии распределения, рассчитанная на основе данных выборки. Виды выборочных дисперсий:

смещённая;
несмещённая, или исправленная

Содержание

1 Определения
2 Замечание
3 Свойства выборочных дисперсий
4 См. также

Определения[править | править код]

Пусть $X_{1},ldots ,X_{n},ldots$ — выборка из распределения вероятности. Тогда

выборочная дисперсия — это случайная величина

$S_{n}^{2}={frac {1}{n}}sum limits _{{i=1}}^{n}left(X_{i}-{bar {X}}right)^{2}={frac {1}{n}}sum limits _{{i=1}}^{n}X_{i}^{2}-left({frac {1}{n}}sum limits _{{i=1}}^{n}X_{i}right)^{2}$

где символ обозначает выборочное среднее;

несмещённая (исправленная) дисперсия — это случайная величина

$S^{2}={frac {1}{n-1}}sum limits _{{i=1}}^{n}left(X_{i}-{bar {X}}right)^{2}$

Замечание[править | править код]

Очевидно,

$S^{2}={frac {n}{n-1}}S_{n}^{2}$

Свойства выборочных дисперсий[править | править код]

Выборочная дисперсия является теоретической дисперсией выборочного распределения. Более точно, пусть — выборочная функция распределения данной выборки. Тогда для любого фиксированного функция является (неслучайной) функцией дискретного распределения. Дисперсия этого распределения равна $S_{n}^{2}(omega )$ .

Обе выборочные дисперсии являются состоятельными оценками теоретической дисперсии. Если ${mathrm {D}}[X_{i}]=sigma ^{2}<infty$ , то

$S_{n}^{2}to ^{{!!!!!!{mathbb {P}}}};sigma ^{2}$

$S^{2}to ^{{!!!!!!{mathbb {P}}}};sigma ^{2}$

где символ « $to ^{{!!!!!!{mathbb {P}}}}$ » обозначает сходимость по вероятности.

Выборочная дисперсия является смещённой оценкой теоретической дисперсии, а исправленная выборочная дисперсия — несмещённой:

${mathbb {E}}left[S_{n}^{2}right]={frac {n-1}{n}}sigma ^{2}$

${mathbb {E}}left[S^{2}right]=sigma ^{2}$

Выборочная дисперсия нормального распределения имеет распределение хи-квадрат. Пусть $X_{i}sim {mathrm {N}}(mu ,sigma ^{2}),;i=1,2,ldots$ . Тогда

$(n-1){frac {S^{2}}{sigma ^{2}}}equiv n{frac {S_{n}^{2}}{sigma ^{2}}}sim chi ^{2}(n-1)$

См. также[править | править код]

Дисперсия случайной величины
Выборочное среднее
Несмещённая оценка
Дисперсия Аллана
Доверительный интервал для дисперсии нормальной выборки

Источник

Несмещенная оценка выборочной дисперсии

Краткая теория

Пусть из генеральной совокупности в результате

независимых наблюдений над количественным
признаком

извлечена повторная выборка объема

При этом

Требуется по данным выборки оценить (приближенно найти) неизвестную
генеральную дисперсию

.
Если в качестве оценки генеральной дисперсии принять выборочную дисперсию, то
эта оценка будет приводить в систематическим ошибкам, давая заниженное значение
генеральной дисперсии. Объясняется это тем, что, как можно доказать, выборочная
дисперсия является смещенной оценкой

,
другими словами, математическое ожидание выборочной дисперсии не равно
оцениваемой генеральной дисперсии, а равно:

Легко «исправить» выборочную дисперсию так, чтобы ее математическое
ожидание было равно генеральной дисперсии. Достаточно для этого умножить

на дробь

.
Сделав это, получим исправленную дисперсию, которую обычно обозначают через

Исправленная дисперсия является, конечно, несмещенной оценкой
генеральной дисперсии. Действительно:

Итак, в качестве оценки генеральной дисперсии принимают
исправленную дисперсию:

Для оценки среднего квадратического
отклонения генеральной совокупности используют исправленное среднее квадратическое отклонение, которое равно квадратному корню
из исправленной дисперсии:

При достаточно больших значениях

объема выборки выборочная и исправленная
дисперсия отличаются мало. На практике используются исправленной дисперсией,
если примерно

Пример решения задачи

Задача

Найти
несмещенную выборочную дисперсию на основании данного распределения выборки.

Решение

На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:

ВКонтакте
WhatsApp
Telegram

Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.

Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.

Выборочная дисперсия является смещенной оценкой генеральной дисперсии, поэтому в статистике применяют также исправленную выборочную дисперсию, которая является несмещенной оценкой генеральной дисперсии.

Сумма
частот:

Вычислим
среднюю:

Средняя квадратов:

Несмещенная
выборочная дисперсия:

Ответ:

Кроме этой задачи на другой странице сайта есть

пример расчета исправленной выборочной дисперсии и среднего квадратического отклонения для интервального вариационного ряда

Источник

Выборочная дисперсия, описание

Связь выборочной и генеральной дисперсии

Как вычислить выборочную дисперсию

Исправленная дисперсия

Для чего применяют исправленную выборочную дисперсию

§ 10. Формула для вычисления дисперсии

§11. Групповая, внутригрупповая, межгрупповая и общая дисперсии

Генеральная дисперсия

Выборочная дисперсия

Исправленная дисперсия

Пример задачи на нахождение дисперсии и среднего квадратического отклонения

Содержание

Определения[править | править код]

Замечание[править | править код]

Свойства выборочных дисперсий[править | править код]

См. также[править | править код]

Несмещенная оценка выборочной дисперсии

Задача

Вам также может понравиться

Как в биглионе найти свой купон

Как найти вещь которую потерял месяц назад

Как исправить тройку в журнале

Добавить комментарий Отменить ответ