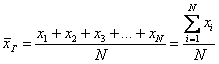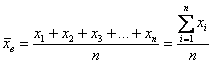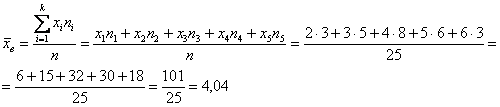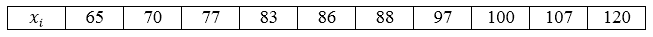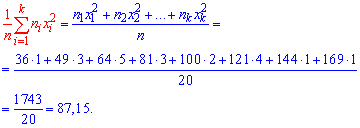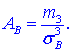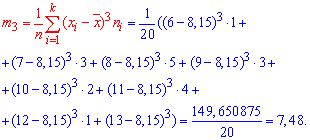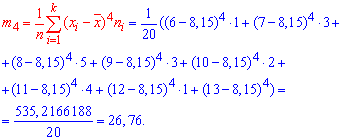Как найти выборочную среднюю результатов измерения - Сайт, где вы сможете решить свои вопросы

3.1. Показатели центральной тенденции

Простейший пример такого показателя нам уже встречался – это среднее арифметическое значение. Но средней

дело не ограничивается, впрочем, обо всём по порядку:

3.1.1. Генеральная и выборочная средняя

Пусть исследуется некоторая генеральная совокупность объёма , а именно её числовая характеристика , не важно, дискретная или непрерывная.

Генеральной средней называют среднее арифметическое всех значений этой совокупности:

Если среди чисел есть одинаковые (что

характерно для дискретного ряда), то формулу можно записать в более компактном

виде:
, где:
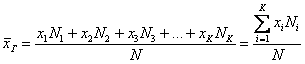
варианта повторяется раз;
варианта – раз;
варианта – раз;
…
варианта – раз.

Живой пример вычисления генеральной средней встретился в Примере 2, но чтобы не занудничать, я даже не буду

напоминать его содержание. Далее.

Как мы помним, обработка всей генеральной совокупности часто затруднена либо невозможна, и поэтому из неё организуют представительную выборку объема , и на основании исследования этой выборки делают вывод обо всей совокупности.

Выборочной средней называется среднее арифметическое всех значений выборки:

и при наличии одинаковых вариант формула запишется компактнее:
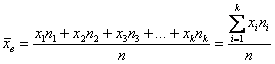
– как сумма произведений вариант на соответствующие частоты , делённая на объём совокупности .

Выборочная средняя позволяет достаточно

точно оценить истинное значение , при этом, чем

больше выборка, тем точнее будет эта оценка.

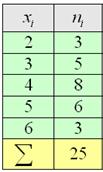
Практику начнём с дискретного вариационного ряда и знакомого условия:

Пример 8

По результатам выборочного исследования рабочих цеха были установлены их квалификационные разряды: 4, 5, 6, 4, 4, 2, 3, 5, 4,

4, 5, 2, 3, 3, 4, 5, 5, 2, 3, 6, 5, 4, 6, 4, 3.

Это числа из Примера 4, но теперь нам требуется: вычислить выборочную среднюю, и, не отходя от станка, найти моду

и медиану.

Как решать задачу? Если нам даны первичные данные (конкретные варианты ), то их можно тупо просуммировать и разделить результат на объём

выборки:
– средний квалификационный разряд рабочих

цеха.

Но здесь удобнее составить вариационный ряд:

и использовать «цивилизованную» формулу:

3.1.2. Мода

3. Основные показатели статистической совокупности

| Оглавление |

Источник

Эксперт по предмету «Математика»

Задать вопрос автору статьи

Генеральная средняя

Пусть нам дана генеральная совокупность относительно случайной величины $X$. Для начала напомним следующее определение:

Определение 1

Генеральная совокупность — совокупность случайно отобранных объектов данного вида, над которыми проводят наблюдения с целью получения конкретных значений случайной величины, проводимых в неизменных условиях при изучении одной случайной величины данного вида.

Определение 2

Генеральная средняя — среднее арифметическое значений вариант генеральной совокупности.

Пусть значения вариант $x_1, x_2,dots ,x_k$ имеют, соответственно, частоты $n_1, n_2,dots ,n_k$. Тогда генеральная средняя вычисляется по формуле:

Сделаем домашку
с вашим ребенком за 380 ₽

Уделите время себе, а мы сделаем всю домашку с вашим ребенком в режиме online

Бесплатное пробное занятие

*количество мест ограничено

Рассмотрим частный случай. Пусть все варианты $x_1, x_2,dots ,x_k$ различны. В этом случае $n_1, n_2,dots ,n_k=1$. Получаем, что в этом случае генеральная средняя вычисляется по формуле:

Выборочная средняя

Пусть нам дана выборочная совокупность относительно случайной величины $X$. Для начала напомним следующее определение:

Определение 3

Выборочная совокупность — часть отобранных объектов из генеральной совокупности.

Определение 4

Выборочная средняя — среднее арифметическое значений вариант выборочной совокупности.

Пусть значения вариант $x_1, x_2,dots ,x_k$ имеют, соответственно, частоты $n_1, n_2,dots ,n_k$. Тогда выборочная средняя вычисляется по формуле:

Рассмотрим частный случай. Пусть все варианты $x_1, x_2,dots ,x_k$ различны. В этом случае $n_1, n_2,dots ,n_k=1$. Получаем, что в этом случае выборочная средняя вычисляется по формуле:

«Средняя выборки: генеральная, выборочная» 👇

!!! В случае, когда значение вариант не являются дискретными, а представляют из себя интервалы, то в формулах для вычисления генеральной или выборочной средних значений за значение $x_i$ принимается значение середины интервала, которому принадлежит $x_i.$

Примеры задач на нахождение средней выборки

Пример 1

В магазин завезли 10 видов шоколадных конфет. По ним проведена следующая выборка по цене за килограмм: 70, 65, 97, 83, 120, 107, 77, 88, 100, 86. Построить ряд распределения данной генеральной совокупности и найти её генеральное среднее.

Решение.

Видим, что все значения вариант различны, поэтому частоты равны единице. Ряд распределения можно записать следующим образом, перечислив значения вариант в порядке возрастания:

Рисунок 1.

Так как наша совокупность является генеральной и все варианты различны, то мы будем пользоваться следующей формулой:

[overline{x_г}=frac{sumlimits^k_{i=1}{x_i}}{n}]

Получим:

[overline{x_г}=frac{65+70+77+83+86+88+97+100+107+120}{10}=89,3]

Ответ: 89,3.

Пример 2

Выборочная совокупность задана следующей таблицей распределения:

Рисунок 2.

Найти среднее выборочное данной совокупности.

Решение.

Для нахождения значения выборочной средней будем пользоваться следующей формулой:

[overline{x_в}=frac{sumlimits^k_{i=1}{x_in_i}}{n}]

Обычно, для наглядности и удобности вычислений составляется расчетная таблица, в которую входят необходимые промежуточные вычисления. В нашем случае составим таблицу со следующей «шапкой»:

Рисунок 3.

Внизу таблицы также добавляется строка «итог», в которой подсчитывается сумма по всем значениям столбцов. Проведя необходимые вычисления, получим следующую расчетную таблицу:

Рисунок 4.

Используя формулу, получим:

[overline{x_в}=frac{sumlimits^k_{i=1}{x_in_i}}{n}=frac{305}{20}=15,25]

Ответ: 15,25.

Пример 3

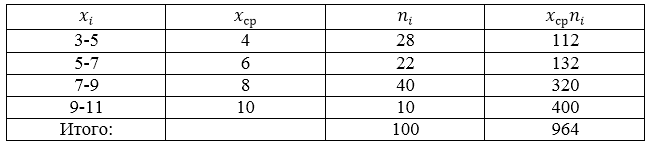
Проводится социальный опрос среди 100 пенсионеров об уровне их пенсии. Получена следующая таблица распределения результатов опроса (размер пенсии указан в тысячах рублей):

Рисунок 5.

Найти среднее выборочное данной совокупности.

Данная совокупность является выборочной, поэтому будем пользоваться следующей формулой:

[overline{x_в}=frac{sumlimits^k_{i=1}{x_in_i}}{n}]

Составим, для начала, расчетную таблицу.

Рисунок 6.

Получаем:

[overline{x_в}=frac{sumlimits^k_{i=1}{x_in_i}}{n}=frac{964}{100}=9,64]

Ответ: 9,64.

Находи статьи и создавай свой список литературы по ГОСТу

Поиск по теме

Источник

Цель
– научить студентов основным способам
расчета точечных характеристик выборочной
совокупности.

Средние
величины

Для
того чтобы получить характеристику не
отдельных объектов, а всей группы в
целом, определяют среднюю величину
признака. В зависимости от исследуемых
объектов и от поставленной задачи
среднюю величину вычисляют различными
способами. Средние значения признака
могут представлять: средняя арифметическая,
средняя геометрическая, средняя
квадратическая, средняя гармоническая,
мода, медиана и другие.

Средняя
арифметическая

Выборочная
средняя арифметическая является оценкой
генеральной средней и отражает уровень,
по отношению к которому колеблются
значения вариант в ней.

Средняя
арифметическая может быть рассчитана
во всех случаях по формуле:
,
где–
средняя арифметическая;
–
сумма всех вариант (дат) ряда; n
– объем
выборки.

Пример
2.1. Было
проведено измерение высоты 13 растений
сои (в см). Данные измерений следующие:
82, 77, 74, 74, 73, 66, 64, 63, 63, 62, 54, 44, 43. Необходимо
рассчитать значение средней арифметической.

Порядок работы.

1.
Подсчитывается число вариант (дат): n
= 13.

2.
Суммируются все варианты данной
совокупности:=
839.

3.
Сумма вариант делится на число вариант
=
839/13 = 64,5 см

Следует
обратить внимание на то, что измерение
растений проводилось в целых величинах,
а полученный результат имеет точность
до десятых. Это в принципе не верно, так
как статистические расчеты не могут
повысить точность измерений. Поэтому,
в нашем случае средняя арифметическая
будет равна 65 см.

Взвешенная
средняя арифметическая

Выборочная
взвешенная средняя арифметическая
используется тогда, когда значения
вариант выборки имеют разный математический
вес.

,
где
– математический
вес варианты
.

Пример
2.2. В
кормовой смеси содержится следующее
количество отдельных компонентов:

Компонент	Содержание в смеси, кг	Содержание протеина, %
Сено	50	3
Резаная солома	10	1
Жмых подсолнечника	20	33
Пшеничные отруби	11	11

Требуется
определить содержание перевариваемого
протеина в килограмме смеси.

Датами
признака будет содержание белка в каждом
компоненте, а их математическими весами
– физические веса компонентов, находящихся
в смеси.

Порядок
работы:

1.
Умножаются значения признака на их
математические веса: 3·50+1·10+33·20+11·20 =
1040

2.
Находится сумма математических весов
компонентов (n)
50+10+20+20 = 100

3.
Делим первое значение на второе 1040/100=
10,4% или 10%

Таким
образом, в каждом килограмме кормовой
смеси содержится 100 г перевариваемого
белка.

Пример
2.3. Данные
о продолжительности периода вегетации
сортов ячменя преобразованы во взвешенный
вариационный ряд и представлены в
таблице.

Границы класса	Середина класса,	Частота класса,
57,5- 62,4	60	2	120
62,5-67,4	65	30	1950
67,5-72,4	70	34	2380
72,5-77,4	75	62	4650
77,5-82,4	80	74	5920
82,5-87,4	85	8	680
87,5-92,5	90	4	360

Найти
среднее значение периода вегетации
сортов ячменя.

В
том случае, когда имеется взвешенный
вариационный ряд, также может использоваться
формула взвешенной средней арифметической,
где:

– частота
(математический вес) класса;
–
середина классового интервала.

Расчеты производятся
в следующем порядке.

1.
Умножаем варианты на их частоты: 60·2 =
120 и т. д.

2.
Суммируем эти произведения; 120+1950…680+360
= 16060.

3.
Полученную сумму делим на объем выборки
(n
= 214)
=
16060/214= 75,1

Таким
образом, продолжительность вегетационного
периода составляет 75 дней.

Пример
2.4. Найдем
общую среднюю арифметическую высоты
растений гелениума осеннего за четыре
года наблюдений по данным, приведенным
в таблице.

Год наблюдения	Средняя арифметическая,	Объем выборки,
1978	87	16	1392
1979	135	16	2160
1980	103	20	2060
1981	89	18	1602

Формула
взвешенной средней арифметической
используется и в случае необходимости
получить общую среднюю составной
выборки, для каждой, из отдельных частей
которой средние арифметические уже
известны.

Общая средняя
будет равна:

=
103 см

Пример
2.5.
Рассчитайте
медиану периода вегетации для
статистической совокупности сортов
ячменя по данным из примера 2.3.

Медианой называется
варианта (или дата), разделяющая
вариационный ряд на две равные по числу
вариант части. Она рассчитывается по
формуле:

,
где
–
медиана;–
начала класса, в котором находится
медиана;–
величина классового интервала;n
– объем
выборки; L
– сумма частот классов, предшествующих
классу, в котором находится медиана;
–
частота медианного класса.

Рассчитаем
медиану периода вегетации для совокупности
сортов ячменя. Порядковый номер медианной
варианты: 0,5 (214 + 1) = 107,5. Класс, в котором
находится медиана, определяется путем
накопления частот. Так, в таблице из
примера 3 сумма частот сверху вниз равна:
2 + 30 + 34 + 62 = 128. Поскольку между 107 и 128
вариантами должна находиться медиана,
накопление частот прекращаем и за начало
медианного класса принимаем 72,5, т.е.
меньшую границу класса: 72, 5 – 77,4, среднее
значение которого 75, а частота 62.

Отсюда
по формуле
=
72,5 +дня.

Пример
2.6.
Рассчитайте моду периода вегетации
сортов ячменя на основании данных
таблицы из примера 3.

Модой называется
точка на оси абсцисс, соответствующая
максимальной частоте теоретической
кривой распределения вариант. Вычисляется
мода по формуле:

,
где Mo–
мода;
–
начало модального класса;–
величина классового интервала;–
частота класса, предшествующего
модальному;–
частота модального класса;–
частота класса, следующего за модальным.

Определим
моду продолжительности периода вегетации
статистической совокупности сортов
ячменя по выше приведенной формуле:

Mo
= 77,5 +

Показатели
варьирования (разнообразия)

В
биологии используются несколько
показателей разнообразия. Самыми
простыми из них являются лимиты (lim)
и размах варьирования (R).
Лимиты и размах определяются следующим
простым способом:

lim
=
и
R
=
–

,
где

и

наименьшая и наибольшая дата статистической
совокупности. Так для задачи с определением
продолжительности вегетационного
периода у сортов ячменя (пример 1.1.) lim
= 6090, а
R
= 92–60 = 32.

Однако
наиболее широкое использование в
исследованиях получили среднее
квадратическое отклонение (σ) или сигма
и дисперсия – среднее квадратическое
отклонение в квадрате (σ).
Среднее квадратическое отклонение и
дисперсия оценивают величину колебаний
значений вариант около их средней
арифметической и служат кроме того для
расчета других биометрических показателей.

Среднее квадратическое
отклонение вычисляется по формуле

σ
= +,
где σ – среднее квадратическое отклонение;– знак суммирования;–
варианты (даты) совокупности;–
средняя арифметическая;n
– объем
выборки.

Пример
2.7.
Необходимо рассчитать варьирование
растений сои по высоте (данные из примера
2.1).

Вычисление
выборочного среднего квадратического
отклонения по приведенной формуле
проводится в следующем порядке.

1.
Определяется средняя арифметическая.
Для данного ряда она вычислена в примере
1. и равна
=
64,538.

2.
Находится отклонение вариант путем
вычисления от каждой из них средней
арифметической:
–.
Вычитая: 82–64,538 = 17, 462: 77 – 64,538 и т.д. (см.
таблицу). Сумма всех разностей должна
быть равна нулю.

3. Возводятся в
квадрат отклонения и получается их
сумма:

=
1721, 231.

4.
Вычисляется среднее квадратическое
отклонение по формуле:

σ
= +=
11,98.

Варианта,	–
82	17,462	304,921
77	12,462	155,301
74	9,462	89,529
74	9,462	89,529
73	8,462	71,605
66	1,462	2,137
64	-0,538	0,289
63	-1,538	2,365
63	-1,538	2,365
62	-2,538	6,441
54	-10,538	111,049
44	-20,538	421,809
43	-21,538	463,885
	0,006	1721,231

В
промежуточных вычислениях показателей
обычно сохраняется число знаков,
достаточное для получения необходимой
точности, сам же показатель приводится
в результате с числом знаков, имеющим
реальное значение, т.е. среднее
квадратическое отклонение высоты сои
равно 12 см. Дисперсия этого признака
(σ)
равна144 (в отличии от среднего
квадратического отклонения дисперсия
это статистика не поименованная),lim
= 4382,
а
R
= 39.

Пример
2.8.
Известны
средние арифметические и средние
квадратические отклонения для массы
тела и длины ног домашней и дикой птицы.
Необходимо объективно сравнить
изменчивость этих признаков у двух
выборочных совокупностей.

Объект	Признак	Варьирование, σ	Средняя арифметическая,	Коэффициент вариации – Cv, %
Куры	Длина ног	1 см	10 см	= 10%
Масса тела	0,6 кг	3 кг	= 20%
Страусы	Длина ног	6 см	150 см	= 4%
Масса тела	10 кг	100 кг	= 10%

Среднее квадратическое
отклонение и дисперсия могут служить
для сравнения разнообразия статистических
совокупностей только при соблюдении
следующих условий:

1. При сравнении
одинаковых признаков;

2.
Если средние, сравниваемых статистических
совокупностей не очень сильно различаются.

В
противном случае используются не
абсолютные, а относительные показатели
вариации, среди которых чаще используется
коэффициент вариации (Cv).
Он вычисляется по формуле:

Cv
=
100%
и представляет собой среднее квадратическое
отклонение, выраженное в процентах от
величины средней арифметической.

Действительно
по величине сигмы невозможно установить,
какой признак более разнообразен: нельзя
сравнить 1 см длины ног с 0,6 кг массы или
6 см длины с 10 кг массы. Кроме того, 1 см
для мелкой птицы несравним с 6 см для
крупной. Это затруднение при решении
задачи снято с помощью коэффициента
вариации: у домашней птицы признаки
более разнообразны по сравнению с дикой
птицей, для которой сказывается действие
стабилизирующего отбора. Длина ног
имеет явно меньшее разнообразие по
сравнению с разнообразием массы, у кур
это связано с отсутствием селекции по
длине ног, у страусов сказывается более
жесткий стабилизирующий отбор.

Варьирование
считается слабым, если коэффициент
вариации не превышает 10%, средним, когда
он составляет 11 – 25%, и значительным при
величине более 25%.

Пример
2.9.
Необходимо
вычислить среднюю дисперсию для четырех
групп измерений диаметра цветков
гелениума осеннего по данным таблицы

Группа	Дисперсия диаметра цветка, мм	Объем выборки
1	2,00	7
2	3,35	5
3	2,95	8
4	4,37	9

В примере 2.4. было
показано, как объединить выборки по их
средним арифметическим. Часто при этом
требуется также найти и среднюю дисперсию
объединенной выборки. Она может быть
рассчитана по формуле:

σ=,
где σ–
средняя дисперсия; σ– дисперсии частных выборок;– объемы частных выборок;k
– число
частных выборок.

По выше приведенной
формуле

σ=

Статистические
ошибки точечных оценок

Выборочная
средняя, выборочная дисперсия, среднее
квадратическое отклонение, коэффициент
вариации являются оценками соответствующих
генеральных параметров. Это точечные
оценки, представляющие собой не интервалы,
а числа, вычисляемые по случайной
выборке. Выборочные характеристики,
как правило, не совпадают по абсолютной
величине с соответствующими им
генеральными параметрами. Величина
отклонения статистики от ее генерального
параметра называют статистической
ошибкой или ошибкой репрезентативности.

Ошибка
средней арифметической вычисляется по
формуле

,
где
–
ошибка средней арифметической; σ –
среднее квадратическое отклонение;n
– объем выборки.

Показатель точности
оценки определяется по следующей
формуле:

Достоверность
средней арифметической оценивается
путем сравнения фактического значения
критерия Стьюдента с его табличным (или
стандартным) значением, которое зависит
от числа степеней свободы и принимаемого
уровня значимости.

,
где t–
фактический (или наблюдаемый) критерий
Стьюдента.

Число
степеней свободы для выборочной средней
равно k
= n
– 1.

Обычно
используются следующие три уровня
значимости в порядке возрастания
строгости оценки достоверности статистик:
,=1%,=
0,1%. Им соответствуют в том же порядке
возрастания строгости оценки, следующие
доверительные уровни:= 95%,=
99%,=
99,9%. И те и другие, также могут быть
выражены в долях. Для биологических
исследований во многих случаях достаточно
принимать 5% уровень значимости, или 95%
доверительный уровень, при котором
подтверждается существенность выводов
в 95 случаях из 100.

Пример
2.10.
Требуется
рассчитать статистическую ошибку,
показатель точности и достоверность
средней арифметической высоты растений
сои по данным примера 1. Ранее была
рассчитана средняя арифметическая,
которая равна 65 см (пример 2.1) и среднее
квадратическое отклонение – 12 см (пример
2.7) при n
= 13.

Ошибка средней
арифметической равна

=
см.
(как правило, ошибка записывается с
точностью на один знак больше после
запятой, чем средняя арифметическая)

Точность
определения выборочной средней
арифметической равна

Sc
=
=
5,1%. Она считается вполне удовлетворительной,
если коэффициент Sc
не превышает 3 – 5%.

Фактический
критерий Стьюдента равен
==
19,5, число степеней свободыk
= 13–1=12. Табличное значение критерия
Стьюдента для 5% уровня значимости равно
2,179 и на 0,15 уровне значимости равно
4,318. Полученное выше значение критерия
19,5 значительно выше табличного, поэтому
средняя арифметическая вполне достоверна
даже при самой строгой оценке, т.е. на
0,1% уровне значимости.

Пример
2.11.
Необходимо сравнить на точность
определения средние:
=
86,1±0,7 см и=
17,4±0,2 см. Так как средние выражены разными
единицами, судить по абсолютной величине
их ошибок о том, какая из них определена
более точно, нельзя. Ответить на этот
вопрос позволяет коэффициентSc

Sc;
Sc

Из расчетов видно,
что первая средняя определена более
точно, чем вторая.

Пример
2.12.
Из 1050
обследованных растений ячменя 66 особей
оказалось мутантами, что составляет
6,3% от всего числа растений. Требуется
оценить достоверность доли мутантных
растений. В задаче имеет место
альтернативное распределение. Ошибка
доли определяется по формуле:

,
где p
– доля особей
с изучаемым признаком, выраженная часть
единицы или в процентах, она же и средняя
арифметическая; q
– доля особей
без этого признака; n
– объем всей выборки (1050). Для приведенных
данных
.
Точность опыта будет равнаSc
=
=
11,9%, что является низким показателем
точности проведенного исследования.

Ошибка среднего
квадратического отклонения вычисляется
по формуле:

или
для небольших выборок (при n<
30) по формуле
.

Ошибка
дисперсии рассчитывается по аналогичной
формуле
.

Пример
2.13.
Необходимо рассчитать среднее
квадратическое отклонение и его ошибку
для продолжительности вегетации ячменя,
пользуясь данными примера 2.3, где
представлен взвешенный вариационный
ряд.

Для
расчета среднего квадратического
отклонения можно воспользоваться
формулойгде σ – среднее квадратическое отклонение;–
варианты совокупности;f
– частота
;– средняя арифметическая;n
– объем
выборки. Так как, мы располагаем данными
преобразованными во взвешенный
вариационный ряд то аналогично с задачей
на взвешенную среднюю арифметическую
принимаем:

– за частоту
(математический вес) класса;
– за
середину классового интервала. Подставив
в формулу данные, получим:

Ошибка
среднего квадратического отклонения
будет равна

Таким
образом, в нашем примере среднее
квадратическое отклонение продолжительности
вегетации сортов ячменя равно σ = 6 ± 0,3
дня.

Вопросы для
самоконтроля:

Какие
две группы показателей позволяют
характеризовать вариационные ряды?
Что
такое медиана, мода?
Что
такое размах варьирования и лимиты?
Приведите
формулу средней арифметической.
Могут
ли совпасть значения
,Me,
Мо?
Каковы
свойства средней арифметической?
В
чем заключается прямой способ вычисления

?
Каковы
свойства дисперсии?
Среднее
крадратическое отклонение как мерило
изменчивости совокупности. Общая
формула для него.
Степени
свободы. Значение этого показателя при
вычислении σ
и σ².
При каких значениях n
более точным
является использование числа степеней
свободы, а не количества вариант
(наблюдений)?
Почему

и σ являются
основными характеристиками вариационного
ряда?
Какова
зависимость между величиной статистической
ошибки средней и объемом совокупности?

Задачи для
самостоятельного решения.

1.
В результате подсчета количества
лепестков в цветках седмичника был
построен следующий вариационный ряд:

x_i	5	6	7	8
f_i	1	31	130	2

Определите
среднее количество лепестков и их
варьирование в цветках седмичника.
Отобразите данные графически (15 баллов)

2. В
результате измерения длины бобов фасоли
(в мм) был построен следующий вариационный
ряд (x_i
– середина классового интервала):

x_i	17	19	21	23	25	27	29	31	33
f_i	10	44	122	160	128	64	25	5	1

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Сейчас Вы научитесь находить числовые характеристики статистического распределения выборки. Примеры подобраны на основании индивидуальных заданий по теории вероятностей, которые задавали студентам ЛНУ им. И. Франка. Ответы послужат для студентов математических дисциплин хорошей инструкцией на экзаменах и тестах. Подобные решения точно используют в обучении экономисты , поскольку именно им задавали все что приведено ниже. ВУЗы Киева, Одессы, Харькова и других городов Украины имеют подобную систему обучения поэтому много полезного для себя должен взять каждый студент. Задачи различной тематики связаны между собой линками в конце статьи, поэтому можете найти то, что Вам нужно.

Индивидуальное задание 1
Вариант 11

Задача 1. Построить статистическое распределение выборки, записать эмпирическую функцию распределения и вычислить такие числовые характеристики:

выборочное среднее;
выборочную дисперсию;;
подправленную дисперсию;
выборочное среднее квадратичное отклонение;
подправленное среднее квадратичное отклонение;
размах выборки;
медиану;
моду;
квантильное отклонение;
коэффициент вариации;
коэффициент асимметрии;
эксцесс для выборки:

Выборка задана рядом 11, 9, 8, 7, 8, 11, 10, 9, 12, 7, 6, 11, 8, 7, 10, 9, 11, 8, 13, 8.

Решение:
Запишем выборку в виде вариационного ряда (в порядке возрастания):
6; 7; 7; 7; 8; 8; 8; 8; 8; 9; 9; 9; 10; 10; 11; 11; 11; 11; 12; 13.
Далее записываем статистическое распределение выборки в виде дискретного статистического распределения частот:

Эмпирическую функцию распределения определим по формуле

Здесь n_x – количество элементов выборки которые меньше х. Используя таблицу и учитывая что объем выборки равен n = 20, запишем эмпирическую функцию распределения:

Далее вычислим числовые характеристики статистического распределения выборки.
Выборочное среднее вычисляем по формуле

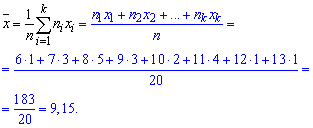
Выборочную дисперсию находим по формуле

Выборочное среднее, что фигурирует в формуле дисперсии в квадрате найдено выше. Остается все подставить в формулу

Подправленную дисперсию вычисляем согласно формулы

Выборочное среднее квадратичное отклонение вычисляем по формуле

Подправленное среднее квадратичное отклонение вычисляем как корень из подправленной дисперсии

Размах выборки вычисляем как разность между наибольшим и наименьшим значениями вариант, то есть:

Медиану находим по 2 формулам:
если число n – четное;
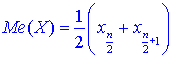
если число n – нечетное.
Здесь берем индексы в x_i согласно нумерации варианта в вариационном ряду.
В нашем случае n = 20, поэтому

Мода – это варианта которая в вариационном ряду случается чаще всего, то есть

Квантильное отклонение находят по формуле

где – первый квантиль, – третий квантиль.
Квантили получаем при разбивке вариационного ряда на 4 равные части.
Для заданного статистического распределения квантильное отклонения примет значение

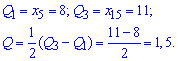
Коэффициент вариации равный процентному отношению подправленного среднего квадратичного к выборочному среднему

Коэффициент асимметрии находим по формуле

Здесь 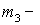центральный эмпирический момент 3-го порядка,

Подставляем в формулу коэффициента асимметрии

Эксцессом статистического распределения выборки называется число, которое вычисляют по формуле:

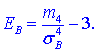
Здесь m₄ центральный эмпирический момент 4-го порядка. Находим момент

а далее эксцесс
Теперь Вы имеете все необходимые формулы чтобы найти числовые характеристики статистического распределения. Как найти моду, медиану и дисперсию должен знать каждый студент, который изучает теорию вероятностей.