Линейный коэффициент корреляции
Краткая теория
Под теснотой связи между
двумя величинами понимают степень сопряженности между ними, которая
обнаруживается с изменением изучаемых величин. Если каждому заданному
значению
соответствуют
близкие друг другу значения
, то связь считается тесной (сильной); если
же значения
сильно
разбросаны, то связь считается менее тесной.
Рассмотрим наиболее важный
для практики и теории случай линейной зависимости вида:
При тесной корреляционной
связи корреляционное поле представляет собой более или менее сжатый эллипс. Две
корреляционные зависимости переменной
от
приведены на рисунке.
Очевидно, что в случае (а)
зависимость между переменными менее тесная, чем в случае (б), так как точки
корреляционного поля (а) дальше отстоят от линии регрессии, чем точки поля (б).
Перейдем к оценке тесноты
линейной корреляционной зависимости. Для показателя тесноты связи нужная такая
стандартная система единиц измерения, в которой данные по различным
характеристикам оказались бы сравнимы между собой. Статистика знает такую
систему единиц. Эта система использует в качестве единицы измерения переменной
ее среднее квадратическое отклонение
.
Учтем, что
и запишем
уравнение парной линейной зависимости
в эквивалентном виде:
В этой системе величина:
показывает, на сколько
величин
изменится
в среднем
, когда
увеличится
на одно
.
Величина
является
показателем тесноты связи и называется линейным коэффициентом корреляции. Коэффициент
корреляции, определяемый по выборочным данным, называется выборочным коэффициентом корреляции.
Если
, то корреляционная связь между переменными
называется прямой, если
– обратной.
Приведем другие модификации
формулы для расчета линейного коэффициента корреляции:
или
Наиболее часто для расчета
используют формулу, получаемую простыми преобразованиями:
По этой формуле
находится
непосредственно из данных наблюдений и на значении
не
скажутся округления данных, связанных с расчетом средних и дисперсий.
Линейный выборочный
коэффициент корреляции
(при
достаточно большом объеме выборки
) обладает следующими свойствами:
-
Коэффициент корреляции
принимает значения на отрезке
, т.е.
. При этом, чем ближе по модулю
к
единице – тем теснее связь.
При
корреляционная
связь представляет собой линейную функциональную зависимость. При этом все
наблюдаемые значения располагаются на прямой линии.
При
линейная
корреляционная связь отсутствует. При этом линия регрессии параллельна оси
.
Расчет линейного коэффициента корреляции предполагает, что
переменные
и
распределены нормально. В других случаях
(когда распределения
и
отклоняются от нормальных) линейный
коэффициент корреляции не следует рассматривать как строгую меру взаимосвязи
переменных.
Пример решения задачи
Задача
Компания,
занимающаяся продажей радиоаппаратуры, установила на видеомагнитофон
определенной модели цену, дифференцированную по регионам. Следующие данные
показывают цены на видеомагнитофон в 10 различных регионах о соответствующее им
число продаж:
|
Число продаж, шт. |
420 | 380 | 350 | 400 | 440 | 380 | 450 | 425 | 430 | 480 |
| Цена, тыс.руб. | 5.6 | 6.0 | 6.5 | 6.0 | 5.0 | 6.4 | 4.5 | 5.0 | 5.7 | 4.4 |
Рассчитайте
выборочный коэффициент линейной корреляции и проверьте его значимость
при
.
Решение
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Составим
расчетную таблицу:
Вычислим
линейный коэффициент корреляции:
Вывод
Связь
между числом продаж и ценой очень тесная, обратная – с уменьшением цены
увеличивается объем продаж.
Проверим
значимость коэффициента корреляции:
По таблице критических точек t-критерия Стьюдента (по уровню значимости
и числу степеней свободы
) находим:
– коэффициент корреляции значим.
Кроме этой задачи на другой странице сайта есть еще
задача на расчет коэффициента корреляции, коэффициента детерминации, построение линии линейной регрессии и корреляционного поля.
Коэффициент корреляции вводится как
величина, которая служит мерой тесноты
(силы) линейной корреляционной зависимости
признаков.
Рассмотрим сначала эксперименты, в
которых одновременно измеряются только
две величины (обозначим их Y
иX ). Пусть
проведеноn независимых
совместных измерений признаковY
иX , в результате
которых полученоnпар чисел:
(x1,
y1),
(x2,
y2),
(x3,
y3),
…, (xi
, yi
), …, (xn,
yn).
(4.7)
Такую совокупность пар чисел можно
рассматривать как случайную выборку
из генеральной совокупности всех
возможных значений пары (Y
,X). Поэтому получаемое
по этим данным значение коэффициента
корреляции называют выборочным.
Выборочный коэффициент корреляции
определяется равенством
 , (4.8)
, (4.8)
где yi
– экспериментальное значение
величиныY ,
соответствующееxi
;
n – объем
выборки;
![]() – выборочные средние признаковX
– выборочные средние признаковX
иY ;
![]() –выборочныесредние квадратичные
–выборочныесредние квадратичные
отклонения признаковX
иY .
Если вместо выборочных использовать
исправленныесредние квадратичные
отклоненияsx,sy
, то вычисление выборочного
коэффициента корреляции производится
по формуле
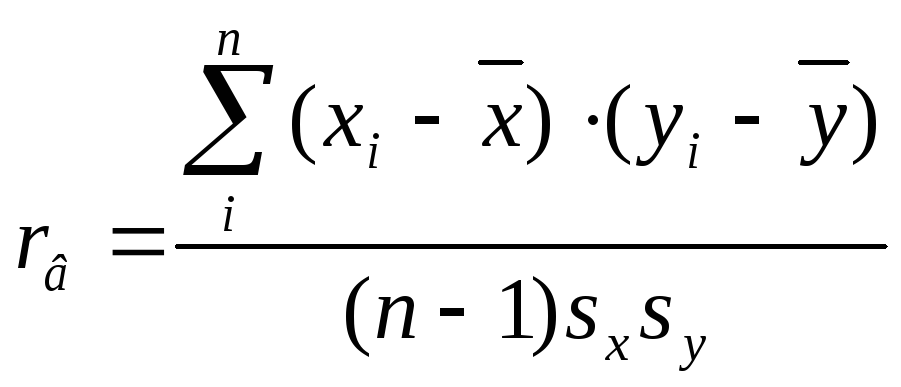 .
.
(4.9)
Почему введенное таким образом выражение
для rв способно служить мерой тесноты
корреляционной связи? Дело в том, что
выражение дляrв
является суммой произведений так
называемых нормированных отклонений.
Нормированное отклонениеt(xi)
вариантыxiесть разность между значениемxiварианты и ее средним значением,
отнесенная к среднему квадратичному
отклонению этой варианты:![]() .
.
Аналогично![]() есть нормированное отклонение
есть нормированное отклонение
вариантыyi
. Используя нормированные отклонения,
выражение дляrвможно представить в видеrв=![]() .
.
При коррелированности (т.е. наличии
сопряженности изменения) признаковX
иY величиныt(xi)
иt(yi)
принимают положительные и отрицательные
значения некоторым регулярным образом,
поэтому произведенияt(xi)
t(yi)
входят в![]() большей
большей
частью с одинаковым знаком, что
обеспечивает отличиеrв
от нуля. Кроме того, при
коррелированности признаковX
иY и модули
величинt(xi)
иt(yi)
меняются согласованно: например, в
случае линейной корреляции большим по
модулю значениямt(xi)
соответствуют, как правило, большие по
модулю значения t(yi),
что также приводит к отличиюrв
от нуля. Наоборот, при отсутствии
корреляции знаки величинt(xi)
иt(yi)
будут меняться чисто случайным образом,
из-за чего число положительных слагаемых
в сумме![]() будет примерно равно числу отрицательных,
будет примерно равно числу отрицательных,
что приведет к их взаимному сокращению
и равенствуrв =
0.
Существует много различных рабочих
формул для вычисления rв
прямым способом, т.е. при
непосредственном использовании
полученных в результате измерений
значенийxi
иyi
. Здесь приведены лишь наиболее
употребимые из них. Выражение
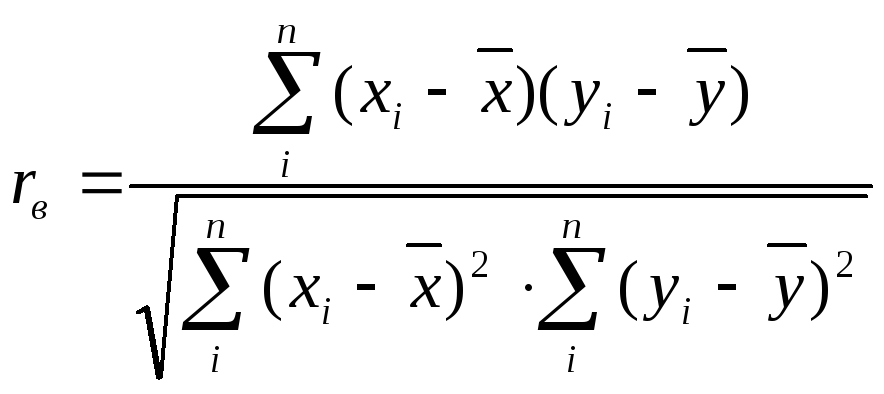 (4.10)
(4.10)
получается из (4.8) заменой
![]() и
и![]() выражениями
выражениями и
и в соответствии с их определением. В этом
в соответствии с их определением. В этом
выражении используются только отклонения
вариант от средних.
Еще одна формула для вычисления rвполучается в результате преобразования
числителя в выражении (4.9):

Отсюда получаем
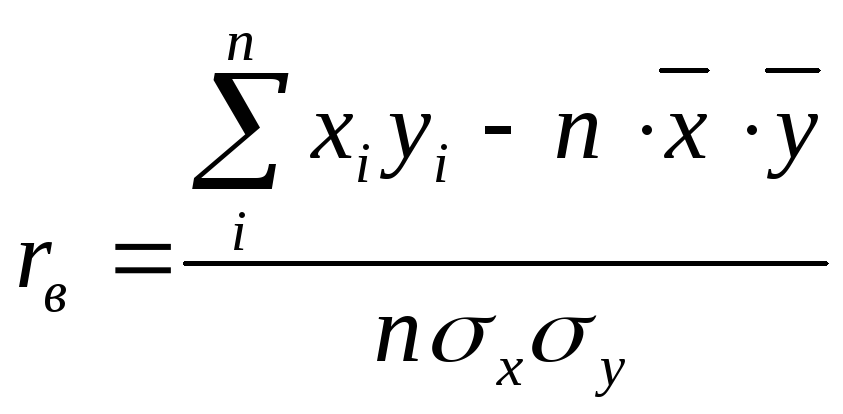 (4.11)
(4.11)
или
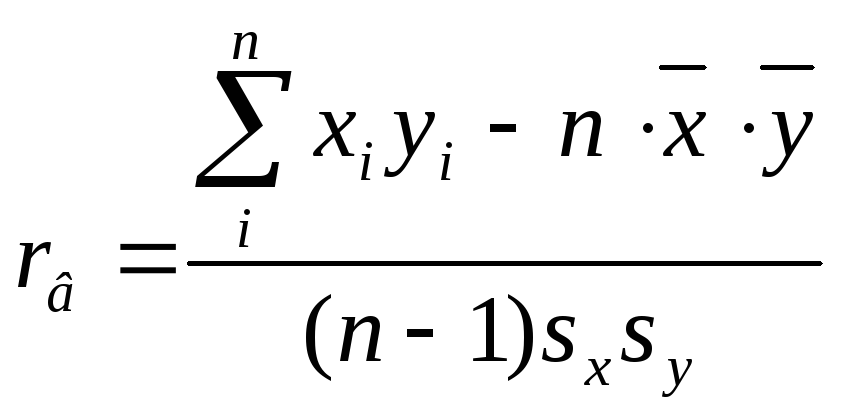 . (4.12)
. (4.12)
Формулы (4.8 ), (4.9) и (4.10 ) для вычисления
выборочного коэффициента корреляции
применимы и в случаях, когда данные
измерений не могут быть сгруппированы,
из-за того, что различные значения xi
иyi
величинX иY
наблюдаются по одному разу, и в тех
случаях, когда данные могли бы быть
сгруппированы, но решено группировку
не делать.
Если данные n
экспериментов по совместному измерению
значений величинY
иX сгруппированы
и представлены в виде корреляционной
таблицы (типа приведенной в 4.4.2.), то
выборочный коэффициент корреляции
удобно вычислять по формуле
![]() , (4.13)
, (4.13)
где x,y
– варианты (наблюдавшиеся значения)
признаковX иY
;
nxy
– частота (число появлений)
наблюдавшейся пары вариант (x
,y );
n – объем
выборки (![]() );
);
![]() – выборочные средние признаковX
– выборочные средние признаковX
иY ;
![]() – выборочные средние квадратичные
– выборочные средние квадратичные
отклонения признаковX
иY .
Если использовать исправленныесредние квадратичные отклоненияsx,sy
, то
![]() .
.
(4.14)
Важно отметить, что выборочный коэффициент
корреляции rв и угловой коэффициентk
прямой линии регрессии (4.4) связаны
между собой соотношением
![]() (4.15)
(4.15)
или
![]() .
.
(4.16)
Это выражение не только дает еще один
способ вычисления коэффициента
корреляции, но и явно указывает на то,
что rв является мерой именно линейной
корреляционной связи.
Пример 4.3. Проверить прямым вычислением
справедливость формулы (4.15) по данным
примера 4.2.
Решение. По данным примера 4.2.
![]()
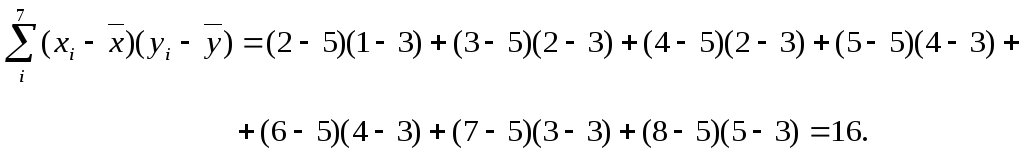
Выборочные дисперсии равны
![]() ,
,
![]() .
.
Выборочные средние квадратичные
отклонения равны
![]()
Отсюда
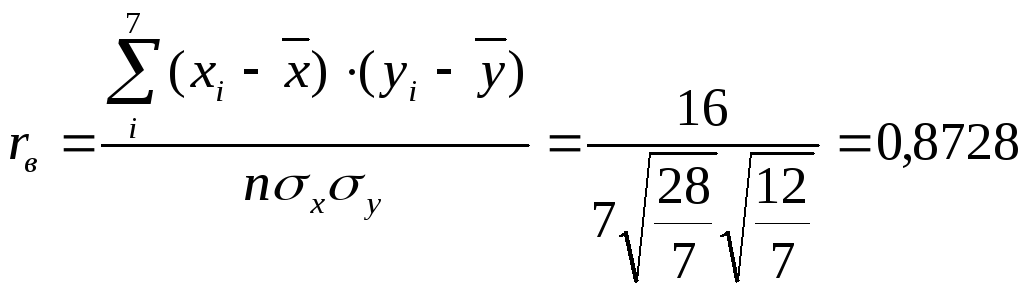 .
.
С другой стороны
![]()
Если вместо выборочных использовать
исправленные средние квадратичные
отклонения, которые оказываются в данном
случае равными sx
=![]() ,sy
,sy
=
![]() ,
,
то
![]() Е
Е
Какие значения rв
можно считать большими, а какие
средними или малыми? Оказывается, что
при наличии корреляции степень влияния
изменений одного признака на изменения
другого может быть выражена квадратом
коэффициента корреляции![]() .
.
Это значит, что приrв
= 0,9 81% вариации одного признака
обусловлен вариацией другого признака,
в остальных же 19% случаев совпадение
или несовпадение вариаций признаков
по знаку и величине является чисто
случайным. Приrв
= 0,3 такая обусловленность имеет
место менее, чем для 10% вариаций. Таким
образом, корреляцию (связь) принято
считать: очень тесной, если![]() ;
;
тесной, если![]() ;
;
средней (значительной), если![]() ;
;
умеренной, если![]() ;
;
слабой, если![]()
Изучаемые признаки X
иYчасто имеют
различную размерность, но коэффициент
корреляцииrвесть всегда величинабезразмерная.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Обнаружение взаимосвязей между явлениями – одна из главных задач статистического анализа. На то есть две причины. Первая. Если известно, что один процесс зависит от другого, то на первый можно оказывать влияние через второй. Вторая. Даже если причинно-следственная связь отсутствует, то по изменению одного показателя можно предсказать изменение другого.
Взаимосвязь двух переменных проявляется в совместной вариации: при изменении одного показателя имеет место тенденция изменения другого. Такая взаимосвязь называется корреляцией, а раздел статистики, который занимается взаимосвязями – корреляционный анализ.
Корреляция – это, простыми словами, взаимосвязанное изменение показателей. Она характеризуется направлением, формой и теснотой. Ниже представлены примеры корреляционной связи.
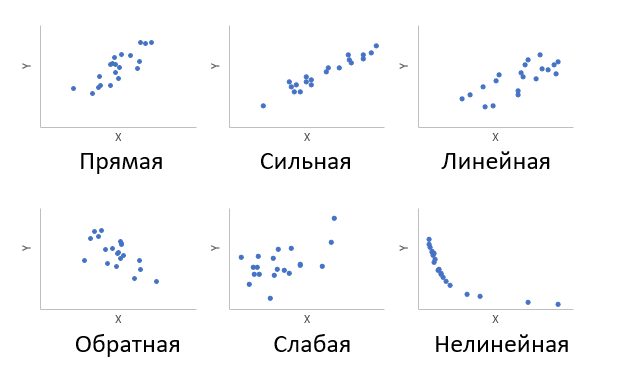
Далее будет рассматриваться только линейная корреляция. На диаграмме рассеяния (график корреляции) изображена взаимосвязь двух переменных X и Y. Пунктиром показаны средние.
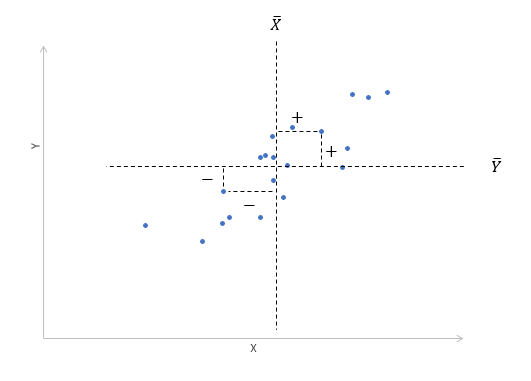
При положительном отклонении X от своей средней, Y также в большинстве случаев отклоняется в положительную сторону от своей средней. Для X меньше среднего, Y, как правило, тоже ниже среднего. Это прямая или положительная корреляция. Бывает обратная или отрицательная корреляция, когда положительное отклонение от средней X ассоциируется с отрицательным отклонением от средней Y или наоборот.
Линейность корреляции проявляется в том, что точки расположены вдоль прямой линии. Положительный или отрицательный наклон такой линии определяется направлением взаимосвязи.
Крайне важная характеристика корреляции – теснота. Чем теснее взаимосвязь, тем ближе к прямой точки на диаграмме. Как же ее измерить?
Складывать отклонения каждого показателя от своей средней нет смысла, получим нуль. Похожая проблема встречалась при измерении вариации, а точнее дисперсии. Там эту проблему обходят через возведение каждого отклонения в квадрат.
![]()
Квадрат отклонения от средней измеряет вариацию показателя как бы относительно самого себя. Если второй множитель в числителе заменить на отклонение от средней второго показателя, то получится совместная вариация двух переменных, которая называется ковариацией.
![]()
Чем больше пар имеют одинаковый знак отклонения от средней, тем больше сумма в числителе (произведение двух отрицательных чисел также дает положительное число). Большая положительная ковариация говорит о прямой взаимосвязи между переменными. Обратная взаимосвязь дает отрицательную ковариацию. Если количество совпадающих по знаку отклонений примерно равно количеству не совпадающих, то ковариация стремится к нулю, что говорит об отсутствии линейной взаимосвязи.
Таким образом, чем больше по модулю ковариация, тем теснее линейная взаимосвязь. Однако значение ковариации зависит от масштаба данных, поэтому невозможно сравнивать корреляцию для разных переменных. Можно определить только направление по знаку. Для получения стандартизованной величины тесноты взаимосвязи нужно избавиться от единиц измерения путем деления ковариации на произведение стандартных отклонений обеих переменных. В итоге получится формула коэффициента корреляции Пирсона.
![]()
Показатель имеет полное название линейный коэффициент корреляции Пирсона или просто коэффициент корреляции.
Коэффициент корреляции показывает тесноту линейной взаимосвязи и изменяется в диапазоне от -1 до 1. -1 (минус один) означает полную (функциональную) линейную обратную взаимосвязь. 1 (один) – полную (функциональную) линейную положительную взаимосвязь. 0 – отсутствие линейной корреляции (но не обязательно взаимосвязи). На практике всегда получаются промежуточные значения. Для наглядности ниже представлены несколько примеров с разными значениями коэффициента корреляции.
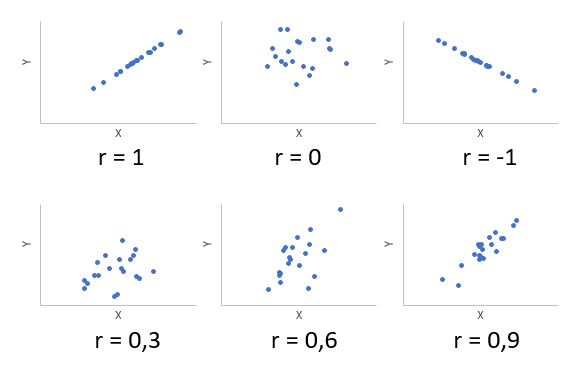
Таким образом, ковариация и корреляция отражают тесноту линейной взаимосвязи. Последняя используется намного чаще, т.к. является относительным показателем и не имеет единиц измерения.
Диаграммы рассеяния дают наглядное представление, что измеряет коэффициент корреляции. Однако нужна более формальная интерпретация. Эту роль выполняет квадрат коэффициента корреляции r2, который называется коэффициентом детерминации, и обычно применяется при оценке качества регрессионных моделей. Снова представьте линию, вокруг которой расположены точки.
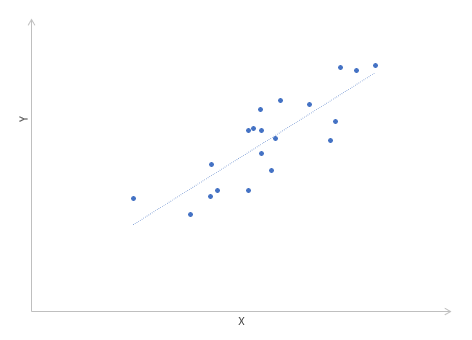
Линейная функция является моделью взаимосвязи между X иY и показывает ожидаемое значение Y при заданном X. Коэффициент детерминации – это соотношение дисперсии ожидаемых Y (точек на прямой линии) к общей дисперсии Y, или доля объясненной вариации Y. При r = 0,1 r2 = 0,01 или 1%, при r = 0,5 r2 = 0,25 или 25%.
Выборочный коэффициент корреляции
Коэффициент корреляции обычно рассчитывают по выборке. Значит, у аналитика в распоряжении не истинное значение, а оценка, которая всегда ошибочна. Если выборка была репрезентативной, то истинное значение коэффициента корреляции находится где-то относительно недалеко от оценки. Насколько далеко, можно определить через доверительные интервалы.
Согласно Центральное Предельной Теореме распределение оценки любого показателя стремится к нормальному с ростом выборки. Но есть проблемка. Распределение коэффициента корреляции вблизи придельных значений не является симметричным. Ниже пример распределения при истинном коэффициенте корреляции ρ = 0,86.
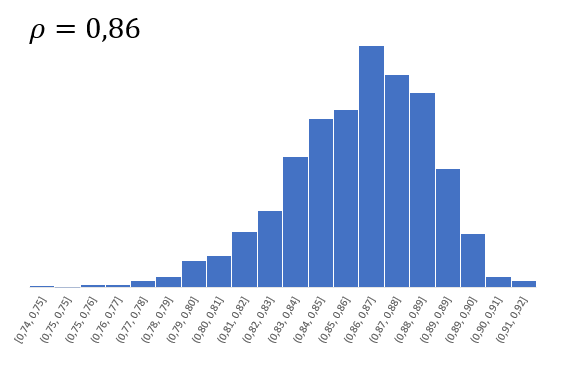
Предельное значение не дает выйти за 1 и, как бы «поджимает» распределение справа. Симметричная ситуация наблюдается, если коэффициент корреляции близок к -1.
В общем рассчитывать на свойства нормального распределения нельзя. Поэтому Фишер предложил провести преобразование выборочного коэффициента корреляции по формуле:
![]()
Распределение z для тех же r имеет следующий вид.
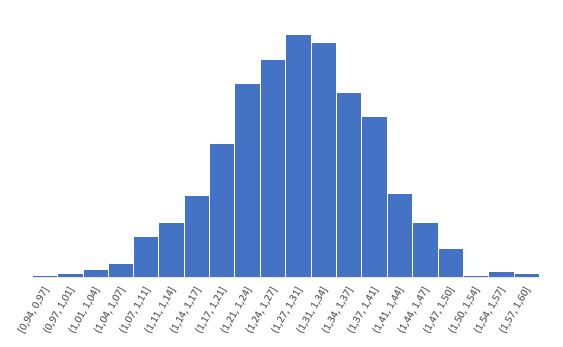
Намного ближе к нормальному. Стандартная ошибка z равна:
![]()
Далее исходя из свойств нормального распределения несложно найти верхнюю и нижнюю границы доверительного интервала для z. Определим квантиль стандартного нормального распределения для заданной доверительной вероятности, т.е. количество стандартных отклонений от центра распределения.
![]()
cγ – квантиль стандартного нормального распределения;
N-1 – функция обратного стандартного распределения;
γ – доверительная вероятность (часто 95%).
Затем рассчитаем границы доверительного интервала.
Нижняя граница z:
![]()
Верхняя граница z:
![]()
Теперь обратным преобразованием Фишера из z вернемся к r.
Нижняя граница r:
![]()
Верхняя граница r:
![]()
Это была теоретическая часть. Переходим к практике расчетов.
Как посчитать коэффициент корреляции в Excel
Корреляционный анализ в Excel лучше начинать с визуализации.
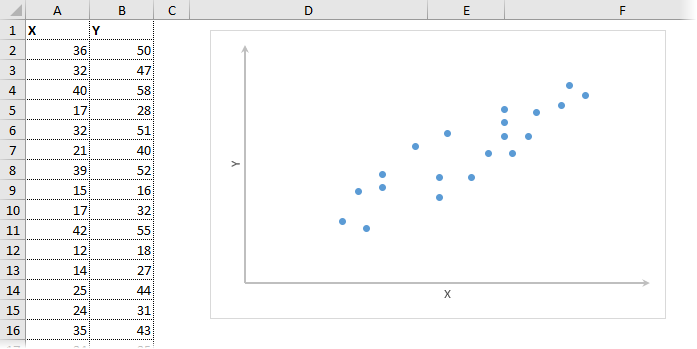
На диаграмме видна взаимосвязь двух переменных. Рассчитаем коэффициент парной корреляции с помощью функции Excel КОРРЕЛ. В аргументах нужно указать два диапазона.

Коэффициент корреляции 0,88 показывает довольно тесную взаимосвязь между двумя показателями. Но это лишь оценка, поэтому переходим к интервальному оцениванию.
Расчет доверительного интервала для коэффициента корреляции в Excel
В Эксель нет готовых функций для расчета доверительного интервала коэффициента корреляции, как для средней арифметической. Поэтому план такой:
— Делаем преобразование Фишера для r.
— На основе нормальной модели рассчитываем доверительный интервал для z.
— Делаем обратное преобразование Фишера из z в r.
Удивительно, но для преобразования Фишера в Excel есть специальная функция ФИШЕР.
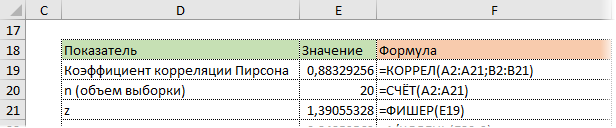
Стандартная ошибка z легко подсчитывается с помощью формулы.
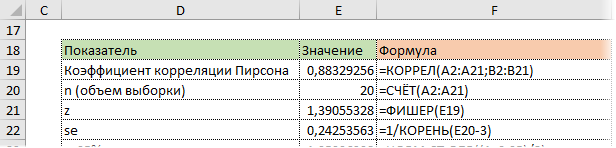
Используя функцию НОРМ.СТ.ОБР, определим квантиль нормального распределения. Доверительную вероятность возьмем 95%.
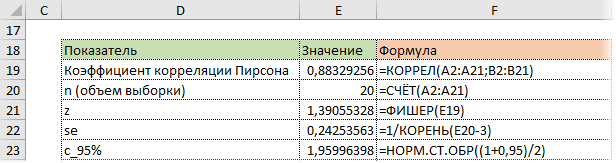
Значение 1,96 хорошо известно любому опытному аналитику. В пределах ±1,96σ от средней находится 95% нормально распределенных величин.
Используя z, стандартную ошибку и квантиль, легко определим доверительные границы z.
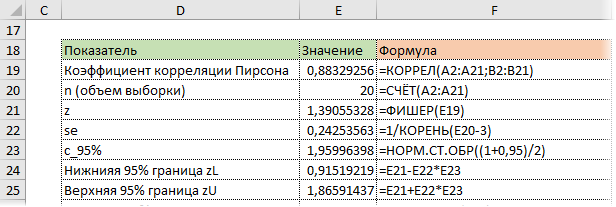
Последний шаг – обратное преобразование Фишера из z назад в r с помощью функции Excel ФИШЕРОБР. Получим доверительный интервал коэффициента корреляции.
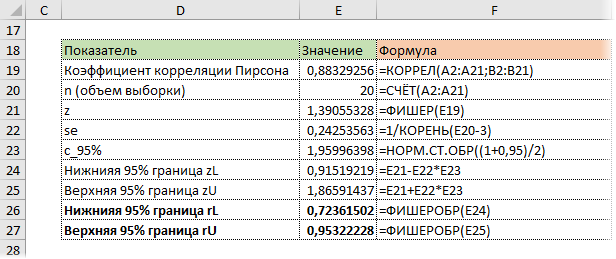
Нижняя граница 95%-го доверительного интервала коэффициента корреляции – 0,724, верхняя граница – 0,953.
Надо пояснить, что значит значимая корреляция. Коэффициент корреляции статистически значим, если его доверительный интервал не включает 0, то есть истинное значение по генеральной совокупности наверняка имеет тот же знак, что и выборочная оценка.
Несколько важных замечаний
1. Коэффициент корреляции Пирсона чувствителен к выбросам. Одно аномальное значение может существенно исказить коэффициент. Поэтому перед проведением анализа следует проверить и при необходимости удалить выбросы. Другой вариант – перейти к ранговому коэффициенту корреляции Спирмена. Рассчитывается также, только не по исходным значениям, а по их рангам (пример показан в ролике под статьей).
2. Синоним корреляции – это взаимосвязь или совместная вариация. Поэтому наличие корреляции (r ≠ 0) еще не означает причинно-следственную связь между переменными. Вполне возможно, что совместная вариация обусловлена влиянием третьей переменной. Совместное изменение переменных без причинно-следственной связи называется ложная корреляция.
3. Отсутствие линейной корреляции (r = 0) не означает отсутствие взаимосвязи. Она может быть нелинейной. Частично эту проблему решает ранговая корреляция Спирмена, которая показывает совместный рост или снижение рангов, независимо от формы взаимосвязи.
В видео показан расчет коэффициента корреляции Пирсона с доверительными интервалами, ранговый коэффициент корреляции Спирмена.
↓ Скачать файл с примером ↓
Поделиться в социальных сетях:
Корреляционный анализ. Линейная корреляция. Выборочный коэффициент корреляции.
Корреляционный анализ занимается степенью связи между двумя случайными величинами Х и Y.
Корреляционный анализ экспериментальных данных для двух случайных величин заключает в себе следующие основные приемы:
1. Вычисление выборочных коэффициентов корреляции.
2. Составление корреляционной таблицы.
3. Проверка статистической гипотезы значимости связи.
ОПРЕДЕЛЕНИЕ. Корреляционная зависимость между случайными величинами Х и Y называется линейной корреляцией, если обе функции регрессии f(x) и φ(x) являются линейными. В этом случае обе линии регрессии являются прямыми; они называется прямыми регрессии.
Для достаточно полного описания особенностей корреляционной зависимости между величинами недостаточно определить форму этой зависимости и в случае линейной зависимости оценить ее силу по величине коэффициента регрессии. Например, ясно, что корреляционная зависимость возраста Y учеников средней школы от года Х их обучения в школе является, как правило, более тесной, чем аналогичная зависимость возраста студентов высшего учебного заведения от года обучения, поскольку среди студентов одного и того же года обучения в вузе обычно наблюдается больший разброс в возраcте, чем у школьников одного и того же класса.
Для оценки тесноты линейных корреляционных зависимостей между величинами Х и Y по результатам выборочных наблюдений вводится понятие выборочного коэффициента линейной корреляции, определяемого формулой:
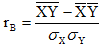 (7)
(7)
где σX и σY выборочные средние квадратические отклонения величин Х и Y, которые вычисляются по формулам:
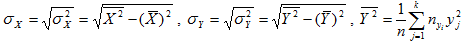 (8)
(8)
Следует отметить, что основной смысл выборочного коэффициента линейной корреляции rB состоит в том, что он представляет собой эмпирическую (т.е. найденную по результатам наблюдений над величинами Х и Y) оценку соответствующего генерального коэффициента линейной корреляции r: r=rB (9)
Принимая во внимание формулы:
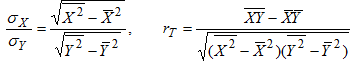
видим, что выборочное уравнение линейной регрессии Y на Х имеет вид:
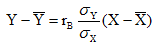 (10)
(10)
где 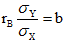 . То же можно сказать о выборочном уравнений линейной регрессии Х на Y:
. То же можно сказать о выборочном уравнений линейной регрессии Х на Y:
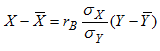 (11)
(11)
Основные свойства выборочного коэффициента линейной корреляции:
1. Коэффициент корреляции двух величин, не связанных линейной корреляционной зависимостью, равен нулю.
2. Коэффициент корреляции двух величин, связанных линейной корреляционной зависимостью, равен 1 в случае возрастающей зависимости и -1 в случае убывающей зависимости.
3. Абсолютная величина коэффициента корреляции двух величин, связанных линейной корреляционной зависимостью, удовлетворяет неравенству 0<|r|<1. При этом коэффициент корреляции положителен, если корреляционная зависимость возрастающая, и отрицателен, если корреляционная зависимость убывающая.
4. Чем ближе |r| к 1, тем теснее прямолинейная корреляция между величинами Y, X.
По своему характеру корреляционная связь может быть прямой и обратной, а по силе – сильной, средней, слабой. Кроме того, связь может отсутствовать или быть полной.
Сила и характер связи между параметрами
| Сила связи |
Характер связи |
|
| Прямая (+) | Обратная (-) | |
| Полная | 1 | -1 |
| Сильная | От 0,7 до 1 | От -0,7 до -1 |
| Средняя | От 0,3 до 0,7 | От -0,3 до -0,7 |
| Слабая | От 0,3 до 0 | От -0,3 до 0 |
| Связь отсутсвует | 0 | 0 |
Пример 4. Изучалась зависимость между двумя величинами Y и Х. Результаты наблюдений приведены в таблице в виде двумерной выборки объема 11:
| X | 68 | 37 | 50 | 53 | 75 | 66 | 52 | 65 | 74 | 65 | 54 |
| Y | 114 | 149 | 146 | 141 | 114 | 112 | 124 | 105 | 141 | 120 | 124 |
Требуется:
1) Вычислить выборочный коэффициент корреляции;
2) Оценить характер и силу корреляционной зависимости;
3) Написать уравнение линейной регрессии Y на Х.
Решение. По известным формулам:
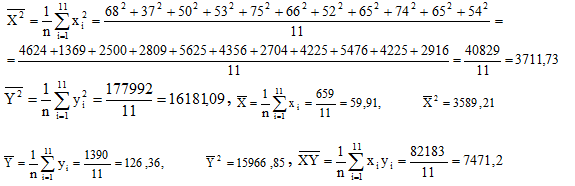
Отсюда, по (7) и (8):
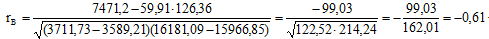
Таким образом, следует сделать вывод, что рассматриваемая корреляционная зависимость между величинами Х и Y является по характеру – обратной, по силе – средней.
3) Уравнение линейной регрессии Y на Х:
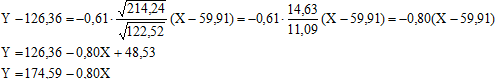
Пример 5. Изучалась зависимость между качеством Y (%) и количеством Х (шт). Результаты наблюдений приведены в виде корреляционной таблицы:
| YX | 18 | 22 | 26 | 30 | ny |
| 70 | 5 | 5 | |||
| 75 | 7 | 46 | 1 | 54 | |
| 80 | 29 | 72 | 101 | ||
| 85 | 29 | 8 |
37 |
||
| 90 | 3 | 3 | |||
| nx | 12 | 75 | 102 | 11 | 200 |
Требуется вычислить выборочный коэффициент линейной корреляции зависимости Y от Х.
Решение. Для упрощения вычислений перейдем к новым переменным – условным вариантам (ui, vi), воспользовавшись формулами (*) (§3) при h1=4, h2=5, x0=26, y0=80. Для удобства перепишем данную таблицу в новых обозначениях:
| uv | -2 | -1 | 0 | 1 | nv |
| -2 | 5 | 5 | |||
| -1 | 7 | 46 | 1 | 54 | |
| 0 | 29 | 72 | 101 | ||
| 1 | 29 | 8 |
37 |
||
| 2 | 3 | 3 | |||
| nu | 12 | 75 | 102 | 11 | 200 |
Имеем при xi=ui и yj=vj:
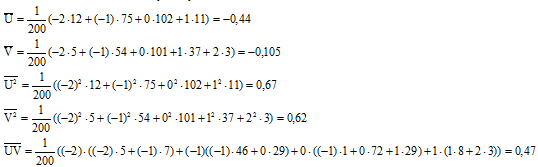
Таким образом:
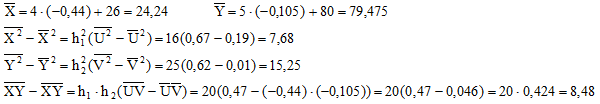
Отсюда, 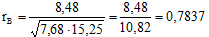
Вывод: Корреляционная зависимость между величинами Х и Y – прямая и сильная.
Добавлять комментарии могут только зарегистрированные пользователи.
Регистрация Вход
