Как найти вычет числа по модулю - Сайт, где вы сможете решить свои вопросы

Элементы теории чисел.

Понятие
вычета по модулю

Целые числа a и b
сравнимы по модулю n (целому числу,
неравному нулю), если выполняется условие

a=b+k•n

для некоторого
целого числа k. В этом случае обычно
используется следующая запись:

a=b {mod n}

Сравнимость a и b
по модулю n означает, что n делит a-b нацело:

n | (a-b)

Если b≥0, a=b {mod n} и
|b|<n, то b называют вычетом числа a по
модулю n. Вычет равен остатку от
целочисленного деления числа a на число
n. Операцию нахождения вычета числа a по
модулю n называют приведением числа a
по модулю n.

-a
{mod n} = -a+n {mod n}

n=0
{mod n}

Примеры:

3+10
{mod 12} = 1 {mod 12} («арифметика»
часов);

-5 {mod 7} = 2 {mod 7}.

Полным набором
вычетов по модулю n называется множество
целых чисел от нуля до n-1:

{0, 1, 2, … , n-1}

Вычеты по модулю
n с применением операций сложения и
умножения образуют коммутативное
кольцо, в котором справедливы законы
ассоциативности, коммутативности и
дистрибутивности.

аддитивности

(a+b)
{mod n} = (a {mod n} + b {mod n}) {mod n}

мультипликативности

(a•b)
{mod n} = (a {mod n} • b {mod n}) {mod n}

сохранения
степени

a^b
{mod n} = (a {mod n})^b
{mod n}

Данные
свойства операций над вычетами позволяют
либо сначала вычислять вычеты, а затем
выполнять операцию, либо сначала
выполнять операцию, а затем вычислять
вычеты. Операция вычисления вычета
является гомоморфным
отображением кольца
целых чисел в кольцо вычетов по модулю
n.

Наибольшим
общим делителем (НОД)
целых чисел a
и b
называется наибольшее целое число, на
которое делятся без остатка a
и b.
Простым
числом называется
целое число, которое делится без остатка
только на единицу и на себя.
Целые
числа a
и b
называются взаимно
простыми,
если выполняется условие НОД(a,
b)=1.

Целое
число y
называется мультипликативно
обратным целому
числу x
по модулю n,
если выполняется условие x•y
{mod
n}
= 1. Мультипликативно обратное целое
число существует только тогда, когда x
и n
– взаимно простые числа. Если целые
числа a
и n
не являются взаимно простыми, то сравнение
a^-1=x
{mod
n}
не имеет решения.

Функция
Эйлера

Если
из полного набора вычетов по модулю n
выделить подмножество вычетов, взаимно
простых с n,
то получим приведенный
набор вычетов.
Например:

{0, 1, 2, 3, 4, 5, 6, 7, 8, 9,
10} – полный набор вычетов по модулю 11.
Приведенным набором вычетов будет то
же подмножество целых чисел за исключением
нуля.

{0, 1, 2, 3, 4, 5, 6, 7, 8, 9}
– полный набор вычетов по модулю 10.
Приведенным набором вычетов будет
подмножество целых чисел {1, 3, 7, 9}.

Очевидно,
что если n
является простым числом, то приведенный
набор вычетов по модулю n
всегда содержит n-1
элемент (все целые числа от единицы до
n-1).
Значением
функции
Эйлера φ(n)
будет количество элементов в приведенном
наборе вычетов по модулю n.
Если n
– простое число, то φ(n)=n-1
и φ(n²)=n•(n-1).
Если n=p•q
(p
и q
– простые числа и p≠q),
то φ(n)=(p-1)•(q-1).

Китайская
теорема об остатках (1-й век н.э.)

Если

m₁,
m₂,
…, m_k
– попарно взаимно простые числа, большие
1 (модули);
M=m₁∙m₂∙
…∙m_k
(произведение модулей);
a₁,
a₂,
…, a_k
− вычеты по модулям m₁,
m₂,
…, m_k
неотрицательного числа x,
меньшего M,
то

где
M_i=M/m_i
и N_i
– мультипликативно обратное к M_i

по
модулю m_i
(M_i∙N_i=1
{mod
m_i}).

Малая
теорема Ферма

Если
a
– целое число, n
– простое число и НОД(a,
n)=1,
то

aⁿ^-1=1
{mod n}.

Теорема
Эйлера

Является
обобщением малой теоремы Ферма: если
целые числа a
и n
являются взаимно простыми (НОД(a,
n)=1),
то

a^φ⁽ⁿ⁾=1
{mod n}.

Причины
использования вычетов в криптографии

Выполнение обратных
операций (логарифмирование, извлечение
корня, разложение на простые сомножители
– факторизация) гораздо более трудоемко,
чем выполнение прямых операций (возведения
в степень или произведения).

При вычислениях
с вычетами ограничивается диапазон
возможных промежуточных значений и
результата (например, a25{mod
n}=((((a2∙a)2)2)2)∙a{mod n}).

Способы симметричного
шифрования.

Перестановки.
Подстановки
(замены).
Гаммирование.

Шифры
перестановок

Биты (или символы)
открытого текста переставляются в
соответствии с задаваемым ключом
шифрования правилом:

“
i, 1≤i≤n C_i=P_k[i],
где

P=<P₁,
P₂,
… , P_i,
… , P_n>
– открытый текст;
n – длина
открытого текста;
C=<C₁,
C₂,
… , C_i,
… , C_n>
– шифротекст;
k=<k₁,
k₂,
…, k_i,
… , k_n>
– ключ шифрования.
При расшифровании
применяется обратная перестановка:
“
i, 1≤i≤n P_k[i]=
C_i.
Очевидно, что при
шифровании перестановкой ключ должен
удовлетворять условию:
“k_iÎk
1≤k_i≤n
Ù
“
k_i,
k_jÎk
(i≠j)
k_i≠k_j.

Пример.
Пусть надо зашифровать слово «связной»
(n=7) с помощью ключа k={4, 2, 1, 7, 6, 3, 5}. В
результате шифрования мы получаем
шифротекст «звсйоян».

Если длина ключа
меньше длины открытого текста, то можно
разбить открытый текст на блоки, длина
которых равна длине ключа, и последовательно
применить ключ перестановки к каждому
блоку открытого текста. Если длина
открытого текста не кратна длине ключа,
то последний блок может быть дополнен
пробелами или нулями.

Можно использовать
и другой прием. После разбиения открытого
текста длиной n на блоки, длина которых
равна длине ключа m, открытый текст
записывается в таблицу с числом столбцов,
равным длине ключа (каждый блок открытого
текста записывается в столбец таблицы).
Количество строк таблицы в этом случае
будет равно наименьшему целому числу,
не меньшему n/m. Затем столбцы полученной
таблицы переставляются в соответствии
с ключом перестановки, а шифротекст
считывается по строкам таблицы.

При расшифровании
шифротекст записывается в таблицу того
же размера по строкам, затем происходит
обратная перестановка столбцов в
соответствии с ключом, после чего
расшифрованный текст считывается из
таблицы по столбцам.
Достоинством
шифрования перестановкой является
высокая скорость получения шифротекста.
К недостаткам
шифрования перестановкой относятся
сохранение частотных характеристик
открытого текста после его шифрования
(символы открытого текста лишь меняют
свои позиции в шифротексте) и малое
число возможных ключей шифрования.

Шифры
подстановок

При
шифровании с помощью подстановки
(замены)
каждый символ открытого текста заменяется
другим символом одного и того же
(одноалфавитная
подстановка)
или разных (многоалфавитная
подстановка)
алфавитов в соответствии с определяемым
ключом шифрования правилом.

Одноалфавитная
подстановка

“
i, 1≤i≤n C_i=P_i+k
{mod m}, где

P=<P₁,
P₂,
… , P_i,
… , P_n>
– открытый текст;
n – длина
открытого текста;
A={A₁,
A₂,
… , A_m}
– алфавит символов открытого текста
(“
i,
1≤i≤n
P_iÎA);
C=<C₁,
C₂,
… , C_i,
… , C_n>
– шифротекст;
k
– ключ шифрования (0≤k<m);

“a_iÎA,
1≤i≤m a_i+k
{mod m}=a_i+k{mod

m}.

При
расшифровании символ шифротекста
заменяется символом, номер которого в
используемом алфавите больше номера
символа шифротекста на величину m-k
(m
– мощность используемого алфавита, а
k
– ключ шифрования; применяется операция
сложения в кольце вычетов по модулю
m):

”
i, 1≤i≤n C_i=P_i+m-k
{mod m}

Пример. При
шифровании открытого текста «наступайте»
с помощью одноалфавитной подстановки
по ключу 3 (так называемой подстановки
Цезаря) получаем шифротекст «ргфхцтгмхз».

К основным
недостаткам относится:

сохранение частоты
появления различных символов открытого
текста в шифротексте (одинаковые символы
открытого текста остаются одинаковыми
и в шифротексте);
малое число
возможных ключей.

Многоалфавитная
подстановка

“
i, 1≤i≤n C_i=P_i+k_i
{mod m}, где

P=<P₁,
P₂,
… , P_i,
… , P_n>
– открытый текст;
n – длина
открытого текста;
A={A₁,
A₂,
… , A_m}
– алфавит символов открытого текста
(“
i,
1≤i≤n
P_iÎA);
C=<C₁,
C₂,
… , C_i,
… , C_n>
– шифротекст;
k=<k₁,
k₂,
… , k_i,
… , k_n>
– ключ шифрования (“
i,
1≤i≤n
0≤k_i<m);

“a_iÎA,
1≤i≤m a_i+k
{mod m}=a_i+k{mod

m}.

Расшифрование:

“
i, 1≤i≤n C_i=P_i+m-k_i
{mod m}.

Если
длина ключа меньше длины открытого
текста, то необходимо разбить открытый
текст на блоки, длина которых равна
длине ключа, и последовательно применить
ключ подстановки к каждому блоку
открытого текста. Если длина открытого
текста не кратна длине ключа, то для
шифрования последнего блока надо взять
только первые l
элементов ключа (l
– длина последнего блока).

К достоинствам
относится то, что в шифротексте маскируется
частота появления различных символов
открытого текста. Поэтому криптоаналитик
не может при вскрытии шифра использовать
частотный словарь букв естественного
языка.

Шифры
гаммирования

Шифротекст
получается путем наложения на открытый
текст гаммы
шифра с помощью какой-либо обратимой
операции (как правило, поразрядного
сложения по модулю 2):

“
i, 1≤i≤n C_i=P_i
Å
G_i,
где

P=<P₁,
P₂,
… , P_i,
… , P_n>
– открытый текст;
n – длина
открытого текста;
C=<C₁,
C₂,
… , C_i,
… , C_n>
– шифротекст;
G=<G₁,
G₂,
… , G_i,
… , G_n>
– гамма шифра;
Å
– операция поразрядного сложения по
модулю 2.

Расшифрование
заключается в повторном наложении той
же гаммы шифра на шифротекст:

“
i, 1≤i≤n P_i=C_i
Å
G_i.

Гамма
шифра вычисляется с помощью программного
или аппаратного датчика
(генератора)
псевдослучайных чисел,
параметры которого определяются ключом
шифрования.

Источник

Сравне́ние двух целых чисел по мо́дулю натурального числа — математическая операция, позволяющая ответить на вопрос о том, дают ли два выбранных целых числа при делении на один и тот же остаток. Любое целое число при делении на дает один из возможных остатков: число от 0 до m-1 ; это значит, что все целые числа можно разделить на групп, каждая из которых отвечает определённому остатку от деления на . Эти группы называются классами вычетов по модулю , а содержащиеся в них целые числа — вычетами по модулю ^[⇨].

Арифметические операции с остатками чисел по фиксированному модулю образуют мо́дульную арифме́тику или модуля́рную арифметику^[1]^[2], которая широко применяется в математике, информатике и криптографии^[3].

История[править | править код]

Предпосылкой к созданию теории сравнений стало восстановление сочинений Диофанта, которые были выпущены в подлиннике и с латинским переводом, благодаря Баше де Мезириаку, в 1621 году. Их изучение привело Ферма́ к открытиям, которые по значению существенно опередили своё время. Например, в письме к Френиклю де Бесси^ru_fr^[4] 18 октября 1640 года он сообщил без доказательства теорему, впоследствии получившую название малой теоремы Ферма. В современной формулировке теорема утверждает, что если — простое число и — целое число, не делящееся на , то

$a^{p-1}equiv 1{pmod {p}}$

Первое доказательство этой теоремы принадлежит Лейбницу, причём он открыл указанную теорему независимо от Ферма́ не позднее 1683 года и сообщил об этом с приведением точного доказательства Бернулли. Кроме этого, Лейбницем был предложен прообраз формулировки теоремы Вильсона.

Позже изучение вопросов, посвященных теории чисел и теории сравнений, было продолжено Эйлером, который ввел квадратичный закон взаимности и обобщил теорему Ферма, установив, что

$a^{varphi (n)}equiv 1{pmod {n}},$

где — функция Эйлера.

Понятие и символьное обозначение сравнений было введено Гауссом, как важный инструмент для обоснования его арифметической теории, работа над которой была начата им в 1797 году. В начале этого периода Гауссу ещё не были известны труды его предшественников, поэтому результаты его работы, изложенные в первых трёх главах его книги «Арифметические исследования» (1801 год), были в основном уже известны, однако методы, которые он использовал для доказательств, оказались абсолютно новыми, имеющими высшую важность для развития теории чисел. Используя эти методы, Гаусс преобразовал все накопленные до него сведения, связанные с операциями сравнения по модулю, в стройную теорию, которая впервые была изложена в этой же книге. Кроме этого, он исследовал сравнения первой и второй степени, теорию квадратичных вычетов и связанный с ней квадратичный закон взаимности^[5].

Определения[править | править код]

Сравнимость чисел и записывается в виде формулы (сравнения):

Число называется модулем сравнения.

Определение сравнимости чисел и по модулю равносильно любому из следующих утверждений:

Например, числа 32 и −10 сравнимы по модулю 7, так как оба числа при делении на 7 дают остаток 4:

Также числа 32 и -10 сравнимы по модулю 7, так как их разность делится на 7 и к тому же имеет место представление

Свойства сравнимости по модулю[править | править код]

Для фиксированного натурального числа отношение сравнимости по модулю обладает следующими свойствами:

Таким образом, отношение сравнимости по модулю является отношением эквивалентности на множестве целых чисел^[8].

Кроме вышеперечисленных свойств, для сравнений справедливы следующие утверждения:

Доказательство

Пусть

Следовательно

где

— некое целое число.

Так как является делителем числа , то

где

— некое целое число.

Следовательно

где

по определению.

Следствие:

Для того, чтобы числа

были сравнимы по модулю

, каноническое разложение на простые сомножители которого имеет вид

$m = prod_{i=1}^d p_i^{alpha_i},$

необходимо и достаточно, чтобы

${displaystyle aequiv b{pmod {p_{i}^{alpha _{i}}}},}$

где

^[9].

Операции со сравнениями[править | править код]

Сравнения по одному и тому же модулю обладают многими свойствами обычных равенств. Например, их можно складывать, вычитать и перемножать: если числа $a_{1},a_{2},ldots ,a_{n}$ и $b_{1},b_{2},ldots ,b_{n}$ попарно сравнимы по модулю , то их суммы $a_{1}+a_{2}+ldots +a_{n}$ и ${displaystyle b_{1}+b_{2}+ldots +b_{n}}$ , а также произведения и тоже сравнимы по модулю :

${displaystyle (a_{1}+a_{2}+ldots +a_{n})equiv (b_{1}+b_{2}+ldots +b_{n}){pmod {m}};}$

${displaystyle (a_{1}cdot a_{2}cdot ldots cdot a_{n})equiv (b_{1}cdot b_{2}cdot ldots cdot b_{n}){pmod {m}}.}$

При этом нельзя выполнять эти операции со сравнениями, если их модули не совпадают^[9].

К обеим частям сравнения можно прибавить одно и то же число :

{displaystyle (a+c)equiv (b+c){pmod {m}}.}

Также можно перенести число из одной части сравнения в другую со сменой знака:

Если числа и сравнимы по модулю , то их степени a^k и $b^{k}$ тоже сравнимы по модулю при любом натуральном ^[7]:

${displaystyle a^{k}equiv b^{k}{pmod {m}}.}$

K любой из частей сравнения можно прибавить целое число, кратное модулю, то есть, если числа и сравнимы по модулю некоторого числа , то и a + t_1 сравнимо с ${displaystyle b+t_{2}}$ по модулю , где $t_{1}$ и $t_{2}$ — произвольные целые числа, кратные :

${displaystyle (a+t_{1})equiv (b+t_{2}){pmod {m}}.}$

Также обе части сравнения и модуль можно умножить на одно и то же число, то есть, если числа и сравнимы по модулю некоторого целого числа , то и числа и сравнимы по модулю числа , где — целое:

Сравнения, однако, нельзя, вообще говоря, делить друг на друга или на другие числа. Пример: , однако, сократив в 2 раза, мы получаем ошибочное сравнение: . Правила сокращения для сравнений следующие.

Можно делить обе части сравнения на число, но только взаимно простое с модулем: если

и НОД

то

Если, число не взаимно просто с модулем, как было в примере, указанном выше, то сокращать на нельзя.

Можно одновременно разделить обе части сравнения и модуль на их общий делитель:

если , то ^[9].

Пример[править | править код]

Применение сравнений позволяет легко получать разнообразные признаки делимости. Например, выведем признак делимости натурального числа N на 7. Запишем в виде (то есть отделим цифру единиц). Условие, что делится нацело на 7, можно записать в виде: Умножим это сравнение на

{displaystyle -20a-2bequiv 0{pmod {7}}.}

Или, прибавив слева число кратное модулю:

Отсюда вытекает следующий признак делимости на 7: надо вычесть из числа десятков удвоенное число единиц, затем повторять эту операцию до тех пор, пока не получится двузначное или однозначное число; если оно делится на 7, то и исходное число делится. Например, пусть Алгоритм проверки^[10]:

${displaystyle N_{1}=2262-2cdot 4=2254; N_{2}=225-2cdot 4=217;N_{3}=21-2cdot 7=7}$

Вывод: 22624 делится на 7.

Связанные определения[править | править код]

Классы вычетов[править | править код]

Множество всех чисел, сравнимых с по модулю , называется классом вычетов по модулю , и обычно обозначается [a]_m или bar a_m . Таким образом, сравнение равносильно равенству классов вычетов ^[11].

Любое число класса вычетов называется вычетом по модулю . Пусть для определённости ― остаток от деления любого из представителей выбранного класса на , тогда любое число из этого класса вычетов можно представить в виде , где — целое. Вычет, равный остатку ( при ) называется наименьшим неотрицательным вычетом, а вычет rho (), самый малый по абсолютной величине, называется абсолютно наименьшим вычетом. При ${displaystyle r<{frac {m}{2}}}$ получаем, что rho =r , в противном случае . Если — чётное и $r = frac{m}{2}$ , то $rho = -frac{m}{2}$ ^[12].

Поскольку сравнимость по модулю является отношением эквивалентности на множестве целых чисел , то классы вычетов по модулю представляют собой классы эквивалентности; их количество равно .

Множество всех классов вычетов по модулю обозначается $mathbb {Z} _{m}$ или ^[13] или ^[14].

Операции сложения и умножения на индуцируют соответствующие операции на множестве $mathbb {Z} _{m}$ :

${displaystyle [a]_{m}+[b]_{m}=[a+b]_{m};}$

${displaystyle [a]_{m}cdot [b]_{m}=[acdot b]_{m}.}$

Относительно этих операций множество $mathbb {Z} _{m}$ является конечным кольцом, а для простого — конечным полем^[6].

Системы вычетов[править | править код]

Система вычетов позволяет осуществлять арифметические операции над конечным набором чисел, не выходя за его пределы.
Полная система вычетов по модулю ― любой набор из попарно несравнимых по модулю целых чисел.
Обычно в качестве полной системы вычетов по модулю берётся одно из двух множеств:

наименьшие неотрицательные вычеты, то есть числа:

или абсолютно наименьшие вычеты, состоящие в случае нечётного из чисел

${displaystyle 0,pm 1,pm 2,ldots ,pm {frac {m-1}{2}}}$

и в случае чётного

из чисел

${displaystyle 0,pm 1,pm 2,ldots ,pm left({frac {m}{2}}-1right),-{frac {m}{2}}}$

Максимальный набор попарно несравнимых по модулю чисел, взаимно простых с , называется приведённой системой вычетов по модулю . Всякая приведённая система вычетов по модулю содержит элементов, где — функция Эйлера^[12].

Например, для числа m=42 полная система вычетов может быть представлена числами 0, 1, 2, 3, …, 21, 22, 23, …, 39, 40, 41, а приведённая — 1, 5, 11, 13, 17, 19, 23, 25, 29, 31, 37, 41.

Сравнения в кольце многочленов над полем[править | править код]

Рассматривается кольцо многочленов K[x] над полем . Два многочлена $g_{1}$ и
$g_{2}$ , принадлежащие выбранному кольцу, называются сравнимыми по модулю многочлена , если их разность g_1-g_2 делится на без остатка. Сравнение обозначается следующим образом:

${displaystyle g_{1}equiv g_{2}{pmod {f}}.}$

Так же, как и в кольце целых чисел, такие сравнения можно складывать, вычитать и перемножать^[15].

Решение сравнений[править | править код]

Сравнения первой степени[править | править код]

В теории чисел, криптографии и других областях науки часто возникает задача поиска решений сравнения первой степени вида

{displaystyle acdot xequiv b{pmod {m}}.}

Решение такого сравнения начинается с вычисления d = НОД (a,m) . При этом возможны два случая:

${displaystyle a_{1}xequiv b_{1}{pmod {m_{1}}},}$

где ${displaystyle a_{1}={frac {a}{d}},}$

$b_1 = frac{b}{d}$

и $m_1 = frac{m}{d}$

являются целыми числами, причём $a_{1}$

взаимно просты. Поэтому число $a_{1}$

можно обратить по модулю m_1

, то есть найти такое число

, что ${displaystyle ccdot a_{1}equiv 1{pmod {m_{1}}}}$

(другими словами, ${displaystyle cequiv a_{1}^{-1}{pmod {m_{1}}}}$

). Теперь решение находится умножением полученного сравнения на

${displaystyle xequiv ca_{1}xequiv cb_{1}equiv a_{1}^{-1}b_{1}{pmod {m_{1}}}.}$

Практическое вычисление значения можно осуществить разными способами: с помощью теоремы Эйлера, алгоритма Евклида, теории цепных дробей (см. алгоритм) и др. В частности, теорема Эйлера позволяет записать значение в виде:

${displaystyle cequiv a_{1}^{-1}equiv a_{1}^{varphi (m_{1})-1}{pmod {m_{1}}}}$

^[16].

Примеры[править | править код]

Пример 1. Для сравнения

имеем d=2 , поэтому по модулю 22 сравнение имеет два решения. Заменим 26 на 4, сравнимое с ним по модулю 22, и затем сократим все три числа на 2:

Поскольку 3 взаимно просто с модулем 11, то его можно обратить по модулю 11 и найти

${displaystyle 3^{-1}equiv 4{pmod {11}}}$

Умножая сравнение на 4, получаем решение по модулю 11:

эквивалентное совокупности двух решений по модулю 22:

Пример 2. Дано сравнение:

Отметим, что модуль 65537

— простое число.

Первый способ решения — воспользоваться соотношением Безу. С помощью алгоритма Евклида или программы, приведенной в статье о соотношении Безу, находим, что это соотношение для чисел 100 и 65537 имеет вид:

{displaystyle 17695cdot 100+(-27)cdot 65537=1,}

или

Умножив обе части этого сравнения на 41, получим:

Отсюда следует, что 725495 есть решение исходного сравнения. Удобнее заменить его на сравнимое с ним 4588 (остаток от деления 725495 на 65537 ). Ответ:

Второй способ решения, более простой и быстрый, не требует построения соотношения Безу, но также эквивалентен алгоритму Евклида.

Шаг 1. Делим модуль на коэффициент при x с остатком: . Умножим обе части исходного сравнения на частное 655 и прибавим 37x ; получим: , но левая часть кратна 65537 , то есть сравнима с нулём, откуда:

{displaystyle 37xequiv -26855{pmod {65537}}}

Мы получили при коэффициент 37 вместо 100. На каждом следующем шаге уменьшаем аналогично, пока не получим единицу.

Шаг 2. Аналогично делим на новый коэффициент при x: . Умножим обе части сравнения, полученного в предыдущем шаге, на частное 1771 и прибавим 10x ; снова заменив левую часть на ноль, получим:

заменяем на его остаток при делении на 65537, равный 45880 :

Далее можно было бы сделать аналогично ещё 5 шагов, но проще разделить обе части сравнения на 10 и сразу получить результат:

Сравнения второй степени[править | править код]

Сравнения второй степени по простому модулю m имеет следующий общий вид:

$c_0x^2+c_1x+c equiv 0pmod {m}.$

Это выражение можно привести к виду

${displaystyle (x+b)^{2}equiv a{pmod {m}},}$

а при замене упрощается до

${displaystyle z^{2}equiv a{pmod {m}}.}$

Решение этого сравнения сводится к выяснению, является ли данное число квадратичным вычетом (с помощью квадратичного закона взаимности) и последующему вычислению квадратного корня по данному модулю^[17]. Для вычисления квадратного корня из квадратичного вычета существует вероятностный метод Берлекэмпа и детерминированный алгоритм Тонелли — Шенкса.

Системы сравнений[править | править код]

Китайская теорема об остатках утверждает, что система сравнений с попарно взаимно простыми модулями $m_{1},m_{2},ldots ,m_{n}$ :

${begin{cases}xequiv a_{1}{pmod {m_{1}}}\xequiv a_{2}{pmod {m_{2}}}\ldots \xequiv a_{n}{pmod {m_{n}}}end{cases}}$

всегда разрешима, и её решение единственно по модулю ${displaystyle m_{1}cdot m_{2}cdot ldots cdot m_{n}}$ .

Другими словами, китайская теорема об остатках утверждает, что кольцо вычетов по модулю произведения нескольких попарно взаимно простых чисел является прямым произведением соответствующих множителям колец вычетов.

Применение[править | править код]

Модульная арифметика используются в теории чисел, теории групп, теории колец, теории узлов, общей алгебре, криптографии, информатике, химии и других областях.

Например, сравнения часто применяются для вычисления контрольных сумм, используемых в идентификаторах. Так, для определения ошибок при вводе международного номера банковского счета используется сравнение по модулю 97^[18].

В криптографии сравнения можно встретить в системах с открытым ключом, использующих, например, алгоритм RSA или протокол Диффи — Хеллмана. Также, модульная арифметика обеспечивает конечные поля, над которыми затем строятся эллиптические кривые, и используется в различных протоколах с симметричным ключом (AES, IDEA)^[19].

В химии последняя цифра в регистрационном номере CAS является значением контрольной суммы, которая вычисляется путём сложения последней цифры номера, умноженной на 1, второй справа цифры, умноженной на 2, третьей, умноженной на три и так далее до первой слева цифры, завершаясь вычислением остатка от деления на 10^[20]

См. также[править | править код]

Сложение по модулю 2
Возведение в степень по модулю
Показатель числа по модулю
Алгоритмы быстрого возведения в степень по модулю

Примечания[править | править код]

↑ Вельшенбах М. Глава 5. Модульная математика: вычисление в классах вычетов. // Криптография на Си и C++ в действии. — М.: «Триумф», 2004. — С. 81—95. — 464 с. — ISBN 5-89392-083-X.
↑ Материалы международной научной конференции “Модулярная арифметика”. Виртуальный компьютерный музей (2005). Дата обращения: 31 июля 2010. Архивировано 5 октября 2007 года.
↑ Егоров А. А. Сравнения по модулю и арифметика остатков // Квант. — 1970. — № 5. — С. 28—33. Архивировано 4 марта 2016 года.
↑ Французский математик, член французской академии наук с 1666.
↑ Вилейтнер Г. Глава III. Теория чисел // История математики от Декарта до середины XIX / пер. с нем. под. ред. А. П. Юшкевича. — М.: Государственное издательство физико-математической литературы, 1960. — С. 69—84. — 467 с. Архивная копия от 24 сентября 2015 на Wayback Machine
↑ ¹ ² Степанов С. А. Глава 1. Основные понятия // Сравнения. — М.: «Знание», 1975. — С. 3—9. — 64 с. Архивная копия от 24 августа 2015 на Wayback Machine
↑ ¹ ² Виноградов И. М. Основы теории чисел. — М.—Л.: Гос. изд. технико-теоретической литературы, 1952. — С. 41—45. — 180 с. Архивная копия от 1 июля 2020 на Wayback Machine
↑ Сизый, 2008, с. 88.
↑ ¹ ² ³ Сагалович, 2010, с. 25—29.
↑ Нестеренко, 2008, с. 86—87.
↑ Бухштаб А. А. Глава 8. Классы // Теория чисел. — М.: «Просвещение», 1966. — С. 77—78. — 384 с. Архивная копия от 20 ноября 2015 на Wayback Machine
↑ ¹ ² Сагалович, 2010, с. 29—32.
↑ Сизый, 2008, с. 87—88,91.
↑ Лидл Р., Нидеррайтер Г. Конечные поля. В 2-х тт. — М.: Мир, 1998. — С. 27 (Пример 1.37). — 430 с. — ISBN 5-03-000065-8.
↑ Фадеев Д. К. Глава VII. Сравнение в кольце полиномов и расширения полей // Лекции по алгебре. — М.: «Наука», 1984. — С. 197—198. — 416 с.
↑ Сизый, 2008, с. 105—109.
↑ Бухштаб А. А. Глава 21. Сравнения 2-й степени по простому модулю, Глава 22. Сравнения второй степени по составному модулю // Теория чисел. — М.: «Просвещение», 1966. — С. 172—201. — 384 с. Архивная копия от 20 ноября 2015 на Wayback Machine
↑ Harald Niederreiter, Arne Winterhof. Applied Number Theory. — «Springer», 2015. — С. 369. — 442 с. — ISBN 978-3-319-22321-6.
↑ Коблиц Н. Курс теории чисел и криптографии / пер. с англ. М. А. Михайловой и В. Е. Тараканова под ред. А. М. Зубкова. — М.: Научное изд-во ТВП, 2001. — С. 96, 105—109, 200—209. — 262 с. — ISBN 5-85484-012-X.
↑ Check Digit Verification of CAS Registry Numbers (англ.). Архивировано 8 декабря 2015 года.

Литература[править | править код]

Бухштаб А. А. Теория чисел. — М.: «Просвещение», 1966. — 384 с.
Вейль А. Основы теории чисел. — М.: Мир, 1972.
Виленкин Н. Я. Сравнения и классы вычетов // Квант. — 1978. — № 10. — С. 4—8.
Виноградов И. М. Основы теории чисел. — М.—Л.: Гос. изд. технико-теоретической литературы, 1952. — 180 с.
Коблиц Н. Курс теории чисел и криптографии / пер. с англ. М. А. Михайловой и В. Е. Тараканова,под ред. А. М. Зубкова. — М.: Научное изд-во ТВП, 2001. — 254 с. — ISBN 5-85484-012-X.
Материалы международной научной конференции “Модулярная арифметика”. Виртуальный компьютерный музей (2005). Дата обращения: 31 июля 2010.
Нестеренко Ю. В. Теория чисел. — М.: Издательский центр «Академия», 2008. — С. 132—133. — 272 с. — ISBN 9785769546464.
Сагалович Ю. Л. Введение в алгебраические коды — 2-е изд. — М.: ИППИ РАН, 2010. — 320 с. — ISBN 978-5-901158-14-2
Сизый С. В. §4. Теория сравнений // Лекции по теории чисел. — М.: Физматлит, 2008. — 192 с. — ISBN 978-5-9221-0741-9.

Источник

А что, если сумма цифр нашего числа все-таки не кратна 9? Возьмем, например, число 3457. Следуя алгоритму, означенному чуть выше, мы можем представить 3457 (сумма цифр которого равна 19) как 3(999) + 4(99) + 5(9) + 7 + 12, то есть 3457 – это 7 + 12 = 19, что чуть больше, чем кратное девятке 18. А если 19 = 18 + 1, значит, и 3457 ровно на единицу больше ближайшего кратного 9 числа. К тому же выводу можно прийти, сложив цифры числа 19, потом – цифры числа 10, то есть вот какая последовательность у нас получается:

3457 ? 19 ? 10 ? 1

Процесс сложения между собой цифр числа и повторение этой операции до тех пор, пока не получится однозначное число, называется вычислением вычета по модулю 9, ведь на каждом этапе вы занимаетесь тем, что вычитаете число, кратное 9. Получаемое в итоге однозначное число называется цифровым корнем изначального числа. Например, числовой корень 3457 – 1, а 3456 – 9. Давайте попробуем вкратце суммировать все сказанное. Для каждого натурального n:

Если цифровой корень n равен 9, n кратно 9.

В ином случае цифровой корень будет равен остатку, получаемому от деления n на 9.

Алгебраически, обозначив цифровой корень числа n как r, получаем:

n = 9x + r

где x – целое число. Вычисление вычета по 9 – забавный способ проверить результаты, полученные в результате сложения, вычитания и умножения. Например, сумма верна, если ее цифровой корень равен сумме цифровых корней складываемых чисел. Хотите конкретнее? Давайте посчитаем

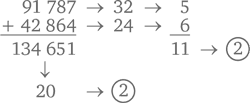
Обратите внимание, что цифровые корни слагаемых чисел равны 5 и 6, а цифровой корень их суммы (11) равен 2. И совсем не случайно, что цифровой корень результата (134 651) тоже имеет цифровой корень, равный 2. Причина всего это кроется в следующей алгебраической формуле:

(9x + r₁) + (9y + r₂) = 9(x + y) + (r₁ + r₂)

Если числа не совпадают, вы наверняка где-то ошиблись. И вот что важно: даже если числа совпадают, это еще не значит, что ответ верный, хотя в 90 % случаев проверка результата цифровыми корнями работает безотказно и позволяет быстро найти ошибку. Однако, случайно поменяв местами две цифры, вы этого не заметите, ведь сумма цифр от этого не изменится. А вот появление неправильного числа говорит об ошибке, если только ошибка не связана с заменой 0 на 9 или 9 на 0. Этот же метод можно использовать, когда нам нужно сложить друг с другом длинный столбец чисел. Представим, вы зашли в магазин и купили несколько продуктов по следующим ценам:

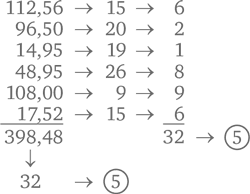
Складывая цифры результата, мы видим, что его цифровой корень – 5, а сумма цифровых корней равна 32, что подтверждает его правильность, потому что цифровой корень 32 – тоже 5. При проверке результата вычитания метод тоже отлично работает. Возьмем для примера те же числа, что были у нас в позапрошлом примере:

Разность будет равна 48 923, ее цифровой корень – 8. Работая с цифровыми корнями уменьшаемого и вычитаемого, видим, что 5 – 6 = –1. Но страшного в этом ничего нет – мы сделали все абсолютно правильно, потому что –1 + 9 = 8, да и прибавление (или вычитание) числа, кратного 9, к нашему ответу (или из нашего ответа) не меняет значение цифрового корня. По той же логике разница с 0 также верна при цифровом корне, равном 9.

А теперь неплохо было бы собрать вместе полученные нами знания и придумать еще один фокус (вроде того, который мы демонстрировали в предисловии). Просто следуйте инструкциям, хотите – с калькулятором, хотите – без.

1. Задумайте любое дву– или трехзначное число.

2. Сложите между собой его цифры.

3. Вычтите результат из задуманного числа.

4. Сложите между собой цифры полученной разности.

5. Если получилось четное число, умножьте его на 5.

6. Если нечетное – на 10.

7. Вычтите 15.

Получилось 75, да?

Если вы начали, например, с 47, вы сначала посчитали 4 + 7 = 11, а потом – 47 – 11 = 36. Дальше было 3 + 6 = 9 – нечетное число, умножив которое на 10, получаем 90, а 90 – 15 = 75. А может, вы начали с трехзначного числа – 831, например? Тогда 8 + 3 + 1 = 12, потом 831 – 12 = 819, а затем 8 + 1 + 9 = 18 – четное число. Дальше делаем 18 ? 5 = 90, вычитаем 15 и получаем те же 75.

Секрет тут в том, что, если цифровая сумма изначального числа равна T, само число должно быть на T больше, чем ближайшее число, кратное 9. Когда мы вычитаем из загаданного числа T, мы гарантированно получаем результат, который можно разделить на 9 без остатка, при этом он меньше 999, а значит, сумма его цифр будет равна либо 9, либо 18 (если вернуться к нашему примеру с 47, цифровая его сумма – 11; мы вычитаем 11 до 36 с цифровой суммой 9). И после следующего шага единственным вариантом остается 90 (как произведение 9 ? 10 или 18 ? 5) и 75 – точно, как в наших примерах.

Теперь предлагаю посмотреть, как работает вычисление вычета по девятке с умножением. Возьмем те же числа и попробуем посчитать:

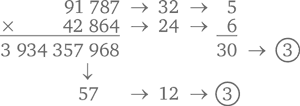
При умножении вычисление вычета по девятке работает на основе метода FOIL, о котором мы говорили в главе 2. Так, в нашем последнем примере цифровые корни справа говорят нам, что множители имеют формы 9x + 5 и 9y + 6, где x и y – целые числа. И когда мы их перемножаем, получаем

(9x + 5)(9y + 6) = 81xy + 54x + 45y + 30 = 9(9xy + 6x + 5y) + 30 = (число, кратное 9) + (27 + 3) = (число, кратное 9) + 3

При делении вычисление вычета по модулю 9 обычно не используется, но я не могу не показать вам поистине чудесный метод деления на 9. Иногда его называют «ведическим». Возьмем

12 302 ? 9

Представим это в следующем виде:

Продублируем первую цифру над чертой, там же – но уже над последней цифрой – напишем литеру R (для обозначения остатка), вот так:

А дальше будем складывать числа попарно, как это показано чуть ниже, обводя их овалом, и записывать результаты над чертой. Сумма 1 и 2, обведенных овалом, равна 3, поэтому следующим числом нашего частного будет 3.

Потом 3 + 3 = 6.

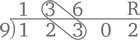
Затем 6 + 0 = 6.

И завершаем все остатком: 6 + 2 = 8.

И вот наш ответ: 12 302 ? 9 = 1366 с остатком 8. Так легко, что даже не верится, правда? Приведем еще один пример:

31 415 ? 9

Чтобы сэкономить бумагу, сразу дадим полную картину:

Начиная вверху с 3, мы складываем 3 + 1 = 4, потом 4 + 4 = 8, потом 8 + 1 = 9, и в конце – 9 + 5 = 14. Получается 3489 и 14 в остатке. Но раз 14 = 9 + 5, нам нужно добавить 1 к частному, чтобы получилось 3490 и 5 в остатке.

А вот простой вопрос с чарующим своей стройностью ответом. Проверьте, пожалуйста (на бумаге или в уме), правильно ли, что

111 111 ? 9 = 12 345 с остатком 6

Мы уже знаем, что, если остаток равен или больше 9, мы просто вычитаем из него эту девятку, а к частному прибавляем 1. Примерно то же происходит, когда сумма складываемых нами при делении чисел превышает 9. Мы сначала это запоминаем, потом вычитаем из результата 9 и продолжаем считать так же, как и считали. Например, при решении 4821 ? 9, мы делаем вот что:

Начинаем мы с 4, но поскольку 4 + 8 = 12, единицу мы пишем над четверкой (чтобы не забыть), а потом вычитаем 9 из 12, чтобы дальше написать 3. Затем идет 3 + 2 = 5, а после этого – 5 + 1 = 6; в результате получаем 535 с остатком 6 – взгляните:

Когда слишком многое «идет на ум», вычислять становится сложнее. Попробуем 98 765 ? 9.

Мы начинаем с 9, складываем 9 + 8 = 17, отмечаем запоминаемую единицу и вычитаем 9, чтобы получить вторую цифру – 8. Дальше у нас идет 8 + 7 = 15, мы отмечаем еще одну единицу и пишем 15 – 9 = 6. 6 + 6 = 12 – значит, «на ум идет» уже третья единица, – считаем 12 – 9 = 3. И остаток: 3 + 5 = 8. С учетом запомненных единиц получаем 10 973 с остатком 8.

Отступление

Если вам уже нравится деление на 9, попробуйте делить на 91. Возьмите любое двузначное число и просто делите его на 91 без остановки, множа количество знаков после запятой, пока не надоест. И никаких столбиков, никаких калькуляторов! Нет, кроме шуток! Вот, смотрите:

53 ? 91 = 0,582417…

Если говорить конкретнее, ответ тут – 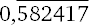, где линия над цифрами 582417 означает, что они повторяются до бесконечности. Откуда эти числа берутся? На самом деле это деление ничуть не сложнее умножения исходного двузначного числа на 11. С помощью метода, о котором мы говорили в главе 1, считаем 53 ? 11 = 583. Вычитаем из этого числа единицу и получаем первую половину нашего ответа, а именно – 0,582. Вторая половина – это разность, полученная при вычитании первой половины из 999: 999 – 582 = 417. В результате получаем .

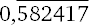Еще один пример – 78 ? 91. Здесь 78 ? 11 = 858, то есть ответ будет начинаться с 857. Затем 999 – 857 = 142, поэтому 78 ? 91 = 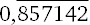. Это число нам уже встречалось в главе 1, потому что 78/91 легко упрощается до 6/7.

Метод этот работает, потому что 91 ? 11 = 1001. Поэтому в первом примере А так как 1/1001 = , мы получаем повторяющуюся часть нашего ответа из 583 ? 999 = 583 000 – 583 = 582 417.

91 = 13 ? 7 дает нам отличный способ делить числа на 13, усложняя их, чтобы получить в знаменателе 91. Например, 1/13 = 7/91, а так как 7 ? 11 = 077, у нас получается

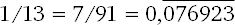
Точно так же 2/13 = 14/91 = , потому что 14 ? 11 = 154.

Источник

Содержание

1 Сравнения по модулю
2 Арифметика сравнений
- 2.1 Свойства сравнений
3 Полная и приведенная система вычетов
4 Решение линейных систем по модулю
- 4.1 Примеры решения

Сравнения по модулю

Будем рассматривать целые числа в связи с остатками от деления их на данное целое число m, которое назовем модулем.
Каждому целому числу отвечает определенный остаток от деления его на m. Если двум целым a и b отвечает один и тот же остаток r, то они называются сравнимыми по модулю m.

Сравнимость для a и b записывается так :

Сравнимость чисел a и b по модулю m равносильна:

а. Возможности представить a в форме , где t — целое.
б. Делимости на m.
- Действительно, из следует , откуда , и , где .
- Обратно, из , представляя b в форме , выводим , где , значит .

Арифметика сравнений

Свойства сравнений

1. Два числа, сравнимые с третьим сравнимы между собой.
- Легко выводится из пункта “а”.

2. Сравнения можно почленно складывать.
- Представляем сравнения, как в пункте “а” и складываем.

3. Сравнения можно почленно перемножать.
- Представляем сравнения, как в пункте “а”, перемножаем, получим , где N—целое.

4. Обе части сравнения можно разделить на их общий делитель, если последний взаимно прост с модулем.
- Действительно, из , следует, что , поэтому .

5. Обе части сравнения можно умножить на одно и тоже число.
- Действительно, из , следует , и, следовательно, .

6. Обе части сравнения и модуль можно разделить на их общий делитель.
- Действительно, пусть , отсюда , и, следовательно, .

7. Если сравнение имеет место по нескольким модулям, то оно имеет место и по модулю равному НОК этих модулей.
- В самом деле, из следует, что разность делится на все модули . Поэтому она должна делиться и на их НОК.

8. Если сравнение имеет место по модулю m, то оно имеет место и по модулю d, равному любому делителю числа m.
- Следует из пункта “б”.

9. Если одна часть сравнения и модуль делятся на некоторое число, то и другая сторона сравнения должна делиться на это число.
- Следует из пункта “а”.

10. Если , то .
- Следует из пункта “а” по свойству НОДа.

Полная и приведенная система вычетов

Числа равноостаточные(сравнимые по модулю m) образуют класс чисел по модулю m.
Из такого определения следует, что всем числам класса отвечает один остаток r, и мы получим все числа класса,
если в форме заставим t пробегать все целые числа. Таким образом для каждого значения остатка имеется свой класс чисел.

Любое число класса называется вычетом по модулю m. Вычет получаемый при , равный самому остатку r,
называется наименьшим неотрицательным вычетом.

Любые m чисел, попарно несравнимые по модулю m, образуют полную систему вычетов по этому модулю.

Согласно 10 свойству сравнений, числа одного класса по модулю m имеют одинаковый НОД. Особенно важны классы, содержащие числа, взаимно простые с модулем. Взяв вычет от каждого такого класса, получим приведенную систему вычетов по модулю m.

Решение линейных систем по модулю

Пусть . Сравнение невозможно, если b не делится на d. При b, кратном d, сравнение имеет d решений.
Поиск решений:
,
Составим новое сравнение ,
обозначим его . Пусть его решением будет , тогда остальные решения найдутся по следующей формуле: (следует понимать, что вычет по модулю, поэтому в этой формуле можно сменить знак, для удобства), всего решений будет d. Если нахождение не является очевидным, то следует воспользоваться теорией цепных дробей, и тогда , где – числитель подходящей дроби.

Примеры решения

Пример 1.

Найдем НОД
Перейдем к новому сравнению
Легко находится
Тогда ответом будет

Пример 2.

Найдем НОД , 75 кратно 3, значит имеем 3 решения
Перейдем к новому сравнению
Воспользуемся цепными дробями, в нашем случае , значит
Тогда ответом будет .

Источник

Введение в модулярную арифметику

Время на прочтение
6 мин

Количество просмотров 67K

В обычной жизни мы обычно пользуемся позиционной системой счисления. В позиционной системе счисления значение каждого числового знака (цифры) в записи числа зависит от его позиции (разряда) [1]. Однако существуют и так называемые «непозиционные системы счисления», к одной из которых относится «система остаточных классов» (СОК) (или в оригинале Residue Number System (RNS)), являющаяся основой модулярной арифметики. Модулярная арифметика базируется на «Китайской теореме об остатках» [2], которая для нашего случая звучит следующим образом:

Для любой системы взаимно простых чисел p₁, … p_n, любое число X из диапазона [0; M), где M = p₁*p₂*…*p_n взаимооднозначно представимо в виде вектора (a₁, a₂, …, a_n), где a_i = X%p_i (здесь и далее «%» — операция взятия остатка от целочисленного деления X на p_i).
p₁, … p_n – модули системы
a₁, a₂, …, a_n – остатки (вычеты) числа по заданной системе модулей

На первый взгляд непонятно какое преимущество может дать такая система, однако существует 2 свойства, которые позволяют эффективно использовать модулярную арифметику в некоторых областях микроэлектроники:

Отсутствие переноса разрядов в сложении и умножении. Пусть нам дано два числа X₁ и X₂, представленные в виде системы остатков (x₁₁, x₁₂, …, x_1n) и (x₂₁, x₂₂, …, x_2n) по системе взаимнопростых чисел (p₁, p₂, …, p_n). В этом случае:
X₃ = X₁ + X₂ = ((x₁₁+x₂₁)%p₁, (x₁₂+x₂₂)%p₂, …, (x_1n+x_2n)%p_n)
X₄ = X₁ * X₂ = ((x₁₁*x₂₁)%p₁, (x₁₂*x₂₂)%p₂, …, (x_1n*x_2n)%p_n)
То есть что бы сложить или умножить два числа, достаточно сложить или умножить соответствующие элементы вектора, что для микроэлектроники означает, что это можно сделать параллельно и из-за малых размерностей p₁, p₂, …, p_n сделать очень быстро.
Ошибка в одной позиции вектора не влияет на расчеты в других позициях вектора. В отличие от позиционной системы счисления все элементы вектора равнозначны и ошибка в одном из них ведет всего лишь к сокращению динамического диапазона. Этот факт позволяет проектировать устройства с повышенной отказоустойчивостью и коррекцией ошибок.

Но не всё так гладко, как хотелось бы. В отличие от позиционной системы счисления, следующие операции (называемые «немодульными») выполняются сложнее, чем в позиционной системе счисления: сравнение чисел, контроль переполнения, деление, квадратный корень и.т.д. Первые успешные попытки применения модулярной арифметики в микроэлектронике были предприняты ещё в 1950-х годах, но из-за сложностей с немодульными операциями интерес несколько утих. Однако в настоящее время модулярная арифметика снова возвращается в микроэлектронику по следующим причинам:

большое распространение мобильных процессоров, в которых требуется высокая скорость при маленьком потреблении энергии. Отсутствие переноса в арифметических операциях сложения/умножения позволяет снизить потребление энергии.
увеличивающаяся плотность элементов на кристалле в некоторых случаях не позволяет провести полное тестирование, поэтому растет важность устойчивости процессоров к возможным ошибкам.
появление специализированных процессоров с большим числом операций над векторами, которые требуют высокой скорости и включают в себя преимущественно сложение и умножение чисел (как пример умножение матриц, скалярное произведение векторов, преобразования Фурье и.т.д).

В данный момент модулярная арифметика применяется в следующих областях: цифровая обработка сигналов, криптография, обработка изображений/аудио/видео и.т.д.

Прямое преобразование

Прямое преобразование из позиционной системы счисления (обычно в двоичном виде) в систему счисления в остатках заключается в нахождении остатков от деления по каждому из модулей системы.

Пример: Пусть требуется найти представление числа X = 25 по системе модулей (3, 5, 7). X = (25%3, 25%5, 25%7) = (1, 0, 4).

Реализация нахождения вычета в микроэлектронике по заданному модулю строится на следующих свойствах вычетов:
(a+b) % p = (a%p + b%p)%p
(a*b) % p = (a%p * b%p)%p

Любое число X можно записать в виде X%p = (x_n-1*2^n-1 + x_n-2*2^n-2 + x₀*2⁰)%p = ((x_n-1)%p*2^n-1%p) + ((x_n-2)%p*2^n-2%p) + … + x₀%p)%p. Поскольку в данном случае x_n-1, … x₀ равны 0 или 1, то фактически нам требуется сложить вычеты вида (2ⁱ%p).

Пример: пусть задано число 25 или в двоичной системе счисления 11001 и требуется найти остаток по модулю 7.
25%7 = (1*2⁴ + 1*2³ + 0*2² + 0*¹ + 1*2⁰)%7 = (2⁴%7 + 2³%7 + 1%7)%7 = (2 + 1 + 1)%7 = 4

Систему используемых модулей подбирают под конкретную задачу. Например, для представления 32-х битных чисел достаточно следующей системы модулей: (7, 11, 13, 17, 19, 23, 29, 31) – все они взаимнопросты друг с другом, их произведение равно 6685349671 > 4294967296. Каждый из модулей не превышает 5 бит, то есть операции сложения и умножения будут производиться над 5-битными числами.
Особое значение так же имеет система модулей вида: (2ⁿ-1, 2ⁿ, 2ⁿ+1) в связи с тем, что прямое и обратное преобразование для них выполняется простейшим образом. Что бы получить остаток от деления на 2ⁿ достаточно взять последние n цифр двоичного представления числа.

Арифметические операции

Пример: пусть задана система модулей (3, 5, 7), то есть мы можем выполнять операции, результат которых не превышает 3*5*7 = 105. Умножим два числа 8 и 10.
8 = (8%3, 8%5, 8%7) = (2, 3, 1)
10 = (10%3, 10%5, 10%7) = (1, 0, 3)
8*10 = ((2*1)%3, (3*0)%5, (1*3)%7) = (2, 0, 3)
Проверяем
80 = (80%3, 80%5, 80%7) = (2, 0, 3)

Обратное преобразование

Обратное преобразование из системы счисления в остаточных классах в позиционную систему счисления производится одним из двух способов:

На базе Китайской теоремы об остатках или системы ортогональных базисов
На базе полиадического кода (другие названия mixed-radix system, система, со смешанным основанием)

Остальные предложенные в различной литературе способы, по сути, являются смесью этих двух.

Способ, основанный на Китайской теореме об остатках, базируется на следующей идее:
X = (x₁, x₂, … x_n) = (x₁, 0, …, 0) + (0, x₂, …, 0) + … + (0, 0, …., x_n) = x₁*(1, 0, …, 0) + x₂*(0, 1, …, 0) + … + x_n*(0, 0, …, 1).
То есть для обратного преобразования требуется найти систему ортогональных базисов B1 = (1, 0, …, 0), B2 = (0, 1, …, 0), …, BN = (0, 0, …, 1). Эти вектора находятся один раз для заданного базиса, а для их поиска требуется решить уравнение вида: (M_i*b_i)%p_i = 1, где M_i = M/p_i, а b_i – искомое число. В этом случае позиционное представление B_i = M_i*b_i и
X = (x₁*(M₁*b₁) + x₂*(M₂*b₂) + … + x_n*(M_n*b_n))%M

Пример: пусть задана система модулей (3, 5, 7), найдем значения M_i и b_i (0 < i <= 3)
M = 3*5*7 = 105
M₁ = 105/3 = 35
M₂ = 105/5 = 21
M₃ = 105/7 = 15
(35*b₁)%3 = 1 => b₁ = 2
(21*b₂)%5 = 1 => b₂ = 1
(15*b₃)%7 = 1 => b₃ = 1
Теперь преобразуем какое-нибудь число в системе остаточных классов. Положим
X = (2, 3, 1) = (2*35*2 + 3*21*1 + 1*15*1)%105 = (140 + 63 + 15)%105 = 218%105 = 8

Минус этого метода заключается в том, что для обратного преобразования требуется умножение и сложение больших чисел (M₁, …, M_n), а так же операция взятия остатка по модулю большого числа M.

Способ на базе полиадического кода, базируется на идее, что любое число X может быть представлено в системе взаимно простых чисел p₁, … p_n, как [4]:
X = a₁ + a₂*p₁ + a₃*p₁*p₂ +… + a_n-1*p₁*p₂*…*p_n-2 + a_n*p₁*p₂*…*p_n-1, где 0 < a_i < p_i

X%p₁ = x₁ = a₁
(X – a₁)%p₂ = (x₂ — a₁)%p₂ = (a₂*p₁)%p₂ => a₂ = ((p₁^-1)%p₂*(x₂ — a₁))%p₂
(X — a₁ — a₂*p₁)%p₃ = (a₃*p₁*p₂)%p₃ => a₃ = ((p₂^-1)%p₃*((p₁^-1)%p₃*(x₃ — a₁) — a₂))%p₃
…

Для использования этого метода требуются константы вида (p_i^-1)%p_k^-1. Можно также заметить, что начинать вычисление a₃ можно, как только появилось значение a₁. На основе этого метода можно строить конвеерные преобразователи.

Пример: Рассмотрим тот же пример — найдем позиционное представление числа X = (2, 3, 1) в системе модулей (3, 5, 7)

a₁ = x₁ = 2

a₂ = ((p₁^-1)%p₂*(x₂ — a₁))%p₂ = ((3^-1)%5*(3 — 2))%5 = 2*1 = 2

a₃ = ((p₂^-1)%p₃*((p₁^-1)%p₃*(x₃ — a₁) — a₂))%p₃ = ((5^-1)%7*((3^-1)%7*(1 — 2) — 2))%7 = (3*(5*(1-2)-2))%7 = (3*(-7))%7 = 0

X = a₁ + a₂*p₁ + a₃*p₁*p₂ = a₁ + 3*a₂ + 15*a₃ = 2 + 3*2 + 15*0 = 8

Замечание: что бы найти константу вида (3^-1)%5 требуется решить уравнение (3*x)%5 = 1, где 0 <= x < 5

P.S.

Статья написана несколько сумбурно, потому что тема достаточно большая и в одну статью вместить все не представляется возможным. В следующих статьях я попробую расписать более подробно различные аспекты модулярной арифметики. На Хабре же я не нашел вообще ничего что относится к этой теме, только краткие упоминания в других статьях, поэтому и было решено написать небольшой обзор с простенькими примерами. Для тех, кого тема заинтересовала, рекомендую прочитать книгу номер [3] из списка литературы (на английском языке), она написана доступным языком с большим количеством примеров.

Литература

[1] ru.wikipedia.org/wiki/%D0%9F%D0%BE%D0%B7%D0%B8%D1%86%D0%B8%D0%BE%D0%BD%D0%BD%D0%B0%D1%8F_%D1%81%D0%B8%D1%81%D1%82%D0%B5%D0%BC%D0%B0_%D1%81%D1%87%D0%B8%D1%81%D0%BB%D0%B5%D0%BD%D0%B8%D1%8F
[2] ru.wikipedia.org/wiki/%D0%9A%D0%B8%D1%82%D0%B0%D0%B9%D1%81%D0%BA%D0%B0%D1%8F_%D1%82%D0%B5%D0%BE%D1%80%D0%B5%D0%BC%D0%B0_%D0%BE%D0%B1_%D0%BE%D1%81%D1%82%D0%B0%D1%82%D0%BA%D0%B0%D1%85
[3] Amos Omondi, Benjamin Premkumar, Residue Number Systems: Theory and Implementation, 2007.
[4] M. A. Soderstrand, W. K. Jenkins, G. A. Jullien and F. J. Taylor. 1986. Residue Number System Arithmetic: Modern Applications in Digital Signal Processing, IEEE Press, New York.

Источник

Элементы теории чисел.

История[править | править код]

Определения[править | править код]

Свойства сравнимости по модулю[править | править код]

Операции со сравнениями[править | править код]

Пример[править | править код]

Связанные определения[править | править код]

Классы вычетов[править | править код]

Системы вычетов[править | править код]

Сравнения в кольце многочленов над полем[править | править код]

Решение сравнений[править | править код]

Сравнения первой степени[править | править код]

Примеры[править | править код]

Сравнения второй степени[править | править код]

Системы сравнений[править | править код]

Применение[править | править код]

См. также[править | править код]

Примечания[править | править код]

Литература[править | править код]

Содержание

Сравнения по модулю

Арифметика сравнений

Свойства сравнений

Полная и приведенная система вычетов

Решение линейных систем по модулю

Примеры решения

Введение в модулярную арифметику

Прямое преобразование

Арифметические операции

Обратное преобразование

P.S.

Литература

Вам также может понравиться

Как найти диагональ прямоугольника зная одну сторону

Как найти мальчика подростка

Как найти где пожить

Добавить комментарий Отменить ответ