Как найти вычет существенно особой точки

Вычеты и их применение

Определение вычета

Пусть $z_0in overline{mathbb{C}}$ — изолированная особая точка функции f(z) . По определению изолированной особой точки существует некоторая окрестность этой точки, в которой f(z) — аналитическая. Напомним, что для $z_0in mathbb{C}$ эта окрестность имеет вид 0<|z-z_0|<R , а для z_0=infty — R<|z|<infty .

Рассмотрим произвольный контур gamma , принадлежащий такой окрестности и являющийся границей некоторой области, содержащей z_0 (рис 4.2,а).

По следствию из основной теоремы Коши интеграл $textstyle{ointlimits_{gamma} f(z),dz}$ имеет одно и то же значение, независимо от вида кривой gamma , т.е. интеграл характеризует поведение функции f(z) в особой точке z_0 и, следовательно, может быть использован для исследования функции как некоторая числовая характеристика.

Вычетом функции f(z) в изолированной особой точке $z_0~(z_0in overline{mathbb{C}})$ называется интеграл $frac{1}{2pi i}ointlimits_{gamma} f(z),dz$ , где gamma — контур, принадлежащий окрестности точки z_0 и охватывающий ее. Обход контура — положительный, т.е. область им ограниченная и принадлежащая окрестности z_0 при обходе расположена слева: для $z_0in mathbb{C}$ — обход против часовой стрелки (рис. 4.2,а), для z_0=infty — по часовой стрелке (рис. 4.2,б). Обозначается вычет $mathop{operatorname{res}}limits_{z_0} f(z)$ (res — residu (фр.) — вычитать):

$begin{gathered} mathop{operatorname{res}}limits_{z_0}f(z)= frac{1}{2pi i} ointlimits_{gamma} f(z),dz,quad gammain O(z_0)setminus z_0colon 0<|z-z_0|<R,\[2pt] mathop{operatorname{res}}limits_{infty}f(z)= frac{1}{2pi i} ointlimits_{gamma} f(z),dz,quad gammain O(infty)setminus inftycolon R<|z|<infty. end{gathered}$

(4.16)

Так как в окрестности изолированной особой точки функция разлагается в ряд Лорана, то, используя формулы для коэффициентов ряда Лорана и сравнивая их с (4.16), замечаем, что можно сделать следующее заключение.

Рис. 4.2.

Утверждение 4.5. Вычет функции в изолированной особой точке равен коэффициенту $c_{-1}$ при первой отрицательной степени в разложении функции в ряд Лорана в окрестности этой точки, т.е. при $frac{1}{z-z_0}$ для $z_0in mathbb{C}$ , и этому коэффициенту, взятому с противоположным знаком, для z_0=inftycolon

$mathop{operatorname{res}}limits_{z_0}f(z)=c_{-1},quad z_0in mathbb{C},$

(4.17)

$mathop{operatorname{res}}limits_{infty} f(z)=-c_{-1},quad z_0=infty.$

(4.18)

С помощью вычетов можно записать в другой форме основную теорему Коши для сложного контура.

Действительно, пусть функция в области имеет особых точек z_k,~ k=1,2,ldots,n . Можно рассмотреть контуры gamma_kin D , которые являются границами непересекающихся областей D_k , таких, что каждая из особых точек z_k (изолированных особых точек) принадлежит одной из D_k (рис. 4.3,а), а интеграл по gamma_k согласно определению (см. формулу (4.16)) есть $2pi i mathop{operatorname{res}}limits_{z_k}f(z)$ .

Кроме того, для любого контура , ограничивающего область , которой принадлежат все особые точки функции f(z) , и контура gamma — границы окрестности бесконечно удаленной точки справедливо равенство $ointlimits_{gamma}f(z),dz=-ointlimits_{C}f(z),dz$ (обход на gamma по часовой стрелке (рис. 4.3,б)). Из этих рассуждений и формулы (4.16) получаем следующие утверждения.

Рис. 4.3.

Основная теорема о вычетах

Утверждение 4.6 (основная теорема о вычетах). Если функция f(z) -аналитическая в overline{D} за исключением конечного числа особых точек z_kin D , то справедливо равенство (где — граница области ):

$ointlimits_{C}f(z),dz= 2pi i sum_{k=1}^{n} mathop{operatorname{res}}limits_{z_k} f(z),quad z_kin D.$

(4.19)

Обобщенная теорема о вычетах

Утверждение 4.7 (обобщенная теорема о вычетах). Сумма вычетов функции f(z) во всех ее особых точках, включая бесконечно удаленную точку, равна нулю:

$sum_{k=1}^{n} mathop{operatorname{res}}limits_{z_k}f(z)+ mathop{operatorname{res}}limits_{infty}f(z)=0.$

(4.20)

Пример 4.22. Найти вычеты следующих функций в их особых точках: а) $f(z)= frac{z+2}{z^2-2z-3}$ ; б) $f(z)=frac{z+2}{(z+1)^2(z-3)}$ .

Решение

Особыми точками функций являются точки z_1=-1,~ z_2=3,~ z_3=infty . Записываем разложения функций в ряд Лорана в окрестности этих точек (см. примеры 3.31, 3.33 и 3.34):

а)

$begin{aligned}f(z)&= frac{-1}{4}cdot frac{1}{z+1}-sum_{n=0}^{infty} frac{5(z+1)^n}{4^{n+2}},quad 0<|z+1|<4;\ f(z)&= frac{5}{4}cdot frac{1}{z-3}-sum_{n=0}^{infty} frac{(-1)^{n+1}}{4^{n+2}}(z+1)^n,quad 0<|z-3|<4;\ f(z)&= sum_{n=1}^{infty} frac{(-1)^n+5cdot3^{n-1}}{4}cdot frac{1}{z^n},quad |z|<3. end{aligned}$

Из этих разложений находим:

$mathop{operatorname{res}}limits_{-1}f(z)=c_{-1}=frac{-1}{4},;quad mathop{operatorname{res}}limits_{3}f(z)=c_{-1}= frac{5}{4},;quad mathop{operatorname{res}}limits_{infty}f(z)=-c_{-1}=-left(frac{-1+5cdot3^0}{4}right)=-1.$

Полученный результат иллюстрирует обобщенную теорему о вычетах:

$mathop{operatorname{res}}limits_{-1}f(z)+ mathop{operatorname{res}}limits_{3}f(z)+ mathop{operatorname{res}}limits_{infty}f(z)=0.$

Заметим также, что здесь точки z_1 и z_2 — простые полюсы, а z=infty — устранимая особая точка.

б)

$begin{aligned}f(z)&= frac{-5}{16}cdot frac{1}{z+1}+ frac{-1}{4}cdotfrac{1}{(z+ 1)^2}-sum_{n=0}^{infty} frac{5(z+1)^n}{16cdot4^{n+1}},,quad 0<|z+1|<4;\ f(z)&= frac{5}{16}cdot frac{1}{z-3}+ sum_{n=0}^{infty} frac{(-1)^{n+1}(n+6)}{4^{n+3}}(z-3)^n,quad 0<|z-3|<4.end{aligned}$

Из этих разложений имеем:

$mathop{operatorname{res}}limits_{-1}f(z)=c_{-1}=-frac{5}{16},;qquad mathop{operatorname{res}}limits_{3}f(z)=c_{-1}=frac{5}{16},.$

Вычет в бесконечно удаленной точке z=infty можно найти, используя обобщенную теорию о вычетах: $mathop{operatorname{res}}limits_{infty}f(z)=-left(mathop{operatorname{res}}limits_{3}f(z)+ mathop{operatorname{res}}limits_{-1}f(z)right)=0$ . Этот же результат получим, если запишем разложение функции в области |z|>3 -окрестности z=infty

Заметим, что для этой функции z_1 — Pi(2) , z_2 — Pi(1) , а z=infty — устранимая особая точка.

Пример 4.23. Найти вычеты следующих функций в особых точках: а) $f(z)=z^3exp frac{1}{z}$ ; б) $f(z)=frac{1-cos z}{z^2}$ .

Решение

Пример 4.24. Найти вычеты следующих функций в их особых точках: a) $sin! left(1+frac{1}{z}right)$ ; б) $(z-1)expfrac{1}{z-2}$ .

Решение

Конечные особые точки функций являются существенно особыми точками. Это z=0 для первой функции и z=2 для второй. Разложим функции в ряды в окрестностях этих точек и найдем вычеты по формуле (4.17):

а)

$begin{aligned}sin! left(1+frac{1}{z}right)&= sin1cdotcos frac{1}{z}+cos1cdotsin frac{1}{z}= sin1cdot left(1-frac{1}{2!z^2}+ldotsright)+ cos1cdot left(frac{1}{z}-frac{1}{z^33!}+ ldotsright)=\ &=sin1+cos1cdot frac{1}{z}-frac{sin1}{2!}cdot frac{1}{z^2}-ldots end{aligned}$

Следовательно, $mathop{operatorname{res}}limits_{z=0}f(z)= c_{-1}=cos1$ .

Так как у рассматриваемой функции другах конечных особых точек нет, то по формуле (4.20) $mathop{operatorname{res}}limits_{infty}f(z)=-cos1$ . Заметим, что z=infty — устранимая особая точка для данной функции f(z) ;

б)

$begin{aligned}(z-1)exp frac{1}{z-2}&= (z-2+1)exp frac{1}{z-2}= (z-2)exp frac{1}{z-2}+exp frac{1}{z-2}=\ &=(z-2)! left(1+frac{1}{z-2}+frac{1}{2!(z-2)^2}+ldotsright)+ left(1+frac{1}{z-2}+frac{1}{2!(z-2)^2}+ldots right)=\ &=2+(z-2)+ frac{1}{z-2}! left(1+frac{1}{2!}right)+ frac{1}{(z-2)^2}! left(frac{1}{2!}+ frac{1}{3!}right)+ldots,end{aligned}$

поэтому $mathop{operatorname{res}}limits_{z=2}f(z)= 1+frac{1}{2!}= frac{3}{2}$ . Поскольку нет другах конечных особых точек, то по формуле (4.20) $mathop{operatorname{res}}limits_{z=infty}f(z)=-frac{3}{2}$ . Точка z=infty является полюсом первого порядка данной f(z) .

Вычисление вычетов в полюсе и устранимой особой точке

В рассмотренных выше примерах при нахождении вычетов использовались формулы (4.17),(4.18) , т.е. функции раскладывались в ряды Лорана. При этом знание типа особой точки, в которой вычисляется вычет функции, не является обязательным. Таким методом всегда определяется вычет в тех случаях, когда заранее предполагается, что особая точка — существенно особая точка для функции. В случае устранимой особой точки и полюсов задачу вычисления вычета по формуле (4.17) можно заменить некоторыми практически более удобными формулами и правилами. Вывод этих формул и правил в общем виде, очевидно, связан с исследованием разложения функции в ряд в окрестности особой точки, а тип особой точки определяется по поведению функции, т.е. вычислением предела.

Так, если $limlimits_{zto z_0}f(z)neinfty$ и z_0 — конечная особая точка, то в разложении функции в ряд Лорана в окрестности z_0 , согласно утверждению 4.1, отсутствует главная часть. Следовательно, $c_{-1}=0$ и $mathop{operatorname{res}}limits_{z=z_0}f(z)=0$ .

Если $limlimits_{zto z_0}f(z)=infty$ и z_0 — полюс функции f(z) , то можно определить порядок полюса, также не прибегая к разложению функции в ряд, используя утверждение 4.3. Пусть z_0 — Pi(n) функции f(z) , тогда разложение функции в ряд в окрестности z_0 имеет вид (4.6). Умножив обе части равенства на (z-z_0)^n и продифференцировав результат (n-1) раз, получим выражение

$frac{d^{n-1}}{dz^{n-1}}bigl[f(z)cdot (z-z_0)^nbigr]= (n-1)!c_{-1}+ n! c_0(z-z_0)+ldots,$

из которого определяем $c_{-1}= frac{1}{(n-1)!} limlimits_{zto z_0}frac{d^{n-1}}{dz^{n-1}} bigl[f(z)cdot (z-z_0)^nbigr]$ .

В частности, при n=1 имеем $c_{-1}= limlimits_{zto z_0}bigl[f(z)cdot (z-z_0)bigr]$ . Последнее равенство принимает наиболее удобную форму для функции вида $f(z)= frac{varphi(z)}{psi(z)}$ , где varphi(z),,psi(z) — аналитические вточке z_0 функции и varphi(z_0)ne0,~ psi(z_0)=0,~ psi'(z_0)ne0 . А именно:

$c_{-1}= limlimits_{zto z_0} frac{varphi(z)(z-z_0)}{psi(z)}= limlimits_{zto z_0} frac{varphi(z)}{dfrac{psi(z)-psi(z_0)}{z-z_0}}= frac{varphi(z_0)}{psi'(z_0)},.$

Результат приведенных рассуждений запишем в виде утверждения.
Утверждение 4.8

1. Если конечная особая точка z_0 является устранимой особой точкой функции f(z) , то (где z_0 — устранимая особая точка)

$mathop{operatorname{res}}limits_{z=z_0}f(z)=0,quad z_0in mathbb{C}.$

(4.21)

2. Если z_0 полюс порядка п функции $f(z),~ z_0in mathbb{C}$ , то

$mathop{operatorname{res}}limits_{z_0}f(z)= frac{1}{(n-1)!} limlimits_{zto z_0} frac{d^{n-1}}{dz^{n-1}} bigl[f(z)cdot (z-z_0)^nbigr],quad z_0-Pi(n);$

(4.22)

$mathop{operatorname{res}}limits_{z_0}f(z)= limlimits_{zto z_0} bigl[f(z)cdot (z-z_0)bigr],quad z_0-Pi(1).$

(4.23)

3. Если z_0 — Pi(1) функции $f(z)=frac{varphi(z)}{psi(z)}$ , где varphi(z),,psi(z) — аналитические в точке z_0 функции и varphi(z_0)ne0,~ psi(z_0)=0,~ psi'(z_0)ne0 , то

$mathop{operatorname{res}}limits_{z_0}frac{varphi(z)}{psi(z)}= frac{varphi(z_0)}{psi'(z_0)},.$

(4.24)

Алгоритм вычисления вычета функции

Замечание 4.6. Формула (4.22) дает следующий алгоритм вычисления вычета функции в полюсе порядка .

1. Умножить f(z) на (z-z_0)^n , где — порядок полюса z_0 , и получить функцию varphi(z)=f(z)cdot (z-z_0)^n .

2. Найти производную функции varphi(z) порядка $(n-1)colon, psi(z)= varphi^{(n-1)}(z)$ .

3. В соответствии с (4.22) найти $mathop{operatorname{res}}limits_{z_0}f(z)= frac{1}{(n-1)!} limlimits_{zto z_0}psi(z)$ .

Пример 4.25. Найти вычеты в конечных особых точках функций:

$f_1(z)= frac{z+2}{z^2-2z-3},,qquad f_2(z)= frac{z+2}{(z+1)^2(z-3)},,qquad f_3(z)= frac{1-cos z}{z^2},.$

Решение

Конечными особыми точками f_1(z) являются z_1=-1 и z_2=3 — полюсы первого порядка, причем в каждом случае функцию можно представить в виде, допускающем применение формулы (4.24). Используя эту формулу, находим

$mathop{operatorname{res}}limits_{z=-1} frac{z+2}{z^2-2z-3}= left.{frac{z+2}{(z^2-2z-3)'}}right|_{z=-1}= left.{frac{z+2}{2z-2}}right|_{z=-1}= -frac{1}{4},;quad mathop{operatorname{res}}limits_{z=3}frac{z+2}{z^2-2z-3}= left.{frac{z+2}{2z-2}}right|_{z=3}= frac{5}{4},.$

Для функции f_2(z) точка z=3 также является Pi(1) и выполняются условия применимости формулы (4.24) . При этом функцию удобно представить в виде $f_2(z)= frac{z+2}{(z+1)^2}frac{1}{z-3}$ . Применяя формулу (4.24), находим

$mathop{operatorname{res}}limits_{z=3}f_2(z)= frac{z+2}{(z+1)^2}frac{1}{z-3}= left.{ frac{z+2}{(z+1)^2}frac{1}{(z-3)'}}right|_{z=3}= left.{frac{z+2}{(z+1)^2}}right|_{z=3}= frac{5}{16},.$

Точка z=-1 для f_2(z) — полюс второго порядка. Применяем формулу (4.22) при n=2 . Запишем решение согласно алгоритму.

1. Умножаем f_2(z) на (z+1)^2 и записываем функцию $varphi(z)= f_2(z)cdot(z+1)^2= frac{z+2}{z-3}$ .

2. Находим производную функции varphi(z)colon

$varphi'(z)= left(right)'= frac{z-3-(z+2)}{(z-3)^2}= frac{-5}{(z-3)^2}= psi(z).$

3. Используя (4.22), получаем $mathop{operatorname{res}}limits_{z=-1} f_2(z)= frac{1}{1!} limlimits_{zto-1} frac{-5}{(z-3)^2}=-frac{5}{16}$ .

Для функции $f_3(z)= frac{1-cos z}{z^2}$ единственная конечная особая точка z=0 является устранимой особой точкой, поэтому $mathop{operatorname{res}}limits_{z=0}f_3(z)=0$ (согласно (4.21)).

Все полученные результаты соответствуют результатам примеров 4.22 и 4.23.

Пример 4.26. Найти вычеты следующих функций в особых точках: а) $frac{z+2i}{z^3+8i}$ ; б) $frac{z-2i}{z^3+8i}$ ;

Решение

В заключение раздела рассмотрим бесконечно удаленную точку в случае, когда она является устранимой особой точкой для f(z) . Разложение функции в ряд Лорана имеет вид (4.5). Коэффициент $c_{-1}$ можно определить из этого равенства следующим образом: $c_{-1}= limlimits_{ztoinfty} bigl[(f(z)-c_0)cdot zbigr]$ . Так как, очевидно, $c_0= limlimits_{ztoinfty}f(z)$ , то, доопределяя функцию, положим $f(infty)= limlimits_{ztoinfty}f(z)=c_0$ . Получаем формулу для вычисления вычета в z=infty — устранимой особой точке функции f(z)colon

$mathop{operatorname{res}}limits_{z=infty} f(z)=-c_{-1}= limlimits_{ztoinfty}bigl[f(infty)-f(z)bigr]z.$

(4.25)

В частности, если z=infty является нулем функции f(z) , то есть $limlimits_{ztoinfty}f(z)=0$ , то формула принимает вид

$mathop{operatorname{res}}limits_{z=infty}f(z)= limlimits_{ztoinfty}bigl(-zcdot f(z)bigr).$

(4.26)

Пример 4.27. Найти вычеты в бесконечно удаленной точке z=infty функций:

а) $f_1(z)=frac{z+2}{z^2-2z+3},~~ f_2(z)= frac{z+2}{(z+1)^2(z-3)}$ ; б) $f_3(z)= frac{3z^2+z}{z^2+z-4}$ .

Решение

а) Точка z=infty — устранимая особая точка для этих функций и $f(infty)= limlimits_{ztoinfty}f(z)=0$ . Поэтому вычеты этих функций находим по формуле (4.26):

$mathop{operatorname{res}}limits_{z=infty}f_1(z)=-limlimits_{ztoinfty} frac{z(z+2)}{z^2-2z-3}=-1,qquad mathop{operatorname{res}}limits_{z=infty}f_2(z)=-limlimits_{ztoinfty} frac{(z+2)z}{(z+1)^2(z-3)}=0.$

Результат совпадает с полученным в примере 4.22.

б) Точка z=infty — устранимая особая точка для f(z) , так как $limlimits_{ztoinfty}f(z)=3$ . Вычет находим по формуле (4.25):

$mathop{operatorname{res}}limits_{z=infty}f(z)= limlimits_{ztoinfty}! left(3-frac{3z^2+z}{z^2+z-4}right)cdot z= limlimits_{ztoinfty} frac{(2z-12)z}{z^2+z-4} =2.$

Математический форум (помощь с решением задач, обсуждение вопросов по математике).

Кнопка "Поделиться"

Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.

Источник

Это следует из
определения устранимой особой точки:
главная часть ряда Лорана отсутствует,
все коэффициенты с отрицательными
индексами равны нулю,
=0.

19.7.3.2. Вычеты в полюсах.

19.7.3.2.1. Если а
– простой полюс функции
,
то
.

Док-во.
Простой полюс – полюс первого порядка,
поэтому разложение в ряд Лорана начинается
с минус первой степени:
.
Тогда
,
и
.

19.7.3.2.2.
Пусть
,
где

и

– аналитические в окрестности точки а
функции. Если а
– простой нуль функции
,
и
,
то
.

Док-во.
Если а
– простой нуль функции
,
и
,
то а
– простой полюс функции
.
Тогда, по предыдущему утверждению,

19.7.3.2.3. Если а
– полюс функции

n–го
порядка, то
.

Док-во.
Так как точка

– полюс n-го
порядка функции
,
то.
.
Для того, чтобы удалить особенность в
точке а,
умножим

на
:

.
Теперь, чтобы убрать первые члены этой
формулы и добраться до
,
дифференцируем это произведение n-1
раз:
,

……………………………………………………………………………………………………………………….,

,
откуда и следует доказываемая формула.

19.7.3.3. Вычет в существенно особой точке находится из разложения функции в ряд Лорана.

19.7.3.4. Примеры нахождения вычетов.

1.
.

Эта функция имеет
единственную особую точку –
.
Функция

при

– бесконечно малая второго порядка,

– четвертого, поэтому можно предположить,
что существует конечный
,
т.е.

– устранимая особая точка. Доказываем
строго:

– устранимая особая точка.

Можно решить эту
задачу по-другому. Так как
,
то
,

.
Понятно, что разложение этой функции
по степеням z
не будет содержать членов с отрицательными
степенями, т.е.

– устранимая особая точка.

2.
.

Особая точка –
.
Разлагаем функцию в ряд по степеням
:

.
Разложение содержит бесконечное
количество слагаемых с отрицательными
степенями
,
следовательно,

– существенно особая точка.
.

3.
.

Особые точки –
те, в которых
.
Эти точки являются простыми нулями
знаменателя, так как
.
Числитель
,
поэтому точки

– простые полюса. Вычеты находим по
формуле
:

4.
.

Особые точки –
те, в которых
.
В этих точках предел знаменателя
;
во всех точках
,
за исключением
,
числитель отличен от нуля, поэтому
,
следовательно, эти точки – полюса. Для
определения порядка этих полюсов найдём
порядок нуля знаменателя:
,
следовательно, эти полюса имеют второй
порядок (при
).
В точке

функция представляет собой неопределённость

,
однако, если вспомнить, что
,
эта неопределённость раскрывается
просто:
,
т.е. функция имеет конечный предел,
следовательно,

– устранимая особая точка.

Вычет в устранимой
особой точке равен нулю, поэтому
.
В остальных точках применяем формулу

при n=2:

(меняем переменную

(к последнему
пределу применяем правило Лопиталя)
.

19.7.4.
Основная теорема о вычетах. Пусть
функция

аналитична во всех точках ограниченной
замкнутой области
,
границей которой является контур L,
за исключением конечного числа особых
точек
,
расположенных внутри L.
Тогда
.

Док-во.
Окружим каждую особою точку
,
контуром

таким, чтобы все контуры лежали в области
D
и не пересекались. В области, ограниченной
контурами L,

,
функция аналитична, поэтому по 19.5.2.2.
Теореме Коши для многосвязной области

.
По определению вычета,
,
следовательно,
,
что и требовалось доказать.

П
римеры
вычисления интегралов с помощью основной
теоремы о вычетах.

1.
,
где L
– квадрат
.

Обе особые точки
подынтегральной функции –

и

– расположены внутри контура L,
поэтому
.
Точка

-полюс первого порядка,
.
Точка

– нуль первого порядка и для числителя,
и для знаменателя; докажем, что это –
устранимая особая точка подынтегральной
функции. Пусть
,
тогда
,
и
,
конечный предел существует, поэтому,
действительно, это – устранимая особая
точка, и
.
По основной теореме о вычетах
.

2
.

.
В примере 2 раздела 19.7.3.4.
Примеры нахождения вычетов
мы доказали, что точка

– существенно особая точка подынтегральной
функции, и
,
поэтому
.

.
Здесь подынтегральная функция

имеет две особых точки, расположенных
в области, находящейся внутри контура:

(простой полюс) и

(полюс второго порядка).
,

;

.
Внутри контура расположена одна особая
точка подынтегральной функции
:

.
Это – существенно особая точка, поэтому
для нахождения вычета необходимо найти
коэффициент

разложения

в ряд Лорана в окрестности этой точки.

;

,
однако нет необходимости выписывать
произведение этих рядов, достаточно
только собрать те попарные произведения,
которые дают минус первую степень
переменной
:

.
Легко сообразить, что это ряд для

при
,
т.е.
,
и
.

19.7.5.
Бесконечно удалённая особая точка.
Будем считать точку

особой точкой любой аналитической
функции. В разделе 19.1.6.
Окрестности точек плоскости

мы определили окрестности этой точки
как внешности кругов с центром в начале
координат:
.
Точка

является изолированной особой точкой
аналитической функции
,
если в некоторой окрестности этой точки
нет других особых точек этой функции.
Для определения типа этой особой точки
сделаем замену переменной
,
при этом точка

переходит в точку
,
функция

примет вид
.
Типом особой точки

функции

будем называть тип особой точки

функции
.
Если разложение функции

по степеням

в окрестности точки
,
т.е. при достаточно больших по модулю
значениях
,
имеет вид
,
то, заменив

на
,
получим
.
Таким образом, при такой замене переменной
главная и правильная части ряда Лорана
меняются местами, и тип особой точки

определяется количеством слагаемых в
правильной части разложения функции в
ряд Лорана по степеням

в окрестности точки
.
Поэтому

1. Точка

– устранимая особая точка, если в этом
разложении правильная часть отсутствует
(за исключением, возможно, члена
);

2. Точка

– полюс n-го
порядка, если правильная часть
заканчивается слагаемым
;

3. Точка

– существенно особая точка, если правильная
часть содержит бесконечно много членов.

При этом остаются
справедливыми признаки типов особых
точек по значению
:
если

– устранимая особая точка, то этот предел
существует и конечен, если

– полюс, то этот предел бесконечен, если

– существенно особая точка, то этот
предел не существует (ни конечный, ни
бесконечный).

Примеры: 1.
.
Функция уже является многочленом по
степеням
,
старшая степень – шестая, поэтому

– полюс шестого порядка.

Этот же результат
можно получить по-другому. Заменим

на
,
тогда
.
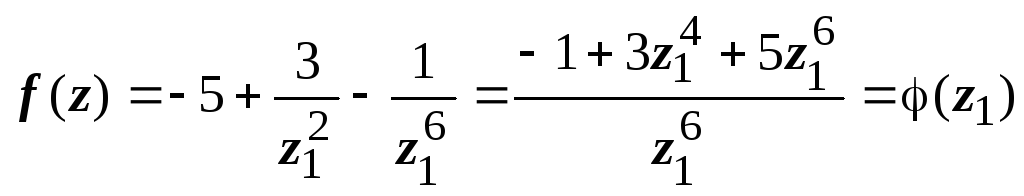Для функции

точка

– полюс шестого порядка, поэтому для

точка

– полюс шестого порядка.

2.
.
Для этой функции получить разложение
по степеням

затруднительно, поэтому найдём
:

;
предел существует и конечен, поэтому
точка

– устранимая особая точка.

3.
.
Правильная часть разложения по степеням

содержит бесконечно много слагаемых,
поэтому

– существенно особая точка. По другому
этот факт можно установить исходя из
того, что

не существует.

В
ычет
функции в бесконечно удалённой особой
точке. Для
конечной особой точки

,
где

– контур, не содержащий других, кроме
,
особых точек, проходимый так, что область,
им ограниченная и содержащая особую
точку, остаётся слева (против часовой
стрелке). Определим

аналогичным образом:
,
где

– контур, ограничивающий такую окрестность

точки
,
которая не содержит других особых точек,
и проходимый так, что эта окрестность
остаётся слева (по часовой стрелке).
Таким образом, все остальные (конечные)
особые точки функции должны находиться
внутри контура
.
Изменим направление обхода контура
:

.
По основной теореме о вычетах
,
где суммирование ведётся по всем конечным
особым точкам. Поэтому, окончательно,

,
т.е. вычет в бесконечно
удалённой особой точке равен сумме
вычетов по всем конечным особым точкам,
взятой с противоположным знаком.
Как следствие, имеет место теорема
о полной сумме вычетов:
если функция

аналитична всюду в плоскости С,
за исключением конечного числа особых
точек
,
то сумма вычетов во всех конечных особых
точках и вычета в бесконечности равна
нулю.

Отметим, что если

– устранимая особая точка, то вычет в
ней может быть отличен от нуля. Так для
функции
,
очевидно,
;

– единственная конечная особая точка
этой функции, поэтому
,
несмотря на то, что
,
т.е.

– устранимая особая точка.

143

Соседние файлы в папке lekciiTFKP

Источник

Содержание

Глава 6. Вычеты функций и их применение

Вычет функции относительно изолированной особой точки. Основная теорема о вычетах

Вычетом функции $f(z)$ относительно изолированной особой точки $z_0$ называется коэффициент $c_{-1}$ при $(z-z_0)^{-1}$ в разложении в ряд Лорана функции $f(z)$ в окрестности $z_0$.
$$
mbox{Res }f(z_0) = c_{-1}.
$$

Вычетом функции $f(z)$ относительно изолированной особой точки $z_0$ называется интеграл
$$
mbox{Res }f(z_0) =frac1{2pi i}ointlimits_L f(z),dz,
$$ где $L$ – произвольный контур в кольце $0<|z-z_0|<R$, ориентированный против часовой стрелки ($L$ должен окружать точку $z_0$).

Основная теорема о вычетах (Коши)

Пусть функция $f(z)$ является аналитической всюду в замкнутой области $overline D$, за исключением конечного
числа изолированных особых точек $z_1,z_2,dots,z_N$, лежащих внутри области $D$. Тогда $$
ointlimits_L f(z),dz=2pi isumlimits_{k=1}^N
mbox{Res }f(z_k),
$$ где $L$ – полная граница области $D$, проходимая в положительном направлении.

Вычисление вычетов в конечных особых точках

Вычет в устранимой особой точке равен $0$.

Если $z_0$ – существенно особая точка, то имеется только один способ вычисления вычета – разложение функции в ряд Лорана и определение коэффициента $c_{-1}$.

Для нахождения вычета в полюсе есть несколько приемов.

* Для простого полюса можно воспользоваться формулой:
begin{equation}label{1}
mbox{Res }f(z_0)=limlimits_{zto z_0}
Big(f(z)(z-z_0)Big).
end{equation}
* Для полюса порядка $m$:
begin{equation}label{2}
mbox{Res }f(z_0)=frac1{(m-1)!}limlimits_{zto z_0}
frac{d^{m-1}}{dz^{m-1}}Big(f(z)(z-z_0)^mBig).
end{equation}
* Для простого полюса в случае функции $ f(z)=frac{g(z)}{varphi(z)}$, где
$g(z)$ и $varphi(z)$ – аналитические функции в окрестности точки $z_0$ и $g(z_0)neq 0$, а для $varphi(z)$ точка $z_0$ есть нуль первого порядка (для $f(z)$ же точка $z_0$ есть полюс первого порядка):
begin{equation}label{3}
mbox{Res }f(z_0)=frac{g(z_0)}{varphi'(z_0)}.
end{equation}

Вычислить
$$ I=ointlimits_{|z-i|=2}frac{z-7}{z^2(z-1)(z-5i)},dz. $$

Строим контур интегрирования – окружность $|z-i|=2$. Подынтегральная функция имеет особые точки $z_1=0$, $z_2=1$ и $z_3=5i$. Точка $5i$ не
лежит внутри контура интегрирования. Точка $z_1=0$ – полюс 2-го порядка, $z_2=1$ – полюс 1-го порядка. По основной теореме о вычетах получаем $$ I=2pi ibig(mbox{Res }f(0)+mbox{Res }f(1)big). $$ По формуле для вычисления вычета в полюсе 2-го порядка
$$
mbox{Res }f(0)=frac1{1!}limlimits_{zto0}left(
left(frac{(z-7)z^2}{z^2(z-1)(z-5i)}right)’right)=
$$ $$ =limlimits_{zto0}frac{(z-1)(z-5i)-(z-7)(2z-1-5i)} {(z-1)^2(z-5i)^2}=frac{7+30i}{25}. $$ Для простого полюса вычет равен $$
mbox{Res }f(1)
=limlimits_{zto1}frac{(z-7)(z-1)}{z^2(z-1)(z-5i)} =-frac6{1-i}. $$

Окончательно, $$ I=2pi ileft(frac{7+30i}{25}-frac6{1-i}right) =pileft(frac{24}5-frac{106}{25}iright). $$

О бесконечно удаленной точке $z=infty$

Выберем любое $r geqslant0$. Разложим функцию $f(z)$ по степеням $z$ во внешности круга $|z|> r$, которое иногда
называют окрестностью бесконечно удаленной точки, $$ f(z)=sumlimits_{-infty}^infty c_kz^k=F_1(z)+F_2(z) =sumlimits_{k=1}^infty
c_kz^k +sumlimits_{k=0}^inftyfrac{c_{-k}}{z^k}. $$ В этом случае $F_1(z)$ называют главной частью, а $F_2(z)$ – правильной частью.

В зависимости от поведения функции
$f(z)$ в окрестности $z=infty$ введена следующая классификация:

– Особенность в точке $z=infty$ устранимая, если все
$c_k=0$, $k=1,2,ldots$, т.е. если $f(z)=F_2(z)$ для $|z|>r$. В этом случае $$
limlimits_{ztoinfty}f(z)=c_0.
$$ Очевидно, что $$
frac1{2pi mathbf i }ointlimits_{L^-}f(z),dz=-c_{-1},
$$ где $L^-$ – произвольный контур, ориентированный по часовой стрелке, содержащий внутри себя окружность $|z|=r$.

Можно считать, что точка $z=infty$ находится внутри контура $L^-$. Если двигаться по контуру $L^-$ по часовой
стрелке, то точка $z=infty$ остается слева.

Видим, что в случае, когда $z=infty$ – устранимая особая точка, то вычет не обязательно
равен нулю!

– Точка $z=infty$ есть полюс порядка $m$, если
$f(z)=sumlimits_{k=1}^m c_k z^k+F_2(z)$ и $c_mne0$. В этом случае, очевидно, $$
limlimits_{ztoinfty}f(z)=infty.
$$

$$
ointlimits_{L^-}f(z),dz=sumlimits_{k=0}^infty c_{-k}
ointlimits_{L^-}frac{dz}{z^k}+sumlimits_{k=1}^m c_k
ointlimits_{L^-}z^k,dz=
$$ $$ =-c_{-1}intlimits_Lfrac{dz}z=-2pimathbf i c_{-1}, $$ потому, что $displaystyleointlimits_{L^-}z^k,dz=-ointlimits_L z^k,dz=0$, когда
$kne-1$;

– Точка $z=infty$ является существенно особой точкой, если
$f(z)=sumlimits_{k=1}^infty c_kz^k+F_2(z)$ и имеется бесконечное число чисел $c_k$, не равных нулю. В данном случае функция из-за первого слагаемого не имеет предела при $ztoinfty$.
$$
ointlimits_{L^-}f(z),dz=sumlimits_{k=-infty}^infty c_k
ointlimits_{L^-}z^k,dz=-2pi mathbf i c_{-1}.
$$

Вычетом функции $f(z)$ в бесконечно удаленной точке
называется $$
mbox{Res }f(infty)=frac1{2pi mathbf i }ointlimits_{L^-}f(z),dz,
$$ где $L^-$ – произвольный замкнутый контур, ориентированный по часовой стрелке, принадлежащий множеству $|z|>r$ (где функция $f(z)$
аналитична).

Кроме того, если $f(z)=sumlimits_{k=-infty }^infty c_kz^k$ – ряд Лорана функции во внешности окружности $|z|=r$, то
$$
mbox{Res }f(infty)=-c_{-1}.
$$

Теорема о сумме вычетов

Пусть функция $f(z)$ аналитична на всей плоскости $z$ за исключением конечного числа изолированных особых точек $z_1,z_2,dots,z_N$. Тогда сумма всех вычетов этой функции, включая вычет в бесконечно удаленной точке, равна нулю:
$$ sumlimits_{k=1}^Nmbox{Res }f(z_k)+mbox{Res }f(infty)=0. $$

Вычислить интеграл $ointlimits_{|z|=2}frac{z^{20},dz}{(2z^3+1)^2(z^4-1)^3}$.

Р е ш е н и е.

Все особые точки $z_k=sqrt[4]{1}$, $sqrt[3]{-0,5}$ лежат в круге $|z|=2$. Вычисление вычетов в этих точках довольно
затруднительно, поэтому воспользуемся формулой $$ I=2pi isumlimits_{k=1}^infty mbox{Res }f(z_k)=-2pi imbox{Res }f(infty). $$ Представим функцию в
виде $$
frac{z^{20}}{4z^6left(1+cfrac1{2z^3}right)^2z^{12}
left(1-cfrac1{z^4}right)^3}=
$$ $$ =frac{z^2}4left(1-frac1{2z^3}+frac1{4z^6}-dotsright)^2
left(1+frac1{z^4}+frac1{z^8}right)^3=frac{z^2}4-frac1{4z}
+dots . $$

Тогда $mbox{Res }f(infty)=dfrac14$ и интеграл равен $-2pi imbox{Res }f(infty)=-dfrac{pi i}2$.

О т в е т: $-dfrac{pi i}2$.

Вычисление определенных интегралов с помощью вычетов

Некоторые определенные интегралы от функций вещественного переменного удается преобразовать в интеграл по замкнутому контуру от функции комплексного переменного, что позволяет применить для вычисления этих интегралов основную теорему о вычетах. Часто удается достаточно просто получить ответ и в тех случаях, когда применение других методов анализа
оказывается затруднительным.

I. Интеграл вида $I=intlimits_0^{2pi}R(cos{x},sin{x}),dx,$

где $R(u,v)$ – рациональная функция двух переменных.

Подстановка $z=e^{itheta}$ даст для $$
begin{array}{l}
costheta=dfrac12left(e^{itheta}+e^{-itheta}right)
=dfrac12left(z+dfrac1zright), \
sintheta=dfrac1{2i}left(e^{itheta}-e^{-itheta}right)
=dfrac{-i}2left(z-dfrac1zright), \ dtheta=dfrac{dz}{iz}
end{array}
$$ и превратит вещественный интеграл в комплексный. При изменении $theta$ от $0$ до $2pi$ комплексная переменная пробегает
замкнутый контур – окружность $|z|=1$ в положительном направлении. Окончательно интеграл примет вид $$
I=frac1iointlimits_{|z|=1}Fleft(z+frac1z,z-frac1zright)
frac{dz}{z},.
$$

Вычислить интеграл
$$
intlimits_0^{2pi}frac{dx}{a+cos x},quad a>1.
$$

Р е ш е н и е.

Положим $e^{ix}=z$. При изменении $x$ от 0 до $2pi$ переменная $z$ пробегает окружность $|z|=1$ в положительном направлении.
Выразим $$
cos x=frac12left(e^{ix}+e^{-ix}right)=frac{z^2+1}{2z},
$$ и $$ dz=ie^{ix}dx=izdx,quadhbox{откуда}quad dx=frac{dz}{iz}. $$ Тогда $$
I=ointlimits_{|z|=1}frac{dz}{izleft(cfrac{z^2+1}{2z}+aright)} =frac2iointlimits_{|z|=1}frac{dz}{z^2+2az+1}. $$

Корни знаменателя $z_1=-a+sqrt{a^2-1}$, $z_2=-a-sqrt{a^2-1}$ — простые полюсы, $|z_1|<1$ и $z_1$ лежит внутри круга $|z|=1$: $$
mbox{Res }f(z_1)=frac1{z-z_2}Big|_{z=z_1}=frac1{2sqrt{a^2-1}}.
$$ Исходный интеграл равен $dfrac2icdotdfrac{2pi i}{2sqrt{a^2-1}} =dfrac{2pi}{sqrt{a^2-1}}$.

О т в е т:
$dfrac{2pi}{sqrt{a^2-1}}$.

II. Несобственный интеграл от рациональной функции $I=intlimits_{-infty}^infty R(x),dx=intlimits_{-infty}^infty frac{P_m(x)}{Q_n(x)},dx$,

где $P_m(x)$ и $Q_n(x)$ — многочлены степеней $m$ и $n$ соответственно.

Если знаменатель $Q_n(x)$ не имеет нулей на действительной оси, и $ngeqslant m+2$, тогда
begin{equation*}
intlimits_{-infty}^infty R(x),dx = 2pi mathbf i sumlimits_{k=1}^n mbox{Res }R(z_k),
end{equation*}
где вычеты берутся во всех полюсах $z_k$ функции $R(z)$, расположенных в верхней полуплоскости $mbox{Im }z>0$.

Вычислить интеграл $ I=intlimits_{-infty}^inftyfrac{dx}{x^4+1}.$

Р е ш е н и е.

Аналитическое продолжение подынтегральной функции в верхнюю полуплоскость, а именно функция $$ f(z)=frac1{z^4+1}, $$
удовлетворяет всем условиям, относящимся к вычислению интегралов с помощью вычетов. Особыми точками
функции в верхней полуплоскости являются точки $$ z_k=e^{tfrac{ipi}4(2k+1)},quad k=0,1, $$ причем обе эти точки – полюсы 1-го порядка.
Поэтому $$ I=2pi isumlimits_{k=0}^1 mbox{Res }f(z_k)=frac{pisqrt2}2. $$

III. Несобственные интегралы вида $I=intlimits_{-infty}^infty R(x)cos{lambda x},dx, ,, I=intlimits_{-infty}^infty R(x)sin{lambda x},dx$,

где $R(x)=P_m(x)/Q_n(x)$ – правильная рациональная дробь, не имеющая особых точек на действительной оси. Тогда
begin{equation*}
intlimits_{-infty}^infty R(x)cos{lambda x},dx = mbox{Re }left( 2pi mathbf i sumlimits_{k}
mbox{Res }R(z_k)e^{mathbf i lambda z_k}right),
end{equation*}
begin{equation*}
intlimits_{-infty}^infty R(x)sin{lambda x},dx = mbox{Im }left( 2pi mathbf i sumlimits_{k}
mbox{Res }R(z_k)e^{mathbf i lambda z_k}right),
end{equation*}
где вычеты берутся во всех полюсах $z_k$ функции $R(z)$, расположенных в верхней полуплоскости $mbox{Im }z>0$.

Интегралы вычисляются с помощью леммы Жордана:

Лемма Жордана

Пусть функция $f(z)$ аналитична в полуплоскости $mbox{Im }z>0$, за исключением конечного числа изолированных особых точек, и пусть
$M(R)$ есть максимум модуля $f(z)$ на полуокружности $gamma_{R}={zin mathbb C_{}: |z|=R, mbox{Im } z >0 }$.

Если $M(R)to0$ при $Rtoinfty$, то для любого действительного числа $lambda>0$
$$
intlimits_{gamma_R}f(z)e^{mathbf i lambda z},dzto0quadhbox{при}quad
Rtoinfty, $$

Для $lambda<0$ в условиях леммы нужно заменить верхнюю полуплоскость на нижнюю и соответственно верхнюю полуокружность на нижнюю.

Вычислить интеграл $ I=intlimits_{-infty}^inftyfrac{cosalpha x}{x^2+a^2},dx,, a>0, alpha>0$.

Р е ш е н и е.

Чтобы иметь возможность воспользоваться леммой Жордана, заметим, что в силу формулы Эйлера $$ I=mbox{Re }I_1
=mbox{Re}intlimits_{-infty}^infty frac{e^{mathbf i alpha x}} {x^2+a^2},dx. $$

Аналитическое продолжение подынтегральной функции интеграла $I_1$ – функция $dfrac{e^{mathbf i alpha z}}{z^2+a^2}$ имеет в верхней полуплоскости единственную особую точку $z_1=ia$, являющуюся простым полюсом. Поэтому по основной теореме о вычетах $$ I_1=2pi
mathbf i mbox{Res }left(frac{e^{mathbf i alpha z}}{z^2+a^2}Big|_{z=mathbf i a}
right)=fracpi{a}e^{-alpha a}quadhbox{и}quad
I=fracpi{a}e^{-alpha a}. $$

Логарифмический вычет. Принцип аргумента

Логарифмической производной функции $f(z)$ называется производная ее логарифма $left(ln {f(z)}right)’= frac{f'(z)}{f(z)}$.

Пусть $z_0$ – нуль порядка $n$, $z_1$ – полюс порядка $p$.
Запишем разложения в ряд Лорана логарифмической производной в окрестности нуля и полюса функции $f(z)$.
$$
left(ln {f(z)}right)’= frac{n}{z-z_0}+b_1+b_2(z-z_0)+dots quad Rightarrow
$$
$n$-кратный нуль функции $f(z)$ является для логарифмической производной простым полюсом, причем вычет логарифмической производной в этой точке равен кратности нуля, то есть $n$.
$$
left(ln {f(z)}right)’= frac{-p}{z-z_1}+c_1+c_2(z-z_1)+dots quad Rightarrow
$$
$p$-кратный полюс функции $f(z)$ является для логарифмической производной простым полюсом, причем вычет логарифмической производной в этой точке равен порядку полюса, взятому с обратным знаком, то есть $-p$.

Логарифмическим вычетом функции $f(z)$ в точке $z=a$ называется вычет ее логарифмической производной $ frac{f'(z)}{f(z)}$ в этой точке, т.е. значение
$$
mbox{Res }frac{f'(z)}{f(z)}=frac{1}{2pi mathbf i}ointlimits_{L} frac{f'(z)}{f(z)}dz,
$$
где в качестве контура $L$ интегрирования можно взять любую окружность с центром в точке $z=a$, целиком лежащую в указанной проколотой окрестности этой точки.

Если $f(z)$ является аналитической функцией на замкнутом контуре $L$ и не имеет нулей на этом контуре, то значение
$$
mbox{Res } frac{f'(z)}{f(z)}=frac{1}{2pi mathbf i}ointlimits_{L} frac{f'(z)}{f(z)}dz
$$
называют логарифмическим вычетом функции $f(z)$ относительно контура $L$.

Теорема о логарифмическом вычете

Логарифмический вычет многочлена $P_n(z)$ степени $n$ относительно контура $L$, на котором нет нулей $P_n(z)$, равен числу нулей многочлена (с учетом их кратности) внутри контура.

Принцип аргумента

Пусть непостоянная функция $f(z)$ аналитична всюду в односвязной области $D$ и на ее границе – кусочно-гладком контуре $L$, кроме, возможно, некоторого конечного числа полюсов. Пусть также функция имеет конечное число нулей, причем на контуре $L$ нет ни нулей, ни полюсов функции. Тогда приращение аргумента функции $f(z)$ при обходе в положительном направлении контура $L$ равно произведению $2pi$ на разность числа нулей и полюсов функции $f(z)$, расположенных в области $D$, причем каждый нуль следует считать сколько раз, какова его кратность, а каждый полюс – каков его порядок.
$$
Delta_Larg f(z)=2pi(N-P),
$$
$$
N=q_1+q_2+ldots+q_m, quad P=p_1+p_2+ldots+p_k,
$$
$q_i$ – кратность нуля $a_i$, $i=1,ldots,m$, $p_j$ – кратность полюса $b_j$, $j=1,ldots,k$.

Теорема Руше

Пусть функции $f(z)$ и $varphi(z)$ являются аналитическими в замкнутой области $D$, причем на границе $C$ этой области имеет место неравенство: $|f(z)|_{C}>|varphi(z)|_{C}$. Тогда полное число нулей (с учетом их кратности) в $D$ функции $F(z)=f(z)+varphi(z)$ равно полному числу нулей (с учетом их кратности) функции $f(z)$.

Найти число нулей функции $F(z)=z^8-4z^5+z^2-1$ в единичном круге.

Пусть $f(z)=-4z^5$, $varphi(z)=z^8+z^2-1$. Граница $C$ заданной области – единичный круг $|z|=1$.

$$
|z|=1: ,, begin{aligned} &|f(z)=|-4z^5|=4|z|^5=4, \ &|varphi(z)|leqslant|z|^8+|z|^2+1=3 ,, Rightarrow \ &|f(z)|>|varphi(z)| end{aligned}.
$$

Выполнены все условия теоремы Руше. Функция $f(z)$ имеет корень $z=0$ кратности $5$, лежащий в $|z|<1$. Значит, $F(z)=f(z)+varphi(z)$ имеет пять нулей в единичном круге.

Найти число корней уравнения $z^4-8z+10=0$ в кольце 1<|z|<3

Найдем число корней $N_1$ в области $|z|<1$ и число корней $N_2$ в области $|z|<3$. Тогда число корней в кольце 1<|z|<3 будет равно $N=N_2-N_1$.

а) $|z|<1$.

Пусть $F(z)=f(z)+varphi(z)$, где $f(z)=10$, $varphi(z)=z^4-8z$.
На границе $C$ единичного круга имеем:
$$
|z|=1: ,, |f(z)|=10, |varphi(z)|leqslant|z|^4+8|z|=9,, Rightarrow ,, |f(z)>|varphi(z)|.
$$
Выполнены все условия теоремы Руше. Функция $f(z)$ в области $|z|<1$ не имеет нулей. Следовательно и уравнение $F(z)=0$ не имеет корней в единичном круге. $N_1=0$.

б) $|z|<3$.

В итоге получаем: $N=N_2-N_1=4-0=4$

Источник

Лекция 9.

Вычеты и их применение.

Вычетом функции f(z) в точке z₀ называется коэффициент при z^-1 в разложении функции в ряд Лорана в окрестности этой точки.

Эквивалентное определение: вычетом функции f(z) в точке z₀ называется . В самом деле, коэффициент ряда Лорана равен . Поэтому .

Вычисление вычетов в точке конечной плоскости.

Для различных типов особых точек (правильная, полюс, существенно особая) различны алгоритмы вычисления вычетов функции в этих точках.

Если z₀– правильная особая точка, то ряд Лорана превращается в ряд Тейлора, в котором нет отрицательных степеней , поэтому =0.

Если z₀ – полюс первого порядка, то разложение в ряд Лорана в окрестности этой точки не содержит степеней , ниже, чем –1 и содержит степень -1. Разложение выглядит так.