Вычеты и их применение
Определение вычета
Пусть — изолированная особая точка функции
. По определению изолированной особой точки существует некоторая окрестность этой точки, в которой
— аналитическая. Напомним, что для
эта окрестность имеет вид
, а для
—
.
Рассмотрим произвольный контур , принадлежащий такой окрестности и являющийся границей некоторой области, содержащей
(рис 4.2,а).
По следствию из основной теоремы Коши интеграл имеет одно и то же значение, независимо от вида кривой
, т.е. интеграл характеризует поведение функции
в особой точке
и, следовательно, может быть использован для исследования функции как некоторая числовая характеристика.
Вычетом функции в изолированной особой точке
называется интеграл
, где
— контур, принадлежащий окрестности точки
и охватывающий ее. Обход контура — положительный, т.е. область им ограниченная и принадлежащая окрестности
при обходе расположена слева: для
— обход против часовой стрелки (рис. 4.2,а), для
— по часовой стрелке (рис. 4.2,б). Обозначается вычет
(res — residu (фр.) — вычитать):
(4.16)
Так как в окрестности изолированной особой точки функция разлагается в ряд Лорана, то, используя формулы для коэффициентов ряда Лорана и сравнивая их с (4.16), замечаем, что можно сделать следующее заключение.
Утверждение 4.5. Вычет функции в изолированной особой точке равен коэффициенту при первой отрицательной степени в разложении функции в ряд Лорана в окрестности этой точки, т.е. при
для
, и этому коэффициенту, взятому с противоположным знаком, для
(4.17)
(4.18)
С помощью вычетов можно записать в другой форме основную теорему Коши для сложного контура.
Действительно, пусть функция в области имеет
особых точек
. Можно рассмотреть контуры
, которые являются границами непересекающихся областей
, таких, что каждая из особых точек
(изолированных особых точек) принадлежит одной из
(рис. 4.3,а), а интеграл по
согласно определению (см. формулу (4.16)) есть
.
Кроме того, для любого контура , ограничивающего область
, которой принадлежат все особые точки функции
, и контура
— границы окрестности бесконечно удаленной точки справедливо равенство
(обход на
по часовой стрелке (рис. 4.3,б)). Из этих рассуждений и формулы (4.16) получаем следующие утверждения.
Основная теорема о вычетах
Утверждение 4.6 (основная теорема о вычетах). Если функция -аналитическая в
за исключением конечного числа особых точек
, то справедливо равенство (где
— граница области
):
(4.19)
Обобщенная теорема о вычетах
Утверждение 4.7 (обобщенная теорема о вычетах). Сумма вычетов функции во всех ее особых точках, включая бесконечно удаленную точку, равна нулю:
(4.20)
Пример 4.22. Найти вычеты следующих функций в их особых точках: а) ; б)
.
Решение
Особыми точками функций являются точки . Записываем разложения функций в ряд Лорана в окрестности этих точек (см. примеры 3.31, 3.33 и 3.34):
а)
Из этих разложений находим:
Полученный результат иллюстрирует обобщенную теорему о вычетах:
Заметим также, что здесь точки и
— простые полюсы, а
— устранимая особая точка.
б)
Из этих разложений имеем:
Вычет в бесконечно удаленной точке можно найти, используя обобщенную теорию о вычетах:
. Этот же результат получим, если запишем разложение функции в области
-окрестности
Заметим, что для этой функции —
,
—
, а
— устранимая особая точка.
Пример 4.23. Найти вычеты следующих функций в особых точках: а) ; б)
.
Решение
Пример 4.24. Найти вычеты следующих функций в их особых точках: a) ; б)
.
Решение
Конечные особые точки функций являются существенно особыми точками. Это для первой функции и
для второй. Разложим функции в ряды в окрестностях этих точек и найдем вычеты по формуле (4.17):
а)
Следовательно, .
Так как у рассматриваемой функции другах конечных особых точек нет, то по формуле (4.20) . Заметим, что
— устранимая особая точка для данной функции
;
б)
поэтому . Поскольку нет другах конечных особых точек, то по формуле (4.20)
. Точка
является полюсом первого порядка данной
.
Вычисление вычетов в полюсе и устранимой особой точке
В рассмотренных выше примерах при нахождении вычетов использовались формулы (4.17),(4.18) , т.е. функции раскладывались в ряды Лорана. При этом знание типа особой точки, в которой вычисляется вычет функции, не является обязательным. Таким методом всегда определяется вычет в тех случаях, когда заранее предполагается, что особая точка — существенно особая точка для функции. В случае устранимой особой точки и полюсов задачу вычисления вычета по формуле (4.17) можно заменить некоторыми практически более удобными формулами и правилами. Вывод этих формул и правил в общем виде, очевидно, связан с исследованием разложения функции в ряд в окрестности особой точки, а тип особой точки определяется по поведению функции, т.е. вычислением предела.
Так, если и
— конечная особая точка, то в разложении функции в ряд Лорана в окрестности
, согласно утверждению 4.1, отсутствует главная часть. Следовательно,
и
.
Если и
— полюс функции
, то можно определить порядок полюса, также не прибегая к разложению функции в ряд, используя утверждение 4.3. Пусть
—
функции
, тогда разложение функции в ряд в окрестности
имеет вид (4.6). Умножив обе части равенства на
и продифференцировав результат
раз, получим выражение
из которого определяем .
В частности, при имеем
. Последнее равенство принимает наиболее удобную форму для функции вида
, где
— аналитические вточке
функции и
. А именно:
Результат приведенных рассуждений запишем в виде утверждения.
Утверждение 4.8
1. Если конечная особая точка является устранимой особой точкой функции
, то (где
— устранимая особая точка)
(4.21)
2. Если полюс порядка п функции
, то
(4.22)
(4.23)
3. Если —
функции
, где
— аналитические в точке
функции и
, то
(4.24)
Алгоритм вычисления вычета функции
Замечание 4.6. Формула (4.22) дает следующий алгоритм вычисления вычета функции в полюсе порядка .
1. Умножить на
, где
— порядок полюса
, и получить функцию
.
2. Найти производную функции порядка
.
3. В соответствии с (4.22) найти .
Пример 4.25. Найти вычеты в конечных особых точках функций:
Решение
Конечными особыми точками являются
и
— полюсы первого порядка, причем в каждом случае функцию можно представить в виде, допускающем применение формулы (4.24). Используя эту формулу, находим
Для функции точка
также является
и выполняются условия применимости формулы (4.24) . При этом функцию удобно представить в виде
. Применяя формулу (4.24), находим
Точка для
— полюс второго порядка. Применяем формулу (4.22) при
. Запишем решение согласно алгоритму.
1. Умножаем на
и записываем функцию
.
2. Находим производную функции
3. Используя (4.22), получаем .
Для функции единственная конечная особая точка
является устранимой особой точкой, поэтому
(согласно (4.21)).
Все полученные результаты соответствуют результатам примеров 4.22 и 4.23.
Пример 4.26. Найти вычеты следующих функций в особых точках: а) ; б)
;
Решение
В заключение раздела рассмотрим бесконечно удаленную точку в случае, когда она является устранимой особой точкой для . Разложение функции в ряд Лорана имеет вид (4.5). Коэффициент
можно определить из этого равенства следующим образом:
. Так как, очевидно,
, то, доопределяя функцию, положим
. Получаем формулу для вычисления вычета в
— устранимой особой точке функции
(4.25)
В частности, если является нулем функции
, то есть
, то формула принимает вид
(4.26)
Пример 4.27. Найти вычеты в бесконечно удаленной точке функций:
а) ; б)
.
Решение
а) Точка — устранимая особая точка для этих функций и
. Поэтому вычеты этих функций находим по формуле (4.26):
Результат совпадает с полученным в примере 4.22.
б) Точка — устранимая особая точка для
, так как
. Вычет находим по формуле (4.25):
Математический форум (помощь с решением задач, обсуждение вопросов по математике).
Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.
-
Теоретический минимум
Вычетом функции
![[IMG]](http://corum.mephist.ru/tex/images/4d8eb2503f655a0ddd6fc14b31088756.gif) в особой точке
в особой точке ![[IMG]](http://corum.mephist.ru/tex/images/34b06aae8f117a184418f76b61e93ff9.gif) по определению называется величина
по определению называется величина
![[IMG]](http://corum.mephist.ru/tex/images/158c67854e74c53d781e5c318dc893b2.gif)
Контур интегрирования должен охватывать только одну особую точку![[IMG]](http://corum.mephist.ru/tex/images/34b06aae8f117a184418f76b61e93ff9.gif) , причём она должна быть изолированной
, причём она должна быть изолированной
и являться точкой однозначного характера.
Обычно по определению вычеты не вычисляют: это неудобно. Можно показать, что вычет функции в точке представляет собой
коэффициент при минус первой степени в разложении функции в ряд Лорана в окрестности данной точки. Это упрощает вычисление,
так как появляется возможность использовать приёмы разложения функции в ряд Лорана, не связанные с вычислением контурных
интегралов. Тут многое зависит от вида особой точки. В разложении функции в ряд Лорана в окрестности устранимой особой точки
отрицательные степени отсутствуют. Следовательно, и вычет в такой точке равен нулю. Разложение в ряд Лорана в окрестности полюса
содержит конечное число отрицательных степеней. В этом случае для полюса n-го порядка
![[IMG]](http://corum.mephist.ru/tex/images/dec252f42b1f3460b2884a62d55c5bc2.gif)
Чаще всего применяется именно эта формула. Для простого полюса (полюса первого порядка) формула сильно упрощается:
![[IMG]](http://corum.mephist.ru/tex/images/1786941a9bed4ff1c2877005620c4880.gif)
Отдельно рассматривается вычет в бесконечно удалённой точке. Он равен взятому с противоположным знаком коэффициенту при
минус первой степени разложения функции в ряд Лорана в окрестности бесконечно удалённой точки.Вычеты находят применение при вычислении интегралов по основной теореме о вычетах.
Примеры вычисления вычетовПример 1. Вычет функции в простом полюсе.
Найдём вычет функции![[IMG]](http://corum.mephist.ru/tex/images/d4b50e652f49367354e3bf0ea0b9004c.gif) в точке
в точке ![[IMG]](http://corum.mephist.ru/tex/images/7c894f6cedac5ed39070fb450a9423b3.gif) .
.![[IMG]](http://corum.mephist.ru/tex/images/aa605951ab5109c0ce9258c32018bf97.gif)
Пример 2. Вычет функции в полюсе третьего порядка.
Найдём вычет функции![[IMG]](http://corum.mephist.ru/tex/images/c3c91d2c9121128764963ba9c9b72ad2.gif) в точке
в точке ![[IMG]](http://corum.mephist.ru/tex/images/40c988e7538d8db23b784ae0eeae3c00.gif) .
.Убедиться в том, что точка
![[IMG]](http://corum.mephist.ru/tex/images/40c988e7538d8db23b784ae0eeae3c00.gif) – полюс третьего порядка, достаточно просто. Котангенс в числителе сам по себе имеет в этой
– полюс третьего порядка, достаточно просто. Котангенс в числителе сам по себе имеет в этой
точке простой полюс, функция![[IMG]](http://corum.mephist.ru/tex/images/8d5153f733b4234a1df6be8942f6c103.gif) в знаменателе делает данную точку полюсом именно третьего порядка.
в знаменателе делает данную точку полюсом именно третьего порядка.
![[IMG]](http://corum.mephist.ru/tex/images/3095de41ea3906dd0ae434327bb23bf3.gif)
![[IMG]](http://corum.mephist.ru/tex/images/23cf622ac2cdeeea6f15a8ebfdd35bfc.gif)
![[IMG]](http://corum.mephist.ru/tex/images/8295f72184d9d346671fe65ba1c8730c.gif)
![[IMG]](http://corum.mephist.ru/tex/images/fb122f95595a543b355ee79ed46da852.gif)
Для вычисления этого предела раскладываем функции в числителе в ряд Тейлора. Причём так как в знаменателе
сразу получится третья степень – в первом же слагаемом, то и в числителе следует проводить разложение до кубических слагаемых:
![[IMG]](http://corum.mephist.ru/tex/images/135dbea134bf6bf6fdc1c1606e270716.gif) .
.
Примечание. Этот расчёт приходится проделывать при вычислении значения дзета-функции Римана![[IMG]](http://corum.mephist.ru/tex/images/c7085352fc56baab9176b386033a1554.gif) .
.Пример 3. Вычет функции в полюсе второго порядка.
Найдём вычет функции![[IMG]](http://corum.mephist.ru/tex/images/d23fa9ab96abed48dfa9ab55e691d352.gif) в точке
в точке ![[IMG]](http://corum.mephist.ru/tex/images/1509fe9b0302d871413424ae4a96c70a.gif) .
.Хотя особая точка
![[IMG]](http://corum.mephist.ru/tex/images/1509fe9b0302d871413424ae4a96c70a.gif) является полюсом второго порядка, пользоваться приведённой выше общей формулой для
является полюсом второго порядка, пользоваться приведённой выше общей формулой для
вычетов в полюсах не будем. Проведём разложение в ряд Лорана:
![[IMG]](http://corum.mephist.ru/tex/images/9ab84eab90ab28e3b92a9ce0f151d6a1.gif)
![[IMG]](http://corum.mephist.ru/tex/images/035703880b44aa0eb44788bd482b30aa.gif)
Видно, что коэффициент при минус первой степени равен![[IMG]](http://corum.mephist.ru/tex/images/0d54236da20594ec13fc81b209733931.gif) . Это и есть искомый вычет.
. Это и есть искомый вычет.Пример 4. Вычет функции в бесконечно удалённой точке.
Найдём вычет функции![[IMG]](http://corum.mephist.ru/tex/images/f1f63d00bae67f87c9f539fd3ba0f600.gif) в бесконечно удалённой точке.
в бесконечно удалённой точке.Представим функцию в следующем виде:
![[IMG]](http://corum.mephist.ru/tex/images/95dcc47856eebd397cebafb5dfb11d1e.gif)
Экспоненту можно разложить в ряд по известной формуле, для дроби используем разложение, представляющее собой сумму геометрической прогрессии:
![[IMG]](http://corum.mephist.ru/tex/images/22dca48886044a394b430dce941f12a3.gif)
Видно, что после перемножения скобок при минус первой степени останется число 2. Следовательно, вычет равен (-2). -

BA3a
for love and rock-n-roll
VIPПомнится, когда нам Теляковский рассказывал про вычеты, я сидел с открытым ртом и думал «вау, как красиво».
-
Реквестирую аналогичную тему про особые точки :huh: Завтра сдавать.
-

Sean33
агрессия и злоба
Модератор
VIPSchufter, большое спасибо! Как раз во время!
-
panicdoctor, да, такая формула есть, конечно. Но на мой взгляд лучше помнить общую формулу для вычета в полюсе
любого порядка, чем помнить дополнительно ещё одну формулу. Тем более, что в простом полюсе вычет обычно находится легко. :huh:
Но подчеркну: формула есть, если есть желание – ей можно пользоваться. Просто высказал своё мнение.
Поделиться этой страницей

В рассмотренных выше примерах при
нахождении вычетов функции раскладывались
в ряды Лорана. При этом знание типа
особой точки, в которой вычисляется
вычет функции, не является обязательным.
Таким методом всегда определяется вычет
в тех случаях, когда заранее предполагается,
что особая точка — существенно особая
точка для функции. В случае устранимой
особой точки и полюсов задачу вычисления
можно заменить некоторыми практически
более удобными формулами и правилами.
Вывод этих формул и правил в общем виде
связан с исследованием разложения
функции в ряд в окрестности особой
точки, а тип особой точки определяется
по поведению функции, т.е. вычислением
предела.
Если
![]()
и
![]()
─
конечная особая точка, то в разложении
функции в ряд Лорана в окрестности![]()
,
отсутствует главная часть, следовательно,![]()
и
![]()
Если
![]()
т.е.
−полюс
функции
![]()
то
можно определить порядок полюса, не
прибегая к разложению функции в ряд и
используя утверждение 4.3. Пусть точка
─
полюс порядка n
функции, тогда разложение функции в
ряд в окрестности точки имеет вид
![]()
![]()
,
![]()
![]()
.
Умножив обе части этих равенств на
![]()
и продифференцировав результат (n-1)
раз, получим выражение
![]()
,из
которого определяем![]()
при
n =1
![]()
.
Последнее равенство принимает наиболее
удобную форму для функции вида
![]()
,
где
![]()
аналитические функции в точке z0
и
![]()
,а именно:
.
Результат приведенных рассуждений
запишем в виде утверждения.
Утверждение
1. Если конечная особая точка z0
является устранимой особой точкой
функции , то ![]()
![]()
устранимая
особая точка. (4.5)
2.Если
─полюс
порядка n
функции ,![]()
то
![]()
![]()
─полюс
порядка n
(4.6)
![]()
─
простой полюс.
(4.7)
3. Если
─простой
полюс. функции
![]()
где
![]()
аналитические
функции в точке z0
и
![]()
то
![]()
(4.8)
Замечание
Формула (4.7) дает следующий алгоритм
вычисления вычета функции в полюсе
порядка n .
1.Умножить на
,
где n
порядок полюса z0,
и получить функцию
![]()
2. Найти производную функции порядка
![]()
![]()
:
3. В соответствии с (4.7) найти
![]()
Пример 1. Найти
вычеты в конечных особых точках функций:
а)
![]()
б)![]()
в)![]()
а) Конечныe особые точки
z1=-1
и z2 =3
─ простые полюсы, поэтому используя
формулу (4.8),можно найти вычеты функции
в указанных точках в виде
![]()
![]()
б) для функции
![]()
особые точки
![]()
и
![]()
.
1) Точка ─простой полюс и выполняются
условия применимости формулы (4.8) . При
этом функцию удобно представить в виде
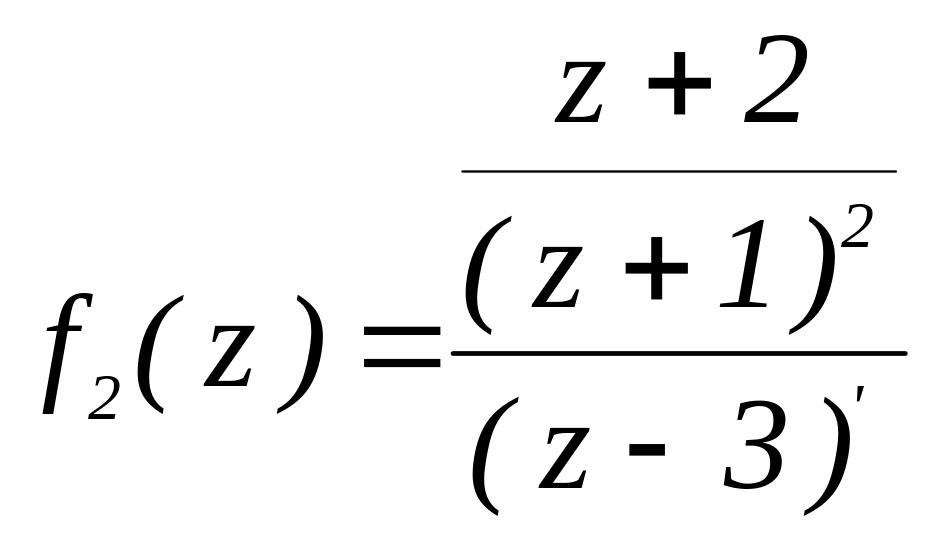
.
Применяя формулу (4.8), находим

2)
Точка z2
=-1
для полюс
второго порядка. Применяя формулу (4.6)
при n=
2,
запишем решение согласно алгоритму
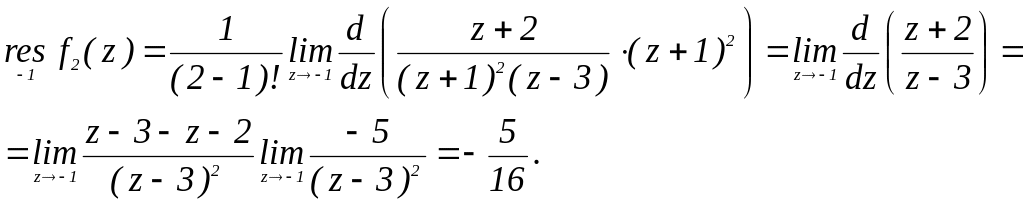
в) Для функции
![]()
единственная конечная особая точка─
устранимая особая точка
,
поэтому согласно формуле (4.5)
![]()
Все полученные результаты соответствуют
результатам примеров 1 и 2 §1.
Пример 2. Найти
вычеты следующих функций в особых
точках:
а)
![]()
б)
![]()
Особыми точками функций являются нули
знаменателя ─корни уравнения
![]()
или
![]()
, находим
![]()
и два других корня квадратного уравнения
![]()
,т.е.
![]()
,
![]()
.
а)Для
![]()
все три особые точки ─простые
полюсы.
Находим вычеты в них по формуле (4.8):
![]()
![]()
![]()
![]()
что можно проверить, разложив
в
ряд в окрестности z=∞
т.е. в области
![]()
.
б) Для
![]()
точка
![]()
─устранимая
особая точка, так как
![]()
,
поэтому
![]()
.
2)Точки и ─простые полюсы, поэтому
вычеты находим, как и в предыдущем случае
или по формуле (4.7):
![]()
![]()
Вычет функции в z=∞
можно получить по формуле (4.4):
![]()
В заключение рассмотрим вычет в бесконечно
удаленной точке в случае, когда она
является устранимой особой точкой для
. Разложение функции в ряд Лорана имеет
вид
![]()
![]()
Коэффициент ![]()
можно
определить из этого равенства следующим
образом:
![]()
Так как
![]()
,
то доопределим функцию, положив
![]()
Получаем формулу для вычисления вычета
в точке
![]()
─
устранимой особой точке функции
![]()
(4.9)
В частности, если
![]()
является нулем функции
,т.е.![]()
,
то формула принимает вид
![]()
.
(4.10)
Пример 3. Найти вычеты в
функций:
a)
![]()
б)
![]()
а) Точка
![]()
─устранимая
особая точка этих функций и
![]()
.
Поэтому
вычеты этих функций находим по формуле
(4.26):
![]()
![]()
Результат совпадает с полученным в
примере 1(а) §2.
б) Точка
─устранимая
особая точка для
![]()
,
так как
![]()
.
Вычет находим по формуле (4.9):
![]()
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Содержание
Глава 6. Вычеты функций и их применение
Вычет функции относительно изолированной особой точки. Основная теорема о вычетах
Вычетом функции $f(z)$ относительно изолированной особой точки $z_0$ называется коэффициент $c_{-1}$ при $(z-z_0)^{-1}$ в разложении в ряд Лорана функции $f(z)$ в окрестности $z_0$.
$$
mbox{Res }f(z_0) = c_{-1}.
$$
Вычетом функции $f(z)$ относительно изолированной особой точки $z_0$ называется интеграл
$$
mbox{Res }f(z_0) =frac1{2pi i}ointlimits_L f(z),dz,
$$ где $L$ – произвольный контур в кольце $0<|z-z_0|<R$, ориентированный против часовой стрелки ($L$ должен окружать точку $z_0$).
Т
Основная теорема о вычетах (Коши)
Пусть функция $f(z)$ является аналитической всюду в замкнутой области $overline D$, за исключением конечного
числа изолированных особых точек $z_1,z_2,dots,z_N$, лежащих внутри области $D$. Тогда $$
ointlimits_L f(z),dz=2pi isumlimits_{k=1}^N
mbox{Res }f(z_k),
$$ где $L$ – полная граница области $D$, проходимая в положительном направлении.
Вычисление вычетов в конечных особых точках
Вычет в устранимой особой точке равен $0$.
Если $z_0$ – существенно особая точка, то имеется только один способ вычисления вычета – разложение функции в ряд Лорана и определение коэффициента $c_{-1}$.
Для нахождения вычета в полюсе есть несколько приемов.
* Для простого полюса можно воспользоваться формулой:
begin{equation}label{1}
mbox{Res }f(z_0)=limlimits_{zto z_0}
Big(f(z)(z-z_0)Big).
end{equation}
* Для полюса порядка $m$:
begin{equation}label{2}
mbox{Res }f(z_0)=frac1{(m-1)!}limlimits_{zto z_0}
frac{d^{m-1}}{dz^{m-1}}Big(f(z)(z-z_0)^mBig).
end{equation}
* Для простого полюса в случае функции $ f(z)=frac{g(z)}{varphi(z)}$, где
$g(z)$ и $varphi(z)$ – аналитические функции в окрестности точки $z_0$ и $g(z_0)neq 0$, а для $varphi(z)$ точка $z_0$ есть нуль первого порядка (для $f(z)$ же точка $z_0$ есть полюс первого порядка):
begin{equation}label{3}
mbox{Res }f(z_0)=frac{g(z_0)}{varphi'(z_0)}.
end{equation}
П
Вычислить
$$ I=ointlimits_{|z-i|=2}frac{z-7}{z^2(z-1)(z-5i)},dz. $$
Строим контур интегрирования – окружность $|z-i|=2$. Подынтегральная функция имеет особые точки $z_1=0$, $z_2=1$ и $z_3=5i$. Точка $5i$ не
лежит внутри контура интегрирования. Точка $z_1=0$ – полюс 2-го порядка, $z_2=1$ – полюс 1-го порядка. По основной теореме о вычетах получаем $$ I=2pi ibig(mbox{Res }f(0)+mbox{Res }f(1)big). $$ По формуле для вычисления вычета в полюсе 2-го порядка
$$
mbox{Res }f(0)=frac1{1!}limlimits_{zto0}left(
left(frac{(z-7)z^2}{z^2(z-1)(z-5i)}right)’right)=
$$ $$ =limlimits_{zto0}frac{(z-1)(z-5i)-(z-7)(2z-1-5i)} {(z-1)^2(z-5i)^2}=frac{7+30i}{25}. $$ Для простого полюса вычет равен $$
mbox{Res }f(1)
=limlimits_{zto1}frac{(z-7)(z-1)}{z^2(z-1)(z-5i)} =-frac6{1-i}. $$
Окончательно, $$ I=2pi ileft(frac{7+30i}{25}-frac6{1-i}right) =pileft(frac{24}5-frac{106}{25}iright). $$
О бесконечно удаленной точке $z=infty$
Выберем любое $r geqslant0$. Разложим функцию $f(z)$ по степеням $z$ во внешности круга $|z|> r$, которое иногда
называют окрестностью бесконечно удаленной точки, $$ f(z)=sumlimits_{-infty}^infty c_kz^k=F_1(z)+F_2(z) =sumlimits_{k=1}^infty
c_kz^k +sumlimits_{k=0}^inftyfrac{c_{-k}}{z^k}. $$ В этом случае $F_1(z)$ называют главной частью, а $F_2(z)$ – правильной частью.
В зависимости от поведения функции
$f(z)$ в окрестности $z=infty$ введена следующая классификация:
– Особенность в точке $z=infty$ устранимая, если все
$c_k=0$, $k=1,2,ldots$, т.е. если $f(z)=F_2(z)$ для $|z|>r$. В этом случае $$
limlimits_{ztoinfty}f(z)=c_0.
$$ Очевидно, что $$
frac1{2pi mathbf i }ointlimits_{L^-}f(z),dz=-c_{-1},
$$ где $L^-$ – произвольный контур, ориентированный по часовой стрелке, содержащий внутри себя окружность $|z|=r$.
Можно считать, что точка $z=infty$ находится внутри контура $L^-$. Если двигаться по контуру $L^-$ по часовой
стрелке, то точка $z=infty$ остается слева.
Видим, что в случае, когда $z=infty$ – устранимая особая точка, то вычет не обязательно
равен нулю!
– Точка $z=infty$ есть полюс порядка $m$, если
$f(z)=sumlimits_{k=1}^m c_k z^k+F_2(z)$ и $c_mne0$. В этом случае, очевидно, $$
limlimits_{ztoinfty}f(z)=infty.
$$
$$
ointlimits_{L^-}f(z),dz=sumlimits_{k=0}^infty c_{-k}
ointlimits_{L^-}frac{dz}{z^k}+sumlimits_{k=1}^m c_k
ointlimits_{L^-}z^k,dz=
$$ $$ =-c_{-1}intlimits_Lfrac{dz}z=-2pimathbf i c_{-1}, $$ потому, что $displaystyleointlimits_{L^-}z^k,dz=-ointlimits_L z^k,dz=0$, когда
$kne-1$;
– Точка $z=infty$ является существенно особой точкой, если
$f(z)=sumlimits_{k=1}^infty c_kz^k+F_2(z)$ и имеется бесконечное число чисел $c_k$, не равных нулю. В данном случае функция из-за первого слагаемого не имеет предела при $ztoinfty$.
$$
ointlimits_{L^-}f(z),dz=sumlimits_{k=-infty}^infty c_k
ointlimits_{L^-}z^k,dz=-2pi mathbf i c_{-1}.
$$
Вычетом функции $f(z)$ в бесконечно удаленной точке
называется $$
mbox{Res }f(infty)=frac1{2pi mathbf i }ointlimits_{L^-}f(z),dz,
$$ где $L^-$ – произвольный замкнутый контур, ориентированный по часовой стрелке, принадлежащий множеству $|z|>r$ (где функция $f(z)$
аналитична).
Кроме того, если $f(z)=sumlimits_{k=-infty }^infty c_kz^k$ – ряд Лорана функции во внешности окружности $|z|=r$, то
$$
mbox{Res }f(infty)=-c_{-1}.
$$
Т
Теорема о сумме вычетов
Пусть функция $f(z)$ аналитична на всей плоскости $z$ за исключением конечного числа изолированных особых точек $z_1,z_2,dots,z_N$. Тогда сумма всех вычетов этой функции, включая вычет в бесконечно удаленной точке, равна нулю:
$$ sumlimits_{k=1}^Nmbox{Res }f(z_k)+mbox{Res }f(infty)=0. $$
П
Вычислить интеграл $ointlimits_{|z|=2}frac{z^{20},dz}{(2z^3+1)^2(z^4-1)^3}$.
Р е ш е н и е.
Все особые точки $z_k=sqrt[4]{1}$, $sqrt[3]{-0,5}$ лежат в круге $|z|=2$. Вычисление вычетов в этих точках довольно
затруднительно, поэтому воспользуемся формулой $$ I=2pi isumlimits_{k=1}^infty mbox{Res }f(z_k)=-2pi imbox{Res }f(infty). $$ Представим функцию в
виде $$
frac{z^{20}}{4z^6left(1+cfrac1{2z^3}right)^2z^{12}
left(1-cfrac1{z^4}right)^3}=
$$ $$ =frac{z^2}4left(1-frac1{2z^3}+frac1{4z^6}-dotsright)^2
left(1+frac1{z^4}+frac1{z^8}right)^3=frac{z^2}4-frac1{4z}
+dots . $$
Тогда $mbox{Res }f(infty)=dfrac14$ и интеграл равен $-2pi imbox{Res }f(infty)=-dfrac{pi i}2$.
О т в е т: $-dfrac{pi i}2$.
Вычисление определенных интегралов с помощью вычетов
Некоторые определенные интегралы от функций вещественного переменного удается преобразовать в интеграл по замкнутому контуру от функции комплексного переменного, что позволяет применить для вычисления этих интегралов основную теорему о вычетах. Часто удается достаточно просто получить ответ и в тех случаях, когда применение других методов анализа
оказывается затруднительным.
I. Интеграл вида $I=intlimits_0^{2pi}R(cos{x},sin{x}),dx,$
где $R(u,v)$ – рациональная функция двух переменных.
Подстановка $z=e^{itheta}$ даст для $$
begin{array}{l}
costheta=dfrac12left(e^{itheta}+e^{-itheta}right)
=dfrac12left(z+dfrac1zright), \
sintheta=dfrac1{2i}left(e^{itheta}-e^{-itheta}right)
=dfrac{-i}2left(z-dfrac1zright), \ dtheta=dfrac{dz}{iz}
end{array}
$$ и превратит вещественный интеграл в комплексный. При изменении $theta$ от $0$ до $2pi$ комплексная переменная пробегает
замкнутый контур – окружность $|z|=1$ в положительном направлении. Окончательно интеграл примет вид $$
I=frac1iointlimits_{|z|=1}Fleft(z+frac1z,z-frac1zright)
frac{dz}{z},.
$$
П
Вычислить интеграл
$$
intlimits_0^{2pi}frac{dx}{a+cos x},quad a>1.
$$
Р е ш е н и е.
Положим $e^{ix}=z$. При изменении $x$ от 0 до $2pi$ переменная $z$ пробегает окружность $|z|=1$ в положительном направлении.
Выразим $$
cos x=frac12left(e^{ix}+e^{-ix}right)=frac{z^2+1}{2z},
$$ и $$ dz=ie^{ix}dx=izdx,quadhbox{откуда}quad dx=frac{dz}{iz}. $$ Тогда $$
I=ointlimits_{|z|=1}frac{dz}{izleft(cfrac{z^2+1}{2z}+aright)} =frac2iointlimits_{|z|=1}frac{dz}{z^2+2az+1}. $$
Корни знаменателя $z_1=-a+sqrt{a^2-1}$, $z_2=-a-sqrt{a^2-1}$ — простые полюсы, $|z_1|<1$ и $z_1$ лежит внутри круга $|z|=1$: $$
mbox{Res }f(z_1)=frac1{z-z_2}Big|_{z=z_1}=frac1{2sqrt{a^2-1}}.
$$ Исходный интеграл равен $dfrac2icdotdfrac{2pi i}{2sqrt{a^2-1}} =dfrac{2pi}{sqrt{a^2-1}}$.
О т в е т:
$dfrac{2pi}{sqrt{a^2-1}}$.
II. Несобственный интеграл от рациональной функции $I=intlimits_{-infty}^infty R(x),dx=intlimits_{-infty}^infty frac{P_m(x)}{Q_n(x)},dx$,
где $P_m(x)$ и $Q_n(x)$ — многочлены степеней $m$ и $n$ соответственно.
Если знаменатель $Q_n(x)$ не имеет нулей на действительной оси, и $ngeqslant m+2$, тогда
begin{equation*}
intlimits_{-infty}^infty R(x),dx = 2pi mathbf i sumlimits_{k=1}^n mbox{Res }R(z_k),
end{equation*}
где вычеты берутся во всех полюсах $z_k$ функции $R(z)$, расположенных в верхней полуплоскости $mbox{Im }z>0$.
П
Вычислить интеграл $ I=intlimits_{-infty}^inftyfrac{dx}{x^4+1}.$
Р е ш е н и е.
Аналитическое продолжение подынтегральной функции в верхнюю полуплоскость, а именно функция $$ f(z)=frac1{z^4+1}, $$
удовлетворяет всем условиям, относящимся к вычислению интегралов с помощью вычетов. Особыми точками
функции в верхней полуплоскости являются точки $$ z_k=e^{tfrac{ipi}4(2k+1)},quad k=0,1, $$ причем обе эти точки – полюсы 1-го порядка.
Поэтому $$ I=2pi isumlimits_{k=0}^1 mbox{Res }f(z_k)=frac{pisqrt2}2. $$
III. Несобственные интегралы вида $I=intlimits_{-infty}^infty R(x)cos{lambda x},dx, ,, I=intlimits_{-infty}^infty R(x)sin{lambda x},dx$,
где $R(x)=P_m(x)/Q_n(x)$ – правильная рациональная дробь, не имеющая особых точек на действительной оси. Тогда
begin{equation*}
intlimits_{-infty}^infty R(x)cos{lambda x},dx = mbox{Re }left( 2pi mathbf i sumlimits_{k}
mbox{Res }R(z_k)e^{mathbf i lambda z_k}right),
end{equation*}
begin{equation*}
intlimits_{-infty}^infty R(x)sin{lambda x},dx = mbox{Im }left( 2pi mathbf i sumlimits_{k}
mbox{Res }R(z_k)e^{mathbf i lambda z_k}right),
end{equation*}
где вычеты берутся во всех полюсах $z_k$ функции $R(z)$, расположенных в верхней полуплоскости $mbox{Im }z>0$.
Интегралы вычисляются с помощью леммы Жордана:
Лемма Жордана
Л
Лемма Жордана
Пусть функция $f(z)$ аналитична в полуплоскости $mbox{Im }z>0$, за исключением конечного числа изолированных особых точек, и пусть
$M(R)$ есть максимум модуля $f(z)$ на полуокружности $gamma_{R}={zin mathbb C_{}: |z|=R, mbox{Im } z >0 }$.
Если $M(R)to0$ при $Rtoinfty$, то для любого действительного числа $lambda>0$
$$
intlimits_{gamma_R}f(z)e^{mathbf i lambda z},dzto0quadhbox{при}quad
Rtoinfty, $$
Для $lambda<0$ в условиях леммы нужно заменить верхнюю полуплоскость на нижнюю и соответственно верхнюю полуокружность на нижнюю.
П
Вычислить интеграл $ I=intlimits_{-infty}^inftyfrac{cosalpha x}{x^2+a^2},dx,, a>0, alpha>0$.
Р е ш е н и е.
Чтобы иметь возможность воспользоваться леммой Жордана, заметим, что в силу формулы Эйлера $$ I=mbox{Re }I_1
=mbox{Re}intlimits_{-infty}^infty frac{e^{mathbf i alpha x}} {x^2+a^2},dx. $$
Аналитическое продолжение подынтегральной функции интеграла $I_1$ – функция $dfrac{e^{mathbf i alpha z}}{z^2+a^2}$ имеет в верхней полуплоскости единственную особую точку $z_1=ia$, являющуюся простым полюсом. Поэтому по основной теореме о вычетах $$ I_1=2pi
mathbf i mbox{Res }left(frac{e^{mathbf i alpha z}}{z^2+a^2}Big|_{z=mathbf i a}
right)=fracpi{a}e^{-alpha a}quadhbox{и}quad
I=fracpi{a}e^{-alpha a}. $$
Логарифмический вычет. Принцип аргумента
Логарифмической производной функции $f(z)$ называется производная ее логарифма $left(ln {f(z)}right)’= frac{f'(z)}{f(z)}$.
Пусть $z_0$ – нуль порядка $n$, $z_1$ – полюс порядка $p$.
Запишем разложения в ряд Лорана логарифмической производной в окрестности нуля и полюса функции $f(z)$.
$$
left(ln {f(z)}right)’= frac{n}{z-z_0}+b_1+b_2(z-z_0)+dots quad Rightarrow
$$
$n$-кратный нуль функции $f(z)$ является для логарифмической производной простым полюсом, причем вычет логарифмической производной в этой точке равен кратности нуля, то есть $n$.
$$
left(ln {f(z)}right)’= frac{-p}{z-z_1}+c_1+c_2(z-z_1)+dots quad Rightarrow
$$
$p$-кратный полюс функции $f(z)$ является для логарифмической производной простым полюсом, причем вычет логарифмической производной в этой точке равен порядку полюса, взятому с обратным знаком, то есть $-p$.
Логарифмическим вычетом функции $f(z)$ в точке $z=a$ называется вычет ее логарифмической производной $ frac{f'(z)}{f(z)}$ в этой точке, т.е. значение
$$
mbox{Res }frac{f'(z)}{f(z)}=frac{1}{2pi mathbf i}ointlimits_{L} frac{f'(z)}{f(z)}dz,
$$
где в качестве контура $L$ интегрирования можно взять любую окружность с центром в точке $z=a$, целиком лежащую в указанной проколотой окрестности этой точки.
Если $f(z)$ является аналитической функцией на замкнутом контуре $L$ и не имеет нулей на этом контуре, то значение
$$
mbox{Res } frac{f'(z)}{f(z)}=frac{1}{2pi mathbf i}ointlimits_{L} frac{f'(z)}{f(z)}dz
$$
называют логарифмическим вычетом функции $f(z)$ относительно контура $L$.
Т
Теорема о логарифмическом вычете
Пусть непостоянная функция $f(z)$ аналитична всюду в односвязной области $D$ и на ее границе – кусочно-гладком контуре $L$, кроме, возможно, некоторого конечного числа полюсов. Пусть также функция имеет конечное число нулей, причем на контуре $L$ нет ни нулей, ни полюсов функции. Тогда
$$
mbox{Res } frac{f'(z)}{f(z)}=N-P,
$$
где $N$ и $P$ – общее количество нулей и полюсов функции $f(z)$ в $D$, причем каждый нуль следует считать сколько раз, какова его кратность, а каждый полюс – каков его порядок.
Логарифмический вычет многочлена $P_n(z)$ степени $n$ относительно контура $L$, на котором нет нулей $P_n(z)$, равен числу нулей многочлена (с учетом их кратности) внутри контура.
Т
Принцип аргумента
Пусть непостоянная функция $f(z)$ аналитична всюду в односвязной области $D$ и на ее границе – кусочно-гладком контуре $L$, кроме, возможно, некоторого конечного числа полюсов. Пусть также функция имеет конечное число нулей, причем на контуре $L$ нет ни нулей, ни полюсов функции. Тогда приращение аргумента функции $f(z)$ при обходе в положительном направлении контура $L$ равно произведению $2pi$ на разность числа нулей и полюсов функции $f(z)$, расположенных в области $D$, причем каждый нуль следует считать сколько раз, какова его кратность, а каждый полюс – каков его порядок.
$$
Delta_Larg f(z)=2pi(N-P),
$$
$$
N=q_1+q_2+ldots+q_m, quad P=p_1+p_2+ldots+p_k,
$$
$q_i$ – кратность нуля $a_i$, $i=1,ldots,m$, $p_j$ – кратность полюса $b_j$, $j=1,ldots,k$.
Теорема Руше
Т
Теорема Руше
Пусть функции $f(z)$ и $varphi(z)$ являются аналитическими в замкнутой области $D$, причем на границе $C$ этой области имеет место неравенство: $|f(z)|_{C}>|varphi(z)|_{C}$. Тогда полное число нулей (с учетом их кратности) в $D$ функции $F(z)=f(z)+varphi(z)$ равно полному числу нулей (с учетом их кратности) функции $f(z)$.
П
Найти число нулей функции $F(z)=z^8-4z^5+z^2-1$ в единичном круге.
Пусть $f(z)=-4z^5$, $varphi(z)=z^8+z^2-1$. Граница $C$ заданной области – единичный круг $|z|=1$.
$$
|z|=1: ,, begin{aligned} &|f(z)=|-4z^5|=4|z|^5=4, \ &|varphi(z)|leqslant|z|^8+|z|^2+1=3 ,, Rightarrow \ &|f(z)|>|varphi(z)| end{aligned}.
$$
Выполнены все условия теоремы Руше. Функция $f(z)$ имеет корень $z=0$ кратности $5$, лежащий в $|z|<1$. Значит, $F(z)=f(z)+varphi(z)$ имеет пять нулей в единичном круге.
П
Найти число корней уравнения $z^4-8z+10=0$ в кольце 1<|z|<3
Найдем число корней $N_1$ в области $|z|<1$ и число корней $N_2$ в области $|z|<3$. Тогда число корней в кольце 1<|z|<3 будет равно $N=N_2-N_1$.
а) $|z|<1$.
Пусть $F(z)=f(z)+varphi(z)$, где $f(z)=10$, $varphi(z)=z^4-8z$.
На границе $C$ единичного круга имеем:
$$
|z|=1: ,, |f(z)|=10, |varphi(z)|leqslant|z|^4+8|z|=9,, Rightarrow ,, |f(z)>|varphi(z)|.
$$
Выполнены все условия теоремы Руше. Функция $f(z)$ в области $|z|<1$ не имеет нулей. Следовательно и уравнение $F(z)=0$ не имеет корней в единичном круге. $N_1=0$.
б) $|z|<3$.
Для круга $|z|<3$ выберем другие $f(z)$ и $varphi(z)$:
$$
f(z)=z^4, ,, |f(z)|_C=3^4=81.
$$
$$
varphi(z)=-8z+10, ,, |varphi(z)|_cleqslant24+10=34< |f(z)|.
$$
Функция $f(z)$ в области $|z|<3$ имеет корень $z=0$ кратности $4$, следовательно, по теореме Руше, функция $F(z)=f(z)+varphi(z)$ имеет четыре нуля в области $|z|<3$, то есть $N_2=4$.
В итоге получаем: $N=N_2-N_1=4-0=4$
Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 30 января 2021 года; проверки требует 1 правка.
У этого термина существуют и другие значения, см. Вычет.
Вы́чет в компле́ксном анализе — объект (число, форма или когомологический класс формы), характеризующий локальные свойства заданной функции или формы.
Теория вычетов одного комплексного переменного была в основном разработана Коши в 1825—1829 годы. Кроме него, важные результаты были получены Эрмитом, Сохоцким, Линделёфом. В 1887 году Пуанкаре обобщил интегральную теорему Коши и понятие вычета на случай двух переменных[1], с этого момента и берёт своё начало многомерная теория вычетов. Однако оказалось, что обобщить это понятие можно различными способами.
Для обозначения вычета аналитической функции 

![{mathop {{mathrm {Res}}}}left[f(z),z_{0}right]](https://wikimedia.org/api/rest_v1/media/math/render/svg/05fb3658be76d3f72c40db48852fc3d41b78931c)
![{displaystyle {text{Выч}}left[f(z),z_{0}right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/edaed72b5637ef03c8a85c67ba5d1c6bbf00e85d)
Одномерный комплексный анализ[править | править код]
Вычет функции[править | править код]
Вычетом мероморфной функции 




Для комплекснозначной функции 



.
В силу голоморфности функции 



В некоторой окрестности точки 




Вычет в «бесконечности»[править | править код]
Для возможности более полного изучения свойств функции вводится понятие вычета в бесконечности, при этом она рассматривается как функция на сфере Римана. Пусть бесконечно удалённая точка является изолированной особой точкой 
.
Цикл интегрирования в этом определении ориентирован положительно, то есть против часовой стрелки.
Аналогично предыдущему случаю вычет в бесконечности имеет представление и в виде коэффициента лорановского разложения в окрестности бесконечно удалённой точки:
.
Вычет дифференциальной формы[править | править код]
С точки зрения анализа на многообразиях вводить специальное определение для некоторой выделенной точки сферы Римана (в данном случае, бесконечно удалённой) неестественно. Более того, такой подход затруднительно обобщить на более высокие размерности. Поэтому понятие вычета вводится не для функций, а для дифференциальных 
.
На первый взгляд разницы в определениях никакой, однако теперь 

Логарифмические вычеты[править | править код]
Интеграл 


Понятие логарифмического вычета используется для доказательства теоремы Руше и основной теоремы алгебры.
Способы вычисления вычетов[править | править код]
Согласно определению вычет может быть вычислен как контурный интеграл, однако в общем случае это довольно трудоёмко. Поэтому на практике пользуются, в основном, следствиями из определения.
В устранимой особой точке 




В полюсе 

,
частный случай 
.
Если функция 






.
Очень часто, особенно в случае существенно особых точек, удобно вычислять вычет пользуясь разложением функции в ряд Лорана. Например, 

Приложения теории вычетов[править | править код]
В большинстве случаев теория вычетов применяется для вычисления разного рода интегральных выражений с помощью основной теоремы о вычетах. Часто полезной в данных случаях бывает лемма Жордана.
Вычисления определённых интегралов от тригонометрических функций[править | править код]
Пусть функция 




.
Вычисление несобственных интегралов[править | править код]
Для вычисления несобственных интегралов с применением теории вычетов используют следующие две леммы:
1. Пусть функция 



.
2. Пусть функция 




При этом интегралы в левых частях равенств не обязаны существовать и поэтому понимаются только лишь в смысле главного значения (по Коши).
Многомерный комплексный анализ[править | править код]
Форма-вычет и класс-вычет[править | править код]
Локальный вычет[править | править код]
Вычетный поток[править | править код]
Примечания[править | править код]
- ↑ H. Poincaré. Sur les résidues des intégrales doubles // Acta Math. — 1887. — № 9. — С. 321—380. — doi:10.1007/BF02406742.
- ↑ Свешников А. Г., Тихонов А. Н. Теория функций комплексной переменной. — 3-е изд., доп. — М.: Наука, 1974. — 320 с.
Литература[править | править код]
- Шабат Б. В. Введение в комплексный анализ. — М.: Наука, 1976.
- Свешников А. Г., Тихонов А. Н. Теория функций комплексной переменной. — М.: Наука, 1979.
- Айзенберг Л. А., Южаков А. П. Интегральные представления и вычеты в многомерном комплексном анализе. — Новосибирск: Наука, 1979.
- Цих А. К. Многомерные вычеты и их применения. — Новосибирск: Наука, 1988.

