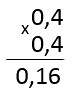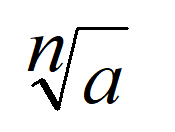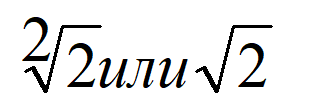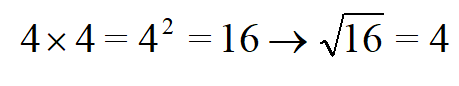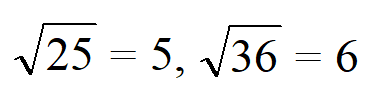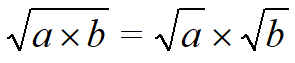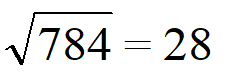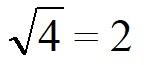Загрузить PDF
Загрузить PDF
До появления калькуляторов студенты и преподаватели вычисляли квадратные корни вручную. Существует несколько способов вычисления квадратного корня числа вручную. Некоторые из них предлагают только приблизительное решение, другие дают точный ответ.
-
1
Разложите подкоренное число на множители, которые являются квадратными числами. В зависимости от подкоренного числа, вы получите приблизительный или точный ответ. Квадратные числа – числа, из которых можно извлечь целый квадратный корень. Множители – числа, которые при перемножении дают исходное число.[1]
Например, множителями числа 8 являются 2 и 4, так как 2 х 4 = 8, числа 25, 36, 49 являются квадратными числами, так как √25 = 5, √36 = 6, √49 = 7. Квадратные множители – это множители, которые являются квадратными числами. Сначала попытайтесь разложить подкоренное число на квадратные множители.- Например, вычислите квадратный корень из 400 (вручную). Сначала попытайтесь разложить 400 на квадратные множители. 400 кратно 100, то есть делится на 25 – это квадратное число. Разделив 400 на 25, вы получите 16. Число 16 также является квадратным числом. Таким образом, 400 можно разложить на квадратные множители 25 и 16, то есть 25 х 16 = 400.
- Записать это можно следующим образом: √400 = √(25 х 16).
-
2
Квадратные корень из произведения некоторых членов равен произведению квадратных корней из каждого члена, то есть √(а х b) = √a x √b.[2]
Воспользуйтесь этим правилом и извлеките квадратный корень из каждого квадратного множителя и перемножьте полученные результаты, чтобы найти ответ.- В нашем примере извлеките корень из 25 и из 16.
- √(25 х 16)
- √25 х √16
- 5 х 4 = 20
- В нашем примере извлеките корень из 25 и из 16.
-
3
Если подкоренное число не раскладывается на два квадратных множителя (а так происходит в большинстве случаев), вы не сможете найти точный ответ в виде целого числа. Но вы можете упростить задачу, разложив подкоренное число на квадратный множитель и обыкновенный множитель (число, из которого целый квадратный корень извлечь нельзя). Затем вы извлечете квадратный корень из квадратного множителя и будете извлекать корень из обыкновенного множителя.
- Например, вычислите квадратный корень из числа 147. Число 147 нельзя разложить на два квадратных множителя, но его можно разложить на следующие множители: 49 и 3. Решите задачу следующим образом:
- √147
- = √(49 х 3)
- = √49 х √3
- = 7√3
- Например, вычислите квадратный корень из числа 147. Число 147 нельзя разложить на два квадратных множителя, но его можно разложить на следующие множители: 49 и 3. Решите задачу следующим образом:
-
4
Если нужно, оцените значение корня. Теперь можно оценить значение корня (найти приблизительное значение), сравнив его со значениями корней квадратных чисел, находящихся ближе всего (с обеих сторон на числовой прямой) к подкоренному числу. Вы получите значение корня в виде десятичной дроби, которую необходимо умножить на число, стоящее за знаком корня.
- Вернемся к нашему примеру. Подкоренное число 3. Ближайшими к нему квадратными числами будут числа 1 (√1 = 1) и 4 (√4 = 2). Таким образом, значение √3 расположено между 1 и 2. Та как значение √3, вероятно, ближе к 2, чем к 1, то наша оценка: √3 = 1,7. Умножаем это значение на число у знака корня: 7 х 1,7 = 11,9. Если вы сделаете расчеты на калькуляторе, то получите 12,13, что довольно близко к нашему ответу.
- Этот метод также работает с большими числами. Например, рассмотрим √35. Подкоренное число 35. Ближайшими к нему квадратными числами будут числа 25 (√25 = 5) и 36 (√36 = 6). Таким образом, значение √35 расположено между 5 и 6. Так как значение √35 намного ближе к 6, чем к 5 (потому что 35 всего на 1 меньше 36), то можно заявить, что √35 немного меньше 6. Проверка на калькуляторе дает нам ответ 5,92 – мы были правы.
- Вернемся к нашему примеру. Подкоренное число 3. Ближайшими к нему квадратными числами будут числа 1 (√1 = 1) и 4 (√4 = 2). Таким образом, значение √3 расположено между 1 и 2. Та как значение √3, вероятно, ближе к 2, чем к 1, то наша оценка: √3 = 1,7. Умножаем это значение на число у знака корня: 7 х 1,7 = 11,9. Если вы сделаете расчеты на калькуляторе, то получите 12,13, что довольно близко к нашему ответу.
-
5
Еще один способ – разложите подкоренное число на простые множители. Простые множители – числа, которые делятся только на 1 и самих себя. Запишите простые множители в ряд и найдите пары одинаковых множителей. Такие множители можно вынести за знак корня.
- Например, вычислите квадратный корень из 45. Раскладываем подкоренное число на простые множители: 45 = 9 х 5, а 9 = 3 х 3. Таким образом, √45 = √(3 х 3 х 5). 3 можно вынести за знак корня: √45 = 3√5. Теперь можно оценить √5.
- Рассмотрим другой пример: √88.
- √88
- = √(2 х 44)
- = √ (2 х 4 х 11)
- = √ (2 х 2 х 2 х 11). Вы получили три множителя 2; возьмите пару из них и вынесите за знак корня.
- = 2√(2 х 11) = 2√2 х √11. Теперь можно оценить √2 и √11 и найти приблизительный ответ.
Реклама
При помощи деления в столбик
-
1
Этот метод включает процесс, аналогичный делению в столбик, и дает точный ответ. Сначала проведите вертикальную линию, делящую лист на две половины, а затем справа и немного ниже верхнего края листа к вертикальной линии пририсуйте горизонтальную линию. Теперь разделите подкоренное число на пары чисел, начиная с дробной части после запятой. Так, число 79520789182,47897 записывается как “7 95 20 78 91 82, 47 89 70”.
- Для примера вычислим квадратный корень числа 780,14. Нарисуйте две линии (как показано на рисунке) и слева сверху напишите данное число в виде “7 80, 14”. Это нормально, что первая слева цифра является непарной цифрой. Ответ (корень из данного числа) будете записывать справа сверху.
-
2
Для первой слева пары чисел (или одного числа) найдите наибольшее целое число n, квадрат которого меньше или равен рассматриваемой паре чисел (или одного числа). Другими словами, найдите квадратное число, которое расположено ближе всего к первой слева паре чисел (или одному числу), но меньше ее, и извлеките квадратный корень из этого квадратного числа; вы получите число n. Напишите найденное n сверху справа, а квадрат n запишите снизу справа.
- В нашем случае, первым слева числом будет число 7. Далее, 4 < 7, то есть 22 < 7 и n = 2. Напишите 2 сверху справа – это первая цифра в искомом квадратном корне. Напишите 2×2=4 справа снизу; вам понадобится это число для последующих вычислений.
-
3
Вычтите квадрат числа n, которое вы только что нашли, из первой слева пары чисел (или одного числа). Результат вычисления запишите под вычитаемым (квадратом числа n).
- В нашем примере вычтите 4 из 7 и получите 3.
-
4
Снесите вторую пару чисел и запишите ее около значения, полученного в предыдущем шаге. Затем удвойте число сверху справа и запишите полученный результат снизу справа с добавлением “_×_=”.
- В нашем примере второй парой чисел является “80”. Запишите “80” после 3. Затем, удвоенное число сверху справа дает 4. Запишите “4_×_=” снизу справа.
-
5
Заполните прочерки справа. Найдите такое наибольшее число на место прочерков справа (вместо прочерков нужно подставить одно и тоже число), чтобы результат умножения был меньше или равен текущему числу слева.
- В нашем случае, если вместо прочерков поставить число 8, то 48 х 8 = 384, что больше 380. Поэтому 8 – слишком большое число, а вот 7 подойдет. Напишите 7 вместо прочерков и получите: 47 х 7 = 329. Запишите 7 сверху справа – это вторая цифра в искомом квадратном корне числа 780,14.
-
6
Вычтите полученное число из текущего числа слева. Запишите результат из предыдущего шага под текущим числом слева, найдите разницу и запишите ее под вычитаемым.
- В нашем примере, вычтите 329 из 380, что равно 51.
-
7
Повторите шаг 4. Если сносимой парой чисел является дробная часть исходного числа, то поставьте разделитель (запятую) целой и дробной частей в искомом квадратном корне сверху справа. Слева снесите вниз следующую пару чисел. Удвойте число сверху справа и запишите полученный результат снизу справа с добавлением “_×_=”.
- В нашем примере следующей сносимой парой чисел будет дробная часть числа 780.14, поэтому поставьте разделитель целой и дробной частей в искомом квадратном корне сверху справа. Снесите 14 и запишите снизу слева. Удвоенным числом сверху справа (27) будет 54, поэтому напишите “54_×_=” снизу справа.
-
8
Повторите шаги 5 и 6. Найдите такое наибольшее число на место прочерков справа (вместо прочерков нужно подставить одно и тоже число), чтобы результат умножения был меньше или равен текущему числу слева.
- В нашем примере 549 х 9 = 4941, что меньше текущего числа слева (5114). Напишите 9 сверху справа и вычтите результат умножения из текущего числа слева: 5114 – 4941 = 173.
-
9
Если для квадратного корня вам необходимо найти больше знаков после запятой, напишите пару нулей у текущего числа слева и повторяйте шаги 4, 5 и 6. Повторяйте шаги, до тех пор пока не получите нужную вам точность ответа (число знаков после запятой).
Реклама
Понимание процесса
-
1
Для усвоения данного метода представьте число, квадратный корень которого необходимо найти, как площадь квадрата S. В этом случае вы будете искать длину стороны L такого квадрата. Вычисляем такое значение L, при котором L² = S.
-
2
Задайте букву для каждой цифры в ответе. Обозначим через A первую цифру в значении L (искомый квадратный корень). B будет второй цифрой, C – третьей и так далее.
-
3
Задайте букву для каждой пары первых цифр. Обозначим через Sa первую пару цифр в значении S, через Sb – вторую пару цифр и так далее.
-
4
Уясните связь данного метода с делением в столбик. Как и в операции деления, где каждый раз нас интересует только одна следующая цифра делимого числа, при вычислении квадратного корня мы последовательно работаем с парой цифр (для получения одной следующей цифры в значении квадратного корня).
-
5
Рассмотрим первую пару цифр Sa числа S (Sa = 7 в нашем примере) и найдем ее квадратный корень. В этом случае первой цифрой A искомого значения квадратного корня будет такая цифра, квадрат которой меньше или равен Sa (то есть ищем такое A, при котором выполняется неравенство A² ≤ Sa < (A+1)²). В нашем примере, S1 = 7, и 2² ≤ 7 < 3²; таким образом A = 2.
- Допустим, что нужно разделить 88962 на 7; здесь первый шаг будет аналогичным: рассматриваем первую цифру делимого числа 88962 (8) и подбираем такое наибольшее число, которое при умножении на 7 дает значение меньшее или равное 8. То есть ищем такое число d, при котором верно неравенство: 7×d ≤ 8 < 7×(d+1). В этом случае d будет равно 1.
-
6
Мысленно представьте квадрат, площадь которого вам нужно вычислить. Вы ищите L, то есть длину стороны квадрата, площадь которого равна S. A, B, C – цифры в числе L. Записать можно иначе: 10А + B = L (для двузначного числа) или 100А + 10В + С = L (для трехзначного числа) и так далее.
- Пусть (10A+B)² = L² = S = 100A² + 2×10A×B + B². Запомните, что 10A+B – это такое число, у которого цифра B означает единицы, а цифра A – десятки. Например, если A=1 и B=2, то 10A+B равно числу 12.(10A+B)² – это площадь всего квадрата, 100A² – площадь большого внутреннего квадрата, B² – площадь малого внутреннего квадрата, 10A×B – площадь каждого из двух прямоугольников. Сложив площади описанных фигур, вы найдете площадь исходного квадрата.
-
7
Вычтите A² из Sa. Для учета множителя 100 снесите одну пару цифр (Sb) из S: вам нужно, чтобы “SaSb” было равным общей площади квадрата, и из нее вычтите 100A² (площадь большого квадрата). В результате получите число N1, стоящее слева в шаге 4 (N = 380 в нашем примере). N1 = 2×10A×B + B² (площадь двух прямоугольников плюс площадь малого квадрата).
-
8
Выражение N1 = 2×10A×B + B² можно записать как N1 = (2×10A + B) × B. В нашем примере вам известно значение N1 (=380) и A(=2) и необходимо вычислить B. Скорее всего, B не является целым числом, поэтому необходимо найти наибольшее целое B, удовлетворяющее условию: (2×10A + B) × B ≤ N1. При этом B+1 будет слишком большим, поэтому N1 < (2×10A + (B+1)) × (B+1).
-
9
Решите уравнение. Для решения умножьте A на 2, переведите результат в десятки (что эквивалентно умножению на 10), поместите B в положение единиц, и умножьте это число на B. Это число (2×10A + B) × B и это выражение абсолютно идентичны записи “N_×_=” (где N=2×A) сверху справа в шаге 4. А в шаге 5 вы находите наибольшее целое B, которое ставится на место прочерков и соответствует неравенству: (2×10A + B) × B ≤ N1.
-
10
Вычтите площадь (2×10A + B) × B из общей площади (слева в шаге 6). Так вы получите площадь S-(10A+B)², которая еще не учитывалась (и которая поможет вычислить следующие цифры).
-
11
Для вычисления следующей цифры C повторите процесс. Слева снесите следующую пару цифр (Sc) из S для получения N2 и найдите наибольшее C, удовлетворяющее условию (2×10×(10A+B)+C) × C ≤ N2 (что эквивалентно двукратному написанию числа из пары цифр “A B” с соответствующим “_×_=”, и нахождению наибольшего числа, которое можно подставить вместо прочерков).
Реклама
Советы
- Перемещение десятичного разделителя при увеличении числа на 2 цифры (множитель 100), перемещает десятичный разделить на одну цифру в значении квадратного корня этого числа (множитель 10).
- В нашем примере, 1,73 может считаться остатком: 780,14 = 27,9² + 1,73.
- Данный метод верен для любых чисел.
- Записывайте процесс вычисления в том виде, который вам наиболее удобен. Например, некоторые записывают результат над исходным числом.
- Альтернативный метод с использованием непрерывных дробей включает формулу: √z = √(x^2+y) = x + y/(2x + y/(2x + y/(2x + …))). Например, для вычисления квадратного корня из 780,14, целым числом, квадрат которого близок к 780,14 будет число 28, поэтому z=780,14, x=28, y=-3,86. Подставляя эти значения в уравнение и решая его в упрощении до х+у/(2x), уже в младших членах получаем результат 78207/2800 или около 27,931(1), а в следующих членах 4374188/156607 или около 27,930986(5). Решение каждого последующего члена добавляет около 3 цифр к дробной доли по сравнению с предыдущем членом.
Реклама
Предупреждения
- Не забудьте разделить число на пары, начиная с дробной части числа. Например, разделяя 79520789182,47897 как “79 52 07 89 18 2,4 78 97″, вы получите бессмысленное число.
Реклама
Похожие статьи
Источники
Об этой статье
Эту страницу просматривали 926 223 раза.
Была ли эта статья полезной?
Квадра́тный ко́рень из числа 






Наиболее часто под 

У каждого положительного вещественного числа существуют два противоположных по знаку квадратных корня. Например, квадратными корнями из числа 9 являются 





Пример для вещественных чисел: 

Если требуется учесть двузначность корня, перед радикалом ставится знак плюс-минус[2]; например, так делается в формуле решения квадратного уравнения 
Например, √25 = 5, поскольку
25 = 5 ⋅ 5, или
52 (5 «в квадрате»)
История[править | править код]
Первые задачи, связанные с извлечением квадратного корня, обнаружены в трудах вавилонских математиков. Среди таких задач[4]:
- Применение теоремы Пифагора для нахождения стороны прямоугольного треугольника по известным двум другим сторонам.
- Нахождение стороны квадрата, площадь которого задана.
- Решение квадратных уравнений.
Вавилонская глиняная табличка YBC 7289 с пометками. Диагональ отображает приближение 
Вавилонская глиняная табличка YBC 7289 из вавилонской коллекции Йельского университета была создана между 1800 и 1600 годами до н. э. и демонстрирует √2 и √2/2 соответственно в шестидесятиричной системе счисления: 1;24,51,10 и 0;42,25,35 на квадрате, пересечённом двумя диагоналями[5]. (1;24,51,10) по основанию 60 соответствует 1,41421296, что является правильным значением с точностью до 5 десятичных знаков: 
Древние греки сделали важное открытие: 
Средневековые европейские математики (например, Кардано) обозначали квадратный корень[9] символом Rx, сокращение от слова «radix». Современное обозначение впервые употребил немецкий математик Кристоф Рудольф, из школы коссистов (то есть алгебраистов), в 1525 году[10]. Происходит этот символ от стилизованной первой буквы того же слова «radix». Черта над подкоренным выражением вначале отсутствовала; её позже ввёл Декарт («Геометрии», 1637) для иной цели (вместо скобок), и эта черта вскоре слилась со знаком корня.
После появления формулы Кардано (XVI век) началось применение в математике мнимых чисел, понимаемых как квадратные корни из отрицательных чисел[11]. Основы техники работы с комплексными числами разработал в XVI веке Рафаэль Бомбелли, который также предложил оригинальный метод вычисления корней (с помощью цепных дробей). Открытие формулы Муавра (1707) показало, что извлечение корня любой степени из комплексного числа всегда возможно и не приводит к новому типу чисел[12].
Комплексные корни произвольной степени в начале XIX века глубоко исследовал Гаусс, хотя первые результаты принадлежат Эйлеру[13]. Чрезвычайно важным открытием (Галуа) стало доказательство того факта, что не все алгебраические числа (корни многочленов) могут быть получены из натуральных с помощью четырёх действий арифметики и извлечения корней[14].
Квадратные корни из чисел[править | править код]
Рациональные числа[править | править код]
При рациональных 



Непрерывная дробь для корня из рационального числа всегда является периодической (возможно, с предпериодом), что позволяет, с одной стороны, легко вычислять хорошие рациональные приближения к рациональным числам с помощью линейных рекурсий, а с другой стороны ограничивает точность приближения: 


Примеры разложения корней из натуральных чисел от 2 до 10 в непрерывные дроби:
-
= [1; 2, 2, …] = [1; 1, 2, 1, 2, …] = [2] = [2; 4, 4, …] = [2; 2, 4, 2, 4, …] = [2; 1, 1, 1, 4, 1, 1, 1, 4, …] = [2; 1, 4, 1, 4, …] = [3] = [3; 6, 6, …]
Действительные (вещественные) числа[править | править код]
Для любого положительного числа 
Неотрицательный квадратный корень из неотрицательного числа 

Основные свойства вещественного квадратного корня (все подкоренные выражения считаются неотрицательными):
К комплексным числам, учитывая двузначность корня, все эти свойства неприменимы (см. ниже пример ошибки).
Комплексные числа[править | править код]
Квадратных корней из любого ненулевого комплексного числа всегда ровно два, они противоположны по знаку. Для корней в комплексной области понятие арифметического корня не вводится, знак радикала обычно либо не используется, либо обозначает не функцию корня, а множество всех корней. В последнем случае, во избежание ошибок, знак радикала не должен использоваться в арифметических операциях. Распространённая ошибка:
(что, конечно, неверно)
Ошибка возникла из-за того, что комплексный квадратный корень является двузначной функцией, и его нельзя использовать в арифметических действиях.
Для извлечения квадратного корня из комплексного числа удобно использовать экспоненциальную форму записи комплексного числа: если
,
то (см. Формула Муавра)
,
где корень из модуля понимается в смысле арифметического значения, а k может принимать значения k = 0 и k = 1, таким образом, в итоге получаются два различных результата.
Существует и чисто алгебраическое представление для корня из 

Здесь sgn — функция «знак». Формула легко проверяется возведением 
Пример: для квадратного корня из 

Квадратный корень как элементарная функция[править | править код]
Квадратный корень является элементарной функцией и частным случаем степенной функции 


Производная функции квадратного корня вычисляется по формуле:
Как функция комплексного переменного корень — двузначная функция, два листа которой соединяются в нуле (см. подробнее Комплексный анализ).
В элементарной геометрии[править | править код]
Квадратные корни тесно связаны с элементарной геометрией: если дан отрезок длины 1, то с помощью циркуля и линейки можно построить те и только те отрезки, длина которых записывается выражениями, содержащими целые числа, знаки четырёх действий арифметики, квадратные корни и ничего сверх того[20].
В информатике[править | править код]
Во многих языках программирования функционального уровня (а также языках разметки типа LaTeX) функция квадратного корня обозначается как sqrt (от англ. square root «квадратный корень»).
Применение[править | править код]
Квадратные корни используются повсеместно в математике и естественных науках, например:
Алгоритмы нахождения квадратного корня[править | править код]
Разложение в ряд Тейлора[править | править код]
при
.
Грубая оценка[править | править код]
Многие алгоритмы вычисления квадратных корней из положительного действительного числа S требуют некоторого начального значения. Если начальное значение слишком далеко от настоящего значения корня, вычисления замедляются. Поэтому полезно иметь грубую оценку, которая может быть очень неточна, но легко вычисляется. Если S ≥ 1, пусть D будет числом цифр S слева от десятичной запятой. Если S < 1, пусть D будет числом нулей, идущих подряд, справа от десятичной запятой, взятое со знаком минус. Тогда грубая оценка выглядит так:
- Если D нечётно, D = 2n + 1, тогда используем
- Если D чётно, D = 2n + 2, тогда используем
Два и шесть используются потому, что ![{displaystyle {sqrt {sqrt {1cdot 10}}}={sqrt[{4}]{10}}approx 2}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a2eeb6a3f3bd5de4533a82fdb3dfd8d86223ffc1)
![{sqrt {{sqrt {10cdot 100}}}}={sqrt[ {4}]{1000}}approx 6,.](https://wikimedia.org/api/rest_v1/media/math/render/svg/95b0b8d8cc44d57a544d6398144d88707458ffa0)
При работе в двоичной системе (как внутри компьютеров), следует использовать другую оценку 
Геометрическое извлечение квадратного корня[править | править код]
Построение для геометрического извлечения квадратного корня
Так как треугольники 




В частности, если 


Итерационный аналитический алгоритм[править | править код]
Данный способ был известен уже в Древнем Вавилоне. Он позволяет найти приближённое значение квадратного корня с любой точностью,
Последовательные приближения рассчитываются по формуле:
тогда 
Этот метод сходится очень быстро. Например, если для 

В заключительном значении верны все приведённые цифры, кроме последней.
Столбиком[править | править код]
Этот способ позволяет найти приближённое значение корня из любого действительного числа с любой наперёд заданной точностью. К недостаткам способа можно отнести увеличивающуюся сложность вычисления с увеличением количества найденных цифр.
Для ручного извлечения корня применяется запись, похожая на деление столбиком. Выписывается число, корень которого ищем. Справа от него будем постепенно получать цифры искомого корня. Пусть извлекается корень из числа N с конечным числом знаков после запятой. Для начала мысленно или метками разобьём число N на группы по две цифры слева и справа от десятичной точки. При необходимости группы дополняются нулями — целая часть дополняется слева, дробная справа. Так, 31234,567 можно представить как 03 12 34, 56 70. В отличие от деления, снос производится такими группами по 2 цифры.
- Записать число N (в примере — 69696) на листке.
- Найти
, квадрат которого меньше или равен группе старших разрядов числа N (старшая группа — самая левая, не равная нулю), а квадрат
больше группы старших разрядов числа. Записать найденное
справа от N (это очередная цифра искомого корня). (На первом шаге примера
, а
).
- Записать квадрат
под старшей группой разрядов. Провести вычитание из старшей группы разрядов N выписанного квадрата числа
и записать результат вычитания под ними.
- Слева от этого результата вычитания провести вертикальную черту и слева от черты записать число, равное уже найденным цифрам результата (мы их выписываем справа от N), умноженное на 20. Назовём это число
. (На первом шаге примера это число просто есть
, на втором
).
- Произвести снос следующей группы цифр, то есть дописать следующие две цифры числа N справа от результата вычитания. Назовем
число, полученное соединением результата вычитания и очередной группы из двух цифр. (На первом шаге примера это число
, на втором
). Если сносится первая группа после десятичной точки числа N, то нужно поставить точку справа от уже найденных цифр искомого корня.
- Теперь нужно найти такое
, что
меньше или равно
, но
больше, чем
. Записать найденное
справа от N как очередную цифру искомого корня. Вполне возможно, что
окажется равным нулю. Это ничего не меняет — записываем 0 справа от уже найденных цифр корня. (На первом шаге примера это число 6, так как
, но
) Если число найденных цифр уже удовлетворяет искомой точности, прекращаем процесс вычисления.
- Записать число
под
. Провести вычитание столбиком числа
из
и записать результат вычитания под ними. Перейти к шагу 4.
Наглядное описание алгоритма:
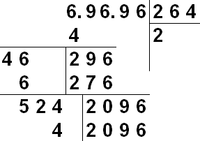
Вариации и обобщения[править | править код]
Квадратный корень из 

Чаще всего рассматривают такие обобщения в алгебраических кольцах.
Если кольцо есть область целостности, то квадратных корней из ненулевого элемента может быть либо два, либо ни одного. В самом деле, если имеются два корня 



В теории чисел рассматривается конечное кольцо вычетов по модулю 


Корни для кватернионов имеют много общего с комплексными, но есть и существенные особенности. Квадратный кватернионный корень обычно имеет 2 значения, но если подкоренное выражение — отрицательное вещественное число, то значений бесконечно много. Например, квадратные корни из 
Для кольца квадратных матриц доказано, что если матрица положительно определена, то положительно определённый квадратный корень из матрицы существует и единственен[24]. Для матриц других типов корней может быть сколько угодно (в том числе ни одного).
Квадратные корни вводятся также для функций[25], операторов[26] и других математических объектов.
См. также[править | править код]
- Быстрый инверсный квадратный корень
- Вложенные радикалы
- День квадратного корня
- Кубический корень
Примечания[править | править код]
- ↑ Математическая энциклопедия (в 5 томах), 1982.
- ↑ 1 2 Элементарная математика, 1976, с. 49.
- ↑ 1 2 Корн Г., Корн Т. Справочник по математике, 1970, с. 33.
- ↑ История математики, 1970—1972, Том I, С. 42—46.
- ↑ Analysis of YBC 7289 (англ.). ubc.ca. Дата обращения: 19 января 2015. Архивировано 12 марта 2020 года.
- ↑ История математики, 1970—1972, Том I, С. 47.
- ↑ История математики, 1970—1972, Том I, С. 169—171.
- ↑ Башмакова И. Г. Становление алгебры (из истории математических идей). — М.: Знание, 1979. — С. 23. — (Новое в жизни, науке, технике. Математика, кибернетика, № 9).
- ↑ Никифоровский В. А. Из истории алгебры XVI-XVII вв. — М.: Наука, 1979. — С. 81. — 208 с. — (История науки и техники).
- ↑ Знаки математические // Математическая энциклопедия. — М.: Советская Энциклопедия, 1982. — Т. 2. Архивировано 20 ноября 2012 года.
- ↑ История математики, 1970—1972, Том I, С. 296—298.
- ↑ История математики, 1970—1972, Том III, С. 56—59.
- ↑ История математики, 1970—1972, Том III, С. 62.
- ↑ Колмогоров А. Н., Юшкевич А. П. (ред.). Математика XIX века. Математическая логика, алгебра, теория чисел, теория вероятностей. — М.: Наука, 1978. — Т. I. — С. 58—66.
- ↑ Теорема Лиувилля о приближении алгебраических чисел
- ↑ Хинчин, 1960.
- ↑ Фихтенгольц, 4.
- ↑ Cooke, 2008.
- ↑ Фихтенгольц, 2.
- ↑ Курант, Роббинс, 2000.
- ↑ Курант, Роббинс, 2000, с. 148.
- ↑ Виноградов И. М. Основы теории чисел. — М.—Л.: ГИТТЛ, 1952. — С. 71. — 180 с. Архивировано 4 ноября 2011 года.
- ↑ Porteous, Ian R. Clifford Algebras and the Classical Groups. Cambridge, 1995, page 60.
- ↑ См., например: Гантмахер Ф. Р. Теория матриц. М.: ГИТТЛ, 1953, С. 212—219, или: Воеводин В., Воеводин В. Энциклопедия линейной алгебры. Электронная система ЛИНЕАЛ. Спб.: БХВ-Петербург, 2006.
- ↑ См., например: Ершов Л. В., Райхмист Р. Б. Построение графиков функций. М.: Просвещение, 1984, или: * Каплан И. А. Практические занятия по высшей математике. — Харьков: Изд-во ХГУ, 1966.
- ↑ См., например: Хатсон В., Пим Дж. Приложения функционального анализа и теории операторов. М.: Мир, 1983, или: Халмош П. Гильбертово пространство в задачах. М.: Мир, 1970.
Литература[править | править код]
- Воеводин В. В. Энциклопедия линейной алгебры. Электронная система ЛИНЕАЛ. — Санкт-Петербург: БХВ-Петербург, 2006.
- Ершов Л. В., Райхмист Р. Б. Построение графиков функций. — Москва: Просвещение, 1984.
- Зайцев В. В., Рыжков В. В., Сканави М. И. Элементарная математика. Повторительный курс. — Издание третье. — М.: Наука, 1976. — 591 с.
- История математики, в трёх томах / Под редакцией А. П. Юшкевича. — М.: Наука, 1970—1972.
- Корень // Математическая энциклопедия (в 5 томах). — Москва: Советская Энциклопедия, 1982. — Т. 3.
- Корн Г., Корн Т. Справочник по математике (для научных работников и инженеров). — 2-е изд.. — Москва: Наука, 1970. — 720 с.
- Курант Р., Роббинс Г. ГЛАВА III Геометрические построения. Алгебра числовых полей // Что такое математика?. — Москва: МЦНМО, 2000.
- Понятов А. Откуда вырос арифметический корень? // Наука и жизнь. — 2022. — № 8. — С. 81—89.
- Фихтенгольц Г. М. Введение, § 4 // [Мат. анализ на EqWorld Курс дифференциального и интегрального исчисления]. — Т. 1.
- Фихтенгольц Г. М. Глава 2, § 1 // [Мат. анализ на EqWorld Курс дифференциального и интегрального исчисления]. — Т. 1.
- Халмош П. Гильбертово пространство в задачах. — Москва: Мир, 1970.
- Хатсон В., Пим Дж. Приложения функционального анализа и теории операторов. — Москва: Мир, 1983.
- Хинчин А. Я. §§ 4, 10 // Цепные дроби. — Москва: ГИФМЛ, 1960.
- Cooke, Roger. Classical algebra: its nature, origins, and uses (англ.). — John Wiley and Sons, 2008. — P. 59. — ISBN 0-470-25952-3.
Ссылки[править | править код]
- Алгоритмы вычисления квадратного корня (англ.). Дата обращения: 12 октября 2006. Архивировано 19 ноября 2010 года.
- Соловьев Ю. Старый алгоритм. Дата обращения: 6 ноября 2006. Архивировано 3 марта 2016 года.
Download Article
Download Article
In the days before calculators, students and professors alike had to calculate square roots by hand. Several different methods have evolved for tackling this daunting process, some giving a rough approximation, others giving an exact value. To learn how to find a number’s square root using only simple operations, please see Step 1 below to get started.
-
1
Divide your number into perfect square factors. This method uses a number’s factors to find a number’s square root (depending on the number, this can be an exact numerical answer or a close estimate). A number’s factors are any set of other numbers that multiply together to make it.[1]
For instance, you could say that the factors of 8 are 2 and 4 because 2 × 4 = 8. Perfect squares, on the other hand, are whole numbers that are the product of other whole numbers. For instance, 25, 36, and 49 are perfect squares because they are 52, 62, and 72, respectively. Perfect square factors are, as you may have guessed, factors that are also perfect squares. To start finding a square root via prime factorization, first, try to reduce your number into its perfect square factors.[2]
- Let’s use an example. We want to find the square root of 400 by hand. To begin, we divide the number into perfect square factors. Since 400 is a multiple of 100, we know that it’s evenly divisible by 25 – a perfect square. Quick mental division lets us know that 25 goes into 400 16 times. 16, coincidentally, is also a perfect square. Thus, the perfect square factors of 400 are 25 and 16 because 25 × 16 = 400.
- We would write this as: Sqrt(400) = Sqrt(25 × 16)
- You can also try multiplying different numbers by themselves and see if they give you the correct answer. Let’s say you were trying to find the square root of 81—you could multiply 7 by 7 to get 49, which is too low. You could go a little higher and multiply 10 by 10 to get 100, which is too high. You could then go a little lower and multiply 9 by 9. This would give you 81, making 9 your square root.
-
2
Take the square roots of your perfect square factors. The product property of square roots states that for any given numbers a and b, Sqrt(a × b) = Sqrt(a) × Sqrt(b). Because of this property, we can now take the square roots of our perfect square factors and multiply them together to get our answer.[3]
- In our example, we would take the square roots of 25 and 16. See below:
- Sqrt(25 × 16)
- Sqrt(25) × Sqrt(16)
- 5 × 4 = 20
Advertisement
- In our example, we would take the square roots of 25 and 16. See below:
-
3
Reduce your answer to simplest terms, if your number doesn’t factor perfectly. In real life, more often than not, the numbers you’ll need to find square roots for won’t be nice round numbers with obvious perfect square factors like 400. In these cases, it may not be possible to find the exact answer as an integer. Instead, by finding any perfect square factors that you can, you can find the answer in terms of a smaller, simpler, easier-to-manage square root. To do this, reduce your number to a combination of perfect square factors and non-perfect square factors, then simplify.[4]
- Let’s use the square root of 147 as an example. 147 isn’t the product of two perfect squares, so we can’t get an exact integer value as above. However, it is the product of one perfect square and another number – 49 and 3. We can use this information to write our answer in simplest terms as follows:
- Sqrt(147)
- = Sqrt(49 × 3)
- = Sqrt(49) × Sqrt(3)
- = 7 × Sqrt(3)
- Let’s use the square root of 147 as an example. 147 isn’t the product of two perfect squares, so we can’t get an exact integer value as above. However, it is the product of one perfect square and another number – 49 and 3. We can use this information to write our answer in simplest terms as follows:
-
4
Estimate, if necessary. With your square root in simplest terms, it’s usually fairly easy to get a rough estimate of a numerical answer by guessing the value of any remaining square roots and multiplying through. One way to guide your estimates is to find the perfect squares on either side of the number in your square root. You’ll know that the decimal value of the number in your square root is somewhere between these two numbers, so you’ll be able to guess in between them.
- Let’s return to our example. Since 22 = 4 and 12 = 1, we know that Sqrt(3) is between 1 and 2 – probably closer to 2 than to 1. We’ll estimate 1.7. 7 × 1.7 = 11.9 If we check our work in a calculator, we can see that we’re fairly close to the actual answer of 12.13.
- This works for larger numbers as well. For example, Sqrt(35) can be estimated to be between 5 and 6 (probably very close to 6). 52 = 25 and 62 = 36. 35 is between 25 and 36, so its square root must be between 5 and 6. Since 35 is just one away from 36, we can say with confidence that its square root is just lower than 6. Checking with a calculator gives us an answer of about 5.92 – we were right.
- Let’s return to our example. Since 22 = 4 and 12 = 1, we know that Sqrt(3) is between 1 and 2 – probably closer to 2 than to 1. We’ll estimate 1.7. 7 × 1.7 = 11.9 If we check our work in a calculator, we can see that we’re fairly close to the actual answer of 12.13.
-
5
Reduce your number to its lowest common factors as a first step. Finding perfect square factors isn’t necessary if you can easily determine a number’s prime factors (factors that are also prime numbers). Write your number out in terms of its lowest common factors. Then, look for matching pairs of prime numbers among your factors. When you find two prime factors that match, remove both these numbers from the square root and place one of these numbers outside the square root.[5]
- As an example, let’s find the square root of 45 using this method. We know that 45 = 9 × 5 and we know that 9 = 3 × 3. Thus, we can write our square root in terms of its factors like this: Sqrt(3 × 3 × 5). Simply remove the 3’s and put one 3 outside the square root to get your square root in simplest terms: (3)Sqrt(5). From here, it’s simple to estimate.
- As one final example problem, let’s try to find the square root of 88:
- Sqrt(88)
- = Sqrt(2 × 44)
- = Sqrt(2 × 4 × 11)
- = Sqrt(2 × 2 × 2 × 11). We have several 2’s in our square root. Since 2 is a prime number, we can remove a pair and put one outside the square root.
- = Our square root in simplest terms is (2) Sqrt(2 × 11) or (2) Sqrt(2) Sqrt(11). From here, we can estimate Sqrt(2) and Sqrt(11) and find an approximate answer if we wish.
Advertisement
Using a Long Division Algorithm
-
1
Separate your number’s digits into pairs. This method uses a process similar to long division to find an exact square root digit-by-digit. Though it’s not essential, you may find that it’s easiest to perform this process if you visually organize your workspace and your number into workable chunks. First, draw a vertical line separating your work area into two sections, then draw a shorter horizontal line near the top of the right section to divide the right section into a small upper section and a larger lower section. Next, separate your number’s digits into pairs, starting from the decimal point. For instance, following this rule, 79,520,789,182.47897 becomes “7 95 20 78 91 82. 47 89 70”. Write your number at the top of the left space.[6]
- As an example, let’s try calculating the square root of 780.14. Draw two lines to divide your workspace as above and write “7 80. 14” at the top of the left space. It’s O.K. that the leftmost chunk is a lone number, rather than a pair of numbers. You will write your answer (the square root of 780.14.) in the top right space.
-
2
Find the largest integer n whose square is lesser than or equal to the leftmost number (or pair). Start with the leftmost “chunk” of your number, whether this is a pair or a single number. Find the largest perfect square that’s less than or equal to this chunk, then take the square root of this perfect square. This number is n. Write n in the top right space and write the square of n in the bottom right quadrant.
- In our example, the leftmost “chunk” is the number 7. Since we know that 22 = 4 ≤ 7 < 32 = 9, we can say that n = 2 because it’s the largest integer whose square is less than or equal to 7. Write 2 in the top right quadrant. This is the first digit of our answer. Write 4 (the square of 2) in the bottom right quadrant. This number will be important in the next step.
-
3
Subtract the number you just calculated from the leftmost pair. As with long division, the next step is to subtract the square we just found from the chunk we just analyzed. Write this number underneath the first chunk and subtract, writing your answer underneath.[7]
- In our example, we would write 4 below 7, then subtract. This gives us an answer of 3.
-
4
Drop down the next pair. Move the next “chunk” in the number whose square root you’re solving for down next to the subtracted value you just found. Next multiply the number in the top right quadrant by two and write it in the bottom right quadrant. Next to the number you just wrote down, set aside space for a multiplication problem you’ll do in the next step by writing ‘”_×_=”‘.
- In our example, the next pair in our number is “80”. Write “80” next to the 3 in the left quadrant. Next, multiply the number in the top right by two. This number is 2, so 2 × 2 = 4. Write “‘4″‘ in the bottom right quadrant, followed by _×_=.
-
5
Fill in the blank spaces in the right quadrant. You must fill each blank space you’ve just written in the right quadrant with the same integer. This integer must be the largest integer that allows the result of the multiplication problem in the right quadrant to be lower than or equal to the current number on the left.[8]
- In our example, filling in the blank spaces with 8, gives us 4(8) × 8 = 48 × 8 = 384. This is greater than 380. Therefore, 8 is too big, but 7 will probably work. Write 7 in the blank spaces and solve: 4(7) × 7 = 329. 7 checks out because 329 is less than 380. Write 7 in the top right quadrant. This is the second digit in the square root of 780.14.
-
6
Subtract the number you just calculated from the current number on the left. Continue with the long-division style chain of subtraction. Take the result of the multiplication problem in the right quadrant and subtract it from the current number on the left, writing your answer below.
- In our example, we would subtract 329 from 380, which gives us 51.
-
7
Repeat step 4. Drop the next chunk of the number you’re finding the square root of down. When you reach the decimal point in your number, write a decimal point in your answer in the top right quadrant. Then, multiply the number in the top right by 2 and write it next to the blank multiplication problem (“_ × _”) as above.
- In our example, since we are now encountering the decimal point in 780.14, write a decimal point after our current answer the top right. Next, drop the next pair (14) down in the left quadrant. Two times the number on the top right (27) is 54, so write “54 _×_=” in the bottom right quadrant.
-
8
Repeat step 5 and 6. Find the biggest digit to fill in the blanks on the right that gives an answer lesser than or equal to the current number on the left. Then, solve the problem.[9]
- In our example, 549 × 9 = 4941, which is lower than or equal to the number on the left (5114). 549 × 10 = 5490, which is too high, so 9 is our answer. Write 9 as the next digit in the top right quadrant and subtract the result of the multiplication from the number on the left: 5114 minus 4941 is 173.
-
9
Continue to calculate digits. Drop a pair of zeros on the left, and repeat steps 4, 5 and 6. For added accuracy, continue repeating this process to find the hundredth, thousandth, etc. places in your answer. Proceed through this cycle until you find your answer to the desired decimal place.
Advertisement
Understanding the Process
-
1
Consider the number you are calculating the square root of as the area S of a square. Because a square’s area is L2 where L is the length of one of its sides, therefore, by trying to find the square root of your number, you are trying to calculate the length L of the side of that square.
-
2
Specify letter variables for each digit of your answer. Assign the variable A as the first digit of L (the square root we are trying to calculate). B will be its second digit, C its third, and so on.
-
3
Specify letter variables for each “chunk” of your starting number. Assign the variable Sato the first pair of digits in S (your starting value), Sb the second pair of digits, etc.
-
4
Understand this method’s connection to long division. This method of finding a square root is essentially a long division problem that divides your starting number by its square root, thus giving its square root as an answer. Just like in a long division problem, in which you are only interested by the next one digit at a time, here, you are interested by the next two digits at a time (which correspond to the next digit at a time for the square root).
-
5
Find the biggest number whose square is less than or equal to Sa. The first digit A in our answer is then the biggest integer where the square does not exceed Sa (meaning A so that A² ≤ Sa < (A+1)²). In our example, Sa = 7, and 2² ≤ 7 < 3², so A = 2.
- Note that, for instance, if you wanted to divide 88962 by 7 via long division, the first step would be similar: you would be looking at the first digit of 88962 (8) and you would want the biggest digit that, when multiplied by 7, is lower than or equal to 8. Essentially, you’re finding d so that 7×d ≤ 8 < 7×(d+1). In this case, d would be equal to 1.
-
6
Visualize the square whose area you are beginning to solve. Your answer, the square root of your starting number, is L, which describes the length of a square with area S (your starting number). Your values for A,B,C, represent the digits in the value L. Another way of saying this is that, for a two-digit answer, 10A + B = L, while for a three-digit answer, 100A +10B + C = L, and so on.
- In our example, (10A+B)² = L2 = S = 100A² + 2×10A×B + B². Remember that 10A+B represents our answer L with B in the units position and A in the tens position. For instance, with A=1 and B=2, 10A+B is simply the number 12. (10A+B)² is the area of the whole square, while 100A² the area of the biggest square inside, B² is the area of the smallest square, and 10A×B is the area of each of the two remaining rectangles. By performing this long, convoluted process, we find the area of the entire square by adding up the areas of the squares and rectangles inside it.
-
7
Subtract A² from Sa. Drop one pair (Sb) of digits from S. Sa Sb is nearly the total area of the square, which you just subtracted the area of the bigger internal square from. The remainder is can be though of as the number N1, which we obtained in step 4 (N1 =380 in our example). N1 is equal to 2×10A×B + B² (area of the two rectangles plus area of the small square).
-
8
Look for N1 = 2×10A×B + B², also written as N1 = (2×10A + B) × B. In our example, you already know N1 (380) and A (2), so you need to find B. B is most likely not going to be an integer, so you must actually find the biggest integer B so that (2×10A + B) × B ≤ N1. So, you have: N1 < (2×10A + (B+1)) × (B+1).)
-
9
Solve. To solve this equation, multiply A by 2, shift it in the position of the tens (which is equivalent to multiplying by 10), place B in the position of the units, and multiply the resulting number by B. In other words, solve (2×10A + B) × B. This is exactly what you do when you write “N_×_=” (with N=2×A) in the bottom right quadrant in step 4. In step 5, you find the biggest integer B that fits on the underscore so that (2×10A + B) × B ≤ N1.
-
10
Subtract the area (2×10A + B) × B from the total area. This gives you the area S-(10A+B)² not yet accounted for (and which will be used to calculate the next digits in a similar fashion).
-
11
To calculate the next digit C, repeat the process. Drop the next pair (Sc) from S to obtain N2 on the left, and look for the biggest C so you have (2×10×(10A+B)+C) × C ≤ N2 (equivalent to writing two times the two-digit number “A B” followed by “_×_=” . Look for the biggest digit that fits in the blanks that gives an answer that is less than or equal to N2, as before.
Advertisement
Add New Question
-
Question
Is 28 a perfect number?
Yes. A “perfect” number is a positive integer which is the sum of all of its positive divisors (except itself). Thus, 28 = 1 + 2 + 4 + 7 + 14.
-
Question
What is the square root of 0.000121?
.011. If you are calculating it by hand, here’s what to do: 121’s sqrt is 11. To get .000121, you simply find an amount of 0’s after the decimal point and the number 11 afterwards. Then multiply by itself. .011*.011= .000121.
-
Question
Can I write the cube root of x as (1/x)^1/3?
No, it’s (x)^1/3.
See more answers
Ask a Question
200 characters left
Include your email address to get a message when this question is answered.
Submit
Advertisement
-
This method works for any base, not just in base 10 (decimal).
-
In the example, 1.73 can be considered to be a “remainder” : 780.14 = 27.9² + 1.73.
-
Moving the decimal point by an increment of two digits in a number (factor of 100), moves the decimal point by increments of one digit in its square root (factor of 10).
Show More Tips
Advertisement
-
Be sure to separate the digits into pairs from the decimal point. Separating 79,520,789,182.47897 as “79 52 07 89 18 2.4 78 97″ will yield a useless number.
Advertisement
Calculator
References
About This Article
Article SummaryX
To calculate a square root by hand, first estimate the answer by finding the 2 perfect square roots that the number is between. A perfect square root is any square root that’s a whole number. For example, if you’re trying to find the square root of 7, first you’d need to find the first perfect square below 7, which is 4, and the first perfect square above 7, which is 9. Then, find the square root of each perfect square. The square root of 4 is 2, and the square root of 9 is 3. Therefore, you know that the square root of 7 falls somewhere between 2 and 3. Now, divide your number by one of the perfect square roots you found. For example, you would divide 7 by either 2 or 3. If you were to choose 3, your answer would be 2.33. Next, find the average of that number and the perfect square root. To find the average in this example, add 2.33 and 2, then divide by 2 and get 2.16. Repeat the process using the average you got. First, divide the number you’re trying to find the square root of by the average. Then, find the average of that number and the original average by adding them together and dividing by 2. For example, first you would divide 7, the number you started with, by 2.16, the average you calculated, and get 3.24. Then, you’d add 3.24 to 2.16, the old average, and divide by 2 to find the new average, which is 2.7. Now, multiply your answer by itself to see how close it is to the square root of the number you started with. In this example, 2.7 multiplied by itself is equal to 7.29, which is 0.29 away from 7. To get closer to 7, you would just repeat the process. Keep dividing the number you started with by the average of that number and the perfect square, using that number and the old average to find the new average, and multiplying the new average by itself until it equals your starting number. If you want to learn how to use the long division algorithm to find the square root, keep reading the article!
Did this summary help you?
Thanks to all authors for creating a page that has been read 2,542,415 times.
Reader Success Stories
-
“I needed a refresher. This was great! I went to give a quick Google search on how to solve X-roots by hand, and it…” more
Did this article help you?
В уроке «Степень числа»
мы проходили, что возвести в квадрат число означает умножить число на само себя.
Кратко запись числа в квадрате выглядит следующим образом:
3 · 3 = 32 = 9
Но как быть, если нам нужно получить обратный результат?
Например, узнать, какое число при возведении в квадрат дало бы число «9»?
Запомните!
Нахождение исходного числа, которое в квадрате дало бы требуемое, называется
извлечением квадратного корня.
Извлечение квадратного корня — это действие, обратное возведению в квадрат.
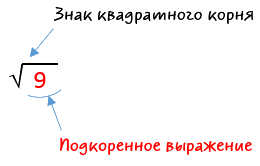
У квадратного корня есть специальный знак.
Исходя из вычислений выше, нетрудно догадаться, что число, которое в квадрате дает «9»,
это число «3». Запись извлечения квадратного корня из числа «9» выглядит так:
√9 = 3
Читаем запись: «Арифметический квадратный корень из девяти». Можно опустить слово «арифметический».
Словосочетания «арифметический квадратный корень» и «квадратный корень» полностью равнозначны.
Число под знаком корня называют подкоренным выражением.
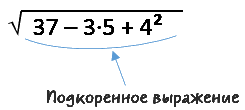
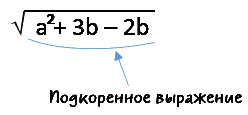
Подкоренное выражение может быть представлено не только одним числом.
Всё, что находится под знаком корня, называют подкоренным выражением. Оно может сожержать как числа, так и буквы.
Запомните!
Извлекать квадратный корень можно только из положительного числа.
-
√−9
= … нельзя извлекать квадратный корень из отрицательного числа; -
√64 = 8
-
√−1,44
= … нельзя извлекать квадратный корень из отрицательного числа; -
√256 = 16
Квадратный корень из нуля
Запомните!
Квадратный корень из нуля равен нулю.
√0 = 0
Квадратный корень из единицы
Запомните!
Квадратный корень из единицы равен единице.
√1 = 1
Как найти квадратный корень из числа
Квадратные корни из целых чисел, чьи квадраты известны, вычислить довольно просто.
Для этого достаточно выучить таблицу квадратов.
Чаще всего в задачах школьного курса математики требуется найти квадратный корень из квадратов чисел от
1 до 20.
Решение примеров с квадратными корнями
Разбор примера
Вычислить арифметический квадратный корень из числа.
- √81 = 9
- √64 = 8
- √100 = 10
Как найти квадратный корень из десятичной дроби
Важно!
При нахождении квадратного корня из десятичной дроби нужно выполнить следующие действия:
- забыть про запятую в исходной десятичной дроби и представить её в виде целого числа;
- вычислить для целого числа квадратный корень;
- полученное целое число заменить на десятичную дробь (поставить запятую исходя из
правила умножения десятичных дробей).
Более подробно разберем на примере ниже.
Разбор примера
Вычислить квадратный корень из десятичной дроби «0,16».
√0,16 =
По первому пункту правила забудем про запятую в десятичной дроби и представим ее в виде целого числа «16».
Нетрудно вспомнить, какое число в квадрате дает «16». Это число
«4».
√16 = 4
√0,16 = …
Вспомним правило умножения десятичных дробей.
Количество знаков после запятой в результате умножения десятичных дробей равняется сумме количества знаков после запятой каждой
дроби.
Т.е., например, при умножении «0,15» на
«0,3» в полученном произведении будет десятичная дробь с тремя знаками после запятой.
0,15 · 0,3 = 0,045
Значит, при вычислении квадратного корня
√0,16
нам нужно найти десятичную дробь, у которой был бы только один знак после запятой.
Мы исходим из того, что в результате умножения десятичной дроби на саму себя в результате должно было получиться
два знака после запятой, как у десятичной дроби «0,16».
Получается, что ответ — десятичная дробь «0,4».
√0,16 = 0,4
Убедимся, что квадрат десятичной дроби
«0,42» дает
«0,16».
Умножим в столбик «0,4» на
«0,4».
Рассмотрим другой пример вычисления квадратного корня из десятичной дроби. Вычислить:
√1,44 =
Представим вместо десятичной дроби «1,44» целое число
«144». Какое число в квадрате даст «144»?
Ответ — число «12».
122 = 144
√144 = 12
√1,44 = …
Так как в десятичной дроби «1,44» — два знака после запятой, значит в десятичной дроби,
которая дала в квадрате «1,44» должен быть один знак после запятой.
√1,44 = 1,2
Убедимся, что «1,22» дает в квадрате «1,44».
1,22 = 1,2 · 1,2 = 1,44
Квадратные корни из чисел
√2,
√3,
√5,
√6,
и т.п.
Не из всех чисел удается легко извлечь квадратный корень. Например, совершенно неочевидно, чему равен
√2
или
√3
и т.п.
В самом деле, какое число в квадрате даст «2»? Или число «3»?
Такое число не будет целым. Более того, оно представляет из себя
непериодическую десятичную дробь
и входит в
множество иррациональных чисел.
Что делать, когда в ответе остаются подобные квадратные корни? Как, например, в примере ниже:
√15 − 2 · 4 =
√15 − 8 =
√7
Нет такого целого числа, которое бы дало в квадрате число «7».
Поэтому, перед завершением задачи внимательно читайте её условие.
Если в задаче дополнительно ничего не сказано об обязательном вычислении всех квадратных корней, тогда ответ можно
оставить с корнем.
√15 − 2 · 4 =
√15 − 8 =
√7
Если в задании сказано, что необходимо вычислить все квадратные корни с помощью микрокалькулятора,
то после вычисления квадратного корня на калькуляторе
округлите результат до необходимого количества знаков.
Текст задания в таком случае может быть написан следующим образом:
«Вычислить. Квадратные корни найти с помощью калькулятора и округлить с точностью до
«0,001».
√15 − 2 · 4 =
√15 − 8 =
√7 ≈ 2,646
Ваши комментарии
Важно!
Чтобы оставить комментарий, вам нужно войти на наш сайт при помощи
«ВКонтакте».

Оставить комментарий:
14 июля 2016 в 18:32
Temur Uldashev
Профиль
Благодарили: 0
Сообщений: 2
Temur Uldashev
Профиль
Благодарили: 0
Сообщений: 2
Всем доброго времени суток! Прошу помочь с примером который я не могу решить, по теме «Квадратные корни. Задачи на вычесление» пример выглядит так:
??28-16?3 ( то есть выражение 28-16?3 еще под двумя корнями, не только 28, а все выражение!)
0
Спасибо
Ответить
15 июля 2016 в 0:04
Ответ для Temur Uldashev
Евгений Фёдоров
Профиль
Благодарили: 0
Сообщений: 60
Евгений Фёдоров
Профиль
Благодарили: 0
Сообщений: 60
?(28 ? 16?3) = 4 ? 2?3.
Скобки не знешь?
0
Спасибо
Ответить
15 июля 2016 в 6:53
Ответ для Temur Uldashev
Temur Uldashev
Профиль
Благодарили: 0
Сообщений: 2
Temur Uldashev
Профиль
Благодарили: 0
Сообщений: 2
Затупил. Но и вы не правильно подсказали. Я уже решил ответ ?3-1
0
Спасибо
Ответить
16 июля 2016 в 22:58
Ответ для Temur Uldashev
Евгений Фёдоров
Профиль
Благодарили: 0
Сообщений: 60
Евгений Фёдоров
Профиль
Благодарили: 0
Сообщений: 60
Чушь не пори.
Спасибо скажи, что тебе подсказали.
0
Спасибо
Ответить
21 июля 2016 в 13:24
Ответ для Temur Uldashev
Евгений Фёдоров
Профиль
Благодарили: 0
Сообщений: 60
Евгений Фёдоров
Профиль
Благодарили: 0
Сообщений: 60
Что не верно у меня, митрофанушка?
0
Спасибо
Ответить
23 ноября 2015 в 15:15
Ксюша Новикова
Профиль
Благодарили: 0
Сообщений: 1
Ксюша Новикова
Профиль
Благодарили: 0
Сообщений: 1
0
Спасибо
Ответить
16 сентября 2016 в 14:23
Ответ для Ксюша Новикова
Евгений Колосов
Профиль
Благодарили: 12
Сообщений: 197
Евгений Колосов
Профиль
Благодарили: 12
Сообщений: 197
1,38 · ?361 = 1,38 · 19 = 26,22
0
Спасибо
Ответить
16 сентября 2015 в 16:11
Макс Простов
Профиль
Благодарили: 0
Сообщений: 4
Макс Простов
Профиль
Благодарили: 0
Сообщений: 4
Расположите в порядке возрастания Корни:3V16, 7V19, 8V13 срочно)))))
0
Спасибо
Ответить
9 сентября 2016 в 9:41
Ответ для Макс Простов
Евгений Колосов
Профиль
Благодарили: 12
Сообщений: 197
Евгений Колосов
Профиль
Благодарили: 12
Сообщений: 197
?16 = 4
?19 ? 4,35
?13 ? 3,61
3 · 4 = 12
7 · 4,35 = 30,45
8 · 3,61 = 28,88
Ответ: 3?16, 8?13, 7?19
0
Спасибо
Ответить
Необходимо произвести сложные расчеты, а электронного вычислительного устройства под рукой не оказалось? Воспользуйтесь онлайн программой — калькулятором корней. Она поможет:
- найти квадратные или кубические корни из заданных чисел;
- выполнить математическое действие с дробными степенями.
| Число знаков после запятой: |
|
√ |
Как вычислять квадратный корень вручную —методом подбора находить подходящие значения. Рассмотрим, как это делать.
Что такое квадратный корень
Корень n степени натурального числа a — число, n степень которого равна a (подкоренное число). Обозначается корень символом √. Его называют радикалом.
Каждое математическое действие имеет противодействие: сложение→вычитание, умножение→деление, возведение в степень→извлечение корня.
Квадратным корнем из числа a будет число, квадрат которого равен a. Из этого следует ответ на вопрос, как вычислить корень из числа? Нужно подобрать число, которое во второй степени будет равно значению под корнем.
Обычно 2 не пишут над знаком корня. Поскольку это самая маленькая степень, а соответственно если нет числа, то подразумевается показатель 2. Решаем: чтобы вычислить корень квадратный из 16, нужно найти число, при возведении которого во вторую степень получиться 16.
Проводим расчеты вручную
Вычисления методом разложения на простые множители выполняется двумя способами, в зависимости от того, какое подкоренное число:
1.Целое, которое можно разложить на квадратные множители и получить точный ответ.
Квадратные числа — числа, из которых можно извлечь корень без остатка. А множители — числа, которые при перемножении дают исходное число.
Например:
25, 36, 49 — квадратные числа, поскольку:
Получается, что квадратные множители — множители, которые являются квадратными числами.
Возьмем 784 и извлечем из него корень.
| Раскладываем число на квадратные множители. Число 784 кратно 4, значит первый квадратный множитель — 4 x 4 = 16. Делим 784 на 16 получаем 49 — это тоже квадратное число 7 x 7 = 16. | 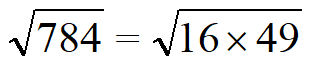 |
| Применим правило
Извлекаем корень из каждого квадратного множителя, умножаем результаты и получаем ответ. |
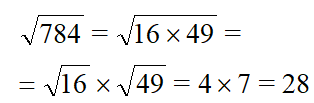
Ответ. |
2.Неделимое. Его нельзя разложить на квадратные множители.
Такие примеры встречаются чаще, чем с целыми числами. Их решение не будет точным, другими словами целым. Оно будет дробным и приблизительным. Упростить задачу поможет разложение подкоренного числа на квадратный множитель и число, из которого извлечь квадратный корень нельзя.
| Раскладываем число 252 на квадратный и обычный множитель. | 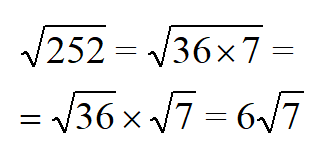 |
| Оцениваем значение корня. Для этого подбираем два квадратных числа, которые стоят впереди и сзади подкоренного числа в цифровой линейки. | Подкоренное число — 7. Значит ближайшее большее квадратное число будет 8, а меньшее 4.
Значит
|
| Оцениваем значение | Вероятнее √7 ближе к 2. Подбираем таким образом, чтобы при умножении этого числа на само себя получилось 7.
2,7 x 2,7 = 7,2. Не подходит, так как 7,2>7, берем меньшее 2,6 x 2,6 = 6,76. Оставляем, ведь 6,76~7. |
| Вычисляем корень | 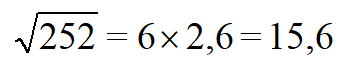 |
Как вычислить корень из сложного числа? Тоже методом оценивая значения корня.
При делении в столбик получается максимально точный ответ при извлечении корня.
| Возьмите лист бумаги и расчертите его так, чтобы вертикальная линия находилась посередине, а горизонтальная была с ее правой стороны и ниже начала. | 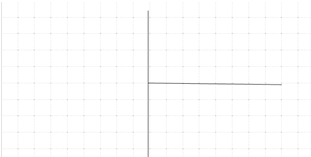 |
| Разбейте подкоренное число на пары чисел. Десятичные дроби делят так:
— целую часть справа налево; — число после запятой слева направо. |
Пример: 3459842,825694 → 3 45 98 42, 82 56 94
795,28 → 7 95, 28 Допускается, что вначале остается непарное число. |
| Для первого числа (или пары) подбираем наибольшее число n. Его квадрат должен быть меньше или равен значению первого числа (пары чисел).
Извлеките из этого числа корень — √n. Запишите полученный результат сверху справа, а квадрат этого числа — снизу справа. У нас первая 7. Ближайшее квадратное число — 4. Оно меньше 7, а 4 = |
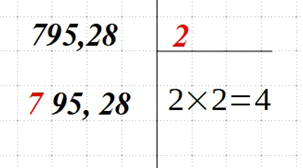 |
| Вычтите найденный квадрат числа n из первого числа (пары). Результат запишите под 7.
А верхнее число справа удвойте и запишите справа выражение 4_х_=_. Примечание: числа должны быть одинаковыми. |
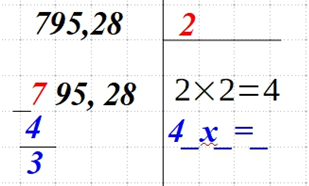 |
| Подбираем число для выражения с прочерками. Для этого найдите такое число, чтобы полученное произведение не было больше или равнялось текущему числу слева. В нашем случае это 8. | 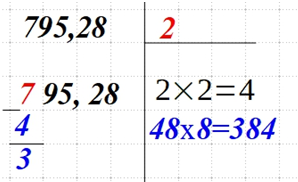 |
| Запишите найденное число в верхнем правом углу. Это второе число из искомого корня.
Снесите следующую пару чисел и запишите возле полученной разницы слева. |
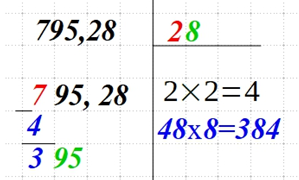 |
| Вычтите полученное справа произведение из числа слева.
Удваиваем число, которое расположено справа вверху и записываем выражение с прочерками. |
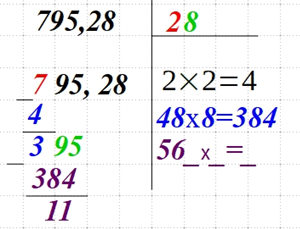 |
| Сносим к получившейся разнице еще пару чисел. Если это числа дробной части, то есть расположены за запятой, то и в верхнем правом углу возле последней цифры искомого квадратного корня ставим запятую.
Заполняем прочерки в выражении справа, подбирая число так, чтобы полученное произведение было меньше или равно разницы выражения слева. |
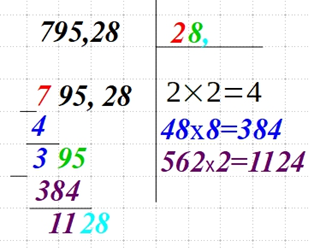 |
| Если необходимо большее количества знаков после запятой, то дописывайте возле текущей цифры слева и повторяйте действия: вычитание слева, удваиваем число в верхнем правом углу, записываем выражение прочерками, подбираем множители для него и так далее. | 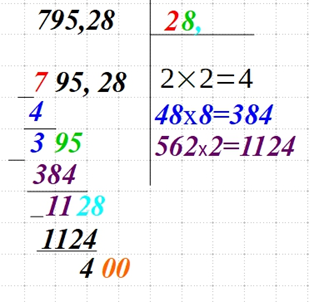 |
Как думаете сколько времени вы потратите на такие расчеты? Сложно, долго, запутанно. Тогда почему бы не упростить себе задачу? Воспользуйтесь нашей программой, которая поможет произвести быстрые и точные расчеты.
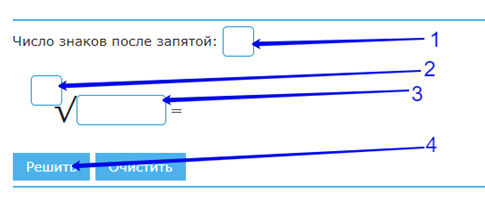
Алгоритм действий
1. Введите желаемое количество знаков после запятой.
2. Укажите степень корня (если он больше 2).
3. Введите число, из которого планируете извлечь корень.
4. Нажмите кнопку «Решить».
Вычисление самых сложных математических действий с онлайн калькулятором станет простым! Экономьте время и проводите расчеты с CALCON.RU.