Как найти вычислительную сложность алгоритма

Оценка сложности алгоритмов

Не так давно мне предложили вести курс основ теории алгоритмов в одном московском лицее. Я, конечно, с удовольствием согласился. В понедельник была первая лекция на которой я постарался объяснить ребятам методы оценки сложности алгоритмов. Я думаю, что некоторым читателям Хабра эта информация тоже может оказаться полезной, или по крайней мере интересной.
Существует несколько способов измерения сложности алгоритма. Программисты обычно сосредотачивают внимание на скорости алгоритма, но не менее важны и другие показатели – требования к объёму памяти, свободному месте на диске. Использование быстрого алгоритма не приведёт к ожидаемым результатам, если для его работы понадобится больше памяти, чем есть у компьютера.

Память или время

Многие алгоритмы предлагают выбор между объёмом памяти и скоростью. Задачу можно решить быстро, использую большой объём памяти, или медленнее, занимая меньший объём.
Типичным примером в данном случае служит алгоритм поиска кратчайшего пути. Представив карту города в виде сети, можно написать алгоритм для определения кратчайшего расстояния между двумя любыми точками этой сети. Чтобы не вычислять эти расстояния всякий раз, когда они нам нужны, мы можем вывести кратчайшие расстояния между всеми точками и сохранить результаты в таблице. Когда нам понадобится узнать кратчайшее расстояние между двумя заданными точками, мы можем просто взять готовое расстояние из таблицы.
Результат будет получен мгновенно, но это потребует огромного объёма памяти. Карта большого города может содержать десятки тысяч точек. Тогда, описанная выше таблица, должна содержать более 10 млрд. ячеек. Т.е. для того, чтобы повысить быстродействие алгоритма, необходимо использовать дополнительные 10 Гб памяти.
Из этой зависимости проистекает идея объёмно-временной сложности. При таком подходе алгоритм оценивается, как с точки зрении скорости выполнения, так и с точки зрения потреблённой памяти.
Мы будем уделять основное внимание временной сложности, но, тем не менее, обязательно будем оговаривать и объём потребляемой памяти.

Оценка порядка

При сравнении различных алгоритмов важно знать, как их сложность зависит от объёма входных данных. Допустим, при сортировке одним методом обработка тысячи чисел занимает 1 с., а обработка миллиона чисел – 10 с., при использовании другого алгоритма может потребоваться 2 с. и 5 с. соответственно. В таких условиях нельзя однозначно сказать, какой алгоритм лучше.
В общем случае сложность алгоритма можно оценить по порядку величины. Алгоритм имеет сложность O(f(n)), если при увеличении размерности входных данных N, время выполнения алгоритма возрастает с той же скоростью, что и функция f(N). Рассмотрим код, который для матрицы A[NxN] находит максимальный элемент в каждой строке.
for i:=1 to N do
begin
max:=A[i,1];
for j:=1 to N do
begin
if A[i,j]>max then
max:=A[i,j]
end;
writeln(max);
end;
В этом алгоритме переменная i меняется от 1 до N. При каждом изменении i, переменная j тоже меняется от 1 до N. Во время каждой из N итераций внешнего цикла, внутренний цикл тоже выполняется N раз. Общее количество итераций внутреннего цикла равно N*N. Это определяет сложность алгоритма O(N^2).
Оценивая порядок сложности алгоритма, необходимо использовать только ту часть, которая возрастает быстрее всего. Предположим, что рабочий цикл описывается выражением N^3+N. В таком случае его сложность будет равна O(N^3). Рассмотрение быстро растущей части функции позволяет оценить поведение алгоритма при увеличении N. Например, при N=100, то разница между N^3+N=1000100 и N=1000000 равна всего лишь 100, что составляет 0,01%.
При вычислении O можно не учитывать постоянные множители в выражениях. Алгоритм с рабочим шагом 3N^3 рассматривается, как O(N^3). Это делает зависимость отношения O(N) от изменения размера задачи более очевидной.

Определение сложности

Наиболее сложными частями программы обычно является выполнение циклов и вызов процедур. В предыдущем примере весь алгоритм выполнен с помощью двух циклов.
Если одна процедура вызывает другую, то необходимо более тщательно оценить сложность последней. Если в ней выполняется определённое число инструкций (например, вывод на печать), то на оценку сложности это практически не влияет. Если же в вызываемой процедуре выполняется O(N) шагов, то функция может значительно усложнить алгоритм. Если же процедура вызывается внутри цикла, то влияние может быть намного больше.
В качестве примера рассмотрим две процедуры: Slow со сложностью O(N^3) и Fast со сложностью O(N^2).
procedure Slow;
var
i,j,k: integer;
begin
for i:=1 to N do
for j:=1 to N do
for k:=1 to N do
{какое-то действие}
end;
procedure Fast;
var
i,j: integer;
begin
for i:=1 to N do
for j:=1 to N do
Slow;
end;
procedure Both;
begin
Fast;
end;
Если во внутренних циклах процедуры Fast происходит вызов процедуры Slow, то сложности процедур перемножаются. В данном случае сложность алгоритма составляет O(N^2 )*O(N^3 )=O(N^5).
Если же основная программа вызывает процедуры по очереди, то их сложности складываются: O(N^2 )+O(N^3 )=O(N^3). Следующий фрагмент имеет именно такую сложность:
procedure Slow;
var
i,j,k: integer;
begin
for i:=1 to N do
for j:=1 to N do
for k:=1 to N do
{какое-то действие}
end;
procedure Fast;
var
i,j: integer;
begin
for i:=1 to N do
for j:=1 to N do
{какое-то действие}
end;
procedure Both;
begin
Fast;
Slow;
end;

Сложность рекурсивных алгоритмов

Простая рекурсия

Напомним, что рекурсивными процедурами называются процедуры, которые вызывают сами себя. Их сложность определить довольно тяжело. Сложность этих алгоритмов зависит не только от сложности внутренних циклов, но и от количества итераций рекурсии. Рекурсивная процедура может выглядеть достаточно простой, но она может серьёзно усложнить программу, многократно вызывая себя.
Рассмотрим рекурсивную реализацию вычисления факториала:
function Factorial(n: Word): integer;
begin
if n > 1 then
Factorial:=n*Factorial(n-1)
else
Factorial:=1;
end;
Эта процедура выполняется N раз, таким образом, вычислительная сложность этого алгоритма равна O(N).

Многократная рекурсия

Рекурсивный алгоритм, который вызывает себя несколько раз, называется многократной рекурсией. Такие процедуры гораздо сложнее анализировать, кроме того, они могут сделать алгоритм гораздо сложнее.
Рассмотрим такую процедуру:
procedure DoubleRecursive(N: integer);
begin
if N>0 then
begin
DoubleRecursive(N-1);
DoubleRecursive(N-1);
end;
end;
Поскольку процедура вызывается дважды, можно было бы предположить, что её рабочий цикл будет равен O(2N)=O(N). Но на самом деле ситуация гораздо сложнее. Если внимательно исследовать этот алгоритм, то станет очевидно, что его сложность равна O(2^(N+1)-1)=O(2^N). Всегда надо помнить, что анализ сложности рекурсивных алгоритмов весьма нетривиальная задача.

Объёмная сложность рекурсивных алгоритмов

Для всех рекурсивных алгоритмов очень важно понятие объёмной сложности. При каждом вызове процедура запрашивает небольшой объём памяти, но этот объём может значительно увеличиваться в процессе рекурсивных вызовов. По этой причине всегда необходимо проводить хотя бы поверхностный анализ объёмной сложности рекурсивных процедур.

Средний и наихудший случай

Оценка сложности алгоритма до порядка является верхней границей сложности алгоритмов. Если программа имеет большой порядок сложности, это вовсе не означает, что алгоритм будет выполняться действительно долго. На некоторых наборах данных выполнение алгоритма занимает намного меньше времени, чем можно предположить на основе их сложности. Например, рассмотрим код, который ищет заданный элемент в векторе A.
function Locate(data: integer): integer;
var
i: integer;
fl: boolean;
begin
fl:=false; i:=1;
while (not fl) and (i<=N) do
begin
if A[i]=data then
fl:=true
else
i:=i+1;
end;
if not fl then
i:=0;
Locate:=I;
end;
Если искомый элемент находится в конце списка, то программе придётся выполнить N шагов. В таком случае сложность алгоритма составит O(N). В этом наихудшем случае время работы алгоритма будем максимальным.
С другой стороны, искомый элемент может находится в списке на первой позиции. Алгоритму придётся сделать всего один шаг. Такой случай называется наилучшим и его сложность можно оценить, как O(1).
Оба эти случая маловероятны. Нас больше всего интересует ожидаемый вариант. Если элемента списка изначально беспорядочно смешаны, то искомый элемент может оказаться в любом месте списка. В среднем потребуется сделать N/2 сравнений, чтобы найти требуемый элемент. Значит сложность этого алгоритма в среднем составляет O(N/2)=O(N).
В данном случае средняя и ожидаемая сложность совпадают, но для многих алгоритмов наихудший случай сильно отличается от ожидаемого. Например, алгоритм быстрой сортировки в наихудшем случае имеет сложность порядка O(N^2), в то время как ожидаемое поведение описывается оценкой O(N*log(N)), что много быстрее.

Общие функции оценки сложности

Сейчас мы перечислим некоторые функции, которые чаще всего используются для вычисления сложности. Функции перечислены в порядке возрастания сложности. Чем выше в этом списке находится функция, тем быстрее будет выполняться алгоритм с такой оценкой.
1. C – константа
2. log(log(N))
3. log(N)
4. N^C, 0<C<1
5. N
6. N*log(N)
7. N^C, C>1
8. C^N, C>1
9. N!
Если мы хотим оценить сложность алгоритма, уравнение сложности которого содержит несколько этих функций, то уравнение можно сократить до функции, расположенной ниже в таблице. Например, O(log(N)+N!)=O(N!).
Если алгоритм вызывается редко и для небольших объёмов данных, то приемлемой можно считать сложность O(N^2), если же алгоритм работает в реальном времени, то не всегда достаточно производительности O(N).
Обычно алгоритмы со сложностью N*log(N) работают с хорошей скоростью. Алгоритмы со сложностью N^C можно использовать только при небольших значениях C. Вычислительная сложность алгоритмов, порядок которых определяется функциями C^N и N! очень велика, поэтому такие алгоритмы могут использоваться только для обработки небольшого объёма данных.
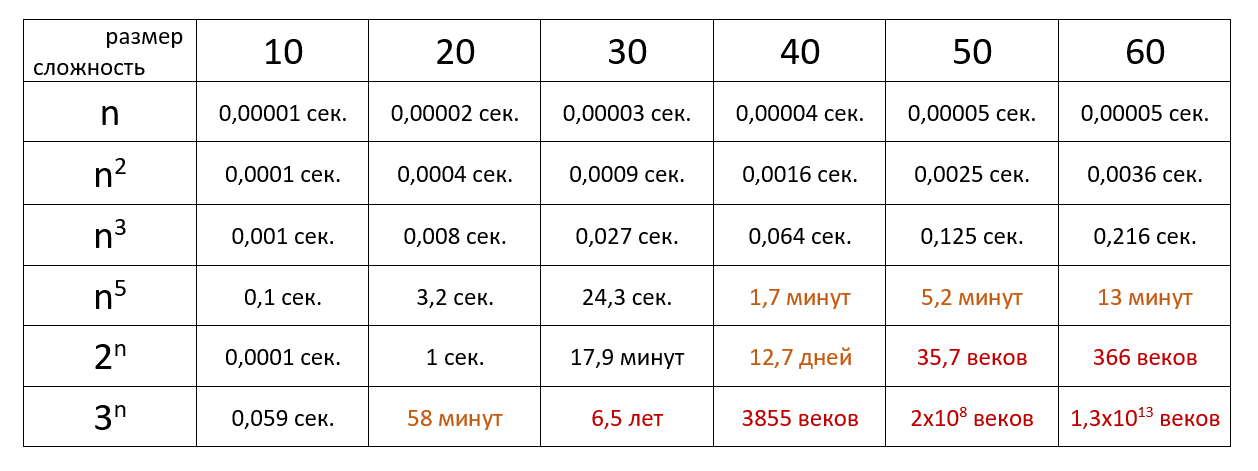
В заключение приведём таблицу, которая показывает, как долго компьютер, осуществляющий миллион операций в секунду, будет выполнять некоторые медленные алгоритмы.

Наверняка вы не раз сталкивались с обозначениями вроде O(log n) или слышали фразы типа «логарифмическая вычислительная сложность» в адрес каких-либо алгоритмов. И если вы хотите стать хорошим программистом, но так и не понимаете, что это значит, — данная статья для вас.

Оценка сложности

Сложность алгоритмов обычно оценивают по времени выполнения или по используемой памяти. В обоих случаях сложность зависит от размеров входных данных: массив из 100 элементов будет обработан быстрее, чем аналогичный из 1000. При этом точное время мало кого интересует: оно зависит от процессора, типа данных, языка программирования и множества других параметров. Важна лишь асимптотическая сложность, т. е. сложность при стремлении размера входных данных к бесконечности.

Допустим, некоторому алгоритму нужно выполнить 4n3 + 7n условных операций, чтобы обработать n элементов входных данных. При увеличении n на итоговое время работы будет значительно больше влиять возведение n в куб, чем умножение его на 4 или же прибавление 7n. Тогда говорят, что временная сложность этого алгоритма равна О(n3), т. е. зависит от размера входных данных кубически.

Использование заглавной буквы О (или так называемая О-нотация) пришло из математики, где её применяют для сравнения асимптотического поведения функций. Формально O(f(n)) означает, что время работы алгоритма (или объём занимаемой памяти) растёт в зависимости от объёма входных данных не быстрее, чем некоторая константа, умноженная на f(n).

Примеры

O(n) — линейная сложность

Такой сложностью обладает, например, алгоритм поиска наибольшего элемента в не отсортированном массиве. Нам придётся пройтись по всем n элементам массива, чтобы понять, какой из них максимальный.

O(log n) — логарифмическая сложность

Простейший пример — бинарный поиск. Если массив отсортирован, мы можем проверить, есть ли в нём какое-то конкретное значение, методом деления пополам. Проверим средний элемент, если он больше искомого, то отбросим вторую половину массива — там его точно нет. Если же меньше, то наоборот — отбросим начальную половину. И так будем продолжать делить пополам, в итоге проверим log n элементов.

O(n²) — квадратичная сложность

Такую сложность имеет, например, алгоритм сортировки вставками. В канонической реализации он представляет из себя два вложенных цикла: один, чтобы проходить по всему массиву, а второй, чтобы находить место очередному элементу в уже отсортированной части. Таким образом, количество операций будет зависеть от размера массива как n * n, т. е. n2.

Бывают и другие оценки по сложности, но все они основаны на том же принципе.

Также случается, что время работы алгоритма вообще не зависит от размера входных данных. Тогда сложность обозначают как O(1). Например, для определения значения третьего элемента массива не нужно ни запоминать элементы, ни проходить по ним сколько-то раз. Всегда нужно просто дождаться в потоке входных данных третий элемент и это будет результатом, на вычисление которого для любого количества данных нужно одно и то же время.

Аналогично проводят оценку и по памяти, когда это важно. Однако алгоритмы могут использовать значительно больше памяти при увеличении размера входных данных, чем другие, но зато работать быстрее. И наоборот. Это помогает выбирать оптимальные пути решения задач исходя из текущих условий и требований.

Наглядно

Время выполнения алгоритма с определённой сложностью в зависимости от размера входных данных при скорости 10⁶ операций в секунду:

Тут можно посмотреть сложность основных алгоритмов сортировки и работы с данными.

Если хочется подробнее и сложнее, заглядывайте в нашу статью из серии «Алгоритмы и структуры данных для начинающих».

Вычисли́тельная сло́жность — понятие в информатике и теории алгоритмов, обозначающее функцию зависимости объёма работы, которая выполняется некоторым алгоритмом, от размера входных данных. Раздел, изучающий вычислительную сложность, называется теорией сложности вычислений. Объём работы обычно измеряется абстрактными понятиями времени и пространства, называемыми вычислительными ресурсами. Время определяется количеством элементарных шагов, необходимых для решения задачи, тогда как пространство определяется объёмом памяти или места на носителе данных. Таким образом, в этой области предпринимается попытка ответить на центральный вопрос разработки алгоритмов: «как изменится время исполнения и объём занятой памяти в зависимости от размера входа?». Здесь под размером входа понимается длина описания данных задачи в битах (например, в задаче коммивояжёра длина входа почти пропорциональна количеству городов и дорог между ними), а под размером выхода — длина описания решения задачи (наилучшего маршрута в задаче коммивояжёра).

В частности, теория сложности вычислений определяет NP-полные задачи, которые недетерминированная машина Тьюринга может решить за полиномиальное время, тогда как для детерминированной машины Тьюринга полиномиальный алгоритм неизвестен. Обычно это сложные задачи оптимизации, например, задача коммивояжёра.

С теоретической информатикой тесно связаны такие области как анализ алгоритмов и теория вычислимости. Связующим звеном между теоретической информатикой и алгоритмическим анализом является тот факт, что их формирование посвящено анализу необходимого количества ресурсов определённых алгоритмов решения задач, тогда как более общим вопросом является возможность использования алгоритмов для подобных задач. Конкретизируясь, попытаемся классифицировать проблемы, которые могут или не могут быть решены при помощи ограниченных ресурсов. Сильное ограничение доступных ресурсов отличает теорию вычислительной сложности от вычислительной теории, последняя отвечает на вопрос, какие задачи, в принципе, могут быть решены алгоритмически.

Временная и пространственная сложности[править | править код]

Теория сложности вычислений возникла из потребности сравнивать быстродействие алгоритмов, чётко описывать их поведение (время исполнения и объём необходимой памяти) в зависимости от размера входа.

Количество элементарных операций, затраченных алгоритмом для решения конкретного экземпляра задачи, зависит не только от размера входных данных, но и от самих данных. Например, количество операций алгоритма сортировки вставками значительно меньше в случае, если входные данные уже отсортированы. Чтобы избежать подобных трудностей, рассматривают понятие временной сложности алгоритма в худшем случае.

Временная сложность алгоритма (в худшем случае) — это функция от размера входных данных, равная максимальному количеству элементарных операций, проделываемых алгоритмом для решения экземпляра задачи указанного размера.

Аналогично понятию временной сложности в худшем случае определяется понятие временная сложность алгоритма в наилучшем случае. Также рассматривают понятие среднее время работы алгоритма, то есть математическое ожидание времени работы алгоритма. Иногда говорят просто: «Временная сложность алгоритма» или «Время работы алгоритма», имея в виду временную сложность алгоритма в худшем, наилучшем или среднем случае (в зависимости от контекста).

По аналогии с временной сложностью, определяют пространственную сложность алгоритма, только здесь говорят не о количестве элементарных операций, а об объёме используемой памяти.

Асимптотическая сложность[править | править код]

Несмотря на то, что функция временной сложности алгоритма в некоторых случаях может быть определена точно, в большинстве случаев искать точное её значение бессмысленно. Дело в том, что во-первых, точное значение временной сложности зависит от определения элементарных операций (например, сложность можно измерять в количестве арифметических операций, битовых операций или операций на машине Тьюринга), а во-вторых, при увеличении размера входных данных вклад постоянных множителей и слагаемых низших порядков, фигурирующих в выражении для точного времени работы, становится крайне незначительным.

Рассмотрение входных данных большого размера и оценка порядка роста времени работы алгоритма приводят к понятию асимптотической сложности алгоритма. При этом алгоритм с меньшей асимптотической сложностью является более эффективным для всех входных данных, за исключением лишь, возможно, данных малого размера. Для записи асимптотической сложности алгоритмов используются асимптотические обозначения:

Обозначение	Интуитивное объяснение	Определение
	ограничена сверху функцией (с точностью до постоянного множителя) асимптотически	или
	ограничена снизу функцией (с точностью до постоянного множителя) асимптотически
	ограничена снизу и сверху функцией асимптотически
	доминирует над асимптотически
	доминирует над асимптотически
	эквивалентна асимптотически

Примеры[править | править код]

• «почистить ковёр пылесосом» требует время, линейно зависящее от его площади (), то есть на ковёр, площадь которого больше в два раза, уйдет в два раза больше времени. Соответственно, при увеличении площади ковра в сто тысяч раз объём работы увеличивается строго пропорционально в сто тысяч раз, и т. п.
• «найти имя в телефонной книге» требует всего лишь времени, логарифмически зависящего от количества записей (), так как, открыв книгу примерно в середине, мы уменьшаем размер «оставшейся проблемы» вдвое (за счет сортировки имен по алфавиту). Таким образом, в книге объёмом в 1000 страниц любое имя находится не больше, чем за раз (открываний книги). При увеличении объёма страниц до ста тысяч проблема все ещё решается за заходов. (См. Двоичный поиск.)

Замечания[править | править код]

Поскольку , в асимптотической оценке сложности часто пишут «логарифм» без упоминания основания — например, .

Необходимо подчеркнуть, что степень роста наихудшего времени выполнения — не единственный или самый важный критерий оценки алгоритмов и программ. Приведем несколько соображений, позволяющих посмотреть на критерий времени выполнения с других точек зрения:

Если создаваемая программа будет использована только несколько раз, тогда стоимость написания и отладки программы будет доминировать в общей стоимости программы, то есть фактическое время выполнения не окажет существенного влияния на общую стоимость. В этом случае следует предпочесть алгоритм, наиболее простой для реализации.

Если программа будет работать только с «малыми» входными данными, то степень роста времени выполнения будет иметь меньшее значение, чем константа, присутствующая в формуле времени выполнения^[1]. Вместе с тем и понятие «малости» входных данных зависит от точного времени выполнения конкурирующих алгоритмов. Существуют алгоритмы, такие как алгоритм целочисленного умножения, асимптотически самые эффективные, но которые никогда не используют на практике даже для больших задач, так как их константы пропорциональности значительно превосходят подобные константы других, более простых и менее «эффективных» алгоритмов. Другой пример — фибоначчиевы кучи, несмотря на асимптотическую эффективность, с практической точки зрения программная сложность реализации и большие значения констант в формулах времени работы делают их менее привлекательными, чем обычные бинарные деревья^[1].

Известны случаи, когда эффективные алгоритмы требуют таких больших объёмов машинной памяти (без возможности использования внешних средств хранения), что этот фактор сводит на нет преимущество «эффективности» алгоритма. Таким образом, часто важна не только «сложность по времени», но и «сложность по памяти» (пространственная сложность).

В численных алгоритмах точность и устойчивость алгоритмов не менее важны, чем их временная эффективность.

Классы сложности[править | править код]

Класс сложности — это множество задач распознавания, для решения которых существуют алгоритмы, схожие по вычислительной сложности. Два важных представителя:

Класс P[править | править код]

Класс P вмещает все те проблемы, решение которых считается «быстрым», то есть время решения которых полиномиально зависит от размера входа. Сюда относится сортировка, поиск в массиве, выяснение связности графов и многие другие.

Класс NP[править | править код]

Класс NP содержит задачи, которые недетерминированная машина Тьюринга в состоянии решить за полиномиальное количество шагов от размера входных данных. Их решение может быть проверено детерминированной машиной Тьюринга за полиномиальное количество шагов. Следует заметить, что недетерминированная машина Тьюринга является лишь абстрактной моделью, в то время как современные компьютеры соответствуют детерминированной машине Тьюринга с ограниченной памятью. Поскольку детерминированная машина Тьюринга может рассматриваться как специальный случай недетерминированной машины Тьюринга, класс NP включает в себя класс P, а также некоторые проблемы, для решения которых известны лишь алгоритмы, экспоненциально зависящие от размера входа (то есть неэффективные для больших входов). В класс NP входят многие знаменитые проблемы, такие как задача коммивояжёра, задача выполнимости булевых формул, факторизация и др.

Проблема равенства классов P и NP[править | править код]

Вопрос о равенстве этих двух классов считается одной из самых сложных открытых проблем в области теоретической информатики. Математический институт Клэя включил эту проблему в список проблем тысячелетия, предложив награду размером в один миллион долларов США за её решение.

См. также[править | править код]

• Временная сложность алгоритма
• Класс сложности
• Алгебраическая сложность
• Скорость сходимости
• Алгоритм
• Аппроксимация
• Сведение
• «O» большое и «o» малое
• Пределы вычислений

Примечания[править | править код]

Ссылки[править | править код]

• Гирш Э. А. «Сложность вычислений и основы криптографии». Курс лекций описывающий основы сложности вычислений и криптографии.
• Юрий Лифшиц «Современные задачи теоретической информатики». Курс лекций по алгоритмам для NP-трудных задач.
• А. А. Разборов. Theoretical Computer Science: взгляд математика // Компьютерра. — 2001. — № 2. (недоступная ссылка) (альтернативная ссылка)
• А. А. Разборов. О сложности вычислений // Математическое просвещение. — МЦНМО, 1999. — № 3. — С. 127—141.

Кадр: фильм «Мальчишник в Вегасе»

Онлайн-журнал для тех, кто влюблён в код и информационные технологии. Пишем для айтишников и об айтишниках.

Валерий Жила

об эксперте

Software Engineer, разрабатывает системы управления городской инфраструктурой для мегаполисов. Основная деятельность: backend, database engineering. Ведёт твиттер @ValeriiZhyla и пишет научные работы по DevOps.

---

---

Сегодня я расскажу о сложности алгоритмов, или, как её часто называют, Big O Notation. Статья рассчитана на новичков, поэтому постараюсь изложить идеи и концепции просто, не теряя важных деталей.

Алгоритмы описывают с помощью двух характеристик — времени и памяти.

Время — это… время, которое нужно алгоритму для обработки данных. Например, для маленького массива — 10 секунд, а для массива побольше — 100 секунд. Интуитивно понятно, что время выполнения алгоритма зависит от размера массива.

Но есть проблема: секунды, минуты и часы — это не очень показательные единицы измерения. Кроме того, время работы алгоритма зависит от железа, на котором он выполняется, и других внешних факторов. Поэтому время считают не в секундах и часах, а в количестве операций, которые алгоритм совершит. Это надёжная и, главное, независимая от железа метрика.

Когда говорят о Time Complexity или просто Time, то речь идёт именно о количестве операций. Для простоты расчётов разница в скорости между операциями обычно опускается. Поэтому, несмотря на то, что деление чисел с плавающей точкой требует от процессора больше действий, чем сложение целых чисел, обе операции в теории алгоритмов считаются равными по сложности.

Запомните: в О-нотации на операции с одной или двумя переменными вроде i++, a * b, a / 1024, max(a,b) уходит всего одна единица времени.

Память, или место, — это объём оперативной памяти, который потребуется алгоритму для работы. Одна переменная — это одна ячейка памяти, а массив с тысячей ячеек — тысяча ячеек памяти.

В теории алгоритмов все ячейки считаются равноценными. Например, int a на 4 байта и double b на 8 байт имеют один вес. Потребление памяти обычно называется Space Complexity или просто Space, редко — Memory.

Алгоритмы, которые используют исходный массив как рабочее пространство, называют in-place. Они потребляют мало памяти и создают одиночные переменные — без копий исходного массива и промежуточных структур данных. Алгоритмы, требующие дополнительной памяти, называют out-of-place. Прежде чем использовать алгоритм, надо понять, хватит ли на него памяти, и если нет — поискать менее прожорливые альтернативы.

Статья написана на основе треда Валерия в его аккаунте в Twitter. Автор благодарит @usehex за помощь в создании материала.

Давайте вспомним 8-й класс и разберёмся: что значит запись O(n) с математической точки зрения. При расчёте Big O Notation используют два правила:

Константы откидываются. Нас интересует только часть формулы, которая зависит от размера входных данных. Проще говоря, это само число n, его степени, логарифмы, факториалы и экспоненты, где число находится в степени n.

Примеры:

O(3n) = O(n)

O(10000 n^2) = O(n^2)

O(2n * log n) = O(n * log n)

Если в O есть сумма, нас интересует самое быстрорастущее слагаемое. Это называется асимптотической оценкой сложности.

Примеры:

O(n^2 + n) = O(n^2)

O(n^3 + 100n * log n) = O(n^3)

O(n! + 999) = O(n!)

O(1,1^n + n^100) = O(1,1^n)

У каждого алгоритма есть худший, средний и лучший сценарии работы — в зависимости от того, насколько удачно выбраны входные данные. Часто их называют случаями.

Худший случай (worst case) — это когда входные данные требуют максимальных затрат времени и памяти.

Например, если мы хотим отсортировать массив по возрастанию (Ascending Order, коротко ASC), то для простых алгоритмов сортировки худшим случаем будет массив, отсортированный по убыванию (Descending Order, коротко DESC).

Для алгоритма поиска элемента в неотсортированном массиве worst case — это когда искомый элемент находится в конце массива или если элемента нет вообще.

Лучший случай (best case) — полная противоположность worst case, самые удачные входные данные. Правильно отсортированный массив, с которым алгоритму сортировки вообще ничего делать не нужно. В случае поиска — когда алгоритм находит нужный элемент с первого раза.

Средний случай (average case) — самый хитрый из тройки. Интуитивно понятно, что он сидит между best case и worst case, но далеко не всегда понятно, где именно. Часто он совпадает с worst case и всегда хуже best case, если best case не совпадает с worst case. Да, иногда они совпадают.

Как определяют средний случай? Считают статистически усреднённый результат: берут алгоритм, прокручивают его с разными данными, составляют сводку результатов и смотрят, вокруг какой функции распределились результаты. В общем, расчёт average case — дело сложное. А мы приступаем к конкретным алгоритмам.

Начнём с самого простого алгоритма — линейного поиска, он же linear search. Дальнейшее объяснение подразумевает, что вы знаете, что такое числа и как устроены массивы. Напомню, это всего лишь набор проиндексированных ячеек.

Допустим, у нас есть массив целых чисел arr, содержащий n элементов. Вообще, количество элементов, размер строк, массивов, списков и графов в алгоритмах всегда обозначают буквой n или N. Ещё дано целое число x. Для удобства обусловимся, что arr точно содержит x.

Задача: найти, на каком месте в массиве arr находится элемент 3, и вернуть его индекс.

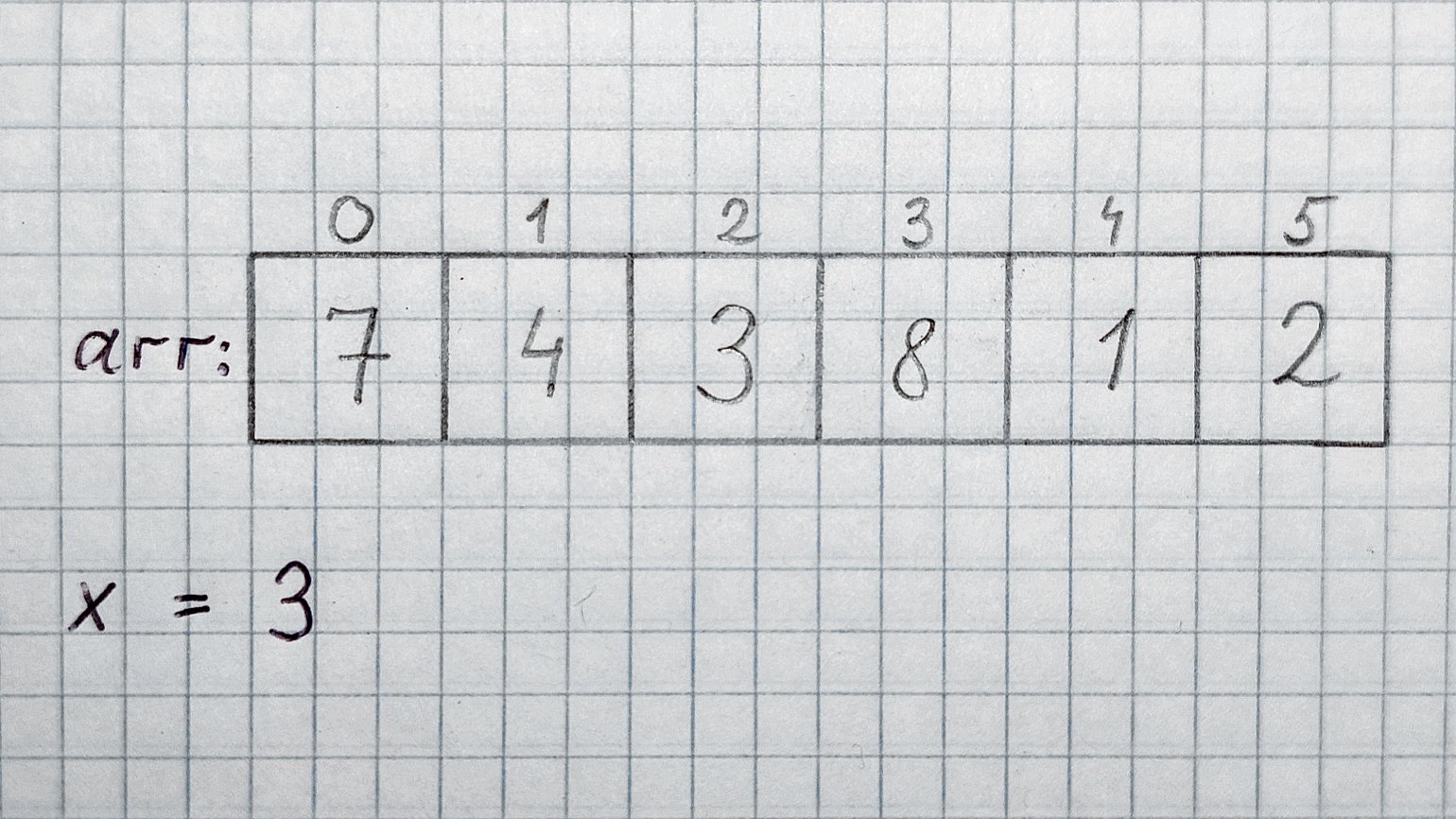
Меткий человеческий глаз сразу видит, что искомый элемент содержится в ячейке с индексом 2, то есть в arr[2]. А менее зоркий компьютер будет перебирать ячейки друг за другом: arr[0], arr[1]… и так далее, пока не встретит тройку или конец массива, если тройки в нём нет.

Теперь разберём случаи:

Worst case. Больше всего шагов потребуется, если искомое число стоит в конце массива. В этом случае придётся перебрать все n ячеек, прочитать их содержимое и сравнить с искомым числом. Получается, worst case равен O(n). В нашем массиве худшему случаю соответствует x = 2.

Best case. Если бы искомое число стояло в самом начале массива, то мы бы получили ответ уже в первой ячейке. Best case линейного поиска — O(1). Именно так обозначается константное время в Big O Notation. В нашем массиве best case наблюдается при x = 7.

Average case. В среднем случае результаты будут равномерно распределены по массиву. Средний элемент можно рассчитать по формуле (n + 1) / 2, но так как мы отбрасываем константы, то получаем просто n. Значит, average case равен O(n). Хотя иногда в среднем случае константы оставляют, потому что запись O(n / 2) даёт чуть больше информации.

Хорошо, мы уже три минуты обсуждаем linear search, но до сих пор не видели кода. Потерпите, скоро всё будет. Но сперва познакомимся с очень полезным инструментом — псевдокодом.

Разработчики пишут на разных языках программирования. Одни похожи друг на друга, а другие — сильно различаются. Часто мы точно знаем, какую операцию хотим выполнить, но не уверены в том, как она выглядит в конкретном языке.

Возьмём хотя бы получение длины массива. По историческим причинам практически во всех языках эта операция называется по-разному: .length, length(), len(), size(), .size — попробуй угадай! Как же объяснить свой код коллегам, которые пишут на другом языке? Написать программу на псевдокоде.

Псевдокод — достаточно формальный, но не слишком требовательный к мелочам инструмент для изложения мыслей, не связанный с конкретным языком программирования.

Прелесть псевдокода в том, что конкретных правил для его написания нет. Я, например, предпочитаю использовать смесь синтаксиса Python и C: обозначаю вложенность с помощью отступов и называю методы в стиле Python.

А вот и пример псевдокода для нашей задачи, со всеми допущениями и упрощениями. Метод должен возвращать -1, если arr пуст или не содержит x:

 int linear_search(int[] arr, int x):
	if arr is empty:
		return -1
	for i in 0..n:
		if (arr[i] == x):
			return i
	return -1	//x was not found

В псевдокоде часто используют -1 в качестве invalid index, а если алгоритм возвращает объекты — null, nil (то же самое, что и null) или специальный символ «ничего», похожий на перевёрнутую букву «т». Также встречаются конструкции для исключений, вроде throw error (“Very Bad”).

Уметь писать псевдокод полезно. Например, с его помощью можно решать задачи на доске на технических собеседованиях. Я пишу код на бумаге и доске почти так же, как в компьютере, но ещё явно выделяю отступы — иначе строчки кода разъезжаются куда глаза глядят:

Следующая остановка — binary search, он же бинарный, или двоичный, поиск.

В чём отличие бинарного поиска от уже знакомого линейного? Чтобы его применить, массив arr должен быть отсортирован. В нашем случае — по возрастанию.

Часто binary search объясняют на примере с телефонным справочником. Возможно, многие читатели никогда не видели такую приблуду — это большая книга со списками телефонных номеров, отсортированных по фамилиям и именам жителей. Для простоты забудем об именах.

Итак, есть огромный справочник на тысячу страниц с десятками тысяч пар «фамилия — номер», отсортированных по фамилиям. Допустим, мы хотим найти номер человека по фамилии Жила. Как бы мы действовали в случае с линейным поиском? Открыли бы книгу и начали её перебирать, строчку за строчкой, страницу за страницей: Астафьев… Безье… Варнава… Ги… До товарища Жилы он дошёл бы за пару часов, а вот господин Янтарный заставил бы алгоритм попотеть ещё дольше.

Бинарный поиск мудрее и хитрее. Он открывает книгу ровно посередине и смотрит на фамилию, например Мельник — буква «М». Книга отсортирована по фамилиям, и алгоритм знает, что буква «Ж» идёт перед «М».

Алгоритм «разрывает» книгу пополам и выкидывает часть с буквами, которые идут после «М»: «Н», «О», «П»… «Я». Затем открывает оставшуюся половинку посередине — на этот раз на фамилии Ежов. Уже близко, но Ежов не Жила, а ещё буква «Ж» идёт после буквы «Е». Разрываем книгу пополам, а левую половину с буквами от «А» до «Е» выбрасываем. Алгоритм продолжает рвать книгу пополам до тех пор, пока не останется единственная измятая страничка с заветной фамилией и номером.

Перенесём этот принцип на массивы. У нас есть отсортированный массив arr и число 7, которое нужно найти. Почему поиск называется бинарным? Дело в том, что алгоритм на каждом шаге уменьшает проблему в два раза. Он буквально отрезает на каждом шаге половину arr, в которой гарантированно нет искомого числа.

На каждом шаге мы проверяем только середину. При этом есть три варианта развития событий:

• попадаем в 7 — тогда проблема решена;
• нашли число меньше 7 — отрезаем левую половину и ищем в правой половине;
• нашли число больше 7 — отрезаем правую половину и ищем в левой половине.

Почему это работает? Вспомните про требование к отсортированности массива, и всё встанет на свои места.

Итак, смотрим в середину. Карандаш будет служить нам указателем.

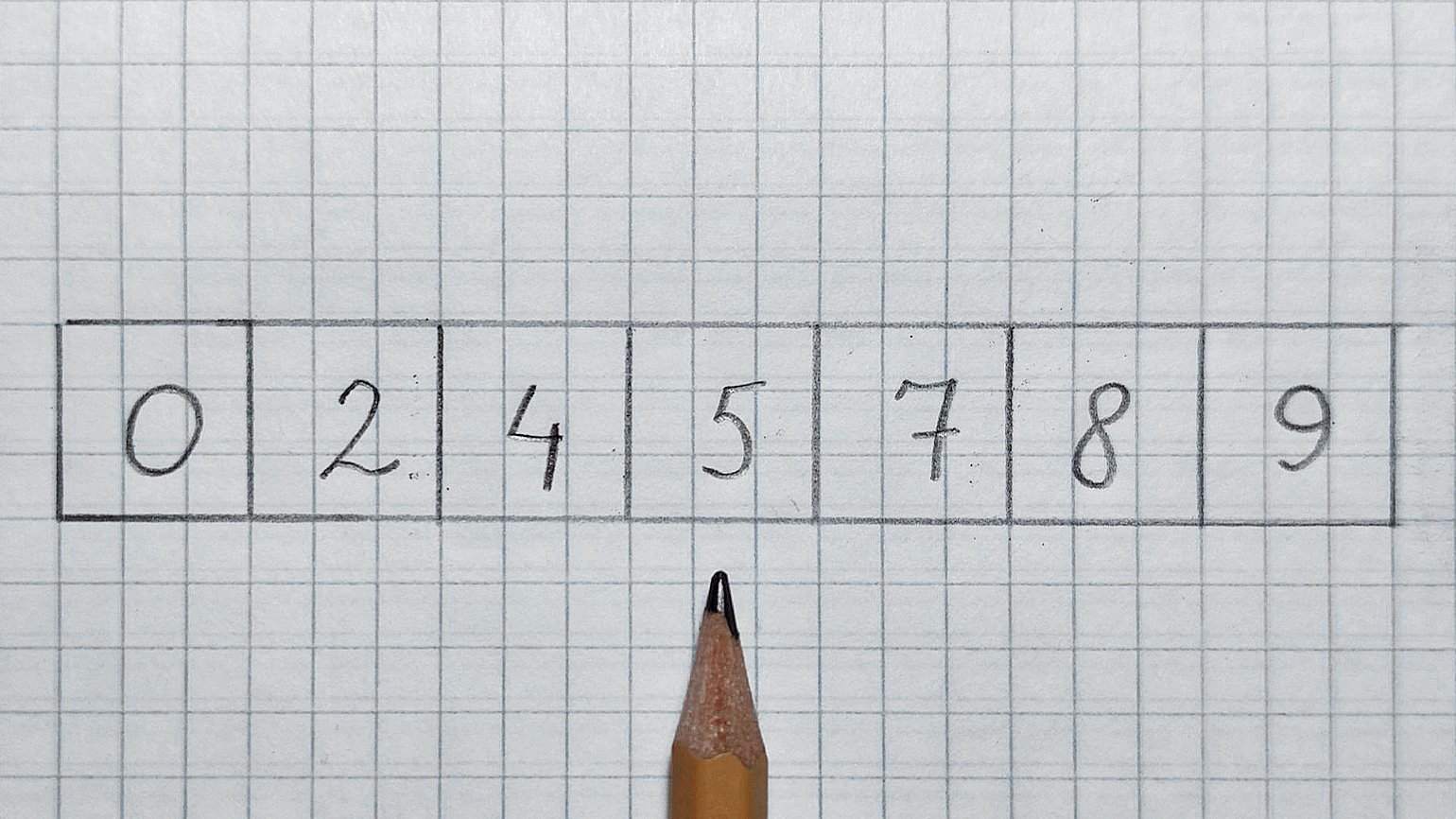
В середине находится число 5, оно меньше 7. Значит, отрезаем левую половину и проверенное число. Смотрим в середину оставшегося массива:

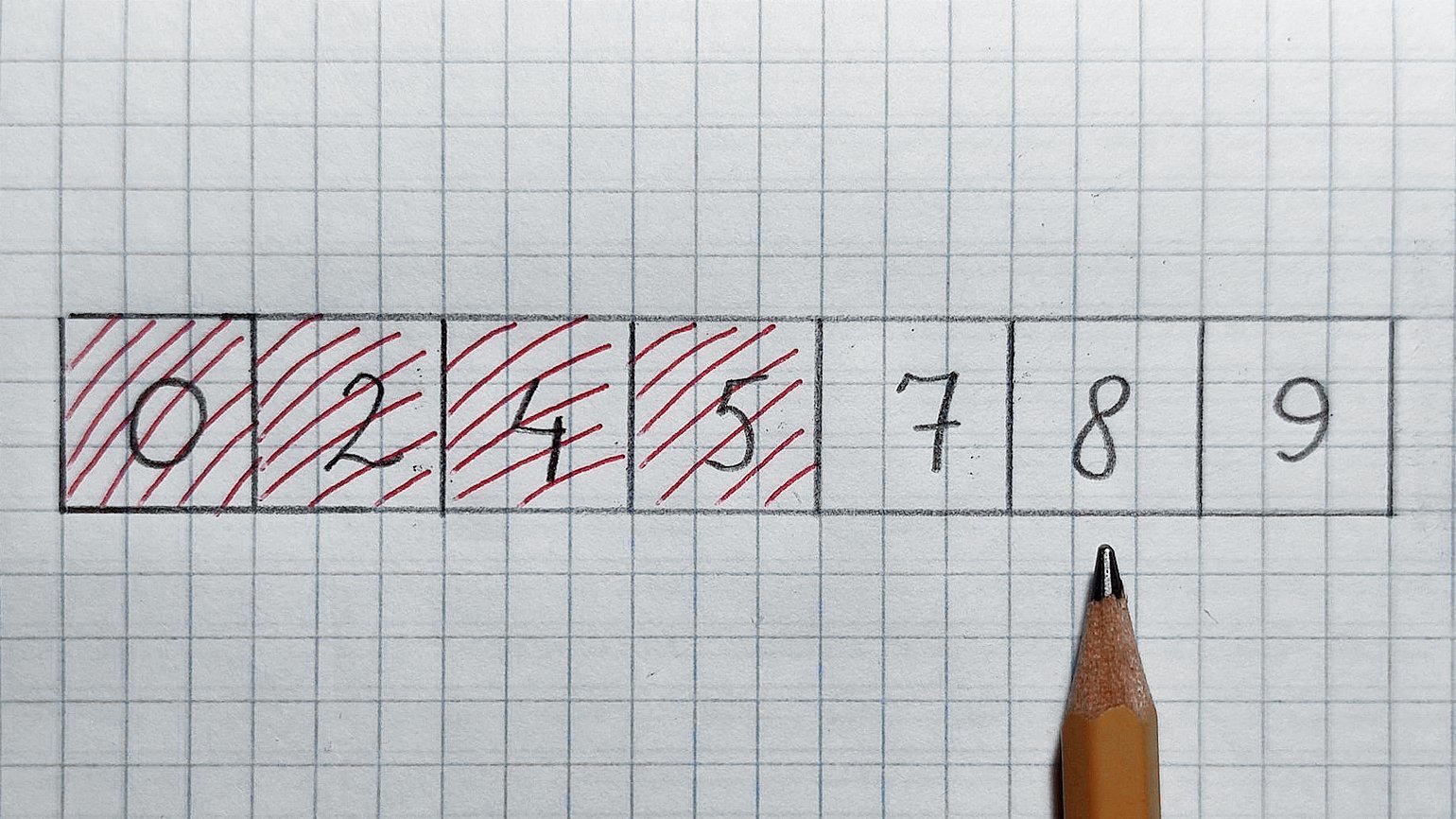
В середине число 8, оно больше 7. Значит, отрезаем правую половинку и проверенное число. Остаётся число 7 — как раз его мы и искали. Поздравляю!

Теперь давайте попробуем записать это в виде красивого псевдокода. Как обычно, назовём середину mid и будем перемещать «окно наблюдения», ограниченное двумя индексами — low (левая граница) и high (правая граница).

int binary_search(int [] arr, int low, int high, int x):
	if high >= low:
		mid = round_down((low + high)/2)
		if arr[mid] == x:  // check middle element
			return mid
		else if arr[mid] > x:  // recursive check left hals
			return binary_search(arr, low, mid-1, x)
		else:  // recursive check right half
			return binary_search(arr, mid+1, high, x)
	else:
		return -1  // x was not found

Алгоритм организован рекурсивно, то есть вызывает сам себя на строках 7 и 9. Есть итеративный вариант с циклом, без рекурсии, но он кажется мне уродливым. Если не находим искомый элемент, возвращаем -1. В начале работы алгоритма значение low совпадает с началом массива, а high — с его концом. И они бегут навстречу друг другу…

Чтобы запускать алгоритм, не задумываясь о начальных значениях индексов low и high, можно написать такую функцию-обёртку:

 int binary_search(int [] arr, int x):
	if arr_is_empty:
		return -1
	lower_bound == 0
	upper_bound == arr.length -1
	return binary_search(arr, lower_bound, upper_bound, x)

Посчитаем сложность бинарного поиска:

Best case. Как и у линейного поиска, лучший случай равен O(1), ведь искомое число может находиться в середине массива, и тогда мы найдём его с первой попытки.

Worst case. Чтобы найти худший случай, нужно ответить на вопрос: «Сколько раз нужно разделить массив на 2, чтобы в нём остался один элемент?» Или найти минимальное число k, при котором справедливо 2^k ≥ n.

Надеюсь, что большинство читателей смогут вычислить k. Но на всякий случай подскажу решение: k = log n по основанию 2 (в алгоритмах практически все логарифмы двоичные). Поэтому worst case бинарного поиска — O(log n).

Average case. Он тоже равен O(log n). И если для линейного поиска average case в два раза лучше, чем worst case, то тут они обычно отличаются всего на несколько шагов.

Часто студенты спрашивают: «Зачем нужен линейный поиск, если бинарный обходит его по всем позициям?» Отвечаю: линейный поиск работает с любыми массивами, а бинарный — только с отсортированными.

Мы дошли до важного принципа: чем сложнее структура данных, тем более быстрые алгоритмы к ней можно применять. Отсортированный массив — более сложная структура, чем неотсортированный. Забегу вперёд и скажу, что сортировка в общем случае требует от O(n * log(n)) до O(n^2) времени.

Создать дополнительные структуры данных несложно, вот только это не бесплатное удовольствие. Они едят много памяти. Как правило, O(n). Отсюда вытекает довольно логичный, но обидный вывод: время и память — «взаимообмениваемые» ресурсы. Алгоритм можно ускорить, пожертвовав памятью, или решать задачу медленно, зато in-place. Кроме того, почти всегда есть промежуточный вариант.

Решить одну и ту же проблему зачастую можно тремя способами. Задача разработчика — выбрать самый подходящий.

Мы рассмотрели два алгоритма и увидели примеры их сложности. Но так и не поговорили о том, как эту сложность определять. Есть три основных способа.

Первый и наиболее часто используемый способ. Именно так мы определяли сложность linear search и binary search. Обобщим эти примеры.

Первый случай. Есть алгоритм some_function, который выполняет действие А, а после него — действие В. На А и В нужно K и J операций соответственно.

int some_function():
	action_A() // K operations
	action_B() // J operations

В случае последовательного выполнения действий сложность алгоритма будет равна O(K + J), а значит, O(max (K, J)). Например, если А равно n^2, а В — n, то сложность алгоритма будет равна O(n^2 + n). Но мы уже знаем, что нас интересует только самая быстрорастущая часть. Значит, ответ будет O(n^2).

Второй случай. Посчитаем сложность действий или вызова методов в циклах. Размер массива равен n, а над каждым элементом будет выполнено действие А (n раз). А дальше всё зависит от «содержимого» A.

Посчитаем сложность бинарного поиска:

int some_function(int [] arr):
	n = arr.length
	for i in 0..n:
	    action_A() // K operations

Если на каждом шаге A работает с одним элементом, то, независимо от количества операций, получим сложность O(n). Если же A обрабатывает arr целиком, то алгоритм совершит n операций n раз. Тогда получим O(n * n) = O(n^2). По такой же логике можно получить O(n * log n), O(n^3) и так далее.

Третий случай — комбо. Для закрепления соединим оба случая. Допустим, действие А требует log(n) операций, а действие В — n операций. На всякий случай напомню: в алгоритмах всегда идёт речь о двоичных логарифмах.

Добавим действие С с пятью операциями и вот что получим:

int some_function(int [] arr):
	n = arr.length
	for i in 0..n:
	    for j in 0..n:
	        action_A(arr) // log(n) operations
	    action_B(arr) // n operations
   action_C() // 5 operations

O(n * (n * log(n) + n) + 5) = O(n^2 * log(n) + n^2 + 5) = O(n^2 * log(n)).

Мы видим, что самая дорогая часть алгоритма — действие А, которое выполняется во вложенном цикле. Поэтому именно оно доминирует в функции.

Есть разновидность определения на глаз — амортизационный анализ. Это относительно редкий, но достойный упоминания гость. В двух словах его можно объяснить так: если на X «дешёвых» операций (например, с O(1)) приходится одна «дорогая» (например, с O(n)), то на большом количестве операций суммарная сложность получится неотличимой от O(1).

Частый пациент амортизационного анализа — динамический массив. Это массив, который при переполнении создаёт новый, больше оригинального в два раза. При этом элементы старого массива копируются в новый.

Практически всегда добавление элементов в такой массив «дёшево» — требует лишь одной операции. Но когда он заполняется, приходится тратить силы: создавать новый массив и копировать N старых элементов в новый. Но так как массив каждый раз увеличивается в два раза, переполнения случаются всё реже и реже, поэтому average case добавления элемента равен O(1).

Слабое место прикидывания на глаз — рекурсия. С ней и правда приходится тяжко. Поэтому для оценки сложности рекурсивных алгоритмов широко используют мастер-теорему.

По сути, это набор правил по оценке сложности. Он учитывает, сколько новых ветвей рекурсии создаётся на каждом шаге и на сколько частей дробятся данные в каждом шаге рекурсии. Это если вкратце.

Метод Монте-Карло применяют довольно редко — только если первые два применить невозможно. Особенно часто с его помощью описывают производительность систем, состоящих из множества алгоритмов.

Суть метода: берём алгоритм и гоняем его на случайных данных разного размера, замеряем время и память. Полученные измерения выкладываем на отдельные графики для памяти и времени. А затем автоматически вычисляется функция, которая лучше всего описывает полученное облако точек.

На протяжении всей статьи мы говорили про Big O Notation. А теперь сюрприз: это только одна из пяти существующих нотаций. Вот они слева направо: Намджун, Чонгук, Чингачгук… простите, не удержался. Сверху вниз: Small o, Big O, Big Theta, Big Omega, Small omega. f — это реальная функция сложности нашего алгоритма, а g — асимптотическая.

Несколько слов об этой весёлой компании:

• Big O обозначает верхнюю границу сложности алгоритма. Это идеальный инструмент для поиска worst case.
• Big Omega (которая пишется как подкова) обозначает нижнюю границу сложности, и её правильнее использовать для поиска best case.
• Big Theta (пишется как О с чёрточкой) располагается между О и омегой и показывает точную функцию сложности алгоритма. С её помощью правильнее искать average case.
• Small o и Small omega находятся по краям этой иерархии и используются в основном для сравнения алгоритмов между собой.

«Правильнее» в данном контексте означает — с точки зрения математических пейперов по алгоритмам. А в статьях и рабочей документации, как правило, во всех случаях используют «Большое „О“».

Если хотите подробнее узнать об остальных нотациях, посмотрите интересный видос на эту тему. Также полезно понимать, как сильно отличаются скорости возрастания различных функций. Вот хороший cheat sheet по сложности алгоритмов и наглядная картинка с графиками оттуда:

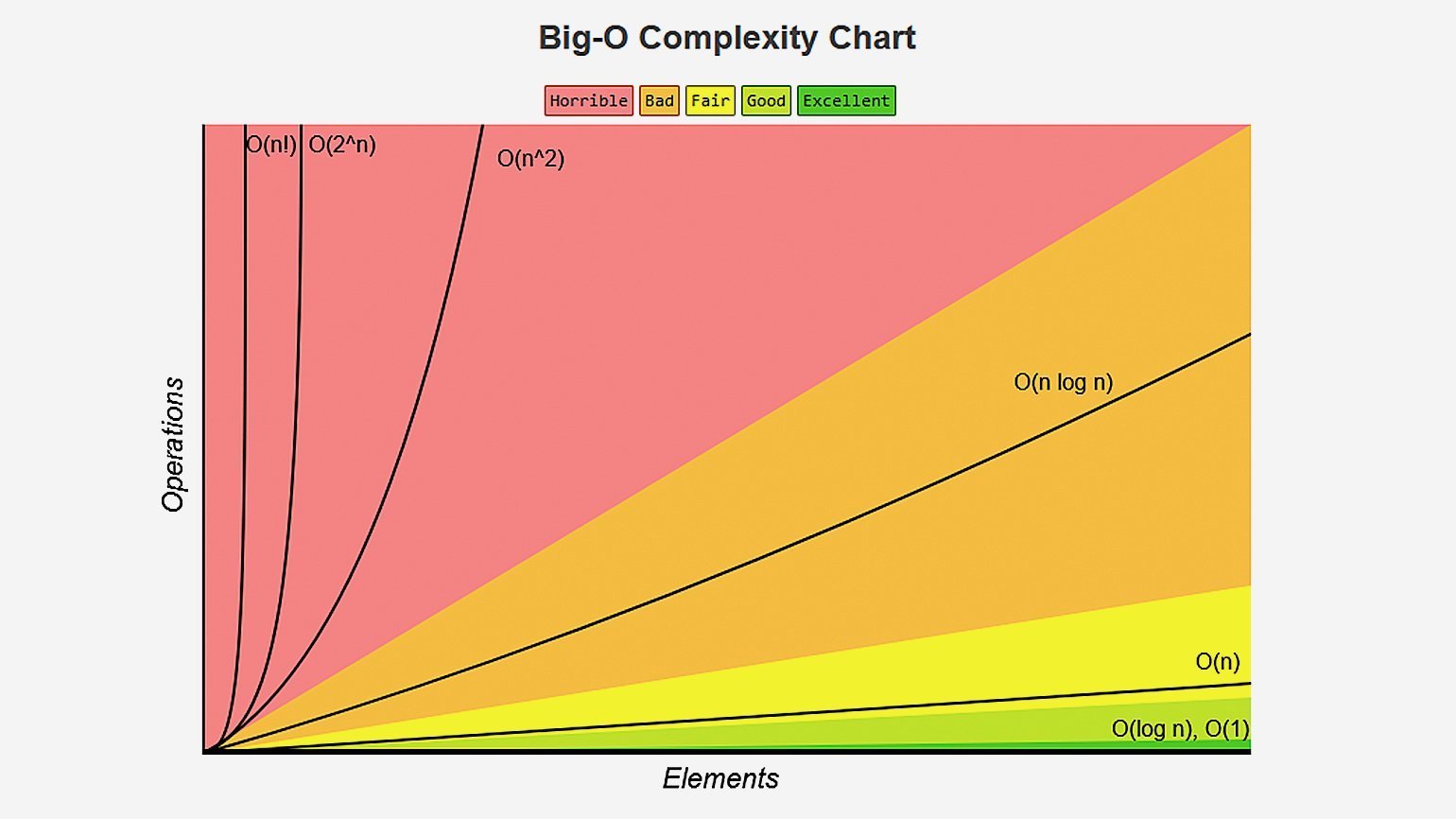
Хоть картинка и наглядная, она плохо передаёт всю бездну, лежащую между функциями. Поэтому я склепал таблицу со значениями времени для разных функций и N. За время одной операции взял 1 наносекунду:

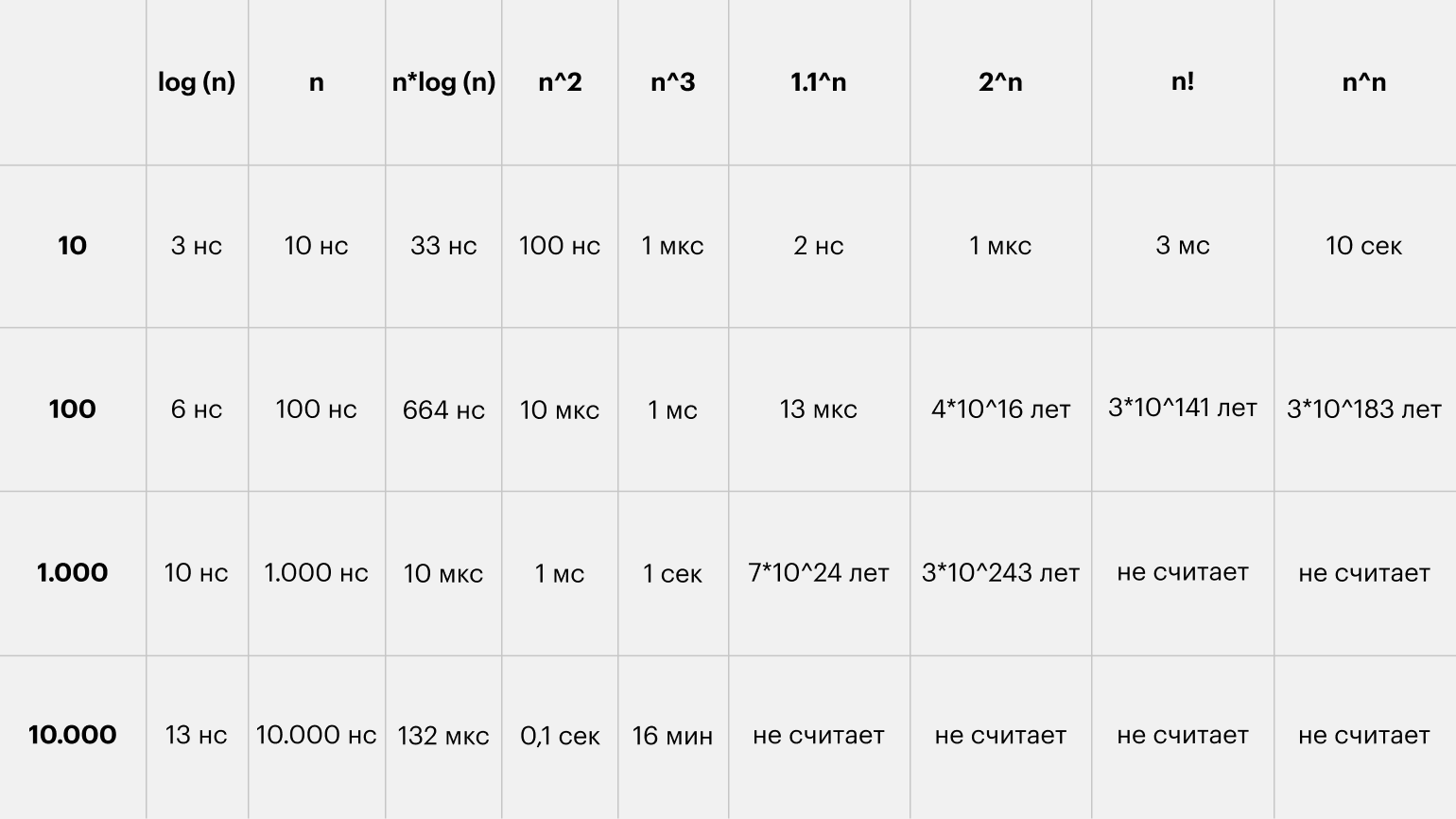
В последнем разделе поговорим о скрытых константах. Это хитрая штука, там собака зарыта.

Возьмём умножение матриц. При размерности матрицы n * n наивный алгоритм, который многие знают с начальных курсов универа, «строчка на столбик» имеет кубическую временную сложность O(n^3). Кубическая, зато честная. Без констант и O(10000 * n^3) под капотом. И памяти не ест — только время.

У Валерия есть отдельный тред об умножении матриц.

В некоторых алгоритмах умножения матриц степень n сильно «порезана». Самые «быстрые» из них выдают время около O(n^2,37). Какой персик, правда? Почему бы нам не забыть про «наивный» алгоритм?

Проблема в том, что у таких алгоритмов огромные константы. В пейперах гонятся за более компактной экспонентой, а степени отбрасываются. Я не нашёл внятных значений констант. Даже авторы оригинальных пейперов называют их просто «очень большими».

Давайте от балды возьмём не очень большую константу 100 и сравним n^3 c 100 * n^2,37. Правая функция даёт выигрыш по сравнению с левой для n, начинающихся с 1495. А ведь мы взяли довольно скромную константу. Подозреваю, что на практике они не в пример больше…

В то же время умножение матриц 1495 × 1495 — очень редкий случай. А матрицы миллиард на миллиард точно нигде не встретишь. Да простит меня Император Душнил с «Хабра» за вольное допущение 🙂

Такие алгоритмы называются галактическими, потому что дают выигрыш только на масштабах, нерелевантных для нас. А в программном умножении матриц, если я правильно помню курс алгоритмов и умею читать «Википедию», очень любят алгоритм Штрассена с его O(2,807) и маленькими константами. Но и те, к сожалению, жрут слишком много памяти.

В прошлой статье мы разбирались,что такое бенчмаркинг кода и как с его помощью оценивать производительность кода. В этой же поговорим про оценку сложности алгоритмов. А чтобы всё было наглядно, вместе попробуем оценить алгоритмы, которые используются для решения задачки на собеседовании в Google.

Задач такого плана полным-полно на платформах типа LeetCode, CodeWars и других. И их ценность не в том, чтоб заучить различные алгоритмы сортировок, которые вы никогда не будете на практике писать самостоятельно, а в том, чтоб увидеть типичные проблемы, с которыми вы можете столкнуться в практических задачах при разработке.

Оценка сложности алгоритмов

Зачем вообще оценивать сложность алгоритмов и какие способы оценки бывают?

Понимать сложность алгоритмов важно и по следующим причинам:

• без этих знаний вы не сможете отличить суб-оптимальный код от оптимального и оптимизировать его;
• каждый средний или большой проект рано или поздно будет оперировать большим объёмом данных. Важно, чтоб ваши алгоритмы это предусматривали и не стали бомбой замедленного действия;
• если вы не понимаете концепции оценки сложности алгоритмов, вы, скорее всего, будете писать низкопроизводительный код по умолчанию.

Способы же оценки сложности существуют следующие:

O большое (O(n)) — позволяет оценить верхнюю границу сложности алгоритмов. Это отношение количества входных данных для алгоритма ко времени, за которое алгоритм сможет их обработать. Простыми словами, это максимальное время работы алгоритма при работе с большими объёмами данных.

o малое (o(n)) — позволяет оценить верхнюю границу, исключая точную оценку.

Омега (Ω(n)) — позволяет оценить нижнюю границу сложности.

Тета (Θ ()) — позволяет получить точную оценку сложности.

В большинстве IT-компаний для оценки сложности используют только большое O (BigO notation), поскольку чаще всего достаточно представлять, как быстро будет расти количество операций при увеличении входных данных в худшем случае. Остальные типы оценок используются редко.

Если представить график распространённых сложностей алгоритмов, они будут выглядеть вот так:

Если условно разделить сложности на зоны, то сложности вида O(log n), O(1) или O(C) можно будет отнести к зоне Excellent. Такие алгоритмы вне зависимости от объёмов данных будут выполняться очень быстро — практически мгновенно.

Алгоритмы сложности O(n) можно отнести к зоне Fair — к алгоритмам, сложность которых растёт предсказуемо и линейно. Например, если 100 элементов ваш алгоритм обрабатывает за 10 секунд, то 1000 он обработает примерно за 100 секунд. Не лучший результат, но предсказуемый.

Алгоритмы из красной зоны Horrible со сложностями O(N^2) и выше трудно отнести к высокопроизводительным. НО!  Тут всё сильно зависит от объёмов входных данных. Если вы уверены, что у вас всегда будет небольшой объём данных (например, 100 элементов), и обрабатываться он будет в приемлемое для вас время, то всё в порядке, такие алгоритмы тоже можно использовать. Но если же вы не уверены в постоянности объёмов данных (может прийти и 10 000 элементов вместо 100) — лучше всё-таки задуматься над оптимизацией алгоритмов.

Оценка сложности по времени и по памяти

Оценку сложности алгоритмов следует проводить не только по времени выполнения, но и по потребляемой памяти. Например, для ускорения вычислений можно создать какую-нибудь промежуточную структуру данных типа массива или стека для ускорения алгоритма и кеширования результатов. Это приведёт к дополнительным затратам памяти, но при этом может существенно ускорить вычисления.

Однако если ваш алгоритм для выполнения будет требовать больше памяти, чем может предоставить ваш ПК, вы не получите ожидаемой производительности. А возможно код и вовсе будет выполнен некорректно.

Немного практики:правила расчета сложности

Пример 1:

Возьмём для начала простой алгоритм присвоения переменной:

Какова его сложность по времени и по памяти?

С одной стороны, нас может ввести в заблуждение массив данных data неизвестной размерности. Но брать его в расчёт при оценке сложности внутреннего алгоритма будет некорректно.

Правило 1: внешние данные не учитываются в сложности алгоритма.

Получается, наш алгоритм состоит только из одной строчки: var a = data[target];

Доступ к элементу массива по индексу — известная операция со сложностью O(1) или O(C). Соответственно, и весь алгоритм по времени у нас займет O(1).

Дополнительная же память выделяется только под одну переменную. А значит, объём данных, которые мы будем передавать (хоть 1 000, хоть 10 000), не скажется на финальном результате. Соответственно, сложность по памяти у нас так же — O(1) или O(C).

Для упрощения записи дальше я везде буду писать O(C) вместо O(1), C в этом случае — это константа. Она может равняться 1, 2 или даже 100 — для современных компьютеров это число не принципиально, поскольку и 1, и 100 операций выполняются практически за одно и то же время.

Пример 2:

Рассмотрим второй алгоритм, очень похожий на первый:

Влияет ли размерность входного массива data на количество операций в нём? Нет.

А на выделенную память? Тоже нет.

Сложность этого алгоритма по времени выполнения можно было бы оценить как O(2*C) — поскольку у нас выполняется в два раза больше операций, чем в предыдущем примере, 2 присваивания вместо 1. Но у нас и на этот счёт есть правило:

Правило 2: опускать константные множители, если они не влияют на результат кардинальным образом.

Если принять это правило в расчёт, сложность этого алгоритма будет такой же, как и в первом примере — O(C) по времени и O(C) по памяти.

Пример 3:

В третьем примере добавим в наш алгоритм цикл для обработки данных:

Как мы видим, количество операций, которые будет выполнять цикл, напрямую зависит от количества входных данных: больше элементов в data — больше циклов обработки потребуется для получения финального результата.

Казалось бы, если взять в учёт каждую строчку кода нашего алгоритма, то получилось бы что-то такое:

И тогда финальная сложность алгоритма получится O(C)+O(n). Но тут опять вмешивается новое правило:

Правило 3: опускать элементы оценки, которые меньше максимальной сложности алгоритма.

Поясню: если у вас O(C)+O(n), результирующая сложность будет O(n), поскольку O(n) будет расти всегда быстрее, чем O(C).

Еще один пример — O(n)+O(n^2). При такой сложности у нас N^2 всегда растёт быстрее, чем N, а значит O(n) мы отбрасываем и остаётся только O(n^2).

Итак, сложность нашего третьего примера — O(n).

Пример 4:

В четвёртом примере добавим на вход уже двумерный массив.

И для его обработки нам теперь нужно два цикла. Оба этих цикла будут зависеть от размерности входных данных data.

Правило 4: вложенные сложности перемножаются.

Сложность внешнего цикла в нашем примере — O(N), сложность внутреннего цикла — O(N) (или O(M), если массив не квадратный). Согласно правилу, две эти сложности должны быть умножены. В результате максимальная сложность всего алгоритма будет равна O(N^2).

Пример 5:

А что мы видим тут? Цикл — уже известная нам сложность O(n), но внутри вызывается функция Alg4() из предыдущего примера:

Если мы вспомним её сложность O(n^2), а также правило 4, то получим, что сложность этого алгоритма — O(n^3) при всей его визуальной минималистичности.

Правило 5: включайте в оценку общей сложности алгоритма оценки всех вложенных вызовов функций.

Именно поэтому важно понимать сложность методов синтаксического сахара вроде LINQ — чтоб была возможность оценить, как метод будет вести себя при увеличении объёмов данных. При использовании их в коде без понимания внутреннего устройства вы рискуете получить очень высокую сложность алгоритма, который будет захлебываться при увеличении входящих данных.

Приведу пример минималистичного алгоритма, который выглядит хорошо и компактно (ни в коем случае не претендует на эталонный код), но станет бомбой замедленного действия при работе с большими объёмами данных:

Что мы тут видим? Цикл = O(n), Where = от O(1) до O(n), в зависимости от типа хранящихся внутри данных, Contains = O(n).

Итого сложность такого алгоритма будет от O(n^2) до O(n^3) по времени выполнения.

ToArray() будет выделять на каждой итерации дополнительную память под копию массива, а значит сложность по памяти составит O(n^2).

Задачка от Google

Возьмём для нашего финального оценивания задачку, которую дают на собеседовании в Google.

Подробный разбор задачи и алгоритмы решения можно посмотреть вот в этом видео от Саши Лукина. Рекомендую посмотреть его перед тем, как продолжить читать эту статью.

Вкратце, цель алгоритма — найти в массиве два любых числа, которые в сумме дали бы нам искомое число target.

Решение 1: полный проход по массиву

Сложность по времени: O(n^2)

Сложность по памяти: O(С)

Это решение в лоб. Не самое оптимальное, поскольку время быстро растёт при увеличении количества элементов, но зато дополнительную память мы особо не потребляем.

Решение 2: используем HashSet

Проходимся по массиву и добавляем элементы, которые мы уже проверили, в HashSet. Если HashSet содержит недостающий для суммы элемент, значит всё хорошо, мы закончили и можем возвращать результат.

Сложность по времени: O(n)

Сложность по памяти: O(n)

Это как раз пример того, как можно выиграть в производительности, выделив дополнительную память для промежуточных структур.

Решение 3: используем бинарный поиск

Алгоритм бинарного поиска имеет известную сложность — O(log(n)). O(n) нам добавилась от внешнего цикла for, а всё, что внутри цикла while — это и есть алгоритм бинарного поиска. Согласно Правилу 4 сложности перемножаются.

Сложность по времени: O(n*log(n))

Сложность по памяти: O(С)

Решение 4: используем метод двух указателей

Двигаем левый и правый указатели к центру, пока они не сойдутся или не найдется пара подходящих нам значений.

Сложность по времени: O(n)

Сложность по памяти: O(С)

И это — самый оптимальный из всех вариантов решения, не использующий дополнительной памяти и совершающий наименьшее количество операций.

Бенчмаркинг решений

Теперь, зная сложности всех четырёх вариантов решения, попробуем провести бенчмаркинг этого кода и посмотреть, как алгоритмы будут вести себя на различных наборах данных.

Результаты будут следующими:

Что же мы тут видим?

За baseline решения мы берём прямой проход массиву FindPairWithFullWalkthrough. На 10 объектах он отрабатывает в среднем за 20 наносекунд и занимает второе место по производительности.

Быстрее на малом объёме данных выполняется только наш самый оптимальный вариант решения — FindPairUsingTwoPointersMethod.

Вариант же с HashSet занял в 8 раз больше времени для работы с малым объёмом данных и потребовал выделения дополнительной памяти, которую потом нужно будет собрать Garbage Collector-у.

На 1 000 же элементов вариант с полным проходом по циклу (FindPairWithFullWalkthrough) начал заметно отставать от остальных алгоритмов. Причиной этому — его сложность O(n^2), которая растёт заметно быстрее всех остальных сложностей.

На 10 000 элементах алгоритму с полным проходом потребовалось и вовсе 9,7 секунды для завершения расчетов, в то время как остальные справлялись за 0.1 секунды и меньше. А самый оптимальный вариант решения и вовсе нашёл решение за 3 миллисекунды.

Заключение

Мы разобрались, как оценивать сложность алгоритмов, а также узнали, как с помощью BenchmarkDotNet проследить связь между сложностью алгоритмов и временем выполнения кода. Это позволит нам ещё до выполнения бенчмаркинга приблизительно оценить — хороший код вы написали или нет.

---

Фото в заголовке: by Joshua Sortino on Unsplash

Автор: Антон Воротынцев

Редактура: Марина Медведева