Деление
с остатком и вычитание
Цели:
дать представление о том, как деление с остатком
можно выполнить с помощью вычитания; учить сравнивать запись на деление с
остатком и запись вычитания одного и того же числа несколько раз; формировать
умение записывать решение задачи с помощью деления с остатком; выполнять
деление с остатком для данных пар чисел с помощью вычитания.
Ход урока
I. Устный счет.
1.
Игра «Угадай-ка!». Вычеркните числа, которые не входят в таблицу умножения.
Если задание выполнено верно, то вы прочитаете загадку. Отгадайте ее.
2.
Запишите буквами свойства арифметических действий:
а) переместительное,
сочетательное и распределительное свойства сложения и умножения;
б)
правило вычитания числа из суммы;
в)
правило вычитания суммы из числа.
3.
Математические ребусы.
4.
Выполните деление с остатком и сделайте проверку.
47 : 5 54
: 7 71 : 9
63 : 8 39
: 6 65 : 7
II. Работа по
учебнику.
Задание 191.
Сравните между собой записи из одного столбика.
41 : 19 = 2 (ост. 3) 56
: 17 = 3 (ост. 5)
41 – 19 – 19 = 3 56
– 17 – 17 – 17 = 5
– Как с помощью вычитания найти
остаток от деления одного числа на другое? Обратите внимание на то, сколько раз
делитель вычитали из делимого. В каждом из рассмотренных случаев сравните это
число с неполным частным.
Задание 192.
Вычислите значения разности.
53 – 7 · 7 = 53 – 49 + 4
– Используя полученное равенство,
запишите результат деления с остатком числа 53 на число 7.
53 : 7 = 7 (ост. 4)
Задание 193.
Представьте разность 69 – 6 в виде произведения двух множителей, один из
которых равен 9. 69 – 6 = 9 · 7
– Используя полученное равенство,
запишите результат деления с остатком числа 69 на число 9 и на число 7.
69 : 9 = 7 (ост. 6) 69
: 7 = 9 (ост. 6)
Задание 194.
Прочитайте задачу. Что известно? Что требуется узнать? Запишите решение задачи
с помощью деления с остатком.
Решение: 150 : 35
= 4 (ост. 10)
Ответ:
получилось 4 полных мешка, 10 кг осталось.
Задание 195. Выполните
деление с остатком для следующих пар чисел с помощью вычитания.
а) 387 : 350 = 1 (ост. 37) б)
927 : 291 = 3 (ост. 48)
387 – 350 · 1 = 37 927
– 293 · 3 = 48
в) 1003 : 250 = 4 (ост. 3)
1003 – 250 · 4 = 3
III. Фронтальная
работа.
–
Выберите рисунок, которому соответствуют все три записи:
3 · 4
+ 2 = 14 14 : 3 = 4 (ост. 2) 14 : 4 = 3 (ост. 2)
Выполните
такие же записи к другим рисункам.
–
Сделайте рисунки, которые соответствуют записям:
10 : 5
= 2 14 : 7 = 2
13 : 5
= 2 (ост. 3) 15 : 7 = 2 (ост. 1)
12 : 4
= 3 12 : 6 = 2
14 : 4
= 3 (ост. 2) 15 : 6 = 2 (ост. 3)
21 : 7
= 3 18 : 3 = 6
25 : 7
= 3 (ост. 4) 20 : 3 = 6 (ост. 2)
IV. Итог урока.
– Как выполнить деление с остатком
с помощью вычитания?
Содержание:
Действие вычитание и компоненты вычитания
Связь вычитания и сложения
Свойства разности
Как вычесть сумму из числа и число из суммы
Изменение разности при изменении вычитаемого и/или уменьшаемого
Правила вычитания разности
Вычитание однозначного числа
Вычитание в столбик многозначных чисел
Проверка действий сложение и вычитание
Пройти тест по теме «Сложение и вычитание натуральных чисел» можно по ссылке. Проверьте свои знания!
Мы можем не только собирать в группы различные предметы, то есть, складывать их, но и забирать из существующей группы определенное их количество.
Например, в кошельке было 1850 рублей. В магазине было потрачено 780 рублей. Чтобы узнать, сколько осталось денег, можно вытащить кошелек и пересчитать их. Но можно поступить по-другому: из той суммы, которая была в кошельке, отнять ту сумму, что была потрачена в магазине. Разница этих чисел, то есть, на сколько единиц изначальная сумма денег больше той суммы, которую потратили, и будет остатком денег.
Разность (или остаток) – это такое число, которое получится, если от одного числа отнять другое, то есть, от всех единиц одного числа отнять все единицы, которые содержатся в другом числе.
Уменьшаемое – это то число, от которого мы отнимаем единицы другого числа.
Вычитаемое – это число, которое мы вычитаем из другого числа. То есть, то число, на количество единиц которого мы уменьшаем другое число.
Вычитание – это арифметическое действие, которое выполняется для получения разности двух или нескольких чисел.
то есть, совершить действие вычитания – это найти такое число, которое получится, если от данного числа отнять определенное количество единиц другого числа.
Компоненты вычитания:
Про действие вычитание также говорят, что нужно из одного числа вычесть другое, или одно число уменьшить на другое.
Совершая вычитание натуральных чисел, вы должны помнить, что из одного натурального числа можно вычесть только равное ему или меньшее натуральное число. Действительно, мы никак не можем отобрать единиц предметов больше, чем их есть в наличии.
Поэтому, уменьшаемое натуральное число всегда больше или равное вычитаемому. Другими словами, мы всегда вычитаем из большего меньшее или из равного равное.
Связь вычитания и сложения
Действие вычитание непосредственно связано с действием сложение.
Действительно, когда мы ищем сумму, мы складываем все единицы, из которых состоят числа, вместе. То есть, получаем число, которое складывается из разных чисел.
А когда мы ищем разность, мы из одного числа (уменьшаемое) отнимаем некоторое количество единиц (вычитаемое), которые входят в его состав, и получаем другое количество единиц. То есть, получаем число (разность), которое также составляло уменьшаемое, пока от него не отняли вычитаемое. Поэтому разность и имеет второе название – остаток – то, что осталось от числа, после вычитания его части.
Из этого мы можем сделать вывод, что, если сложить обратно обе части одного числа (разность и вычитаемое), то мы получим уменьшаемое.
Поэтому, вычитание и сложение – это взаимно обратные действия. Если нам известна сумма двух слагаемых, мы можем превратить ее в разность двух чисел, и наоборот, разность можно перевести в сумму.
Уменьшаемое – это сумма вычитаемого и разности. То есть, разность и вычитаемое – это слагаемые.
Когда мы складываем числа, слагаемые нам известны, и нужно вычислить их сумму. А когда мы вычитаем, нам даются сумма (уменьшаемое) и одно из слагаемых (вычитаемое) этой суммы, а второе слагаемое (разность) нам нужно вычислить.
Рассмотрим это на примере. Мы нашли разность 8-5=3. Это означает, что мы разложили одно данное нам число 8 на два: 5 (данное нам уменьшаемое) и 3 (найденная нами разность). Но мы знаем, что состав числа – это слагаемые, которые в сумме дают нам это самое число. Поэтому, найденную нами разность чисел мы можем превратить в сумму чисел, сложив остаток с вычитаемым: 3+5=8.
Свойства разности натуральных чисел
Свойства разности натуральных чисел состоят из:
- Правила вычитания суммы из числа и числа из суммы;
- Зависимость разности от изменения уменьшаемого или вычитаемого.
- Правило вычитания разности из числа;
Рассмотрим каждый пункт подробнее.
Правила вычитания суммы из числа и числа из суммы
Как вычесть сумму из числа
Чтобы найти разность числа и суммы чисел нужно из данного числа вычесть последовательно каждое слагаемое суммы.
То есть, сначала мы находим разность между данным числом и первым слагаемым, потом от этой полученной разности отнимаем второе слагаемое, третье, и так далее до последнего слагаемого суммы.
Действительно, так как сумма – это объединение всех слагаемых, то очевидно, что, отнимая последовательно каждое слагаемое, каждое ее составляющее число, мы в конце концов отнимем всю сумму.
Рассмотрим это на примере из урока сложение чисел.
325+(12+64+5) = 325+81 = 406
Я запишу это в виде разности:
406-(12+64+5) = 325
и покажу, что результат будет равен первому слагаемому:
406—12 = 394;
394-64 = 330;
330-5 = 325.
Как видите, все верно.
Как вычесть число из суммы
Чтобы найти разность суммы чисел и некоторого числа, нужно отнять это число от какого-нибудь подходящего слагаемого этой суммы.
То есть, мы сначала находим разность одного из слагаемых и данного числа, а потом складываем получившийся результат последовательно с остальными слагаемыми.
Действительно, вы знаете, что, если уменьшить одно из слагаемых на какое-то число, то и сумма уменьшится на это же самое число. Следовательно, если нам нужно сумму чисел уменьшить на какое-то число, то для этого достаточно уменьшить на это число одно из слагаемых суммы.
Для рассмотрения я возьму тот же пример, только сумму расчленю на слагаемые, а слагаемое в скобках заменю суммой:
325+81 = (191+65+150)
Превращаю выражение в разность:
(191+65+150)-81 = 325
и покажу, что результат также будет равен первому слагаемому:
191-81 = 110;
110+65 = 175;
175+150 = 325
или
150-81 = 69;
69+191 = 260;
260+65 = 325.
Я недаром написал в правиле, что нужно отнимать от подходящего слагаемого суммы, потому что, если оно будет меньше вычитаемого, то оно нам не подходит. Так, в нашем примере 65<81.
Отсюда следует, что это правило применимо не к любой сумме натуральных чисел, а только к той, в которой хотя бы одно из слагаемых больше, чем вычитаемое.
Как меняется разность при изменении вычитаемого или уменьшаемого
Изменение разности при изменении вычитаемого и уменьшаемого является следствием описанных в уроке изменений суммы чисел с изменением ее слагаемых.
Если уменьшаемое увеличить на некоторое количество единиц, то и разность увеличится на такое же количество единиц.
Если уменьшаемое уменьшить на некоторое количество единиц, то и разность уменьшится на такое же количество единиц.
Если вычитаемое увеличить на некоторое количество единиц, то разность уменьшится на такое же количество единиц.
Если вычитаемое уменьшить на некоторое количество единиц, то разность увеличится на такое же количество единиц.
Если сразу оба числа, и уменьшаемое, и вычитаемое, увеличить или уменьшить на одно и то же количество единиц, то разность не изменится.
Правила вычитания разности
Если нужно вычесть из числа разность других чисел, можно воспользоваться одним из двух способов:
1. Прибавить к данному числу вычитаемое, и из получившейся суммы вычесть уменьшаемое;
2. Вычесть из данного числа уменьшаемое, а потом результат этого действия сложить с вычитаемым.
Это свойство выводится из предыдущих, рассмотренных нами.
Рассмотрим на примере 22-(17—3).
Для начала вычислим обычным способом: сперва узнаем разность в скобках (это будет 17-3=14), а потом вычтем 14 из 22. Получится 22-14=8.
22-(17—3) = 8
Теперь вернемся к исходному примеру и отнимем от 22 не разность 17-3, то есть, не 17 без 3 единиц, а все число 17.
22—17 = 5
Но мы ведь отняли больше, чем нужно было, поэтому нам нужно вернуть лишне взятые 3 единицы обратно, а именно, прибавить их к полученному результату.
5+3 = 8
Попробуем решить другим путем: увеличим и уменьшаемое (данное число), и вычитаемое (разность в скобках) на одно и то же число 3. Получим:
22+3-(17+3-3)
Так как 22+3=25, а 3-3=0, то в итоге получается:
25-17+0 = 8
Как видите, оба способа показали верный результат.
Вычитание однозначного числа
Вы сможете без каких-либо трудностей совершать вычитание любых чисел, если сперва хорошо натренируете себя вычитать однозначные числа в уме из однозначных и двухзначных.
А поскольку вычитание – это действие обратное сложению, тогда необходимо просто выучить на память все суммы однозначных чисел. Пользуясь ими, мы легко сможем получить необходимые вам разности.
Например, нам нужно найти разность чисел 17 и 8. Для этого нам необходимо вспомнить, какое число при сложении с числом 8 дает сумму 17? Это число 9, потому что 8+9=17. Значит, если от 17 отнять 8, мы получим: 17-8=9.
Хорошо натренировавшись в нахождении разности чисел из суммы однозначных чисел, можно переходить к более сложным случаям вычитания. Подробно эти приемы рассмотрены в разделе рубрики «Устный счет».
Вычитание в столбик многозначных чисел
Так же, как и сложение, разность многозначных чисел удобно находить, используя вычитание в столбик.
Вычитание в столбик – это способ нахождения разности чисел при помощи их записи друг под другом таким образом, чтобы соответствующие разряды разных чисел находились на одной вертикали (один под другим), и последующего вычисления.
Давайте найдем разность чисел 52063-4825.
Запишем их друг под другом таким образом, чтобы совпадали соответствующие разряды обоих чисел, т.е. единицы под единицами, десятки под десятками и т.д. После этого, под вторым слагаемым проводим горизонтальную черту, а между слагаемыми ставим знак действия, т.е. минус. У нас получилась такая запись:

Вычитание в столбик выполняется подобным способом, как и при сложении, только теперь мы отнимаем единицы от единиц, десятки от десятков и так далее.
От 3 единиц в уменьшаемом мы не можем отнять 5 единиц вычитаемого, поскольку 3<5. Поэтому, мы раскладываем соседние 6 десятков на 5 десятков и 1 десяток. Этот десяток содержит 10 единиц, которые мы складываем с 3 имеющимися в уменьшаемом единицами. Теперь у нас есть 13 единиц, и мы можем отнять от них 5, получим 8 единиц. Записываем их под чертой в разряде простых единиц, а над цифрой разряда десятков в уменьшаемом ставим одну точку, чтобы не забыть, что 1 десяток единиц мы оттуда уже забрали.
Переходим к десяткам. У уменьшаемого в разряде десятков мы уже забрали 1 десяток, о чем нам напоминает поставленная точка. Поэтому, мы отнимаем 2 десятка вычитаемого не от 6, а от 5 десятков, потому что 6-1=5.
5>2, значит, действие вычитания возможно: 5-2=3. Пишем цифру 3 под чертой в разряде десятков, и переходим к сотням.
Сотен в уменьшаемом у нас нет, поэтому мы смотрим, сколько в числе содержится тысяч? Их тоже 0. Смотрим следующий разряд. Здесь у нас 5 десятков тысяч. Из них мы берем 1 десяток тысяч (ставим точку над цифрой 5 в уменьшаемом), что составляет 10 тысяч единиц. Из них (из взятых в десятках тысячах) мы занимаем 1 тысячу для того, чтобы закончить вычитание в разряде сотен (ставим точку над цифрой 0 в разряде тысяч уменьшаемого).
1 тысяча единиц – это 10 сотен. Кроме этих занятых, больше в уменьшаемом сотен нет. В вычитаемом 8 сотен, поэтому находим разность сотен уменьшаемого и вычитаемого: 10-8=2. Пишем результат под чертой в разряде сотен.
В разряде тысяч уменьшаемого у нас осталось 9 тысяч единиц (потому что 1 тысячу мы отдали для разряда сотен в качестве 10 сотен). Отнимаем от нее 4 тысячи вычитаемого, получаем: 9-4=5, которые записываем под чертой в разряде тысяч.
Десятков тысяч в уменьшаемом осталось 5-1=4 (помните, мы для разряда сотен занимали?), в вычитаемом их нет совсем, то есть, 0. Поэтому мы просто сносим цифру 4 в результат под черту в разряд десятков тысяч.
После нахождения разности чисел способом вычитания в столбик записываем ответ в строчном примере:
50063-4825 = 45238.
Как проверить действия сложение и вычитание?
После того, как вы закончили арифметическое действие, нужно проверить правильность ответа, то есть, удостовериться, что вычисление было сделано без ошибок.
Проверить сложение можно двумя способами: обратным сложением и вычитанием.
Обратное сложение означает, что мы меняем слагаемые местами, и складываем их еще раз. Если результат будет такой же, как и после первого сложения, значит, вычисление было верным.
Например, в уроке сложение чисел мы находили сумму: 5728+803 = 6531. Проверим правильность результата способом обратного сложения:
Как видите, сложив слагаемые в другом порядке, мы получили тот же самый результат, а значит, вычисление было правильным.
Проверка сложения вычитанием – это способ, при котором нужно из суммы, которую получили после выполнения действия сложение, отнять одно из слагаемых. Если результат этого вычитания будет равен второму слагаемому (или сумме остальных слагаемых, если их больше двух), значит сложение было выполнено верно.
Проверим эту же сумму вычитанием: отнимем от результата 6531 слагаемое 5728.
И этот способ проверки показал правильность нашего решения.
Проверить вычитание также возможно и сложением, и другим вычитанием.
Проверка вычитания сложением основана на взаимосвязи вычитания и сложения. Зная, что уменьшаемое – это сумма, а остаток и вычитаемое – это слагаемые, мы можем сложить между собой вычитаемое и остаток, и, если получим в результате уменьшаемое, значит, мы правильно сделали действие.
Вот так выглядит проверка вычитания сложением на примере вычисленной на этом уроке разницы 50063-4825 = 45238:
Проверка вычитания вычитанием также основывается на взаимосвязи вычитания и сложения, а также на переместительном законе сложения. Так как уменьшаемое – это сумма двух слагаемых: вычитаемого и остатка, и сумма не зависит от порядка сложения слагаемых, то очевидно, что мы можем отнять от уменьшаемого остаток. Если результат этого действия будет равен вычитаемому, значит наша первая разность вычислена верно.
Проверка той же самой разницы вычитанием:
Многие числа нельзя разделить нацело, при делении часто присутствует остаток, отличный от нуля. В этой статье мы разберем способы деления натуральных чисел с остатком и подробно рассмотрим их применение на примерах.
Начнем с деления натуральных чисел с остатком в столбик, затем рассмотрим деление с помощью последовательного вычитания. Наконец, закончим разбором метода подбора неполного частного. Приведем алгоритм деления с остатком для наиболее общего случая и покажем, как проводить проверку результата деления натуральных чисел с остатком.
Деление натуральных чисел столбиком с остатком
Это один из самых удобных способов деления. Подробно он описан в отдельной статье, посвященной делению натуральных чисел столбиком. Здесь мы не будем приводить всю теорию заново, но сконцентрируемся именно на случае деления с остатком.
Приведем решение примера, так как понять суть метода проще всего на практике.
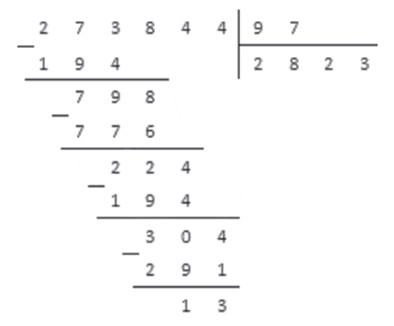
Разделим натуральное число 273844 на натуральное число 97.
Проводим деление столбиком и записываем:
Результат: неполное частное от деления равно 2823, а остаток равен 13.
Деление чисел с остатком через последовательное вычитание
Чтобы найти неполное частное и остаток, можно прибегнуть к последовательному вычитанию делителя из делимого. Этот способ не всегда целесообразен, однако в некоторых случаях его очень удобно применять. Вновь обратимся к примеру.
Пусть у нас есть 7 яблок. Нам нужно эти 7 яблок разложить в пакеты по 3 яблока. Иными словами, 7 разделить на 3.
Возьмем из начального количества яблок 3 штуки и положим в один пакет. У нас останется 7-3=4 яблока. Теперь, из оставшихся яблок снова отнимаем 3 штуки и кладем уже в другой пакет. Остается 4-3=1 яблоко.
1 яблоко – это остаток от деления, так как на этом этапе мы уже не можем сформировать еще один пакет с тремя яблоками и деление, по сути, завершено. Результат деления:
7÷3=2 (остаток 1)
Это значит, что число 3 как бы умещается в числе 7 два раза, а единица – остаток, меньший чем 3.
Рассмотрим еще один пример. На этот раз, приведем только математические выкладки, не прибегая к аналогиям.
Вычислим: 145÷46.
145-46=99.
Число 99 больше, чем 46, поэтому продолжаем последовательное вычитание делителя:
99-46=53.
Повторяем эту операцию еще раз:
53-46=7
В результате, нам понадобилось последовательно вычесть делитель из делимого 3 раза до того, как мы получили остаток – результат вычитания, который меньше делителя. В нашем случае остатком является число 7.
145÷46=3 (остаток 7).
Метод последовательного вычитания непригоден, когда делимое меньше делителя. В таком случае можно сразу записать ответ: неполное частное равно нулю, а остаток равен самому делимому.
Если a<b, то a÷b=0 (остаток a).
Например:
12÷36=0 (остаток 12)47÷88=0 (остаток 47)
Также касательно метода последовательного вычитания нужно отметить, что он удобен только в случаях, когда вся операция деления сводится к небольшому количеству вычитаний. Если делимое во много раз больше делителя, использование этого метода будет нецелесообразно и связано с множеством громоздких вычислений.
Метод подбора неполного частного
При делении натуральных чисел с остатком можно вычислить результат методом подбора неполного частного. Покажем, как можно вести процесс подбора, и на чем он основан.
Во-первых, определим, среди каких чисел нужно искать неполное частное. Из самого определения процесса деления понятно, что неполное частное равно нулю, либо является одним из натуральных чисел 1, 2, 3 и т.д.
Во-вторых, установим связь между делителем, делимым, неполным частным и остатком. Рассмотрим уравнение d=a-b·c. Здесь d – остаток от деления, a – делимое, b – делитель, с – неполное частное.
В-третьих, не будем забывать, что остаток всегда меньше делителя.
Теперь рассмотрим непосредственно процесс подбора. Делимое a и делитель b известны нам с самого начала. В качестве неполного частного с будем последовательно принимать числа из ряда 0, 1, 2, 3 и т.д. Применяя формулу d=a-b·c и вычисляя полученное значение с делителем, закончим процесс, когда остаток d будет меньше, чем делитель b. Число, взятое за с на этом шаге и будет неполным частным.
Разберем применение этого метода на примере.
Разделим 267 на 21.
a=267; b=21. Подберем неполное частное.
Используем формулу d=a-b·c и будем последовательно перебирать c, придавая ему значения 0, 1, 2, 3 и т.д.
Если с=0, имеем: d=a-b·c=267-21·0=267. Число 267 больше, чем 21, поэтому продолжаем подстановку.
При с=1 имеем: d=a-b·c=267-21·1=246. Т.к. 246>21, снова повторяем процесс.
При с=2 имеем: d=a-b·c=267-21·2=267-42=225; 225>21.
При с=3 имеем: d=a-b·c=267-21·3=267-63=204; 204>21.
…
При с=12 имеем: d=a-b·c=267-21·12=267-252=15;15<21.
На этом этапе процесс деления можно считать законченным. Неполное частное с=12, а остаток деления равен 15.
Алгоритм деления натуральных чисел с остатком
Когда рассмотренные выше методы подбора неполного частного и последовательного вычитания требуют слишком громоздких вычислений, для деления с остатком применяется следующий метод. Рассмотрим алгоритм деления натурального числа a на число b с остатком.
Вспомним, что в случае, когда a<b, неполное частное равно нулю, а остаток равен делимомому a. Мы будем рассматривать случай, когда a>b.
Сформулируем три вопроса и ответим на них:
- Что там известно?
- Что нам нужно найти?
- Как мы будем это делать?
Изначально известными являются делимое и делитель: a и b.
Найти нужно неполное частное c и остаток d.
Приведем формулу, которая задает связь между делимым, делителем, неполным частным и остатком. a=b·c+d. Именно это соотношение мы и возьмем за основу алгоритма деления натуральных чисел с остатком. Делимое a нужно представить в виде суммы a=b·c+d, тогда мы найдем искомые величины.
Алгоритм деления, благодаря которому мы представим a в виде суммы a=b·c+d очень схож с алгоритмом деления натуральных чисел без остатка. Приведем ниже шаги алгоритма на примере деления числа 899 на 47.
1. Первым делом смотрим на делимое и делитель. Выясняем и запоминаем, на сколько знаков число в записи делимого больше числа в делителе. В нашем конкретном примере в делимом три знака, а в делителе – два.
3-2=1
Запомним это число.
2. Справа в записи делителя допишем число нулей, определенное разницей между количеством знаков в делимом и делителе. В нашем случае нужно дописать один нуль. Если записанное число больше делимого, то нужно из запомненного в первом пункте числа вычесть единицу.
В нашем примере справа от 47 дописываем нуль. Так как 470<899, запомненное в предыдущем пункте число не нужно уменьшать на единицу. Таким образом, число 1 так и остается у нас в памяти.
3. Справа к цифре 1 приписываем количество нулей, равное числу, определенному в предыдущем пункте. В нашем примере, приписывая к единице один нуль, получаем число 10. В результате данного действия мы получили рабочую единицу разряда, с которым будем работать дальше.
4. Будем последовательно умножать делитель на 1, 2, 3.. и т.д. единицы рабочего разряда, пока не получим число, которое больше или равно делимому.
Рабочий разряд в нашем примере – десятки. После умножения делителя на одну единицу рабочего разряда, получаем 470.
470<899, поэтому умножаем на еще одну единицу рабочего разряда. Получаем: 47·20=940; 940>899.
Число, которое мы получили на предпоследнем шаге (470=47·10) является первым из искомых слагаемых.
5. Найдем разность между делимым и первым найденным слагаемым. Если полученное число больше делителя, то переходим к нахождению второго слагаемого.
Шаги 1-5 повторяем, однако в качестве делимого принимаем полученное здесь число. Если снова получаем число, большее, чем делитель, снова по-кругу повторяем пункты 1-5, но уже с новым числом в качестве делимого. Продолжаем, пока полученное здесь число не будет меньше делителя. Переходим к завершающему этапу. Забегая вперед, скажем, что последнее полученное число и будет равно остатку.
Обратимся к примеру. 899-470=429, 429>47. Повторяем шаги 1-5 алгоритма с числом 429, взятым в качестве делимого.
1. В записи числа 429 на один знак больше, чем в записи числа 47. Запоминаем разницу – число 1.
2. В записи делимого справа дописываем один нуль. Получаем число 470. Так как 470>429, из запомненного в предыдущем пункте числа 1 вычитаем 1 и получаем 1-1=0. Запоминаем 0.
3. Так как в предыдущем пункте мы получили число 0 и запомнили его, нам не нужно прибавлять ни одного нуля к единице справа. Таким образом, рабочим разрядом являются единицы
4. Последовательно умножим делитель 47 на 1, 2, 3 .. и т.д. Не будем приводить подробные выкладки, а обратим внимание на конечный результат: 47·9=423<429, 47·10=470>429. Таким образом, второе искомое слагаемое – 47·9=423.
5. Разность между 429 и 423 равна числу 6. Так как 6<47, это третье, и последнее искомое слагаемое. Перейдем к завершающему этапу алгоритма деления столбиком.
6. Целью предыдущих действий было представление делимого в виде суммы нескольких слагаемых. Для нашего примера мы получили 899=470+423+6. Вспоминаем, что 470=47·10, 423=47·9. Перепишем равенство:
899=47·10+47·9+6
Применим распределительное свойство умножения.
899=47·10+47·9+6=47·(10+9)+6
899=47·19+6.
Таким образом, мы представили делимое в виде уже данной ранее формулы a=b·c+d.
Искомые неизвестные:неполное частное с=19, остаток d=6.
Безусловно, при решении практических примеров нет нужды расписывать все действия так подробно. Покажем это:
Разделим числа 42252 и 68.
Используем алгоритм. Первые пять шагов дают первое слагаемое – число 40800=68·600.
Снова повторяем первые пять шагов алгоритма с числом 1452=42252-40800 и получаем второе слагаемое 1360=68·20
Третий раз проходим шаги аглоритма, но у же с новым числом 92=1452-1360. Третье слагаемое равно 68=68·1. Остаток равен 24=92-68.
В результате получаем:
42252=40800+1360+68+24=68·600+68·20+68·1+24==68·(600+20+1)+24=68·621+24
Неполное частное равно 621, остаток равен 24.
Деление натуральных чисел с остатком. Проверка результата
Деление натуральных чисел с остатком, особенно при больших числах, довольно трудоемкий и громоздкий процесс. Допустить ошибку в вычислениях может каждый. Именно поэтому, проверка результата деления поможет понять, все ли вы сделали правильно. Проверка результата деления натуральных чисел с остатком выполняется в два этапа.
На первом этапе проверяем, не получился ли остаток больше делителя. Если нет, то все хорошо. Иначе, можно сделать вывод, что что-то пошло не так.
Остаток всегда меньше делителя!
На втором этапе проверяется справедливость равенства a=b·c+d. Если равенство после подстановки значений оказывается верным, то и деление было выполнено без ошибок.
Проверим, верно ли, что 506÷28=17 (остаток 30).
Сравниваем остаток и делитель: 30>28.
Значит, деление выполнено неверно.
Школьник разделил 121 на 13 и получил в результате неполное частное 9 с остатком 5. Правильно ли он сделал?
Чтобы узнать это, сначала сравниваем остаток и делитель: 5<13.
Первый пункт проверки пройден, переходим ко второму.
Запишем формулу a=b·c+d. a=121; b=13; c=9; d=5.
Подставляем значения и сравниваем результаты
13·9+5=117+5=122; 121≠122
Значит, в вычисления школьника где-то закралась ошибка.
Студент выполнял лабораторную работу по физике. В ходе выполнения ему понадобилось разделить 5998 на 111. В результате у него получилось число 54 с остатком 4. Все ли правильно посчитано?
Проверим! Остаток 4 меньше, чем делитель 111, поэтому переходим ко второму этапу проверки.
Используем формулу a=b·c+d, где a=5998; b=111; c=54; d=4.
После подстановки, имеем:
5998=111·54+4=5994+4=5998.
Равенство корректно, а значит, и деление выполнено верно.
Деление с остатком
- Как делить с остатком?
- Проверка деления с остатком
Деление с остатком — это деление одного числа на другое, при котором остаток не равен нулю.
Как делить с остатком?
Выполнить деление не всегда возможно, так как бывают случаи, когда одно число не делится на другое. Например, число 11 не делится на 3, так как нет такого натурального числа, при умножении которого на 3 получилось бы 11.
Когда деление невозможно выполнить условились делить не всё делимое, а только наибольшую его часть, какая только может разделиться на делитель. В данном примере наибольшая часть делимого, которая может быть разделена на 3 — это 9 (в результате получим 3), оставшаяся меньшая часть делимого — 2 не разделится на 3.
Говоря о делении 11 на 3, 11 по прежнему называется делимым, 3 — делителем, результат деления — число 3, называют неполным частным, а число 2 — остатком от деления. Само деление в этом случае называют делением с остатком.
Неполное частное — это наибольшее число, которое при умножении на делитель даёт произведение, не превосходящее делимого. Остаток — это разность между делимым и этим произведением. Остаток всегда меньше делителя, иначе его тоже можно было бы поделить на делитель.
Остаток всегда меньше делителя.
Деление с остатком можно записывать так:
27 : 7 = 3 (ост. 6),
где 27 — это делимое, 7 — делитель, 3 — неполное частное, а 6 — остаток.
Если при делении одного натурального числа на другое в остатке получается 0, то говорят, что первое число делится на второе нацело. Например, 4 делится на 2 нацело. Число 5 не делится на 2 нацело. Слово нацело обычно опускают для краткости и говорят: такое-то число делится на другое, например: 4 делится на 2, а 5 не делится на 2.
Пример. Выполнить деление с остатком:
1) 19 : 6;
2) 27 : 5;
3) 60 : 8.
Решение:
1) 19 : 6 = 3 (ост. 1);
2) 27 : 5 = 5 (ост. 2);
3) 60 : 8 = 7 (ост. 4).
Задание. Какие остатки могут получаться при делении на 3? на 6? на 8?
Решение: Так как остаток всегда меньше делителя то:
- при делении на 3 остаток может быть 2 или 1;
- при делении на 6 в остатке может получится 5, 4, 3, 2 или 1;
- при делении на 8 остаток будет равен 7, 6, 5, 4, 3, 2 или 1.
Проверка деления с остатком
Рассмотрим выражение:
15 : 2 = 7 (ост. 1),
где 15 — это делимое, 2 — делитель, 7 — неполное частное, а 1 — остаток.
Чтобы узнать правильно ли было выполнено деление с остатком, можно неполное частное умножить на делитель (или наоборот) и к полученному произведению прибавить остаток. Если в результате получится число, равное делимому, то деление с остатком выполнено верно:
7 · 2 + 1 = 15
или
2 · 7 + 1 = 15.
Онлайн калькулятор определит остаток от деления чисел, поможет проверить себя при решении уроков и примеров на деление. Деление с остатком (деление по модулю) — это арифметическая операция, в результате выполнения которой получается два целых числа: неполное частное и остаток от деления.
Остаток всегда должен быть меньше делителя. Если при делении остаток равен нулю, то это значит, что делимое делиться нацело или без остатка на делитель.
×
Пожалуйста напишите с чем связна такая низкая оценка:
×
Для установки калькулятора на iPhone – просто добавьте страницу
«На главный экран»

Для установки калькулятора на Android – просто добавьте страницу
«На главный экран»