Как найти вычитание в уравнении

Поиск вычитаемого, уменьшаемого и разности для первоклассников

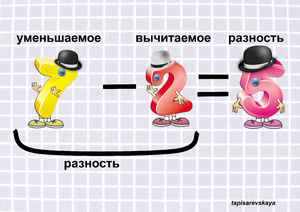Длинная дорога в мир знаний начинается с первых примеров, простых уравнений и задач. В нашей статье мы рассмотрим уравнение вычитания, которое, как известно, состоит из трёх частей: уменьшаемое, вычитаемое, разность.

Теперь рассмотрим правила вычисления каждого из этих компонентов на простых примерах.

Чтобы сделать юным математикам понимание азов науки проще и доступнее, представим эти сложные и пугающие термины именами чисел в уравнении. Ведь у каждого человека есть имя, по которому к нему обращаются, чтобы о чем-то спросить, что-то рассказать, обменяться информацией. Учитель в классе, вызывая ученика к доске, смотрит на него и называет по имени. Так и мы, глядя на числа в уравнении, можем очень легко понять, какое число как зовут. А после уже и обратиться к числу, чтобы правильно решить уравнение или даже найти потерявшееся число, об этом чуть позже.

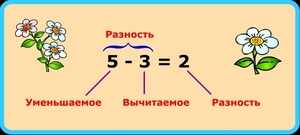
Но, ничего не зная о числах в уравнении, давайте сначала с ними познакомимся. Для этого приведем пример: уравнение 5−3= 2. Первое и самое большое число 5 после того, как мы от него отняли 3, становится меньше, уменьшается. Поэтому в мире математики его так и называют — Уменьшаемое. Второе число 3, которое мы отнимаем от первого, тоже легко узнать и запомнить — оно Вычитаемое. Глядя на третье число 2, мы видим разницу между Уменьшаемым и Вычитаемым — это Разность, то, что мы получили в результате вычитания. Вот так.

Как найти неизвестные

Мы познакомились с тремя братьями:

Но бывают случаи, когда какое-то из чисел теряется или просто неизвестно. Что же делать? Все очень просто — для того, чтобы такое число найти, нам нужно знать только два других значения, а также несколько правил математики, и, конечно, уметь ими пользоваться. Начнём с самой лёгкой ситуации, когда нам нужно найти Разность.

Как найти разность

Представим, что мы купили 7 яблок, подарили 3 яблока своей сестре и оставили какое-то количество себе. Уменьшаемое — это наши 7 яблок, число которых уменьшилось. Вычитаемое — это те 3 подаренных нами яблока. Разность — это количество оставшихся яблок. Что сделать, чтобы узнать это количество? Решить уравнение 7−3= 4. Таким образом, хотя мы и подарили 3 яблока сестре, у нас ещё осталось 4.

Правило поиска уменьшаемого

Теперь узнаем, что делать, если потерялось Уменьшаемое.

• Допустим, мы купили один килограмм яблок. Пришли домой, съели 4 яблока, и у нас в корзине осталось 6. Как узнать, сколько яблок у нас было? Ведь мы покупали килограмм, но точное количество не посчитали. В данном случае Уменьшаемое — это как раз и есть первоначальное количество яблок. Вычитаемое — это то число, которое мы съели, а Разность — оставшиеся. Мы не знаем число яблок, которые у нас были, поэтому поставим вместо него букву Х. У нас получается вот такой пример: X-4=6. Чтобы найти неизвестное Уменьшаемое, надо к Вычитаемому прибавить Разность, вот такое простое правило. То есть сложить 3+6=10. И вот оно, наше Уменьшаемое 10.
• Теперь, чтобы быть уверенными, сделаем небольшую проверку — подставим все на свои места и вычислим разность. Итак, 10 -4= 6. Разность совпадает, а значит мы сделали все верно. У нас было 10 яблок, мы съели 4, осталось 6.

Как найти вычитаемое

Рассмотрим, что делать, если потерялось Вычитаемое. Представим, что мы купили 7 яблок, принесли домой и ушли гулять, а когда вернулись — осталось всего 4. Вычитаемым в этом случае будет то количество яблок, которое кто-то съел в наше отсутствие. Давайте обозначим это число в виде буквы Y. Получится уравнение 7-Y=4. Чтобы найти неизвестное вычитаемое, надо знать простое правило и сделать следующее — из Уменьшаемого отнять Разность, то есть 7 -4= 3. Наше неизвестное значение отыскалось, это 3. Ура! Теперь мы знаем, сколько было съедено.

На всякий случай можно проверить наши успехи и подставить отыскавшееся Вычитаемое в исходный пример. 7−3= 4. Разность не изменилась, а значит мы сделали все правильно. Было 7 яблок, съели 3, осталось 4.

Правила очень простые, но, чтобы быть уверенными и ничего не забыть, можно поступить так — самому для себя придумать лёгкий и понятный пример на вычитание и, решая другие примеры, отыскивать неизвестные значения, просто подставляя цифры и легко находить правильный ответ. Например, 5−3= 2. Мы уже знаем, как найти и Уменьшаемое 5, и Вычитаемое 3, поэтому решая более сложное уравнение, скажем, 25-Х= 13, мы можем вспомнить наш простой пример и понять, что, чтобы найти неизвестное Вычитаемое, нужно лишь отнять от 25 число 13, то есть 25 -13= 12.

Ну вот, теперь мы познакомились с вычитанием, его главными участниками.

Мы умеем отличать их друг от друга, находить, если они неизвестны и решать любые уравнения с их участием. Пусть эти знания помогут и пригодятся вам в начале интересного и увлекательного пути в страну Математики. Удачи!

Нахождение неизвестного слагаемого, множителя: правила, примеры, решения

Чтобы научиться быстро и успешно решать уравнения, нужно начать с самых простых правил и примеров. В первую очередь надо научиться решать уравнения, слева у которых стоит разность, сумма, частное или произведение некоторых чисел с одним неизвестным, а справа другое число. Иными словами, в этих уравнениях есть одно неизвестное слагаемое и либо уменьшаемое с вычитаемым, либо делимое с делителем и т.д. Именно об уравнениях такого типа мы с вами поговорим.

Эта статья посвящена основным правилам, позволяющим найти множители, неизвестные слагаемые и др. Все теоретические положения будем сразу пояснять на конкретных примерах.

Нахождение неизвестного слагаемого

Допустим, у нас есть некоторое количество шариков в двух вазах, например, 9 . Мы знаем, что во второй вазе 4 шарика. Как найти количество во второй? Запишем эту задачу в математическом виде, обозначив число, которое нужно найти, как x. Согласно первоначальному условию, это число вместе с 4 образуют 9 , значит, можно записать уравнение 4 + x = 9 . Слева у нас получилась сумма с одним неизвестным слагаемым, справа – значение этой суммы. Как найти x ? Для этого надо использовать правило:

Для нахождения неизвестного слагаемого надо вычесть известное из суммы.

В данном случае мы придаем вычитанию смысл, который является обратным смыслу сложения. Иначе говоря, есть определенная связь между действиями сложения и вычитания, которую можно в буквенном виде выразить так: если a + b = c , то c − a = b и c − b = a , и наоборот, из выражений c − a = b и c − b = a можно вывести, что a + b = c .

Зная это правило, мы можем найти одно неизвестное слагаемое, используя известное и сумму. Какое именно слагаемое мы знаем, первое или второе, в данном случае неважно. Посмотрим, как применить данное правило на практике.

Возьмем то уравнение, что у нас получилось выше: 4 + x = 9 . Согласно правилу, нам нужно вычесть из известной суммы, равной 9 , известное слагаемое, равное 4 . Вычтем одно натуральное число из другого: 9 – 4 = 5 . Мы получили нужное нам слагаемое, равное 5 .

Обычно решения подобных уравнений записывают следующим образом:

1. Первым пишется исходное уравнение.
2. Далее мы записываем уравнение, которое получилось после того, как мы применили правило вычисления неизвестного слагаемого.
3. После этого пишем уравнение, которое получилось после всех действий с числами.

Такая форма записи нужна для того, чтобы проиллюстрировать последовательную замену исходного уравнения равносильными и отобразить процесс нахождения корня. Решение нашего простого уравнения, приведенного выше, правильно будет записать так:

4 + x = 9 , x = 9 − 4 , x = 5 .

Мы можем проверить правильность полученного ответа. Подставим то, что у нас получилось, в исходное уравнение и посмотрим, выйдет ли из него верное числовое равенство. Подставим 5 в 4 + x = 9 и получим: 4 + 5 = 9 . Равенство 9 = 9 верное, значит, неизвестное слагаемое было найдено правильно. Если бы равенство оказалось неверным, то нам следовало бы вернуться к решению и перепроверить его, поскольку это знак допущенной ошибки. Как правило, чаще всего это бывает вычислительная ошибка или применение неверного правила.

Нахождение неизвестного вычитаемого или уменьшаемого

Как мы уже упоминали в первом пункте, между процессами сложения и вычитания существует определенная связь. С ее помощью можно сформулировать правило, которое поможет найти неизвестное уменьшаемое, когда мы знаем разность и вычитаемое, или же неизвестное вычитаемое через уменьшаемое или разность. Запишем эти два правила по очереди и покажем, как применять их при решении задач.

Для нахождения неизвестного уменьшаемого надо прибавить вычитаемое к разности.

Например, у нас есть уравнение x – 6 = 10 . Неизвестно уменьшаемое. Согласно правилу, нам надо прибавить к разности 10 вычитаемое 6 , получим 16 . То есть исходное уменьшаемое равно шестнадцати. Запишем все решение целиком:

x − 6 = 10 , x = 10 + 6 , x = 16 .

Проверим получившийся результат, добавив получившееся число в исходное уравнение: 16 – 6 = 10 . Равенство 16 – 16 будет верным, значит, мы все подсчитали правильно.

Переходим к следующему правилу.

Для нахождения неизвестного вычитаемого надо вычесть разность из уменьшаемого.

Воспользуемся правилом для решения уравнения 10 – x = 8 . Мы не знаем вычитаемого, поэтому нам надо из 10 вычесть разность, т.е. 10 – 8 = 2 . Значит, искомое вычитаемое равно двум. Вот вся запись решения:

10 – x = 8 , x = 10 – 8 , x = 2 .

Сделаем проверку на правильность, подставив двойку в исходное уравнение. Получим верное равенство 10 – 2 = 8 и убедимся, что найденное нами значение будет правильным.

Перед тем, как перейти к другим правилам, отметим, что существует правило переноса любых слагаемых из одной части уравнения в другую с заменой знака на противоположный. Все приведенные выше правила ему полностью соответствуют.

Нахождение неизвестного множителя

Посмотрим на два уравнения: x · 2 = 20 и 3 · x = 12 . В обоих нам известно значение произведения и один из множителей, необходимо найти второй. Для этого нам надо воспользоваться другим правилом.

Для нахождения неизвестного множителя нужно выполнить деление произведения на известный множитель.

Данное правило базируется на смысле, который является обратным смыслу умножения. Между умножением и делением есть следующая связь: a · b = c при a и b , не равных 0 , c : a = b , c : b = c и наоборот.

Вычислим неизвестный множитель в первом уравнении, разделив известное частное 20 на известный множитель 2 . Проводим деление натуральных чисел и получаем 10 . Запишем последовательность равенств:

x · 2 = 20 x = 20 : 2 x = 10 .

Подставляем десятку в исходное равенство и получаем, что 2 · 10 = 20 . Значение неизвестного множителя было выполнено правильно.

Уточним, что в случае, если один из множителей нулевой, данное правило применять нельзя. Так, уравнение x · 0 = 11 с его помощью решить мы не можем. Эта запись не имеет смысла, поскольку для решения надо разделить 11 на 0 , а деление на нуль не определено. Подробнее о подобных случаях мы рассказали в статье, посвященной линейным уравнениям.

Когда мы применяем это правило, мы, по сути, делим обе части уравнения на другой множитель, отличный от 0 . Существует отдельное правило, согласно которому можно проводить такое деление, и оно не повлияет на корни уравнения, и то, о чем мы писали в этом пункте, с ним полностью согласовано.

Нахождение неизвестного делимого или делителя

Еще один случай, который нам нужно рассмотреть, – это нахождение неизвестного делимого, если мы знаем делитель и частное, а также нахождение делителя при известном частном и делимом. Сформулировать это правило мы можем с помощью уже упомянутой здесь связи между умножением и делением.

Для нахождения неизвестного делимого нужно умножить делитель на частное.

Посмотрим, как применяется данное правило.

Решим с его помощью уравнение x : 3 = 5 . Перемножаем между собой известное частное и известный делитель и получаем 15 , которое и будет нужным нам делимым.

Вот краткая запись всего решения:

x : 3 = 5 , x = 3 · 5 , x = 15 .

Проверка показывает, что мы все подсчитали верно, ведь при делении 15 на 3 действительно получается 5 . Верное числовое равенство – свидетельство правильного решения.

Указанное правило можно интерпретировать как умножение правой и левой части уравнения на одинаковое отличное от 0 число. Это преобразование никак не влияет на корни уравнения.

Переходим к следующему правилу.

Для нахождения неизвестного делителя нужно разделить делимое на частное.

Возьмем простой пример – уравнение 21 : x = 3 . Для его решения разделим известное делимое 21 на частное 3 и получим 7 . Это и будет искомый делитель. Теперь оформляем решение правильно:

21 : x = 3 , x = 21 : 3 , x = 7 .

Удостоверимся в верности результата, подставив семерку в исходное уравнение. 21 : 7 = 3 , так что корень уравнения был вычислен верно.

Важно отметить, что это правило применимо только для случаев, когда частное не равно нулю, ведь в противном случае нам опять же придется делить на 0 . Если же частным будет нуль, возможны два варианта. Если делимое также равно нулю и уравнение выглядит как 0 : x = 0 , то значение переменной будет любым, то есть данное уравнение имеет бесконечное число корней. А вот уравнение с частным, равным 0 , с делимым, отличным от 0 , решений иметь не будет, поскольку таких значений делителя не существует. Примером может быть уравнение 5 : x = 0 , которое не имеет ни одного корня.

Последовательное применение правил

Зачастую на практике встречаются более сложные задачи, в которых правила нахождения слагаемых, уменьшаемых, вычитаемых, множителей, делимых и частных нужно применять последовательно. Приведем пример.

У нас есть уравнение вида 3 · x + 1 = 7 . Вычисляем неизвестное слагаемое 3 · x , отняв от 7 единицу. Получим в итоге 3 · x = 7 − 1 , потом 3 · x = 6 . Это уравнение решить очень просто: делим 6 на 3 и получаем корень исходного уравнения.

Вот краткая запись решения еще одного уравнения ( 2 · x − 7 ) : 3 − 5 = 2 :

( 2 · x − 7 ) : 3 − 5 = 2 , ( 2 · x − 7 ) : 3 = 2 + 5 , ( 2 · x − 7 ) : 3 = 7 , 2 · x − 7 = 7 · 3 , 2 · x − 7 = 21 , 2 · x = 21 + 7 , 2 · x = 28 , x = 28 : 2 , x = 14 .

Нахождение неизвестного слагаемого, множителя, и т.п., правила, примеры, решения

Долгий путь наработки навыков решения уравнений начинается с решения самых первых и относительно простых уравнений. Под такими уравнениями мы подразумеваем уравнения, в левой части которых находится сумма, разность, произведение или частное двух чисел, одно из которых неизвестно, а в правой части стоит число. То есть, эти уравнения содержат неизвестное слагаемое, уменьшаемое, вычитаемое, множитель, делимое или делитель. О решении таких уравнений и пойдет речь в этой статье.

Здесь мы приведем правила, позволяющие находить неизвестное слагаемое, множитель и т.п. Причем будем сразу рассматривать применение этих правил на практике, решая характерные уравнения.

Навигация по странице.

Чтобы найти неизвестное слагаемое, надо…

Женя с Колей решили покушать яблок, для чего начали их сшибать с яблони. Женя добыл 3 яблока, а в конце процесса у мальчиков оказалось 8 яблок. Сколько яблок сшиб Коля?

Для перевода этой типично задачи на математический язык, обозначим неизвестное число яблок, которые сшиб Коля, через x . Тогда по условию 3 Жениных яблока и x Колиных вместе составляют 8 яблок. Последней фразе соответствует уравнение вида 3+x=8 . В левой части этого уравнения находится сумма, содержащая неизвестное слагаемое, в правой части стоит значение этой суммы – число 8 . Так как же найти интересующее нас неизвестное слагаемое x ?

Для этого существует следующее правило: чтобы найти неизвестное слагаемое, надо из суммы вычесть известное слагаемое.

Это правило объясняется тем, что вычитанию придается смысл, обратный смыслу сложения. Иными словами, между сложением и вычитанием чисел существует связь, которая выражается в следующем: из того, что a+b=c следует, что c−a=b и c−b=a , и наоборот, из c−a=b , как и из c−b=a следует, что a+b=c .

Озвученное правило позволяет по одному известному слагаемому и известной сумме определить другое неизвестное слагаемое. При этом не имеет значения, какое из слагаемых неизвестно, первое или второе. Рассмотрим его применение на примере.

Вернемся к нашему уравнению 3+x=8 . Согласно правилу, нам надо из известной суммы 8 вычесть известное слагаемое 3 . То есть, выполняем вычитание натуральных чисел: 8−3=5 , так мы нашли нужное нам неизвестное слагаемое, оно равно 5 .

Принята следующая форма записи решения подобных уравнений:

• сначала записывают исходное уравнение,
• ниже – уравнение, получающееся после применения правила нахождения неизвестного слагаемого,
• наконец, еще ниже, записывают уравнение, полученное после выполнения действий с числами.

Смысл такой формы записи заключается в том, что исходное уравнение последовательно заменяется равносильными уравнениями, из которых в итоге становится очевиден корень исходного уравнения. Подробно об этом говорят на уроках алгебры в 7 классе, а пока оформим решение нашего уравнения уровня 3 класса:
3+x=8 ,
x=8−3 ,
x=5 .

Чтобы убедиться в правильности полученного ответа, желательно сделать проверку. Для этого полученный корень уравнения надо подставить в исходное уравнение и посмотреть, дает ли это верное числовое равенство.

Итак, подставляем в исходное уравнение 3+x=8 вместо x число 5 , получаем 3+5=8 – это равенство верное, следовательно, мы правильно нашли неизвестное слагаемое. Если бы при проверке мы получили неверное числовое равенство, то это указало бы нам на то, что мы неверно решили уравнение. Основными причинами этого могут быть либо применение не того правила, которое нужно, либо вычислительные ошибки.

Как найти неизвестное уменьшаемое, вычитаемое?

Связь между сложением и вычитанием чисел, про которую мы уже упоминали в предыдущем пункте, позволяет получить правило нахождения неизвестного уменьшаемого через известное вычитаемое и разность, а также правило нахождения неизвестного вычитаемого через известное уменьшаемое и разность. Будем формулировать их по очереди, и сразу приводить решение соответствующих уравнений.

Чтобы найти неизвестное уменьшаемое, надо к разности прибавить вычитаемое.

Для примера рассмотрим уравнение x−2=5 . Оно содержит неизвестное уменьшаемое. Приведенное правило нам указывает, что для его отыскания мы должны к известной разности 5 прибавить известное вычитаемое 2 , имеем 5+2=7 . Таким образом, искомое уменьшаемое равно семи.

Если опустить пояснения, то решение записывается так:
x−2=5 ,
x=5+2 ,
x=7 .

Для самоконтроля выполним проверку. Подставляем в исходное уравнение найденное уменьшаемое, при этом получаем числовое равенство 7−2=5 . Оно верное, поэтому, можно быть уверенным, что мы верно определили значение неизвестного уменьшаемого.

Можно переходить к нахождению неизвестного вычитаемого. Оно находится с помощью сложения по следующему правилу: чтобы найти неизвестное вычитаемое, надо из уменьшаемого вычесть разность.

Решим уравнение вида 9−x=4 с помощью записанного правила. В этом уравнении неизвестным является вычитаемое. Чтобы его найти, нам надо от известного уменьшаемого 9 отнять известную разность 4 , имеем 9−4=5 . Таким образом, искомое вычитаемое равно пяти.

Приведем краткий вариант решения этого уравнения:
9−x=4 ,
x=9−4 ,
x=5 .

Остается лишь проверить правильность найденного вычитаемого. Сделаем проверку, для чего подставим в исходное уравнение вместо x найденное значение 5 , при этом получаем числовое равенство 9−5=4 . Оно верное, поэтому найденное нами значение вычитаемого правильное.

И прежде чем переходить к следующему правилу заметим, что в 6 классе рассматривается правило решения уравнений, которое позволяет выполнять перенос любого слагаемого из одной части уравнения в другую с противоположным знаком. Так вот все рассмотренные выше правила нахождения неизвестного слагаемого, уменьшаемого и вычитаемого с ним полностью согласованы.

Чтобы найти неизвестный множитель, надо…

Давайте взглянем на уравнения x·3=12 и 2·y=6 . В них неизвестное число является множителем в левой части, а произведение и второй множитель известны. Для нахождения неизвестного множителя можно использовать такое правило: чтобы найти неизвестный множитель, надо произведение разделить на известный множитель.

В основе этого правила лежит то, что делению чисел мы придали смысл, обратный смыслу умножения. То есть, между умножением и делением существует связь: из равенства a·b=c , в котором a≠0 и b≠0 следует, что c:a=b и c:b=c , и обратно.

Для примера найдем неизвестный множитель уравнения x·3=12 . Согласно правилу нам надо разделить известное произведение 12 на известный множитель 3 . Проведем деление натуральных чисел: 12:3=4 . Таким образом, неизвестный множитель равен 4 .

Кратко решение уравнения записывается в виде последовательности равенств:
x·3=12 ,
x=12:3 ,
x=4 .

Желательно еще сделать проверку результата: подставляем в исходное уравнение вместо буквы найденное значение, получаем 4·3=12 – верное числовое равенство, поэтому мы верно нашли значение неизвестного множителя.

Отдельно нужно обратить внимание на то, что озвученное правило нельзя применять для нахождения неизвестного множителя, когда другой множитель равен нулю. Например, это правило не подходит для решения уравнения x·0=11 . Действительно, если в этом случае придерживаться правила, то чтобы найти неизвестный множитель нам надо выполнить деление произведения 11 на другой множитель, равный нулю, а на нуль делить нельзя. Эти случаи мы подробно обсудим при разговоре о линейных уравнениях.

И еще один момент: действуя по изученному правилу, мы фактически выполняем деление обеих частей уравнения на отличный от нуля известный множитель. В 6 классе будет сказано, что обе части уравнения можно умножать и делить на одно и то же отличное от нуля число, это не влияет на корни уравнения.

Как найти неизвестное делимое, делитель?

В рамках нашей темы осталось разобраться, как найти неизвестное делимое при известном делителе и частном, а также как найти неизвестный делитель при известном делимом и частном. Ответить на эти вопросы позволяет уже упомянутая в предыдущем пункте связь между умножением и делением.

Чтобы найти неизвестное делимое, надо частное умножить на делитель.

Рассмотрим его применение на примере. Решим уравнение x:5=9 . Чтобы найти неизвестное делимое этого уравнения надо согласно правилу умножить известное частное 9 на известный делитель 5 , то есть, выполняем умножение натуральных чисел: 9·5=45 . Таким образом, искомое делимое равно 45 .

Покажем краткую запись решения:
x:5=9 ,
x=9·5 ,
x=45 .

Проверка подтверждает, что значение неизвестного делимого найдено верно. Действительно, при подстановке в исходное уравнение вместо переменной x числа 45 оно обращается в верное числовое равенство 45:5=9 .

Заметим, что разобранное правило можно трактовать как умножение обеих частей уравнения на известный делитель. Такое преобразование не влияет на корни уравнения.

Переходим к правилу нахождения неизвестного делителя: чтобы найти неизвестный делитель, надо делимое разделить на частное.

Рассмотрим пример. Найдем неизвестный делитель из уравнения 18:x=3 . Для этого нам нужно известное делимое 18 разделить на известное частное 3 , имеем 18:3=6 . Таким образом, искомый делитель равен шести.

Решение можно оформить и так:
18:x=3 ,
x=18:3 ,
x=6 .

Проверим этот результат для надежности: 18:6=3 – верное числовое равенство, следовательно, корень уравнения найден верно.

Понятно, что данное правило можно применять только тогда, когда частное отлично от нуля, чтобы не столкнуться с делением на нуль. Когда частное равно нулю, то возможны два случая. Если при этом делимое равно нулю, то есть, уравнение имеет вид 0:x=0 , то этому уравнению удовлетворяет любое отличное от нуля значение делителя. Иными словами, корнями такого уравнения являются любые числа, не равные нулю. Если же при равном нулю частном делимое отлично от нуля, то ни при каких значениях делителя исходное уравнение не обращается в верное числовое равенство, то есть, уравнение не имеет корней. Для иллюстрации приведем уравнение 5:x=0 , оно не имеет решений.

Совместное использование правил

Последовательное применение правил нахождения неизвестного слагаемого, уменьшаемого, вычитаемого, множителя, делимого и делителя позволяет решать и уравнения с единственной переменной более сложного вида. Разберемся с этим на примере.

Рассмотрим уравнение 3·x+1=7 . Сначала мы можем найти неизвестное слагаемое 3·x , для этого надо от суммы 7 отнять известное слагаемое 1 , получаем 3·x=7−1 и дальше 3·x=6 . Теперь осталось найти неизвестный множитель, разделив произведение 6 на известный множитель 3 , имеем x=6:3 , откуда x=2 . Так найден корень исходного уравнения.

Для закрепления материала приведем краткое решение еще одного уравнения (2·x−7):3−5=2 .
(2·x−7):3−5=2 ,
(2·x−7):3=2+5 ,
(2·x−7):3=7 ,
2·x−7=7·3 ,
2·x−7=21 ,
2·x=21+7 ,
2·x=28 ,
x=28:2 ,
x=14 .

[spoiler title=”источники:”]

http://zaochnik.com/spravochnik/matematika/systems/nahozhdenie-neizvestnogo-slagaemogo-mnozhitelja/

http://www.cleverstudents.ru/equations/finding_of_unknown_addend_minuend_factor.html

[/spoiler]

Математика, 3 класс

Урок № 3.Решение уравнений с неизвестным уменьшаемым.

Решение уравнений с неизвестным вычитаемым

Перечень вопросов, рассматриваемых в теме:

– Что такое уравнение?

– Как найти неизвестное уменьшаемое?

– Как найти неизвестное вычитаемое?

Глоссарий по теме:

Уравнение – равенство с неизвестным.

Уменьшаемое – компонент вычитания. Число, из которого производят вычитание.

Вычитаемое – компонент вычитания. Число, с помощью которого вычитают.

Разность – результат вычитания.

Основная и дополнительная литература по теме урока:

1. Моро М. И., Бантова М. А. и др. Математика 3 класс. Учебник для общеобразовательных организаций М.; Просвещение, 2017. – с. 8-9.
2. Моро М. И., Волкова С. И. Математика. Рабочая тетрадь 3 класс. Часть 1. М.; Просвещение, 2016. – с. 7.
3. М. И. Моро, С. И. Волкова. Для тех, кто любит математику 3 класс. Учебное пособие для общеобразовательных организаций. М.; Просвещение, 2018. – с. 4-6.

Теоретический материал для самостоятельного изучения

Рассмотрим группы уравнений. Чем они отличаются?

В первой группе записана сумма чисел. Неизвестный компонент в уравнениях – слагаемое.

Вспомним: чтобы найти неизвестное слагаемое, надо из суммы вычесть известное слагаемое. В первом уравнение х = 29; во втором – х = 23.

Во второй группе уравнений записана разность чисел. Компоненты вычитания: уменьшаемое, вычитаемое. Результат вычитания – разность. Неизвестным в уравнениях может быть уменьшаемое или вычитаемое.

Рассмотрим рисунок и составим равенства

8 – 6 = 2 2 + 6 = 8 8 – 2 = 6

Вывод: если к разности прибавить вычитаемое, то получим уменьшаемое.

Это правило позволит решать уравнения, в которых неизвестное число – уменьшаемое.

Вывод: если из уменьшаемого вычесть разность, то получим вычитаемое.

Это правило позволит решать уравнения, в которых неизвестное число – вычитаемое.

При решении любого уравнения обязательно пользуемся алгоритмом решения уравнения.

Алгоритм:

1. Прочитать уравнение и определить компоненты действий;
2. Определить неизвестный компонент;
3. Вспомнить правило для его нахождения;
4. Применить это правило;
5. Выполнить вычисления;
6. Записать ответ;
7. Выполнить проверку правильности решения.

Применим знания в решении уравнений.

Х – 36 = 40

В уравнение неизвестно уменьшаемое. Вспоминаем правило: чтобы найти уменьшаемое, нужно к разности прибавить вычитаемое. Применяем правило и вычисляем.

Х = 40 + 36

Х = 76

Необходимо выполнить проверку.

76 – 36 = 40

Производим вычисления в левой части равенства.

40 = 40

Уравнение решено верно.

Решим следующее уравнение.

82 – х = 5

В уравнение неизвестно вычитаемое. Вспоминаем правило для его нахождения: чтобы найти неизвестное вычитаемое, надо из уменьшаемого вычесть разность.

Применяем правило и производим вычисление.

Х = 82 – 5

Х = 77

Выполняем проверку.

82 – 77 = 5

5 = 5

Выполним тренировочные задания.

1. Выберите значения х, которые получатся при решении уравнения:

Х – 28 = 40

Х = 16;

Х = 68;

Х = 12.

Правильный ответ:

Х = 68.

2. Образуйте пары: компоненты вычитания – их названия. Соедините линиями.

Правильный ответ:

• Мне нравится 

 
 

Инфоурок

›

Математика

›Другие методич. материалы›Памятка “Нахождение неизвестных компонентов сложения и вычитания в уравнениях”

Памятка “Нахождение неизвестных компонентов сложения и вычитания в уравнениях”

В уравнениях неизвестное обычно обозначается строчной латинской буквой. Чаще всего используют буквы
«x» [икс] и «y» [игрек].

• Корень уравнения — это значение буквы, при котором из уравнения получается верное числовое равенство.
• Решить уравнение — значит найти все его корни или убедиться, что корней нет.

Информация для родителей

Уважаемые родители, обращаем ваше внимание на то, что в начальной школе и в 5 классе дети НЕ знают тему
«Отрицательные числа».

Поэтому они должны решать уравнения, используя только
свойства сложения, вычитания, умножения и деления. Методы решения уравнений для 5 класса приведены ниже.

Не пытайтесь объяснить решение уравнений через перенос чисел и букв
из одной части уравнения в другую с изменением знака.

Освежить знания по понятиям, связанным со сложением, вычитанием, умножением и делением вы можете в уроке
«Законы арифметики».

Решение уравнений на сложение и вычитание

Как найти неизвестное слагаемое x + 9 = 15	Как найти неизвестное уменьшаемое x − 14 = 2	Как найти неизвестное вычитаемое 5 − x = 3
Чтобы найти неизвестное слагаемое, надо от суммы отнять известное слагаемое.	Чтобы найти неизвестное уменьшаемое, надо к разности прибавить вычитаемое.	Чтобы найти неизвестное вычитаемое, надо от уменьшаемого отнять разность.
x + 9 = 15 x = 15 − 9 x = 6 Проверка 6 + 9 = 15 15 = 15	x − 14 = 2 x = 14 + 2 x = 16 Проверка 16 − 2 = 14 14 = 14	5 − x = 3 x = 5 − 3 x = 2 Проверка 5 − 2 = 3 3 = 3

Решение уравнений на умножение и деление

Как найти неизвестный множитель y · 4 = 12	Как найти неизвестное делимое y : 7 = 2	Как найти неизвестный делитель 8 : y = 4
Чтобы найти неизвестный множитель, надо произведение разделить на известный множитель.	Чтобы найти неизвестное делимое, надо частное умножить на делитель.	Чтобы найти неизвестный делитель, надо делимое разделить на частное.
y · 4 = 12 y = 12 : 4 y = 3 Проверка 3 · 4 = 12 12 = 12	y : 7 = 2 y = 2 · 7 y = 14 Проверка 14 : 7 = 2 2 = 2	8 : y = 4 y = 8 : 4 y = 2 Проверка 8 : 2 = 4 4 = 4

---

Ваши комментарии

Оставить комментарий:

---