Как найти кол-во теплоты, выделяемое при неупругом столкновении двух тел? Известны обе массы и обе скорости
Наталия Дмитриева
Ученик
(98),
закрыт
8 лет назад
ВиталийГорностаев
Мастер
(2365)
10 лет назад
Обозначим скорости тел до столкновения V1 V2
Общая скорость после столкновения U
Закон сохранения импульса m1*V1+m2*V2=U*(m1+m2)
Отсюда U=(m1*V1+m2*V2)/(m1+m2)
Кинетическая энергия до столкновения Ek1=m1*(V1)^2+m2*(V2)^2
Кинетическая энергия после столкновения Ek2=(m1+m2)*(U)^2
Количество теплоты Q=Ek2-Ek1
2014-05-31 ![]()
Какое количество тепла выделится при лобовом ударе двух свинцовых шаров массой m = 1 кг каждый, скользящих без вращении на абсолютно гладкой горизонтальной поверхности по одной прямой в одном направлении? Скорость первого шара $v_{1}=10 см/с$, скорость второго $v_{2} = 20 см/с$. Удар шаров считать абсолютно неупругим
Решение:
Так как удар абсолютно неупругий, то после удара оба шара будут двигаться с одинаковой скоростью $v$. Согласно закону сохранения импульса
$mv_{1}+mv_{2}=2mu$.
Отсюда
$v=frac{v_{1}+v_{2}}{2}$.
До столкновения шары обладали кинетической энергией
$W_{1}=frac{mv_{1}^{2}}{2}+frac{mv_{2}^{2}}{2}$.
После удара их кинетическая энергия равна
$W_{2}=2 frac{mv^{2}}{2}= frac{m(v_{1}+v_{2})^{2}}{4}$.
В результате удара кинетическая энергия системы уменьшается на величину
$Delta = W_{1} – W_{2}=frac{m}{4}(v_{1}-v_{2})^{2} = 0,0025 Дж$.
Эта энергия и переходит в тепло.
Задача решена у другого автора не верно..
И это сразу видно.
Действительно, по условию задачи первый шарик, брошенный под углом находится в точке столкновения в максимальной точке подъёма, а это значит, что вертикальная составляющая скорости v cos a=0
другой же шарик по условию задачи имеет нулевую горизонтальную составляющую, скорости, поскольку брошен вертикально..
Значит в точке столкновения первый шарик имеет только горизонтальную скорость v sin A (неизменную во время всего полёта шарика, если не учитывать горизонтальную силу типа ветра), а другой – только вертикальную, которую можно легко найти из условий:
v cos A – gt = 0 (равнозамедленное движение вертикальной составляющей первого шарика, при этом в верхней точке вертикальная составляющая будет нулевой, что показано справа)
v – gt = v1 (скорость второго шарика в момент столкновения, также описываемая уравнением равнозамеделенного движения)
из первого уравнения находим t и подставляем во второе уравнение..
v – g (v cos A/g) = v1
откуда:
v(1-cos A)=v1
Теперь складываем вертикальную и горизонтальные составляющие скорости векторно:
sqrt((v sin A)^2+(v(1-cos A)^2)
или:
v sqrt((sin A)^2+(1-cos A)^2)
Далее раскрываем равенство и учитывая тригонометрическое выражение:
cos^2+sin^2=1
получим:
V sum=sqrt(2)v sqrt(1-cosA)
Теперь согласно закону сохранения энергии, с учётом того, что удар абсолютно неупругий кинетическая энергия обоих шариков переходит в тепло:
E = 2(m (V sum)^2)/2
E= 2 m v (1- cos A)
Откуда:
E= 2 0,1 10 (1- 0,5) = 1 Дж..
Примером применения
законов сохранения импульса и энергии
при решении реальной физической
задачи является удар абсолютно упругих
и неупругих тел.
Удар
(или соударение)
—
это столкновение двух или более тел,
при котором взаимодействие длится очень
короткое время. Исходя из данного
определения, кроме явлений, которые
можно отнести к ударам в прямом смысле
этого слова
28
(столкновения
атомов или биллиардных шаров), сюда
можно отнести и такие, как удар человека
о землю при прыжке с трамвая и т. д. При
ударе в телах возникают столь
значительные внутренние силы, что
внешними силами, действующими на
них, можно пренебречь. Это позволяет
рассматривать соударяющиеся тела
как замкнутую систему и применять к ней
законы сохранения.
Тела
во время удара претерпевают деформацию.
Сущность удара заключается в том,
что кинетическая энергия относительного
движения соударяющихся тел на короткое
время преобразуется в энергию упругой
деформации. Во время удара имеет
место перераспределение энергии между
соударяющимися телами. Наблюдения
показывают, что относительная скорость
тел после удара не достигает своего
прежнего значения. Это объясняется
тем, что нет идеально упругих тел и
идеально гладких поверхностей.
Отношение нормальных составляющих
относительной скорости тел после и до
удара называется коэффициентом
восстановления :
=
v’n/vn.
Если
для сталкивающихся тел =0,
то такие тела называются абсолютно
неупругими, если
=1—абсолютно
упругими.
На
практике для всех тел 0<<1
(например, для стальных шаров 0,56,
для шаров из слоновой кости 0,89,
для свинца 0).
Однако в некоторых случаях тела можно
с большой точностью рассматривать либо
как абсолютно упругие, либо как
абсолютно неупругие.
Прямая,
проходящая через точку соприкосновения
тел и нормальная к поверхности их
соприкосновения, называется линией
удара. Удар
называется центральным,
если
тела до удара движутся вдоль прямой,
проходящей через их центры масс. Мы
будем рассматривать только центральные
абсолютно упругие и абсолютно
неупругие удары.
Абсолютно
упругий удар — столкновение
двух тел, в результате которого в обоих
взаимодействующих телах не остается
никаких деформаций и вся кинетическая
энергия, которой обладали тела до удара,
после удара снова превращается в
кинетическую энергию

.
Для абсолютно
упругого удара выполняются закон
сохранения импульса и закон сохранения
кинетической энергии.
Обозначим
скорости шаров массами m1
и
m2
до удара через v1
и
v2,
после
удара — через v’1
и
v’2
(рис.
18). При прямом центральном ударе
векторы скоростей шаров до и после удара
лежат на прямой линии, соединяющей их
центры. Проекции векторов скорости на
эту линию равны модулям скоростей. Их
направления учтем знаками: положительное
значение припишем движению вправо,
отрицательное — движению влево.
При указанных
допущениях законы сохранения имеют вид

Произведя
соответствующие преобразования в
выражениях (15.1) и (15.2), получим
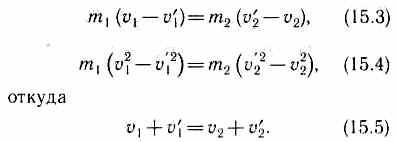
Решая уравнения
(15.3) и (15.5), находим

Разберем несколько
примеров.
29

Проанализируем
выражения (15.8) и (15.9) для двух шаров
различных масс:
а) m1
=m2.
Если
второй шар до удара висел неподвижно
(v2=0)
(рис.
19), то после удара остановится первый
шар (v’1=0),
а второй будет двигаться с той же
скоростью и в том же направлении, в
котором двигался первый шар до удара
(v’2
= v1);
б)
m1>m2.

Первый
шар продолжает двигаться в том же
направлении, как и до удара, но с меньшей
скоростью (v’1<v1).
Скорость
второго шара после удара больше, чем
скорость первого после удара (v’2>v’1)
(рис.20);

в)
m1<m2.
Направление
движения первого шара при ударе изменяется
— шар отскакивает обратно. Второй шар
движется в ту же сторону, в которую
двигался первый шар до удара, но с меньшей
скоростью, т.е. v’2<v1
(рис.
21);
г)
m2>>m1
(например,
столкновение шара со стеной). Из уравнений
(15.8) и (15.9) следует, что v’1=-v1,
v’22m1v1/m20.

2) При
m1=m2
выражения
(15.6) и (15.7) будут иметь вид
v’1=v2,
v’2=v1,
т. е. шары равной
массы «обмениваются» скоростями.
Абсолютно
неупругий удар — столкновение
двух тел, в результате которого тела
объединяются, двигаясь дальше как единое
целое.

Продемонстрировать
абсолютно неупругий удар можно с
помощью шаров из пластилина (глины),
движущихся навстречу друг другу (рис.
22).
Если
массы шаров m1
и
m2,
их скорости до удара v1
и
v2,
то,
используя закон сохранения импульса,
можно записать

Если
шары движутся навстречу друг другу, то
они вместе будут продолжать двигаться
в ту сторону, в которую двигался шар,
обладающий большим импульсом. В частном
случае если массы шаров равны (m1=m2),
то
v
= (v1+v2)/2.
Выясним, как
изменяется кинетическая энергия
шаров при центральном абсолютно
неупругом ударе. Так как в процессе
соударения шаров между ними дей-
30
ствуют силы,
зависящие не от самих деформаций, а от
их скоростей, то мы имеем дело с силами,
подобными силам трения, поэтому закон
сохранения механической энергии не
должен соблюдаться. Вследствие деформации
происходит «потеря» кинетической
энергии, перешедшей в тепловую или
другие формы энергии. Эту «потерю» можно
определить по разности кинетической
энергии тел до и после удара:
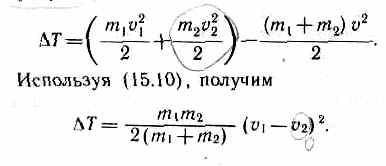
Если
ударяемое тело было первоначально
неподвижно (v2=0),
то

Когда
m2>>m1
(масса
неподвижного тела очень большая), то
v<<v1
и
почти
вся кинетическая энергия тела при ударе
переходит в другие формы энергии.
Поэтому, например, для получения
значительной деформации наковальня
должна быть массивнее молотка.
Наоборот, при забивании гвоздей в стену
масса молотка должна быть гораздо
большей (m1>>m2),
тогда
vv1
и
практически вся энергия затрачивается
на возможно большее перемещение гвоздя,
а не на остаточную деформацию стены.
Абсолютно неупругий
удар — пример того, как происходит
«потеря» механической энергии под
действием диссипативных сил.
Контрольные
вопросы
• В чем различие
между понятиями энергии и работы?
• Как найти
работу переменной силы?
• Какую работу
совершает равнодействующая всех сил,
приложенных к телу, равномерно движущемуся
по окружности?
• Что такое
мощность? Вывести ее формулу.
• Дайте определения
и выведите формулы для известных вам
видов механической энергии. • Какова
связь между силой и потенциальной
энергией?
• Почему изменение
потенциальной энергии обусловлено
только работой консервативных сил?
• В чем заключается
закон сохранения механической энергии?
Для каких систем он выполняется?
• Необходимо
ли условие замкнутости системы для
выполнения закона сохранения механической
энергии?
• В чем физическая
сущность закона сохранения и превращения
энергии? Почему он является фундаментальным
законом природы?
• Каким свойством
времени обусловливается справедливость
закона сохранения механической энергии?
• Что такое
потенциальная яма? потенциальный барьер?
• Какие заключения
о характере движения тел можно сделать
из анализа потенциальных кривых?
• Как
охарактеризовать положения устойчивого
и неустойчивого равновесия? В чем их
различие?
• Чем отличается
абсолютно упругий удар от абсолютно
неупругого?
• Как определить
скорости тел после центрального абсолютно
упругого удара? Следствием каких законов
являются эти выражения?
31
Задачи
3.1. Определить:
1) работу поднятия груза по наклонной
плоскости; 2) среднюю и 3) максимальную
мощности подъемного устройства, если
масса груза 10 кг, длина наклонной
плоскости 2 м, угол ее наклона к горизонту
45°, коэффициент трения 0,1 и время подъема
2 с. [1) 170 Дж; 2) 85 Вт; 3) 173 Вт |
3.2. С башни высотой
35 м горизонтально брошен камень массой
0,3 кг. Пренебрегая сопротивлением
воздуха, определить: 1) скорость, с которой
брошен камень, если через 1 с после начала
движения его кинетическая энергия 60
Дж; 2) потенциальную энергию камня через
1 с после начала движения. [1) 17,4 м/с; 2)
88,6 Дж ]
3.3. Пренебрегая
трением, определить наименьшую высоту,
с которой должна скатываться тележка
с человеком по желобу, переходящему в
петлю радиусом 10 м, чтобы она сделала
полную петлю и не выпала из желоба. [25
м]
3.4.
Пуля массой m=
10 г, летевшая горизонтально со скоростью
v
= 500 м/с, попадает в баллистический
маятник длиной l=
1 м и массой М = 5 кг и застревает в нем.
Определить угол отклонения маятника.
[ 18°30′ ]
3.5.
Зависимость потенциальной энергии
частицы в центральном силовом поле от
расстояния r
до
центра
поля задается выражением П(r)
=A/r2
-B/r,
где А
и
В —
положительные постоянные.
Определить
значение r0,
соответствующее
равновесному положению частицы. Является
ли это положение положением устойчивого
равновесия? [r0
= 2А/В]
3.6.
При центральном абсолютно упругом ударе
движущееся тело массой m1
ударяется
в покоящееся тело массой m2,
в результате чего скорость первого тела
уменьшается в n=
1,5 раза. Определить: 1) отношение m1/m2;
2)
кинетическую энергию T’2,
с
которой начнет двигаться второе
тело, если первоначальная кинетическая
энергия первого тела T1
=
1000 Дж. [ 1) 5; 2) 555 Дж ]
3.7.
Тело массой m1=4
кг движется со скоростью v1=3
м/с
и ударяется о неподвижное тело такой
же массы. Считая удар центральным и
неупругим, определить количество
теплоты, выделившееся при ударе. [9 Дж ]
* У. Гамильтон
(1805—1865) — ирландский математик и
физик.
Соседние файлы в папке Трофимова
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- Печать
Страницы: 1 2 [3] 4 5 … 7
Тема: Законы сохранения из сборника Савченко Н.Е. (Прочитано 91300 раз)
0 Пользователей и 1 Гость просматривают эту тему.
226. На невесомом стержне длиной l = 75 см укреплены два одинаковых шара массой m каждый. Один шар укреплен на конце стержня, другой — посередине (рис. 1). Стержень может колебаться в вертикальной плоскости вокруг точки А. Какую горизонтальную скорость нужно сообщить нижнему концу стержня, чтобы стержень отклонился до горизонтального положения?
Решение. Задачу решим, используя закон сохранения энергии. За нулевую высоту примем высоту, на которой находится нижний шарик (рис. 2).
Полная механическая энергия двух тел в начальном состоянии. Если сообщить скорость υ1 нижнему шарику, то верхний шарик также будет иметь некоторую скорость υ2. Найдем эту скорость (υ2). Так как шарики закреплены на одном стержне, то при движении стержня (по дуге) у них будет одинаковые угловые скорости, т.е.
ω1 = ω2 или υ1/R1 = υ2/R2,
где R1 = l, R2 = l/2 (второй шарик посередине). Поэтому
υ1/l = 2υ2/l, υ2 = υ1/2.
Тогда
[ W_{0} = m cdot gcdot h_{1} +frac{m cdot upsilon _{1}^{2}}{2} + frac{m cdot upsilon _{2}^{2}}{2} = m cdot g cdot h_{1} + frac{m cdot upsilon _{1}^{2}}{2} + frac{m cdot upsilon _{1}^{2}}{8} = m cdot g cdot h_{1} + frac{5m cdot upsilon _{1}^{2}}{8}, ]
где h1 = l/2.
Полная механическая энергия тела в конечном состоянии
W = 2m⋅g⋅h2,
где h2 = l.
Так как на систему не действует внешняя сила, то выполняется закон сохранения механической энергии:
[ mcdot gcdot h_{1} + frac{5m cdot upsilon _{1}^{2}}{8} = 2m cdot gcdot h_{2}, ; ; ; g cdot frac{l}{2} + frac{5 upsilon _{1}^{2}}{8} = 2g cdot l, ]
[ frac{5upsilon _{1}^{2}}{8} = frac{3g cdot l}{2}, ; ; ; upsilon_{1} = sqrt{frac{12g cdot l}{5}} ],
υ1 = 4,2 м/с.

Записан
227. Шарик подвешен на невесомом прямом стержне длиной l. Какую минимальную скорость в горизонтальном направлении необходимо сообщить шарику, чтобы он сделал полный оборот в вертикальной плоскости?
Примечание. Для груза на жестком стержне минимальная скорость груза (υ0) в нижней точке соответствует случаю, когда верхняя точка проходится им со скоростью чуть больше нуля, т.е. υ ≈ 0.
Решение. Задачу решим, используя закон сохранения энергии. За нулевую высоту примем нижнюю точку окружности (рис. 1).
Полная механическая энергия тела в начальном состоянии
[ W_{0} = frac{m cdot upsilon _{0}^{2}}{2}. ]
Полная механическая энергия тела в конечном состоянии
W = m⋅g⋅h = 2m⋅g⋅l.
Так как на систему не действует внешняя сила, то выполняется закон сохранения механической энергии:
[ frac{m cdot upsilon _{0}^{2}}{2} = 2m cdot g cdot l, , , , upsilon _{0} = sqrt{4g cdot l} = 2 cdot sqrt{g cdot l}. ]

Записан
228. Найти количество теплоты, которое выделилось при абсолютно неупругом соударении двух шаров, двигавшихся навстречу друг другу. Масса первого шара m1 = 0,4 кг, его скорость υ1 = 3 м/с. Масса второго шара m2 = 0,2 кг, скорость υ2 = 12 м/с.
Решение. При неупругом ударе выделяется количество теплоты, равное
Q = W0 – W.
Найдем энергии W0 и W. За нулевую высоту примем высоту поверхности, по которой двигаются шары.
Полная механическая энергия тел в начальном состоянии
[ W_{0} =frac{m_{1} cdot upsilon _{1}^{2}}{2} + frac{m_{2} cdot upsilon_{2}^{2}}{2}. ]
Полная механическая энергия тел в конечном состоянии
[ W = frac{left(m_{1} + m_{2} right)cdot upsilon ^{2}}{2},;;; (1) ]
где υ — скорость шаров после столкновения.
Так как удар неупругий, то выполняется закон сохранения импульса. Воспользуемся им для нахождения скорости шаров υ после столкновения (рис. 1):
[ m_{1} cdot vec{upsilon }_{1} + m_{2} cdot vec{upsilon }_{2} = left(m_{1} + m_{2} right) cdot vec{upsilon}, ]
0Х: m1⋅υ1 – m2⋅υ2 = (m1 + m2)⋅υх.
Тогда
[ upsilon _{x} = frac{m_{1} cdot upsilon _{1} -m_{2} cdot upsilon _{2} }{m_{1} +m_{2} } . ]
После подстановки в уравнение (1) получаем
[ W=frac{m_{1} +m_{2}}{2} cdot left(frac{m_{1} cdot upsilon _{1} -m_{2} cdot upsilon _{2} }{m_{1} + m_{2}} right)^{2} = frac{left(m_{1} cdot upsilon _{1} -m_{2} cdot upsilon _{2} right)^{2}}{2cdot left(m_{1} +m_{2} right)}.
]
Количество теплоты, которое выделится при неупругом ударе шаров, будет равно (подробнее смотри рис. 2)
[ Q = frac{m_{1} cdot upsilon _{1}^{2}}{2} + frac{m_{2} cdot upsilon _{2}^{2}}{2} -frac{left(m_{1} cdot upsilon _{1} -m_{2} cdot upsilon _{2} right)^{2}}{2 cdot left(m_{1} + m_{2} right)} = frac{m_{1} cdot m_{2} cdot left(upsilon _{1} + upsilon _{2} right)^{2}}{2 cdot left(m_{1} + m_{2} right)}, ]
Q = 15 Дж.

Записан
229. Брусок массой m1 движется по гладкой горизонтальной поверхности со скоростью υ1. Пуля массой m2, летевшая в горизонтальном направлении со скоростью υ2, застревает в бруске. Угол между векторами υ1 и υ2 α = 90°. Определить, какое количество теплоты выделилось в бруске.
Решение. При неупругом ударе выделяется количество теплоты, равное
Q = W0 – W.
Найдем энергии W0 и W. За нулевую высоту примем высоту поверхности, по которой двигается брусок.
Полная механическая энергия тел в начальном состоянии
[ W_{0} =frac{m_{1} cdot upsilon _{1}^{2}}{2} + frac{m_{2} cdot upsilon_{2}^{2}}{2}.
]
Полная механическая энергия тел в конечном состоянии
[ W = frac{left(m_{1} + m_{2} right)cdot upsilon ^{2}}{2},;;; (1) ]
где υ — скорость бруска и пули после столкновения.
Так как удар неупругий, то выполняется закон сохранения импульса. Воспользуемся им для нахождения скорости υ бруска с пулей после столкновения (рис. 1):
[ m_{1} cdot vec{upsilon }_{1} + m_{2} cdot vec{upsilon }_{2} = left(m_{1} + m_{2} right) cdot vec{upsilon}, ]
0Х: m1⋅υ1 = (m1 + m2)⋅υх,
0Y: m2⋅υ2 = (m1 + m2)⋅υy.
Тогда
[ upsilon ^{2} = upsilon _{x}^{2} +upsilon _{y}^{2} =left(frac{m_{1} cdot upsilon _{1} }{m_{1} +m_{2}} right)^{2} +left(frac{m_{2} cdot upsilon _{2}}{m_{1} +m_{2} } right)^{2} =frac{left(m_{1} cdot upsilon _{1} right)^{2} +left(m_{2} cdot upsilon _{2} right)^{2} }{left(m_{1} +m_{2} right)^{2}}. ]
После подстановки в уравнение (1) получаем
[ W = frac{m_{1} +m_{2}}{2} cdot frac{left(m_{1} cdot upsilon _{1} right)^{2} +left(m_{2} cdot upsilon _{2} right)^{2}}{left(m_{ 1} +m_{2} right)^{2}} = frac{left(m_{1} cdot upsilon _{1} right)^{2} +left(m_{2} cdot upsilon _{2} right)^{2}}{2cdot left(m_{1} +m_{2} right)}. ]
Количество теплоты, которое выделится при неупругом ударе шаров, будет равно (подробнее смотри рис. 2)
[ Q = frac{m_{1} cdot upsilon _{1}^{2}}{2} +frac{m_{2} cdot upsilon _{2}^{2}}{2} -frac{left(m_{1} cdot upsilon _{1} right)^{2} + left(m_{2} cdot upsilon _{2} right)^{2}}{2cdot left(m_{1} +m_{2} right)} = frac{m_{1} cdot m_{2} cdot left(upsilon _{1}^{2} +upsilon _{2}^{2} right)}{2 cdot left(m_{1} +m_{2} right)}. ]

Записан
231. Шар массой m1, движущийся со скоростью υ10 по горизонтальной поверхности, сталкивается с неподвижным шаром массой m2. Между шарами происходит абсолютно упругий центральный удар. Определить скорости шаров после удара.
Решение. При абсолютно упругом ударе выполняются законы сохранения и импульса системы, и ее механической энергии. За нулевую высоту примем высоту поверхности, по которой двигаются шары.
Запишем оба закона сохранения и учтем, что после упругого удара второй шар начнет двигаться вправо (рис. 1):
0X: m1⋅υ10 = m1⋅υ1x + m2⋅υ2,
[ frac{m_{1} cdot upsilon _{10}^{2} }{2} =frac{m_{1} cdot upsilon _{1x}^{2} }{2} +frac{m_{2} cdot upsilon _{2}^{2}}{2}.
]
Получили систему двух уравнений с двумя неизвестными (υ1x и υ2). Решим ее. Например
[ upsilon _{1x} = frac{m_{1} cdot upsilon _{10} -m_{2} cdot upsilon _{2} }{m_{1}}, , , , m_{1} cdot upsilon _{10}^{2} = m_{1} cdot frac{left(m_{1} cdot upsilon _{10} -m_{2} cdot upsilon _{2} right)^{2}}{m_{1}^{2}} +m_{2} cdot upsilon _{2}^{2},
]
υ2 = 0 м/с или
[ upsilon _{2} =frac{2m_{1} cdot upsilon _{10}}{m_{1} +m_{2}}. ]
Подробнее решение смотри рис. 2.
Первый ответ (υ2 = 0 м/с) при упругом ударе невозможен.
Найдем скорость первого шара:
[ upsilon _{1x} =frac{1}{m_{1}} cdot left(m_{1} cdot upsilon _{10} -m_{2} cdot frac{2m_{1} cdot upsilon _{10}}{m_{1} +m_{2}} right)=frac{left(m_{1} +m_{2} right)cdot upsilon _{10} -2m_{2} cdot upsilon _{10}}{m_{1} +m_{2}} =frac{left(m_{1} -m_{2} right)cdot upsilon _{10}}{m_{1} +m_{2}}. ]
Если проекция скорости υ1x > 0, то первый шар будет двигаться вдоль оси 0Х, т.е. продолжать двигаться в ту же сторону, если υ1x < 0, то первый шар начнет двигаться в обратную сторону.

Записан
232. Самолет пикирует вертикально вниз с высоты h1 = 1,5 км до высоты h2 = 500 м. Его начальная скорость υ1 = 360 км/ч, а при выходе из пике υ2 = 540 км/ч. Найти силу сопротивления воздуха, считая ее постоянной. Масса самолета m = 2,0 т, двигатель самолета не работает. Ускорение свободного падения g считать равным 10 м/с2.
Решение. Задачу решим, используя закон сохранения энергии. За нулевую высоту примем поверхность Земли.
Полная механическая энергия самолета в начальном состоянии
[ W_{0} = frac{m cdot upsilon_{1}^{2}}{2} +m cdot g cdot h_{1}.;;; (1) ]
Полная механическая энергия тела в конечном состоянии
[ W = frac{m cdot upsilon_{2}^{2}}{2} +m cdot g cdot h_{2}.;;; (2) ]
На самолет действует внешняя сила Fc — сила сопротивления воздуха. Работа этой силы равна
Av = Fc⋅Δr⋅cos α, (3)
где Δr = h1 – h2, α = 180° (т.к. сила сопротивления направлена в противоположную сторону скорости движения).
Запишем закон изменения механической энергии
Аv = W – W0.
Распишем данное выражение с учетом уравнений (1)-(3)
[ -F_{c} cdot left(h_{1} – h_{2} right) = left(frac{m cdot upsilon_{2}^{2}}{2} +m cdot g cdot h_{2} right)-left(frac{mcdot upsilon _{1}^{2}}{2} +m cdot g cdot h_{1} right) = mcdot left(frac{upsilon _{2}^{2} -upsilon _{1}^{2}}{2} -gcdot left(h_{1} -h_{2} right)right),
]
[ F_{c} = mcdot left(g-frac{upsilon_{2}^{2} -upsilon_{1}^{2}}{2 cdot left(h_{1} -h_{2} right)} right), ]
Fc = 7,5⋅103 Н.

Записан
233. Камень брошен под углом к горизонту с высоты H с начальной скоростью υ0. С какой скоростью камень упадет на поверхность земли? Решить без применения кинематических уравнений. Сопротивление воздуха не учитывать.
Решение. Задачу решим, используя закон сохранения энергии. За нулевую высоту примем поверхность земли (рис. 1).
Полная механическая энергия тела в начальном состоянии
[ W_{0} =frac{m cdot upsilon _{0}^{2}}{2} +m cdot g cdot H. ]
Полная механическая энергия тела в конечном состоянии
[ W = frac{m cdot upsilon ^{2}}{2}. ]
Так как на систему не действует внешняя сила (сопротивление воздуха не учитывать), то выполняется закон сохранения механической энергии
[ frac{m cdot upsilon _{0}^{2}}{2} +m cdot gcdot H=frac{mcdot upsilon ^{2}}{2}, , , , frac{upsilon ^{2}}{2} = frac{upsilon _{0}^{2}}{2} + g cdot H, , , , upsilon = sqrt{upsilon _{0}^{2} +2g cdot H}.
]

Записан
234. Пуля, летящая со скоростью υ0, пробивает несколько одинаковых досок, расположенных на некотором расстоянии друг от друга. В какой по счету доске пуля застрянет, если ее скорость после прохождения первой доски υ1 = 0,8υ0?
Решение. Задачу решим, используя закон сохранения энергии. За нулевую высоту примем высоту, на которой находится пуля, поэтому Wp0 = Wp = 0.
Рассмотрим вначале случай, когда пуля проходит через одну доску.
Полная механическая энергия тела в начальном состоянии
W0 = m⋅υ02/2.
Полная механическая энергия тела в конечном состоянии
W = m⋅υ12/2.
На пулю действует внешняя сила Fc – сила сопротивления доски. Работа этой силы равна
Av = Fc⋅Δr⋅cos α,
где Δr = d — толщина доски, α = 180° (т.к. сила сопротивления направлена в противоположную сторону скорости движения пули).
Запишем закон изменения механической энергии
Аv = W – W0,
или
[ -F_{c} cdot d=frac{m cdot upsilon _{1}^{2} }{2} -frac{m cdot upsilon _{0}^{2}}{2}, ; ; ; F_{c} = frac{m}{2d} cdot left(upsilon _{0}^{2} -upsilon _{1}^{2} right).;;; (1) ]
Рассмотрим теперь случай, когда пуля проходит через N досок и застревает в последней.
Полная механическая энергия тела в начальном состоянии
W0 = m⋅υ02/2.
Полная механическая энергия тела в конечном состоянии
W = 0.
Работа силы сопротивления всех досок равна
Av2 = –Fc⋅N⋅d,
где Fc найдем из уравнения (1).
Запишем закон изменения механической энергии
Аv2 = W – W0,
или
[ -F_{c} cdot Ncdot d = -frac{m cdot upsilon _{0}^{2}}{2}, ; ; ; N = frac{m cdot upsilon _{0}^{2}}{2dcdot F_{c}} = frac{m cdot upsilon _{0}^{2} cdot 2d}{2d cdot m cdot left(upsilon _{0}^{2} -upsilon _{1}^{2} right)} = frac{upsilon _{0}^{2}}{upsilon _{0}^{2} -upsilon _{1}^{2}}, ]
[ N = frac{upsilon _{0}^{2}}{upsilon _{0}^{2} -0,64upsilon _{0}^{2}} = frac{1}{0,36} = 2,8. ]
Ответ. В третьей доске.

Записан
235. Пуля массой m, летящая горизонтально со скоростью υ, попадает в ящик с песком массой M, подвешенный на жестком невесомом стержне длиной l, который шарнирно укреплен за верхний конец («баллистический маятник»), и застревает в нем. Стержень может вращаться вокруг горизонтальной оси, перпендикулярной направлению скорости пули. Пренебрегая размерами ящика, определить максимальный угол отклонения стержня от вертикали.
Решение. Так как пуля застревает в ящике, то применять сразу закон сохранения энергии нельзя. Рассмотрим вначале процесс столкновения пули и ящика (неупругий удар), затем движение системы ящик-пуля на стержне.
Процесс столкновения пули и ящика (рис. 1). Так как удар неупругий, то для нахождения скорости системы ящик-пуля воспользуемся законом сохранения импульса:
[ mcdot vec{upsilon } = left(m+M right) cdot vec{upsilon }_{1}, ]
0Х: m⋅υ = (m + M)⋅υ1
или
[ upsilon _{1} = frac{m cdot upsilon }{m+M}. ] (1)
Процесс движения системы ящик-пуля на стержне. Силой сопротивления, по умолчанию, пренебрегаем, поэтому теперь можем применять закон сохранения энергии. За нулевую высоту примем высоту, на которой находится ящик в нижнем положении (рис. 2).
Полная механическая энергия системы ящик-пуля в начальном состоянии (с учетом уравнения (1))
[ W_{0} = frac{left(m+Mright) cdot upsilon _{1}^{2}}{2} = frac{m+M}{2} cdot left(frac{m cdot upsilon }{m+M} right)^{2} = frac{m^{2} cdot upsilon ^{2}}{2cdot left(m+Mright)}. ]
Полная механическая энергия системы ящик-пуля в конечном состоянии. Максимальный угол α отклонения стержня от вертикали будет в тот момент, когда система достигнет максимальной высоты и их скорость υ2 = 0, т.е.
W = (m + M)⋅g⋅h,
где h = AB = OB – OA = l – l⋅cos α = l⋅(1 – cos α).
Из закона сохранения механической энергии следует, что
[ frac{m^{2} cdot upsilon ^{2}}{2 cdot left(m+Mright)} = left(m+M right) cdot g cdot l cdot left(1-cos alpha right), , , , 1-cos alpha = frac{m^{2} cdot upsilon ^{2}}{2 cdot left(m+M right)^{2} cdot g cdot l}, ]
[ cos alpha = 1-frac{m^{2} cdot upsilon ^{2}}{2 cdot left(m+Mright)^{2} cdot g cdot l}, ; ; ; alpha = arccos left(1-frac{m^{2} cdot upsilon ^{2}}{2 cdot left(m+Mright)^{2} cdot g cdot l} right).;;; (2) ]
Примечание. Так как –1 ≤ cos α ≤ 1, то уравнение (2) можно применять если
[ -1 le 1-frac{m^{2} cdot upsilon ^{2}}{2 cdot left(m+M right)^{2} cdot g cdot l}, ; ; ; frac{m^{2} cdot upsilon ^{2}}{left(m+ M right)^{2} cdot g cdot l} le 4. ]
Если это неравенство не выполняется, то угол α = 180°, и система совершает полный оборот.

Записан
239. Конькобежец массой M = 60 кг, стоя на льду, бросает в горизонтальном направлении шайбу массой m = 0,3 кг со скоростью υ = 40 м/с. На какое расстояние откатится при этом конькобежец, если коэффициент трения коньков о лед μ = 0,004?
Подобная задача (с другими числовыми значениями) решена на форуме: Конькобежец на коньках бросает мяч.
Ответ. 0,5 м.

Записан
- Печать
Страницы: 1 2 [3] 4 5 … 7

