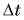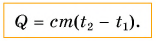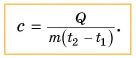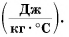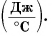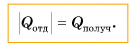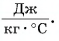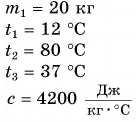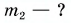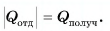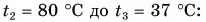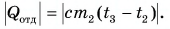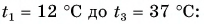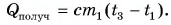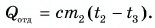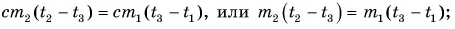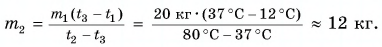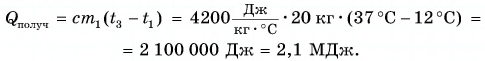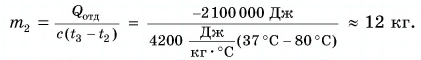Как найти выделяемое количество теплоты формула

Количество теплоты — еще один изученный нами вид энергии. Эту энергию тело получает или отдает при теплопередаче. Мы установили, что количество теплоты, необходимое для нагревания тела, зависит от массы тела, разности температур и рода вещества. Нам известен физический смысл удельной теплоемкости и некоторые ее табличные значения для разных веществ. В этом уроке мы перейдем к численному расчету количества теплоты, необходимой для нагревания тела или выделяемого им при охлаждении. 

Зачем это нужно? На самом деле, на практике очень часто используют подобные расчеты.

При строительстве зданий и проектировании систем отопления важно знать, какое количество теплоты необходимо отдавать для полного обогрева всех помещений. С другой стороны, также необходима информация о том, какое количество теплоты будет уходить через окна, стены и двери. 

Формула для расчета количества теплоты

Допустим, на нужно узнать, какое количество теплоты получила при нагревании железная деталь. Масса детали $3 space кг$. Деталь нагрелась от $20 degree C$ до $300 degree C$. 

Возьмем значение теплоемкости железа из таблицы — $460 frac{Дж}{кг cdot degree C}$. Объясним смысл этой величины: на нагревание куска железа массой $1 space кг$ на $1 degree C$ необходимо затратить количество теплоты, равное $460 space Дж$. 

• Масса детали у нас в 3 раза больше, значит, на ее нагрев потребуется в 3 раза большее количество теплоты — $1380 space Дж$
• Температура изменилась не на $1 degree C$, а на $280 degree C$
• Значит, необходимо в 280 раз большее количество теплоты: $1380 space Дж cdot 280 = 386 400 space Дж$

Тогда, формула для расчета количества теплоты, необходимой для нагревания тела или выделяемого им при охлаждении примет вид:

$Q = cm(t_2 — t_1)$,

где $Q$ — количество теплоты,
$c$ — удельная теплоемкость вещества, из которого состоит тело,
$m$ — масса тела,
$t_1$ — начальная температура тела,
$t_2$ — конечная температура тела.

Чтобы рассчитать количество теплоты, которое необходимо затратить для нагревания тела или выделяемое им при охлаждении, нужно удельную теплоемкость умножить на массу тела и на разность конечной и начальной температур.

Рассмотрим подробнее особенности расчета количества теплоты на примерах решения задач.

Расчет количества теплоты, затраченного на нагревание двух тел

В железный котелок массой $4 space кг$ налили воду массой $10 space кг$ (рисунок 1). Их температура $25 degree C$. Какое количество теплоты нужно затратить, чтобы нагреть котелок и воду до температуры $100 degree C$?

Обратите внимание, что нагреваться будут сразу два тела: и котелок, и вода в нем. Между постоянно будет происходить теплообмен. Поэтому их температуры мы можем считать одинаковыми. 

Отметим, что массы котелка и воды различные. Также они имеют различные теплоемкости. Значит, полученные ими количества теплоты будет различными.

Теперь мы можем записать условие задачи и решить ее.

Дано:
$m_1 = 4 space кг$
$c_1 = 460 frac{Дж}{кг cdot degree C}$
$m_2 = 10 space кг$
$c_2 = 4200 frac{Дж}{кг cdot degree C}$
$t_1 = 25 degree C$
$t_2 = 100 degree C$

Q-?

Посмотреть решение и ответ

Скрыть

Расчет количества теплоты при смешивании жидкостей

Горячую воду разбавили холодной и получили температуру смеси $30 degree C$. Горячей воды с температурой $100 degree C$ при этом было $0.3 space кг$. Холодная вода имела массу $1.4 space кг$ и температуру $15 degree C$. Рассчитайте, какое количество теплоты было отдано горячей водой при остывании и получила холодная вода при нагревании. Сравните эти количества теплоты.

Дано:
$c_1 = c_2 = c = 4200 frac{Дж}{кг cdot degree C}$
$m_1 = 0.3 space кг$
$m_2 = 1.4 space кг$
$t_1 = 100 degree C$
$t_2 = 15 degree C$
$t = 30 degree C$

$Q_1 — ?$
$Q_2 — ?$

Посмотреть решение и ответ

Скрыть

В ходе решения этой задачи мы увидели, что количество теплоты, отданное горячей водой, и количество теплоты, полученное холодной водой, равны. Другие опыты дают схожие результаты. 

Значит,

Если между телами происходит теплоообмен, то внутренняя энергия всех нагревающихся тел увеличивается на столько, на сколько уменьшается внутренняя энергия остывающих тел.

На практике часто получается так, что отданная горячей водой энергия больше, чем полученная холодной. На самом деле, горячая вода при охлаждении передает какую-то часть своей внутренней энергии воздуху и сосуду, в котором происходит смешивание.

Есть 2 способа учесть этот фактор:

• Если мы максимально сократим потери энергии, то добьемся приблизительного равенства отданной и полученной энергий
• Если рассчитать и учесть потери энергии, то можно получить точное равенство

Расчет температуры при известной величине количества теплоты

При нагревании куска меди было затрачено $22 space кДж$. Масса этого куска составляет $300 space г$. Начальная температура была равна $20 degree C$. До какой температуры нагрели кусок меди?

$t_2 — ?$

Посмотреть решение и ответ

Скрыть

Расчет количества теплоты при нагревании и охлаждении:

Вы уже знаете, что изменить внутреннюю энергию тела можно передачей ему количества теплоты. Как связано изменение внутренней энергии тела, т. е. количество теплоты, с характеристиками самого тела?

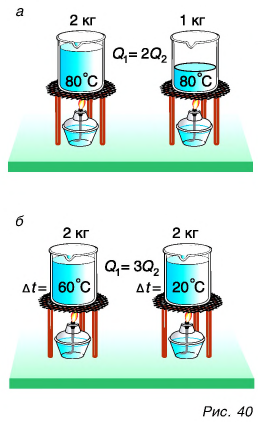
Внутренняя энергия тела есть суммарная энергия всех его частиц. Значит, если массу данного тела увеличить в два или три раза, то и количество теплоты, необходимое для его нагревания на одно и то же число градусов, увеличится в два или три раза. Например, на нагревание двух килограммов воды от 20 °C до 80 °C потребуется в два раза больше теплоты, чем на нагревание одного килограмма воды (рис. 40, а).

Очевидно также, что для нагревания воды на

Из этих рассуждений следует подтвержденный опытами вывод. Количество теплоты, необходимое для нагревания тела, прямо пропорционально его массе и изменению температуры.

А зависит ли количество теплоты, идущее на нагревание, от рода вещества, которое нагревается?

Для ответа на этот вопрос проведем опыт. В два одинаковых стакана нальем по 150 г подсолнечного масла и воды. Поместим в них термометры и поставим на нагреватель (рис. 41).

Получив за одинаковое время от нагревателя равное с водой количество теплоты, масло нагрелось больше, чем вода. Значит, для изменения температуры масла на одну и ту же величину требуется меньше теплоты, чем для изменения температуры такой же массы воды.

Поэтому для всех веществ вводят специальную величину — удельную теплоемкость вещества. Эту величину обозначают буквой с (от лат. capacite — емкость, вместимость). Теперь мы можем записать строгую формулу для количества теплоты, необходимого для нагревания:

Выразим из этой формулы с:

Удельная теплоемкость есть физическая величина, численно равная количеству теплоты, которое необходимо передать 1 кг данного вещества, чтобы изменить его температуру на 1 °C. Удельная теплоемкость измеряется в джоулях на килограмм-градус Цельсия

Для любознательных:

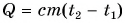
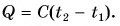
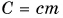
Часто формулу записывают в виде  Здесь величина называется теплоемкостью тела (обратите внимание — не вещества). Она численно равна количеству теплоты, необходимому для нагревания всей массы тела на 1 °C. Измеряется теплоемкость тела в джоулях на градус Цельсия 

В таблице 1 представлены значения удельной теплоемкости различных веществ (в различных состояниях). Как следует из этой таблицы, среди жидкостей максимальное значение удельной теплоемкости имеет вода: для нагревания 1 кг воды на 1 °C требуется 4200 Дж теплоты — это почти в 2,5 раза больше, чем для нагревания 1 кг подсолнечного масла, и в 35 раз больше, чем для нагревания 1 кг ртути.

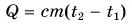
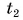
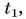
Формула дает возможность найти и выделяемую при охлаждении тела теплоту. Так как конечная температура остывшего тела меньше начальной  то изменение температуры оказывается отрицательным числом. Значит, и выделяемое телом количество теплоты выражается отрицательным числом, что обозначает не рост, а убыль внутренней энергии тела.

В заключение заметим, что при теплообмене двух или нескольких тел абсолютное значение количества теплоты, которое отдано более нагретым телом (телами), равно количеству теплоты, которое получено более холодным телом (телами):

Это равенство называется уравнением теплового баланса и выражает, по сути, закон сохранения энергии. Оно справедливо при отсутствии потерь теплоты.
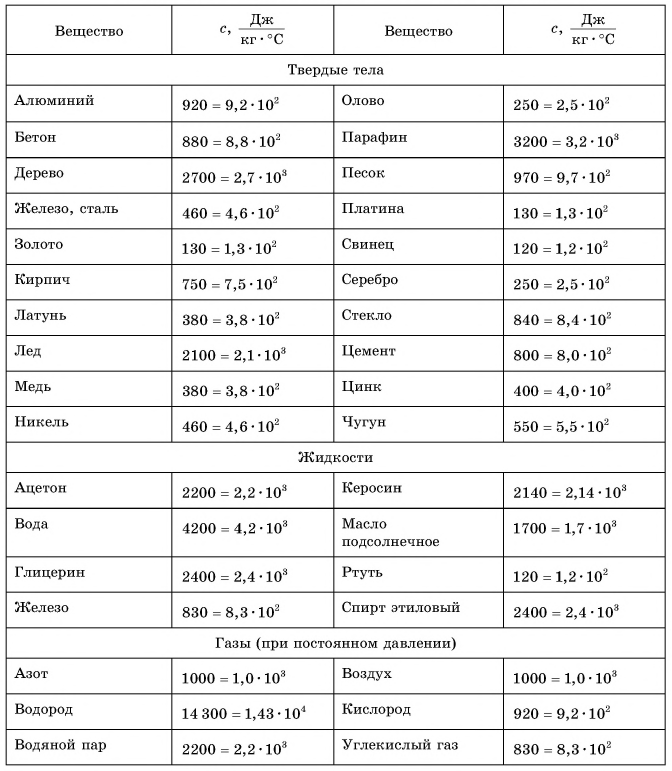
Таблица 1. Удельная теплоемкость некоторых веществ

Главные выводы:

1. Количество теплоты, необходимое для нагревания тела (выделившееся при охлаждении), прямо пропорционально его массе, изменению температуры тела и зависит от вещества тела.
2. Удельная теплоемкость вещества численно равна количеству теплоты, которое надо передать 1 кг данного вещества, чтобы изменить его температуру на 1 °C.
3. При теплообмене количество теплоты, отданное более горячим телом, равно по модулю количеству теплоты, полученному более холодным телом, если нет потерь теплоты.

• Заказать решение задач по физике

Пример решения задачи:

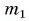
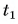
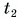
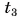
Для купания ребенка в ванночку влили холодную воду массой = 20 кг при температуре  = 12 °C. Какую массу горячей воды при температуре = 80 °C нужно добавить в ванночку, чтобы окончательная температура воды стала = 37 °C? Удельная теплоемкость воды с = 4200
Дано:

Решение

По закону сохранения энергии

Отдавала теплоту горячая вода, изменяя свою температуру от

Холодная вода получила эту теплоту и нагрелась от

Так как нас интересует только модуль  то можно записать:

Тогда

При решении мы пренебрегали потерями теплоты на нагревание ванночки, окружающего воздуха и т. д.

Возможен и другой вариант решения.

Рассчитаем сначала количество теплоты, которое было получено холодной водой:

Полагая, что эта теплота отдана горячей водой, запишем: 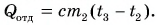 Выразим искомую массу:

Ответ:

Вычисление количества теплоты при нагревании и охлаждении тела

Данный урок посвящен вычислению количества теплоты при нагревании тела или выделяемого им при охлаждении.

Умение вычислять необходимое количество теплоты является очень важным. Это может понадобиться, к примеру, при вычислении количества теплоты, которое необходимо сообщить воде для обогрева помещения.

Рис. 1. Количество теплоты, которое необходимо сообщить воде для обогрева помещения

Или для вычисления количества теплоты, которое выделяется при сжигании топлива в различных двигателях:

Рис. 2. Количество теплоты, которое выделяется при сжигании топлива в двигателе

Также эти знания нужны, например, чтобы определить количество теплоты, которое выделяется Солнцем и попадает на Землю:

Рис. 3. Количество теплоты, выделяемое Солнцем и попадающее на Землю

Для вычисления количества теплоты необходимо знать три вещи (рис. 4):

• массу тела (которую, обычно, можно измерить с помощью весов);
• разность температур, на которую необходимо нагреть тело или охладить его (обычно измеряется с помощью термометра);
• удельную теплоемкость тела (которую можно определить по таблице).

Рис. 4. Что необходимо знать для определения 

Формула, по которой вычисляется количество теплоты, выглядит так:

.

В этой формуле фигурируют следующие величины:

 – количество теплоты, измеряется в джоулях (Дж);

 – удельная теплоемкость вещества, измеряется в ;

 – разность температур, измеряется в градусах Цельсия ().

Задача на вычисление количества теплоты

Рассмотрим задачу на вычисление количества теплоты.

Задача

В медном стакане массой  грамм находится вода объемом  литра при температуре . Какое количество теплоты необходимо передать стакану с водой, чтобы его температура стала равна ?

Рис. 5. Иллюстрация условия задачи

Сначала запишем краткое условие (Дано) и переведем все величины в систему интернационал (СИ).

Решение:

Сначала определи,  какие еще величины потребуются нам для решения данной задачи. По таблице удельной теплоемкости (табл. 1) находим  (удельная теплоемкость меди, так как по условию стакан медный),  (удельная теплоемкость воды, так как по условию в стакане находится вода). Кроме того, мы знаем, что для вычисления количества теплоты нам понадобится масса воды. По условию нам дан лишь объем. Поэтому из таблицы возьмем плотность воды:  (табл. 2).

Табл. 1. Удельная теплоемкость некоторых веществ,

Табл. 2. Плотности некоторых жидкостей

Теперь у нас есть все необходимое для решения данной задачи.

Заметим, что итоговое количество теплоты будет состоять из суммы количества теплоты, необходимого для нагревания медного стакана и количества теплоты, необходимого для нагревания воды в нем:

Рассчитаем сначала количество теплоты, необходимое для нагревания медного стакана:

Прежде чем вычислить количество теплоты, необходимое для нагревания воды, рассчитаем массу воды по формуле, хорошо знакомой нам из 7 класса:

, тогда

.

Теперь можем вычислить:

Тогда можем вычислить:

Напомним, что  означает: килоджоули. Приставка «кило» означает , то есть .

Ответ:.

Таблица для нахождения величин, входящих в формулу количества теплоты

Для удобства решения задач на нахождение количества теплоты (так называемые прямые задачи) и связанных с этим понятием величин можно пользоваться следующей таблицей.

Табл. 3. Готовые формулы для вычисления величин

Формулу для конечной температуры попробуйте вывести самостоятельно.

Стоит отметить, что, конечно же, запоминать эти формулы не нужно. Главное – помнить базовую формулу и уметь выводить из нее все необходимые величины.

На следующем уроке мы проведем лабораторную работу, цель которой – научиться экспериментально определять удельную теплоемкость твердого тела.

Список литературы:

1. Генденштейн Л.Э, Кайдалов А.Б., Кожевников В.Б. / Под ред. Орлова В.А., Ройзена И.И. Физика 8. – М.: Мнемозина.
2. Перышкин А.В. Физика 8. – М.: Дрофа, 2010.
3. Фадеева А.А., Засов А.В., Киселев Д.Ф. Физика 8. – М.: Просвещение.

Дополнительные рекомендованные ссылки на ресурсы сети Интернет

1. Интернет-портал «» (Источник)

Домашнее задание

1. Стр. 25, параграф 9, вопросы № 1-4, упражнение 4. Перышкин А.В. Физика 8. – М.: Дрофа, 2010.
2. Найдите формулу для нахождения конечной температуры по аналогии с начальной температурой из приведенной в уроке таблицы.
3. Стальная деталь массой  при обработке на токарном станке нагрелась на . Сколько энергии потратил двигатель на нагрев детали?
4. Какое количество теплоты отдает стакан кипятка объемом , охлаждаясь до температуры ?

Количество теплоты. Удельная теплоемкость вещества

Количеством теплоты называют количественную меру изменения внутренней энергии тела при теплообмене.

Количество теплоты — это энергия, которую тело отдает при теплообмене (без совершения работы). Количество теплоты, как и энергия, измеряется в джоулях (Дж).

Удельная теплоемкость вещества

Теплоемкость — это количество теплоты, поглощаемой телом при нагревании на $1$ градус.

Теплоемкость тела обозначается заглавной латинской буквой С.

От чего зависит теплоемкость тела? Прежде всего, от его массы. Ясно, что для нагрева, например, $1$ килограмма воды потребуется больше тепла, чем для нагрева $200$ граммов.

А от рода вещества? Проделаем опыт. Возьмем два одинаковых сосуда и, налив в один из них воду массой $400$ г, а в другой — растительное масло массой $400$ г, начнем их нагревать с помощью одинаковых горелок. Наблюдая за показаниями термометров, мы увидим, что масло нагревается быстрее. Чтобы нагреть воду и масло до одной и той же температуры, воду следует нагревать дольше. Но чем дольше мы нагреваем воду, тем большее количество теплоты она получает от горелки.

Таким образом, для нагревания одной и той же массы разных веществ до одинаковой температуры требуется разное количество теплоты. Количество теплоты, необходимое для нагревания тела и, следовательно, его теплоемкость зависят от рода вещества, из которого состоит это тело.

Так, например, чтобы увеличить на $1°$С температуру воды массой $1$ кг, требуется количество теплоты, равное $4200$ Дж, а для нагревания на $1°$С такой же массы подсолнечного масла необходимо количество теплоты, равное $1700$ Дж.

Физическая величина, показывающая, какое количество теплоты требуется для нагревания $1$ кг вещества на $1°$С, называется удельной теплоемкостью этого вещества.

У каждого вещества своя удельная теплоемкость, которая обозначается латинской буквой $с$ и измеряется в джоулях на килограмм-градус (Дж/(кг$·°$С)).

Удельная теплоемкость одного и того же вещества в разных агрегатных состояниях (твердом, жидком и газообразном) различна. Например, удельная теплоемкость воды равна $4200$ Дж/(кг$·°$С), а удельная теплоемкость льда $2100$ Дж/(кг$·°$С); алюминий в твердом состоянии имеет удельную теплоемкость, равную $920$ Дж/(кг$·°$С), а в жидком — $1080$ Дж/(кг$·°$С).

Заметим, что вода имеет очень большую удельную теплоемкость. Поэтому вода в морях и океанах, нагреваясь летом, поглощает из воздуха большое количество тепла. Благодаря этому в тех местах, которые расположены вблизи больших водоемов, лето не бывает таким жарким, как в местах, удаленных от воды.

Расчет количества теплоты, необходимого для нагревания тела или выделяемого им при охлаждении

Из вышеизложенного ясно, что количество теплоты, необходимое для нагревания тела, зависит от рода вещества, из которого состоит тело (т. е. его удельной теплоемкости), и от массы тела. Ясно также, что количество теплоты зависит от того, на сколько градусов мы собираемся увеличить температуру тела.

Итак, чтобы определить количество теплоты, необходимое для нагревания тела или выделяемое им при охлаждении, нужно удельную теплоемкость тела умножить на его массу и на разность между его конечной и начальной температурами:

$Q=cm(t_2-t_1)$

где $Q$ — количество теплоты, $c$ — удельная теплоемкость, $m$ — масса тела, $t_1$ — начальная температура, $t_2$ — конечная температура.

При нагревании тела $t_2 > t_1$ и, следовательно, $Q > 0$. При охлаждении тела $t_2 < t_1$ и, следовательно, $Q < 0$.

В случае, если известна теплоемкость всего тела $С, Q$ определяется по формуле

$Q=C(t_2-t_1)$

Удельная теплота парообразования, плавления, сгорания

Теплота парообразования (теплота испарения) — количество теплоты, которое необходимо сообщить веществу (при постоянном давлении и постоянной температуре) для полного превращения жидкого вещества в пар.

Теплота парообразования равна количеству теплоты, выделяющемуся при конденсации пара в жидкость.

Превращение жидкости в пар при постоянной температуре не ведет к увеличению кинетической энергии молекул, но сопровождается увеличением их потенциальной энергии, т. к. расстояние между молекулами существенно увеличивается.

Удельная теплота парообразования и конденсации. Опытами установлено, что для полного обращения в пар $1$ кг воды (при температуре кипения) необходимо затратить $2.3$ МДж энергии. Для обращения в пар других жидкостей требуется иное количество теплоты. Например, для спирта оно составляет $0.9$ МДж.

Физическая величина, показывающая, какое количество теплоты необходимо, чтобы обратить жидкость массой $1$ кг в пар без изменения температуры, называется удельной теплотой парообразования.

Удельную теплоту парообразования обозначают буквой $r$ и измеряют в джоулях на килограмм (Дж/кг).

Количество теплоты, необходимое для парообразования (или выделяющееся при конденсации). Чтобы вычислить количество теплоты $Q$, необходимое для превращения в пар жидкости любой массы, взятой при температуре кипения, нужно удельную теплоту парообразования $r$ умножить на массу $m$:

$Q=rm$

При конденсации пара происходит выделение такого же количества теплоты:

$Q=-rm$

Удельная теплота плавления

Теплота плавления — это количество теплоты, которое необходимо сообщить веществу при постоянном давлении и постоянной температуре, равной температуре плавления, чтобы полностью перевести его из твердого кристаллического состояния в жидкое.

Теплота плавления равна тому количеству теплоты, которое выделяется при кристаллизации вещества из жидкого состояния.

При плавлении вся подводимая к веществу теплота идет на увеличение потенциальной энергии его молекул. Кинетическая энергия не меняется, поскольку плавление идет при постоянной температуре.

Изучая на опыте плавление различных веществ одной и той же массы, можно заметить, что для превращения их в жидкость требуется разное количество теплоты. Например, для того чтобы расплавить один килограмм льда, нужно затратить $332$ Дж энергии, а для того чтобы расплавить $1$ кг свинца — $25$ кДж.

Физическая величина, показывающая, какое количество теплоты необходимо сообщить кристаллическому телу массой $1$ кг, чтобы при температуре плавления полностью перевести его в жидкое состояние, называется удельной теплотой плавления.

Удельную теплоту плавления измеряют в джоулях на килограмм (Дж/кг) и обозначают греческой буквой $λ$ (лямбда).

Удельная теплота кристаллизации равна удельной теплоте плавления, поскольку при кристаллизации выделяется такое же количество теплоты, какое поглощается при плавлении. Так, например, при замерзании воды массой $1$ кг выделяются те же $332$ Дж энергии, которые нужны для превращения такой же массы льда в воду.

Чтобы найти количество теплоты, необходимое для плавления кристаллического тела произвольной массы, или теплоту плавления, надо удельную теплоту плавления этого тела умножить на его массу:

$Q=λm$

Количество теплоты, выделяемое телом, считается отрицательным. Поэтому при расчете количества теплоты, выделяющегося при кристаллизации вещества массой $m$, следует пользоваться той же формулой, но со знаком «минус»:

$-Q=λm$

Удельная теплота сгорания

Теплота сгорания (или теплотворная способность, калорийность) — это количество теплоты, выделяющейся при полном сгорании топлива.

Для нагревания тел часто используют энергию, выделяющуюся при сгорании топлива. Обычное топливо (уголь, нефть, бензин) содержит углерод. При горении атомы углерода соединяются с атомами кислорода, содержащегося в воздухе, в результате чего образуются молекулы углекислого газа. Кинетическая энергия этих молекул оказывается большей, чем у исходных частиц. Увеличение кинетической энергии молекул в процессе горения называют выделением энергии. Энергия, выделяющаяся при полном сгорании топлива, и есть теплота сгорания этого топлива.

Теплота сгорания топлива зависит от вида топлива и его массы. Чем больше масса топлива, тем больше количество теплоты, выделяющейся при его полном сгорании.

Физическая величина, показывающая, какое количество теплоты выделяется при полном сгорании топлива массой $1$ кг, называется удельной теплотой сгорания топлива.

Удельную теплоту сгорания обозначают буквой $q$ и измеряют в джоулях на килограмм (Дж/кг).

Количество теплоты $Q$, выделяющееся при сгорании $m$ кг топлива, определяют по формуле:

$Q=qm$

Чтобы найти количество теплоты, выделяющееся при полном сгорании топлива произвольной массы, нужно удельную теплоту сгорания этого топлива умножить на его массу.

Уравнение теплового баланса

В замкнутой (изолированной от внешних тел) термодинамической системе изменение внутренней энергии какого-либо тела системы $∆U_i$ не может приводить к изменению внутренней энергии всей системы. Следовательно,

$∆U_1+∆U_2+∆U_3+…+∆U_n=∑↙{i}↖{n}∆U_i=0$

Если внутри системы не совершается работа никакими телами, то, согласно первому закону термодинамики, изменение внутренней энергии любого тела происходит только за счет обмена теплом с другими телами этой системы: $∆U_i=Q_i$. Учитывая ($∆U_1+∆U_2+∆U_3+…+∆U_n=∑↙{i}↖{n}∆U_i=0$), получим:

$Q_1+Q_2+Q_3+…+Q_n=∑↙{i}↖{n}Q_i=0$

Это уравнение называется уравнением теплового баланса. Здесь $Q_i$ — количество теплоты, полученное или отданное $i$-м телом. Любое из количеств теплоты $Q_i$ может означать теплоту, выделяемую или поглощаемую при плавлении какого-либо тела, сгорании топлива, испарении или конденсации пара, если такие процессы происходят с различными телами системы, и будут определятся соответствующими соотношениями.

Уравнение теплового баланса является математическим выражением закона сохранения энергии при теплообмене.