Ядерные реакции
-
Темы кодификатора ЕГЭ: ядерные реакции, деление и синтез ядер.
-
Энергетический выход ядерной реакции
-
Деление ядер
-
Цепная ядерная реакция
-
Термоядерная реакция
Автор статьи — профессиональный репетитор, автор учебных пособий для подготовки к ЕГЭ Игорь Вячеславович Яковлев
Темы кодификатора ЕГЭ: ядерные реакции, деление и синтез ядер.
В предыдущем листке мы неоднократно говорили о расщеплении атомного ядра на составные части. Но как этого добиться в действительности? В результате каких физических процессов можно разбить ядро?
Наблюдения радиоактивного распада в изменяющихся внешних условиях — а именно, при различных давлениях и температурах, в электрических и магнитных полях — показали, что скорость радиоактивного распада от этих условий не зависит. Никаких превращений химических элементов друг в друга все эти факторы вызвать не способны. Очевидно, изменения энергии тут слишком малы, чтобы повлиять на атомное ядро — так ветер, обдувающий кирпичный дом, не в состоянии его разрушить.
Но разрушить дом можно артиллерийским снарядом. И Резерфорд в 1919 году решил воспользоваться наиболее мощными «снарядами», которые имелись тогда в распоряжении. Это были -частицы, вылетающие с энергией около 5 МэВ при радиоактивном распаде урана. (Как вы помните, это те самые снаряды, которыми он восемь лет назад бомбардировал лист золотой фольги в своих знаменитых опытах, породивших планетарную модель атома.)
Правда, превращений золота в другие химические элементы в тех экспериментах не наблюдалось. Ядро золота само по себе весьма прочное, да и к тому же содержит довольно много протонов; они создают сильное кулоновское поле, отталкивающее
-частицу и не подпускающее её слишком близко к ядру. А ведь для разбивания ядра
-снаряд должен сблизиться с ядром настолько, чтобы включились ядерные силы! Что ж, раз большое количество протонов мешает — может, взять ядро полегче, где протонов мало?
Резерфорд подверг бомбардировке ядра азота и в результате осуществил первую в истории физики ядерную реакцию:
(1)
В правой части (1) мы видим продукты реакции — изотоп кислорода и протон.
Стало ясно, что для изучения ядерных реакций нужно располагать частицами-снарядами высоких энергий. Такую возможность дают ускорители элементарных частиц. Ускорители имеют два серьёзных преимущества перед естественными «радиоактивными пушками».
1. В ускорителях можно разгонять любые заряженные частицы. В особенности это касается протонов, которые при естественном распаде ядер не появляются. Протоны хороши тем, что несут минимальный заряд, а значит — испытывают наименьшее кулоновское отталкивание со стороны ядер-мишеней.
2. Ускорители позволяют достичь энергий, на несколько порядков превышающие энергию α-частиц при радиоактивном распаде. Например, в Большом адронном коллайдере протоны разгоняются до энергий в несколько ТэВ; это в миллион раз больше, чем 5 МэВ у -частиц в реакции (1), осуществлённой Резерфордом.
Так, с помощью протонов, прошедших через ускоритель, в 1932 году удалось разбить ядро лития (получив при этом две -частицы):
(2)
Ядерные реакции дали возможность искусственного превращения химических элементов.
Кроме того, в продуктах реакций стали обнаруживаться новые, не известные ранее частицы. Например, при облучении бериллия -частицами в том же 1932 году был открыт нейтрон:
(3)
Нейтроны замечательно подходят для раскалывания ядер: не имея электрического заряда, они беспрепятственно проникают внутрь ядра. (При этом ускорять нейтроны не надо — медленные нейтроны легче проникают в ядра. Нейтроны, оказывается, нужно даже замедлять, и делается это пропусканием нейтронов через обычную воду.) Так, при облучении азота нейтронами протекает следующая реакция:
(4)
к оглавлению ▴
Энергетический выход ядерной реакции
Обсуждая энергию связи, мы видели, что в результате ядерных процессов масса системы частиц не остаётся постоянной. Это, в свою очередь, приводит к тому, что кинетическая энергия продуктов ядерной реакции отличается от кинетической энергии исходных частиц.
Прежде всего напомним, что полная энергия частицы массы
складывается из её энергии покоя
и кинетической энергии
:
Пусть в результате столкновения частиц и
происходит ядерная реакция, продуктами которой служат частицы
и
:
(5)
Полная энергия системы частиц сохраняется:
то есть
(6)
Кинетическая энергия исходных частиц равна . Кинетическая энергия продуктов реакции равна
. Энергетический выход
ядерной реакции — это разность кинетических энергий продуктов реакции и исходных частиц:
Из (6) легко получаем:
(7)
Если , то говорят, что реакция идёт с выделением энергии: кинетическая энергия продуктов реакции больше кинетической энергии исходных частиц. Из (7) мы видим, что в этом случае суммарная масса продуктов реакции меньше суммарной массы исходных частиц.
Если же , то реакция идёт с поглощением энергии: кинетическая энергия продуктов реакции меньше кинетической энергии исходных частиц. Суммарная масса продуктов реакции в этом случае больше суммарной массы исходных частиц.
Таким образом, термины «выделение» и «поглощение» энергии не должны вызывать недоумение: они относятся только к кинетической энергии частиц. Полная энергия системы частиц, разумеется, в любой реакции остаётся неизменной.
Чтобы посчитать энергетический выход ядерной реакции (5), действуем по следующему алгоритму.
1. С помощью таблицы масс нейтральных атомов находим и
, выраженные в а. е. м. (для нахождения массы ядра не забываем вычесть из массы нейтрального атома массу электронов).
2. Вычисляем массу исходных частиц, массу
продуктов реакции и находим разность масс
.
3. Умножаем на
и получаем величину
, выраженную в МэВ.
Мы сейчас подробно рассмотрим вычисление энергетического выхода на двух примерах бомбардировки ядер лития
: сначала — протонами, затем —
-частицами.
В первом случае имеем уже упоминавшуюся выше реакцию (2):
Масса атома лития равна
а. е. м. Масса электрона равна
а. е. м. Вычитая из массы атома массу трёх его электронов, получаем массу ядра лития
:
а. е. м.
Масса протона равна а. е. м., так что масса исходных частиц:
а. е. м.
Переходим к продуктам реакции. Масса атома гелия равна а. е. м. Вычитаем массу электронов и находим массу ядра гелия
:
а. е. м.
Умножая на , получаем массу продуктов реакции:
а. е. м.
Масса, как видим, уменьшилась ; это означает, что наша реакция идёт с выделением энергии. Разность масс:
а. е. м.
Выделившаяся энергия:
МэВ.
Теперь рассмотрим второй пример. При бомбардировке ядер лития -частицами происходит реакция:
(8)
Массы исходных ядер нам уже известны; остаётся сосчитать их суммарную массу:
а. е. м.
Из таблицы берём массу атома бора (она равна
а. е. м.); вычитаем массу пяти электронов и получаем массу ядра атома бора:
а. е. м.
Масса нейтрона равна а. е. м. Находим массу продуктов реакции:
а. е. м.
На сей раз масса увеличилась , то есть реакция идёт с поглощением энергии.
Разность масс равна:
а. е. м.
Энергетический выход реакции:
МэВ.
Таким образом, в реакции (8) поглощается энергия МэВ. Это означает, что суммарная кинетическая энергия продуктов реакции (ядра бора и нейтрона) на
МэВ меньше, чем суммарная кинетическая энергия исходных частиц (ядра лития и
-частицы). Поэтому чтобы данная реакция в принципе осуществилась, энергия исходных частиц должна быть не меньше
МэВ.
к оглавлению ▴
Деление ядер
Бомбардируя ядра урана медленным нейтронами, немецкие физики Ган и Штрассман обнаружили появление элементов средней части периодической системы: бария, криптона, стронция, рубидия, цезия и т. д. Так было открыто деление ядер урана.
На рис. 1 мы видим процесс деления ядра (изображение с сайта oup.co.uk.). Захватывая нейтрон, ядро урана делится на два осколка, и при этом освобождаются два-три нейтрона.

Рис. 1. Деление ядра урана
Осколки являются ядрами радиоактивных изотопов элементов середины таблицы Менделеева. Обычно один из осколков больше другого. Например, при бомбардировке урана могут встречаться такие комбинации осколков (как говорят, реакция идёт по следующим каналам).
• Барий и криптон:
• Цезий и рубидий:
• Ксенон и стронций:
В каждой из этих реакций выделяется очень большая энергия — порядка МэВ. Сравните эту величину с найденным выше энергетическим выходом реакции (2), равным
МэВ! Откуда берётся такое количество энергии?
Начнём с того, что из-за большого числа протонов ( штуки), упакованных в ядре урана, кулоновские силы отталкивания, распирающие ядро, очень велики. Ядерные силы, конечно, ещё в состоянии удерживать ядро от распада, но могучий кулоновский фактор готов сказать своё слово в любой момент. И такой момент настаёт, когда в ядре застревает нейтрон (рис. 2 – изображение с сайта investingreenenergy.com).

Рис. 2. Деформация, колебания и разрыв ядра
Застрявший нейтрон вызывает деформацию ядра. Начнутся колебания формы ядра, которые могут стать столь интенсивными, что ядро вытянется в «гантельку». Короткодействующие ядерные силы, скрепляющие небольшое число соседних нуклонов перешейка, не справятся с силами электрического отталкивания половинок гантельки, и в результате ядро разорвётся.
Осколки разлетятся с огромной скоростью — около скорости света. Они и уносят большую часть высвобождающейся энергии (около
МэВ из
).
Деление тяжёлых ядер можно истолковать с точки зрения уже известного нам графика зависимости удельной энергии связи ядра от его массового числа (рис. 3).

Рис. 3. Деление тяжёлых ядер энергетически выгодно
Цветом выделена область , в которой удельная энергия связи достигает наибольшего значения
МэВ/нуклон. Это область наиболее устойчивых ядер. Справа от этой области удельная энергия связи плавно уменьшается до
МэВ/нуклон у ядра урана.
Процесс превращения менее устойчивых ядер в более устойчивые является энергетически выгодным и сопровождается выделением энергии. При делении ядра урана, как видим, удельная энергия связи повышается примерно на МэВ/нуклон; эта энергия как раз и выделяется в процессе деления. Умножив это на число нуклонов в ядре урана, получим приблизительно те самые
МэВ энергетического выхода, о которых говорилось выше.
к оглавлению ▴
Цепная ядерная реакция
Появление двух-трёх нейтронов в процессе деления ядра урана — важнейший факт. Эти нейтроны «первого поколения» могут попасть в новые ядра и вызвать их деление; в результате деления новых ядер возникнут нейтроны «второго поколения», которые попадут в следующие ядра и вызовут их деление; возникнут нейтроны «третьего поколения», которые приведут к делению очередных ядер и т. д. Так идёт цепная ядерная реакция, в ходе которой высвобождается колоссальное количество энергии.
Для протекания цепной ядерной реакции необходимо, чтобы число высвободившихся нейтронов в очередном поколении было не меньше числа
нейтронов в предыдущем поколении. Величина
называеся коэффициентом размножения нейтронов. Таким образом, цепная реакция идёт при условии . Если
, то цепная реакция не возникает.
В случае происходит лавинообразное нарастание числа освобождающихся нейтронов, и цепная реакция становится неуправляемой. Так происходит взрыв атомной бомбы.
В ядерных реакторах происходит управляемая цепная реакция деления с коэффициентом размножения . Стационарное течение управляемой цепной реакции обеспечивается введением в активную зону реактора (то есть в ту область, где протекает реакция) специальных управляющих стержней, поглощающих нейтроны. При полностью введённых стержнях поглощение ими нейтронов настолько велико, что
и реакция не идёт. В процессе запуска реактора стержни постепенно выводят из активной зоны, пока выделяемая мощность не достигнет требуемого уровня. Этот уровень тщательно контролируется, и при его превышении включаются устройства, вводящие управляющие стержни назад в активную зону.
к оглавлению ▴
Термоядерная реакция
Наряду с реакцией деления тяжёлых ядер энергетически возможным оказывается и обратный в некотором смысле процесс — синтез лёгких ядер, то есть слияние ядер лёгких элементов (расположенных в начале периодической таблицы) с образованием более тяжёлого ядра.
Чтобы началось слияние ядер, их нужно сблизить вплотную — чтобы вступили в действие ядерные силы. Для такого сближения нужно преодолеть кулоновское отталкивание ядер, резко возрастающее с уменьшением расстояния между ними. Это возможно лишь при очень большой кинетической энергии ядер, а значит — при очень высокой температуре (в десятки и сотни миллионов градусов). Поэтому реакция ядерного синтеза называется термоядерной реакцией.
В качестве примера термоядерной реакции приведём реакцию слияния ядер дейтерия и трития (тяжёлого и сверхтяжёлого изотопов водорода), в результате которой образуется ядро гелия и нейтрон:
(9)
Эта реакция идёт с выделением энергии, равной МэВ (попробуйте сами провести расчёты и получить данную величину). Это очень много, если учесть, что в реакции участвуют всего
нуклонов! В самом деле, в расчёте на один нуклон в реакции (9) выделяется энергия примерно
МэВ, в то время как при делении ядра урана выделяется «всего»
МэВ на нуклон.
Таким образом, термоядерные реакции служат источником ещё большего количества энергии, чем реакции деления ядер. С физической точки зрения это понятно: энергия реакции ядерного деления есть в основном кинетическая энергия осколков, разогнанных электрическими силами отталкивания, а при ядерном синтезе энергия высвобождается в результате разгона нуклонов навстречу друг другу под действием куда более мощных ядерных сил притяжения.
Проще говоря, при делении ядер высвобождается энергия электрического взаимодействия, а при синтезе ядер — энергия сильного (ядерного) взаимодействия.
В недрах звёзд достигаются температуры, подходящие для синтеза ядер. Свет Солнца и далёких звёзд несёт энергию, выделяющуяся в термоядерных реакциях — при слиянии ядер водорода в ядра гелия и последующем слиянии ядер гелия в ядра более тяжёлых элементов, расположенных в средней части периодической системы. Направление термоядерного синтеза показано на рис. 4; синтез лёгких ядер энергетически выгоден, так как направлен в сторону увеличения удельной энергии связи ядра.

Рис. 4. Синтез лёгких ядер энергетически выгоден
Неуправляемая термоядерная реакция осуществляется при взрыве водородной бомбы. Сначала взрывается встроенная атомная бомба — это нужно для создания высокой температуры на первой ступени термоядерного взрыва. При достижении необходимой температуры в термоядерном горючем бомбы начинаются реакции синтеза, и происходит взрыв собственно водородной бомбы.
Осуществление управляемой термоядерной реакции остаётся пока нерешённой проблемой, над которой физики работают уже более полувека. Если удастся добиться управляемого течения термоядерного синтеза, то человечество получит в своё распоряжение фактически неограниченный источник энергии. Это чрезвычайно важная задача, стоящая перед нынешним и будущими поколениями — в свете угрожающей перспективы истощения нефтегазовых ресурсов нашей планеты.
Благодарим за то, что пользуйтесь нашими статьями.
Информация на странице «Ядерные реакции» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам.
Чтобы успешно сдать необходимые и поступить в ВУЗ или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из данного раздела.
Публикация обновлена:
08.05.2023
Данная тема будет посвящена решению задач на применение
законов сохранения для ядерных реакций, а также научимся рассчитывать
энергетический выход ядерных реакций.
Задача 1. Напишите ядерную реакцию, происходящую при
бомбардировке бериллия α-частицами и сопровождающуюся
выбиванием нейтронов. Изотоп какого элемента образуется при такой реакции?
РЕШЕНИЕ
По условию задачи в результате взаимодействия ядра бериллия с
a-частицей образуется изотоп
некоторого элемента и вылетает нейтрон.
Известно, что в результате ядерных реакций должны выполняться
законы сохранения. В частности, должен выполняться закон сохранения заряда, то
есть суммарный заряд частиц, вступивших в реакцию, должен быть равен суммарному
заряду образовавшихся частиц
Также должен выполняться и закон сохранения массового числа,
то есть массовое число вступивших в реакцию частиц равно массовому числу образовавшихся
частиц
По таблице Менделеева находим, что неизвестный элемент в
реакции — это углерод
Ответ: в результате реакции образуется
ядро изотопа углерода.
Задача 2. Определите энергию, освобождающуюся при
слиянии двух атомов дейтерия с образованием атома трития.
|
ДАНО: |
РЕШЕНИЕ Энергия, выделяющаяся при ядерной реакции Запишем ядерную реакцию Закон сохранения заряда Закон сохранения массового числа Поскольку зарядовое и массовое число равняются 1, то неизвестным Тогда ядерная реакция будет иметь вид Определим сумму масс частиц до реакции Сумма масс частиц после реакции Тогда энергия, выделяющаяся при ядерной реакции равна |
|
|
Ответ: в результате реакции выделилось
4 МэВ энергии.
Задача 3. Вычислите коэффициент полезного действия
двигателей атомной подводной лодки, если их мощность 72 МВт, а реактор
расходует 200 г урана в сутки. Считать, что вследствие деления одного ядра
атома урана выделяется 200 МэВ энергии.
|
ДАНО: |
СИ |
РЕШЕНИЕ Запишем формулу для вычисления коэффициента полезного Полная мощность Количество урана-235 Энергия, выделяемая реактором за сутки Тогда полная мощность Коэффициент полезного действия двигателя |
|
|
Ответ: КПД двигателей атомной
подводной лодки составляет 38%.
Задача 4. Ядро радия 88226Ra испытывает a-распад. Определите отношение
импульсов и кинетических энергий образовавшихся a-частиц и нового ядра, если до распада ядро
радия покоилось.
|
ДАНО: |
РЕШЕНИЕ Импульс α-частицы Импульс нового ядра: Закон сохранения импульса Кинетическая энергия α-частицы: Кинетическая энергия нового ядра: Тогда отношение кинетических энергий равно Реакция α-распада: Закон сохранения массового числа: Отношение кинетических энергий: |
|
|
Ответ: отношение импульсов равно 1, а
отношение кинетических энергий — 55,5.
Задача 5. Найдите энергетический выход реакции, в
которой в результате бомбардировки ядра бериллия протоном, образуется изотоп 36Li и
вылетает a-частица, если
известно, что кинетическая энергия водорода равна 5,45 МэВ, ядра гелия —
4 МэВ и что ядро гелия вылетело под углом 90º к направлению движения
водорода. Ядро-мишень бериллия неподвижно.
|
ДАНО: |
РЕШЕНИЕ Запишем ядерную реакцию Энергетическим выходом ядерной реакции называется разность Энергия частиц вступивших в реакцию Энергия частиц после реакции Кинетическая энергия лития Закон сохранения импульса в проекциях на оси координат: Ох: Оу: Квадрат скорости лития Тогда кинетическая энергия лития Кинетическая энергия водорода Кинетическая энергия гелия Тогда кинетическая энергия лития Энергия частиц после реакции Тогда энергетический выход реакции |
|
|
Ответ: реакция экзотермическая, а ее
энергетический выход составляет 0,01 МэВ или 1,6 ∙ 10−15
Дж.
Задачи, тесты
А. А.
Найдин,
< naidin_anatoli@mail.ru >, МОУ гимназия № 44, г. Новокузнецк, Кемеровская обл.
Расчёт энерговыделения при ядерной реакции
Всё прекрасное так же трудно, как и редко…
Спиноза
Расчёт энерговыделения при ядерных реакциях традиционно труден для учеников средней школы, однако происходящие внутри атомного ядра процессы всегда вызывают у них живой интерес. В школьных учебниках на примерах показано, как определить энергию связи ядра и энергетический выход ядерной реакции, однако совсем не обсуждаются условия протекания ядерной реакции и другие способы расчёта энерговыделения. Попробуем этот недочёт устранить, сгруппировав решаемые на уроке задачи так, чтобы они образовали систему задач, которая будет развивать ученика. Напомним, что ядерные реакции – превращения атомных ядер при взаимодействии с частицами, в том числе с фотонами или друг с другом.
Для протекания ядерной реакции необходимо сближение частиц до расстояний порядка 10–13 см. Что конкретно произойдёт с ядром, зависит от энергии налетающей частицы и энергии связи нуклонов: частица может быть захвачена ядром атома и вызвать ядерную реакцию, может расщепить ядро на фрагменты, может отлететь от ядра при упругом ударе. Ядерные реакции подчиняются законам сохранения электрического заряда, энергии, импульса.
Примеры ядерных реакций (запись комментируют учащиеся):
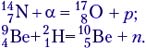
Ядерные реакции могут протекать как с выделением, так и с поглощением энергии. Причём эта энергия по порядку величины в 106 раз больше, чем при химической реакции! Произведём расчёт энерговыделения на примере ядерной реакции:
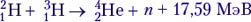
(такие ядерные реакции называются реакциями синтеза):
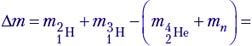 2,01410 а.е.м. + 3,01605 а.е.м. – (4,00260 + 1,00866) а.е.м. = 0,01889 а.е.м. = 0,013136 · 10–27 кг.
2,01410 а.е.м. + 3,01605 а.е.м. – (4,00260 + 1,00866) а.е.м. = 0,01889 а.е.м. = 0,013136 · 10–27 кг.
E = Δmc2 = 0,28221 · 10–11 Дж ≈ 17,6 МэВ.
Ядерные реакции деления покажем на примере одной из возможных схем деления изотопа урана 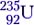 :
:
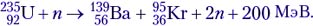
Эта реакция идёт при взрыве атомной бомбы, а также в недрах ядерного реактора. Расчёт энерговыделения производить не будем, но на будущее будем знать, что в среднем на одну реакцию деления изотопа урана выделяется около 200 МэВ энергии.
Реакцию распада удобно показать на примере реакции 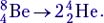 Эта реакция интересна тем, что попытки создать ядро
Эта реакция интересна тем, что попытки создать ядро 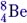 путём двойного α-цикла природа «предпринимала» во время Большого Взрыва, предпринимает и сейчас – в недрах звёзд. Однако это ядро неустойчиво и практически сразу распадается на две α-частицы. Благодаря этому Вселенная в основном состоит из водорода и гелия, а концентрация более тяжёлых элементов в ней незначительна.
путём двойного α-цикла природа «предпринимала» во время Большого Взрыва, предпринимает и сейчас – в недрах звёзд. Однако это ядро неустойчиво и практически сразу распадается на две α-частицы. Благодаря этому Вселенная в основном состоит из водорода и гелия, а концентрация более тяжёлых элементов в ней незначительна.
Сокращённую запись уравнения ядерной реакции покажем на примере реакции 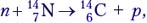 которую записывают в виде
которую записывают в виде 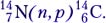
«Установленное Эйнштейном соотношение является основанием для дальнейших, значительно более важных выводов. Радиоактивная отслойка является с этой точки зрения одной из возможностей получения из материи огромных запасов энергии, техническое использование таких запасов энергии в принципе не представляется невыполнимым и совсем недавно Резерфорд получил, по-видимому, подобные количества энергии, – правда, в микроскопическом масштабе, когда ему удалось разложить азот путём радиоактивного расщепления. Но не нужно предаваться иллюзии, будто техническая добыча указанной здесь энергии является вопросом непосредственного будущего и что этим будет достигнуто обесценивание угля; с другой стороны, нельзя возражать и против того, что тут раскрывается одна из серьёзнейших технических проблем».
В.Нернст, 1918
Теперь в процессе решения задач ученикам можно продемонстрировать и другие методы расчёта энерговыделения при ядерной реакции.
«Прибавь ещё один оттенок к радуге…»
У.Шекспир
Задача 1. Одной из наиболее известных реакций термоядерного синтеза является реакция слияния дейтерия и трития: 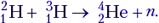 Какая энергия выделяется в этой реакции? Энергия связи дейтерия 2,228 МэВ, трития 8,483 МэВ, гелия 28,294 МэВ.
Какая энергия выделяется в этой реакции? Энергия связи дейтерия 2,228 МэВ, трития 8,483 МэВ, гелия 28,294 МэВ.
Решение. В данной реакции происходит разделение ядер дейтерия и трития на составляющие их частицы, на что затрачивается энергия связи, после чего образуется ядро гелия с выделением энергии. Энергетический выход реакции: Е = 28,294 МэВ – (2,228 МэВ
+ 8,483 МэВ) = 17,583 МэВ. Энергию связи любого ядра ученики уже могут рассчитывать, поэтому для них не представляет большого труда рассчитать энергетический выход любой ядерной реакции таким способом.
Задача 2. Определите энергию реакции 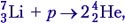 если известно, что энергии связи на один нуклон в ядрах
если известно, что энергии связи на один нуклон в ядрах 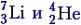 равны соответственно 5,60 и 7,06 МэВ.
равны соответственно 5,60 и 7,06 МэВ.
Решение. Под действием протона ядро лития разрушается, на что затрачивается энергия связи, но при этом возникают два ядра гелия и выделяется энергия Е = 2(4 ∙ 7,06 МэВ/нуклон) – 7 ∙ 5,60 МэВ/нуклон = 17,28 МэВ.
Задача 3. В ядерной реакции 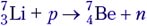 протоны налетают на покоящиеся ядра лития. Если энергия налетающих протонов Е = 1,92 МэВ, то нейтроны, образующиеся в реакции, покоятся. Оцените, какая энергия поглощается в данной реакции. При какой минимальной энергии налетающих протонов эта реакция может идти?
протоны налетают на покоящиеся ядра лития. Если энергия налетающих протонов Е = 1,92 МэВ, то нейтроны, образующиеся в реакции, покоятся. Оцените, какая энергия поглощается в данной реакции. При какой минимальной энергии налетающих протонов эта реакция может идти?
Решение. Это первый пример ядерной реакции, в которой энергия поглощается (Еп). В лабораторной системе отсчёта имеем движущийся со скоростью υ протон и покоящееся ядро лития (рис. а). После ядерной реакции нейтрон неподвижен, а ядро бериллия приобретает некоторую скорость V (рис. б).

По закону сохранения импульса, mpυ = mBeV. Зная массовое число каждой частицы, находим V = (1/7)υ. В лабораторной системе отсчёта 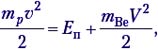 откуда Еп=6/7.
откуда Еп=6/7.
Теперь выясним, при какой минимальной энергии налетающих протонов Е′ эта реакция вообще может идти. В системе отсчёта «центр масс системы протон–ядро лития», которая движется вправо с некоторой скоростью υ′, их импульс mp(υ – υ′) – mLiυ′ = 0, откуда υ′ = 1/8 υ. Если протон обладает минимальной энергией Е′, то в данной системе отсчёта вся она поглощается и возникшие в реакции частицы не разлетаются: 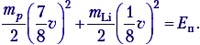 Учитывая, что mLi = 7mp , получим
Учитывая, что mLi = 7mp , получим 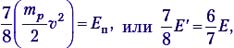 или откуда Е′= 48/49Е.
или откуда Е′= 48/49Е.
Задача 4. Если направить поток протонов на кусок льда из тяжёлой воды D2O, то при минимальной кинетической энергии протонов Е = 1,4 МэВ происходит ядерная реакция с образованием ядер  Какую минимальную энергию надо сообщить ядрам дейтерия, чтобы при их попадании на кусок льда из обычной воды произошла та же ядерная реакция?
Какую минимальную энергию надо сообщить ядрам дейтерия, чтобы при их попадании на кусок льда из обычной воды произошла та же ядерная реакция?
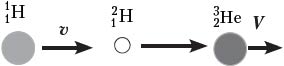
Решение. Запишем закон сохранения импульса и закон сохранения энергии для данной реакции V:
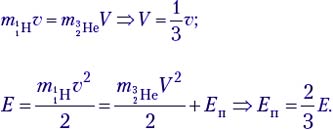
где Еп – энергия, поглощаемая в данной реакции.
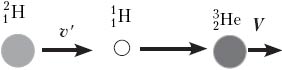
Запишем закон сохранения импульса и закон сохранения энергии для случая, когда ядра дейтерия попадают на кусок льда из обычной воды:
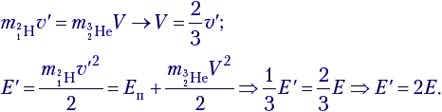
Задача 5. В реакции 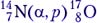 налетающая α-частица имеет кинетическую энергию 7,68 МэВ. Возможна ли такая реакция? Если да, то чему равна полная кинетическая энергия продуктов реакции?
налетающая α-частица имеет кинетическую энергию 7,68 МэВ. Возможна ли такая реакция? Если да, то чему равна полная кинетическая энергия продуктов реакции?
Решение. Найдём дефект массы: 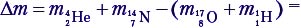 4,00260 + 14,00307 – (16,99913 + 1,00782) = –0,0013 а.е.м.
4,00260 + 14,00307 – (16,99913 + 1,00782) = –0,0013 а.е.м.
Эта реакция идёт с поглощением энергии! Еп = 1,2 МэВ.
Запишем закон сохранения импульса и закон сохранения энергии для этой реакции:
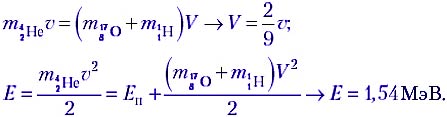
Энергии налетающей частицы вполне достаточно для того, чтобы данная реакция протекала! Полная кинетическая энергия продуктов распада Е – Еп = 6,14 МэВ.
Литература
- Джанколи Д. Физика. – М.: Мир, 1989.
- Савченко О.Я. Задачи по физике. – Новосибирск: НГУ, 1999.
Выход – частица
Cтраница 2
Соответственно прекращение роста выхода частиц при увеличении концентрации углеводорода наступает для бензола значительно раньше, чем для ацетилена. В опытах с ацетиленом, судя по наклону кривой ( рис. 5, кривая 2), максимальный выход частиц еще не был достигнут. По-видимому, максимальный, выход частиц для ацетилена при принятых условиях опытов составляет 2 3 1010 мл-1.
[17]
Точно так же обеспечивают выход частиц в современных ускорителях электронов и протонов при ядерных исследованиях.
[18]
Из анализа результатов по выходу каскадных частиц можно заметить, что для низких энергий выход нуклонов с увеличением атомного номера элемента уменьшается. С повышением энергии выход нуклонов увеличивается; при энергиях порядка 1 Гэв и более начинает увеличиваться выход и с повышением атомного номера ядра-мишени. С увеличением энергии и атомного номера ядра-мишени возрастает относительная часть нейтронов в общем выходе нуклонов.
[19]
Их строят как разность между выходом частиц фракции в целевой продукт и загрязнением другого продукта разделения.
[20]
Для определенности рассматривается задача о выходе частицы, первоначально находившейся в стационарном связанном состоянии, в непрерывный спектр путем туннелирования сквозь барьер. Однако обобщение полученных результатов на другие задачи не представляет труда. Предполагается, что частица находится под действием внутреннего поля t / o, образующего связанное состояние с действительной энергией EQ 0, и поля SU, открывающего барьер.
[21]
С помощью этого уравнения находим точки выхода частицы из магнитной стенки и строим касательные к найденной траектории в этих точках.
[22]
С помощью этого уравнения находим точки выхода частицы из магнитной стенки и в этих точках строим касательные к найденной траектории.
[23]
Нетрудно понять, что отношение скорости выхода частиц из u – й ступени к скорости поступления частиц в систему равно отношению концентраций частиц в А – й ступени каскада и в суспензии, поступающей на вход системы. Таким образом, уравнения (2.29) и (2.31) позволяют определить концентрацию частиц в любой ступени каскада для переходного процесса при постоянной концентрации питания.
[24]
Для смесей метана с ароматическими углеводородами зависимость выхода частиц от концентрации имеет совершенно другой вид. Для малых концентраций бензола и нафталина кривые зависимости выхода частиц от концентрации имеют резко выраженный максимум. Это показывает, что зародыши сажевых частиц из молекул ароматических углеводородов образуются, по-видимому, по другому механизму и со значительно большей скоростью, чем для алифатических углеводородов.
[25]
С увеличением температуры разложения ( рис. 3) выход частиц линейно возрастает.
[27]
Характер кривых, выражающих для разных температур зависимость выхода частиц от концентрации ацетилена, одинаков: повышение концентрации ацетилена приводит сначала к быстрому росту выхода частиц, который затем постепенно замедляется; при концентрациях ацетилена порядка 3 5 – 4 0 % увеличение выхода частиц прекращается. Добавление водорода к смеси, несмотря на значительное повышение температуры ( с 1150 до 1260), тормозит процесс и выход частиц при одинаковых концен – Торп.
[29]
Поверхностные потенциалы следует отличать от доступной измерению работы выхода РГр частицы г, т.е. работы переноса ее из фазы а в точку А, расположенную в вакууме на расстоянии х от границы раздела фаз. Если объемный состав фазы а не изменяется и, следовательно, ц [ сопзг, а поверхностный потенциал этой фазы изменяется, напр. Ха однозначно связано с изменением И ф-лой 5Х – & У. Эта ф-ла лежит основе эксперим.
[30]
Страницы:
1
2
3
4
Ядерная реакция — процесс взаимодействия атомного ядра с другим ядром или элементарной частицей, сопровождающийся изменением состава и структуры ядра, а также выделением вторичных частиц или γ-квантов.
Осуществление ядерной реакции возможно только при сближении ядер атомов вещества вплотную и их попадании в радиус действия ядерных сил. Но ядра любых химических элементов имеют положительный заряд. Поэтому при сближении они отталкиваются за счет действия кулоновских сил. Ядра могут сблизиться друг с другом только в случае, если им сообщить достаточно большую кинетическую энергию. Такую энергию можно им сообщить с помощью специальных ускорителей. Однако для легких ядер достаточно использовать α-частицы или дейтроны — ядро атома дейтерия.
Первая ядерная реакция была осуществлена Э. Резерфордом в 1919 году в опытах по обнаружению протонов в продуктах распада ядер. Ученый бомбардировал атомы азота α-частицами. При соударении частиц происходила ядерная реакция, протекавшая по следующей схеме:
147N+42He→178O+11H
Первая реакция с использованием ускорителей была проведена в 1932 году. Во время нее удалось расщепить атом лития на две α-частицы :
73Li+11H→42He+42He
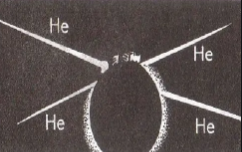
На фотографии треков в камере Вильсона (см. рисунок выше) видно, что ядра гелия разлетаются в разные стороны вдоль одной прямой. Это соответствует закону сохранения импульса (импульс протона много меньше импульса возникающих α-частиц; на фотографии треки протонов не видны).
Внимание! Количество нуклонов до и после реакции есть число постоянное.
Пример №1. При бомбардировке ядер бора 115B протонами получается бериллий 84Be. Какое еще ядро образуется при этой реакции?
Составим схему реакции:
115B+11p=84Be+AZX
Количество нуклонов до и после реакции постоянно. Поэтому зарядовое число нового элемента будет равно разнице суммы зарядов бора и протона и заряда бериллия:
Z=(5+1)−4=2
Массовое число нового элемента будет равно разнице суммы массовых чисел бора и протона и массового числа бериллия:
A=(11+1)−8=4
Вещество с зарядовым числом 2 и массовым числом 4 — гелий. Следовательно, схема получает вид:
115B+11p=84Be+42He
Энергетический выход ядерных реакций
В ядерной реакции по распаду лития при столкновении с быстрым протоном кинетическая энергия двух образующихся ядер гелия оказалась больше кинетической энергии протона, который вступил в реакцию. И разница между ними составила 7,3 МэВ. Это говорит о том, что превращение ядер сопровождается изменением их внутренней энергии, т. е. изменение энергии связи. В рассмотренной реакции удельная энергия связи в ядрах гелия больше удельной энергии связи в ядре лития. Поэтому часть внутренней энергии ядра лития превращается в кинетическую энергию разлетающихся α-частиц.
Изменение энергии связи ядер означает, что суммарная энергия покоя участвующих в реакциях ядер и частиц не остается постоянной. Ведь энергия покоя ядра выражается через энергию связи. В соответствии с законом сохранения энергии изменение кинетической энергии в процессе ядерной реакции равно изменению энергии покоя участвующих в реакции ядер и частиц.
Энергетический выход ядерной реакции — разность энергий покоя ядер и частиц до реакции и после реакции.
Q = (MA + MB – MC – MD)c2 = ΔMc2
где MA и MB – массы исходных продуктов, MC и MD – массы конечных продуктов реакции.
Энергетический выход ядерной реакции равен изменению кинетической энергии частиц, участвующих в реакции. Причем:
- Если суммарная кинетическая энергия ядер и частиц после реакции больше, чем до реакции, то энергия выделяется.
- Если суммарная кинетическая энергия ядер и частиц после реакции меньше, чем до реакции, то энергия поглощается.
Выделяющаяся при ядерных реакциях энергия может быть колоссальной. Но использовать ее при столкновениях ускоренных частиц (или ядер) с неподвижными ядрами мишени практически нельзя. Это связано с тем, что основная часть ускоренных частиц пролетает мимо ядер мишени, не приводя к возникновению реакции.
Пример №2. В результате деления ядра урана 23592U, захватившего нейтрон, образуются ядра бария 14256Ba и криптона 9136Kr, а также три свободных нейтрона. Удельная энергия связи ядер бария 8,38 МэВ/нуклон, криптона – 8,55 МэВ/нуклон и урана – 7,59 МэВ/нуклон. Чему равна энергия, выделенная из одного ядра урана?
Составим схему реакции:
23592U+10n→14256Ba+9136Kr+310n
Из условия задачи известно, сколько энергии имеет каждый нуклон. Нуклон — это 1 протон или нейтрон. Каждый элемент до и после реакции имеет определенные массовые числа:
AU=235
ABa=142
AKr=91
Следовательно, чтобы найти выделившуюся энергию, нужно умножить количество нуклонов на их энергии, а затем найти разность энергий до и после реакции:
Q=EсвUAU−EсвBaABa−EсвKrAKr
Q=7,59·235−8,38·142−8,55·91=−184,36 (МэВ)
Отрицательное число получилось в связи с тем, что суммарная энергия связи ядер образовавшихся элементов больше энергии связи ядра атома урана. Это говорит о том, что энергия при проведении этой реакции будет выделяться в количестве 184,36 МэВ.
Ядерные реакции на нейтронах
Нейтроны не имеют заряда. Поэтому они беспрепятственно проникают в атомные ядра и вызывают их изменения. Например, столкновение нейтрона с ядром атома алюминия может вызвать следующую реакцию:
2713Al+10n→2411Na+42He
Итальянский физик Энрико Ферми, изучавший ядерные реакции на нейтронах, обнаружил, что ядерные превращения вызываются, как быстрыми, так и медленными нейтронами. Причем применение медленных нейтронов часто дает лучшие результаты. Поэтому быстрые нейтроны стали замедлять в воде. После соударения с ядрами водорода, которые по массе примерно равны массе нейтрона, эти нейтроны замедлялись. Их скорость становилась равной скорости теплового движения молекул воды.
Деление ядер урана
В отличие от радиоактивного распада ядер, сопровождающегося испусканием α- или β-частиц, реакции деления —процесс, при котором нестабильное ядро делится на два крупных фрагмента сравнимых масс. В 1939 году немецкие ученые Ган и Штрассман открыли деление ядер урана. Они обнаружили, что при бомбардировке урана нейтронами возникают элементы средней части периодической системы – радиоактивные изотопы бария (Z = 56), криптона (Z = 36) и пр.
Уран встречается в природе в виде двух изотопов: 23892U (99,3 %) и 23592U (0,7 %). При бомбардировке нейтронами ядра обоих изотопов расщепляются на 2 части. Причем реакция деления 23592U лучше идет на медленных нейтронах, в то время как ядра 23892U вступают в реакцию деления только с быстрыми нейтронами, энергия которых составляет около 1 МэВ.
Наибольший интерес для ученых представила реакция деления ядра 23592U. Сегодня известны около 100 различных изотопов с массовыми числами примерно от 90 до 145, которые образуются при делении этого ядра. Две наиболее распространенные реакции деления этого ядра имеют вид:
23592U+10n→14456Ba+8936Kr+310n
23592U+10n→14454Xe+9438Sr+210n
Ядро урана-235 имеет форм шара. При поглощении лишнего нейтрона (рис. а) оно переходит в возбужденное состояние и начинает деформироваться — удлиняться (рис. б). Оно растягивается дальше (рис. в.) до тех пор, пока не распадется с образованием двух новых ядер и испусканием нескольких нейтронов (рис. г).
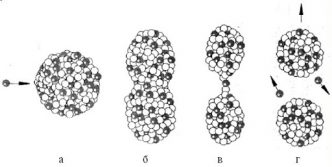
Кинетическая энергия, выделяющаяся при делении одного ядра урана, огромна – порядка 200 МэВ. Оценку выделяющейся при делении ядра энергии можно сделать с помощью понятия удельной энергии связи нуклонов в ядре. Удельная энергия связи нуклонов в ядрах с массовым числом A ≈ 240 порядка 7,6 МэВ/нуклон, в то время как в ядрах с массовыми числами A = 90–145 удельная энергия примерно равна 8,5 МэВ/нуклон. Следовательно, при делении ядра урана освобождается энергия порядка 0,9 МэВ/нуклон или приблизительно 210 МэВ на один атом урана. При полном делении всех ядер, содержащихся в 1 г урана, выделяется такая же энергия, как и при сгорании 3 т угля или 2,5 т нефти.
Цепные ядерные реакции
При делении ядра урана-235, вызванного столкновением с нейтроном, освобождается 2 или 3 нейтрона. При соблюдении некоторых условий эти нейтроны могут попасть в другие ядра урана и вызвать их деление. На этом этапе появятся уже от 4 до 9 нейтронов, способных вызвать новые распады ядер урана и т. д. Такой лавинообразный процесс называется цепной реакцией.
Цепная реакция — ядерная реакция, при которой вызывающие ее частицы (нейтроны), образуются как продукт этой реакции.
Схема цепной реакции урана-235 выглядит так:
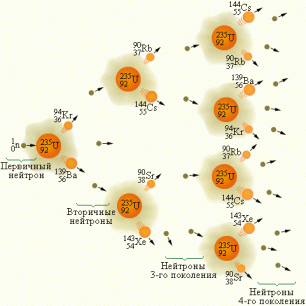
Для осуществления цепной реакции необязательно каждый выделенный нейтрон должен вызывать распад другого ядра урана. Важно лишь, чтобы среднее число освобожденных нейтронов с течением времени не уменьшалось. Такое условие выполняется, если коэффициент размножения нейтронов (k) больше или равен единице: k ≥1.
Коэффициент размножения нейтронов — отношение числа нейтронов в каком-либо «поколении» к числу нейтронов предшествующего поколения.
Коэффициент размножения определяется не только числом нейтронов, образующихся в каждом элементарном акте, но и условиями, в которых протекает реакция – часть нейтронов может поглощаться другими ядрами или выходить из зоны реакции. Нейтроны, освободившиеся при делении ядер урана-235, способны вызвать деление лишь ядер этого же урана, на долю которого в природном уране приходится всего лишь 0,7 %. Такая концентрация оказывается недостаточной для начала цепной реакции. Изотоп урана-238 также может поглощать нейтроны, но при этом не возникает цепной реакции.
Ядерный реактор
Ядерный реактор — устройство, в котором осуществляется и поддерживается управляемая цепная реакция деления некоторых тяжелых ядер.
Первый ядерный реактор был построен в 1942 году в США под руководством Э. Ферми. В нашей стране первый реактор был построен в 1946 году под руководством И. В. Курчатова.
Ядерные энергетические реакторы используются для выработки электроэнергии на атомных электростанциях, в судовых энергетических установках, атомных теплоэлектроцентралях, а также на атомных станциях теплоснабжения.
Основные элементами ядерного реактора:
- ядерное горючее (обычно уран-235);
- замедлитель нейтронов — для получения медленных электронов (тяжелая вода, захватывающая нейтроны, или графит, не захватывающий их);
- теплоноситель для вывода энергии, образующейся при работе реактора (вода, жидкий натрий);
- регулирующие стержни (бор, кадмий) — для регулирования количества высвобожденных электронов (эти вещества способны поглощать много нейтронов);
- защитная оболочка, которая задерживает излучения (железобетон).
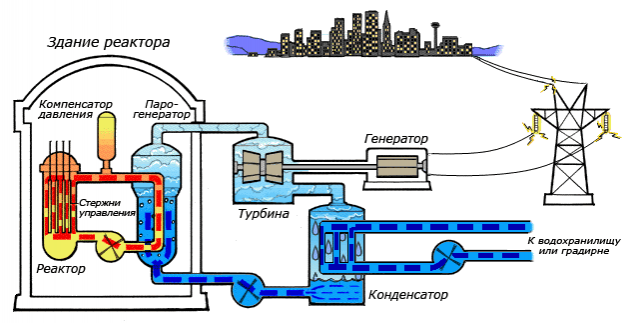
Цепная реакция, как известно, может протекать только при коэффициенте размножения нейтронов k ≥1. Но он может поддерживаться в этом значении только при условии, что масса урана превышает некоторое критическое значение.
Критическая масса — наименьшая масса делящегося вещества, при которой может протекать цепная реакция.
Для чистого урана-235 критическая масса равна 50 кг. При такой массе шар из урана имеет радиус всего 9 см. Если в реакторе использовать оболочку, которая отражает уран, то критическую массу можно снизить до 250 г.
Это интересно! Реактор, работающий на уране-235 и медленных нейтронах, является энергетическим. Его применяют для производства энергии. Но реактор, работающий на уране-235 и быстрых нейтронах, является реактором-размножителем. При распаде 1 кг урана в этом случае образуется 1,5 кг плутония, который также можно использовать как ядерное топливо. При делении урана медленными нейтронами входит в 2,5 раза меньше плутония.
Термоядерные реакции
Масса покоя ядра урана больше суммы масс покоя осколков, на которые делится ядро. Для легких ядер дело обстоит как раз наоборот. Так, масса покоя ядра гелия значительно меньше суммы масс покоя двух ядер тяжелого водорода, на которые можно разделить ядро гелия. Поэтому при слиянии легких ядер масса покоя уменьшается. Следовательно, должна выделяться значительная энергия. Подобного рода реакции слияния легких ядер могут протекать только при очень высоких температурах. Поэтому они называются термоядерными.
Термоядерные реакции — это реакции слияния легких ядер при очень высокой температуре.
Ядра сливаются только при сближении на расстоянии около 10-12 см — тогда они попадают в сферу действия ядерных сил. Этому сближению препятствует кулоновское отталкивание ядер, которое может быть преодолено лишь за счет большой кинетической энергии теплового движения ядер.
Энергия, которая выделяется при термоядерных реакциях в расчете на один нуклон, превышает удельную энергию, выделяющуюся при цепных реакциях деления ядер. Так, при слиянии тяжелого водорода — дейтерия — со сверхтяжелым изотопом водорода — тритием — выделяется около 3,5 МэВ на один нуклон. При делении же урана выделяется примерно 1 МэВ энергии на один нуклон.
Термоядерные реакции играют большую роль в эволюции Вселенной. Энергия излучения Солнца и звезд имеет термоядерное происхождение. По современным представлениям, на ранней стадии развития звезда в основном состоит из водорода. Температура внутри звезды столь велика, что в ней протекают реакции слияния ядер водорода с образованием гелия. Затем при слиянии ядер гелия образуются и более тяжелые элементы.
Если человечество научится управлять термоядерными реакциями, то на Земле появится неисчерпаемый источник энергии. Но пока это невозможно, так как нет таких веществ, которые могли бы выдержать температуру, при которых могут сливаться ядра. Однако неуправляемые реакции проведены уже были. Речь идет о термоядерных бомбах, которые могут уничтожить все человечество.
Задание EF17710
Каково массовое число ядра Х в реакции 95241 Am + 24 He→ X + 2 01 n?
Алгоритм решения
- Записать правило сохранения нуклонов до и после реакции.
- Составить уравнение и вычислить искомое массовое число.
Решение
Количество нуклонов до и после реакции постоянно. Поэтому сумма массовых чисел до реакции и после нее не изменится. Составим уравнение, используя только массовые числа ядер и частиц:
241 + 4 = A + 2
A = 243
Ответ: 243
pазбирался: Алиса Никитина | обсудить разбор
Задание EF18442
Определите массовое и зарядовое число частицы, которая вызывает ядерную реакцию37 Li + … → 48 Вe + 01 n?
Алгоритм решения
- Записать правило сохранения нуклонов до и после реакции.
- Составить уравнение и вычислить искомое массовое число.
- Составить уравнение и вычислить искомое зарядовое число.
Решение
Количество нуклонов до и после реакции постоянно. Поэтому сумма массовых чисел до реакции и после нее не изменится. Составим уравнение, используя только массовые числа ядер и частиц:
7 + А = 8 + 1
A = 2
Составим уравнение, используя только массовые числа ядер и частиц:
3 + Z = 4 + 0
Z = 1
Ответ: 21
pазбирался: Алиса Никитина | обсудить разбор
Задание EF18660
Закону сохранения электрического заряда не противоречит реакция:
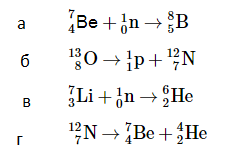
Алгоритм решения
- Записать правило сохранения нуклонов до и после реакции.
- Проверить, где выполняется это правило.
Решение
Количество нуклонов до и после реакции постоянно. Поэтому сумма массовых и зарядовых чисел до реакции и после нее не изменится. Проверим правильность реакций.
Реакция «а»:
7 + 1 = 8
4 + 0 < 5
Реакция «б»:
13 = 1 + 12
8 = 1 + 7
Реакция «в»:
7 + 1 > 6
3 + 0 > 2
Реакция «г»:
12 > 7 + 4
7 > 4 + 2
Подходит только реакция «б».
Ответ: б
pазбирался: Алиса Никитина | обсудить разбор
Алиса Никитина | Просмотров: 2.6k
