Входное и выходное сопротивление
Входное и выходное сопротивление является очень важным в электронике.
Предисловие
Ладно, начнем издалека… Как вы знаете, все электронные устройства состоят из блоков. Их еще часто называют каскады, модули, узлы и тд. В нашей статье будем использовать понятие «блок». Например, источник питания, собранный по этой схеме:
состоит из двух блоков. Я их пометил в красном и зеленом прямоугольниках.
В красном блоке мы получаем постоянное напряжение, а в зеленом блоке мы его стабилизируем. То есть блочная схема будет такой:
Блочная схема — это условное деление. В этом примере мы могли бы даже взять трансформатор, как отдельный блок, который понижает переменное напряжение одного номинала к другому. Как нам удобнее, так и делим на блоки нашу электронную безделушку. Метод «от простого к сложному» полностью работает в нашем мире. На низшем уровне находятся радиоэлементы, на высшем — готовое устройство, например, телевизор.
Ладно, что-то отвлеклись. Как вы поняли, любое устройство состоит из блоков, которые выполняют определенную функцию.
— Ага! Так что же получается? Я могу просто тупо взять готовые блоки и изобрести любое электронное устройство, которое мне придет в голову?
Да! Именно на это нацелена сейчас современная электроника 😉 Микроконтроллеры и конструкторы, типа Arduino, добавляют еще больше гибкости в творческие начинания молодых изобретателей.
На словах все выходит прекрасно, но всегда есть подводные камни, которые следует изучить, чтобы начать проектировать электронные устройства. Некоторые из этих камушков называются входным и выходным сопротивлением.
Думаю, все помнят, что такое сопротивление и что такое резистор. Резистор хоть и обладает сопротивлением, но это активное сопротивление. Катушка индуктивности и конденсатор будут уже обладать, так называемым, реактивным сопротивлением. Но что такое входное и выходное сопротивление? Это уже что-то новенькое. Если прислушаться к этим фразам, то входное сопротивление — это сопротивление какого-то входа, а выходное — сопротивление какого-либо выхода. Ну да, все почти так и есть. И где же нам найти в схеме эти входные и выходные сопротивления? А вот «прячутся» они в самих блоках радиоэлектронных устройств.
Входное сопротивление
Итак, имеем какой-либо блок. Как принято во всем мире, слева — это вход блока, справа — выход.
Как и полагается, этот блок используется в каком-нибудь радиоэлектронном устройстве и выполняет какую-либо функцию. Значит, на его вход будет подаваться какое-то входное напряжение Uвх от другого блока или от источника питания, а на его выходе появится напряжение Uвых (или не появится, если блок является конечным).
Но раз уж мы подаем напряжение на вход (входное напряжение Uвх), следовательно, у нас этот блок будет кушать какую-то силу тока Iвх.
Теперь самое интересное… От чего зависит Iвх ? Вообще, от чего зависит сила тока в цепи? Вспоминаем закон Ома для участка цепи :

Значит, сила тока у нас зависит от напряжения и от сопротивления. Предположим, что напряжение у нас не меняется, следовательно, сила тока в цепи будет зависеть от… СОПРОТИВЛЕНИЯ. Но где нам его найти? А прячется оно в самом каскаде и называется входным сопротивлением.
То есть, разобрав такой блок, внутри него мы можем найти этот резистор? Конечно же нет). Он является своего рода сопротивлением радиоэлементов, соединенных по схеме этого блока. Скажем так, совокупное сопротивление.
Как измерить входное сопротивление
Как мы знаем, на каждый блок подается какой-либо сигнал от предыдущего блока или это может быть даже питание от сети или батареи. Что нам остается сделать?
1)Замерить напряжение Uвх, подаваемое на этот блок
2)Замерить силу тока Iвх, которую потребляет наш блок
3) По закону Ома найти входное сопротивление Rвх.

Если у вас входное сопротивление получается очень большое, чтобы замерить его как можно точнее, используют вот такую схему.
Мы с вами знаем, что если входное сопротивление у нас большое, то входная сила тока в цепи у нас будет очень маленькая (из закона Ома).
Падение напряжения на резисторе R обозначим, как UR





Когда мы проводим эти измерения, имейте ввиду, что напряжение на выходе генератора не должно меняться!
Итак, давайте посчитаем, какой же резистор нам необходимо подобрать, чтобы как можно точнее замерять это входное сопротивление. Допустим, что у нас входное сопротивление Rвх=1 МегаОм, а резистор взяли R=1 КилоОм. Пусть генератор выдает постоянное напряжение U=10 Вольт. В результате, у нас получается цепь с двумя сопротивлениями. Правило делителя напряжения гласит: сумма падений напряжений на всех сопротивлениях в цепи равняется ЭДС генератора.
В результате получается цепь:
Высчитываем силу тока в цепи в Амперах

Получается, что падение напряжения на сопротивлении R в Вольтах будет:

Грубо говоря 0,01 Вольт. Вряд ли вы сможете точно замерить такое маленькое напряжение на своем китайском мультиметре.
Какой отсюда вывод? Для более точного измерения высокого входного сопротивления надо брать добавочное сопротивление также очень большого номинала. В этом случае работает правило шунта: на бОльшем сопротивлении падает бОльшее напряжение, и наоборот, на меньшем сопротивлении падает меньшее напряжение.
Измерение входного сопротивления на практике
Ну все, запарка прошла ;-). Давайте теперь на практике попробуем замерить входное сопротивление какого-либо устройства. Мой взгляд сразу упал на Транзистор-метр. Итак, выставляем на блоке питания рабочее напряжение этого транзистор-метра, то есть 9 Вольт, и во включенном состоянии замеряем потребляемую силу тока. Как замерить силу тока в цепи, читаем в этой статье. По схеме все это будет выглядеть вот так:
Итак, у нас получилось 22,5 миллиАмпер.
Теперь, зная значение потребляемого тока, можно найти по этой формуле входное сопротивление:


Выходное сопротивление
Яркий пример выходного сопротивления — это закон Ома для полной цепи, в котором есть так называемое «внутреннее сопротивление». Кому лень читать про этот закон, вкратце рассмотрим его здесь.
Что мы имели? У нас был автомобильный аккумулятор, с помощью которого мы поджигали галогенную лампочку. Перед тем, как цеплять лампочку, мы замеряли напряжение на клеммах аккумулятора:
И как только подсоединяли лампочку, у нас напряжение на аккумуляторе становилось меньше.
Разница напряжения, то есть 0,3 Вольта (12,09-11,79) у нас падало на так называемом внутреннем сопротивлении r 😉 Оно же и есть ВЫХОДНОЕ СОПРОТИВЛЕНИЕ. Его также называют еще сопротивлением источника или эквивалентным сопротивлением.
У всех аккумуляторов есть это внутреннее сопротивление r, и «цепляется» оно последовательно с источником ЭДС (Е).
Но только ли аккумуляторы и различные батарейки обладают выходным сопротивлением? Не только. Выходным сопротивлением обладают все источники питания. Это может быть блок питания, генератор частоты, либо вообще какой-нибудь усилитель.
В теореме Тевенина (короче, умный мужик такой был) говорилось, что любую цепь, которая имеет две клеммы и содержит в себе туеву кучу различных источников ЭДС и резисторов разного номинала можно привести тупо к источнику ЭДС с каким-то значением напряжения (Eэквивалентное) и с каким-то внутренним сопротивлением (Rэквивалентное).
Eэкв — эквивалентный источник ЭДС
Rэкв — эквивалентное сопротивление
То есть получается, если какой-либо источник напряжения питает нагрузку, значит, в источнике напряжения есть ЭДС и эквивалентное сопротивление, оно же выходное сопротивление.
В режиме холостого хода (то есть, когда к выходным клеммам не подцеплена нагрузка) с помощью мультиметра мы можем замерить ЭДС (E). С замером ЭДС вроде бы понятно, но вот как замерить Rвых ?
В принципе, можно устроить короткое замыкание. То есть замкнуть выходные клеммы толстым медным проводом, по которому у нас будет течь ток короткого замыкания Iкз.
В результате у нас получается замкнутая цепь с одним резистором. Из закона Ома получаем, что

Но есть небольшая загвоздка. Теоретически — формула верна. Но на практике я бы не рекомендовал использовать этот способ. В этом случае сила тока достигает бешеного значения, да вообще, вся схема ведет себя неадекватно.
Измерение выходного сопротивления на практике
Есть другой, более безопасный способ. Не буду повторяться, просто скопирую со статьи закон Ома для полной цепи, где мы находили внутреннее сопротивление аккумулятора. В той статье, мы к акуму цепляли галогенную лампочку, которая была нагрузкой R. В результате по цепи шел электрический ток. На лампочке и на внутреннем сопротивлении у нас падало напряжение, сумма которых равнялась ЭДС.
Итак, для начала замеряем напряжение на аккумуляторе без лампочки.
Так как у нас в этом случае цепь разомкнута (нет внешней нагрузки), следовательно сила тока в цепи I равняется нулю. Значит, и падение напряжение на внутреннем резисторе Ur тоже будет равняться нулю. В итоге, у нас остается только источник ЭДС, у которого мы и замеряем напряжение. В нашем случае E=12,09 Вольт.
Как только мы подсоединили нагрузку, то у нас сразу же упало напряжение на внутреннем резисторе и на нагрузке, в данном случае на лампочке:
Сейчас на нагрузке (на галогенке) у нас упало напряжение UR=11,79 Вольт, следовательно, на внутреннем резисторе падение напряжения составило Ur=E-UR=12,09-11,79=0,3 Вольта. Сила тока в цепи равняется I=4,35 Ампер. Как я уже сказал, ЭДС у нас равняется E=12,09 Вольт. Следовательно, из закона Ома для полной цепи высчитываем, чему у нас будет равняться внутреннее сопротивление r:


Заключение
Входное и выходное сопротивление каскадов (блоков) в электронике играют очень важную роль. В этом мы убедимся, когда начнем рассматривать статью по согласованию узлов радиоэлектронных схем. Все качественные вольтметры и осциллографы также стараются делать с очень высоким входным сопротивлением, чтобы оно меньше сказывалось на замеряемый сигнал и не гасило его амплитуду.
С выходным сопротивлением все намного интереснее. Когда мы подключаем низкоомную нагрузку, то чем больше внутреннее сопротивление, тем больше напряжение падает на внутреннем сопротивлении. То есть в нагрузку будет отдаваться меньшее напряжение, так как разница осядет на внутреннем резисторе. Поэтому, качественные источники питания, типа блока питания либо генератора частоты, пытаются делать как можно с меньшим выходным сопротивлением, чтобы напряжение на выходе «не проседало» при подключении низкоомной нагрузки. Даже если сильно просядет, то мы можем вручную подкорректировать с помощью регулировки выходного напряжения, которые есть в каждом нормальном источнике питания. В некоторых источниках это делается автоматически.
Источник
Расчёт делителя напряжения.
Следует иметь ввиду, что расчёт выходного напряжения U2 справедлив, при сопротивлении нагрузки близком к бесконечности. При низком сопротивлении нагрузки, резистор R2 расчитывается, как два параллельно соединённых резистора.
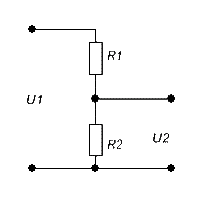
U1 = Входное напряжение
U2 = Выходное напряжение
Расчёт делителя производится по следующей формуле.
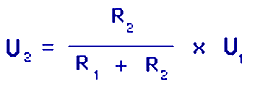
Расчёт позволяет найти любую необходимую величину.
Например; известно входное напряжение, необходимое выходное и имеется R2 определённого номинала. Вводим эти величины и находим R1. И так далее.
Напряжение в дробных частях вводить через “точку”. Например два с половиной вольта = 2.5
Unit Converter
Enter the input voltage (volts), the resistance of resistor 1 (ohms), and the resistance of resistor 2 (ohms) into the calculator to determine the Output Voltage.
- All Electrical Calculators
- Attenuation Calculator
- Parallel Voltage Calculator
- Voltage Divider Calculator
- Thevenin Voltage Calculator
Output Voltage Formula
The following formula is used to calculate the Output Voltage.
- Where Vo is the Output Voltage (volts)
- Vi is the input voltage (volts)
- R1 is the resistance of resistor 1 (ohms)
- R2 is the resistance of resistor 2 (ohms)
To calculate the output voltage, multiply the input voltage by the 1st resistance, then divide by the sum of both resistances.
How to Calculate Output Voltage?
The following example problems outline how to calculate the Output Voltage.
Example Problem #1
- First, determine the input voltage (volts). In this example, the input voltage (volts) is determined to be 140 .
- Next, determine the resistance of resistor 1 (ohms). For this problem, the resistance of resistor 1 (ohms) is measured to be 50 .
- Next, determine the resistance of resistor 2 (ohms). In this case, the resistance of resistor 2 (ohms) is found to be 4.
- Finally, calculate the Output Voltage using the formula above:
Vo = Vi * R2 / (R1+R2)
Inserting the values from above into the equation gives:
Vo = 140 * 50 / (50+4) = 129.62 (volts)
Example Problem #2
Using the same method as above, determine the variables required by the equation. For this example problem, these are provided as follows:
input voltage (volts) = 301
resistance of resistor 1 (ohms) = 4
resistance of resistor 2 (ohms) = 34
Entering these given values into the calculator above yields:
Vo = 301 * 4 / (4+34) = 31.68 (volts)
|
1 / 1 / 0 Регистрация: 19.01.2014 Сообщений: 39 |
|
|
1 |
|
Найти выходное напряжение20.03.2014, 16:12. Показов 5466. Ответов 15
Найти выходное напряжение по закону Кирхгофа
0 |
|
4174 / 2817 / 707 Регистрация: 16.09.2012 Сообщений: 11,466 |
|
|
20.03.2014, 16:46 |
2 |
|
РешениеПреобразуй треугольник в звезду и всё будет просто. Добавлено через 27 минут
1 |
|
1 / 1 / 0 Регистрация: 19.01.2014 Сообщений: 39 |
|
|
20.03.2014, 16:55 [ТС] |
3 |
|
Преобразуй треугольник в звезду и всё будет просто. Можете подсказать, какая система уравнений у Вас получилась?
0 |
|
4174 / 2817 / 707 Регистрация: 16.09.2012 Сообщений: 11,466 |
|
|
20.03.2014, 17:10 |
4 |
|
Можете подсказать, какая система уравнений у Вас получилась? Ты сначала схему преобразуй, а потом поговорим.
1 |
|
1 / 1 / 0 Регистрация: 19.01.2014 Сообщений: 39 |
|
|
20.03.2014, 17:34 [ТС] |
5 |
|
Так? Тогда получается:
0 |
|
7483 / 4147 / 474 Регистрация: 25.08.2012 Сообщений: 11,529 Записей в блоге: 11 |
|
|
20.03.2014, 17:42 |
6 |
|
1 |
|
1 / 1 / 0 Регистрация: 19.01.2014 Сообщений: 39 |
|
|
20.03.2014, 17:47 [ТС] |
7 |
|
Спасибо,исправил
0 |
|
7483 / 4147 / 474 Регистрация: 25.08.2012 Сообщений: 11,529 Записей в блоге: 11 |
|
|
20.03.2014, 17:52 |
8 |
|
Ну и…?
1 |
|
1 / 1 / 0 Регистрация: 19.01.2014 Сообщений: 39 |
|
|
20.03.2014, 18:29 [ТС] |
9 |
|
Поправьте, пожалуйста
0 |
|
4174 / 2817 / 707 Регистрация: 16.09.2012 Сообщений: 11,466 |
|
|
20.03.2014, 18:40 |
10 |
|
В числителе (+) Добавлено через 4 минуты Добавлено через 3 минуты
1 |
|
1 / 1 / 0 Регистрация: 19.01.2014 Сообщений: 39 |
|
|
20.03.2014, 18:47 [ТС] |
11 |
|
Тогда получается: Так? или где-то ошибся?
0 |
|
4174 / 2817 / 707 Регистрация: 16.09.2012 Сообщений: 11,466 |
|
|
20.03.2014, 18:48 |
12 |
|
Всё правильно!
1 |
|
1 / 1 / 0 Регистрация: 19.01.2014 Сообщений: 39 |
|
|
20.03.2014, 18:49 [ТС] |
13 |
|
Но вы же писали, что будет 3.92 ?)
0 |
|
4174 / 2817 / 707 Регистрация: 16.09.2012 Сообщений: 11,466 |
|
|
20.03.2014, 18:52 |
14 |
|
Теперь U=5,5*4,7/6,6=3,917 B.
1 |
|
7483 / 4147 / 474 Регистрация: 25.08.2012 Сообщений: 11,529 Записей в блоге: 11 |
|
|
20.03.2014, 18:53 |
15 |
|
5,5*4,7/(4,7+1,9)
1 |
|
1 / 1 / 0 Регистрация: 19.01.2014 Сообщений: 39 |
|
|
20.03.2014, 18:53 [ТС] |
16 |
|
Огромное Вам спасибо !!
0 |
Главная » Справочник » Делитель напряжения на резисторах. Формула расчета, онлайн калькулятор
Делитель напряжения — это простая схема, которая позволяет получить из высокого напряжения пониженное напряжение.
Используя только два резистора и входное напряжение, мы можем создать выходное напряжение, составляющее определенную часть от входного. Делитель напряжения является одной из наиболее фундаментальных схем в электронике. В вопросе изучения работы делителя напряжения следует отметить два основных момента – это сама схема и формула расчета.
Схема делителя напряжения на резисторах
Схема делителя напряжения включает в себя входной источник напряжения и два резистора. Ниже вы можете увидеть несколько схематических вариантов изображения делителя, но все они несут один и тот же функционал.
 Обозначим резистор, который находится ближе к плюсу входного напряжения (Uin) как R1, а резистор находящийся ближе к минусу как R2. Падение напряжения (Uout) на резисторе R2 — это пониженное напряжение, полученное в результате применения резисторного делителя напряжения.
Обозначим резистор, который находится ближе к плюсу входного напряжения (Uin) как R1, а резистор находящийся ближе к минусу как R2. Падение напряжения (Uout) на резисторе R2 — это пониженное напряжение, полученное в результате применения резисторного делителя напряжения.
Расчет делителя напряжения на резисторах
Расчет делителя напряжения предполагает, что нам известно, по крайней мере, три величины из приведенной выше схемы: входное напряжение и сопротивление обоих резисторов. Зная эти величины, мы можем рассчитать выходное напряжение.
Формула делителя напряжения

Это не сложное упражнение, но очень важное для понимания того, как работает делитель напряжения. Расчет делителя основан на законе Ома.
Для того чтобы узнать какое напряжение будет на выходе делителя, выведем формулу исходя из закона Ома. Предположим, что мы знаем значения Uin, R1 и R2. Теперь на основании этих данных выведем формулу для Uout. Давайте начнем с обозначения токов I1 и I2, которые протекают через резисторы R1 и R2 соответственно:
 Наша цель состоит в том, чтобы вычислить Uout, а это достаточно просто используя закон Ома:
Наша цель состоит в том, чтобы вычислить Uout, а это достаточно просто используя закон Ома:
![]()
Хорошо. Мы знаем значение R2, но пока неизвестно сила тока I2. Но мы знаем кое-что о ней. Мы можем предположить, что I1 равно I2. При этом наша схема будет выглядеть следующим образом:


Тестер транзисторов / ESR-метр / генератор
Многофункциональный прибор для проверки транзисторов, диодов, тиристоров…
Что мы знаем о Uin? Ну, Uin это напряжение на обоих резисторах R1 и R2. Эти резисторы соединены последовательно, при этом их сопротивления суммируются:
![]()
И, на какое-то время, мы можем упростить схему:

Закон Ома для участка цепи в его наиболее простом виде: Uin = I *R. Помня, что R состоит из R1+R2, формула может быть записана в следующем виде:

А так как I1 равно I2, то:

Это уравнение показывает, что выходное напряжение прямо пропорционально входному напряжению и отношению сопротивлений R1 и R2.
Делитель напряжения — калькулятор онлайн
Применение делителя напряжения на резисторах
В радиоэлектронике есть много способов применения делителя напряжения. Вот только некоторые примеры где вы можете обнаружить их.
Потенциометры
Потенциометр представляет собой переменный резистор, который может быть использован для создания регулируемого делителя напряжения.

Изнутри потенциометр представляет собой резистор и скользящий контакт, который делит резистор на две части и передвигается между этими двумя частями. С внешней стороны, как правило, у потенциометра имеется три вывода: два контакта подсоединены к выводам резистора, в то время как третий (центральный) подключен к скользящему контакту.

Если контакты резистора подключения к источнику напряжения (один к минусу, другой к плюсу), то центральный вывод потенциометра будет имитировать делитель напряжения.
Переведите движок потенциометра в верхнее положение и напряжение на выходе будет равно входному напряжению. Теперь переведите движок в крайнее нижнее положение и на выходе будет нулевое напряжение. Если же установить ручку потенциометра в среднее положение, то мы получим половину входного напряжения.
Резистивные датчики
Большинство датчиков применяемых в различных устройствах представляют собой резистивные устройства. Фоторезистор представляет собой переменный резистор, который изменяет свое сопротивление, пропорциональное количеству света, падающего на него. Так же есть и другие датчики, такие как датчики давления, ускорения и термисторы и др.
Так же резистивный делитель напряжения помогает измерить напряжение при помощи микроконтроллера (при наличии АЦП).
Пример работы делителя напряжения на фоторезисторе.
Допустим, сопротивление фоторезистора изменяется от 1 кОм (при освещении) и до 10 кОм (при полной темноте). Если мы дополним схему постоянным сопротивлением примерно 5,6 кОм, то мы можем получить широкий диапазон изменения выходного напряжения при изменении освещенности фоторезистора.


Как мы видим, размах выходного напряжения при уровне освещения от яркого до темного получается в районе 2,45 вольт, что является отличным диапазоном для работы большинства АЦП.

Блок питания 0…30В/3A
Набор для сборки регулируемого блока питания…

 Сообщение было отмечено Evgen57 как решение
Сообщение было отмечено Evgen57 как решение

