У многих учащихся возникают трудности с решением задач, связанных со вращательным движением тел. Также вызывают стопор задачи с блоками. В основном я это понял во время занятий физикой со своими школьниками и студентами. Поэтому я решил написать статью, в которой рассматриваю 7 случаев с небольшими задачами по динамике блоков. Это те основные кирпичики, из которых складываются все типы задач с блоками. В том числе и олимпиадные. Все примеры представлены от простого к сложному. Приятного чтения 🙂
А пока попрошу подписаться на канал в telegram IT mentor . Автор пишет краткие заметки и наблюдения по физике, математике, программированию, железу и технике 💡
Случай 1
Рассмотрим самый простой случай. Идеальная веревка перекидывается через неподвижный идеальный блок. Мы пытаемся удержать груз, прикрепленный на одном конце веревки, с помощью прикладывания силы F на другом конце веревки. Сначала рассмотрим статическое равновесие. Будем определять силу F, которую нам необходимо прикладывать.
Пожалуй, что из задач с блоками этот пример является самым простым. Допущения, принятые здесь, вполне согласуются с реальной жизнью. Но всё таки это сильно упрощенная модель.
1. Выигрыша в силе мы не имеем;
2. На какое расстояние сдвинули веревку, на такое же расстояние поднимется груз;
3. Удобство поднятия груза заключается в выборе направления тяги.
Случай 2
Немного усложним нашу ситуацию, добавив в систему ускорение. Какую силу нужно приложить, чтобы поднять груз с ускорением? Здесь также будем учитывать, что веревка идеальная:
нерастяжимая — поэтому все ускорения равны
невесомая — поэтому для правого конца выполняется условие F = T (для нулевой массы веревки).
Случай 3
Будем продолжать усложнение конфигурации из грузов и блоков. Что если в систему добавить второй блок, который будет висеть на веревке, один конец которой будет подвешен к потолку, а другой конец протянут через неподвижный блок и в итоге удержан нашей силой F. Рассмотрим статической равновесие системы и попробуем найти силу F. Теперь в задаче появляются две веревки:
Первая короткая нить удерживает груз (на рисунке изображена желтым цветом). Вторая длинная нить протянута через блоки, один конец закреплен в потолке, а другой конец удерживается силой F (на рисунке нить обозначена оранжевым цветом).
Мы получили выигрыш в силе в два раза. Простыми словами объяснить это можно так: 50 кг мы сможем удержать, тянув за свободный конец оранжевой веревки так, как будто мы бы удерживали 25 кг в ситуации с одним неподвижным блоком (Случай 1).
Как-то раз, занимаясь в тренажерном зале, я обратил внимание на разговор двух своих друзей. Они рассуждали, что поднимали на бицепс 70 кг в тренажере (так было написано на плитках, когда вставляешь штырек в определенный вес). Мне было интересно и я спросил: «Если в тренажере вы поднимаете 70 кг на бицепс, то почему же не можете поднять штангу в 70 кг также на бицепс?». Вопрос вызвал замешательство… Действительно, они не обращали на это внимание раньше. Вы, мои дорогие читатели, уже наверняка догадались в чем подвох. Конечно же в тренажере был подвижный ролик, тот самый блок, который катался вверх-вниз, удерживываемый тросиком, и давал выигрыш в силе в 2 раза. То есть по факту человек поднимает в этом тренажере 35 кг, а не 70 кг, как написано на плитках. Многие об этом не задумываются 🙂
Подвижный блок можно считать воистину крутым изобретением человечества. Ведь он дает возможность поднять груз, который мы бы никогда не подняли своими силами без этого хитрого приспособления.
Но во всём ли мы выигрываем? Нет, не во всём. Как и любой рычаг, подвижный блок помогает выиграть в силе, но проиграть в расстоянии. Это можно понять, если считать, что работа, выполняемая нами по мерещению груза (изменению его потенциальной энергии в случае подъема) является величиной постоянной ( *здесь мы пока не учитываем трение, которое есть в любых блоках, подшипниках и других механизмах ).
Как видите по рисункам, выиграть можно и в 4 раза, используя только два блока. Такая конструкция часто применяется в подъемных кранах. Однако, чем тяжелее груз, тем медленнее его будут поднимать. Такой же принцип наблюдается в коробке передач автомобиля, такой же принцип работает в переключении скоростей велосипеда. Чем быстрее, тем труднее. Или наоборот, чем легче, тем медленее.
Случай 4
Что если мы усложним наш пример, включив в него ускорение? Здесь важно не забыть учесть тот момент, который мы уже обсуждали в предыдущем пункте. Ускорение центра масс подвижного блока будет в два раза меньше, чем ускорение свободного конца длинной нити, протянутой через два блока. Почему? Попытаюсь это продемонстрировать на рисунке ниже.
Определить соотношение сил и перемещений можно с помощью метода виртуальных перещений. Однажды во время строительства одного из соборов в Швейцарии его архитектору понадобились блоки, позволяющие поднимать на большую высоту особо тяжелые грузы. Он сконструировал сложный полиспаст ( это грузоподъемное устройство, которое натягивается несколькими тросами. подробнее ), но запутался в многочисленных силах натяжения тросов и не смог рассчитать, сколько рабочих будет нужно нанимать для обслуживания грузоподъемного устройства. Архитектор обратился за помощью к известному ученому того времени Иоганну Бернулли (1667 – 1748). Едва взглянув на чертеж, Бернулли сразу же дал ответ. Разумеется, архитектор был очень удивлен и попросил объяснить ему суть решения…
Часто в задаче нужно учесть условия равновесия системы. Для этого определяются силы реакций механических связей. Связи — это ограничения, наложенные на положение отдельных частей системы или их возможные перемещения. Связями могут быть нити, шарниры, блоки. Чем больше связей, тем сложнее проследить за возникающими в них реакциями.
В большинстве случаев мехнические связи обладают интересным свойством, которое Бернулли положил в основу своего простого и изящного способа нахождения условий равновесия механической системы. Напишем это свойство:
Полная работа всех сил реакции, возникающих в связях системы при любых достаточно малых возможных отклонениях системы от положения равновесия, равна нулю.
Замечание: любые возможные отклонения не должны противоречить механическим связям: нити не должны рваться, шарниры не должны ломаться, блоки не должны деформироваться. Это и есть возможные или виртуальные перемещения.
Бернулли сформулировал этот принцип в 1717 году. Получается, что для исследования равновесия системы, достаточно выбрать удобные виртуальные перемещения (мы рисовали это выше), вычислить соответствующую им работу только внешних сил, а затем приравнять её к нулю.
Хотите простейший пример на применение данного метода? Давайте представим, что некоторый груз массой m подвешивают на пружину, и он её растягивает с силой тяжести m•g. При этом в самой пружине возникает сила упругости T. Допустим, груз сместился вниз на маленькую величину Δx. Тогда работа силы тяжести будет равна ΔA₁ = m•g•Δx, а работа силы упругости пружины будет ΔA₂ = − T•Δx. Знак минус здесь стоит потому что сила упругости всегда направлена против перемещения (вспоминайте закон Гука). Тогда, согласно принципу возможных перемещений, сумма работ обеих сил должна быть равна нулю:
ΔA₁ + ΔA₂ = m•g•Δx − T•Δx = 0 откуда получаем T = m•g
Замечание: Конечно же эту задачу можно решить обычным способом. Более того, оба метода будут примерно одинаковы по степени сложности. НО, существуют случаи, когда применение метода возможных перемещений дает более быстрое и простое решение. Иногда позволяет решать задачи, которые не разрешаются на основе обычнх уловий равновесия. Этот метод можно применяться не только для задач механики, но и для задач электростатики или молекулярной физики.
Итак, ускорение повлияет на силы, но не сильно. Мы же помним, что в нашем случае блоки по-прежнему идеальные, то есть их массу мы принимает за ноль (соответственно, момент инерции тоже).
Вот на этом моменте уже хочется обозначить несколько общих принципов решения таких задач.
Алгоритм, общие принципы, замечания
1. При решении нужно выяснить, какие силы действуют на тело, движение которого мы рассматриваем в конкретный момент времени. Все известные силы надо изобразить, сделать рисунок. Понимать со стороны каких тел действуют рассматриваемые силы. Действие одного тело на другое является взаимным (третий закон Ньютона). Бывает такое, что направление силы заранее неизвестно. Здесь не стоит переживать. Выберите то направление, которое вам кажется верным. При проецировании второгой закона Ньютона вы сможете получить численные значения для проекций. И если они будут положительные, то вы угадали с направлением. А если будут отрицательные, то вы не угадали, значит рисунок нужно подкорректировать, инвертировал стрелку, обозначающую силу. Если в задаче рассматривается несколько тел, то разумеется нужно расставить силы, действующие на все тела.
2. Далее осуществляется выбор системы отсчета. Оси (базис XOY) нужно выбирать так, что проекции был как можно более простыми, то есть чтобы как можно большее количество сил были параллельны или перпендикулярны выбранным осям.
3. Для каждого тела в системе записывается второй закон Ньютона. Затем этот закон проецируется на оси выбранного базиса (см 2 пункт). По началу вы можете сразу подставлять в полученную систему уравнений известные вам силы, углы, массы и проекции сил. Однако хорошим тоном является доведения решения до конца в буквенном виде. Если вы сейчас учитесь в школе, то обязательно научитесь оперировать буквами без подстановки чисел.
4. Для решения задач о движении системы тел одних уравнений движения (проекций второго закона Ньютона) может быть недостаточно. Нужна записать ещё все кинематические условия. Эти условия определяют соотношения между ускорениями различных объектов системы, обусловленные связями между ними.
Пример для неподвижных блоков: тела, связанные нерастяжимой нитью (идеальная нить), имеют вдоль этой нити одинаковые по модулю ускорения. И не важно через сколько неподвижных блоков перекинута нить.
Пример для подвижных блоков: При наличии подвижных блоков, ускорение тела (или свободного конца нити), перекинутой через неподвижный блок в два раза больше ускорения тела, прикрепленного к подвижному блоку. Так как за одинаковое время пройденные пути отличаются в два раза (мы это разбирали выше в статье).
5. Во множестве простых задач теоретической механики массой нитей, связывающих тела, пренебрегают. Только тогда натяжение таких нитей одинаково, какое бы мы не взяли сечение на всей длине.
6. Массой блоков также пренебрегают во множестве задач. В этих случаях натяжение нити, перекинутой через такой идеальный блок, можно считать одинаковым по обе стороны блока. В противном случае, если учитывать массу, то натяжения будут разными, угловая скорость будет меняться, то есть у нас появится вращающий момент сил, угловое ускорение и момент инерции реального блока.
7. Очень полезно попытаться понять как будут изменяться искомые величины при изменениях заданных величин. Если вы построите графики таких зависимостей, то сможете лучше разобраться в задаче.
Случай 5
Давайте рассмотрим задачу, в которой мы имеем два разных груза и два разных блока (подвижный и неподвижный.
Задача
Найдите силы натяжения T₁ и T₂ нитей abcd и ce в устройстве с подвижным блоком, изображенном на рисунке. Массы тел соответственно равны m₁ = 2 кг и m₂ = 3 кг.
Решение:
Обратите внимание, что сила натяжения оранжевой длинной веревки abcd меньше, чем сила натяжения короткой желтой веревки ce, хотя на короткой веревке груз висит более легкий, чем на длинной веревке. Получается, что сила натяжения уменьшается при постоянном движении троса.
Случай 6
В задачах на блоки грузы необязательно могут быть подвешены. Бывает так, что грузы скользят по плоскостям, потому как блок опускается под действием силы тяжести груза, прикрепленного к нему. Рассмотрим такой случай.
Задача
На рисунке изображена система движущихся тел, имеющих массы m₁ = m, m₂ = 4m, m₃ = m. Наклонная плоскость составляет с горизонтом угол α = 30°. Трение отсутствует. Определите силы натяжения нитей.
Решение:
Случай 7
Встречаются и более редкие задачи, которые вводят учащихся в замешательство. Это задачи связанные с реальными блоками. Основное отличие заключается в том, что мы учитываем массу блока, а следовательно учитываем его момент инерции. Для раскрутки блока с массой (реального блока) нужен ненулевой момент сил (в сторону вращения). Значит такие задачи отличаются тем, что силы натяжения одной и той же нити на таком блоке будут разные по обе стороны от перегиба нити на блоке. Звучит сложно? Понимаю… Сейчас мы разберемся как это работает на практике.
При описании движения по окружности (другими словами при описании вращения тела) удобно использовать величины угла поворота φ, угловой скорости ω, углового ускорения ε и момента сил M.
Роль массы при вращении тела (или движении по окружности) играет величина J = m·R². Будем называть эту величину моментом инерции. Тогда уравнение вращательного движения по окружности для точки можно записать в виде: J·ε = M. По своей сути последнее уравнение является удобной записью второго закона Ньютона в проекциях на тангенциальное (касатальное) направление при движении по окружности.
Момент инерции является мерой инертности тела. К примеру, камень на длинной верёвке будет раскрутить сложнее, чем на короткой.
Вопрос читателям канала: Почему велосипедной колесо до одной и той же угловой скорости легче раскрутить пацльцем, если прикладывать силу к ободу колеса, чем если прикладывать силу к спицам возле втулки?
Блоки из наших задач выше не являются материальными точками. Поэтому момент инерции для них выводится с помощью суммирования моментов инерции всех частичек (материальных точек), из которых состоит блок.
Наш блок мы будем представлять в виде сплошного диска, сделанного из однородного материала. Момент инерции такого блока J = 1/2·m·R². Возможно, вам непонятно откуда взялась 1/2 ? Тогда выведем формулу…
Вывод формулы для момента инерции кольца и диска (блока) при вращении вокруг оси, проходящей через центр симметрии диска (блока):
Задача с реальным блоком
Через блок, представляющий собой сплошной диск радиусом R, перекинута нить. На нити подвешены грузы массами m₁ и m₂ ( m₂ > m₁). Масса блока m. Определите разность сил натяжения нитей с обеих сторон блока и ускорение грузов. Считать, что нить нерастяжима и не может скользить по блоку.
Решение:
Как видно из решения, больше натягивается та часть нити, в сторону которой происходит вращение блока, то есть та часть, которая разматывает блок. Именно она и может порваться, ведь натяжение в ней больше. Обратим внимание, что разница натяжений в частях нити пропорциальна ускорение грузов и массе блока.
В этой статье разобрано 7 основных случаев, из которых состоят задачи на блоки. И я очень надеюсь, что вам было интересно почитать эту статью. Ибо время на неё было потрачено очень много.
💾 Метод виртуальных перемещений (скачать полезные задачи в pdf)
Ладно, пора заканчивать эту бесконечную статью… А то, боюсь, что до этого момента уже никто не дочитает. Тяжело читать статьи, в которых много математики. Есть и более приятный контент для расслабления.
📚 На Дзен недавно появился интересный канал «Читающий Лингвист». Автор канала пишет замечательные рецензии на зарубежную литературу, рассказывает о прочитанном и делает заметки на околокнижные лингвистические наблюдения.
Советую подписаться на этот авторский канал «Читающего Лингвиста»
Понравилась статья? Поставьте лайк, подпишитесь на канал! Вам не сложно, а мне очень приятно 🙂
Если Вам нужен репетитор по физике, математике или информатике/программированию, Вы можете написать мне или в мою группу Репетитор IT mentor в VK
Библиотека с книгами для физиков, математиков и программистов
Репетитор IT mentor в telegram
Содержание:
Золотое правило механики:
Используя простые механизмы, можно изменять как силу, приложенную к телу, так и путь, от которого зависит значение работы. Означает ли это, что с помощью простых механизмов можно получить выигрыш в работе?
Теоретические сведения
В технике, на производстве и в повседневной жизни используют простой механизм, который называется наклонная плоскость. Это устройство, в котором длинная доска или рейка положена так, что образует некоторый угол с горизонтом. Как правило, этот угол меньше 45о.
Использование наклонной плоскости позволяет получить выигрыш в силе. Выигрыш в работе, как утверждает «золотое правило» механики, получить невозможно. В реальных условиях тот, кто пользуется наклонной плоскостью, даже проигрывает в работе, поскольку при перемещении тела но наклонной плоскости выполняется дополнительная работа по преодолению трения.
Золотое правило механики
Рассмотренные нами простые механизмы применяют при выполнении работы в тех случаях, когда нужно меньшей силой уравновесить большую. Тогда перед нами встаёт вопрос: Простые механизмы дают выигрыш в силе, а дают ли они выигрыш в работе ?
Уравновесим рычаг, приложив к нему две разные по значению силы 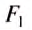
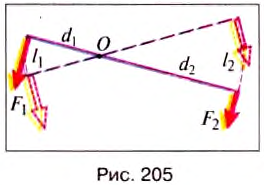
Видим, что теперь в правиле рычага можно заменить отношение плечей сил на отношение путей точек приложения сил, тогда получим: 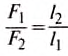 Из свойства пропорции вытекает:
Из свойства пропорции вытекает: 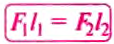
По определению механической работы: 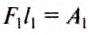 а
а 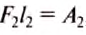 , т. е.
, т. е. 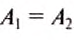 , отсюда делаем следующий вывод.
, отсюда делаем следующий вывод.
Рычаг выигрыша в работе не даёт.
Это касается и других простых механизмов.
Ни один из простых механизмов не даёт выигрыша в работе: во сколько раз выигрываем в силе, во столько же раз проигрываем в расстоянии.
Это правило назвали «золотым правилом» механики.
Дает ли выигрыш в работе простой механизм
Закрепим конец нити на крючке динамометра и прикрепим к ней груз массой 1 кг (рис.124). Начнем равномерно поднимать его вверх. Динамометр покажет, что к нити приложена сила 9,8 Н. Поднимем груз на высоту 0,25 м и рассчитаем работу, которая при этом будет выполнена:
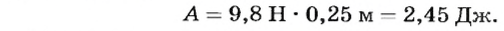
Конец нити закрепим неподвижно на штативе и пропустим ее через подвижный блок, к которому прикреплен груз массой 1 кг.
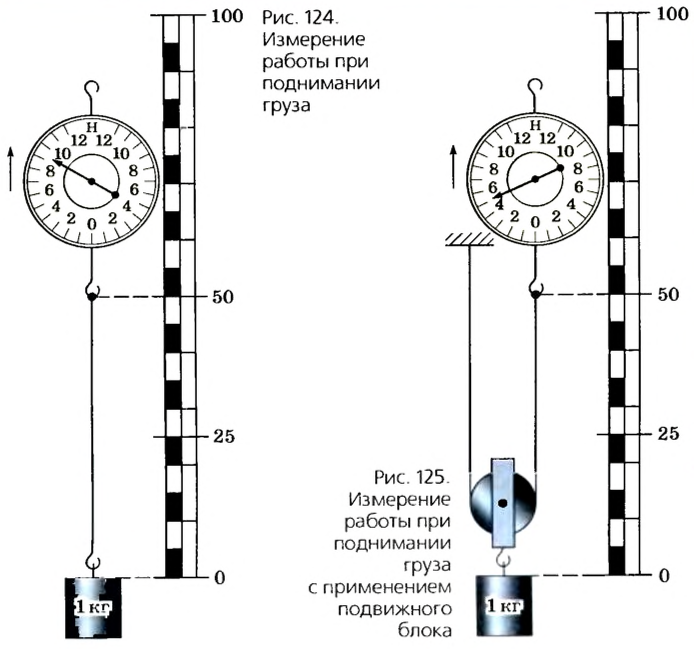
К свободному концу нити прикрепим динамометр и обозначим на линейке положение точки присоединения динамометра (рис. 125). Постепенно будем поднимать динамометр до тех пор, пока груз не переместится на 0,25 м. Динамометр при этом будет показывать силу 4,9 Н, но путь, который прошла точка присоединения динамометра, будет равен 0, 5 м. Выполненная работа в этом случае 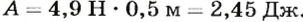
Проанализировав результаты эксперимента, можно сделать вывод, что использовав подвижный блок, мы получили выигрыш в силе в 2 раза, но проиграли в пути, на котором действовала эта сила, тоже в 2 раза. Работа оказалась одинаковой и в первом, и во втором случае.
Итак, поднимать груз при помощи подвижного блока легче, чем без него. Однако путь, на котором действует сила, будет соответственно большим.
Никакого выигрыша в работе блок не дал. Подобное явление можно наблюдать и при использовании рычага и наклонной плоскости. Такая закономерность была замечена учеными еще в античные времена и выражена в «золотом правиле» механики.
«Золотое правило» механики – это когда ни один простой механизм не дает выигрыша в работе. Если выигрываем в силе, то проигрываем в расстоянии.
При использовании простых механизмов оказывается, что при этом имеется даже некоторый проигрыш в работе. Так, выполняя работу с помощью простого механизма, нужно перемещать еще блок или рычаг, имеющих определенный вес, преодолевать силы трения. Эту работу нельзя назвать полезной.
Как оценить качество простого механизма
Чтобы оценить качество какого-либо простого механизма, сравнивают полезную работу, которую необходимо выполнить без этого механизма, с работой, которая выполняется с использованием простого механизма.
Число, показывающее, какую часть от всей выполненной работы 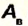 составляет полезная работа
составляет полезная работа 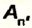 называют коэффициентом полезного действия (КПД):
называют коэффициентом полезного действия (КПД):

В формулах КПД обозначают греческой буквой 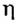 («эта»).
(«эта»).
Коэффициент полезного действия удобно выражать в процентах. Тогда

Коэффициент полезного действия может иметь различные значения. Чем его значение больше, тем лучшим считается механизм. Но ни один исследователь или инженер не смог бы изготовить механизм с КПД большим или равным 100 %. И это не из-за несовершенства технологий. Просто этому мешают законы природы, которые человек не в силах изменить.
Таким образом, чтобы оценить качество механизма, необходимо сравнить выполненную и полезную работу.
- Заказать решение задач по физике
Пример задачи с решением
С помощью подвижного блока массой 2 кг на высоту 5 м подняли груз массой 20 кг. Определить коэффициент полезного действия установки.
Дано:
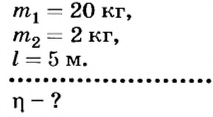
Решение
По определению 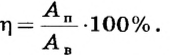
Полезная работа 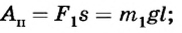
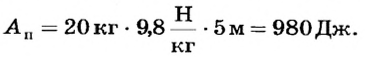
Выполненная работа
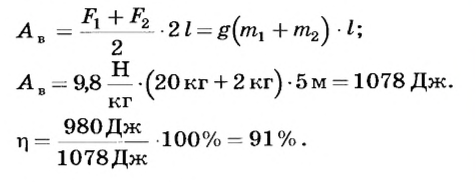
Ответ. 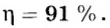
- Потенциальная энергия
- Кинетическая энергия
- Закон сохранения и превращения механической энергии
- Работа, мощность и энергия
- Энергия в физике
- Мощность в физике
- Взаимодействие тел
- Механическая энергия и работа
Простые механизмы.
-
Рычаг.
-
Неподвижный блок.
-
Подвижный блок.
-
Наклонная плоскость.
-
Золотое правило механики.
-
КПД механизма.
Автор — профессиональный репетитор, автор учебных пособий для подготовки к ЕГЭ Игорь Вячеславович Яковлев
Темы кодификатора ЕГЭ: простые механизмы, КПД механизма.
Механизм – это приспособление для преобразования силы (её увеличения или уменьшения).
Простые механизмы – это рычаг и наклонная плоскость.
Рычаг.
Рычаг – это твёрдое тело, которое может вращаться вокруг неподвижной оси. На рис. 1) изображён рычаг с осью вращения . К концам рычага (точкам
и
) приложены силы
и
. Плечи этих сил равны соответственно
и
.
Условие равновесия рычага даётся правилом моментов: , откуда
.
 |
| Рис. 1. Рычаг |
Из этого соотношения следует, что рычаг даёт выигрыш в силе или в расстоянии (смотря по тому, с какой целью он используется) во столько раз, во сколько большее плечо длиннее меньшего.
Например, чтобы усилием 100 Н поднять груз весом 700 Н, нужно взять рычаг с отношением плеч 7 : 1 и положить груз на короткое плечо. Мы выиграем в силе в 7 раз, но во столько же раз проиграем в расстоянии: конец длинного плеча опишет в 7 раз большую дугу, чем конец короткого плеча (то есть груз).
Примерами рычага, дающего выигрыш в силе, являются лопата, ножницы, плоскогубцы. Весло гребца – это рычаг, дающий выигрыш в расстоянии. А обычные рычажные весы являются равноплечим рычагом, не дающим выигрыша ни в расстоянии, ни в силе (в противном случае их можно использовать для обвешивания покупателей).
к оглавлению ▴
Неподвижный блок.
Важной разновидностью рычага является блок – укреплённое в обойме колесо с жёлобом, по которому пропущена верёвка. В большинстве задач верёвка считается невесомой нерастяжимой нитью.
На рис. 2 изображён неподвижный блок, т. е. блок с неподвижной осью вращения (проходящей перпендикулярно плоскости рисунка через точку ).
 |
На правом конце нити в точке закреплён груз весом
. Напомним, что вес тела – это сила, с которой тело давит на опору или растягивает подвес. В данном случае вес
прило жен к точке
, в которой груз крепится к нити.
К левому концу нити в точке приложена сила
.
Плечо силы равно
, где
– радиус блока. Плечо веса
равно
. Значит, неподвижный блок является равноплечим рычагом и потому не даёт выигрыша ни в силе, ни в расстоянии: во-первых, имеем равенство
, а во-вторых, в процессе движении груза и нити перемещение точки
равно перемещению груза.
Зачем же тогда вообще нужен неподвижный блок? Он полезен тем, что позволяет изменить направление усилия. Обычно неподвижный блок используется как часть более сложных механизмов.
к оглавлению ▴
Подвижный блок.
На рис. 3 изображён подвижный блок, ось которого перемещается вместе с грузом. Мы тянем за нить с силой , которая приложена в точке
и направлена вверх. Блок вращается и при этом также движется вверх, поднимая груз, подвешенный на нити
.
 |
В данный момент времени неподвижной точкой является точка , и именно вокруг неё поворачивается блок (он бы “перекатывается” через точку
). Говорят ещё, что через точку
проходит мгновенная ось вращения блока (эта ось направлена перпендикулярно плоскости рисунка).
Вес груза приложен в точке
крепления груза к нити. Плечо силы
равно
.
А вот плечо силы , с которой мы тянем за нить, оказывается в два раза больше: оно равно
. Соответственно, условием равновесия груза является равенство
(что мы и видим на рис. 3: вектор
в два раза короче вектора
).
Следовательно, подвижный блок даёт выигрыш в силе в два раза. При этом, однако, мы в те же два раза проигрываем в расстоянии: чтобы поднять груз на один метр, точку придётся переместить на два метра (то есть вытянуть два метра нити).
У блока на рис. 3 есть один недостаток: тянуть нить вверх (за точку ) – не самая лучшая идея. Согласитесь, что гораздо удобнее тянуть за нить вниз! Вот тут-то нас и выручает неподвижный блок.
 |
На рис. 4 изображён подъёмный механизм, который представляет собой комбинацию подвижного блока с неподвижным. К подвижному блоку подвешен груз, а трос дополнительно перекинут через неподвижный блок, что даёт возможность тянуть за трос вниз для подъёма груза вверх. Внешнее усилие на тросе снова обозначено вектором .
Принципиально данное устройство ничем не отличается от подвижного блока: с его помощью мы также получаем двукратный выигрыш в силе.
к оглавлению ▴
Наклонная плоскость.
Как мы знаем, тяжёлую бочку проще вкатить по наклонным мосткам, чем поднимать вертикально. Мостки, таким образом, являются механизмом, который даёт выигрыш в силе.
В механике подобный механизм называется наклонной плоскостью. Наклонная плоскость – это ровная плоская поверхность, расположенная под некоторым углом к горизонту. В таком случае коротко говорят: “наклонная плоскость с углом
“.
Найдём силу, которую надо приложить к грузу массы , чтобы равномерно поднять его по гладкой наклонной плоскости с углом
. Эта сила
, разумеется, направлена вдоль наклонной плоскости (рис. 5).
 |
Выберем ось так, как показано на рисунке. Поскольку груз движется без ускорения, действующие на него силы уравновешены:
.
Проектируем на ось :
,
откуда
.
Именно такую силу нужно приложить, что двигать груз вверх по наклонной плоскости.
Чтобы равномерно поднимать тот же груз по вертикали, к нему нужно приложить силу, равную . Видно, что
, поскольку
. Наклонная плоскость действительно даёт выигрыш в силе, и тем больший, чем меньше угол
.
Широко применяемыми разновидностями наклонной плоскости являются клин и винт.
к оглавлению ▴
Золотое правило механики.
Простой механизм может дать выигрыш в силе или в расстоянии, но не может дать выигрыша в работе.
Например, рычаг с отношением плеч 2 : 1 даёт выигрыш в силе в два раза. Чтобы на меньшем плече поднять груз весом , нужно к большему плечу приложить силу
. Но для поднятия груза на высоту
большее плечо придётся опустить на
, и совершённая работа будет равна:
т. е. той же величине, что и без использования рычага.
В случае наклонной плоскости мы выигрываем в силе, так как прикладываем к грузу силу , меньшую силы тяжести. Однако, чтобы поднять груз на высоту
над начальным положением, нам нужно пройти путь
вдоль наклонной плоскости. При этом мы совершаем работу
т. е. ту же самую, что и при вертикальном поднятии груза.
Данные факты служат проявлениями так называемого золотого правила механики.
Золотое правило механики. Ни один из простых механизмов не даёт выигрыша в работе. Во сколько раз выигрываем в силе, во столько же раз проигрываем в расстоянии, и наоборот.
Золотое правило механики есть не что иное, как простой вариант закона сохранения энергии.
к оглавлению ▴
КПД механизма.
На практике приходится различать полезную работу A полезн, которую нужно совершить при помощи механизма в идеальных условиях отсутствия каких-либо потерь, и полную работу Aполн,
которая совершается для тех же целей в реальной ситуации.
Полная работа равна сумме:
-полезной работы;
-работы, совершённой против сил трения в различных частях механизма;
-работы, совершённой по перемещению составных элементов механизма.
Так, при подъёме груза рычагом приходится вдобавок совершать работу по преодолению силы трения в оси рычага и по перемещению самого рычага, имеющего некоторый вес.
Полная работа всегда больше полезной. Отношение полезной работы к полной называется коэффициентом полезного действия (КПД) механизма:
=Aполезн/Аполн.
КПД принято выражать в процентах. КПД реальных механизмов всегда меньше 100%.
Вычислим КПД наклонной плоскости с углом при наличии трения. Коэффициент трения между поверхностью наклонной плоскости и грузом равен
.
Пусть груз массы равномерно поднимается вдоль наклонной плоскости под действием силы
из точки
в точку
на высоту
(рис. 6). В направлении, противоположном перемещению, на груз действует сила трения скольжения
.
 |
Ускорения нет, поэтому силы, действующие на груз, уравновешены:
.
Проектируем на ось X:
. (1)
Проектируем на ось Y:
. (2)
Кроме того,
, (3)
Из (2) имеем:
.
Тогда из (3):
.
Подставляя это в (1), получаем:
.
Полная работа равна произведению силы F на путь, пройденный телом вдоль поверхности наклонной плоскости:
Aполн=.
Полезная работа, очевидно, равна:
Аполезн=.
Для искомого КПД получаем:
Если вам нравятся наши материалы – записывайтесь на курсы подготовки к ЕГЭ по физике онлайн
Благодарим за то, что пользуйтесь нашими статьями.
Информация на странице «Простые механизмы.» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам.
Чтобы успешно сдать нужные и поступить в ВУЗ или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из разделов нашего сайта.
Публикация обновлена:
07.05.2023
Введение
Здравствуйте!
Человеческие возможности ограничены: нагруженную тачку вряд ли можно поднять вертикально вверх. А вот заталкивать её по наклонной поверхности с небольшим наклоном гораздо легче (см. рис. 1)

Рис. 1. Работа человека
Но для такого подъёма потребуется больше времени.
Мы постоянно решаем задачу поиска компромисса между потраченным временем и приложенной силой: что лучше – набрать побольше и сделать меньше ходок или не перегружать себя, но сходить туда-обратно больше раз?
Быстрее всего подняться на 5 этаж – по вертикальной лестнице. Но усилие для преодоления каждой ступеньки будет очень большим. Поэтому мы проходим более длинный путь, но на каждый шаг тратим меньше сил (см. рис. 2)

Рис. 2. Два способа затащить кирпичи на этаж
Пандусы для колясок делают с небольшим углом наклона – путь, который надо проехать в таком случае больше, но усилие нужно прикладывать меньше (см. рис. 3)

Рис. 3. Пандусы
Наша сила ограничена – если для перемещения тела нужна большая сила, то путей решения два: разбить задачу на несколько частей или уменьшить требуемую силу, используя различные механизмы.
Простые механизмы
Мы уже знакомы с механизмами, которые позволяют изменять создаваемое давление: нож, лыжи и т.д (см. рис. 4)

Рис. 4. Изменение давления
Для изменения прикладываемой силы люди тоже придумали различные механизмы, которые назвали простыми.
Примеры таких механизмов каждому знакомы: когда папа садится на качели ближе к центру, а вы – дальше и таким образом его уравновешиваете, то используете принцип рычага (см. рис. 5)

Рис. 5. Принцип рычага
Этот же принцип используется в ножницах, дверной ручке и лопате. А пандус – это пример наклонной плоскости (см. рис. 3)
Но для того, чтобы создавать эффективные простые механизмы, нужно научиться точно рассчитывать выигрыш, который они дают.
Условно можно выделить три основных вида простых механизмов: наклонная плоскость, рычаг и блок (см. рис. 6)

Рис. 6. Основные виды простых механизмов
О них и пойдёт речь в уроке, но сначала давайте поймем, как вообще можно уменьшить необходимую для поднятия тела силу.
Почему механизмы «простые»?
Механизмы, о которых пойдет речь в уроке, называют «простыми». Их изобрели еще в глубокой древности и продолжают пользоваться до сих пор (см. рис. 7)

Рис. 7. Принцип действия простых механизмов
Действия этих механизмов основаны на простых механических принципах.
Соединив вместе несколько простых механизмов, можно получить сложный механизм (см. рис. 8)

Рис. 8. Сложный механизм
По сравнению с простыми, сложные механизмы работают более эффективно и позволяют решать более сложные инженерные задачи.
Может ли человек поднять дом? Дом слишком тяжелый, не получится (см. рис. 9)

Рис. 9. Поднятие дома
Но что, если мы разберем его на кирпичи? Конечно, можно сказать, что это будет не совсем дом, но нам важно то, что теперь эта задача человеку под силу. Правда, это займёт больше времени (см. рис. 10)

Рис. 10. Выполнение одной и той же работы
При этом работа будет та же, что и в случае, если бы человек поднимал дом целиком: массу m поднимают на высоту h :
![]()
Получается, возможности человека безграничны, ведь по одному кирпичу можно перенести любой дом, каким бы огромным он ни был? На самом деле, нет – чем больше масса дома (больше кирпичей надо перенести), тем больше времени это займёт.
Можно уменьшить силу, которую мы прикладываем за один подход, но при этом увеличится путь и время подъема. Совершенная работа, или затраченная энергия, при этом останется такой же:
![]()
Это общий принцип действия большинства простых механизмов: выигрывая с их помощью в прикладываемой силе, мы будем проигрывать в расстоянии, которое нужно будет преодолеть (можно взбираться на гору по прямой – получится быстро, но тяжело, а можно – по серпантину – легче, но дольше – (см. рис. 11))

Рис. 11. Общий принцип простых механизмов
Наклонная плоскость
Если друг попросит затащить его вместе с санками на горку, вы, вероятно, сможете это сделать. А смогли бы вы просто поднять друга вместе санками на высоту горки (см. рис. 12)

Рис. 12. Наклонная плоскость
Вряд ли.
В первом случае вы поднимаете санки по склону, во втором – вертикально вверх. В данной ситуации склон является примером простейшего механизма – наклонной плоскости.
Ею часто пользуются грузчики, когда нужно поднять груз на некоторую высоту. Наклонная плоскость позволяет поднять груз, прикладывая меньшую силу. И чем меньше наклон, тем меньше потребуется сила (см. рис. 13)

Рис. 13. Использование наклонной плоскости
Любой, кто катался на санках, это знает: по крутому склону поднимать их наверх намного тяжелее, чем по пологому. Но, используя наклонную плоскость, нужно преодолеть большее расстояние. Длина склона всегда больше высоты горки (см. рис. 14)

Рис. 14. Длина склона всегда больше высоты горки
На математическом языке это звучит так: в прямоугольном треугольнике гипотенуза всегда больше катета.
Итак, можно сказать, что наклонная плоскость даёт выигрыш в силе, но проигрыш в расстоянии. Чем меньше угол наклона, тем больше выигрыш в силе.
Выигрыш-проигрыш
Наклонная плоскость чаще всего используется для подъёма грузов. Конечно, это можно сделать и без неё – поднять груз равномерно, прикладывая силу ![]() (см. рис. 15)
(см. рис. 15)

Рис. 15. Приложенная сила ![]()
Но наклонная плоскость позволяет поднять тот же груз, но приложить при этом меньшую силу (см. рис. 16)

Рис. 16. Прикладывание меньшей силы ![]()
Поскольку нам это выгодно, так и скажем: «мы выиграли в силе». Можно даже указать, во сколько раз меньше получилась сила. Например, «выигрыш в силе в 3 раза» значит, что вместо силы ![]() , нам достаточно приложить силу в 3 раза меньше:
, нам достаточно приложить силу в 3 раза меньше:![]() . При этом мы поднимем тот же груз массой m.
. При этом мы поднимем тот же груз массой m.
Итак, если нам выгодно изменение физической величины, мы говорим о «выигрыше». Ну, а если невыгодно – то о «проигрыше».
Винт
Если свернуть наклонную плоскость (см. рис. 17), то получится ее частный случай – винт!

Рис. 17. Винт
Принцип действия винта рассмотрим на примере шурупа. Вкрутить его легче, чем вбить гвоздь такой же длины.
Если перейти в систему отсчёта, связанную с гвоздём, то стенка относительно гвоздя поднимается вертикально вверх (см. рис. 18)

Рис. 18. Гвоздь и шуруп
А в системе отсчёта, связанной с шурупом, стенка поднимается по шурупу как по спирали (по свёрнутой наклонной плоскости).
За счёт этого получается выигрыш в силе. Но при этом увеличивается пройденный путь. В примере с санками и горкой мы проходили больший путь вдоль плоскости, а здесь мы делаем несколько оборотов отверткой. Точки шурупа проделывают больший путь, чем точки гвоздя.
Клин
Рассмотрим еще один инструмент: топор. Во время первого удара по бревну, топор прорезает его. Тут действует принцип ножа: небольшая площадь, большое давление (см. рис. 19)

Рис. 19. Принцип ножа
Но дальше мы бьём уже по-другому (см. рис. 20)

Рис. 20. Работа топором
Что происходит? Древесина движется вдоль лезвия топора (наклонной плоскости). На нее действует сила реакции опоры перпендикулярно поверхности лезвия (см. рис. 21), и под ее действием древесина раскалывается

Рис. 21. Клин
Топор является примером ещё одного частного случая наклонной плоскости, который называют клином. И снова получаем выигрыш в силе и проигрыш в перемещении – топор вгоняется в бревно на несколько сантиметров, чтобы разъединить его на несколько миллиметров.
Про все виды наклонной плоскости мы можем сказать, что они дают выигрыш в силе. И чем меньше угол у основания плоскости, тем больше этот выигрыш (см. рис. 13) Известных нам математических инструментов пока не хватает, чтобы точно рассчитать этот выигрыш, но чуть позже мы научимся это делать.
Рычаг
Рассмотрим второй из выделенных нами типов простых механизмов.
Представьте: папа сел на качели (см. рис. 22)

Рис. 22. Качели с человеком
Чтобы его уравновесить, вы сядете на качели подальше от центра (см. рис. 23)

Рис. 23. Уравновешивание качелей
Так вы, давя на качели меньшим весом, уравновесите более тяжелого папу.
Подсознательно вы использовали принцип действия простого механизма – рычага. Рычаг – это твердое тело, которое имеет точку опору и может вращаться вокруг неё. Свойствами рычага мы пользуемся, когда толкаем дверь дальше от петель, чтобы её открыть; когда берём лопату поближе к концу черенка и т.д (см. рис. 24)

Рис. 24. Принцип рычага
Чтобы строго сформулировать используемые нами свойства рычага, введём несколько понятий.
У качелей есть точка, которая остается неподвижной и вокруг которой они вращаются (см. рис. 25)

Рис. 25. Точка опоры
Эта точка называется точкой опоры (в ней качели крепятся к опоре). Для лопаты точкой опоры будет точка (см. рис. 26), для ножниц – винтик и т.д.


Рис. 26. Точка опоры для лопаты и ножниц
Итак, у любого рычага есть одна неподвижная точка, которая называется точкой опоры.
Какие силы действуют на качели (см. рис. 27)?

Рис. 27. Качели
1) В точке опоры действует сила реакции опоры. Из-за этого данная точка остаётся неподвижной (см. рис. 28)

Рис. 28. Сила реакции опоры
2) Папа действует на качели своим весом. Эта сила стремится вращать качели против часовой стрелки (см. рис. 29)

Рис. 29. Вес человека
3) Вы тоже действуете на качели своим весом. Эта сила вращает качели по часовой стрелке (см. рис. 30)

Рис. 30. Вес второго человека
Если использовать для рычага модель материальной точки, то получится, что все силы, которые мы описали, действуют вдоль вертикали (вверх или вниз) (см. рис. 31)

Рис. 31. Модель материальной точки
Тогда движение рычага было бы возможно только вверх или вниз. Но рычаг вращается, значит, модель материальной точки для его описания неприменима.
Поэтому рассмотрим не только силы, действующие на рычаг, но и точки их приложения. Все знают, насколько труднее удерживать груз на вытянутой руке, чем на согнутой (см. рис. 32)


Рис. 32. Удерживание груза на вытянутой и согнутой руке
Можно сделать предположение, что чем ближе точка приложения силы к точке опоры, тем меньше её «вклад» в поворот рычага.
Чтобы определять точку приложения силы, введем понятие плеча силы (по аналогии с плечом руки, которая удерживает груз).
Плечо силы – это минимальное расстояние от заданной точки до прямой, вдоль которой действует сила (см. рис. 33)

Рис. 33. Плечо силы
В геометрии мы определили такое расстояние, как перпендикуляр, опущенный из точки опоры на прямую, вдоль которой действует сила.
Чаще всего мы будем рассматривать силы, действующие перпендикулярно рычагу, и плечо силы будет равно расстоянию от точки опоры до точки приложения силы (см. рис. 34)

Рис. 34. Силы, действующие перпендикулярно рычагу
Вращение рычага зависит и от значения силы, и от ее плеча – чем больше сила и длиннее её плечо, тем сильнее будет вращающее действие этой силы (см. рис. 35)

Рис. 35. Вращение рычага
Назовем произведение силы на ее плечо моментом силы.
![]()
Вспомним, что тело сохраняет свою скорость, если действующие на него силы уравновешены. При вращении тела, то же самое можно сказать про момент силы: если моменты сил уравновешены, то тело вращается равномерно или остается в покое (см. рис. 36)

Рис. 36. Моменты сил уравновешены
Вернёмся к примеру с качелями (см. рис. 23): чтобы они уравновесились, моменты двух сил – вашего и папиного веса – также должны быть уравновешены. Момент силы реакции опоры не учитываем: он равен нулю, поскольку плечо этой силы равно нулю (см. рис. 37)

Рис. 37. Момент силы реакции опоры равен 0
Момент веса папы (см. рис. 38):
![]()
Момент вашего веса (см. рис. 38):
![]()

Рис. 38. Моменты силы
Тогда ![]() . Теперь видно: чем больше будет
. Теперь видно: чем больше будет ![]() , тем меньшего достаточно веса
, тем меньшего достаточно веса ![]() . Поэтому, если длина качелей будет достаточной, чтобы взяться подальше от точки опоры, взрослого человека легко уравновесить рукой (см. рис. 39)
. Поэтому, если длина качелей будет достаточной, чтобы взяться подальше от точки опоры, взрослого человека легко уравновесить рукой (см. рис. 39)

Рис. 39. Достаточная длина качелей
Простые механизмы, работающие по тому же принципу, что и качели, называют рычагами. Примерами рычагов, как мы уже сказали, являются лопата, тачка, плоскогубцы (см. рис. 40)


Рис. 40. Примеры рычагов
На примере качелей мы увидели, что с помощью рычага можно получить выигрыш в силе, если увеличить плечо. Вокруг себя вы можете увидеть множество аналогичных примеров:
– дверь вы открываете ближе к краю, а не к петлям: плечо больше, значит, можно прикладывать меньшую силу (см. рис. 41)

Рис. 41. Открывание двери
– у дверной ручки тоже есть своё плечо, чтобы проще было её поворачивать. А вот круглые ручки поворачивать сложнее (см. рис. 42)

Рис. 42. Дверная ручка
Выигрыш в силе для рычага
Давайте вычислим выигрыш в силе для рычага. Чтобы просто поднять тело, нужно приложить силу ![]() (см. рис. 43)
(см. рис. 43)

Рис. 43. Поднятие тела
Посчитаем силу необходимую для поднятия тела с помощью рычага, как мы это делали через моменты сил для качелей (см. рис. 44):
![]()

Рис. 44. Использование рычага
Тогда:
![]()
Например, если ![]() относится к
относится к ![]() как 1 к 3
как 1 к 3 ![]() , то
, то ![]() (см. рис. 45)
(см. рис. 45)

Рис. 45. Отношение длин плеч
Получаем выигрыш в силе в 3 раза.
Увеличивая плечо ![]() , мы можем уменьшать силу. Можно ли это делать неограниченно? Кажется, что да – увеличивая плечо. Но чтобы уменьшить силу в миллион раз, нужно добиться того, чтобы соотношение плеч равнялось миллиону. И чтобы короткое плечо рычага сдвинулось на сантиметр, длинное плечо должно сдвинуться на 10 км – мы много теряем в перемещении (см. рис. 46)
, мы можем уменьшать силу. Можно ли это делать неограниченно? Кажется, что да – увеличивая плечо. Но чтобы уменьшить силу в миллион раз, нужно добиться того, чтобы соотношение плеч равнялось миллиону. И чтобы короткое плечо рычага сдвинулось на сантиметр, длинное плечо должно сдвинуться на 10 км – мы много теряем в перемещении (см. рис. 46)

Рис. 46. Большие потери в перемещении
«Дайте мне точку опоры, и я сдвину Землю»
Архимед сказал: «Дайте мне точку опоры, и я сдвину Землю». И действительно: если будет точка опоры, можно сделать рычаг (см. рис. 47)

Рис. 47. Точка опоры и Земля
Архимед мог бы выбрать такое плечо прикладываемой силы, что выигрыш в силе был бы огромным. И его сил хватило, чтобы сдвинуть Землю. Правда, перемещение длинного конца рычага было бы огромным. В книге Перельмана «Занимательная физика» приводятся расчеты, какой путь должна была бы преодолеть рука Архимеда, чтобы сдвинуть Землю на 1 см, зная массу Земли и силу, которую мог бы приложить человек. Оказывается, даже двигая рычаг со скоростью 1 м/с, за всю свою долгую жизнь Архимед не сдвинул бы Землю даже на толщину тончайшего волоса. Подробнее с этими расчётами Вы можете ознакомиться по ссылке http://allforchildren.ru/sci/perelman2-17.php
Задача 1
Давайте рассчитаем, какой длины должен быть рычаг, чтобы с его помощью хрупкая девушка массой 50 кг смогла приподнять автомобиль массой 1500 кг, надавив на рычаг всем своим весом (см. рис. 48)

Рис. 48. Задача 1
Точку опоры рычага разместим так, чтобы короткое плечо рычага было равно 1 м.
В задаче описан рычаг. Мы знаем, во сколько раз выигрыш в силе дает рычаг:
![]()
Силы прикладываются по разные стороны от опоры рычага, поэтому два плеча рычага в сумме составят его длину:
![]()
Мы составили математическую модель задачи. В нашем случае сила ![]() , действующая на плечо
, действующая на плечо ![]() , – это вес автомобиля
, – это вес автомобиля ![]() , а сила
, а сила ![]() , действующая на плечо
, действующая на плечо ![]() , – вес девушки
, – вес девушки ![]() .
.
Теперь осталось только решить уравнения и найти ответ.
Из первого уравнения найдем плечо ![]() . Большая сила приложена к меньшему плечу рычага, значит
. Большая сила приложена к меньшему плечу рычага, значит ![]() – это и есть короткое плечо, равное 1 м.
– это и есть короткое плечо, равное 1 м.
![]()
![]()
![]()
Длина рычага равна:
![]()
Блок
Третий тип простых механизмов, который мы рассмотрим, – это блоки. Блок – это колесо с желобом, через которое перекинута веревка (см. рис. 49)

Рис. 49. Блок
Использовать этот механизм можно двумя способами. Можно закрепить колесо посредине, к одному концу веревки привязать груз, за другой – тянуть. Такой блок называют неподвижным (сам блок не двигается) (см. рис. 50)

Рис. 50. Неподвижный блок
Груз действует на веревку с силой ![]() . Чтобы удержать веревку нужно также приложить силу
. Чтобы удержать веревку нужно также приложить силу ![]() . То есть, неподвижный блок не даёт выигрыша в силе (см. рис. 51)
. То есть, неподвижный блок не даёт выигрыша в силе (см. рис. 51)

Рис. 51. Выигрыша в силе нет
Но с помощью него можно менять направление силы. Без блока силу для подъема нужно прикладывать вверх, а с помощью блока – в любом направлении (см. рис. 52)

Рис. 52. Прикладывание силы в любом направлении
Второй способ применения блока – закрепить один конец веревки, за второй – тянуть, а груз привязать к центру блока. Такой блок называется подвижным, т.к. он будет двигаться вместе с грузом (см. рис. 53)

Рис. 53. Подвижный блок
Подвижный блок дает выигрыш в силе в 2 раза, но проигрыш в перемещении, тоже в 2 раза. Убедиться в этом можно, проведя мысленный эксперимент.
Представим двух человек на крыше дома, поднимающих груз на подвижном блоке (см. рис. 54)

Рис. 54. Поднятие груза двумя людьми
Понятно, что поднимать вдвоем в 2 раза легче, т.е. каждый из них прикладывает силу, равную ![]() . Изменится ли сила, с которой будет тянуть один человек, если второго заменить жестким креплением? Очевидно, нет (см. рис. 55)
. Изменится ли сила, с которой будет тянуть один человек, если второго заменить жестким креплением? Очевидно, нет (см. рис. 55)

Рис. 55. Поднятие груза одним человеком
За счет чего же происходит выигрыш в силе в 2 раза? При поднятии груза на высоту ![]() освободится h метров веревки с каждой стороны от блока, т.е. один человек вытащит
освободится h метров веревки с каждой стороны от блока, т.е. один человек вытащит ![]() метров веревки (см. рис. 56)
метров веревки (см. рис. 56)

Рис. 56. Проигрыш в перемещении
Таким образом, выигрыш в силе происходит за счет проигрыша в перемещении, как и в большинстве других простых механизмах.
Велосипед
Рассмотрим принцип работы велосипеда. Это сложный механизм, ведь он состоит из множества деталей, которые различным образом взаимодействуют друг с другом. Но мы сейчас сосредоточимся на том, почему крутится колесо, если крутить педали. Детали, которые за это отвечают: педали, шестеренки, цепь и колесо (см. рис. 57)

Рис. 57. Детали, которые отвечают за вращение колеса
Передняя шестеренка жестко скреплена с педалями и вращается вместе в ними. Такой тип механизма называется ворот. Типичный пример применения ворота – колодец (см. рис. 58)

Рис. 58. Тип механизма – ворот
Плечо ручки колодца больше, чем плечо веса ведра с водой. Это позволяет уменьшить силу (по аналогии с рычагом). В велосипеде плечо силы у педалей больше, чем у шестеренок. За счёт этого мы получаем выигрыш в силе. При этом будет проигрыш в перемещении: ноги должны преодолеть большее расстояние, чтобы повернуть педали (см. рис. 59)

Рис. 59. Преодоление большего расстояния
Далее две шестеренки связаны через цепную передачу. Цепь движется с одной скоростью, но одинаково ли быстро будут вращаться шестеренки? Цепь связана с зубцами обеих шестеренок, значит на обеих шестеренках зубцы движутся с одинаковой скоростью ![]() . За время
. За время ![]() каждый зубец пройдет путь
каждый зубец пройдет путь ![]() . Но радиусы у шестеренок разные! Поэтому меньшая шестеренка сделает больше оборотов (см. рис. 60)
. Но радиусы у шестеренок разные! Поэтому меньшая шестеренка сделает больше оборотов (см. рис. 60)

Рис. 60. Обороты шестеренок
И чем меньше будет радиус шестеренки, тем чаще она будет вращаться. Подобным образом работают ременные передачи и сцепленные шестерни (см. рис. 61)


Рис. 61. Ременные передачи и сцепленные шестерни
Итак, мы крутим педали, они вращают переднюю шестеренку. Она через цепь вращает заднюю шестеренку. А та, в свою очередь, сцеплена с задним колесом и заставляет его вращаться (см. рис. 62)

Рис. 62. Вращение колеса
Основные виды механизмов
Давайте еще раз посмотрим на основные виды механизмов, которые мы уже знаем (см. рис. 63)

Рис. 63. Механизмы, с помощью которых можно изменять давление, скорость вращения, величину и направление силы
Можно выделить механизмы, с помощью которых можно изменять давление (нож, лыжи); скорость вращения (шестеренки, валы); величину и направление силы (простые механизмы). К простым механизмам относятся наклонная плоскость (её разновидностями являются винт и клин); рычаг и блоки (подвижный и неподвижный) (см. рис. 64)

Рис. 64. Простые механизмы
Во всех простых механизмах (кроме неподвижного блока) мы получали выигрыш в силе за счет проигрыша в перемещении. Почему так происходит?
На самом деле, ничего нового для нас в этом нет, мы сталкиваемся с одной из эквивалентных формулировок уже известного нам закона сохранения энергии. Прикладывая силу к механизму, мы выполняем работу ![]() . Выполняя работу, мы передаем соответствующую энергию телу. Если наша задача – поднять тело массой m на высоту h – мы должны увеличить его потенциальную энергию на величину
. Выполняя работу, мы передаем соответствующую энергию телу. Если наша задача – поднять тело массой m на высоту h – мы должны увеличить его потенциальную энергию на величину ![]() , значит – выполнить над ним работу
, значит – выполнить над ним работу ![]() (см. рис. 65)
(см. рис. 65)

Рис. 65. Поднятие груза
Рассмотрим идеальный простой механизм, в котором вся выполненная работа ![]() пойдёт на передачу телу энергии. Тогда:
пойдёт на передачу телу энергии. Тогда:
![]()
Значение переданной энергии ![]() фиксировано, поэтому уменьшить силу
фиксировано, поэтому уменьшить силу ![]() можно только в том случае, если увеличится перемещение
можно только в том случае, если увеличится перемещение![]() .
.
Иногда полезно уменьшить перемещение ![]() . Это можно сделать, увеличив прикладываемую силу
. Это можно сделать, увеличив прикладываемую силу ![]() . По этому принципу работает бицепс: мышца немного сокращается (то есть перемещение незначительное), при этом прикладываемая сила должна быть большой (см. рис. 66)
. По этому принципу работает бицепс: мышца немного сокращается (то есть перемещение незначительное), при этом прикладываемая сила должна быть большой (см. рис. 66)

Рис. 66. Работа бицепса
В этом несложно убедиться: как вам легче держать груз – с согнутой рукой или с прямой?
Рычаги, которые используются «наоборот»
Не всегда рычаги используются для того, чтобы совершать работу, прикладывая меньшую силу. Иногда важно выиграть в перемещении, даже если при этом приходится прикладывать бόльшую силу. Так делает рыбак, которому нужно вытащить рыбу, переместить ее на большое расстояние. При этом он использует удочку как рычаг, прикладывая силу ![]() к ее короткому плечу (см. рис. 67)
к ее короткому плечу (см. рис. 67)

Рис. 67. Рыбак
Рычагом является и наша рука. Мышцы руки сокращаются, и рука сгибается в локте, совершая работу (поднимая груз) (см. рис. 66) При этом на кости предплечья действуют с некоторыми силами мышцы и груз. Ось вращения предплечья – локтевой сустав. Из таких рычагов состоит весь наш опорно-двигательный аппарат. И сам термин «плечо рычага» назван так из-за аналогии с плечом одного из рычагов в нашем теле – руки.
Мышцы так устроены, что они при сокращении не могут укорачиваться на те полметра, на которые нам нужно поднять, например, чашку с чаем. Нужно выиграть в перемещении, поэтому мышцы крепятся ближе к суставу, к меньшему плечу рычага. При этом нужно приложить бόльшую силу, но для наших мышц это не проблема.
КПД
Мы рассмотрели идеальные случаи механизмов, в которых не учитывали потери энергии. А ведь при подъеме груза по наклонной плоскости часть энергии уйдет на преодоление трения. В рычаге не избежать потерь на трение в точке опоры. В подвижном и неподвижном блоках энергия будет расходоваться на трение веревки о сам блок, а в подвижном блоке, кроме груза, мы поднимаем и сам блок.
Неизбежные потери
Выполняя любое действие, нельзя обойтись без потерь. Когда мы чистим картошку, вместе со шкуркой срезаем часть самой картошки.
Закупая продукты на неделю, вы помимо стоимости продуктов можете потратить деньги на проезд к магазину, на пакеты, которые нужны только для переноски этих продуктов и т.д.
Когда вы кипятите воду в чайнике, кроме воды нагревается сам чайник и воздух на кухне – это тоже ненужные потери энергии. И т.д.
Так и с механизмами: не вся выполненная ими работа будет нам нужна, но без этих потерь не обойтись, можно только постараться их минимизировать.
Поэтому, для реальных механизмов, вводят величину КПД – коэффициент полезного действия. Она показывает, насколько полезен данный механизм. КПД определяется как отношение полезной работы к выполненной:
![]()
Обычно, для краткости записи, КПД обозначают буквой греческой η («эта»). То есть
![]()
Что же это такое – полезная и выполненная работы?
Нужно понимать, что понятия КПД – не существует в природе. Мы вводим его, чтобы оценивать эффективность механизма. Поэтому сами выбираем, что считать полезной и выполненной работой.
Обычно выполненная работа – это работа внешней силы, которая выполняет подъем тела, действуя на механизм. ![]() (см. рис. 68)
(см. рис. 68)

Рис. 68. Выполненная работа
При подъеме тела полезная работа – это та, которая пошла непосредственно на изменение высоты тела – ведь это и есть наша цель. Тогда ![]() . И в этом случае:
. И в этом случае:
![]()
В других случаях для вычисления КПД нужно сначала понять, какой была цель работы механизма. И из этого определить, что считать полезной работой.
Потренируемся рассчитывать КПД на примере решения задачи в ответвлении.
Задача 2
С помощью подвижного блока массой 0,5 кг поднимают груз массой 4,5 кг. Определите КПД подвижного блока в данном случае (см. рис. 69)

Рис. 69. Задача 2
В задаче речь идет о КПД – это отношение полезной работы к выполненной.
![]()
Нам интересна работа, выполненная силой, с которой рука тянет веревку. Силу эту мы найдем, рассмотрев простой механизм. Запишем силы, действующие на блок: это сила тяжести ![]() , вес груза
, вес груза ![]() и дважды сила натяжения нити
и дважды сила натяжения нити ![]() – с двух концов нити (см. рис. 70)
– с двух концов нити (см. рис. 70)

Рис. 70. Действие сил
По третьему закону Ньютона рука будет тянуть нить с силой, равной по модулю ![]() . По второму закону Ньютона (при нулевом ускорении) запишем:
. По второму закону Ньютона (при нулевом ускорении) запишем:
![]()
Направим ось координат вверх, в проекции на ось координат запишем:
![]()
Полезная работа – это работа по перемещению груза на высоту ![]() :
:
![]()
Чтобы груз поднялся на высоту ![]() , нужно поднять конец веревки на
, нужно поднять конец веревки на ![]() (см. рис. 71), поэтому
(см. рис. 71), поэтому ![]() .
.

Рис. 71. Поднятие груза на высоту 2h
Всё, мы записали в виде уравнений условие задачи и закономерности, которым подчиняется процесс, осталось выразить из этих уравнений КПД.
Из записи второго закона Ньютона получим силу ![]() :
:
![]()
![]()
![]()
![]()
![]() или 90%
или 90%
На сегодняшнем уроке мы познакомились с простыми механизмами и рассмотрели понятие КПД. Спасибо за внимание, до свидания!
Домашнее задание
- Что такое простые механизмы и для чего они нужны? Назовите несколько примеров, где используется принцип простых механизмов.
- Что такое рычаг? Как он работает? За счет чего получается выигрыш в силе?
- Как определяется момент силы?
- Какой блок не дает выигрыша в силе?
Список рекомендованной литературы:
- Соколович Ю.А., Богданова Г.С Физика: Справочник с примерами решения задач. – 2-е издание передел. – X.: Веста: Издательство «Ранок», 2005. – 464 с.
- Ф.Я.Божинова, Н.М. Кирюхин, Е.А. Кирюхина Физика 7 кл.: Учебник. – Х.: Издательство «Ранок», 2007, 192 с.
Рекомендованные ссылки на ресурсы сети Интернет
- Интернет-портал «physbook.ru» (Источник)
- Интернет-портал «dpva» (Источник)
- Интернет-портал «class-fizika.narod.ru» (Источник)
Рассмотрим примеры того, как можно на практике применить условия равновесия твердого тела.
Пример 1. Равноплечие весы
Еще с древнейших времен для определения массы тел люди использовали равноплечие весы (рис. 137). Понять принцип их работы просто, если воспользоваться вторым условием равновесия твердого тела.
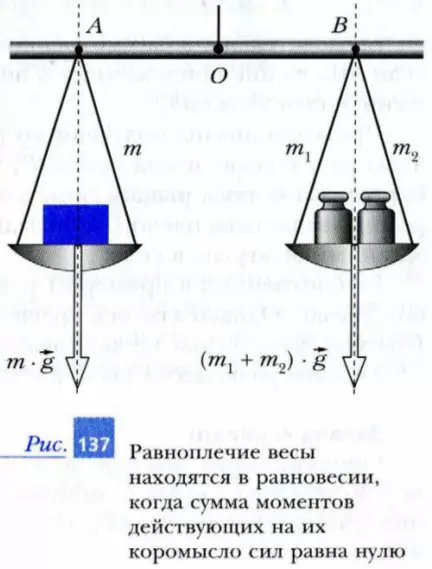
Коромысло весов может поворачиваться вокруг оси, проходящей через точку O. На равных расстояниях от оси вращения коромысла подвешены одинаковые чашки. В одну чашку помещают груз неизвестной массы m, а в другую – набор грузов известной массы, например m1 + m2. Весы будут находиться в равновесии, если стремящиеся развернуть их коромысло положительный момент m · g · OA и отрицательный момент -(m1 + m2) · g · OB будут уравновешивать друг друга. Поэтому условие равновесия коромысла весов можно записать в виде:
m · g · OA – (m1 + m2) · g · OB = 0
Так как плечо OA силы тяжести груза равно плечу OB силы тяжести гирь, то уравнение обратится в тождество при условии, что m = m1 + m2. Таким образом, равноплечие весы будут находиться в равновесии, если суммарная масса гирь будет равна массе взвешиваемого груза.
Если массы груза и гирь не равны друг другу, то коромысло весов начнет разворачиваться в сторону большего по модулю момента силы тяжести (в сторону большей массы). Чашка весов с большей массой начнет опускаться. Добавляя (или уменьшая) число гирь известной массы, можно достичь равновесия и таким образом измерить неизвестную массу груза.
Пример 2. Рычаг
Рычагом называют твердое тело, способное вращаться вокруг неподвижной оси (или опоры). Применение рычага позволяет получить выигрыш в силе – преодолеть действие большей силы, приложив меньшую силу. Каким образом это можно сделать?
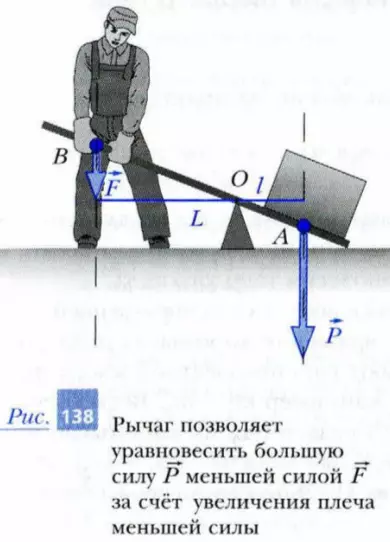
Рассмотрим человека, поднимающего камень весом P с помощью рычага (рис. 138). Человек действует на противоположный конец рычага силой F, направленной вертикально вниз. Под действием моментов сил F и P рычаг может вращаться вокруг оси O. Обозначим плечо силы F символом L, а плечо силы P – символом l. Рычаг будет находиться в равновесии, если сумма вращающих его моментов сил будет равна нулю:
F · L – P · l = 0 или F/P = l/L
Следовательно, в рассмотренном случае рычаг находится в равновесии, если отношение приложенных к нему сил обратно пропорционально отношению плеч этих сил.
Проведем анализ полученного результата. Если плечо L силы F будет в два раза больше плеча l силы P, то для поднятия камня человек должен будет приложить к рычагу силу, в два раза меньшую веса камня. Таким образом, увеличивая плечо L прикладываемой силы, можно получить заранее заданный выигрыш в силе.
Рассмотренные в примере 1 равноплечие весы также представляют собой рычаг. Однако его ось вращения совпадает с серединой коромысла. Поэтому такой рычаг не дает выигрыша в силе.
Условие равновесия рычага можно использовать для решения задач.
Задача «качели»
Старший брат массой M = 60 кг посадил младшего брата массой m = 40 кг на легкую доску качелей на расстоянии L = 3 м от оси ее вращения (рис. 139). Куда должен сесть старший брат, чтобы доска находилась в равновесии?

Решение. Ясно, что старший брат должен сесть с противоположной стороны на таком расстоянии l от оси вращения, чтобы выполнялось условие равновесия доски качелей относительно этой оси: M · g · l – m · g · L = 0.
Следовательно,
l = (m · L) / M = (40 кг · 3 м) / 60 кг = 2 м.
Ответ: чтобы качели находились в равновесии, старший брат должен сесть на расстоянии 2 м от оси вращения качелей.
Найдите силу, с которой доска качелей при этом будет действовать на ось вращения (опору). Массой доски качелей можно пренебречь.
Решение. По третьему закону Ньютона искомая сила F, с которой доска качелей действует на ось вращения (опору), равна по модулю силе N реакции опоры, с которой ось вращения действует на доску. Для того чтобы найти силу N реакции опоры, применим к доске первое условие равновесия твердого тела. На доску действуют три силы (со стороны двух братьев и со стороны оси вращения). Если ось системы отсчета, связанной с Землей, направить вертикально вверх, то первое условие равновесия твердого тела для доски примет вид: N – M · g – m · g = 0. Следовательно, искомая сила направлена вертикально вниз, а ее модуль равен
F = N = (M + m) · g = 1000 Н = 1 кН.
Ответ: модуль силы, с которой доска качелей действует на опору, равен 1 кН.
Мы рассмотрели рычаги, в которых ось вращения находится между точками приложения действующих сил. На практике используют также рычаги, у которых точки приложения сил находятся по одну сторону от оси вращения. Такие рычаги часто называют рычагами второго рода. На рис. 140 изображен подобный рычаг.

Задача «рычаг второго рода»
На каком расстоянии L от точки опоры O (см. рис. 140) должен взяться за легкий рычаг рабочий, чтобы приподнять груз массой M = 200 кг? Линия действия веса этого груза проходит на расстоянии l = 60 см от точки опоры. Рабочий прикладывает к рычагу силу, направленную вертикально вверх, ее модуль F = 600 Н.
Решение. На рычаг действуют вес груза P = M · g и сила F со стороны рабочего. При этом относительно оси вращения (точки опоры O) момент веса груза положителен, а момент силы, приложенной рабочим, отрицателен. Поэтому условие равновесия данного рычага имеет вид:
M · g · l – F · L = 0.
Следовательно, L = (M · g · l) / F = (200 кг ·10 м/с2 · 0,6 м) / 600 Н = 2 м.
Ответ: рабочий должен взяться за рычаг на расстоянии L = 2 м от точки опоры.
Итоги
Рычагом называют твердое тело, способное вращаться вокруг неподвижной оси (или опоры).
Рычаг дает выигрыш в силе, равный отношению плеч сил. При этом отношение модулей приложенных к нему сил обратно пропорционально отношению плеч этих сил.
Вопросы
- Что называют рычагом? Приведите примеры рычагов в быту и в технике.
- Сформулируйте условие равновесия рычага.
- Как с помощью рычага получить выигрыш в силе?
- Чем отличается рычаг первого рода от рычага второго рода?
- Предложите способы определения равноплечности весов.
Упражнения
- Определите массу камня, который приподнимает человек (рис. 138), прикладывая силу F, модуль которой равен 800 Н. Расстояние OB = 3 м, OA = 40 см. Массой рычага пренебречь.
- Соберите группу из пяти человек. Узнайте свои массы и рассчитайте расстояния от точки опоры доски качелей, на которые каждому из вас необходимо сесть, чтобы качели с пятью учащимися находились в равновесии (сделайте рисунок, на котором изобразите действующие на доску силы и их плечи). Для проверки полученного ответа проведите эксперимент с качелями (используйте рулетку).
- Как с помощью неравноплечих весов и набора гирь определить неизвестную массу груза?
- В каком случае палка сильнее давит на плечо путника, показанного на рис. 141, а и б? (Подсказка: определите, рычагом какого рода является палка.)
- Допустим, вам нужно поднять груз массой 100 кг, а вы можете приложить в вертикальном направлении силу не более 200 Н. Какой рычаг второго рода потребуется вам для выполнения задачи? Нарисуйте схему эксперимента, указав на ней силы и их плечи.
