Как найти вынужденное решение - Сайт, где вы сможете решить свои вопросы

8.1. Понятие устойчивости системы

Под устойчивостью системы понимается способность ее возвращаться к состоянию установившегося равновесия
после снятия возмущения, нарушившего это равновесие. Неустойчивая система
непрерывно удаляется от равновесного состояния или совершает вокруг него
колебания с возрастающей амплитудой.

Устойчивость линейной системы определяется не характером возмущения, а структурой
самой системы (рис.61). Говорят, что система устойчива “в малом”,
если определен факт наличия устойчивости, но не определены ее границы. Система
устойчива “в большом”, когда определены границы устойчивости и
то, что реальные отклонения не выходят за эти границы.

В соответствии с классическим методом решение дифференциального уравнения ищется
в виде:

y(t) = y_вын(t) + y_св(t).

Здесь yсв(t) – общее решение однородного дифференциального
уравнения, то есть уравнения с нулевой правой частью:

a_oy⁽ⁿ⁾
+ a₁y^(n-1) +
… + a_(n-1)y’ + a_(n)y
= 0.

Физически это означает, что все внешние
воздействия сняты и система абсолютно свободна, ее движения определяются лишь
собственной структурой. Поэтому решение данного уравнения называется свободной
составляющей общего решения. y_вын(t) – частное решение неоднородного
дифференциального уравнения, под которым понимается уравнение с ненулевой
правой частью. Физически это означает, что к системе приложено внешнее воздействие
u(t). Поэтому вторая составляющая общего решения называется вынужденный.
Она определяет вынужденный установившийся режим работы системы после окончания переходного процесса.

Можно провести аналогию между САУ и пружиной, колебания которой описываются аналогичным дифференциальным уравнением
(рис.62). Оттянем пружину, а затем отпустим, предоставив ее самой себе. Пружина
будет колебаться в соответствии со свободной составляющей решения уравнения,
то есть характер колебаний будет определяться только структурой самой пружины.
Если в момент времени t = 0 подвесить к пружине груз, то на свободные
колебания наложится внешняя сила Р. После затухания колебаний, описываемых
только свободной составляющей общего решения, система перейдет в новый установившийся
режим, характеризуемый вынужденной составляющей y_вын = y(t
).
Если внешнее воздействие само будет изменяться по синусоидальному закону P
= P_osin(t
+ ), то
после затухания переходного процесса система будет совершать вынужденные колебания
с той же частотой, что и вынуждающая сила, то есть y_вын = y_maxsin(t
+ y).

Каждая составляющая общего решения уравнения динамики ищется отдельно. Вынужденная
составляющая ищется на основе решения уравнения статики для данной системы для
времени t
.
Свободная составляющая представляет собой сумму из n отдельных составляющих:
, где p_i
корни характеристического уравнения D(p) = a₀p_n
+ a₁p_n-1 +
a₂p_n-2 + …
+ a_n = 0. Корни могут быть либо вещественными
p_i = a_i,
либо попарно комплексно сопряженными p_i
= a_i ± ji.
Постоянные интегрирования А_i определяются
исходя из начальных и конечных условий, подставляя в общее решение значения
u, y и их производные в моменты времени t = 0 и t
.

Каждому отрицательному вещественному
корню соответствует экспоненциально затухающая во времени составляющая y_св(t)_i,
каждому положительному – экспоненциально расходящаяся, каждому нулевому корню
соответствует y_св(t)_i = const
(рис.63). Пара комплексно сопряженных корней с отрицательной вещественной частью
определяет затухающие колебания с частотой _i,
при положительной вещественной части – расходящиеся колебания, при нулевой –
незатухающие (рис.64).

Так как после снятия возмущения y_вын(t) = 0, то устойчивость
системы определяется только характером свободной составляющей y_св(t).
zПоэтому условие устойчивости систем по Ляпунову формулируется так: в
устойчивой системе свободная составляющая решения уравнения динамики, записанному
в отклонениях, должна стремиться к нулю, то есть затухать.

Исходя из расположения на комплексной
плоскости корни с отрицательными вещественными частями называются левыми,
с положительными – правыми (рис.65).

Поэтому условие устойчивости линейной САУ можно сформулировать следующим образом:
для того, чтобы система была устойчива, необходимо и достаточно, чтобы все корни
ее характеристического уравнения были левыми. Если хотя бы один корень правый,
то система неустойчива. Если один из корней равен нулю (в системах, где a_n
= 0), а остальные левые, то система находится на границе апериодической
устойчивости. Если равны нулю вещественные части одной или нескольких пар
комплексно сопряженных корней, то система находится на границе колебательной
устойчивости.

Правила,
позволяющие судить о знаках корней характеристического уравнения без его решения,
называются критериями устойчивости. Их можно разделить на алгебраические
(основаны на составлении по данному характеристическому уравнению по определенным
правилам алгебраических выражений, по которым можно судить об устойчивости САУ)
и частотные (основаны на исследовании частотных характеристик).

8.2.
Алгебраические критерии устойчивости

8.2.1.
Необходимое условие устойчивости

Характеристическое
уравнение системы с помощью теоремы Виета может быть записано в виде

D(p)
= a_opⁿ + a₁p^n-1
+ a₂p^n-2 + …
+ a_n = a_o(p-p₁)(p-p₂)…(p-p_n)
= 0,

где p₁,
p₂, …, p_n
– корни этого уравнения. Если система устойчива, значит все корни левые, то есть
вещественные части всех корней

отрицательны, что можно записать как
a_i = -|a_i| <
0. Подставим их в уравнение:

a₀(p
+ |a₁|)(p
+ |a₂| – j2)(p
+ |a₂| + j2)…
= 0.

Перемножая комплексно сопряженные выражения,
получим:

a₀(p
+ |a₁|)((p
+ |a₂|)2 + (2)2)…
= 0.

После раскрытия скобок должно получиться выражение

a₀pⁿ
+ a₁p^n-1
+ a₂p^n-2 + … + a_n = 0.

Так
как в скобках нет ни одного отрицательного числа, то ни один из коэффициентов
a₀,a₁,…,a_n
не будет отрицательным. Поэтому необходимым условием устойчивости САУ является
положительность всех коэффициентов характеристического уравнения: a₀
> 0, a₁> 0, … , a_n> 0. В дальнейшем будем рассматривать только уравнения, где
a₀ > 0. В противном случае уравнение
домножается на -1.

Рассмотренное условие является необходиным, но не достаточным
условием. Необходимые и достаточные условия дают алгебраические критерии Рауса
и Гурвица.

8.2.1. Критерий Рауса

Раус предложил критерий устойчивости САУ в виде алгоритма, по которому заполняется
специальная таблица с использованием коэффициентов характеристического уравнения:

1)
в первой строке записываются коэффициенты уравнения с четными индексами в порядке
их возрастания;

2) во второй строке – с нечетными;

3) остальные элементы таблицы определяется по формуле: c_k,i
= c_{k+ 1,i – 2} – ric_{k

+ 1,i – 1}, где ri = c_{1,i – 2}/c_{1,i

– 1}, i 3 –
номер строки, k – номер столбца.

4) Число строк таблицы Рауса на единицу больше
порядка характеристического уравнения.

Ri	ik	1	2	3	4
–	1	c₁₁ = a₀	c₂₁ = a₂	c₃₁ = a₄	…
–	2	c₁₂ = a₁	c₂₂ = a₃	c₃₂ = a₅	…
r₃ = c₁₁/cc₁₂	3	c₁₃ = c₂₁-r₃c₂₂	c₂₃ = c₃₁-r₃c₃₂	c₃₃ = c₄₁-r₃c₄₂	…
r₃ = c₁₁/c₁₂	4	c₁₄ = c₂₂-r₃c₂₃	c₂₄ = c₃₂-r₄c₃₃	c₃₄ = c₄₂-r₄c₄₃	…
…	…	…	…	…	…

Критерий
Рауса: для того, чтобы САУ была устойчива, необходимо и достаточно, чтобы
коэффициенты первого столбца таблицы Рауса c₁₁,
c₁₂, c₁₃,…
были положительными. Если это не выполняется, то система неустойчива, а количество
правых корней равно числу перемен знака в первом столбце.

Достоинство
– критерий прост в использовании независимо от порядка характеристического уравнения.
Он удобен для использования на ЭВМ. Его недостаток – малая наглядность,
трудно судить о степени устойчивости системы, на сколько далеко отстоит она от
границы устойчивости.

8.2.2. Критерий Гурвица

Гурвиц предложил другой критерий
устойчивости. Из коэффициентов характеристического уравнения строится определитель
Гурвица
по алгоритму:

1) по главной диагонали слева направо выставляются все коэффициенты характеристического
уравнения от a₁ до a_n;

2)
от каждого элемента диагонали вверх и вниз достраиваются столбцы определителя
так, чтобы индексы убывали сверху вниз;

3) на место коэффициентов с индексами
меньше нуля или больше n ставятся нули.

Критерий Гурвица: для того,
чтобы САУ была устойчива, необходимо и достаточно, чтобы все n диагональных
миноров определителя Гурвица были положительны. Эти миноры называются определителями
Гурвица.

Рассмотрим примеры применения критерия Гурвица:

1) n = 1 => уравнение динамики: a₀p
+ a₁ = 0. Определитель Гурвица:
= ₁
= a₁> 0 при a₀> 0, то есть условиие устойчивости: a₀
> 0, a₁> 0;

2) n = 2 => уравнение динамики: a₀p²
+ a₁p + a₂
= 0. Определители Гурвица: ₁
= a₁ > 0, D₂
= a₁a₂– a₀a₃ = a₁a₂>
0, так как a₃ = 0, то есть условие
устойчивости: a₀ > 0, a₁
> 0, a₂> 0;

3) n = 3 => уравнение динамики: a₀p³
+ a₁p² + a₂p
+ a₃ = 0. Определители Гурвица: ₁
= a₁ > 0, ₂
= a₁a₂ – a₀a₃> 0, 3
= a₃₂> 0, условие устойчивости: a₀> 0, a₁> 0, a₂> 0, a₃> 0, a₁a₂– a₀a₃
> 0;

Таким образом при n 2
положительность коэффициентов характеристического уравнения является необходимым
и достаточным условием устойчивости САУ. При n > 2 появляются дополнительные
условия.

Критерий Гурвица применяют при n
4. При больших порядках возрастает число определителей и процесс становится
трудоемким. Имеется ряд модификаций данного критерия, расширяющие его возможности.

Недостаток критерия Гурвица
– малая наглядность. Достоинство – удобен для реализации на ЭВМ. Его
часто используют для определения влияния одного из параметров САУ на ее устойчивость.
Так равенство нулю главного определителя _n
= a_n_n-1
= 0 говорит о том, что система находится на границе устойчивости. При этом
либо a_n = 0 – при выполнении остальных
условий система находится на границе апериодической устойчивости, либо предпоследний
минор _n-1
= 0 – при положительности всех остальных миноров система находится на границе
колебательной устойчивости. Параметры САУ определяют значения коэффициентов
уравнения динамики, следовательно изменение любого параметра Ki влияет на значение
определителя _n-1.
Исследуя это влияние можно найти, при каком значении Ki определитель _n-1
станет равен нулю, а потом – отрицательным (рис.67). Это и будет предельное
значение исследуемого параметра, после которого система становится неустойчивой.

Вопросы

Что
понимают под устойчивостью САУ в малом и в большом?
Какой вид имеет решение
уравнения динамики САУ?
Как найти вынужденную составляющую решения уравнения
динамики САУ?
Какой вид имеет свободная составляющая решения уравнения
динамики САУ?
Что такое характеристическое уравнение?
Какой вид
имеют корни характеристического уравнения?
Чем отличаются правые и левые
корни характеристического уравнения?
Сформулируйте условие устойчивости
систем по Ляпунову.
Что такое граница устойчивости?
Что такое
критерии устойчивости?
Сформулируйте необходимое условие устойчивости
САУ.
Сформулируйте критерий Рауса.
Сформулируйте критерий Гурвица.
В
чем достоинства и недостатки алгебраических критериев устойчивости?

Далее…

Источник

Суть задачи анализа.Пусть имеется
некоторая дискретная система,
представленная разностными уравнениями
в форме Коши, либо уравнениями “вход-выход”.
В частности, эти уравнения могут
представлять замкнутую систему
автоматического управления (импульсную
или цифровую), для непрерывной части
которой построена соответствующая
дискретная модель.

Суть всякой задачи анализа во временной
области, в том числе и для дискретных
систем, состоит в том, чтобы при заданном
внешнем воздействии на систему и при
заданных начальных состояниях (начальных
условиях) найти реакцию выхода этой
системы, а также других ее переменных,
которые могут представлять какой-либо
интерес и определять поведение данной
системы. Очевидно, что математически
эта задача сводится к решению разностных
уравнений, описывающих данную систему.

Решение разностных уравнений,
представленных в форме Коши.Рассмотрим
линейную дискретную систему, представленную
с помощью разностных уравнений состояний
с постоянными коэффициентами

(2.6.1)

где
,,– векторы дискретных состояний, входов
и выходов соответственно;,,– числовые матрицы соответствующих
размеров.

Решить разностное уравнение (2.6.1) это
значит, при заданной решетчатой функции
входного воздействия
и при заданном начальном состоянии,
найти решетчатые векторные функции
состоянияи выходадля.
Очевидно, что решение данной задачи
может быть получено с помощью итерационной
процедуры, вытекающей непосредственно
из уравнения дискретных состояний
(2.6.1). Действительно, запишем это уравнение
для моментов.

Продолжая эти итерации легко увидеть,
что для произвольного момента
будем иметь

. (2.6.2)

Полученное выражение позволяет
аналитически определить решение
разностного уравнения (2.6.1) и представляет
собой аналог формулы Коши для непрерывных
систем. При этом следует заметить, что
для ненулевого начального момента
совершенно аналогично можно получить
для

. (2.6.3)

В формулах (2.6.2) и (2.6.3) матричная функция
есть не что иное, как нормированная
фундаментальная матрица стационарной
дискретной системы (2.6.1).

Рассмотрим один из способов аналитического
определения матрицы
.
При этом ограничимся случаем, когда все
собственные числаматрицыразличны. Напомним, что они могут быть
определены как корни характеристического
уравнения

. (2.6.4)

Пусть также
– обозначают собственные векторы матрицы.
Образуем из этих векторов матрицу,
которая по построению является неособой.
Тогда, как известно из теории матриц[11],
можно записать

В результате для матричной функции
будем иметь

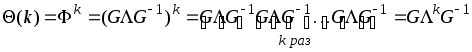При этом очевидно, что
,
и таким образом окончательно получим

. (2.6.5)

Существуют и другие способы нахождения
этой матричной функции.

Заметим, что в более общем нестационарном
случае, когда элементами матриц системы
(2.6.1) являются решетчатые функции, формула
(2.6.3) принимает вид [6]

где нормированная фундаментальная
матрица
становится функцией двух дискретных
аргументов и определяется как решение
следующего матричного разностного
уравнения

, , . (2.6.6)

Возвращаясь к стационарному случаю
нетрудно заметить, что матричная функция
также удовлетворяет уравнению (2.6.6).

Решение разностных уравнений в форме
“вход-выход”.При рассмотрении
этого вопроса ограничимся случаем
односвязной (один вход, один выход)
системы с постоянными параметрами.
Разностное уравнение этой системы,
представленное в форме “вход-выход”
имеет вид

,, (2.6.7)

где
,– известные числа, причем.

Пусть входное воздействие
представляет собой известную решетчатую
функцию, заданную для,
и пусть заданы начальные условия,
определяемыескалярными соотношениями

. (2.6.8)

Требуется определить решетчатую функцию
выхода
для.

Переходя к решению этой задачи, отметим,
что если
задано, то вся правая часть уравнения
(2.6.7) становится известной решетчатой
функцией, которую обозначим как.
Таким образом задача сводится к нахождению
решения неоднородного линейного
разностного уравнения с известной
правой частью

. (2.6.9)

Наряду с уравнением (2.6.9) рассмотрим
соответствующее ему однородное уравнение

. (2.6.10)

Обозначим через
некоторое нетривиальное решение этого
уравнения, которое будем искать в виде,
гденекоторое число. Подставляя функциюв уравнение (2.6.10) получим

Отсюда следует, что
должно быть ненулевым корнем следующего
уравнения

, (2.6.11)

которое, очевидно, является
характеристическим, и которое при
имеетненулевых корней.
Пусть для простоты все корни различны.
Тогда для однородного уравнения (2.6.10)
можно построитьчастных решений,
которые образуют линейно-независимую
систему решетчатых функций[4].
Это означает, что линейная комбинация
этих решений

, (2.6.12)

где
– некоторые константы, также будет
решением уравнения (2.6.10). Действительно,
если обозначить характеристический
полином каки учесть, что,
то, подставляя (2.6.12) в уравнение (2.6.10),
получим

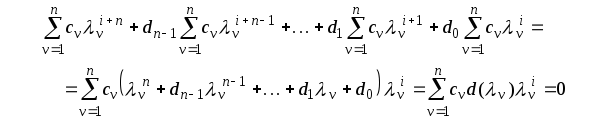
Очевидно, что любое другое решение
уравнения (2.6.10) можно представить в виде
(2.6.12), и таким образом (2.6.12) определяет
собой общее решение однородного
уравнения.

Если среди корней характеристического
полинома есть комплексный корень
,
то поскольку коэффициенты этого полинома
вещественны, найдется и сопряженный к
нему корень,
причемибудут входить в линейную комбинацию
(2.6.12) с комплексно-сопряженными
коэффициентамии.
Сумма двух комплексно-сопряженных
членовможет быть записана как

Таким образом, в случае отсутствия
кратных корней, общее решение
разностного уравнения (2.6.10) представляется
линейной комбинацией решетчатых функций,,,
где– вещественные корни, аи– модули и аргументы комплексно-сопряженных
корней.

Если среди корней имеются кратные, то
можно показать [4],
что функции(,

– число некратных корней) будут
образовывать систему линейно-независимых
решений, если каждому кратному корнюкратностипоставить в соответствие частное решение
вида

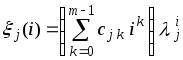, (2.6.13)

где
– некоторые постоянные.

Рассмотрим теперь решение неоднородного
уравнения (2.6.9). Для этого предположим,
что частное решение этого уравнения
,
обусловленное правой частью,
определено. Его обычно называют
вынужденным решением, и оно может быть
найдено, например, по виду правой части
(2.6.9), аналогично тому, как это делается
для непрерывных систем при нахождении
решения линейного неоднородного
дифференциального уравнения с известной
правой частью[12].
Другим способом нахождения
вынужденного решенияявляется метод вариации произвольных
постоянных[4].

Покажем теперь, что искомое общее решение
неоднородного уравнения (2.6.9) определяется
выражением

, (2.6.14)

где
– общее решение однородного уравнения
(2.6.10). Для этого подставим (2.6.14) в исходное
уравнение (2.6.9). Получим

. (2.6.15)

Функция
является частным решением неоднородного
уравнения, поэтому

а функция
есть общее решение однородного уравнения,
и, следовательно, первое слагаемое из
(2.6.15), заключенное в скобки, равно нулю.
Таким образом подстановка (2.6.14) в исходное
уравнение обращает его в тождество, и
таким образом (2.6.14) действительно есть
общее решение неоднородного уравнения.
В частном случае, если все корни
характеристического полинома различны,
то с учетом (2.6.12) это решение примет вид

, (2.6.16)

где постоянные
могут быть определены по заданным
начальным условиям (2.6.8).

Весовая и переходная функции (матрицы)
дискретной системы.Пусть дискретная
система задана разностными уравнениями
в форме Коши (2.6.1). Используя решение
(2.6.2) запишем выражение для выходной
переменной

,. (2.6.17)

В этом выражении матричная функция

(2.6.18)

называется импульсной переходной или
весовой матрицей дискретной системы,
а матричная функция

(2.6.19)

называется переходной матрицей этой
системы.

Чтобы выяснить физический смысл этих
характеристик рассмотрим систему с
одним входом и одним выходом
.
В этом случае характеристики (2.6.18) и
(2.6.19) становятся скалярными, которые
будем обозначать какисоответственно.

Пусть в начальный момент
система (2.6.1) находилась в покое, то есть,
и пусть в моментна систему действует единичный импульс,
определяемый соотношением

. (2.6.20)

Тогда очевидно, что вплоть до момента
выход системы будет нулевым, а прииз (2.6.17) получим

Таким образом, весовая функция дискретной
системы это реакция ее выхода при нулевом
начальном состоянии на единичный импульс
(2.6.20).

Определим теперь при
выход дискретной системы, когда на ее
входе в моментдействует единичная ступенчатая
решетчатая функция, определяемая
соотношением

. (2.6.21)

Тогда из (2.6.17) для
будем иметь

то есть переходная функция это реакция
выхода системы при нулевом начальном
состоянии на единичную ступенчатую
функцию.

Очевидно, что в многомерном случае
элементами весовой матрицыявляются решетчатые функции, определяющие
реакцию соответствующего выхода
дискретной системы при нулевом начальном
состоянии, когда на один из входов
действует единичный импульс, а на
остальных входах сигналы отсутствуют.
Аналогично определяются элементы
переходной матрицы.

Рассмотрим особенность нахождения
переходной функции для дискретной
односвязной (для простоты) системы
заданной в форме “вход-выход”
разностным уравнением (2.6.7). Эта особенность
состоит в том, что начальные условия по
выходной переменной (2.6.8) определяются
не только начальным состоянием системы,
которое при нахождении переходной
функции принимается нулевым, но зависят
также и от решетчатой функции входного
воздействия. Это приводит к тому, что
начальные условия (2.6.8) могут оказаться
ненулевыми. Формально это можно объяснить
также тем, что из-за наличия в правой
части уравнения (2.6.7) смещенных решетчатых
функций
ступенчатое воздействие (2.6.21) начинает
действовать на систему уже в момент.

Определить начальные условия (2.6.8) можно
непосредственно из самого уравнения
(2.6.7). Для этого, полагая
и принимая очевидное условие, чтодля,
запишем это уравнение для моментов.
Тогда нетрудно показать, что начальные
условия определятся следующими
соотношениями

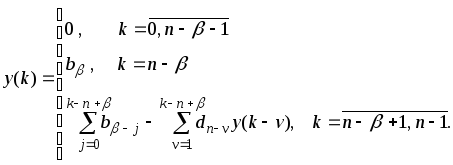(2.6.22)

Заметим, что если до момента
система находилась в покое,
то начальные условия (2.6.8) могут оказаться
ненулевыми не только при.
В частности, если в более общем случае

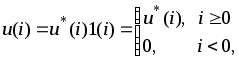
где
– заданная решетчатая функция, то
начальные условия также могут быть
определены по соотношениям (2.6.22), в
которых коэффициентынеобходимо теперь умножить на,
где.

Пример.В качестве примера рассмотрим
односвязную дискретную систему 3-го
порядка, заданную в форме “вход-выход”
следующим разностным уравнением

. (2.6.23)

Пусть до момента
система находилась в покое и пусть
входное воздействиезадано следующей решетчатой функцией

. (2.6.24)

Требуется определить решетчатую функцию
выхода
.

Переходя к решению данной задачи,
составим характеристическое уравнение

решением которого являются следующие
корни

Тогда общее решение соответствующего
однородного уравнения запишется в виде

где
,,– произвольные постоянные.

Найдем вынужденную составляющую решения.
При этом, поскольку в силу (2.6.24) правая
часть заданного разностного уравнения
является гармонической решетчатой
функцией, то и вынужденное решение
также будем искать в виде гармонической
решетчатой функции той же частоты

, (2.6.25)

где
инеизвестные пока константы. Для их
определения подставим (2.6.25) и (2.6.24) в
исходное уравнение

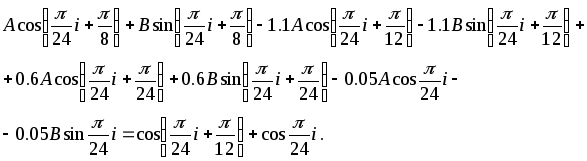
Применяя формулы для
и,
после преобразования и приведения
подобных, получим следующую систему
уравнений

решениями которой будут
и.
Таким образом окончательно общее решение
заданного неоднородного уравнения
(2.6.23) запишется в виде

(2.6.26)

Определим постоянные
.
Для этого найдем сначала начальные
условия,,.
Записывая исходное уравнение (2.6.23) для
моментови учитывая, чтопри,
а также условие (2.6.24) будем иметь

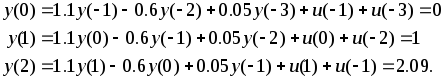
Запишем теперь решение (2.6.26) для моментов
.
Производя необходимые вычисления,
получим следующую систему уравнений

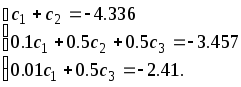
Решениями этой системы являются

,,.

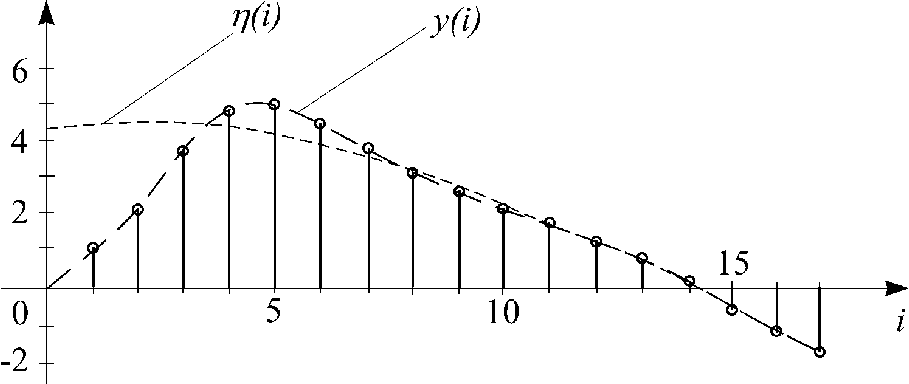
Рис. 2.7.

Таким образом окончательно искомое
решение определится следующей решетчатой
функцией

На рис.2.7приведены графики решетчатых функций
найденного решенияи вынужденной составляющей этого решения.
Заметим, что как следует из (2.6.26) и из
приведенного рисунка, если свободная
составляющаяпри,
то установившаяся реакция дискретной
системы на гармоническое входное
воздействие также является гармонической
решетчатой функцией той же частоты, но
другой амплитуды и фазы.

Соседние файлы в папке DiskretnTau

Источник

Решение дифференциальных уравнений
операционным методом

Постановка задачи

Рассмотрим задачу, наиболее часто встречающуюся в теории дифференциальных уравнений, — задачу Коши для линейных дифференциальных уравнений и систем.

1. Пусть заданы:

а) линейное обыкновенное дифференциальное уравнение с постоянными коэффициентами

$a_{n},frac{d^{n}x}{dt^{n}}+ a_{n-1},frac{d^{n-1}x}{dt^{n-1}}+ ldots+ a_0x=f(t),qquad mathsf{(5.24)}$

где — порядок дифференциального уравнения; $a_n,a_{n-1},ldots,a_0$ — заданные коэффициенты; f(t) — заданная функция;

б) начальные условия:

$x(0)=x_0,quad x'(0)=x'_0,quad ldots,quad x^{(n-1)}(0)=x_0^{n-1}.$

(5.25)

Требуется найти решение x(t) дифференциального уравнения, которое удовлетворяет начальным условиям (решить задачу Коши (5.24),(5.25)).

Замечание 5.6. Переменная в задачах анализа динамических систем имеет смысл времени. Поэтому будем использовать следующие обозначения производных:

$frac{dx}{dt}=x'(t)=dot{x}(t),qquad frac{dx^2}{dt^2}= x''(t)=ddot{x}(t),qquad frac{dx^3}{dt^3}=x'''(t)=dddot{x}(t).$

2. Пусть заданы:

а) система линейных обыкновенных дифференциальных уравнений первого порядка с постоянными коэффициентами, записанная в нормальной форме:

dot{x}= Acdot x(t)+f(t),

(5.26)

где $x=begin{pmatrix}x_1& cdots& x_nend{pmatrix}^T$ — вектор неизвестных; $A=begin{pmatrix} a_{11}&cdots& a_{1n}\ vdots& ddots& vdots\ a_{n1}& cdots& a_{nn}end{pmatrix}$ матрица коэффициентов; $f(t)= begin{pmatrix}f_1(t)& cdots& f_n(t)end{pmatrix}^T$ — заданная вектор-функция;

б) начальные условия (где $x_0= begin{pmatrix}x_{i0}& cdots& x_{n0}end{pmatrix}^T$ — вектор начальных значений):

x(0)=x_0,

(5.27)

Требуется найти решение $x(t)= begin{pmatrix}x_1(t)& cdots& x_n(t)end{pmatrix}^T$ системы, которое удовлетворяет начальным условиям (решение задачи Коши (5.26),(5.27)).

Во многих учебниках изложены классические аналитические и численные методы решения задачи Коши. Здесь будем предполагать, что заданная функция f(t) и искомая функция x(t) принадлежат классу оригиналов. Для решения задач (5.24),(5.25) и (5.26),(5.27) можно применить аппарат операционного исчисления метода решения задач, суть которого состоит в следующем.

Поставленная в классе оригиналов задача переводится с помощью преобразования Лапласа в задачу для изображений. Эта задача решается, и определяете изображение искомой функции. Затем применяется обратное преобразование Лапласа и находится оригинал — решение поставленной задачи.

Алгоритм решения задачи Коши операционным методом

1. Применить преобразование Лапласа: от известных и неизвестных функций перейти к их изображениям, записать уравнение (систему) в изображениях, соответствующее решаемой задаче Коши.

2. Решить полученное уравнение (систему): найти изображение искомого решения.

3. Применить обратное преобразование Лапласа: найти оригинал для полученного в п.2 изображения.

рис. 5.8.

Замечания 5.7

1. Преимущество операционного метода заключается в том, что при его применении функции из пространства оригиналов и производимые над ними операции заменяются функциями и операциями в пространстве изображений, которые оказываются более простыми. Так, вместо дифференциальных уравнений решаются алгебраические уравнения (рис. 5.8).

2. Начальные условия при записи уравнений в изображениях учитываются автоматически, и нет необходимости решать систему для нахождения произвольных постоянных, как это делается при применении классического метода.

3. Операционное исчисление позволяет найти не только частное, но и общее решение уравнения (5.24). Для этого достаточно положить $x^{(k)}(0)=C_k$ . При нахождении общего решения системы (5.26) следует принять x_i(0)=C_i,~i=1,ldots,n .

4. Операционное исчисление можно применять для широкого класса кусочно-непрерывных функций f(t) и функций, заданных графически; для решения уравнений с переменными коэффициентами, уравнений в частных производных, интегральных и интегро-дифференциальных уравнений; для вычисления несобственных интегралов и суммирования рядов.

5. При решении уравнения (системы) для изображений не следует приводить дроби к общему знаменателю, так как следующий этап — нахождение оригинала — связан с представлением дробей в виде суммы.

▼ Примеры 5.30-5.37

Пример 5.30. Решить задачи Коши: а) $x'+x=boldsymbol{1}(t),~ x(0)=frac{1}{2}$ ; б) x'+2x=-3t+2,~ x(0)=0 .

Решение

а) Воспользуемся алгоритмом.

1. Перейдем от оригиналов к изображениям:

$L bigl[x(t)bigr]=X(p);qquad L bigl[x'(t)bigr]=pX(p)-frac{1}{2};qquad L bigl[boldsymbol{1}(t)bigr]=frac{1}{p},.$

Здесь использованы формулы (5.11) и 1 из табл. 5.1. Запишем уравнение для изображений:

$pX(p)-frac{1}{2}+X(p)=frac{1}{p},.$

2. Решим уравнение для изображений:

$pX(p)+X(p)=frac{1}{p}+frac{1}{2}quad Rightarrowquad X(p)= frac{frac{1}{p}+ frac{1}{2}}{p+1}= frac{1}{p(p+1)}+ frac{1}{2}cdot frac{1}{p+1},.$

3. Найдем оригинал для функции X(p) . Применяя формулы 15,6 из табл. 5.1, получаем:

$x(t)= L^{-1} bigl[X(p)bigr]= frac{1}{-1}(e^{-t}-1)+ frac{1}{2},e^{-t}= 1-frac{1}{2},e^{-t}.$

б) Воспользуемся алгоритмом.

1. Перейдем от оригиналов к изображениям:

$L bigl[x(t)bigr]=X(p);qquad L bigl[x'(t)bigr]=pX(p)-x(0)=pX(p);qquad L bigl[f(t)bigr]= L bigl[-3t+2bigr]= frac{-3}{p^2}+frac{2}{p},.$

Здесь использованы формулы 3,2 из табл. 5.1. и (5.11). Запишем уравнение для изображений:

$pX(p)+2X(p)=frac{-3}{p^2}+frac{2}{p},.$

Решим уравнение для изображений: $X(p)=-frac{3}{p^2(p+2)}+frac{2}{p(p+2)}$ .

3. Найдем оригинал для функции X(p) . Применяя формулы 18,15 из табл. 5.1, получаем

$x(t)=-3cdot frac{1}{4}(e^{-2t}-1+2t)+frac{2}{-2}(e^{-2t}-1)=1,!75-1,!5t-1,!75e^{-2t}.$

Пример 5.31. Решить задачу Коши: $x''-3x'+2x=2e^{3t},~ x(0)=1,~ x'(0)=3$ .

Решение

1. Перейдем от оригиналов к изображениям:

$begin{gathered}L bigl[x(p)bigr]=X(p);qquad L bigl[x'(p)bigr]=pX(p)-x(0)=pX(p)-1;\ L bigl[x''(p)bigr]= p^2X(p)-p,x(0)-x'(0)= p^2X(p)-p-3;qquad L bigl[2e^{3t}bigr]=frac{2}{p-3},. end{gathered}$

Запишем уравнение для изображений:

$p^2X(p)-p-3-3pX(p)+3+2X(p)=frac{2}{p-3},.$

2. Решим уравнение для изображений:

$begin{aligned}& p^2X(p)-3pX(p)+2X(p)=frac{2}{p-3}+pquad Rightarrow\ & X(p)= frac{2}{(p-3)(p^2-3p+2)}+ frac{p}{p^2-3p+2}= frac{2+p^2-3p}{(p^2-3p+2)(p-3)}= frac{1}{p-3},. end{aligned}$

3. Найдем оригинал для функции $X(p)colon, x(t)=L^{-1}! left[frac{1}{p-3}right]= e^{3t}$ .

Пример 5.32. Решить задачу Коши x''+4x=cos2t,~ x(0)=1,~ x'(0)=-1 методами операционного исчисления

Решение

1. Перейдем от оригиналов к изображениям:

$L[x(t)]= X(p);qquad L[x''(t)]= p^2X(p)-p,x(0)-x'(0)= p^2X(p)-p+1;qquad L[cos2t]= frac{p}{p^2+4},.$

Запишем уравнение для изображений: $p^2X(p)-p+1+4X(p)=frac{p}{p^2+4}$ .

2. Решим уравнение для изображений:

$p^2X(p)+4X(p)=frac{p}{p^2+4}+p-1qquad Rightarrowquad X(p)= frac{p}{(p^2+4)^2}+ frac{p}{p^2+4}-frac{1}{p^2+4},.$

3. Применяя формулы 10,9,8 из табл. 5.1, найдем оригинал для функции X(p)colon

$x(t)=frac{1}{4},tsin2t+ cos2t-frac{1}{2}sin2t,.$

Пример 5.33. Решить задачи Коши:
а) x'''+x'=0,~~ x(0)=2,~ x'(0)=0,~ x''(0)=-1 ;
б) x'''+6x''+11x'+6x=0,~~ x(0)=1,~ x'(0)=-3,~ x''(0)=9 .

Решение

а) Воспользуемся алгоритмом.

1. Перейдем от оригиналов к изображениям:

L[x(t)]= X(p);quad L[x'''(t)]= p^3X(p)-p^2x(0)-p,x'(0)-x''(0)= p^3X(p)-2p^2+1;quad L[0]=0.

Запишем уравнение для изображений: p^3X(p)-2p^2+1+pX(p)-2=0 .

2. Решим уравнение для изображений:

$p^3X(p)+pX(p)=2p^2+1qquad Rightarrowquad X(p)=frac{2p^2+1}{p^3+p}= frac{p^2+1}{p(p^2+1)}+ frac{p^2}{p(p^2+1)}= frac{1}{p}+ frac{p}{p^2+1},.$

3. Применяя формулы 1,9 из табл. 5.1, найдем оригинал для функции X(p)colon, x(t)=1+cos t .

б) Решим вторую задачу, пользуясь алгоритмом.

1. Перейдем от оригиналов к изображениям:

$begin{gathered}L[x(t)]=X(p);qquad L[x'(t)]=pX(p)-x(0)= pX(p)-1;\ L[x''(t)]=p^2X(p)-p,x(0)-x'(0)= p^2X(p)-p+3;\ L[x'''(t)]=p^3X(p)-p^2x(0)-p,x'(0)-x''(0)= p^3X(p)-p^2+3p-9;quad L[0]=0. end{gathered}$

Запишем уравнение для изображений:

p^3X(p)-p^2+3p-9+ 6p^2X(p)-6p+18+ 11pX(p)-11+6X(p)=0.

2. Решим уравнение для изображений: $X(p)= frac{p^2+3p+2}{p^3+6p^2+11p+6}= ldots= frac{1}{p+3}$ .

3. Найдем оригинал для функции $X(p)colon, x(t)=L^{-1}! left[frac{1}{p+3}right]=e^{-3t}$ .

Пример 5.34. Решить задачу Коши: x'''-3x''+3x'-x=e^t,~ x(0)=1,~ x'(0)=-1,~ x''(0)=1 .

Решение

1. Перейдем от оригиналов к изображениям:

$begin{gathered}Lbigl[x(t)bigr]=X(p);quad Lbigl[x'(t)bigr]=pX(p)-x(0)=pX(p)-1;\[2pt] Lbigl[x''(t)bigr]= p^2X(p)-p,x(0)-x'(0)= p^2X(p)-p+1;\[2pt] Lbigl[x'''(t)bigr]= p^3X(p)-p^2x(0)-p,x'(0)-x''(0)= p^3X(p)-p^2+p-1;quad L[e^t]= frac{1}{p-1},. end{gathered}$

Запишем уравнение для изображений:

$p^3X(p)-p^2+p-1-3p^2X(p)+3 p-3+ 3pX(p)-3-X(p)= frac{1}{p-1},.$

2. Решим уравнение для изображений:

$begin{aligned}X(p)&= frac{1}{(p-1)^4}+ frac{p^2-4p+7}{(p-1)^3}= frac{1}{(p-1)^4}+ frac{(p-1)^2}{(p-1)^3}-frac{2(p-1)}{(p-1)^3}+ frac{4}{(p-1)^3}=\ &= frac{1}{(p-1)^4}+ frac{1}{p-1}-frac{2}{(p-1)^2}+ frac{4}{(p-1)^3}= frac{1}{6}cdot frac{3!}{(p-1)^4}+ frac{1}{p-1}-2cdot frac{1}{(p-1)^2}+ 2cdot frac{2}{(p-1)^3},. end{aligned}$

3. По формулам 7, 6 из табл. 5.1 найдем оригинал для функции $X(p)colon~ x(t)= e^t! left(frac{1}{6},t^3+1-2t+2t^2right)$ .

Пример 5.35. Решить систему ДУ: $begin{cases}x'=x+2y-9t,& x(0)=1,\ y'=2x+y+4e^t,& y(0)=2. end{cases}$ операционным методом.

Решение

1. Перейдем от оригиналов к изображениям:

$begin{gathered}L[x(t)]=X(p);qquad L[y(t)]= Y(p);\ L[x'(t)]= pX(p)-x(0)=pX(p)-1;quad L[y'(t)]= pY(p)-y(0)= pY(p)-2;\ L[9t]=frac{9}{p^2},;qquad L[4e^t]=frac{4}{p-1},. end{gathered}$

Запишем систему уравнений для изображений:

$left{begin{aligned}&pX(p)-1= X(p)+2Y(p)-frac{9}{p^2},;\ &pY(p)-2= 2X(p)+Y(p)+frac{4}{p-1},. end{aligned}right.$

2. Решим систему уравнений для изображений. Из первого уравнения выразим X(p)colon

$X(p)= frac{2Y(p)}{p-1}+frac{1}{p-1}-frac{9}{p^2(p-1)},,$

и подставим во второе: $pY(p)-2= frac{4Y(p)}{p-1}+frac{2}{p-1}-frac{18}{p^2(p-1)}+ Y(p)+ frac{4}{p-1}$ . Отсюда имеем

$Y(p)= frac{2(p-1)}{(p+1)(p-3)}+ frac{6}{(p+1)(p-3)}-frac{18}{p^2(p+1)(p-3)}$

Разложим каждое слагаемое на элементарные дроби:

$begin{gathered}frac{2(p-1)}{(p+1)(p-3)}= frac{1}{p+1}+ frac{1}{p-3},;quad frac{6}{(p+1)(p-3)}=-frac{3}{2}cdot frac{1}{p+1}+ frac{3}{2}cdot frac{1}{p-3},;\ frac{18}{p^2(p+1)(p-3)}= frac{4}{p}-frac{6}{p^2}-frac{9}{2}cdot frac{1}{p+1}+ frac{1}{2}cdot frac{1}{p-3},. end{gathered}$

Тогда $left{begin{aligned}&Y(p)=-frac{4}{p}+frac{6}{p^2}+ frac{4}{p+1}+2cdot frac{1}{p-3},,\ &X(p)=frac{1}{p-1}-frac{3}{p}-frac{3}{p^2}-frac{8}{p(p-1)}+frac{8}{(p+1)(p-1)}+frac{4}{(p-3)(p-1)},. end{aligned}right.$ .

3. По формулам 6, 2, 3, 15, 16 из табл. 5.1 найдем оригиналы для функций X(p) и Y(p)colon

$begin{cases}x(t)=2e^{3t}-4e^{-t}-2e^t+5-3t,;\[2pt] y(t)=-4+6t+4e^{-t}+2e^{3t}. end{cases}$

Пример 5.36. Решить задачу Коши: $begin{cases}x'=y-1,& x(0)=1,\ y'=-x-2y,& y(0)=-1.end{cases}$ .

Решение

1. Перейдем от оригиналов к изображениям:

$begin{gathered}L[x(t)]=X(p);quad L[y(t)]=Y(p);quad L[x'(t)]=pX(p)-x(0)= pX(p)-1;\ L[y'(t)]= pY(p)-y(0)= pY(p)+1;quad L[boldsymbol{1}(t)]= frac{1}{p}. end{gathered}$

Запишем систему уравнений для изображений:

$begin{cases}pX(p)-1= Y(p)-1!!not{phantom{|}},p,\ pY(p)+1=-X(p)-2Y(p). end{cases}$

2. Решим систему уравнений для изображений.

Умножим второе уравнение на , а из первого выразим pX(p)colon

$begin{gathered}pX(p)= Y(p)+1-frac{1}{p},\ p^2Y(p)+p=-pX(p)-2pY(p). end{gathered}$

Отсюда имеем

$p^2Y(p)+p=-Y(p)-1+frac{1}{p}-2Y(p)$ или $Y(p)= frac{1!!not{phantom{|}},p-1-p}{p^2+2p+1}= frac{1}{p(p+1)^2}-frac{1}{p+1}.$

Из второго уравнения системы

$X(p)=-1-(p+2)Y(p)=-1-(p+1)Y(p)-Y(p)=-frac{1}{p(p+1)}-frac{1}{p(p+1)^2}+ frac{1}{p+1}.$

Представим второе слагаемое в виде

$frac{1}{p(p+1)^2}= frac{A}{p}+ frac{B}{p+1}+ frac{C}{(p+1)^2},$

где A,,B,,C — неопределенные коэффициенты. Отсюда находим A(p+1)^2+ Bp(p+1)+ Cp=1 .

При p=-1,~ p=0,~ p=1 последовательно получаем C=-1,~ A=1,~ B=-1colon

$frac{1}{p(p+1)^2}= frac{1}{p}-frac{1}{p+1}-frac{1}{(p+1)^2}.$

Поэтому

$X(p)=-frac{1}{p(p+1)}-frac{1}{p}+ frac{2}{p+1}+ frac{1}{(p+1)^2},quad Y(p)= frac{1}{p}-frac{2}{p+1}-frac{1}{(p+1)^2}.$

3. По формулам 15,2,6,7 из табл. 5.1 найдем оригиналы для функций X(p) и Y(p)colon

$begin{cases}x(t)=2,e^{-t}-2+e^{-t}+t,e^{}= 3,e^{-t}+ t,e^{-t}-2;\ y(t)=1-2,e^{-t}-t,e^{-t}. end{cases}$

Пример 5.37. Решить задачу Коши: $begin{cases}x'_1=-x_2+2,& x_1(0)=-1,\ x'_2=x_1+1,& x_2(0)=0. end{cases}$ .

Решение

Перейдем от оригиналов к изображениям:

$begin{gathered}L[x_1(t)]= X_1(p);qquad L[x_2(t)]= X_2(p);\ L[x'_1(t)]= pX_1(p)-x_1(0)= pX_1(p)+1;qquad L[x'_2(t)]= pX_2(p)-x_2(0)= pX_2(p);\ L[boldsymbol{1}(t)]= frac{1}{p};qquad L[2cdot boldsymbol{1}(t)]= frac{2}{p}. end{gathered}$

Запишем систему уравнений для изображений: $begin{cases}pX_1(p)+1=-X_2(p)+ 2!!not{phantom{|}},p,\ pX_2(p)= X_1(p)+ 1!!not{phantom{|}},p.end{cases}$

2. Решим систему уравнений для изображений. Для этого умножим первое уравнение на и подставим во второе:

$p^2X_1(p)+p=-X_1(p)-frac{1}{p}+2.$

Отсюда получим

$X_1(p)= frac{2}{p^2+1}-frac{1}{p},qquad X_2(p)=-frac{2p}{p^2+1}+1-1+frac{2}{p}=-frac{2p}{p^2+1}+frac{2}{p}.$

3. По формулам 8, 2, 9 из табл. 5.1 найдем оригиналы для функций X_1(p) и X_2(p)colon

$begin{cases}x_1(t)=2sin t-1,\ x_2(t)=2-2cos t.end{cases}$

Замечание 5.8. Во многих практических задачах правая часть дифференциального уравнения задается графически. В этом случае алгоритм решения задачи не изменяется, а для нахождения изображения оригинала, заданного графиком, используются методы, изложенные в разд. 5.1.3.

▼ Примеры 5.38-5.42

рис. 5.9.

Пример 5.38. Решить задачу Коши: x'+x=f(t),~ x(0)=0 , где f(t) — функция, изображенная на рис. 5.9 (а).

Решение

1. Перейдем от оригиналов к изображениям:

L[x(t)]= X(p),qquad L[x'(t)]= pX(p)-x(0)= pX(p).

Функцию f(t) можно записать в форме f(t)= boldsymbol{1}(t)-boldsymbol{1}(t-2) . Ее изображение находится по свойству запаздывания: $F(p)= frac{1}{p}-frac{1}{p},e^{-2p}$ .

Запишем уравнение для изображений: $pX(p)+ X(p)= frac{1}{p}-frac{1}{p},e^{-2p}$ .

2. Решим уравнение для изображений: $X(p)= frac{1}{p(p+1)}- frac{e^{-2p}}{p(p+1)}$ .

3. Найдем оригинал для функции X(p) . Первому слагаемому по формуле 15 из табл. 5.1 соответствует оригинал $1-e^{e^{-t}}$ . Оригинал для второго слагаемого находится по теореме запаздывания (5.9):

$x(t)=1-e^{-t}-bigl[1-e^{-(t-2)}bigr]cdot boldsymbol{1}(t-2).$

Пример 5.39. Решить задачу Коши: x''+x= f(t),~ x(0)=0,~ x'(0)=0 , где f(t) — функция, изображенная на рис. 5.9 (б).

Решение

1. Перейдем от оригиналов к изображениям:

$begin{gathered}L[x(t)]= X(p),qquad Lx'(t)]= pX(p)-x(0)= pX(p);\ L[x''(t)]= p^2X(p)-p,x(0)-x'(0)= p^2=X(p). end{gathered}$

Так как функцию f(t) можно записать в виде

f(t)= cos tcdot bigl[boldsymbol{1}(t)-boldsymbol{1}(t-pi)bigr]= cos t+cos(t-pi)cdot boldsymbol{1}(t-pi),

то по формуле 9 из табл. 5.1 и по теореме запаздывания находим соответствующее изображение:

$X(p)= L[f(t)]= frac{p}{p^2+1}+ frac{p}{p^2+1},e^{-pi,p}.$

Запишем уравнение для изображений: $p^2X(p)+ X(p)= frac{p}{p^2+1}+ frac{p}{p^2+1},e^{-pi,p}$ .

2. Решим уравнение для изображений: $X(p)= frac{p}{(p^2+1)^2}+ frac{p}{(p^2+1)^2},e^{-pi,p}$ .

3. Найдем оригинал для функции X(p) по формуле 10 из табл. 5.1 и с учетом теоремы запаздывания (5.9):

$x(t)= frac{1}{2}tsin{t}+ frac{1}{2}(t-pi)sin(t-pi)cdot boldsymbol{1}(t-pi).$

рис. 5.5.

Пример 5.40. Решить задачу Коши: x''-x'= f(t),~ x(0)=0,~ x'(0)=0 , где f(t) — функция, изображенная на рис. 5.5 (з).

Решение

1. Аналогично примеру 5.39 перейдем от оригиналов к изображениям:

L[x(t)]= X(p),qquad L[x'(t)]= pX(p),qquad L[x''(t)]= p^2X(p).

Согласно результату примера 5.22,п.”з”: $L[f(t)]= frac{1-e^{-p-1}}{p+1}$ .

Запишем уравнение для изображений: $p^2X(p)-pX(p)= frac{1-e^{-p-1}}{p+1}$ .

2. Решим уравнение для изображений:

$X(p)= frac{1}{(p+1)p(p-1)}-frac{1}{e}cdot frac{e^{-p}}{p(p+1)(p-1)}$

3. Найдем оригинал для функции X(p) . Так как

$frac{1}{p(p+1)(p-1)}=-frac{1}{p}+ frac{1}{2}cdot frac{1}{p+1}+ frac{1}{2}cdot frac{1}{p-1}$ , то

$x(t)=-1+ frac{1}{2},e^{-t}+ frac{1}{2},e^t-frac{1}{e}boldsymbol{1}(t-1)left[-1+frac{1}{2},e^{-(t-1)}+ frac{1}{2},e^{t-1}right]!.$

Пример 5.41. Решить задачу Коши: x''+x= f(t),~ x(0)=0,~ x'(0)=0 , где f(t) — функция, изображенная на рис. 5.5 (и).

Решение

1. Перейдем от оригиналов к изображениям:

L[x(t)]= X(p),qquad L[x''(t)]= p^2X(p).

Согласно результату примера 5.22 п.”и” $L[f(t)]= frac{1}{p}-frac{2}{p},e^{-p}+ frac{1}{p},e^{-2p}$ .

Запишем уравнение для изображений:

$p^2X(p)+ X(p)= frac{1}{p}-frac{2}{p},e^{-p}+ frac{1}{p},e^{-2p}.$

2. Решим уравнение для изображений:

$X(p)= frac{1}{p(p^2+1)}-frac{2}{p(p^2+1)},e^{-p}+ frac{1}{p(p^2+1)},e^{-2p}.$

3. Найдем оригинал для функции X(p) . По формуле 17 из табл. 5.1 с учетом теоремы запаздывания (5.9) получаем

x(t)=1-cos t-2cdot bigl[1-cos(t-1)bigr]cdot boldsymbol{1}(t-1)+ bigl[1-cos(t-2)bigr]cdot boldsymbol{1}(t-2).

Пример 5.42. Решить задачу Коши: x''+9x=f(t),~ x(0)=0,~ x'(0)=1 , где f(t) — функция, изображенная на рис. 5.5,г.

Решение

1. Перейдем от оригиналов к изображениям:

L[x(t)]= X(p);quad L[x''(t)]= p^2X(p)-px(0)-x'(0)= p^2X(p)-1;

Согласно результату примера 5.22,г $L[f(t)]= frac{e^{-p}}{p^2}-2cdot frac{e^{-2p}}{p^2}+frac{e^{-3p}}{p^2}$ . Запишем уравнение для изображений:

$p^2X(p)-1+9X(p)= frac{1}{p^2}bigl(e^{-p}-2e^{-2p}+ e^{-3p}bigr)$

2. Решим уравнение для изображений:

$X(p)= frac{1}{p^2+9}+ frac{1}{p^2(p^2+9)}bigl(e^{-p}-2e^{-2p}+ e^{-3p}bigr).$

3. Найдем оригинал для функции X(p) . Заметим, что $frac{1}{p^2(p^2+9)}= frac{1}{9}cdot frac{1}{p^2}-frac{1}{9}cdot frac{1}{p^2+9}$ .

Согласно формулам 8, 3 из табл. 5.1 этому изображению соответствует оригинал $frac{1}{9}t-frac{1}{27}sin3t$ . Раскрывая скобки во втором слагаемом X(p) и при меняя теорему запаздывания при tau=1,~ tau=2,~ tau=3 , получаем:

$begin{gathered}x(t)= frac{}{}sin3t+ left[frac{1}{9}(t-1)-frac{1}{27}sin[3(t-1)]right]cdot boldsymbol{1}(t-1),-\ -left[frac{2}{9}(t-2)-frac{2}{27}sin[3(t-2)]right]cdot boldsymbol{1}(t-2)+ left[frac{1}{9}(t-3)-frac{1}{27}sin[3(t-3)]right]cdot boldsymbol{1}(t-3). end{gathered}$

Применение интеграла Дюамеля и теоремы Бореля

Рассмотрим задачу решения дифференциального уравнения (5.24) с нулевыми начальными условиями:

$x(0)=0,~ x'(0)=0,~ ldots,~ x^{(n-1)}(0)=0.$

(5.28)

Рассмотрим два способа ее решения, применение которых не требует нахождения изображения правой части f(t) дифференциального уравнения.

Первый способ. Наряду с уравнением (5.24) рассмотрим уравнение, получающееся из него при f(t)=boldsymbol{1}(t) , с нулевыми начальными условиями, т.е.

$begin{gathered}a_ncdot h^{(n)}+ldots+a_0cdot h= boldsymbol{1}(t),\ x(0)=0,~ x'(0)=0,~ ldots,~ x^{(n-1)}(0)=0. end{gathered}$

(5.29)

Решением уравнения (5.29) является функция h(t) , которая называется единичной переходной функцией.

Применим к задачам (5.24), (5.28) и (5.29) алгоритм решения задачи Коши, описанный в данном разделе.

Перейдем от оригиналов к изображениям:

$L[x(t)]=X(p),quad L[h(t)]=H(p),quad L[f(t)]=F(p),quad L[boldsymbol{1}(t)]= frac{1}{p},.$

Так как начальные условия нулевые, то $L[x^{(k)}(t)]=p^kX(p),~ L[h^{(k)}(t)]=p^kH(p),~ k=1,2,ldots,n.$ . В результате получаем уравнения в изображениях, соответствующие уравнениям (5.24) и (5.29):

$D(p)X(p)=F(p),~ D(p)H(p)=frac{1}{p}$ , где D(p)=a_np^n+ldots+a_0 — характеристический многочлен.

Исключая D(p) , находим X(p)=pH(p)F(p) . Используя интеграл Дюамеля (5.17), можно найти оригинал

$x(t)= h(0)f(t)+ intlimits_{0}^{t} h'(tau)f(t-tau),dtau,.$

Так как в силу (5.29) h(0)=0 , то окончательно получаем

$x(t)= intlimits_{0}^{t} h'(tau)f(t-tau),dtau,.$

(5.30)

На основании (5.30) можно сформулировать алгоритм решения задачи Коши:

$begin{gathered}a_nx^{(n)}+ldots+a_0x=f(t),\ x(0)=0,~ x'(0)=0,~ ldots,~ x^{(n-1)}(0)=0.end{gathered}$

(5.31)

Алгоритм решения задачи Коши (5.31) с помощью единичной переходной функции

1. Найти единичную переходную функцию h(t) , решая задачу (5.29). Для этого можно применить операционное исчисление или другие методы.

2. Найти производную h'(t) единичной переходной функции.

3. Определить решение задачи (5.31) по формуле (5.30).

Второй способ. В качестве вспомогательного уравнения для решения задачи (5.24),(5.28) рассмотрим уравнение с правой частью f(t)=delta(t) (см. пример 5.10) и нулевыми начальными условиями, т.е.

$begin{gathered}a_nk^{(n)}+ ldots+ a_0k=delta(t),\[2pt] k(0)=0,~ k'(0)=0,~ ldots,~ k^{(n-1)}(0)=0. end{gathered}$

(5.32)

Решением уравнения (5.32) является функция k(t) , которая называется импульсной переходной функцией.

Рассмотрим решение задач Коши (5.31) и (5.32) с помощью преобразования Лапласа. Перейдем от оригиналов к изображениям:

L[k(t)]= K(p);quad L[x(t)]= X(p);quad L[f(t)]= F(p);quad L[delta(t)]=1.

Так как начальные условия нулевые, то

$L bigl[x^{(k)}(t)bigr]= p^kX(p),quad L bigl[k^{(k)}(t)bigr]= p^kK(p),quad k=1,2,ldots,n.$

В результате получаем D(p)X(p)=F(p),~ D(p)K(p)=1 , где D(p)= a_np^n+ ldots+a_0 . Отсюда находим изображение искомого решения X(p)= K(p)F(p) . Согласно теореме Бореля можно найти оригинал по формуле (5.16):

$x(t)= intlimits_{0}^{t} k(tau)f(t-tau),dtau= intlimits_{0}^{t} k(t-tau)f(tau),dtau,.$

(5.33)

Заметим, что между переходными функциями, как следует из сравнения (5.30) и (5.33), имеется связь:

k(t)= h'(t).

(5.34)

На основании формулы (5.33) можно сформулировать алгоритм решения задачи (5.31).

Алгоритм решения задачи Коши (5.31) с помощью импульсной переходной функции

Найти импульсную переходную функцию, решая задачу Коши (5.32). Для этого можно применить операционное исчисление или другие методы [45].

По формуле (5.33) найти решение задачи Коши (5.31).

▼ Примеры 5.43-5.45

Пример 5.43. Решить задачу Коши: x'+x=e^t,~ x(0)=0 .

Решение

Первый способ

1. Составим уравнение (5.29) h'+h=1,~ h(0)=0 для единичной переходной функции и решим его, применяя операционное исчисление:

а) $L[h(t)]= H(p),~~ L[h'(t)]= pH(p),~~ L[boldsymbol{1}(t)]= frac{1}{p};~~ pH(p)+ H(p)= frac{1}{p}$ ;

б) $H(p)= frac{1}{p(p+1)}$ ;

в) $h(t)= L^{_1}[H(p)]=1-e^{-t}$ .

2. Найдем производную единичной переходной функции: $h'(t)=e^{-t}$ .

3. По формуле (5.30) при f(t)=e^t имеем

$x(t)= intlimits_{0}^{t}e^{-tau}e^{t-tau}dtau= e^{t} intlimits_{0}^{t} e^{-2tau} dtau= left.{-frac{1}{2}e^{t}e^{-2tau}}right|_{tau=0}^{tau=t}= frac{1}{2}(e^t-e^{-t}),.$

Второй способ

1. Составим уравнение (5.32) k'+k=delta(t),~ k(0)=0 для импульсной переходной функции и решим его:

а) L[k(t)]= K(p);~~ L[k'(t)]= pK(p);~~ L[delta(t)]=1;~~ pK(p)+ K(p)=1 ;

б) $K(p)= frac{1}{p+1}$ ;

в) $k(t)= L^{-1}[K(p)]= e^{-t}$ .

2. По формуле (5.33) при f(t)= e^t имеем

$x(t)= intlimits_{0}^{t} e^{-tau}e^{t-tau}dtau= frac{1}{2}(e^t-e^{-t}).$

Пример 5.44. Решить задачу Коши: x'+2x=-3t+2,~ x(0)=0 .

Решение

Применим алгоритм решения задачи Коши с помощью единичной переходной функции.

1. Составим уравнение h'+2h=1,~ h(0)=0 для нахождения единичной переходной функции и решим его:

а) $L[h(t)]= H(p),~~ L[h'(t)]= pH(p),~~ L[boldsymbol{1}(t)]= frac{1}{p};~~ pH(p)+ 2H(p)= frac{1}{p}$ ;

б) $H(p)= frac{1}{p(p+2)}$ ;

в) $h(t)= L^{-1}[H(p)]=-frac{1}{2}(e^{-2t}-1)= frac{1}{2}(1-e^{-2t})$ .

2. Найдем производную от единичной переходной функции: $h'(t)= e^{-2t}$ .

3. По формуле (5.30) при f(t)=-3t+2 получаем

$begin{aligned}x(t)&= intlimits_{0}^{t} e^{-2tau}bigl[2-3(t-tau)bigr]dtau= (2-3t) intlimits_{0}^{t} e^{-2tau}dtau+ 3intlimits_{0}^{t} tau,e^{-2tau}dtau=\ &= left.{frac{-2+3t}{2},e^{-2tau}}right|_{0}^{t}-left.{frac{3}{2}tau,e^{-2tau}}right|_{0}^{t}+ frac{3}{2} intlimits_{0}^{t} tau,e^{-2tau}dtau=\ &= left(-1+frac{3}{2},tright)! e^{-2t}+ 1-frac{3}{2},t-frac{3}{2},t,e^{-2t}-frac{3}{4},e^{-2t}+ frac{3}{4}=\ &=1,!75-1,!5t-1,!75e^{-2t}. end{aligned}$

Пример 5.45. Решить задачу Коши: $x''-3x'+2x=2e^{3t},~ x(0)=0,~ x'(0)=0$ .

Решение

Применим алгоритм решения задачи Коши с помощью импульсной переходной функции.

1. Составим уравнение k''-3k'+2k=delta(t),~ k(0)=0,~ k'(0)=0 для импульсной переходной функции и решим его:

a) L[k(t)]= K(p),~ L[k'(t)]= pK(p),~ L[k''(t)]= p^2K(p),~ L[delta(t)]=1,~ p^2K(p)-3pK(p)+ 2K(p)=1 ;

б) $K(p)= frac{1}{p^2-3p+2}= frac{1}{(p-1)(p-2)}$ ;

в) $k(t)= L^{-1}[K(p)]= e^{2t}-e^t$ .

2. По формуле (5.33) имеем

$begin{aligned}x(t)&= intlimits_{0}^{t} (e^{2tau}-e^{tau})2e^{3(t-tau)}dtau= 2e^{3t} intlimits_{0}^{t} (e^{-tau}-e^{-2tau})dtau= left.{2e^{3t}! left(-e^{-tau}+ frac{1}{2}e^{-2tau}right)}right|_{0}^{t}= \ &=-2e^{2t}+e^t+ 2e^{3t}-e^{3t}= e^t-2e^{2t}+ e^{3t}. end{aligned}$

Замечание 5.9. При решении прикладных задач, в частности задачи анализа выходных процессов линейных динамических систем, возникает необходимость в решении задачи, более общей по сравнению с (5.24), (5.25), где правая часть представляет собой линейный дифференциальный оператор над некоторой функцией:

$begin{gathered}a_nx^{(n)}+ ldots+ a_0x= b_m g^{(m)}(t)+ ldots+ b_0g(t),\[2pt] x(0)=x_0,~ x'(0)=x'_0,~ ldots,~ x^{(n-1)}(0)= x_0^{(n-1)}. end{gathered}$

(5.35)

Здесь g(t) — заданная функция; a_,ldots,a_0;~ b_m,ldots,b_0 — постоянные коэффициенты; и — числа, определяющие порядок старшей производной в левой и правой частях уравнения.

В процедуре решения задачи используется принцип суперпозиции: эффект, вызываемый суммой нескольких факторов (начальными условиями и функцией g(t) ), равен сумме эффектов каждого из факторов в отдельности.

Алгоритм решения задачи Коши с помощью принципа суперпозиции

1. Найти решение однородного уравнения (при g(t)equiv 0 ), соответствующего уравнению (5.35) с заданными начальными условиями:

$begin{gathered}a_nx^{(n)}+ldots+ a_0x=0,\ x(0)=x_0,~ x'(0)=x'_0,~ ldots,~ x^{(n-1)}(0)= x^{(n-1)}_{0}.end{gathered}$

(5.36)

Для этого может применяться как операционное исчисление, так и другие методы Полученное решение называется свободным движением и обозначается x_c(t) . Оно характеризует влияние начальных условий. Если начальные условия нулевые, свободное движение отсутствует, т.е. x_c(t)equiv0 .

2. Найти решение неоднородного уравнения с нулевыми начальными условиями:

$begin{gathered}a_nx^{(n)}+ ldots+ a_0x= b_mg^{(m)}+ ldots+ b_0g,\ x(0)=0,~ x'(0)=0,~ ldots,~ x^{(n-1)}(0)=0. end{gathered}$

(5.37)

Полученное решение называется вынужденным движением и обозначается $x_{text{vn}}(t)$ . Оно характеризует влияние функции g(t) . Для его нахождения следует:

а) найти импульсную переходную функцию k_0(t) для уравнения $a_nx^{(n)}+ ldots+a_0x=f(t)$ . Для этого решить задачу (5.32) с применением операционного исчисления:

$begin{gathered}a_n k_{0}^{(n)}+ ldots+a_0k^0= delta(t),\ k_0(0)=0,~ k'_0(0)=0,~ ldots,~ k_0^{(n-1)}(0)=0. end{gathered}$

(5.39)

б) найти импульсную переходную функцию k(t) для уравнения $a_nx^{(n)}+ ldots+ a_0x= b_mg^{(m)}+ ldots+ b_0g$ по формуле

$k(t)= b_m k_0^{(m)}(t)+ ldots+ b_0k_0(t);$

(5.39)

в) найти вынужденное движение по формуле, аналогичной (5.33):

$x_{text{vn}}(t)= intlimits_{0}^{t} k(tau)g(t-tau),dtau,.$

(5.40)

3. Найти решение задачи (5.35) в виде суммы свободного и вынужденного движений:

$x(t)=x_{c}(t)+ x_{text{vn}}(t).$

(5.41)

▼ Примеры 5.46-5.47

Пример 5.46. Найти решение задачи: $x''-2x'+2x= g'(t)-g(t),~ g(t)= e^{3t}cdot boldsymbol{1}(t),~ x(0)=0,~ x'(0)=0$ .

Решение

Решим задачу, используя алгоритм.

1. Найдем решение x_c(t) уравнения (5.36): x''-3x'+2x=0,~ x(0)=0,~ x'(0)=0 . Так как начальные условия нулевые, то, очевидно, x_c(t)equiv0 .

2. Найдем решение уравнения (5.37): x''-3x'+2x=g'-g,~ x(0)=0,~ x'(0)=0 . Для этого:

а) найдем импульсную переходную функцию k_0(t) для уравнения x''-3x'+2x=f(t) , решая уравнение (5.38):

k''_0-3k'_0+2k_0= delta(t),quad k_0(0)=0,~ k'_0(0)=0.

Из п.1 примера 5.45 следует, что $k_0(t)= e^{2t}-e^t$ ;

б) по формуле (5.39) определим импульсную переходную функцию:

$k(t)= 2e^{2t}-e^t-e^{2t}+ e^t=e^{2t};$

в) по формуле (5.40) имеем

$x_{text{vn}}(t)= intlimits_{0}^{t} e^{2tau}e^{3(t-tau)}dtau= e^{3t} intlimits_{0}^{t} e^{-tau}dtau= Bigl.{-e^{3t}e^{-tau}}Bigr|_{0}^{t}= e^{3t}-e^{2t}.$

3. Решение задачи получается по формуле (5.41): $x(t)= x_c(t)+ x_{text{vn}}(t)= e^{3t}-e^{2t}$ .

Пример 5.47. Найти решение задачи: x'''+6x''+11x'+6x= g''+5g'+6g;~~ g(t)=boldsymbol{t},~ x(0)=1,~ x'(0)=-3,~ x''(0)=9 .

Решение

Решим задачу, используя алгоритм.

1. Найдем свободное движение x_c(t) как решение уравнения (5.36):

$begin{gathered}x'''+6x''+11x'+6x=0,\ x(0)=1,~ x'(0)=-3,~ x''(0)=9. end{gathered}$

Согласно результату примера 5.33, пункт “б”, $x_c(t)=e^{-3t}$ .

2. Найдем вынужденное движение как решение уравнения (5.37):

$begin{gathered}x'''+6x''+11x'+6x= g''+5g'+6,\ x(0)=0,quad x'(0)=0,quad x''(0)=0.end{gathered}$

Для этого:

а) найдем импульсную переходную функцию для уравнения x'''+6x''+11x'+6x=f(t) , то есть решим уравнение (5.38):

$begin{gathered}k'''_0+6k''_0+11k'_0+6k_0=delta(t),\ k_0(0)=0,quad k'_0(0)=0,quad k''_0(0)=0. end{gathered}$

Перейдем от оригиналов к изображениям:

L[k_0(t)]= K_0(p);quad L[k'_0(t)]= pK_0(p);quad L[k''_0(t)]= p^2K_0(p);quad L[k'''_0(t)]= p^3K_0(p);quad L[delta(t)]=1.

Запишем уравнение для изображений и решим его:

$begin{gathered}p^3K_0(p)+ 6p^2K_0(p)+ 11pK_0(p)+ 6K_0(p)=1\ Downarrow\ K_0(p)= frac{1}{p^3+6p^2+11p+6}= frac{1}{(p+1)(p+2)(p+3)}= frac{1}{2}cdot frac{1}{p+1}-frac{1}{p+2}+ frac{1}{2}cdot frac{1}{p+3},.end{gathered}$

Найдем оригинал: $k_0(t)= frac{1}{2},e^{-t}-e^{-2t}+ frac{1}{2},e^{-3t}$ ;

б) найдем импульсную переходную функцию k(t) по формуле (5.39):

$k(t)= k''_0+ 5k'_0+ 6k_0= frac{1}{2},e^{-t}-4e^{-2t}+ frac{9}{2},e^{-3t}-frac{5}{2},e^{-t}+ 10e^{-2t}-frac{15}{2},e^{-3t}+ 3e^{-t}-6e^{-2t}+ 3e^{-3t}= e^{-t};$

в) определим вынужденное движение по формуле (5.40):

$x_{text{vn}}(t)= intlimits_{0}^{t} e^{-tau} boldsymbol{1}(t-tau),dtau= Bigl.{-e^{-tau}}Bigr|_{0}^{t}=1-e^{-t}.$

3. Найдем решение задачи по формуле (5.41): $x(t)= e^{-3t}+1-e^{-t}$ .

Математический форум (помощь с решением задач, обсуждение вопросов по математике).

Кнопка "Поделиться"

Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.

Источник

Найти правильное решение в трудной ситуации.

Довольно часто в жизни мы сталкиваемся с непростой ситуацией, когда сложно найти ее правильное решение или верность одного из решений не очевидна. Советы близких и всевозможных знакомых, рекомендации как лучше всего поступить конкретно в вашей ситуации могут лишь еще больше усложнить дело, потому что подчас они противоречивы или не совпадают с вашими желаниями. Универсальных рецептов нет, но наилучшим образом разрешить спорную ситуацию помогут следующие несколько тезисов, правил, которые работают всегда.

Чтобы не сожалеть о принятом решении или не сомневаться в его правильности спустя какое-то время, нужно абстрагироваться от текущей ситуации. А для этого необходимо вспомнить свои главные ценности и вытекающие из них приоритетные цели. Вполне возможно, не все ваши решения будут согласованы с вашими ценностями, и служить на благо жизненно-важных целей, но, по крайней мере, они не должны им противоречить.
Какими бы сложными, неразрешимыми или даже трагическими ни казались возникшие обстоятельства, необходимо задаться вопросом: “А что полезного может мне дать эта ситуация?” В любой обстановке, при любом стечении событий есть что-то жизненно необходимое именно для вас сейчас, в противном случае они не возникли бы. Все ситуации в жизни мы, так или иначе, создаем сами, спровоцировав их ранее принятыми решениями и взглядами на жизнь, себя и других. Чтобы не блуждать в вечной неопределенности, вселенная периодически дает нам обратную связь для дальнейшей корректировки наших мыслей, взглядов и действий. То, что есть сейчас можно рассматривать как меньшее зло из возможных или как вызов, новую ступень для личностного роста.
Чтобы найти в себе силы и мудрость разрешить данную ситуацию наилучшим образом, вспомните, какие качества и свойства вас наиболее привлекают в других людях. Именно эти особенности характера вам сейчас более чем необходимы – их нужно найти в себе, позволить им проявить себя, развивать их и воспитывать. Чтобы взять под контроль ситуацию и не нуждаться в контроле над другими – достаточно управлять собой.
Было бы ошибкой постоянно стремиться избежать неприятностей и проблем. Во-первых, концентрируясь на неприятностях, мы склонны притягивать их в свою жизнь, а во-вторых, это отвлекает внимание от основной желаемой цели. Поэтому самое разумное -самостоятельно представить наилучший сценарий своей жизни и двигаться в выбранном направлении, не страшась трудностей. Они неизбежны, но преодолимы.
Вам во многом должно нравиться то, что вы делаете, то, как, где, в каком окружении живете. Это необходимое условие для счастья и правило счастливых людей. С опорой на то, что вас радует в вашей жизни, с адекватной положительной оценкой себя, вы можете успешно менять то, что вас не устраивает.
Забудьте о своих недостатках, сосредоточьтесь на своих достоинствах, развивайте их и совершенствуйте. Помните, что людей без недостатков не бывает, истинная ценность человека в его проявленных способностях и развитых задатках. Особенно в сложных ситуациях помните о своих прежних достижениях и ранее правильно принятых решениях, они будут мотивировать аналогично вести себя сейчас.
Чтобы научиться принимать себя и свои не самые лучшие, как вы считаете качества, начните относиться к себе с юмором. Ведь юмор снимает напряжение, дает передышку и помогает безболезненно и объективно взглянуть на сложности. И, между прочим, полностью отрицательных черт характера, как известно, не бывает, тому, что вы считаете плохим и недостойным тоже можно найти наилучшее применение. Когда вы подумаете, то обязательно вспомните случаи из жизни, в которых вам пригодилось то, что вы склонны критиковать в себе.
Не меняйте цели, но своевременно корректируйте свое поведение, то, что помогало раньше, возможно уже не имеет прежней силы. Меняйте средства, подцели, но не саму основную цель – жить счастливо! Постарайтесь максимально находиться здесь и сейчас, быть гибким и внимательным, дабы правильно интерпретировать происходящее. И не придавайте слишком большее знание критике окружающих, что бы вы ни сделали, каждый интерпретирует исходя из своего опыта, ценностей и склонен видеть в других уже то, что есть в нем самом. И не видит того, что ему не присуще.
В какую бы нестандартную или неоднозначную ситуацию вы не попали, представьте хотя бы три более-менее подходящих способа выхода из трудностей. Иногда мы зацикливаемся на одной или двух допустимых способах решения задачи, не замечая остальные. Чем больше вариантов, пусть даже невероятных, вы можете придумать и назвать, тем увереннее вы будете себя чувствовать и легче найдете правильное решение среди всех возможных.
Как бы тяжело, больно, грустно вам не было, помните, что ничего не бывает вечным: день сменяет ночь, солнечную погоду – дождливая. Научитесь относиться к трудностям как ко временным, тем более что так оно и есть. В полной мере оценить лучшие мгновения нашей жизни помогают именно черные полосы. А позитивный настрой, надежда на лучшее и вера в себя часто оказываются решающими в преодолении трудностей.

Найти правильное решение в трудной ситуации.

Другие статьи, которые могут быть вам интересны:

Как преодолеть трудности? Копинг тест Лазаруса.
Выход из сложных ситуаций. Тест Хайма борьбы со стрессом.
Копинг стратегии. Тест Преодоление трудных жизненных ситуаций.
Копинг стратегии при конфликте.
Тест жизнестойкости.

Добавить комментарий

Источник

Найти эффективное решение
1. Техники поиска эффективного решения
  1. ]”Успевайте больше за меньшее время вместе с
2. «Копилкой Эффективных Советов»

Найти эффективное решение

Каждый из нас так или иначе постоянно сталкивается с различными задачами и проблемами. Это могут быть проблемы личного и делового характера, нерешенные вопросы, которые с течением времени превращаются в проблемы, личная ответственность за принятие того или иного решения.

Не всегда и у всех получается находить наилучший выход из создавшейся ситуации. Чаще всего для того, чтобы найти эффективное решение, не хватает опыта, мудрости, времени или знаний. Существует множество различных техник нахождения решений, и главная задача состоит в том, какая их техник подходит конкретно вам или конкретной ситуации.

Не так давно появились утверждения о том, что проблем не существуют. Есть только задачи, которые нужно решить. Проблемы существуют только в наших головах. На этот счет есть много мнений, и в принципе, каждый волен думать по-своему. Но так как слово “решение” в большей степени соответствует слову “задача”, давайте постараемся рассматривать свои проблемы как задачи, так их будет проще решить. Мы же все в школе учились решать задачи: с одним неизвестным, с двумя неизвестными, были даже такие, когда исходных данных для ее решения казалось совсем мало.

Вот так и в жизни, когда находишься на первый взгляд в неразрешимой ситуации, сначала кажется, что справиться в одиночку практически невозможно, но начиная распутывать клубок вопросов, становится понятно, что решение найдено и найдено верно.

Как же сделать так, чтобы в любых ситуациях мы действовали по одному и тому же алгоритму, который ранее доказал свою эффективность? Ответ банально простой – создавать свою личную систему принятия решений, и оттачивать мастерство поиска эффективных решений до автоматизма.

“Если мы поймем, что любая проблема или задача имеет решение, то наши мысли будут фокусироваться не нашем отношении к ней, а на том, что сделать, чтобы на одну задачу или проблему стало меньше.”

“Безвыходность положения заключается чаще всего не в отсутствии выхода из него, а в неспособности его найти.”

“Все наши трудности в большей степени связаны с тем, что мы думаем о них, а не с истинным положением вещей. Поэтому проблема заключается не в том, что именно произошло, а в том, как мы реагируем на произошедшее.”

“Парадоксы и закономерности нашей жизни и бизнеса таковы, что за отсутствие проблем, приходится платить… отсутствием успехов!”

Мудрые мысли, афоризмы, порой как отголоски из далеких миров и веков, часто бывают хорошими помощниками и советчиками в разнообразных ситуациях. Это уже чей-то пережитый опыт. Но мы привычно хотим наступать на свои, а не на чужие грабли, поэтому ценность советов чаще всего оцениваем уже после того как…

Давайте посмотрим, как находят решение задач и проблем те, кто уже умеет это делать. Заметьте, что перед нами сейчас стоит важная задача: научиться находить самое эффективное решение.

Техники поиска эффективного решения

1. Убедитесь, что вы решаете ту задачу, которую нужно. Важно на забывать: “Главное внимание – главным вещам”.

2. На второе место я поставлю способность задавать себе нужные вопросы. Вспомните, иногда чей-то вопрос способен в корне изменить отношение к проблеме и взглянуть на нее под другим углом зрения. Вопросы нужны и для того, чтобы проанализировать имеющуюся ситуацию, понять, от чего нужно отталкиваться и какими ресурсами мы обладаем.

Способностью задавать вопросы обладают коучи. Коучем называют такого человека, который профессионально решает чужие задачи. В своей практике коучи используют технику, при которой они искусственно создают ситуацию, в которой человек должен найти свое собственное правильное и эффективное решение. То решение, которое он с большим желанием и удовольствием реализует.

Брайан Трейси утверждает, что успешные люди тратят 25 % всего времени, отведенного на решения задачи. Действительно, наша неспособность определить истинную причину возникновения ситуации привет к тому, что эта проблема может повторяться снова и снова в разных вариациях.

3. Эффективным средством в поиске наиболее эффективного решения может стать обычный мозговой штурм, проведенный в кругу коллег, сотрудников, друзей, членов семьи. В таких случаях говорят: “Одна голова хорошо, а две лучше.” Более того, в такой среде часто возникают идеальные и креативные способы решения задачи. Имея на руках несколько вариантов, главной задачей будет выбрать наилучшее из них. Нелишним в этом случае будет знание о том, как правильно сделать выбор.

4. Эффективным считают метод “Шести думающих шляп”, изобретенным Эдвардом де Боно для оценки провокационных и необычных идей, инновационных предложений и ситуаций.

Учитывая, что коллективное мнение часто представляет собой борьбу разных мнений, метод “Шести думающих шляп” побуждает участников думать параллельно. Для этого участники одевают шляпы разных цветов, и смотрят на задачу в ракурсе соответствующего цвета шляпы. Сначала озвучивается предложение, а затем каждый участник по очереди одевает шляпы:

Белая шляпа – шляпа информации. В белой шляпе можно попросить предоставить дополнительную информацию, цифры, факты, которые помогут оценить ситуацию.

Красная шляпа – шляпа эмоций. Можно описать эмоции, которые вызывает данное предложение.

Желтая шляпа – шляпа оптимизма. Даже если идея кажется плохой, нужно найти в ней положительные стороны.

Черная шляпа – шляпа пессимизма. Даже если идея отличная, надо найти в ней недостатки и угрозы.

Зеленая шляпа – шляпа роста и возможностей. Каждый может предложить способ улучшения идеи для того, чтобы она работала лучше.

Голубая шляпа – шляпа процесса. Одевая шляпу голубого цвета люди включаются в процесс размышления над ним. Цель: выяснить, насколько эффективен данный метод оценки предложения.

С помощью метода “Шести думающих шляп” в корпорациях решают проблемы текучки кадров или обмена электронного документооборота.

5. Найти максимальное количество информации по данному вопросу. В этом случае также появится необходимость выбора из имеющегося арсенала и адаптации чьего-то эффективного решения под конкретную ситуацию. Старайтесь читать хорошую бизнес-литературу, накапливайте знания. Читайте больше, анализируйте прочитанное, запоминайте информацию.

6. Самый любимый и быстрой поиск нужного и эффективного решения – подбросить монетку. Это на случай, когда хороших вариантов так много, что определиться становится трудно.

Встретила по этому поводу перевод стихотворения Питера Хейна:

Коль ты в плену сомнений мук,

В них заперт, словно в клетке.

Мудрей всего, не смейся друг, –

Подбросить вверх монетку.

Лишь в воздух устремиться грош,

Лишь станет мир короче.

Ты неожиданно поймешь,

Чего ты втайне хочешь.

7. Хорошо бы услышать свою интуицию. Иногда, в экстремальных ситуациях, подсознание способно предложить наилучший выход. Доверяя своей интуиции надо помнить о вероятности ошибок.

8. Случайно наткнулась на технику “Лощади”, который, считаю, имеет право на жизнь в некоторых случаях. Когда не остается сил, а решение еще не найдено, ложитесь спать. “Утро вечера мудренее” – говорили наши бабушки. Только перед сном мысленно подумайте о задаче и скажите: “Пусть об этом подумает лошадь”.

Таким образом вы отпускаете проблему, и если навязчивая задача будет беспокоить, говорите себе, что теперь это не ваша задача, что теперь об этом думает Лошадь. Сняв таким образом напряжение и поверив в то, что ответ найдется у Лошади, автор метода советует поблагодарить Лошадь, когда ответ придет вам в голову или вложит в уста другого человека.

9. Техника стакана воды по Методу Сильвы. С помощью этого метода можно задействовать скрытые способности сознания. Это по сути – самовнушение, и оно стимулирует творческие способности нашего мозга за счет использования обоих полушарий.

Перед тем, как лечь спать, наполните стакан чистой водой и выпейте половину. Затем закройте глаза и направьте взгляд слегка вверх. Произнесите мысленно: “Это все, что мне нужно сделать, чтобы найти решение проблемы, о которой я думаю”. После этого отпустите проблему и перестаньте о ней думать – вы передали ее на рассмотрение своему сознанию.

Проснувшись утром, выпейте вторую половину воды и проделайте те же действия, что и перед сном. Люди, использующие этот метода, считают, что решение приходит либо ночью во сне, либо в виде какой-то случайной подсказки. Этот метод очень похож на технику “Лошади”, вероятно, в поисках эффективного решения люди изобрели много подобных способов на тот случай, когда идея совершенно не приходила в голову.

10. А теперь, когда единственное решение все-таки найдено, его можно проверить на соответствие критериям “Каким должно быть эффективное решение”.

Наше решение является обоснованным.
Наше решение является реальным, у нас есть все ресурсы для его осуществления.
Наше решение можно разложить на простые составляющие.
Наше решение своевременно. Его исполнение все еще актуально.
Наше решение является гибким. Его можно адаптировать под изменившиеся условия.
Наше решение должно принести максимальную выгоду.
Наше решение предусматривает контроль над его исполнением.

Друзья, никто из нас не застрахован от принятия неверных решений. Это нужно понимать и постараться избавиться от этого страха. Единственный разумный способ справиться с проблемами и задачами – как можно быстрее создать импульс движения. Не пускать все на самотек, а начать действовать. В процессе движения обязательно появляются средства и пути решения проблемы, обычно скрытые от нас.

Может быть стоит поучиться и узнать, как найти эффективное решение сегодня, чтобы завтра не ошибиться.

Смотрите один из способов принятия решения от Константина Коптелова.

[message type="warning"

`]"Успевайте больше за меньшее время вместе с`

«Копилкой Эффективных Советов»

[/message]

Просмотры: 752

Источник

Решение дифференциальных уравненийоперационным методом

Постановка задачи

Алгоритм решения задачи Коши операционным методом

Применение интеграла Дюамеля и теоремы Бореля

Алгоритм решения задачи Коши (5.31) с помощью единичной переходной функции

Алгоритм решения задачи Коши (5.31) с помощью импульсной переходной функции

Алгоритм решения задачи Коши с помощью принципа суперпозиции

Найти правильное решение в трудной ситуации.

Добавить комментарий

Найти эффективное решение

Техники поиска эффективного решения

]"Успевайте больше за меньшее время вместе с

«Копилкой Эффективных Советов»

Вам также может понравиться

Скайрим пропала серана как найти

Посудомоечная машина хайер ошибка е10 как исправить

Как найти индекс москвы по улице

Добавить комментарий Отменить ответ

Решение дифференциальных уравнений
операционным методом

`]"Успевайте больше за меньшее время вместе с`