Алгоритм Грэхема — алгоритм построения выпуклой оболочки в двумерном пространстве.
В этом алгоритме задача о выпуклой оболочке решается с помощью стека, сформированного из точек-кандидатов. Все точки входного множества заносятся в стек, а потом точки, не являющиеся вершинами выпуклой оболочки, со временем удаляются из него. По завершении работы алгоритма в стеке остаются только вершины оболочки в порядке их обхода против часовой стрелки.
Алгоритм[править | править код]
В качестве входных данных процедуры Graham выступает множество точек Q, где 
Graham(Q) 1) Пусть— точка из множества Q с минимальной координатой y или самая левая из таких точек при наличии совпадений 2) Пусть
— остальные точки множества Q, отсортированные в порядке возрастания полярного угла, измеряемого против часовой стрелки относительно точки
(если полярные углы нескольких точек совпадают, то по расстоянию до точки
) 3) Push(
,S) 4) Push(
,S) 5) for i = 2 to m do 6) while угол, образованный точками NextToTop(S),Top(S) и
, образуют не левый поворот (при движении по ломаной, образованной этими точками, мы движемся прямо или вправо) 7) do Pop(S) 8) Push(
,S) 9) return S
Для определения, образуют ли три точки 




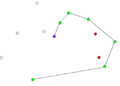
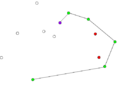
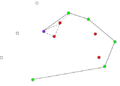
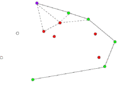
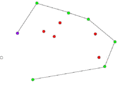
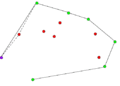
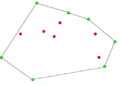
- Пример работы алгоритма Грэхема.
-
-

-
-
-
-
-
-
-
-
-
-
Корректность сканирования по Грэхему[править | править код]
Если процедура Graham обрабатывает множество точек Q, где 
Доказательство[править | править код]
После выполнения строки 2 в нашем распоряжении имеется последовательность точек 












В доказательстве используется сформулированный ниже инвариант цикла. В начале каждой итерации цикла for в строках 6-9 стек S состоит(снизу вверх) только из вершин оболочки CH(
Инициализация. При первом выполнении строки 6 инвариант поддерживается, поскольку в этот момент стек S состоит только из вершин 

Сохранение. При входе в новую итерацию цикла for вверху стека S находится точка 















Покажем, что множество вершин CH(
































Сразу после вытеснения из стека S точки 

Завершение. По завершении цикла выполняется равенство i = m + 1, поэтому из инварианта цикла следует, что стек S состоит только из вершин CH(
Время работы[править | править код]
Время работы процедуры Graham равно 



См. также[править | править код]
- Алгоритм Джарвиса
- Алгоритм Чена
- Алгоритм быстрой оболочки
- Алгоритм монотонных цепочек Эндрю
Литература[править | править код]
- Т. Кормен, Ч. Лейзерсон, Р. Ривест, К. Штайн. Алгоритмы. Построение и анализ = Introduction to Algorithms. — 2-e изд. — “Вильямс”, 2005.
Ссылки[править | править код]
- Реализация на c++
- Реализация на Java
- Реализация на Haskell
Пусть на плоскости задано некоторое количество точек. Оболочкой множества данных точек называется любая замкнутая линия, которая содержит в себе все эти точки.
Соответственно минимальная выпуклая оболочка – это такая оболочка, которая является выпуклым многоугольником наименьшего периметра.


В обработке изображений, распознавании образов и разработке игр часто возникает задача поиска выпуклой оболочки на плоскости. Для этого существуют следующие алгоритмы:
- Алгоритм обхода Джарвиса
- Алгоритм обхода Грэхема
- Алгоритм монотонных цепочек Эндрю
- Алгоритм типа «Разделяй и властвуй»
- Алгоритм «быстрого построения»
- Алгоритм Чана
Рассмотрим некоторые из них.
Алгоритм обхода Джарвиса

Пусть дан массив точек P.
- Необходимо найти точку, которая гарантировано будет входить в выпуклую оболочку; очевидно, что самая левая нижняя точка подходит под это условие.Находим точку с минимальной координатой x и y, и делаем ее текущей H[0].
- Перебираем все оставшиеся точки двойным циклом по i и j. В массив H записываем самую правую точку относительно вектора H[i]P[j]. Для этого находим векторное произведение, и если оно меньше 0, следовательно точка P[j] находится правее точки P[i] относительно H[i].
- Алгоритм завершается тогда, когда в H будет записана стартовая вершина и следовательно линия замкнется.
Псевдокод:
Jarvis(P) 1) H[1] = самая левая нижняя точка массива P; 2) i = 1; 3) do { H[i+1] = любая точка из P (кроме уже попавших в выпуклую оболочку, но включая p[1]); for (для каждой точки j из P, кроме уже попавших в выпуклую оболочку, но включая p[1]) if( векторное произведение(H[i], H[i+1], P[j]) < 0 ): H[i+1] = P[j] i = i + 1; } while P[i] != P[1] 4) return p;

Сложность обхода Джарвиса – O(hn), где n – количество всех вершин и h – количество вершин попавших в выпуклую оболочку.
Алгоритм обхода Грэхема
Сложность данного алгоритма O(nlgn) – следовательно он будет работать быстрее обхода Джарвиса.
1. Как и в предыдущем алгоритме находим самую нижнюю левую точку и делаем ее начальной.
2. Сортируем все оставшиеся точки в порядке их “левизны” относительно начальной точки, с помощью векторного произведения.


3. Как мы видим, получился многоугольник и для того, чтобы сделать его выпуклым необходимо убрать все те точки, в которых выполняется правый поворот (опять же, с помощью векторного произведения).

Код алгоритма на javascript:
function graham() { var minI = 0; //номер нижней левой точки var min = points[0].x; // ищем нижнюю левую точку for (var i = 1; i < points.length; i++) { if (points[i].x < min) { min = points[i].x; minI = i; } } // делаем нижнюю левую точку активной ch[0] = minI; ch[minI] = 0; // сортируем вершины в порядке "левизны" for (var i = 1; i < ch.length - 1; i++) { for (var j = i + 1; j < ch.length; j++) { var cl = classify({ 'x1': points[ ch[0] ].x, 'y1': points[ ch[0] ].y, 'x2': points[ ch[i] ].x, 'y2': points[ ch[i] ].y }, points[ ch[j] ].x, points[ ch[j] ].y) // функция classify считает векторное произведение. // если векторное произведение меньше 0, следовательно вершина j левее вершины i.Меняем их местами if (cl < 0) { temp = ch[i]; ch[i] = ch[j]; ch[j] = temp; } } } //записываем в стек вершины, которые точно входят в оболочку h = []; h[0] = ch[0]; h[1] = ch[1]; for (var i = 2; i < ch.length; i++) { while (classify({ 'x1': points[ h[h.length - 2] ].x, 'y1': points[ h[h.length - 2] ].y, 'x2': points[ h[h.length - 1] ].x, 'y2': points[ h[h.length - 1] ].y }, points[ ch[i] ].x, points[ ch[i] ].y) < 0) { h.pop(); // пока встречается правый поворот, убираем точку из оболочки } h.push(ch[i]); // добавляем новую точку в оболочку } }
Метод Эндрю
В методе обхода Грэхема имеется один недостаток: при упорядочении точек используется сравнение углов. Чтобы исправить этот недостаток, Эндрю предложил следующую модификацию метода обхода Грэхема, в которой вместо сравнения углов применяется сравнение абсцисс точек.
Пусть задано конечное множество M точек плоскости, состоящее из m элементов. Сначала находятся его левая крайняя точка l и правая крайняя точка r этого множества. Для определенности среди точек с наименьшей абсциссой выбирается точка с наименьшей ординатой, а среди точек с наибольшей абсциссой — точка с наибольшей ординатой. Построим прямую, проходящую через точки l и r (см. рис. 1). Множество M разбивается на два подмножества, первое из которых состоит из точек, расположенных выше прямой, и называется верхним подмножеством, а второе состоит из остальных точек и называется нижним подмножеством.

Рис.1. Разбиение, определенное крайними точками
Строится выпуклая оболочка верхнего подмножества вместе с точками l и r. Затем строится выпуклая оболочка нижнего подмножества и точек l и r. В результате получаем две ломанные, которые вместе составляют выпуклый многоугольник, ограничивающий искомую выпуклую оболочку.
Выпуклая оболочка верхнего подмножества и точек l и r строится в два этапа:
Верхние точки вместе с точками l и r сортируются по возрастанию абсцисс. Среди точек с одинаковой абсциссой оставляется лишь верхняя.
Производится просмотр троек pipi+1pi+2 верхних точек. Если вектор pipi+1 расположен слева от pipi+2, то увеличивается i, в противном случае точка pi+1 удаляется из списка (или массива) верхних точек.
Есть еще более быстрый способ поиска – алгоритм Чана. Его идея заключается в том, чтобы разбить множество заданных точек на группы, по m точек в каждой. Для каждой из таких групп строится выпуклая оболочка обходом Грэхема. Затем находится самая нижняя левая точка, и методом Джарвиса строится общая оболочка для всех групп, при этом следующая точка находится быстрее, так как в каждой группе они отсортированы в нужном порядке после обхода Грэхема. Следовательно для нахождения следующей точки оболочки нужно проверить только одну точку из каждой группы.

Конспект готов к прочтению.
| Определение: |
| Выпуклой оболочкой множества точек называется пересечение всех выпуклых множеств, содержащих все заданные точки. |
Ниже приводятся основные алгоритмы построения выпуклых оболочек статического множества. Используются обозначения: – размер входных данных, – размер оболочки.
Содержание
- 1 Алгоритм Джарвиса
- 1.1 Описание Алгоритма
- 1.2 Корректность
- 1.3 Псевдокод
- 1.4 Сложность
- 1.5 Ссылки
- 2 Алгоритм Грэхема
- 2.1 Описание Алгоритма
- 2.2 Корректность
- 2.3 Псевдокод
- 2.4 Сложность
- 2.5 Ссылки
- 3 Алгоритм Эндрю
- 3.1 Описание Алгоритма
- 3.2 Корректность
- 3.3 Псевдокод
- 3.4 Сложность
- 3.5 Ссылки
- 4 Алгоритм Чена
- 4.1 Описание Алгоритма
- 4.2 Сложность
- 4.3 Поиск [math]m[/math]
- 4.4 Ссылки
- 5 Алгоритм QuickHull
- 5.1 Описание Алгоритма
- 5.2 Корректность
- 5.3 Реализация
- 5.4 Псевдокод
- 5.5 Сложность
- 5.6 Ссылки
Алгоритм Джарвиса
По-другому “Gift wrapping algorithm” (Заворачивание подарка).
Он заключается в том, что мы ищем выпуклую оболочку последовательно, против часовой стрелки, начиная с определенной точки.
Описание Алгоритма
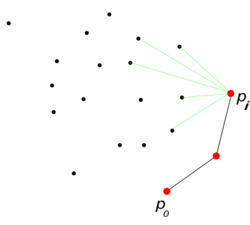
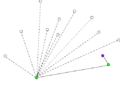
Промежуточный шаг алгоритма. Для точки ищем следующую перебором.
- Возьмем точку нашего множества с самой маленькой у-координатой (если таких несколько, берем самую правую из них). Добавляем ее в ответ.
- На каждом следующем шаге для последнего добавленного ищем среди всех недобавленных точек и с максимальным полярным углом относительно (Если углы равны, надо сравнивать по расстоянию). Добавляем в ответ. Если , заканчиваем алгоритм.
Корректность
Точка , очевидно, принадлежит оболочке. На каждом последующем шаге алгоритма мы получаем прямую , по построению которой все точки множества лежат слева от нее. Значит, выпуклая оболочка состоит из -ых и только из них.
Псевдокод
Inplace-реализация алгоритма. – исходное множество,
Jarvis(S)
find i such that S[i] has the lowest y-coordinate and highest x-coordinate
p0 = S[i]
pi = p0
k = 0
do
k++
for i = k..n
if S[i] has lower angle and higher distance than S[k] in relation to pi
swap(S[i], S[k])
pi = S[k]
while pi != p0
return k
Сложность
Добавление каждой точки в ответ занимает времени, всего точек будет , поэтому итоговая сложность . В худшем случае, когда оболочка состоит из всех точек сложность .
Ссылки
- Английская статья — Wikipedia
- Русская статья — Wikipedia
Алгоритм Грэхема
Алгоритм заключается в том, что мы ищем точки оболочки последовательно, используя стек.
Описание Алгоритма
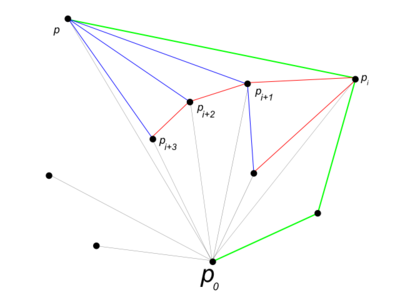
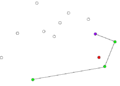
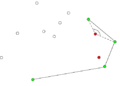
Промежуточный шаг алгоритма. Зелеными линиями обозначена текущая выпуклая оболочка, синими – промежуточные соединения точек, красными – те отрезки, которые раньше входили в оболочку, а сейчас нет. На текущем шаге при добавлении точки последовательно убираем из оболочки точки с -ей до -ой
- Находим точку нашего множества с самой маленькой у-координатой (если таких несколько, берем самую правую из них), добавляем в ответ.
- Сортируем все остальные точки по полярному углу относительно .
- Добавляем в ответ – самую первую из отсортированных точек.
- Берем следующую по счету точку . Пока и две последних точки в текущей оболочке и образуют неправый поворот (вектора и ), удаляем из оболочки .
- Добавляем в оболочку .
- Делаем п.4, пока не закончатся точки.
Корректность
Докажем, что на каждом шаге множество -тых является выпуклой оболочкой всех уже рассмотренных точек. Доказательство проведем по индукции.
- База. Для трех первых точек утверждение, очевидно, выполняется.
- Переход. Пусть для точек оболочки совпадают. Докажем, что и для точек они совпадут.
Рассмотрим истинную оболочку , где – множество всех точек из , видимых из . Так как мы добавляли точки в нашу оболочку против часовой стрелки и так как -тая точка лежит в , то состоит из нескольких подряд идущих последних добавленных в оболочку точек, и именно их мы удаляем на текущем шаге. Поэтому наша оболочка и истинная для точек совпадают.
Тогда по индукции оболочки совпадают и для .
Псевдокод
Inplace-реализация алгоритма. – исходное множество,
Graham(S)
find i such that S[i] has the lowest y-coordinate and highest x-coordinate
swap(S[i], S[1])
sort S[2..n] by angle in relation to S[1]
k = 2
for p = 3..n
while S[k - 1], S[k], S[p] has non-right orientation and k > 1
k--
swap(S[p], S[k + 1])
k++
return k + 1
Сложность
Сортировка точек занимает времени. При обходе каждая точка добавляется в ответ не более одного раза, поэтому сложность этой части – . Суммарное время — .
Ссылки
- Английская статья — Wikipedia
- Русская статья — Wikipedia
Алгоритм Эндрю
Алгоритм, очень похожий на алгоритм Грехема. Он заключается в том, что мы находим самую левую и самую правую точки, ищем для точек над и под этой прямой выпуклую оболочку Грехемом – для них начальные точки будут лежать на , а сортировка по углу относительно далекой точки аналогична сортировке по координате; после этого объединяем две оболочки в одну.
Описание Алгоритма
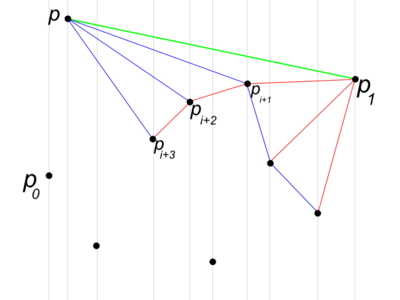
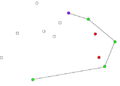
Промежуточный шаг алгоритма. Зелеными линиями обозначена текущая выпуклая оболочка, синими – промежуточные соединения точек, красными – те отрезки, которые раньше входили в оболочку, а сейчас нет. На текущем шаге при добавлении точки последовательно убираем из оболочки точки с -ей до -ой
- Находим самую левую и самую правую точки множества – и .
- Делим множество на две части: точки над и под прямой.
- Для каждой половины ищем выпуклую оболочку Грехемом с условием, что сортируем не по полярному углу, а по координате.
- Сливаем получившиеся оболочки.
Корректность
См. доказательство алгоритма Грехема.
Псевдокод
Inplace-реализация алгоритма. – исходное множество,
Andrew(S)
sort S[1..n] by x-coordinate backward(than by y backward)
k = 2
for p = 3..n
while S[k - 1], S[k], S[p] has non-right orientation
k--
swap(S[p], S[k + 1])
k++
sort S[k + 1..n] by x-coordinate (than by y)
for p = k + 1..n
while S[k - 1], S[k], S[p] has non-right orientation
k--
swap(S[p], S[k + 1])
return k + 1
Сложность
Сортировка точек занимает времени. При обходе каждая точка добавляется в ответ не более одного раза, поэтому сложность двух обходов – . Суммарное время – . Также можно отметить тот факт, что Эндрю в целом работает быстрее чем Грэхем, так как использует всего поворотов, в то время как Грэхем использует поворотов.
Ссылки
- Одно предложение о нем
- Имплементация на 13 языках
Алгоритм Чена
Является комбинацией двух алгоритмов – Джарвиса и Грехема. Недостатком Грэхема является необходимость сортировки всех точек по полярному углу, что занимает достаточно много времени . Джарвис требует перебора всех точек для каждой из точек оболочки, что в худшем случае занимает .
Описание Алгоритма
- Разобьем все множество на произвольные группы по штук в каждой. Будем считать, что нам известно. Тогда всего групп окажется .
- Для каждой группы запускаем Грехема.
- Начиная с самой нижней точки ищем саму выпуклую оболочку Джарвисом, но перебираем не все точки, а по одной из каждой группы.
Сложность
На втором шаге алгоритма в каждой группе оболочка ищется за , общее время – . На третьем шаге поиск каждой следующей точки в каждой группе занимает , так как точки уже отсортированы, и мы можем найти нужную бинпоиском. Тогда поиск по всем группам займет . Всего таких шагов будет , значит общее время – .
Итоговое время – . Несложно видеть, что минимум достигается при . В таком случае сложность равна .
Поиск
Как заранее узнать ? Воспользуемся следующим методом. Положим . Начиная с маленьких будем запускать наш алгоритм, причем если на третьем шаге Джарвис уже сделал шагов, то мы выбрали наше слишком маленьким, будем увеличивать, пока не станет .
Тогда общее время алгоритма –
Ссылки
- Английская статья — Wikipedia
- Русская статья — Wikipedia
Алгоритм QuickHull
Описание Алгоритма
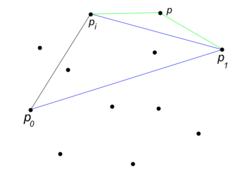
Промежуточный шаг алгоритма. Для прямой нашли точку . Над прямыми и точек нет, поэтому переходим к следующей прямой .
- Найдем самую левую точку и самую правую точку (Если таких несколько, выберем среди таких нижнюю и верхнюю соответственно).
- Возьмем все точки выше прямой .
- Найдем среди этого множества точку , наиболее отдаленную от прямой (если таких несколько, взять самую правую).
- Рекурсивно повторить шаги 2-3 для прямых и , пока есть точки.
- Добавить в ответ точки , полученные в п. 3.
- Повторить пункты 2-5 для (то есть для “нижней” половины).
- Ответ – объединение списков из п. 5 для верхней и нижней половины.
Корректность
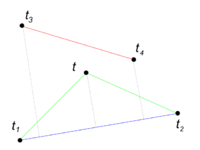
Очевидно, что выпуклая оболочка всего множества является объединением выпуклых оболочек для верхнего и нижнего множества. Докажем, что алгоритм верно строит оболочку для верхнего множества, для нижнего рассуждения аналогичны.
Точки и принадлежат оболочке.
- Пусть какая-то точка входит в нашу оболочку, но не должна.
Назовем эту точку . По алгоритму эта точка появилась как самая удаленная от некой прямой . Так как не входит в оболочку, то существует прямая из настоящей выпуклой оболочки, что лежит снизу от прямой. Тогда какая-то из и удалена от прямой дальше , что противоречит алгоритму.
- Наоборот, пусть какой-то точки в нашей оболочке нет, а должна быть.
Пойдем вниз рекурсии в те ветки, где есть . В какой-то момент окажется внутри некоторого треугольника. Но тогда возникает противоречие с тем, что принадлежит выпуклой оболочке.
Таким образом, наша оболочка совпадает с истинной, а значит алгоритм корректен.
Реализация
Заметим, что длина высоты, опущенная из точки на отрезок , пропорциональна векторному произведению , поэтому для сравнения можно использовать именно это. Векторное произведение эквивалентно предикату поворота, поэтому можно так же использовать и его.
Псевдокод
Inplace-реализация алгоритма. – исходное множество. – рекурсивная функция, находящая оболочку подмножества . В реализации в конце каждого подмножества находятся эл-ты, точно не принадлежащие оболочке.
QuickHull(S) find i such that S[i] has the highest x-coordinate and lowest y-coordinate swap(S[1], S[i]) find i such that S[i] has the lowest x-coordinate and lowest y-coordinate swap(S[n], S[i]) k = partition1(S) // разбиваем на те эл-ты, которые лежат над прямой и на остальные a = quick_hull(S, 1, k) b = quick_hull(S, k + 1, n); swap(S[a..k], S[k + 1, b]) return start + (a - 1) + (b - k - 1)
quick_hull(S, start, end) find i such that S[i], S[start], S[end] has maximum value (a, b) = partition2(S, start, end, S[i]) //свапаем эл-ты S так, чтобы сначала были все эл-ты над прямой S[start]S[i], потом S[i]S[end], потом все остальное c = quick_hull(S, start, a) d = quick_hull(S, a + 1, b) swap(S[c..a], S[a + 1..d]) return start + (a - c) + (d - b)
Сложность
Пусть время, необходимое для нахождения оболочки над некой прямой и множеством точек есть
Тогда , где – множества над полученными прямыми. Отсюда видно, что в худшем случае, алгоритм тратит . На рандомных же данных это число равно
Ссылки
- Английская статья — Wikipedia
Задачи на многоугольники¶
Очень часто геометрические задачи на контестах – это задачи на многоугольники. Некоторые из таких задач мы уже обсудили на предыдущих занятиях. Так мы уже обсудили задачу проверки многоугольника на выпуклость и научились находить площадь многоугольника. Напомним, что такое полярный угол.
Выпуклое множество – такое множество точек, что все точки отрезка, образуемого любыми двумя точками данного множества, также принадлежат данному множеству
Выпуклая оболочка фигуры – такое выпуклое множество точек, что все точки фигуры также лежат в нем.
Минимальная выпуклая оболочка фигуры – это минимальная по площади выпуклая оболочка.
Дано множество точек, требуется построить его минимальную выпуклую оболочку :
Алгоритм Джарвиса(метод заворачивания подарка)¶
Давайте выберем какую-то точку, которая гарантированно попадет в минимальную выпуклую оболочкуо, например обычно берут нижнюю и если таких несколько, то самую левую из них. Теперь давайте по одной набирать точки, как бы заворачивая нашу выпуклую оболочку(отсюда и название). Как же нам найти следующую точку в выпуклую оболочку, давайте пройдемся по точкам, которые мы еще не взяли в МВО и среди них выберем с минимальным полярным углом.

Корректность алгоритма легко доказывается по индукции, так как на первом шагу мы выбрали точку, точно лежащую в МВО, а на i, взяли такую точку, что все остальные лежат в нужной нам стороне.
Асимптотика : для каждой точки выпуклой оболочки мы из всех оставшихся точек будем искать оптимальную – что будет работать за h(размер выпуклой оболочки) * n
Важно помнить, что именно $O(hn)$, а не $O(n^2)$, так как существуют задачи на это¶
Построение за $O(n log n)$¶
Алгоритм Грэхема базируется на следующей идее: Давайте не искать следующую точку каждый раз, а сделаем так, чтобы у нас всегда была оптимальная точка и мы могли бы просто ее достать и проверить.
В прошлом алгоритме мы искали точку, оптимальную по полярному углу, тогда давайте сейчас сразу отсортируем точки по полярному углу и сразу возьмем две первые точки в МВО.
Теперь будем делать следующий алгоритм, пока все точки не будут просмотрены :
1) Возьмем первую из отсортированных точек.
2) Проверем последние три точки из взятых, если они образуют правый поворот, то удалим предпоследнюю точку
Сделать это можно, например, стеком. Код есть ниже.

Асимптотика : Мы просмотрим одну точку и либо удалим ее, либо оставим, то есть сам поиск МВО работает за линейное время, но мы еще делаем сортировку, а $rightarrow$ алгоритм работает за $O(nlog(n))$, при этом его корректность вытекает из предыдущего алгоритма.
Красивая визуализация – https://visualgo.net/en/convexhull
красивое видео – https://www.youtube.com/watch?v=BTgjXwhoMuI
.
Алгоритм Эндрю опирается на то, что вещественные числа не точны и предлагает поменять компаратор и строить не одну выпуклую оболочку, а две :
Давайте выберем самую нижнюю и самую правую точку, затем отсортируем точки по самому простому из возможных компараторов, теперь будем строить две оболочки от самой правой точки и самой левой, в итоге мы получим верхнюю и нижнюю части выпуклой оболочки
Алгоритм Чена¶
Также существует алгоритм, объединяющий Джарвиса и Грэхема(Эндрю) и работающий за $O(nlog(h))$, но он разбираться не будет
Задачи¶
1) Базовые задачи – достаточно простые, например найти длину забора, чтобы ограничить многоугольник и подобные, но есть достаточно интересные задачи, в которых выпуклая оболочка неочевидна, например следующая : Даны $n$ пунктов в городе и $n$ почтальонов, для каждого пункта известно расстояние от почты $c_{i}$. Требуется каждому пункту доставить почту, $i$-ый почтальон просит $a_{i}$ монет, чтобы проснуться и $b_{i}$, чтобы проехать один километр, требуется для каждого пункта сказать, кто доставит почту наиболее выгодно. (Подсказка : $a_{i} + b_{i} * c_{j}$ – это прямая и стоимость доставки от $i$ почтальона к $j$ пункту).
Просмотров 1.7к. Обновлено 23 ноября 2020
Урок из серии «Геометрические алгоритмы»
Вычисление выпуклой оболочки важно не только само по себе, но и как промежуточный этап для многих задач вычислительной геометрии. Например, задача о наиболее удаленных точках. Дано множество из N точек. Нужно выбрать пару максимально удаленных друг от друга точек.
Выпуклой оболочкой конечного числа точек N называется наименьший, выпуклый многоугольник, содержащий все точки из N (некоторые из точек могут быть внутри многоугольника, некоторые на его сторонах, а некоторые будут его вершинами).
Наглядно это можно представить себе так: в точках N вбиваются гвозди, на которые натянута резинка, охватывающая их все – эта резинка и будет выпуклой оболочкой множества гвоздей.
Задача. На плоскости задано множество S точек. Найти вершины выпуклой оболочки этого множества.
Будем перечислять вершины в порядке обхода против часовой стрелки. Для эффективного решения этой задачи существует несколько различных алгоритмов. Приведем наиболее простую реализацию одного из них – алгоритма Джарвиса. Этот алгоритм иногда называют «заворачиванием подарка».
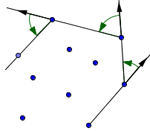
Перечисление точек искомой границы выпуклого многоугольника начнем с правой нижней точки ![]() , которая заведомо принадлежит границе выпуклой оболочки. Обозначим ее координаты
, которая заведомо принадлежит границе выпуклой оболочки. Обозначим ее координаты ![]() . Следующей при указанном порядке обхода будет точка
. Следующей при указанном порядке обхода будет точка ![]() . Она, очевидно, обладает тем свойством, что все остальные точки лежат слева от вектора
. Она, очевидно, обладает тем свойством, что все остальные точки лежат слева от вектора ![]() , т.е. ориентированный угол между векторами
, т.е. ориентированный угол между векторами ![]() и
и ![]() неотрицателен для любой другой точки М нашего множества.
неотрицателен для любой другой точки М нашего множества.
Для кандидата на роль точки ![]() проверяем выполнение условия
проверяем выполнение условия ![]() со всеми точками М. Если точек, удовлетворяющих этому условию несколько, то вершиной искомого многоугольника станет та из них, для которой длина вектора
со всеми точками М. Если точек, удовлетворяющих этому условию несколько, то вершиной искомого многоугольника станет та из них, для которой длина вектора ![]() максимальна.
максимальна.
Будем поступать так и далее.
Допустим, уже найдена i-я вершина ![]() выпуклой оболочки. Для следующей точки
выпуклой оболочки. Для следующей точки ![]() косые произведения
косые произведения ![]() не отрицательны для всех точек М.
не отрицательны для всех точек М.
Если таких точек несколько, то выбираем ту, для которой вектор ![]() имеет наибольшую длину.
имеет наибольшую длину.
Непосредственно поиск такой точки можно осуществить так. Сначала мы можем считать следующей (i+1)-й, любую точку.
Затем вычисляем значение ![]() , рассматривая в качестве М все остальные точки. Если для одной из них указанное выражение меньше нуля, то считаем следующей ее и продолжаем проверку остальных точек (аналогично алгоритму поиска минимального элемента в массиве).
, рассматривая в качестве М все остальные точки. Если для одной из них указанное выражение меньше нуля, то считаем следующей ее и продолжаем проверку остальных точек (аналогично алгоритму поиска минимального элемента в массиве).
Если же значение выражения равно нулю, то сравниваем квадраты длин векторов. Продолжая эту процедуру, мы рано или поздно вернемся к точке ![]() . Это будет означать, что выпуклая оболочка построена.
. Это будет означать, что выпуклая оболочка построена.
Приведем программу решения данной задачи для целочисленных координат.
Множество исходных точек находится в массиве a, а все точки, принадлежащие выпуклой оболочке, будем записывать в массив b.
program geom6;
type vv = record
x,y: longint;
end;
myArray = array[1..100] of vv;
var a, b: myArray;
min,m,i,j,k,n:integer;
input:text;
function vect(a1,a2,b1,b2:vv):longint;
begin
vect:=(a2.x - a1.x)*(b2.y-b1.y)-(b2.x-b1.x)*(a2.y-a1.y)
end;
function dist2(a1,a2:vv):longint; {Квадрат длины вектора}
begin
dist2:=sqr(a2.x-a1.x)+sqr(a2.y-a1.y);
end;{dist2}
procedure Solve(a:myArray; var k: integer; var b:myArray);
{Построение выпуклой оболочки}
var i, j, m: integer;
begin
{ищем правую нижнюю точку}
m:=1;
for i:= 2 to n do
if a[i].y < a[m].y
then m := i
else if (a[i].y = a[m].y) and (a[i].x > a[m].x) then m:=i;
{запишем ее в массив
b
и переставим на первое место в массиве
a
}
b[1] := a[m]; a[m]:= a[1]; a[1]:= b[1];
k:= 1;
min:= 2;
writeln(b[1].x, b[1].y);
repeat
{ищем очередную вершину оболочки}
for j := 2 to n do
if (Vect(b[k],a[min],b[k],a[j])< 0) or
((Vect(b[k],a[min],b[k],a[j])=0) and
(dist2(b[k],a[min])< dist2(b[k],a[j])))
then min:=j;
k:=k+1;
{записана очередная вершина}
b[k]:=a[min];
min:=1;
until (b[k].x = b[1].x)and (b[k].y = b[1].y); {пока ломаная не замкнется}
end; {Solve}
begin{main}
assign(input,'input.pas');
reset(input);
readln(input,n); {количество точек}
for i:= 1 to n do
read(input,a[i].x, a[i].y);
close(input);
solve(a, k, b);
for j := 1 to k-1 do
writeln(b[j].x, ' ',b[j].y)
end.
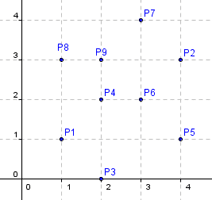
Входные данные: 9 1 1 4 3 2 0 2 2 4 1 3 2 3 4 1 3 2 3
Выходные данные: 2 0 4 1 4 3 3 4 1 3 1 1
На этом мы с вами заканчиваем обзор решения элементарых задач вычислительной геометрии на плоскости. На них опирается решение более сложных , в частности олимпиадных задач.
Надеюсь, что решение последних окажется теперь нам по силам.
С уважением, Вера Господарец.
