Приветствую Вас!
Предлагаю разобрать выражения, содержащие степени как положительные, так и отрицательные, дробные, сложные.
Начнем сначала. Для решения степенных выражений существует несколько правил, и они не меняются на протяжении всей математики. Как бы что не выглядело, в любом случае:
- при умножении степени складываются,
- при делении – вычитаются,
- при возведении степени в степень – перемножаются.
Именно такие определения дает основная масса населения. Но, в данной интерпретации отсутствует главная мысль: основание должно быть одинаковое(!), т.е. то число, которое возводится в степень. Оттуда и ошибки по типу: 2^4×3^3=6^7.
Поэтому, прежде чем выполнять какие-либо действия со степенями, нужно обратить внимание на основания. Если они разные, никаких действий со степенями совершать нельзя. Для начала требуется сделать основания одинаковыми, говоря простым языком. Например:
Это, конечно, самые элементарные примеры, но на них строятся более сложные. Бывает так, что в одном выражении находятся разные основания. В этом случае, если это возможно, нужно получить одинаковые, и выполнить действия:
Теперь об отрицательных степенях. Если какое-либо число стоит в отрицательной степени, то, по сути, это дробное число. Дроби и минуса неудобны, поэтому от них, по возможности, лучше избавиться. Это не всегда возможно, но когда-то мы и могём. Вот один из экзаменационных примеров:
Безусловно, можно высчитать степени и в таком виде как они даны, т.е. -11+4-(-3)=-4. Но это не совсем удобно, и как показывает практика, некоторые ребятишки в 9ом классе не знают как сосчитывать отрицательные числа. Поэтому давайте уберем минуса:
Из примера видно, что число в отрицательной степени из числителя перешло в знаменатель, и наоборот. Это произошло из правил умножения/деления дробных выражений. Помним, что минус в степени показывает, что число дробное. Теперь совокупим несколько приемов. Допустим, такой пример:
Запишем его для удобства в виде дроби, пустив по боку две точечки, и проведем нужные манипуляции:
И не надо ничего мудрить. Всё очень просто. Ну и апогей экзаменационных выражений выглядит примерно так:
Здесь мы сталкиваемся со сложными степенями. И, сложные они не потому, что трудные, а потому, что сложенные. А в каком случае степени складываются? Правильно, при умножении чисел с одинаковыми основаниями. Воспользуемся всё теми же правилами и разложим сложное на простое в обратном направлении и применим вышеуказанные действа:
Благодарю за внимание..
Сложение и вычитание степеней
Как складывать числа со степенями и как вычитать степени — очень просто. Основной принцип такой: выполняется сначала возведение в степень, а уже потом действия сложения и вычитания.
23+ 34= 8 + 81= 89
63— 33= 216 — 27 = 189
- Если есть скобки — начинать вычисления нужно внутри них
- Только потом возводим этот результат из скобок в степень
- Затем выполняем остальные действия: сначала умножение и деление по порядку (слева направо), а в конце — сложение и вычитание по порядку (слева направо)
Сложение степеней с разными показателями
В таком случае действуем согласно общему правилу: сначала выполняем возведение в степень каждого числа, затем — производим сложение.
- 23+ 24= 8 + 16= 24
Сложение степеней с разными основаниями
В целом это ничем не отличается от предыдущего пункта. Могут быть разные основания, но одинаковые показатели. А могут быть и разные основания, и разные показатели. Поэтому сначала выполняем возведение в степень каждого числа, затем — производим сложение.
- 34+ 54=81 + 625 = 706
- 14+ 72= 1+ 49 = 50
Как складывать числа с одинаковыми степенями
Точно так же, как и в предыдущем примере. Если показатели степени одинаковые, а основания разные — нельзя сложить основания и затем эту сумму возводить в степень.
- 63+ 33= 216 + 27 = 243
В уравнениях с этим все проще. Если показатель и основание степени одинаковые (тогда это называется переменная, a2, например) — их коэффициенты можно складывать. Коэффициент — это число перед переменной a2.
- 2a2 + 3a2 = 5a2
2,3, 5 — коэффициенты
a2 — переменная
Если перед переменной в уравнении нет коэффициента, это значит, что он равен 1.
Вычитание степеней с одинаковым основанием
Здесь принцип тот же, что и со сложением: возводим в степень числа и только потом вычитаем их.
- 63— 33= 216 — 27 = 189
Вычитание степеней с разными основаниями
Могут быть разные основания, но одинаковые показатели степени. А могут быть и разные основания, и разные показатели. Поэтому сначала выполняем возведение в степень каждого числа, затем — производим вычитание.
- 54— 44= 625 — 256 = 369
- 74— 32= 2401 — 9 = 2392
Вычитание степеней с одинаковыми показателями
Все точно так же, как и со сложением. Если показатели степени одинаковые, а основания разные — нельзя вычесть основания и затем эту разницу возводить в степень. Сначала возводим каждое число в степень и затем выполняем вычитание.
- 63— 33= 216 — 27 = 189
И та же история с коэффициентами: если показатель степени и основание степени одинаковые (тогда это называется переменная, a2) — их коэффициенты можно вычитать. Коэффициент — это число перед переменной a2.
- 5a2 — 3a2 = 2a2
5, 3, 2 — коэффициенты
a2 — переменная
Если перед переменной в уравнении нет коэффициента, это значит, что он равен 1.
Умножение и деление степеней
Здесь всё не так однозначно, как со сложением и вычитанием — общие правила для всех случаев выделить не получится. Все зависит от оснований и показателей степеней, с которыми нужно выполнить манипуляции.
Например, действия со степенями с разными основаниями будут отличаться от действий с числами, у которых основания одинаковые. Работа с показателями — одинаковыми и разными — тоже отличается. Давайте разбираться.
Умножение степеней с одинаковыми показателями
Чтобы произвести умножение степеней с одинаковыми показателями, нужно перемножить основания, а показатель степени оставить неизменным:
- an · bn = (a · b)n , где
a, b — основание степени (не равное нулю)
n — показатели степени, натуральное число
- a5 · b5 = (a·a·a·a·a) ·(b·b·b·b·b) = (ab)·(ab)·(ab)·(ab)·(ab) = (ab)5
- 35 · 45 = (3·4)5 = 125 = 248 832
- 16a2 = 42·a2 = (4a)2
Умножение степеней с одинаковыми основаниями
Степени с одинаковыми основаниями умножаются путём сложения показателей степеней:
am · an= am+n, где
a — основание степени
m, n — показатели степени, любые натуральные числа
- 35 · 32 = 35 + 2 = 37 = 2 187
- 28 · 81= 28 · 23 = 28 + 3 = 211 = 2048
Умножение степеней с разными основаниями и показателями
Если разные и показатели, и основания, и одна из степеней не преобразуется в число с тем же основанием, как у другой степени (как здесь: 28 · 81= 28 · 23 = 211 = 2048), то производим возведение в степень каждого числа и лишь затем умножаем:
- 33 · 52 = 27·25 = 675
Деление степеней с одинаковыми основаниями и одинаковыми показателями
Деление степеней с одинаковыми основаниями, но разными показателями осуществляется по следующей формуле: показатели отнимаются, а основание остается неизменным.
a — любое число, не равное нулю
m, n — любые натуральные числа такие, что m > n
Деление чисел с одинаковыми показателями степени
При делении степеней с одинаковыми показателями результат частного этих чисел возводится в степень:
- an : bn = (a : b)n , где
a, b — основание степени, любые числа, b ≠ 0,
n — показатель степени, натуральное число
Пример:
Деление степеней с разными основаниями и показателями
Если разные и показатели, и основания, то возводим в степень каждое число и только потом делим:
- 33 ÷52 = 27÷25 = 1,08
Степень с отрицательным показателем и её свойства
Число в минусовой степени равно дроби, числителем которой является единица, а знаменателем данное число с положительным показателем:
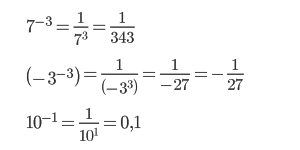
Чтобы разобраться, как возводить число в отрицательную степень, вспомним правило деления степеней с одинаковыми основаниями.
Деление степеней с одинаковыми основаниями, но разными показателями осуществляется по следующей формуле: показатели отнимаются, а основание остается неизменным.
Поэтому если степень делимого будет меньше степени делителя, то в результате получится число с отрицательной степенью:
- a3÷a6=a3 — 6 = a-3
Если записать деление в виде дроби, то при сокращении в числителе останется 1, а в знаменателе число будет иметь положительную степень:
Умножение отрицательных степеней
При умножении отрицательных степеней с одинаковыми основаниями показатели степеней складываются, так же как и при умножении положительных степеней:
am · an = am+n
Деление отрицательных степеней
При делении отрицательных степеней с одинаковыми основаниями из показателя степени делимого вычитается показатель делителя, так же как и при делении положительных степеней:
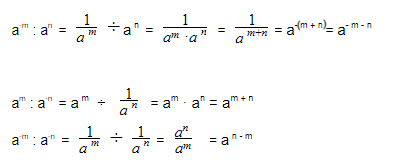
Возведение дроби в отрицательную степень
Чтобы возвести дробь в отрицательную степень, надо возвести в эту степень отдельно числитель и знаменатель:
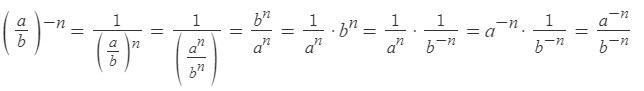
Возведение произведения в отрицательную степень
Чтобы возвести произведение в отрицательную степень, необходимо возвести в эту степень каждый множитель произведения отдельно:
Как представить число в виде степени
Чтобы представить число в виде степени, нужно разложить его на простые множители. Если в произведении встречаются несколько одинаковых сомножителей, то это произведение записывается в виде степени.
Например, представим в виде степени число 243:
243 = 3 × 3 × 3 × 3 × 3 = 35
Формулировка задачи: Найдите значение выражения (степени, с разными основаниями).
Задача входит в состав ЕГЭ по математике базового уровня для 11 класса под номером 2 (Действия со степенями).
Рассмотрим, как решаются подобные задачи на примере.
Пример задачи 1:
Найдите значение выражения 80,76 ∙ 640,12.
Решение:
Найдем значение выражения. Для этого приведем числа к одинаковому основанию и выполним необходимые действия:

Ответ: 8
Пример задачи 2:
Найдите значение выражения: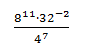
Решение:
Найдем значение выражения. Для этого приведем числа к одинаковому основанию и выполним необходимые действия:

Ответ: 512
Пример задачи 3:
Найдите значение выражения 35-4,7 ∙ 75,7 : 5-3,7.
Решение:
Найдем значение выражения. Для этого приведем числа к одинаковому основанию и выполним необходимые действия:
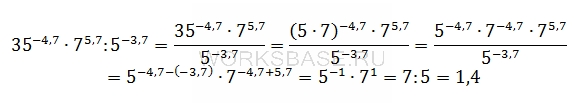
Ответ: 1,4
Пример задачи 4:
Найдите значение выражения: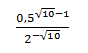
Решение:
Найдем значение выражения. Для этого приведем числа к одинаковому основанию и выполним необходимые действия:
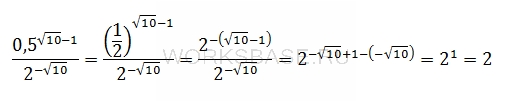
Ответ: 2
Поделитесь статьей с одноклассниками «Найдите значение выражения (степени, с разными основаниями) – как решать».
При копировании материалов с сайта ссылка на источник обязательна. Уважайте труд людей, которые вам помогают.
Нашли ошибку? Выделите текст и нажмите Ctrl + Enter.
|
Например : 2^3 x 4^5 = ? Не знаю удачный ли пример,но что тут надо делать?При умножении и делении надо степени вычитать и складывать,а тут что?
В общем случае с этим ничего не сделать, в вашем конкретном примере можно 4 представить как 2 во 2-й степени. Получится (2^2)^5. Далее, т.к. при возведении степени в степень показатели степеней перемножаются, получаем 2^3 x 2^10 = 2^13 = 8192. Т.е. числа нужно приводить ко одинаковому основанию или показателю степени. Тут 2 правила: X^a * X^b = X^(a+b) X^a * Y^a = (XY)^a. модератор выбрал этот ответ лучшим
Galina7v7 7 лет назад У вас не сложение , или вычитание , а умножение. И это очень меняет дело* В данном примере нужно привести 4 к степени двойки : 4 =2^(2) , тогда 2^(3) * 4^(5) = 2^(3) * [2^(2)]^5 = 2^(3 * 2^(10) = 2 ^ (3+10) = 2 ^ (13) или 2 в 13 степени. Если бы был пример на сложение ,то есть : 2 ^ (3) + 4 ^ (5) = [2 ^( 3) + (2 )]^ 2 ^ 5 = 2 ^ (3) + 2 ^( 10)= 2 ^(3) *[1+2 ^( 7)]. И это совсем другой результат.А правила действий со степенями такие : a ^ (m) * a ^ (n) = a ^ (m+n)a ^(m) a ^ (n) = a ^ (m-n)a^ (m )+ a ^( n) = a ^(m) *[a ^(m-n)+1}Вот это правило очень важное,потому что когда степени стоят как слагаемые,то их нельзя иначе преобразовать,как только вынести общий множитель за скобки. ({a ^ (m)}^n= a ^ (m*n)
Ксарфакс 5 лет назад Если в выражении присутствует возведение в степень, то алгоритм действий различается для умножения/деления и для сложения/вычитания. Начнём с самого простого – умножение и деление степеней с одинаковым основанием. 1) Умножение – основание остаётся тем же, а показатели степени складываем. 2) Деление – основание оставляем, а из показателя степени делимого вычитаем показатель степени делителя.
В этой ситуации затруднений вообще быть не должно. При умножении и делении степеней с разными основаниями порядок алгоритм такой – приводим их к одному основанию (если это можно сделать), а затем выполняем действия по вышеприведённым правилам.
Если основания разные, но при этом показатель степени один и тот же, то нужно перемножить основания и возвести их в степень.
Другое дело, если требуется сложить или вычесть степени. Здесь ситуация разная. Если показатель степени у чисел один и тот же, то можно воспользоваться формулами сокращённого умножения для суммы и разности степеней. В некоторых случаях можно попробовать общий множитель выносится за скобки.
Ну и последний вариант (если первые два способа не применимы) – возводим каждое число в степень и складываем/вычитаем. renard 6 лет назад В вашем примере 2^3•4^5 нужно найти произведение степеней с разными основаниями. Потребуется несколько действий совершить:
Со сложением чисел в одной степени, как и с вычитанием, занимаемся расчетами на калькуляторе или в столбик на бумажке. Хотя есть возможность использовать известные из школьной алгебры формулы сокращенного умножения для вычитания квадратов, для сложения или вычитания кубов. Так можно хоть от степеней избавиться или понизить их. a^2-b^2=(a-b)•(a+b) – так упрощаем разность квадратных чисел. a^3-a^3 = (a+b)•(a^2-ab+b^2)или a^3+b^3=(a-b)•(a^2+ab+b^2) и с неудобными третьими степенями можно распрощаться.
В общем случае ничего с таким умножением сделать нельзя. То есть если требуется умножить 2 в квадрате на 3 в кубе, то это не значит, что мы должны 2 умножить на 3 и возвести результат в 5 степень – ответ получится неверный. Приходится возводить 2 в квадрат, а 3 в куб и только потом перемножать числа. Но если требуется 2 в произвольной степени умножить на 4 в произвольной степени, то мы представляем 4 как 2 в квадрате и просто складываем степени. Если же мы складываем или вычитаем два числа возведенных в степени, то тут нет никакого правила – надо возводить и складывать (вычитать) результат: а^3 + b^4 не упростить да и не надо.
ZoRRoO 8 лет назад На вашем примере нужно привести к одной основе, то есть 4 – это 2^2. Поэтому запишем выражение следующим образом 2^3 x 4^5 = 2^3 x (2^2)^5. Теперь нам нужно избавиться от этих скобочек. Мы знаем, что по правилу степени просто перемножаются, поэтому, у нас получится следующее выражение: 2^3 x 2^10. А теперь у нас есть единая основа, значит мы можем просто сложить степени. Получится такое выражение: 2^13. Ответ будет 8192. Итак, на представленном вами примере мы использовали всего лишь 2 правила, а именно сложение степеней, когда есть одна основа, и умножение их, когда мы возводим одну степень в другую. Конь В Пальто 10 лет назад Ничего кроме выполнения отдельных операций согласно их приоритету, вы тут не сделаете. Если вам нужно сложить два разных числа в разных степенях, то сначала каждое число вы возводите в свою степень и после этого выполняете сложение. Если у двух слагаемых в основании одно число в разных степенях, можно вынести общее кратное: Например, а^x+y + а^x = а^x * (а^y + 1) Если основания разные, но степень одна, то в некоторых простых частных случаях можно воспользоваться алгебраическими формулами вроде: а^2-b^2= (а-b) * (a+b). Но это очень редкие совпадения, расчитывать на которые не стоит.
Azamatik 5 лет назад Пример: 2^3 х 4^5. Для решения этого уравнения нужно привести их к одинаковому основанию: представить 4 как 2 в квадрате (2^2). Изначально у нас было 4^5 > (2^2)^5. Степени умножаем и получаем 2^10. Теперь можно решить это уравнение; 2^3 х2^10. Складываем степени и получаем 2^13. Подобные уравнения решаются именно так: Если основания одинаковые, то складываем степени. Если же показатели степени одинаковые, то нужно основания перемножить и полученный результат возвести в степень.
Odessitka 8 лет назад Если умножать степени с одинаковым основанием, то показатели степени складываются: Например: 2^2 х 2^4 = 2^6 = 64 Если делить степени с одинаковым основанием, то показатели степени вычитаются: Например: 2^4 / 2^2 = 2^2 = 4. Если же умножать или делить степени с разным основанием, то нужно сначала возвести основание в степень, а потом совершать умножение или деление. В вашем случае 2^3 x 4^5 = 8 х 1024 = 8192.
Лолочка611 8 лет назад При умножении степеней, которые имеют одинаковые основания – числа степеней складываются. При делении степеней, которые имеют одинаковые основания – числа степеней вычитаются. А вот если умножать, либо делить степени, которые имеют разные основания, нужно выполнить следующие действия:
Знаете ответ? |
Напоминаем, что в данном уроке разбираются свойства степеней
с натуральными показателями и нулём.
Степени с рациональными показателями и их свойства будут рассмотрены в уроках
для 8 классов.
Степень с натуральным показателем обладает несколькими важными свойствами, которые позволяют
упрощать вычисления в примерах со степенями.
Свойство № 1
Произведение степеней
Запомните!
![]()
При умножении степеней с одинаковыми основаниями основание остаётся без изменений,
а показатели степеней складываются.
am · an = am + n, где
«a» — любое
число, а «m», «n» — любые натуральные числа.
Данное свойство степеней также действует на произведение трёх и более степеней.
Примеры.
- Упростить выражение.
b · b2 · b3 · b4 · b5 =
b 1 + 2 + 3 + 4 + 5 = b15 - Представить в виде степени.
615 · 36 = 615 · 62 = 615 · 62 =
617 - Представить в виде степени.
(0,8)3 · (0,8)12 = (0,8)3 + 12 = (0,8)15
Важно!

Обратите внимание, что в указанном свойстве речь шла только об умножении
степеней с одинаковыми основаниями. Оно не относится к их сложению.
Нельзя заменять сумму
(33 + 32) на 35. Это понятно, если
посчитать
(33 + 32) = (27 + 9) = 36 , а
35 = 243
Свойство № 2
Частное степеней
Запомните!
![]()
При делении степеней с одинаковыми основаниями основание остаётся без изменений,
а из показателя степени делимого вычитают показатель степени делителя.
=
am − n, где
«a» — любое
число, не равное нулю, а «m», «n» — любые
натуральные числа такие, что «m > n».
Примеры.
- Записать частное в виде степени
(2b)5 : (2b)3 = (2b)5 − 3 = (2b)2 - Вычислить.
=
113 − 2 · 4 2 − 1 = 11 · 4 = 44 - Пример. Решить уравнение. Используем свойство частного степеней.
38 : t = 34t = 38 : 34
t = 38 − 4
t = 34
Ответ: t = 34 = 81
Пользуясь свойствами № 1 и № 2, можно легко упрощать выражения и производить вычисления.
- Пример. Упростить выражение.
45m + 6 · 4m + 2 : 44m + 3 =
45m + 6 + m + 2 : 44m + 3 =
46m + 8 − 4m − 3 = 42m + 5 - Пример. Найти значение выражения, используя свойства степени.
=
==
=
=
211 − 5 = 2 6 = 64
Важно!

Обратите внимание, что в свойстве 2 речь шла только
о делении степеней с одинаковыми основаниями.
Нельзя заменять разность
(43 −42) на 41. Это понятно, если посчитать
(43 −42) = (64 − 16) = 48, а
41 = 4
Будьте внимательны!
Свойство № 3
Возведение степени в степень
Запомните!
![]()
При возведении степени в степень основание степени остаётся без изменения, а показатели степеней
перемножаются.
(an)m = an · m, где
«a» — любое
число, а «m», «n» — любые натуральные числа.
- Пример.
(a4)6 = a4 · 6 = a24 - Пример. Представить 320 в виде степени с основанием
32.По свойству возведения степени в степень известно, что при возведении
в степень показатели перемножаются, значит: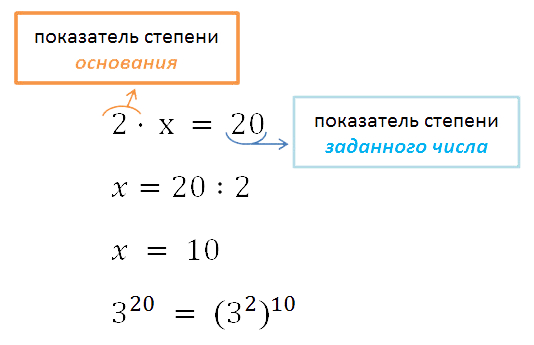
Свойства 4
Степень произведения
Запомните!
![]()
При возведении в степень произведения каждый из множителей
возводится в степень. Затем полученные результаты перемножаются.
(a · b)n = an · bn, где
«a», «b» — любые рациональные
числа; «n» — любое натуральное число.
- Пример 1.
(6 · a2 · b3 · c )2 =
62 · a2 · 2 · b3 · 2
· с 1 · 2 = 36 a4 · b6
· с 2
- Пример 2.
(−x2 · y)6 =( (−1)6 · x2 · 6 · y1 · 6) =
x12 · y6
Важно!

Обратите внимание, что свойство № 4, как и другие свойства степеней,
применяют и в обратном порядке.
(an · bn)=
(a · b) n
То есть, чтобы перемножить степени с одинаковыми
показателями можно перемножить основания, а показатель степени оставить неизменным.
- Пример. Вычислить.
24 · 54 = (2 · 5)4 =
104 = 10 000 - Пример. Вычислить.
0,516 · 216 = (0,5 · 2)16 =
1
В более сложных примерах могут встретиться случаи, когда умножение и деление
надо выполнить над степенями с разными основаниями и разными показателями.
В этом случае советуем поступать следующим образом.
Например,
45 · 32 = 43 ·
42 · 32 = 43 · (4 · 3)2 =
64 · 122 = 64 · 144 = 9216
Пример возведения в степень десятичной дроби.
421 · (−0,25)20 = 4 · 4 20 ·
(−0,25) 20 = 4 · (4 · (−0,25))20 = 4 · (−1)20 =
4 · 1 = 4
Свойства 5
Степень частного (дроби)
Запомните!
![]()
Чтобы возвести в степень частное, можно возвести в эту степень отдельно делимое и делитель,
и первый результат разделить на второй.
(a : b)n = an : bn, где
«a», «b» — любые рациональные
числа, b ≠ 0, n — любое натуральное число.
- Пример. Представить выражение в виде частного степеней.
(5 : 3)12 = 512 : 312
Напоминаем, что частное можно представить в виде дроби. Поэтому
на теме
возведение дроби в степень
мы остановимся более подробно на следующей странице.
Ваши комментарии
Важно!

Чтобы оставить комментарий, вам нужно войти на наш сайт при помощи
«ВКонтакте».

Оставить комментарий:
24 апреля 2023 в 13:57
София Елизарьева

Профиль
Благодарили: 0
Сообщений: 2

София Елизарьева
Профиль
Благодарили: 0
Сообщений: 2
ЛяяялДляля
0
Спасибо
Ответить
24 апреля 2023 в 13:57
София Елизарьева

Профиль
Благодарили: 0
Сообщений: 2

София Елизарьева
Профиль
Благодарили: 0
Сообщений: 2
0
Спасибо
Ответить