Время на прочтение
5 мин
Количество просмотров 2.8K

В данной статье разберемся с выравнием данных, а также решим 17-е задание с сайта pwnable.kr.
Организационная информация
Специально для тех, кто хочет узнавать что-то новое и развиваться в любой из сфер информационной и компьютерной безопасности, я буду писать и рассказывать о следующих категориях:
- PWN;
- криптография (Crypto);
- cетевые технологии (Network);
- реверс (Reverse Engineering);
- стеганография (Stegano);
- поиск и эксплуатация WEB-уязвимостей.
Вдобавок к этому я поделюсь своим опытом в компьютерной криминалистике, анализе малвари и прошивок, атаках на беспроводные сети и локальные вычислительные сети, проведении пентестов и написании эксплоитов.
Чтобы вы могли узнавать о новых статьях, программном обеспечении и другой информации, я создал канал в Telegram и группу для обсуждения любых вопросов в области ИиКБ. Также ваши личные просьбы, вопросы, предложения и рекомендации рассмотрю лично и отвечу всем.
Вся информация представлена исключительно в образовательных целях. Автор этого документа не несёт никакой ответственности за любой ущерб, причиненный кому-либо в результате использования знаний и методов, полученных в результате изучения данного документа.
Выравнивание данных
Выравнивание данных в оперативной памяти компьютера представляет собой особой размещение данных в памяти для ускорения доступа. При работе с памятью процессы в качестве основной единицы используют машинное слово. У различных видов процессоров оно можем быть разного размера: один, два, четыре, восемь и т.д. байтов. При сохранении объектов в памяти может получиться так, что некоторое поле выйдет за пределы этих границ слов. Некоторые процессоры могут работать с невыровненными данными более длительное время, чем с выравненными. А неторые процессоры вообще не могут работать с невыравненными данными.
Для того, чтобы лучше представить себе модель выровненных и невыровненных данных, рассмотрим пример на следующем объекте — структура Data.
struct Data{
int var1;
void* mas[4];
};Так как размер переменной типа int в x32 и x64 процессорах не равно 4 байта, а значение переменной типа void* — 4 и 8 байт соответственно, то в памяти данная структура для процессоров x32 и x64 будет представлена следующим образом.

Процессоры x64 с такой структорой работать не будут, так как данные не выравнены. Для выравнивания данных необходимо добавить в структуру еще одно поле 4 байт.
struct Data{
int var1;
int addition;
void* mas[4];
};Таким образом данные структуры Data для процессоров x64 будут выровнены в памяти.

Решение задания memcpy
Нажимаем на иконку с подписью memcpy, и нам говорят, что нужно подключиться по SSH с паролем guest.
Так же предоставляют исходный код.
// compiled with : gcc -o memcpy memcpy.c -m32 -lm
#include <stdio.h>
#include <string.h>
#include <stdlib.h>
#include <signal.h>
#include <unistd.h>
#include <sys/mman.h>
#include <math.h>
unsigned long long rdtsc(){
asm("rdtsc");
}
char* slow_memcpy(char* dest, const char* src, size_t len){
int i;
for (i=0; i<len; i++) {
dest[i] = src[i];
}
return dest;
}
char* fast_memcpy(char* dest, const char* src, size_t len){
size_t i;
// 64-byte block fast copy
if(len >= 64){
i = len / 64;
len &= (64-1);
while(i-- > 0){
__asm__ __volatile__ (
"movdqa (%0), %%xmm0n"
"movdqa 16(%0), %%xmm1n"
"movdqa 32(%0), %%xmm2n"
"movdqa 48(%0), %%xmm3n"
"movntps %%xmm0, (%1)n"
"movntps %%xmm1, 16(%1)n"
"movntps %%xmm2, 32(%1)n"
"movntps %%xmm3, 48(%1)n"
::"r"(src),"r"(dest):"memory");
dest += 64;
src += 64;
}
}
// byte-to-byte slow copy
if(len) slow_memcpy(dest, src, len);
return dest;
}
int main(void){
setvbuf(stdout, 0, _IONBF, 0);
setvbuf(stdin, 0, _IOLBF, 0);
printf("Hey, I have a boring assignment for CS class.. :(n");
printf("The assignment is simple.n");
printf("-----------------------------------------------------n");
printf("- What is the best implementation of memcpy? -n");
printf("- 1. implement your own slow/fast version of memcpy -n");
printf("- 2. compare them with various size of data -n");
printf("- 3. conclude your experiment and submit report -n");
printf("-----------------------------------------------------n");
printf("This time, just help me out with my experiment and get flagn");
printf("No fancy hacking, I promise :Dn");
unsigned long long t1, t2;
int e;
char* src;
char* dest;
unsigned int low, high;
unsigned int size;
// allocate memory
char* cache1 = mmap(0, 0x4000, 7, MAP_PRIVATE|MAP_ANONYMOUS, -1, 0);
char* cache2 = mmap(0, 0x4000, 7, MAP_PRIVATE|MAP_ANONYMOUS, -1, 0);
src = mmap(0, 0x2000, 7, MAP_PRIVATE|MAP_ANONYMOUS, -1, 0);
size_t sizes[10];
int i=0;
// setup experiment parameters
for(e=4; e<14; e++){ // 2^13 = 8K
low = pow(2,e-1);
high = pow(2,e);
printf("specify the memcpy amount between %d ~ %d : ", low, high);
scanf("%d", &size);
if( size < low || size > high ){
printf("don't mess with the experiment.n");
exit(0);
}
sizes[i++] = size;
}
sleep(1);
printf("ok, lets run the experiment with your configurationn");
sleep(1);
// run experiment
for(i=0; i<10; i++){
size = sizes[i];
printf("experiment %d : memcpy with buffer size %dn", i+1, size);
dest = malloc( size );
memcpy(cache1, cache2, 0x4000); // to eliminate cache effect
t1 = rdtsc();
slow_memcpy(dest, src, size); // byte-to-byte memcpy
t2 = rdtsc();
printf("ellapsed CPU cycles for slow_memcpy : %llun", t2-t1);
memcpy(cache1, cache2, 0x4000); // to eliminate cache effect
t1 = rdtsc();
fast_memcpy(dest, src, size); // block-to-block memcpy
t2 = rdtsc();
printf("ellapsed CPU cycles for fast_memcpy : %llun", t2-t1);
printf("n");
}
printf("thanks for helping my experiment!n");
printf("flag : ----- erased in this source code -----n");
return 0;
}
При подключении мы видим соответствующий баннер.
Давайте узнаем, какие файлы есть на сервере, а также какие мы имеем права.

У нас имеется файл readme. Прочитав его, узнаем, что программа работает на порте 9022.

Подключимся к порту 9022. Нам предлагают эксперимент — сравнить медленную и быструю версию memcpy. Далее программа провесит ввести число в определенном промежутке и выдает отчет о сравнении медленной и быстрой версии функции. Есть одно но: экспериментов 10, а отчетов — 5.
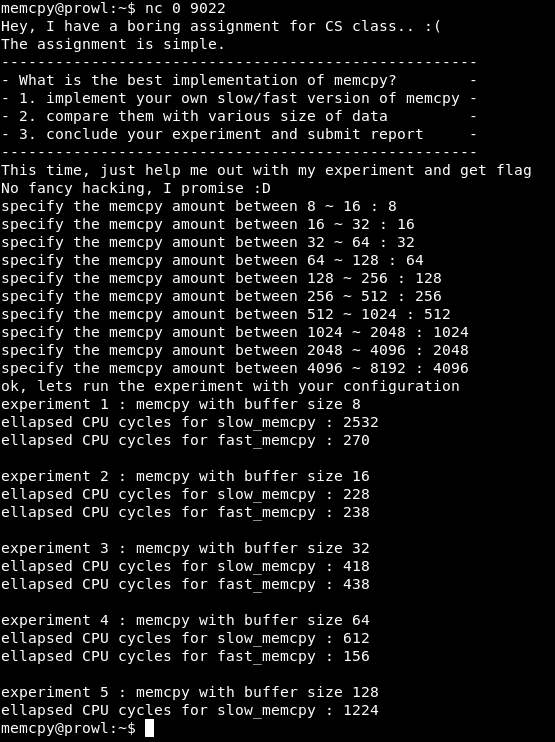
Давайте рабираться почему. Найдем в коде место сравнения результатов.
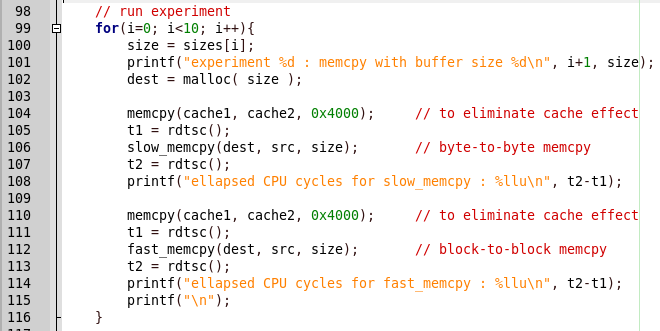
Все просто, сначала вызывается slow_memcpy, потом — fast_memcpy. Но в отчете программы есть вывод о медленной релизации функции, а при вызове быстрой реалиации — программа падает. Посмотрим код быстрой реалиации.
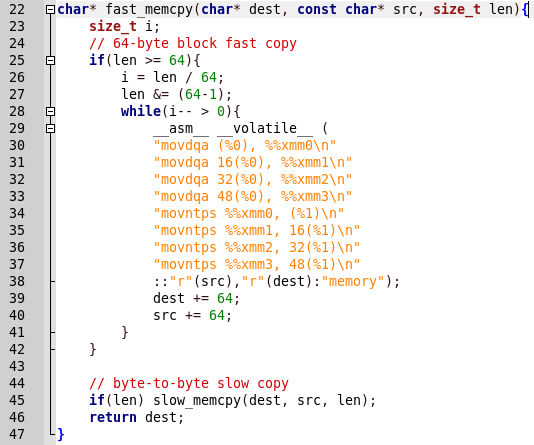
Копирование выполняется с помощью ассемблерных функций. По командам определяем, что это SSE2. Как сказано тут: SSE2 использует восемь 128-битных регистров (xmm0 до xmm7), включённых в архитектуру x86 с вводом расширения SSE, каждый из которых трактуется как 2 последовательных значения с плавающей точкой двойной точности. Тем более, в данном коде ведется работа с выровнеными данными.


Таким образом, работая с невыровненнымми данными, программа может упасть. Выравнивание производится по 128 бит, то есть по 16 байт, значит блоки должны быть равны 16. Нам нужно узнать сколько байт уже есть в первом блоке на куче (пусть X) тогда мы должны каждый передавать программу столько байт (пусть Y), чтобы (X+Y)%16 было равно 0.
Так как все операции занимают блоки кучи, кратные двум, переберем X как 2, 4, 8, т.д. до 16.
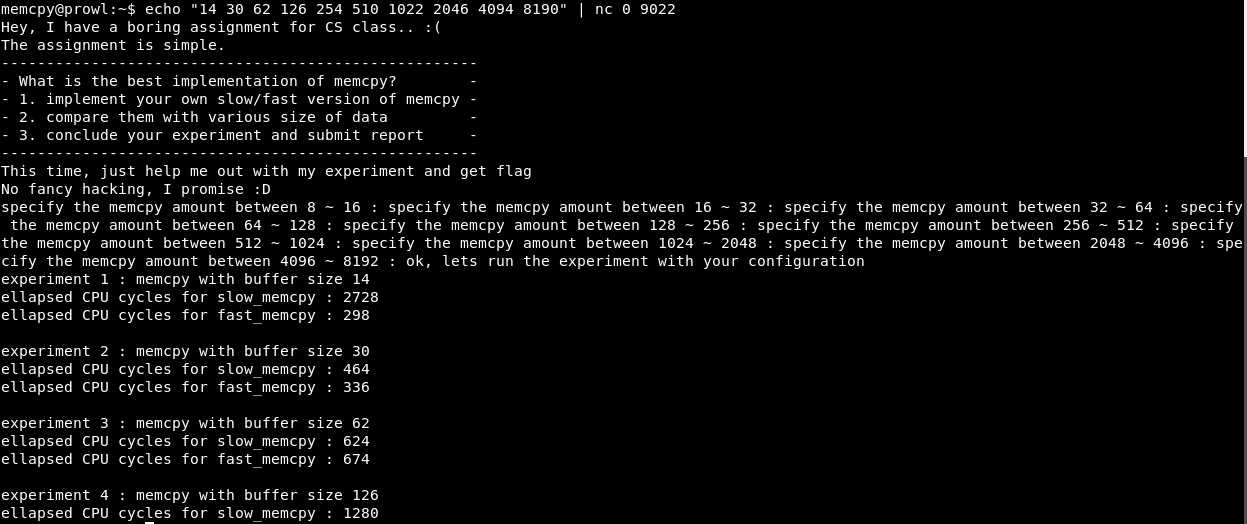
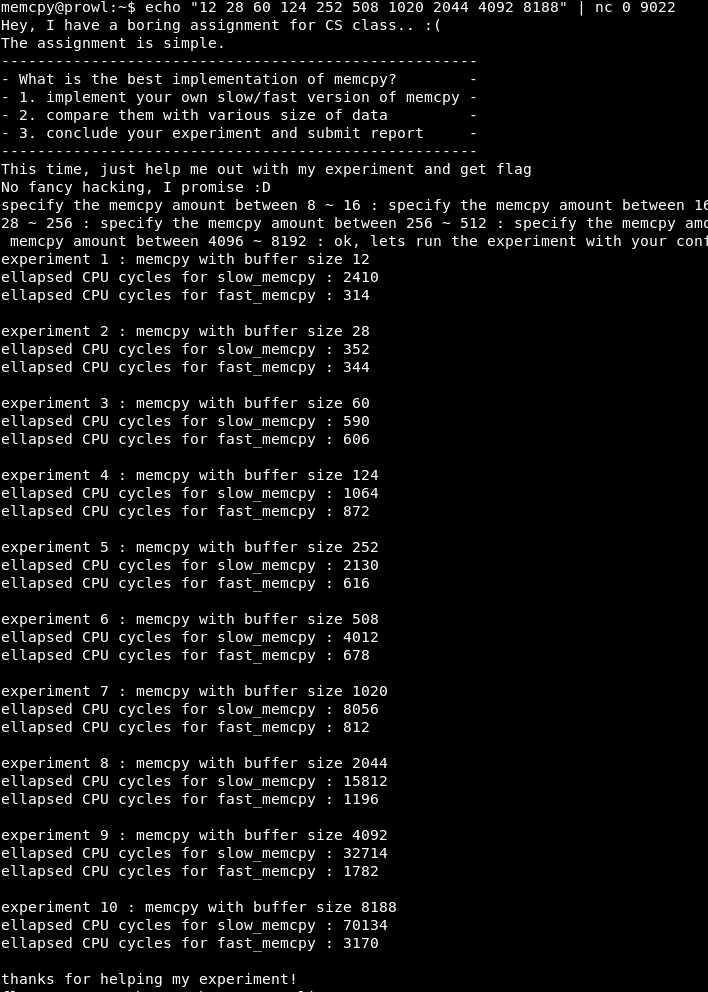
Как видим, при X=4 программа успешно выполняется.

Получаем шелл, читаем флаг, получаем 10 очков.
Вы можете присоединиться к нам в Telegram. В следующий раз разберемся с переполнением кучи.
Выравнивание по уравнению прямой
Уравнение прямой
может быть выражено в виде следующей
формулы:
yt
=ao+a1t,
где yt
– значение выровненного ряда;
ao,
a1 – параметры
прямой линии (которые необходимо
вычислить);
t
– показатель времени.
Задача состоит в
том, чтобы фактические уровни ряда (у)
заменить теоретическими (yt).
Для расчета
параметров прямой линии aoиa1 используем
способ наименьших квадратов, который
дает систему двух уравнений:
 ;
;
где n
– число членов ряда;
у– фактические
уровни ряда;
t
– показатель времени.
Упрощенный расчет
параметров уравнений заключается в
переносе начала координат в середину
ряда динамики (t=0).
В этом случае упрощаются сами нормальные
уравнения, кроме того, уменьшаются
абсолютные значения величин, участвующих
в расчете. Тогда системы нормальных
уравнений для оценивания параметров
прямой (у = a0+a1t)
примут вид:
 .
.
Решая систему
относительно неизвестных параметров,
получим величины параметров соответствующих
полиномов.
Пример 7.7.
Пример. Имеются данные о продажах по
месяцам.
|
Месяц |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
Объем |
18 |
17 |
11 |
16 |
18 |
20 |
27 |
Решение. Составим
рабочую таблицу для расчета параметров
уравнения прямой
|
Месяц |
у |
t |
yt |
t2 |
yt |
|
1 |
18 |
-3 |
-54 |
9 |
14,04 |
|
2 |
17 |
-2 |
-34 |
4 |
15,36 |
|
3 |
11 |
-1 |
-11 |
1 |
16,68 |
|
4 |
16 |
0 |
0 |
0 |
18 |
|
5 |
18 |
1 |
18 |
1 |
19,32 |
|
6 |
20 |
2 |
40 |
4 |
20,64 |
|
7 |
27 |
3 |
78 |
9 |
21,96 |
|
Итого |
126 |
0 |
37 |
28 |
126 |
![]() 126 / 7 = 18,0 a1=
126 / 7 = 18,0 a1=
![]() =37/
=37/
28 = 1,321
Уравнение тренда
yt= 18,0 + 1,321·t
Построим график
фактических уровней и линию, характеризующую
тенденцию динамического ряда.

Методы выявления сезонной компоненты
При рассмотрении
квартальных или месячных данных многих
социально-экономических явлений часто
обнаруживаются определенные, постоянно
повторяющиеся колебания, которые
существенно не изменяются за длительный
период времени. Они являются результатом
влияния природно-климатических условий,
общих экономических факторов, а также
ряда многочисленных разнообразных
факторов, которые частично являются
регулируемыми. В статистике периодические
колебания, которые имеют определенный
и постоянный период, равный годовому
промежутку, носят название «сезонных
колебаний» или «сезонных волн», а
динамический ряд в этом случае называют
тренд-сезонным, или просто сезонным
рядом динамики.
Сезонные колебания
характеризуются специальными показателями
которые называются индексами сезонности
(IS). Совокупность этих
показателей отражает сезонную волну.
Индексами сезонности являются процентные
отношения фактических внутригодовых
уровней к постоянной или переменной
средней.
Для выявления
сезонных колебаний обычно берут данные
за несколько лет, распределенные по
месяцам. Данные за несколько лет (не
менее трех) используются для того, чтобы
выявить устойчивую сезонную волну, на
которой не отражались бы случайные
условия одного года.
Для вычисления
индексов сезонности применяются
различные методы. Если ряд динамики не
содержит явно выраженной тенденциив развитии, то индексы сезонности
вычисляются непосредственно по
эмпирическим данным без их предварительного
выравнивания.
Для каждого месяца
рассчитывается средняя величина уровня,
например, за три года (![]() ),
),
затем из них вычисляется среднемесячный
уровень для всего ряда![]() и в заключение определяется процентное
и в заключение определяется процентное
отношение средних для каждого месяца
к общему среднемесячному уровню ряда,
т. е.
![]() .
.
Если же ряд динамики
содержит определенную тенденцию в
развитии, то прежде чем вычислить
сезонную волну, фактические данные
должны быть обработаны так, чтобы была
выявлена общая тенденция. Обычно для
этого прибегают к аналитическому
выравниванию ряда динамики. По уравнению
вычисляются для каждого месяца (квартала)
выравненные уровни на момент времени
t (![]() ).
).
Затем определяются отношения фактических
данных за месяц (квартал) к соответствующим
выравненным данным:
![]()
И находят средние
арифметические из процентных соотношений,
рассчитанных по одноименным периодам
в процентах:
IS=(I1+I2+…+In):n,
где n
— число одноименных периодов (месяцев,
кварталов).
В общем виде формулу
расчета индекса сезонности данным
способом можно записать так:
![]()
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Одной из задач, возникающих при анализе рядов
динамики, является установление закономерности изменения уровней изучаемого
показателя во времени. В некоторых случаях эта закономерность, общая тенденция
развития объекта вполне ясно отображается уровнями динамического ряда. Но часто
приходится встречаться с такими рядами динамики, когда уровни ряда претерпевают
самые различные изменения (то возрастают, то убывают) и можно говорить лишь об
общей тенденции развития явления, либо о тенденции к росту, либо к снижению. В
этих случаях для определения основной тенденции развития явления, достаточно
устойчивой на протяжении данного периода, используют особые приемы обработки
рядов динамики.
Уровни ряда динамики формируются под совокупным
влиянием множества длительно и кратковременно действующих факторов и в том
числе различного рода случайных обстоятельств.
Выявление основной закономерности изменения уровней
ряда предполагает ее количественное выражение, в некоторой мере свободное от случайных
воздействий. Выявление основной тенденции развития (тренда) называется в
статистике также выравниванием временного ряда, а методы выявления основной
тенденции – методами выравнивания. Выравнивание позволяет характеризовать
особенность изменения во времени данного динамического ряда в наиболее общем
виде как функцию времени, предполагая, что через время можно выразить влияние
всех основных факторов.
Приемы сглаживания динамических рядов (укрупнение
интервала и метод скользящей средней) могут рассматриваться как важное
вспомогательное средство, облегчающее применение других методов и, в частности,
более строгих методов выявления тенденции. Для того чтобы представить
количественную модель, выражающую общую тенденцию изменений уровней
динамического ряда во времени, используется аналитическое выравнивание ряда
динамики.
В этом случае фактические уровни заменяются
уровнями, вычисленными на основе определенной кривой.
Предполагается, что она отражает общую тенденцию изменения во времени
изучаемого показателя.
При аналитическом выравнивании ряда динамики
закономерно изменяющийся уровень изучаемого показателя оценивается как функция
времени
,
Где
–
уровни динамического ряда, вычисленные по соответствующему аналитическому
уравнению на момент времени t.
При выборе формы уравнения следует исходить и из
объема имеющейся информации. Чем больше параметров содержит уравнение тренда,
тем больше должно быть наблюдений при одной и той же степени надежности
оценивания. Выбор формы кривой может осуществляться: и на основе принятого
критерия, в качестве которого может служить сумма квадратов отклонений
фактических значений от значений, рассчитанных по уравнению тренда. Из
совокупности кривых выбирается та, которой соответствует минимальное значение
критерия. Рассмотрим аналитическое выравнивание ряда динамики
по прямой, т.е. аналитическое уравнение вида:
где
-порядковый номер
периодов или моментов времени.
Параметры
и
прямой рассчитываются
по методу наименьших квадратов (МНК).
Система нормальных уравнений в данном
случае имеет вид:
Поиск параметров уравнения можно упростить, если
отсчет времени производить так, чтобы сумма показателей времени изучаемого ряда
динамики была равна нулю
.
При нечетном числе уровней ряда динамики уровень, находящийся в середине ряда, принимается за условное начало отчета времени
(этому периоду или моменту времени придается нулевое значение). Даты времени,
стоящие выше этого уровня, обозначаются натуральными числами со знаками минус,
а ниже -натуральными числами со знаками плюс.
При условии
получим:
Правильность расчета уровней выравниваемого ряда
динамики может быть проверена следующим образом: сумма значений эмпирического
ряда должна совпадать с суммой вычисленных уровней выровненного ряда, т.е.
Аналитическое уравнение представляет собой математическую
модель развития явления и дает выражение статистической закономерности,
проявляющейся в рядах динамики. Следует помнить, что прием аналитического
выравнивания содержит в себе ряд условностей, связанных
прежде всего с тем, что уровни, характеризующие тот или иной динамический ряд,
рассматриваются как функция времени. В действительности же развитие явлений
обусловлено не тем, сколько времени прошло с отправного момента, а тем, какие
факторы влияли на развитие, в каком направлении и с какой интенсивностью. Развитие явлений во времени выступает
как внешнее выражение этих факторов, как их суммарное действие; оказывающее
влияние на изменение уровня в отдельно взятые промежутки или моменты времени.
Выявить основную тенденцию развития явления методом наименьших квадратов можно
лишь тогда, когда выяснено, что изменяющиеся во времени процессы протекают на
всем рассматриваемом промежутке времени одинаково, что их количественное и
качественное изменение происходит под действием одного и того же комплекса основных
факторов, определяющих движение данного ряда динамики.
Модели, учитывающие общие закономерности изменения
экономического явления в изучаемый интервал времени и изменения во времени
влияния комплекса факторов, называют многофакторными динамическими моделями.
Выделим особенности моделей аналитического
выравнивания уровней динамического ряда, накладывающие ограничения на их
использование. Во-первых, динамические ряды, к которым применяется
аппроксимация, должны быть достаточно длинными. Во-вторых, применение
аппроксимации наиболее целесообразно в случае медленно и плавно меняющегося
уровня. В-третьих, аппроксимация как метод моделирования практически не
адаптируется к изменяющимся условиям формирования уровней ряда; при появлении
новых данных построение модели должно быть проведено заново. В-четвертых, при
использовании для расчета параметров уравнения метода наименьших квадратов
(МНК) считается, что значимость информации в пределах отрезка аппроксимации
одинакова независимо от давности полученных данных, в то время как более
поздние данные имеют большую ценность.
Помимо этого, динамические ряды экономических
показателей часто имеют небольшую длину и подвержены значительным колебаниям,
которые аппроксимация предвидеть не может.
Задача
В таблице приведены готовые данные о
трудоемкости производства:
| Год | 2009 | 2010 | 2011 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 |
|
Трудоемкость производства, человек-часов |
8 | 8.4 | 7.6 | 7 | 7.3 | 6.6 | 5.9 | 5 | 5.2 |
-
Провести аналитическое выравнивание ряда динамики по прямой.
Построить точечный и интервальный
прогноз на 2018 год.
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Решение
1) Произведем аналитическое выравнивание ряда по прямой.
Составим расчетную таблицу:
Расчетная вспомогательная таблица 1
| Годы |
|
|
|
|
| 2009 | -4 | 8 | 16 | -32 |
| 2010 | -3 | 8,4 | 9 | -25,2 |
| 2011 | -2 | 7,6 | 4 | -15,2 |
| 2012 | -1 | 7 | 1 | -7 |
| 2013 | 0 | 7,3 | 0 | 0,0 |
| 2014 | 1 | 6,6 | 1 | 6,6 |
| 2015 | 2 | 5,9 | 4 | 11,8 |
| 2016 | 3 | 5 | 9 | 15 |
| 2017 | 4 | 5,2 | 16 | 20,8 |
| Итого | 0 | 61,0 | 60 | -25,2 |
Коэффициенты уравнения линейного тренда найдем по формулам:
Уравнение линейного тренда имеет вид:
2) Составим расчетную таблицу:
Расчетная вспомогательная таблица 2
| Годы |
|
|
Теоретические значения |
|
| 2009 | -4 | 8 | 8,48 | 0,2304 |
| 2010 | -3 | 8,4 | 8,06 | 0,1156 |
| 2011 | -2 | 7,6 | 7,64 | 0,0016 |
| 2012 | -1 | 7 | 7,22 | 0,0484 |
| 2013 | 0 | 7,3 | 6,8 | 0,25 |
| 2014 | 1 | 6,6 | 6,38 | 0,0484 |
| 2015 | 2 | 5,9 | 5,96 | 0,0036 |
| 2016 | 3 | 5 | 5,54 | 0,2916 |
| 2017 | 4 | 5,2 | 5,12 | 0,0064 |
| Итого | — | — | — | 0,996 |
Среднеквадратическая ошибка:
Точечный прогноз на 2018 год (t=5):
Ошибка
прогноза составит:
По таблице критерия Стьюдента,
для доверительной вероятности
(уровня значимости
) находим:
Вывод к задаче
Таким образом
тренд для трудоемкости производства выражается линейным уравнением
.
Согласно прогнозу, в 2018 году трудоемкость производства с вероятностью 0,95
будет лежать в пределах от 3,6 до 5,8 человеко-часов.
Аналитическое выравнивание ряда по прямой
Решение находим с помощью калькулятора.
Линейное уравнение тренда имеет вид y = at + b
1. Находим параметры уравнения методом наименьших квадратов.
Система уравнений
Для наших данных система уравнений имеет вид
Из первого уравнения выражаем а 0 и подставим во второе уравнение
Получаем a0 = -2.89, a1 = 63.27
Уравнение тренда
y = -2.89 t + 63.27
Оценим качество уравнения тренда с помощью ошибки абсолютной аппроксимации.
Поскольку ошибка больше 15%, то данное уравнение не желательно использовать в качестве тренда
Средние значения
т.е. в 39.75 % случаев влияет на изменение данных. Другими словами – точность подбора уравнения тренда – средняя
| t | y | t 2 | y 2 | x ∙ y | y(t) | (y-y cp ) 2 | (y-y(t)) 2 | (t-t p ) 2 | (y-y(t)) : y |
| 1 | 80 | 1 | 6400 | 80 | 60.38 | 1826.44 | 384.99 | 64 | 1569.68 |
| 2 | 79 | 4 | 6241 | 158 | 57.49 | 1741.96 | 462.7 | 49 | 1699.33 |
| 3 | 75 | 9 | 5625 | 225 | 54.6 | 1424.07 | 416.16 | 36 | 1530 |
| 4 | 70 | 16 | 4900 | 280 | 51.71 | 1071.7 | 334.5 | 25 | 1280.26 |
| 5 | 65 | 25 | 4225 | 325 | 48.82 | 769.33 | 261.76 | 16 | 1051.63 |
| 6 | 60 | 36 | 3600 | 360 | 45.93 | 516.96 | 197.92 | 9 | 844.11 |
| 7 | 39 | 49 | 1521 | 273 | 43.04 | 3.02 | 16.34 | 4 | 157.64 |
| 8 | 35 | 64 | 1225 | 280 | 40.15 | 5.12 | 26.55 | 1 | 180.34 |
| 9 | 30 | 81 | 900 | 270 | 37.26 | 52.75 | 52.75 | 0 | 217.89 |
| 10 | 25 | 100 | 625 | 250 | 34.37 | 150.39 | 87.87 | 1 | 234.34 |
| 11 | 20 | 121 | 400 | 220 | 31.48 | 298.02 | 131.89 | 4 | 229.68 |
| 12 | 10 | 144 | 100 | 120 | 28.59 | 743.28 | 345.76 | 9 | 185.95 |
| 13 | 13 | 169 | 169 | 169 | 25.71 | 588.7 | 161.42 | 16 | 165.17 |
| 14 | 19 | 196 | 361 | 266 | 22.82 | 333.54 | 14.56 | 25 | 72.5 |
| 15 | 29 | 225 | 841 | 435 | 19.93 | 68.28 | 82.33 | 36 | 263.14 |
| 16 | 14 | 256 | 196 | 224 | 17.04 | 541.17 | 9.22 | 49 | 42.52 |
| 17 | 20 | 289 | 400 | 340 | 14.15 | 298.02 | 34.25 | 64 | 117.05 |
| 18 | 25 | 324 | 625 | 450 | 11.26 | 150.39 | 188.85 | 81 | 343.55 |
| 171 | 708 | 2109 | 38354 | 4725 | 708 | 11971.68 | 7212.72 | 570 | 10184.79 |
2. Анализ точности определения оценок параметров уравнения тренда.
Анализ точности определения оценок параметров уравнения тренда
По таблице Стьюдента находим Tтабл
Tтабл (n-m-1;a) = (17;0.05) = 1.74
Рассчитаем границы интервала, в котором будет сосредоточено 95% возможных значений Y при неограниченно большом числе наблюдений и t = 10
63.27 + -2.89*10 – 1.74*20.55 ; 63.27 + -2.89*10 – 1.74*20.55
(-1.39;70.14)
Интервальный прогноз.
Определим среднеквадратическую ошибку прогнозируемого показателя.
где L – период упреждения; уn+L – точечный прогноз по модели на (n + L)-й момент времени; n – количество наблюдений во временном ряду; Sy – стандартная ошибка прогнозируемого показателя; Tтабл – табличное значение критерия Стьюдента для уровня значимости а и для числа степеней свободы, равного n — 2.
Точечный прогноз, t = 20: y(20) = -2.89*20 + 63.27 = 5.48
K1 = 49.73
5.48 – 49.73 = -44.25 ; 5.48 + 49.73 = 55.21
t = 20: (-44.25;55.21)
3. Проверка гипотез относительно коэффициентов линейного уравнения тренда.
1) t-статистика. Критерий Стьюдента.
Статистическая значимость коэффициента уравнения подтверждается.
Статистическая значимость коэффициента тренда подтверждается.
Доверительный интервал для коэффициентов уравнения тренда
Определим доверительные интервалы коэффициентов тренда, которые с надежность 95% будут следующими (tтабл=1.74):
(a – tтабл·Sa; a + tтабл·S a)
(-4.3484;-1.4306)
(b – tтабл·S b ; b + tтабл·S b)
(47.898;78.6389)
2) F-статистика. Критерий Фишера.
Fkp = 4.41
Поскольку F > Fkp, то коэффициент детерминации статистически значим
4. Тест Дарбина-Уотсона на наличие автокорреляции остатков для временного ряда.
| y | y(x) | e i = y-y(x) | e 2 | (e i – e i-1 ) 2 |
| 80 | 60.38 | 19.62 | 384.99 | 0 |
| 79 | 57.49 | 21.51 | 462.7 | 3.57 |
| 75 | 54.6 | 20.4 | 416.16 | 1.23 |
| 70 | 51.71 | 18.29 | 334.5 | 4.45 |
| 65 | 48.82 | 16.18 | 261.76 | 4.45 |
| 60 | 45.93 | 14.07 | 197.92 | 4.45 |
| 39 | 43.04 | -4.04 | 16.34 | 327.99 |
| 35 | 40.15 | -5.15 | 26.55 | 1.23 |
| 30 | 37.26 | -7.26 | 52.75 | 4.45 |
| 25 | 34.37 | -9.37 | 87.87 | 4.45 |
| 20 | 31.48 | -11.48 | 131.89 | 4.45 |
| 10 | 28.59 | -18.59 | 345.76 | 50.56 |
| 13 | 25.71 | -12.71 | 161.42 | 34.69 |
| 19 | 22.82 | -3.82 | 14.56 | 79.02 |
| 29 | 19.93 | 9.07 | 82.33 | 166.14 |
| 14 | 17.04 | -3.04 | 9.22 | 146.66 |
| 20 | 14.15 | 5.85 | 34.25 | 79.02 |
| 25 | 11.26 | 13.74 | 188.85 | 62.24 |
| 0 | 0 | 0 | 7212.72 | 6909.71 |
Критические значения d1 и d2 определяются на основе специальных таблиц для требуемого уровня значимости a, числа наблюдений n и количества объясняющих переменных m.
Не обращаясь к таблицам, можно пользоваться приблизительным правилом и считать, что автокорреляция остатков отсутствует, если 1.5
Выравнивание по уравнению прямой линии
Аналитическое выравнивание имеет своей конечной целью получение конкретного уравнения связи между двумя сопряженными признаками. В первую очередь исходные данные наносят на систему координат и по характеру расположения точек определяют функцию для выравнивания. Её график должен проходить максимально близко по отношению ко всем исходным точкам. В данном примере характер расположения точек линейный следовательно выравнивание осуществляем по уравнению прямой.
Как известно, уравнение линейной зависимости общего вида будет иметь вид: y = а x+b.
Вычисление конкретного уравнения сводится к определению числовых значений коэффициентов а, b, для получения которых существует несколько способов. Рассмотрим два, наиболее широко применяемых способа, характеризующихся различной точностью и трудоемкостью:
а) способ координат двух избранных точек, обеспечивающий получение менее точных результатов, но гораздо более простым путем;
б) способ наименьших квадратов, позволяющий получить достаточно точные результаты путем использования координат всех выравниваемых точек (наблюдений).
Остановимся на технике работ при вычислении конкретного уравнения методом координат избранных точек. В этом случае исходные данные изображаются на графике, и производится предварительное выравнивание. Результирующая линия проводится между точками с таким расчетом, чтобы разделить их общее количество на две приблизительно равные части. При этом необходимо стремиться к такому положению, чтобы расстояние между линией и исходными точками было кратчайшим. Для облегчения техники выравнивания и увеличения его точности можно рекомендовать следующий прием. Соединить все выравниваемые точки и постараться провести плановую выравнивающую линию по возможности ближе к этим серединам. При этом желательно провести прямую таким образом, чтобы хотя бы две исходные точки попали на неё. С полученной прямой линии снимаем координаты двух любых точек исходных данных (лежащих на проведенной прямой). Если число наблюдений в классах известно, то следует отдать предпочтение точкам, обеспеченным наибольшим числом наблюдений. В нашем примере в качестве избранных использованы координаты точек классов № 2 и № 6.
Система двух конкретных уравнений приобретет вид

После подстановки координат избранных точек:

После решения системы относительно а и b, получим
Следовательно, полученное конкретное уравнение связи Y/Х (Д/Н) будет иметь вид
Для краткости изложения в последующем тексте полученным уравнениям присвоены определенные номера: уравнение, вычисленное методом координат точек, получает номер I, а уравнение, полученное методом наименьших квадратов – номер II.
Пределы «работы» полученного уравнения по диаметру от 10 см до 46 см.
Рассмотрим технику вычислений при использовании способа наименьших квадратов. Для получения конкретного уравнения в этом случае используются координаты всех точек. Это учитывается при выведении системы уравнений для этого метода. Так, если записать уравнения прямой для каждой точки, а потом просуммировать левые и правые части всех уравнений, то получим следующее:
Так как нам необходимо найти два неизвестных значения (a и b), то в системе должно быть два уравнения. Для получения второго уравнения системы умножим обе части каждого уравнения на соответствующий «х» и просуммируем левые и правые части уравнений. Получим:
Таким образом, мы вывели оба уравнения системы:

Для удобства вычислений числовых значений указанной системы составляется вспомогательная таблица (табл.4.2).
Таблица 4.2
Вспомогательные расчеты для вычисления конкретного уравнения
| Исходные данные | ХY | Х 2 | |
| Х | Y | ||
| 16,00 | 192,00 | ||
| 18,00 | 288,00 | ||
| 20,15 | 403,00 | ||
| 22,14 | 531,36 | ||
| 23,48 | 657,64 | ||
| 23,65 | 756,80 | ||
| 24,62 | 886,32 | ||
| 26,00 | 1040,00 | ||
| 27,00 | 1188,00 | ||
 252 252 |
 201,04 201,04 |
 5943,12 5943,12 |
 8016 8016 |
Подставим итоговые данные в систему уравнений и вычислим коэффициенты а, b, имея в виду, что значение «n» соответствует числу классов по X:

Следовательно, конкретное уравнение будет иметь вид
С целью последующего анализа результатов применения полученных уравнений вычисляются вероятные (теоретические) значения зависимого признака по первому уравнению (yв1) и второму уравнению (yв2). Последние (yв2) сравниваются с исходными (опытными) данными (у). Указанные сравнения (a = y–yв2) производятся по всем классам X, а их результат для прямой линии показан в табл. 4.3.
Таблица 4.3
Сравнение исходных и вероятных высот деревьев, полученных по уравнению прямой линии
| Исходные данные | Вероятные высоты | Отклонения, м | ||
| диаметр, см | высота, м | Ув1 | Ув2 | a = y–yв2 |
| X | Y | |||
| 16,00 | 16,60 | 17,06 | -1,06 | |
| 18,00 | 18,00 | 18,38 | -0,38 | |
| 20,15 | 19,40 | 19,70 | +0,45 | |
| 22,14 | 20,80 | 21,02 | +1,12 | |
| 23,48 | 22,20 | 22,34 | +1,14 | |
| 23,65 | 23,60 | 23,66 | -0,01 | |
| 24,62 | 25,00 | 24,98 | -0,36 | |
| 26,00 | 26,40 | 26,40 | -0,40 | |
| 27,00 | 27,80 | 27,62 | -0,62 | |
| ∑-0,12 |
Приведенные данные позволяют, прежде всего, проверить правильность вычислений, выполненных при получении конкретных уравнений, на предмет обнаружения грубых арифметических ошибок.
Правильность вычисления уравнений связи проверяется путем сравнения исходных значений Y с вероятными (ув), полученными по уравнению I (ув1) и уравнению II (ув2) Критерием правильности вычислений уравнения I будет совпадение вероятных значений ув1 с исходными значениями Y для тех классов, в которых использованы координаты точек в качестве исходных для получения конкретного уравнения I. В нашем примере для уравнения прямой линии значение ув1 равно 18,0, соответствует исходным данным Y во втором классе, то есть также 18,0. Аналогичное положение и в следующем, шестом классе: ув1 =23,6 практически не отличается от Y =23,65. Совпадение Y и 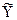 в остальных классах не обязательно и может наступить только случайно.
в остальных классах не обязательно и может наступить только случайно.
Некоторый контроль правильности уравнения II можно получить путем сопоставления Y и ув2 – во всех классах. В этом случае должно наблюдаться такое сочетание знаков (плюс и минус), которое отражает «срединное» положение выравнивающей прямой между выравниваемыми исходными значениями Y.
О явной неправильности полученного уравнения будет свидетельствовать наличие во всех классах только +, равно как и знаков -, а также, если в нескольких начальных классах будут наблюдаться отклонения с одним и тем же знаком ( + или -), а во всех последующих классах с противоположным, а именно:
Заметим, что описанные критерии правильности и вычислений I и II уравнений распространяются и на выравнивание по всем другим линиям связи.
Аналитическое выравнивания ряда динамики по прямой
2. Аналитическое выравнивания ряда динамики по прямой.
Рассмотрим применение метода на следующих данных о производстве продукции предприятием ОАО «Технополис»:
| Год | 1991 | 1992 | 1993 | 1994 | 1995 | 1996 | 1997 | 1998 | 1999 |
| Объем продукции, тыс. ед. | 10,0 | 10,7 | 12,0 | 10,3 | 12,9 | 16,3 | 15,6 | 17,8 | 18,0 |
Примем за точку отсчета 1995г. Тогда условные годы:
| Год | 1991 | 1992 | 1993 | 1994 | 1995 | 1996 | 1997 | 1998 | 1999 |
| t. | -4 | -3 | -2 | -1 | 0 | 1 | 2 | 3 | 4 |
Определим параметры уравнения прямой с использованием программы Excel:
| Годы | Объем продукции, тыс. ед. | Условные годы | yt | y1 | |
| 1 | 2 | 3 | 4 | 5 | 6 |
| 1991 | 10 | -4 | 16 | -40 | 9,3 |
| 1992 | 10,7 | -3 | 9 | -32,1 | 10,41 |
| 1993 | 12 | -2 | 4 | -24 | 11,52 |
| 1994 | -10,3 | -1 | 1 | 10,3 | 12,63 |
| 1995 | 12,9 | 0 | 0 | 0 | 13,74 |
| 1996 | 16,3 | 1 | 1 | 16,3 | 14,85 |
| 1997 | 15,6 | 2 | 4 | 31,2 | 15,96 |
| 1998 | 17,8 | 3 | 9 | 53,4 | 17,07 |
| 1999 | 18 | 4 | 16 | 72 | 18,18 |
| Итого: | 123,6 | 0 | 60 | 66,5 | 123,66 |
Т.к. прямая имеет вид y1 = a0 + а1t , то
а0 = 123,6/9 = 13,74 тыс. ед.;
а1 = 66,5/ 60 = 1,11 тыс. ед;
уравнение прямой имеет вид:
Подставив в это уравнение значение t, получим выровненные теоретические значения.
На рис. представлены графики фактических и теоретических уровней ряда.
Штриховая линия, построенная по значениям y1, показывает тенденцию роста объема производства на данном предприятии.
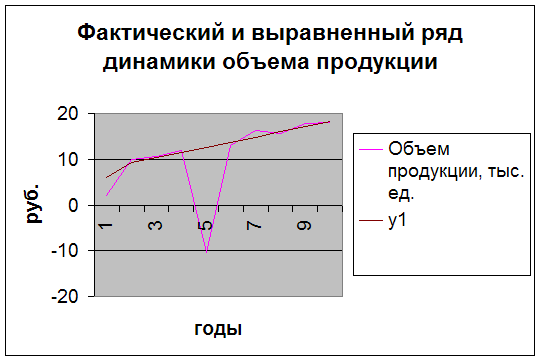
рис. Графики рядов динамики: 1 – фактического, 2 – выровненного.
[spoiler title=”источники:”]
http://lektsii.org/7-19077.html
http://kazedu.com/referat/50642/3
[/spoiler]
Если честно, то просто не обращайте на это внимания. Такая нанооптимизация не понадобится большую часть вашей жизни. Большая часть проблем решается не перестановкой полей структуры, а вдумчивым переписыванием алгоритмов и выбором подходящих структур данных. Хотя конечно знать про это надо.
Итак, смотрите, в чём дело.
Память компьютера работает следующим образом. Память программы можно представить себе как большой массив байт, а адрес — индекс в этом массиве.
[байт 0] [байт 1] [байт 2] [байт 3] [байт 4] [байт 5] [байт 6] [байт 7]...
(Ну или иногда легче представлять так:
... [байт 7] [байт 6] [байт 5] [байт 4] [байт 3] [байт 2] [байт 1] [байт 0]
— вам ещё предстоит узнать про разницу между Big Endian и Little Endian.)
Байт, как минимально адресуемую единицу памяти, можно адресовать как угодно. Но обычно вы работаете с более крупными единицами. Например, это машинное слово: размер регистра процессора. Для 32-битной архитектуры это четырёхбайтовая структура.
Теперь, байты прекрасно организовываются в четвёрки:
[байт 0] [байт 1] [байт 2] [байт 3] [байт 4] [байт 5] [байт 6] [байт 7]...
[ машинное слово 0 ] [ машинное слово 1 ]...
Но заметьте, что в принципе байты можно бы комбинировать в машинные слова и по-другому:
[байт 0] [байт 1] [байт 2] [байт 3] [байт 4] [байт 5] [байт 6] [байт 7] [байт 8]...
[ машинное слово ] [ ещё одно машинное слово ]...
— машинное слово может начинаться по любому адресу!
Так вот, большинство компьютеров устроено так, что машинные слова, скомбинированные в четвёрки верхним образом читаются быстро, а вот машинные слова второго типа (то есть, те, которые не получаются шагами по 4 от нуля) — медленно. (Хотя требования по выравниванию могут быть и сложнее, и не совпадать с кратностью машинного слова.) Хуже того, очень многие архитектуры вовсе не позволяют читать такие слова, и для того, чтобы прочитать вот такое слово:
[байт 0] [байт 1] [байт 2] [байт 3] [байт 4] [байт 5] [байт 6] [байт 7]...
[ машинное слово ]
приходится читать машинные слова по адресу 0 и 4
[байт 0] [байт 1] [байт 2] [байт 3] [байт 4] [байт 5] [байт 6] [байт 7]...
[ нужно это машинное слово ]
[ но приходится читать это ] [ и это ]
выбирать из них нужные байты, перетасовывать и собирать «вручную» в нужное машинное слово! Понятно, что это сложная и сравнительно дорогостоящая операция.
Поэтому компиляторы языка программирования C (да и большинства других тоже) проводят такую оптимизацию: между полями структуры вставляются незначащие байты для того, чтобы у всех полей было хорошее выравнивание.
Пример: для такой структуры:
struct
{
char x; // 1 байт
int y; // 4 байта
char z; // 1 байт
};
память выделяется так:
[ ] [ ] [ ] [ ] [ ] [ ] [ ] [ ] [ ] [ ] [ ] [ ]
[ x ] { потерянные байты } [ y ] [ z ] { потерянные байты }
Если сама структура будет выровнена в памяти (об этом компилятор тоже заботится), то y будет выровнено, и доступ к нему будет быстрым (а на некоторых платформах, напомню, вообще только в этом случае возможен).
Но в этом случае наша структура занимает больше памяти, чем если бы порядок переменных был таким:
[ ] [ ] [ ] [ ] [ ] [ ] [ ] [ ]
[ x ] [ z ] { потеряно } [ y ]
Бóльшая структура означает бóльший расход памяти и бóльшие затраты на копирование, чтение этой структуры и тому подобное. Таким образом, переставив поля структуры, мы можем сэкономить.
Обратите внимание, что на самом деле универсальной оптимизации не существует. Например, для разных архитектур компьютера размер машинного слова будет отличаться. Кроме того, и размеры сколько-нибудь сложных данных могут отличаться тоже, а значит вычисленный оптимальный порядок на одной системе может оказаться очень неоптимальным на другой системе.
Дополнительное чтение по теме (на английском): http://www.catb.org/esr/structure-packing/
