Одной из задач, возникающих при анализе рядов
динамики, является установление закономерности изменения уровней изучаемого
показателя во времени. В некоторых случаях эта закономерность, общая тенденция
развития объекта вполне ясно отображается уровнями динамического ряда. Но часто
приходится встречаться с такими рядами динамики, когда уровни ряда претерпевают
самые различные изменения (то возрастают, то убывают) и можно говорить лишь об
общей тенденции развития явления, либо о тенденции к росту, либо к снижению. В
этих случаях для определения основной тенденции развития явления, достаточно
устойчивой на протяжении данного периода, используют особые приемы обработки
рядов динамики.
Уровни ряда динамики формируются под совокупным
влиянием множества длительно и кратковременно действующих факторов и в том
числе различного рода случайных обстоятельств.
Выявление основной закономерности изменения уровней
ряда предполагает ее количественное выражение, в некоторой мере свободное от случайных
воздействий. Выявление основной тенденции развития (тренда) называется в
статистике также выравниванием временного ряда, а методы выявления основной
тенденции – методами выравнивания. Выравнивание позволяет характеризовать
особенность изменения во времени данного динамического ряда в наиболее общем
виде как функцию времени, предполагая, что через время можно выразить влияние
всех основных факторов.
Приемы сглаживания динамических рядов (укрупнение
интервала и метод скользящей средней) могут рассматриваться как важное
вспомогательное средство, облегчающее применение других методов и, в частности,
более строгих методов выявления тенденции. Для того чтобы представить
количественную модель, выражающую общую тенденцию изменений уровней
динамического ряда во времени, используется аналитическое выравнивание ряда
динамики.
В этом случае фактические уровни заменяются
уровнями, вычисленными на основе определенной кривой.
Предполагается, что она отражает общую тенденцию изменения во времени
изучаемого показателя.
При аналитическом выравнивании ряда динамики
закономерно изменяющийся уровень изучаемого показателя оценивается как функция
времени
,
Где
–
уровни динамического ряда, вычисленные по соответствующему аналитическому
уравнению на момент времени t.
При выборе формы уравнения следует исходить и из
объема имеющейся информации. Чем больше параметров содержит уравнение тренда,
тем больше должно быть наблюдений при одной и той же степени надежности
оценивания. Выбор формы кривой может осуществляться: и на основе принятого
критерия, в качестве которого может служить сумма квадратов отклонений
фактических значений от значений, рассчитанных по уравнению тренда. Из
совокупности кривых выбирается та, которой соответствует минимальное значение
критерия. Рассмотрим аналитическое выравнивание ряда динамики
по прямой, т.е. аналитическое уравнение вида:
где
-порядковый номер
периодов или моментов времени.
Параметры
и
прямой рассчитываются
по методу наименьших квадратов (МНК).
Система нормальных уравнений в данном
случае имеет вид:
Поиск параметров уравнения можно упростить, если
отсчет времени производить так, чтобы сумма показателей времени изучаемого ряда
динамики была равна нулю
.
При нечетном числе уровней ряда динамики уровень, находящийся в середине ряда, принимается за условное начало отчета времени
(этому периоду или моменту времени придается нулевое значение). Даты времени,
стоящие выше этого уровня, обозначаются натуральными числами со знаками минус,
а ниже -натуральными числами со знаками плюс.
При условии
получим:
Правильность расчета уровней выравниваемого ряда
динамики может быть проверена следующим образом: сумма значений эмпирического
ряда должна совпадать с суммой вычисленных уровней выровненного ряда, т.е.
Аналитическое уравнение представляет собой математическую
модель развития явления и дает выражение статистической закономерности,
проявляющейся в рядах динамики. Следует помнить, что прием аналитического
выравнивания содержит в себе ряд условностей, связанных
прежде всего с тем, что уровни, характеризующие тот или иной динамический ряд,
рассматриваются как функция времени. В действительности же развитие явлений
обусловлено не тем, сколько времени прошло с отправного момента, а тем, какие
факторы влияли на развитие, в каком направлении и с какой интенсивностью. Развитие явлений во времени выступает
как внешнее выражение этих факторов, как их суммарное действие; оказывающее
влияние на изменение уровня в отдельно взятые промежутки или моменты времени.
Выявить основную тенденцию развития явления методом наименьших квадратов можно
лишь тогда, когда выяснено, что изменяющиеся во времени процессы протекают на
всем рассматриваемом промежутке времени одинаково, что их количественное и
качественное изменение происходит под действием одного и того же комплекса основных
факторов, определяющих движение данного ряда динамики.
Модели, учитывающие общие закономерности изменения
экономического явления в изучаемый интервал времени и изменения во времени
влияния комплекса факторов, называют многофакторными динамическими моделями.
Выделим особенности моделей аналитического
выравнивания уровней динамического ряда, накладывающие ограничения на их
использование. Во-первых, динамические ряды, к которым применяется
аппроксимация, должны быть достаточно длинными. Во-вторых, применение
аппроксимации наиболее целесообразно в случае медленно и плавно меняющегося
уровня. В-третьих, аппроксимация как метод моделирования практически не
адаптируется к изменяющимся условиям формирования уровней ряда; при появлении
новых данных построение модели должно быть проведено заново. В-четвертых, при
использовании для расчета параметров уравнения метода наименьших квадратов
(МНК) считается, что значимость информации в пределах отрезка аппроксимации
одинакова независимо от давности полученных данных, в то время как более
поздние данные имеют большую ценность.
Помимо этого, динамические ряды экономических
показателей часто имеют небольшую длину и подвержены значительным колебаниям,
которые аппроксимация предвидеть не может.
Задача
В таблице приведены готовые данные о
трудоемкости производства:
| Год | 2009 | 2010 | 2011 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 |
|
Трудоемкость производства, человек-часов |
8 | 8.4 | 7.6 | 7 | 7.3 | 6.6 | 5.9 | 5 | 5.2 |
-
Провести аналитическое выравнивание ряда динамики по прямой.
Построить точечный и интервальный
прогноз на 2018 год.
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Решение
1) Произведем аналитическое выравнивание ряда по прямой.
Составим расчетную таблицу:
Расчетная вспомогательная таблица 1
| Годы |
|
|
|
|
| 2009 | -4 | 8 | 16 | -32 |
| 2010 | -3 | 8,4 | 9 | -25,2 |
| 2011 | -2 | 7,6 | 4 | -15,2 |
| 2012 | -1 | 7 | 1 | -7 |
| 2013 | 0 | 7,3 | 0 | 0,0 |
| 2014 | 1 | 6,6 | 1 | 6,6 |
| 2015 | 2 | 5,9 | 4 | 11,8 |
| 2016 | 3 | 5 | 9 | 15 |
| 2017 | 4 | 5,2 | 16 | 20,8 |
| Итого | 0 | 61,0 | 60 | -25,2 |
Коэффициенты уравнения линейного тренда найдем по формулам:
Уравнение линейного тренда имеет вид:
2) Составим расчетную таблицу:
Расчетная вспомогательная таблица 2
| Годы |
|
|
Теоретические значения |
|
| 2009 | -4 | 8 | 8,48 | 0,2304 |
| 2010 | -3 | 8,4 | 8,06 | 0,1156 |
| 2011 | -2 | 7,6 | 7,64 | 0,0016 |
| 2012 | -1 | 7 | 7,22 | 0,0484 |
| 2013 | 0 | 7,3 | 6,8 | 0,25 |
| 2014 | 1 | 6,6 | 6,38 | 0,0484 |
| 2015 | 2 | 5,9 | 5,96 | 0,0036 |
| 2016 | 3 | 5 | 5,54 | 0,2916 |
| 2017 | 4 | 5,2 | 5,12 | 0,0064 |
| Итого | — | — | — | 0,996 |
Среднеквадратическая ошибка:
Точечный прогноз на 2018 год (t=5):
Ошибка
прогноза составит:
По таблице критерия Стьюдента,
для доверительной вероятности
(уровня значимости
) находим:
Вывод к задаче
Таким образом
тренд для трудоемкости производства выражается линейным уравнением
.
Согласно прогнозу, в 2018 году трудоемкость производства с вероятностью 0,95
будет лежать в пределах от 3,6 до 5,8 человеко-часов.
Наиболее точным и эффективным способом
выявления основной тенденции развития
является аналитическое выравнивание.
При этом фактические уровни ряда динамики
заменяются теоретическими уровнями,
вычисленными на основе определенной
кривой, описываемой аналитическим
выражением. Предполагается, что
теоретическая кривая свободна от
всевозможных колебаний и поэтому
наиболее точно отображает общую тенденцию
изменения во времени изучаемого
показателя.
При аналитическом выравнивании ряда
динамики, его уровни выражаются в виде
функции времени.
![]() (12.1)
(12.1)
где
![]() – теоретический уровень ряда динамики,
– теоретический уровень ряда динамики,
вычисленный по определенному
аналитическом выражению на момент
времени
![]() .
.
Чаще всего при аналитическом выравнивании
используются следующие математические
зависимости:
-
линейная (уравнение прямой):
![]() (12.2)
(12.2)
-
параболическая (уравнение параболы):
![]() (12.3)
(12.3)
-
экспоненциальная (уравнение экспоненты):
![]() (12.4)
(12.4)
-
гиперболическая (уравнение гиперболы):
![]() (12.5)
(12.5)
Выбор формы кривой во многом определяет
результаты выявления тренда. Основанием
для выбора формы кривой может использоваться
содержательный анализ сущности развития
данного явления. Можно опираться на
результаты предыдущих исследований в
данной области.
На практике для этих целей прибегают к
анализу графического изображения
уровней ряда динамики (линейной
диаграммы). Однако из графического
представления эмпирических данных не
всегда удается произвести однозначный
выбор формы кривой (вида уравнения).
Поэтому целесообразно воспользоваться
графическим изображением сглаженных
уровней, в которых случайные и периодические
колебания в некоторой степени оказываются
сглаженными.
При выборе вида аналитической кривойдля выравнивания ряда динамики можно
воспользоваться следующими рекомендациями.
-
Линейная зависимостьиспользуется
в том случае, когда в исходном ряде
динамики наблюдается более или менее
постоянные абсолютные цепные приросты,
не проявляющие тенденции ни к увеличению,
ни к снижению. -
Параболическаязависимостьвыбирается в тех случаях, когда абсолютные
цепные приросты сами по себе обнаруживают
некоторую тенденцию развития, но
абсолютные цепные приросты абсолютных
приростов (разности второго порядка)
никакой тенденции развития не проявляют. -
Экспоненциальные зависимости, если
в исходном динамическом ряде наблюдается
либо более или менее постоянный
относительный рост (устойчивость цепных
темпов роста, темпов прироста,
коэффициентов роста), либо, при отсутствии
точного постоянства, – устойчивость
в изменении показателей относительного
роста (цепных темпов роста цепных же
темпов роста).
Для решения уравнений аналитических
кривых (формулы 12.2 – 12.5) в большинстве
случаев используют метод наименьших
квадратов, который обеспечивает
наименьшую сумму квадратов отклонений
фактических уровней от выровненных
(теоретических).
![]() (12.6)
(12.6)
Рассмотрим технику аналитического
выравнивания ряда динамики с использованием
уравнения прямой, имеющей наиболее
простое выражение, на следующем примере.
Пример. Имеются данные за последние
10 лет по заводу, где производятся запасные
части для тракторов. Эти данные приведены
в табл. 12.3.
-
Для того, чтобы выдвинуть гипотезу о
предполагаемом законе распределения
уровней ряда динамики, построим график
зависимости выпуска продукции от
времени. Такой график для нашего примера
представлен на рис. 12.1.
Таблица 12.3
Выпуск продукции на заводе (тыс. шт.)
|
Годы |
Выпуск продукции, ( |
|
|
|
|
|
1991 |
39,4 |
-9 |
81 |
-354,60 |
39,43 |
|
1992 |
39,8 |
-7 |
49 |
-278,60 |
39,84 |
|
1993 |
40,0 |
-5 |
25 |
-200,00 |
40,25 |
|
1994 |
40,6 |
-3 |
9 |
-121,80 |
40,66 |
|
1995 |
41,4 |
-1 |
1 |
-41,40 |
41,07 |
|
1996 |
41,9 |
+1 |
1 |
41,90 |
41,47 |
|
1997 |
41,9 |
+3 |
9 |
125,70 |
41,88 |
|
1998 |
42,0 |
+5 |
25 |
210,00 |
42,29 |
|
1999 |
42,6 |
+7 |
49 |
298,20 |
42,70 |
|
2000 |
43,1 |
+9 |
81 |
387,90 |
43,11 |
|
Итого: |
412,7 |
0 |
330 |
67,30 |
412,70 |
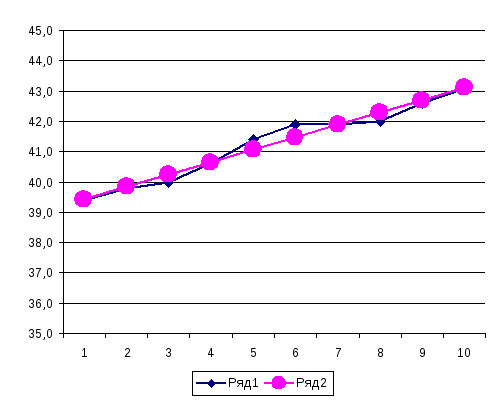
Рис. 12.1. Динамика выпуска продукции по
годам
(ряд 1 – фактические данные (![]() );
);
ряд 2 – выровненные данные (![]() )).
)).
-
По характеру фактических уровней,
принимаем гипотезу о существовании
прямолинейного тренда (динамика выпуска
характеризуется прямой линией). -
Запишем уравнение прямой
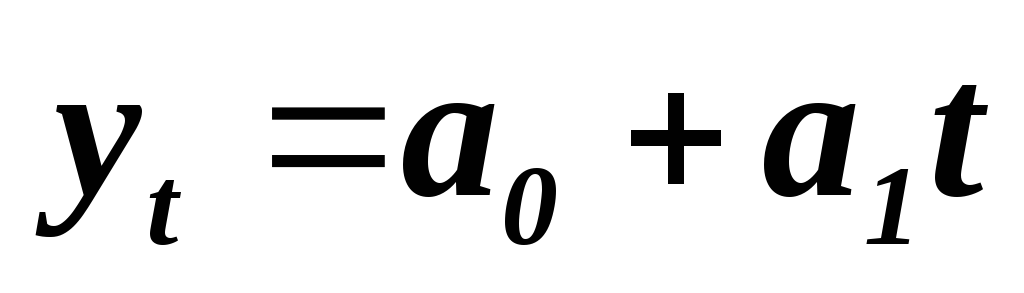 .
. -
Решить это уравнение – значит найти
параметры
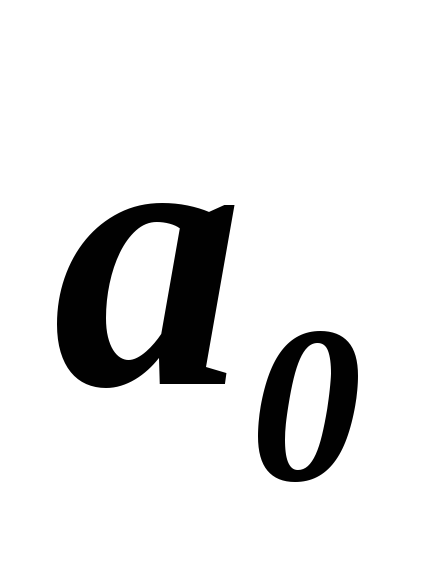 и
и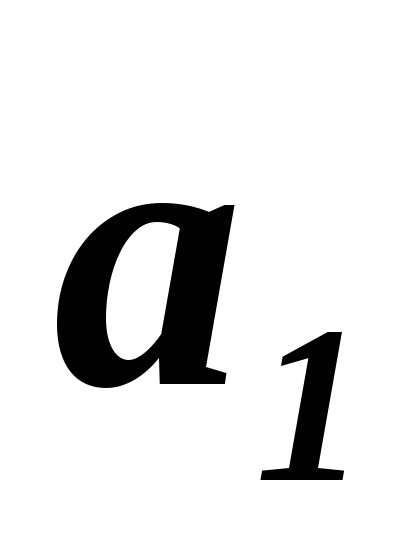 искомой прямой. Наиболее просто найти
искомой прямой. Наиболее просто найти
значение этих параметров можно,
воспользовавшисьметодом наименьших
квадратов. Для этого необходимо
решить систему нормальных уравнений:
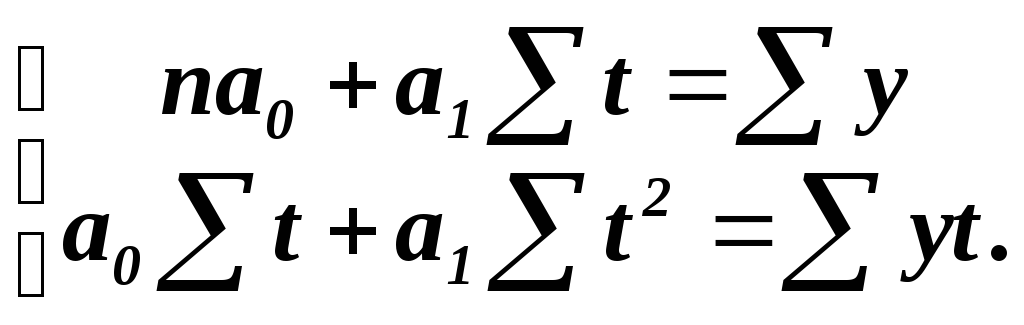 (12.7)
(12.7)
где ![]() – число членов ряда динамики;
– число членов ряда динамики;
![]() – фактические уровни ряда динамики.
– фактические уровни ряда динамики.
Система уравнений упрощается, если
![]() подобрать так, чтобы их сумма равнялась
подобрать так, чтобы их сумма равнялась
нулю, т.е. начало отсчета времени перенести
в середину рассматриваемого периода.
Тогда:
![]() и
и![]() (12.8,
(12.8,
12.9)
В табл. 12.3 производим необходимые расчеты
и тогда:
![]() и
и![]()
Подставим найденные параметры
![]() и
и![]() в уравнение прямой. Искомое уравнение
в уравнение прямой. Искомое уравнение
будет иметь вид:
![]()
По уравнению найдем расчетные значения
выровненных уровней ряда динамики,
подставляя в него значения
![]() из табл. 12.3.
из табл. 12.3.
Полученное уравнение, описывающее
исследуемый ряд динамики, показывает,
что средний уровень производства деталей
составляет 41,27 тыс. шт.в год и ежегодно
увеличивается в среднем на0,20 тыс.
штукв год. Сумма уравнений эмпирического
ряда полностью совпадает с суммой
расчетных значений выровненного ряда.
Аналогичным способом производится
аналитическое выравнивание рядов
динамики с использованием других
уравнений кривых. Однако каждой кривой
соответствует своя система нормальных
уравнений. Так, например, для решения
уравнения параболы система уравнений
имеет вид:
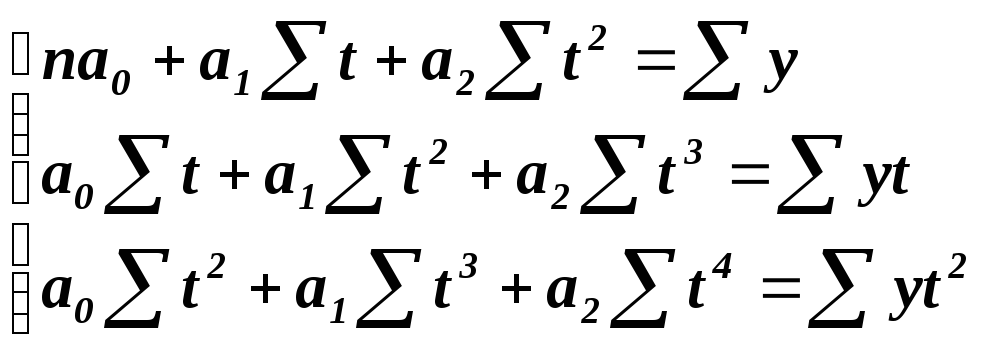 (12.10)
(12.10)
Для решения экспоненциального уравнения,
система нормальных уравнений имеет
вид:
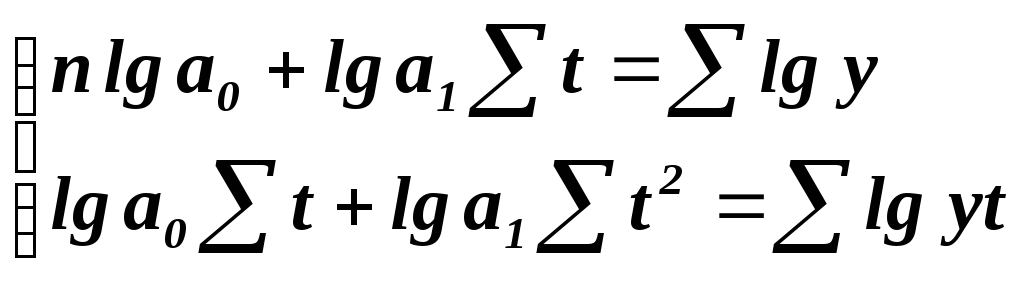 (12.11)
(12.11)
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Динамические ряды — краткое руководство по анализу изменений явлений во времени
Даная статья понятными и простыми терминами объяснит, что же такое динамические ряды, для чего они нужны, как производится анализ полученных данных и какие возможности открываются перед теми, кто владеет методикой данного анализа. Любое явление в области здравоохранения нуждается в тщательной оценке, и здесь знания анализа динамических рядов неоценимы. С помощью динамического ряда можно оценить и спрогнозировать проблематику любой нозологической единицы, сформировать дальнейшую тактику лечения и меры профилактики заболеваний.
Динамический ряд — ряд однородных величин, характеризующих изменение явления во времени.
Целью анализа динамических рядов является:
- выявление закономерности изменения изучаемого явления во времени;
- прогнозирование (экстраполирование) полученных данных на последующие
годы.
Числовые значения, составляющие динамический ряд, называются уровнями ряда (у).
Типы динамических рядов:
- В зависимости от вида уровня ряда:
а) простые (уровень ряда выражен абсолютными числами);
б) сложные (уровень ряда выражен обобщающими коэффициентами).
- В зависимости от способа формирования временного интервала:
а) моментные (данные собираются на определенный момент времени);
б) интервальные (данные собираются за определенный период времени).
- В зависимости от выраженности изменений явления во времени (определяется по коэффициенту корреляции между временем и изучаемым явлением).
а) с выраженной тенденцией (r =0,7 — 1,0);
б) с неустойчивой тенденцией (r =0,3 — 0,69);
в) с отсутствием тенденции ( r = 0 — 0,29).
Основное требование, предъявляемое к анализируемым динамическим рядам, заключается в сопоставимости их уровней. Для оценки сопоставимости проводят предварительный анализ полученных данных по следующим критериям:
- единство территории, на которой проводился сбор данных;
- единая методология учета данных;
- единые временные интервалы, в течение которых проводилась регистрация
данных.
Методика анализа динамических рядов
Методика аналитики предусматривает выполнение последовательных действий:
- Представить полученные данные графически и выявить форму зависимости изучаемого явления от времени.
- Оценить наличие и силу корреляции изучаемого явления от времени.
- Если установлено, что ряд обладает выраженной тенденцией, проводят анализ компонентов динамики ряда: основной тенденции (эволюции, тренда), кратковременных систематических движений и случайных колебаний. Основная задача анализа — разделить эти компоненты и выявить основную закономерность изменения явления во времени. Для выявления и описания тренда динамический ряд подвергают обработке — выравниванию.
Способы выравнивания динамических рядов
Чтобы произвести выравнивание динамических рядов потребуются следующие действия:
- Укрупнение временных интервалов (периодов), в течение которых изучается явление.
- Сглаживание ряда методом скользящей средней.
- Аналитический способ.
При этом способе на основании фактических данных подбирается наиболее подходящее для отражения тенденции развития явления математическое уравнение (аппроксимирующая функция), которое принимается за модель развития явления во времени. Т.е. уровни ряда рассматриваются как функция времени, и задача выравнивания сводится к определению вида функции, отысканию ее параметров по эмпирическим данным и расчету по найденной формуле теоретических выравненных уровней. Наиболее часто используются следующие функции:
а) линейная зависимость:![]()
б) экспоненциальная зависимость:![]()
в) показательная зависимость:![]()
г) параболическая зависимость:![]()
и др.
где a0, a1, а2 — параметры уравнения;
у – теоретический уровень;
t – временной интервал.
В качестве примера возьмем линейную зависимость и проведем выравнивание, используя для нахождения параметров уравнения а0 ,а1 способ наименьших квадратов. Способ наименьших квадратов позволяет найти теоретическую кривую, максимально приближенную к эмпирической, а условие минимума суммы квадратов отклонений теоретических данных от фактических позволяет свести математическое решение задачи к системе нормальных уравнений:
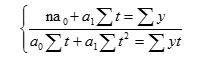
где у — уровни фактического ряда;
n — количество уровней;
t — порядковый номер временного периода.
Эта система уравнений легко упрощается, если «t» присвоить ранги (порядковые номера), ведя отсчет времени от середины ряда. При нечетном ряде середина обозначается через 0, а отсчет рангов ведется через единицу с соответствующим знаком в ту или иную сторону от середины (например: -5,-4,-3,-2,-1, 0,+1.+2,+3,->:4,+5). При четном ряде две средние временные точки обозначаются через +1 и -1, а остальные ранги присваиваются через две единицы (например: -5,-3,-1,+1,+3,+5).
При отсчете времени от середины ряда St = 0 и система нормальных уравнений принимает вид:
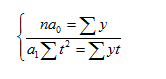
Отсюда находим параметры уравнения:
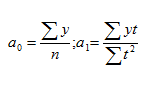
Подставляя в уравнение у = а0 + а1t вместо «t» его ранги, находим выравненные (теоретические) значения уровней ряда и строим теоретическую кривую выравненного динамического ряда.
При использовании аналитического способа всегда отмечается отклонение теоретических уровней от фактических уровней ряда, которое может быть обусловлено как случайными колебаниями, так и неправильно подобранным аппроксимирующим уравнением. В связи с этим заключительным этапом выравнивания динамического ряда аналитическим способом является оценка точности аппроксимации с определенным уровнем значимости.
Оценка точности аппроксимации возможна с помощью нахождения
Для получения точной оценки необходимо найти такие величины:
а) коэффициент вариации:

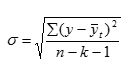
где у- фактический уровень ряда;
yt — теоретический уровень ряда;
k- число параметров уравнения;
n- число уровней ряда.
Аппроксимация считается точной при Cv не более 15%.
б) коэффициент расхождения Тейла:
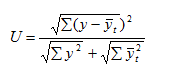
где у — фактический уровень ряда;
yt — теоретический уровень ряда.
Аппроксимация считается точной при U не более 5%
После аналитического выравнивания динамического ряда и описания тренда возможно экстраполировать полученные данные. Экстраполяция — предположение о сохранении тренда, базирующееся на допущении неизменности влияющих факторов и предшествующей тенденции. Осуществляется путем подставления в найденное уравнение аппроксимации не фактического значения временного интервала, а предполагаемого порядкового номера (ранг) того периода, на который прогнозируется результат.
Вычисление основных показателей динамического ряда
Алгоритм вычислений ведущих параметров динамических рядов:
Условные обозначения:
yi- текущий уровень (сравниваемый);
уi-1— базисный уровень (с каким сравнивают);
t- период времени, в течение которого уровень предполагается неизменным.
1.Абсолютный прирост (убыль) :
![]()
2.Темп роста (убыли):
![]()
3.Темп прироста (относительная скорость), темп убыли :
![]()
4.Средний темп прироста (убыли):
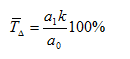
где а0; а1 — параметры уравнения;
k = 1 при нечетном ряде;
k = 2 при четном ряде.
5.1% прироста (убыли): используются при сравнении динамических рядов с уровнями, выраженными различными обобщающими коэффициентами.

Таким образом, с помощью данного руководства по определению и расчетам такого понятия, как, динамические ряды, специалисты различных отраслей медицины, ученые могут эффективно и быстро оценить изменение различных величин в течение времени.
Благодарим за интерес, проявленный к нашей статье, оставайтесь с нами!
Если Вам понравилась статья и оказалась полезной, Вы можете поделиться ею с коллегами и друзьями в социальных сетях:
