Алгебра логики в информатике начинает с 8 класса с изучения отдельных элементов алгебры логики.
По определению алгеброй логики является раздел математики, однако, элементами алгебры логики в информатике могут быть и высказывания.
Высказывание
Высказывание — это предложение, содержание которого можно однозначно определить как ложное иди истинное. И не важно на каком языке это ваысказывание.
Какое же предложение в русском языке является высказыванием?
По факту мы можем выделить повествовательные предложения, побудительные и вопросительные. Но это не говорит нам о том, является предложение высказыванием или не является.
Однозначно можно сказать, что вопросительные и побудительные предложения не могут являться высказыванием.
«Что вы изучаете?» или «Как найти школу № 75?» — эти предложения не являются высказыванием, как и «Сдайте на проверку домашнее задание.» или «Сходите на субботник.»
Повествовательные предложения тоже не все можно назвать высказыванием. главное условие высказывания — это условие при котором можно точно определить истинность или ложность этого высказывания.
«Это предложение является ложным» — повествовательное предложение, которое не является высказыванием. Причина: относительно данного предложения нельзя наверняка сказать ложно оно или истинно.
Если предположить, что предложение истинно, то возникнет между сказанным предложением и его содержанием противоречие.
Если принять, что предложение ложно, то надо признать, что оно истинно.
Построение высказываний
Высказывания могут строиться не только простыми предложениями, но и с использованием различных знаков формальных языков. Например, формальным языком является математика, химия, физика и т.д.
Высказываниями являются следующие предложения:
- Битва при Ватерло́о является последним крупным сражением французского императора Наполеона I.
- Fe (Ферум) — металл и элемент таблицы Менделеева.
- Ра́диус — это отрезок, соединяющий центр окружности с любой точкой, лежащей на окружности, а также длина этого отрезка.
Числовые выражения не являются высказыванием. Однако, используя числовые выражения можно составить высказывание. При этом надо две части этого выражения соединить знаком либо равенства, либо неравенства.
В случае, если в математическом выражении есть переменные, то такое выражение нельзя включить в высказывание до тех пор, пока переменная не будет заменена числом.
Рассмотрим пример.
«5+8 = 15-2»
Это высказывание истинно.
«5+8 > 5 +10»
Это высказывание ложно
«Х>8» не является высказыванием.
Однако, если Х заменить на число из множества (9;+∞), то будет высказывание, истинное высказывание.
В целом, истинность или ложность высказывания можно рассматривать лишь с точки зрения той науки к сфере которой эти выражения относятся. А алгебра логики отвлекается от специфики выражения, от его содержательной части, поэтому все высказывания обозначаются буквами, которые называют логическими переменными.
Алгебра логики определяет правила записи, упрощение и преобразования высказываний и вычислений их значений.
Логические переменные могут быть только 0 или 1.
Оперируя только логическими переменными, алгебра логики сводит все операции к операциями с двоичными данными.
Алгебра логики является основой компьютерных устройств хранения и обработки данных, основой алгоритмизации и программирования.
Далее рассмотрим простые и сложные высказывания.
Практические задания
Приведите примеры как истинных, так и ложных высказываний по следующим изучаемым предметам: истории, математике, литературе.
На уроке рассмотрен материал для подготовки к огэ по информатике, решение задания 3
3-е задание: «Значение логического выражения»
Уровень сложности — базовый,
Максимальный балл — 1,
Примерное время выполнения — 3 минуты.
* до 2020 г — это задание № 2 ОГЭ
Содержание:
- Объяснение 3 задания ОГЭ по информатике
- ОГЭ информатика разбор задания 3
- Актуальное
- Тренировочные
- Для подготовки к решению 3 задания ОГЭ по информатике следует вспомнить знаки сравнения. В логических выражениях используются следующие знаки сравнения:
- В логических выражениях участвуют всего два значения выражений: ИСТИНА и ЛОЖЬ.
- Рассмотрим результат выполнения логических выражений для двух высказываний — А и Б:
- Если отрицание НЕ стоит перед скобкой с выражением, то НЕ ставится перед каждой частью выражения в скобках и при этом операция внутри скобок меняется:
|
> |
больше |
|
< |
меньше |
|
= |
равно |
|
≥ |
больше или равно |
|
≤ |
меньше или равно |
| 1 | А ИЛИ Б = ИСТИНА → | если А=истина И Б=истина |
| 2 | если А=истина И Б=ложь | |
| 3 | если А=ложь И Б=истина | |
| 4 | А ИЛИ Б = ЛОЖЬ → | если А=ложь И Б=ложь |
Вывод: логическое выражение с операцией ИЛИ легче проверить «на ложь»:
с операцией ИЛИ результатом будет ЛОЖЬ только в одном единственном случае, — когда оба выражения — А и Б — ложны
| 1 | А И Б = ИСТИНА → | если А=истина И Б=истина |
| 2 | А И Б = ЛОЖЬ → | если А=истина И Б=ложь |
| 3 | если А=ложь И Б=истина | |
| 4 | если А=ложь И Б=ложь |
Вывод: логическое выражение с операцией И легче проверить «на истинность»:
с операцией И результатом будет ИСТИНА только в одном единственном случае, — когда оба выражения — А и Б — истинны
| Исходные значения | Результат | |
|---|---|---|
| 1 | НЕ А если А=истина |
А = ЛОЖЬ |
| НЕ(5 > 0) | 5 ≤ 0 | |
| 2 | НЕ А если А=ложь |
А = ИСТИНА |
| НЕ(-2 > 0) | -2 ≤ 0 | |
| 3 | НЕ (НЕ А) | = А |
| 1 | НЕ |
| 2 | выражение в скобках |
| 3 | И |
| 4 | ИЛИ |
| 1 | НЕ (А ИЛИ Б) | НЕ А И НЕ Б |
| 2 | НЕ (А И Б) | НЕ А ИЛИ НЕ Б |
ОГЭ информатика разбор задания 3
Подробный видеоразбор по ОГЭ 3 задания:
📹 Видеорешение на RuTube здесь
Актуальное
Значение логического выражения
Разбор задания 3.7. Демонстрационный вариант ОГЭ 2022 г ФИПИ:
Напишите наименьшее число x, для которого истинно высказывание:
(x > 16) И НЕ (x нечётное)
✍ Решение:
- Выполним первую по приоритету операцию — операцию НЕ:
НЕ (x нечётное) результат: x чётное
(x > 16) И (x чётное)
(x > 16) И (x чётное) = ИСТИНА истина истина
Ответ: 18
Разбор задания 3.12:
Напишите наименьшее число x, для которого ложно высказывание:
(x ≤ 15) ИЛИ НЕ (x нечётное)
✍ Решение:
- Выполним первую по приоритету операцию — операцию НЕ:
НЕ (x нечётное) результат: x чётное
(x ≤ 15) ИЛИ (x чётное) = 0 (ложь)
(x ≤ 15) ИЛИ (x чётное) = ЛОЖЬ ложь ложь
Ответ: 17
Тренировочные
Разбор задания 3.1:
Для какого из приведённых значений числа X ложно высказывание:
НЕ (X < 6) ИЛИ (X < 5) ?
1) 7
2) 6
3) 5
4) 4
Подобные задания для тренировки
✍ Решение:
- Выполним первую по приоритету операцию — операцию НЕ:
НЕ (X < 6) (X < 6) - ложь, значит результат: X ≥ 6
(X ≥ 6) ИЛИ (X < 5)
(X ≥ 6) ИЛИ (X < 5) = ЛОЖЬ ложь ложь
1. (X ≥ 6) = ЛОЖЬ => X < 6 2. (X < 5) = ЛОЖЬ => X ≥ 5
5 < 6 и 5 ≥ 5
Ответ: 3
Разбор задания 3.2:
Для какого из приведённых значений числа X истинно высказывание:
(X < 8) И НЕ (X < 7) ?
1) 9
2) 8
3) 7
4) 6
Подобные задания для тренировки
✍ Решение:
- Выполним первую по приоритету операцию — операцию НЕ:
НЕ (X < 7) (X < 7) - ложь, значит результат: X ≥ 7
(X < 8) И (X ≥ 7)
(X < 8) И (X ≥ 7) = ИСТИНА истина истина
1. (X < 8) = ИСТИНА => X < 8 2. (X ≥ 7) = ИСТИНА => X ≥ 7
7 < 8 и 7 ≥ 7
Ответ: 3
Разбор задания 3.3:
Для какого из приведённых имён ЛОЖНО высказывание:
НЕ ((Третья буква согласная) И (Последняя буква гласная)) ?
1) Анна
2) Елена
3) Павел
4) Егор
Подобные задания для тренировки
✍ Решение:
- Обратим внимание на то, что в заданном выражении операция НЕ относится ко всей общей скобке.
- Выполним первую по приоритету операцию — операцию НЕ, по таблице 6 для НЕ перед скобкой с выражением имеем:
НЕ ((Третья буква согласная) И (Последняя буква гласная)) = = (НЕ(Третья буква согласная) ИЛИ НЕ(Последняя буква гласная))
1. НЕ(Третья буква согласная) => Третья буква НЕ согласная 2. НЕ(Последняя буква гласная) => Последняя буква НЕ гласная
(Третья буква не согласная) ИЛИ (Последняя буква не гласная)
(Третья буква не согласная) ИЛИ (Последняя буква не гласная) = ЛОЖЬ
ложь ложь
1. (Третья буква не согласная) = ЛОЖЬ => Третья буква согласная 2. (Последняя буква не гласная) = ЛОЖЬ => Последняя буква гласная
Третья буква "н" согласная и Последняя буква "а" гласная
Ответ: 1
Разбор задания 3.4:
Для какого из приведённых имён ИСТИННО высказывание:
НЕ ((число > 50) ИЛИ НЕ(число четное)) ?
1) 43
2) 50
3) 61
4) 72
Подобные задания для тренировки
✍ Решение:
- Обратим внимание на то, что в заданном выражении операция НЕ относится ко всей общей скобке.
- Выполним первую по приоритету операцию — операцию НЕ в малых скобках:
НЕ(число четное) => число нечетное
НЕ ((число > 50) ИЛИ (число нечетное)) = = (НЕ(число > 50) И НЕ(число нечетное))
1. НЕ(число > 50) => число <= 50 2. НЕ(число нечетное) => число четное
(число <= 50) И (число четное)
(число <= 50) И (число нечетное) = ИСТИНА
истина истина
Ответ: 2
Разбор задания 3.5.:
Для какого из приведённых слов ЛОЖНО высказывание:
(последняя буква согласная) ИЛИ НЕ ((первая буква согласная) И (вторая буква гласная)) ?
1) Тигр
2) Выдра
3) Енот
4) Краб
✍ Решение:
- Обратим внимание на то, что в заданном выражении операция НЕ относится ко всей общей скобке.
- Выполним первую по приоритету операцию — операцию НЕ, по таблице 6 для НЕ перед скобкой с выражением имеем:
НЕ ((первая буква согласная) И (вторая буква гласная)) = = (НЕ(первая буква гласная) ИЛИ НЕ(вторая буква гласная))
1. НЕ(первая буква согласная) => первая буква гласная 2. НЕ(вторая буква гласная) => вторая буква согласная
(первая буква гласная) ИЛИ (вторая буква согласная)
(последняя буква согласная) ИЛИ (первая буква гласная) ИЛИ (вторая буква согласная)
(последняя буква согласная) ИЛИ (первая буква согласная) ИЛИ
ложь ложь
(вторая буква согласная) = ЛОЖЬ
ложь
1. (последняя буква согласная) = ЛОЖЬ => последняя буква гласная 2. (первая буква гласная) = ЛОЖЬ => первая буква согласная 3. (вторая буква согласная) = ЛОЖЬ => вторая буква гласная
Ответ: 2
Разбор задания 3.6:
Для какого из приведённых слов верно высказывание:
(первая буква гласная) И ((последняя буква согласная) ИЛИ (вторая буква согласная)) ?
1) АИДА
2) СЕРГЕЙ
3) СТЕПАН
4) АРТЕМ
Подобные задания для тренировки
✍ Решение:
- Обратим внимание на то, что в заданном выражении находятся большие скобки, с которых необходимо начать решение.
- Внешняя операция, т.е. последняя по приоритету — это операция И. Рассмотрим ее подробней, разделив общее высказывание на две части относительно этой операции:
(первая буква гласная) И ((последняя буква согласная) ИЛИ (вторая буква согласная))
(первая буква гласная) И ((последняя буква согласная) ИЛИ (вторая буква согласная)) истина истина
((последняя буква согласная) ИЛИ (вторая буква согласная))
истина ИЛИ истина
(первая буква гласная) И (или первая или вторая буква в слове согласная) истина истина
Ответ: 4
Осуществление поиска в готовой базе данных по сформулированному условию
* до 2020 г – это задание № 12 ОГЭ
Разбор задания 3.8:
Ниже в табличной форме представлен фрагмент базы данных «Отправление поездов дальнего следования»:
| Пункт назначения | Категория поезда | Время в пути | Вокзал |
|---|---|---|---|
| Рига | скорый | 15:45 | Рижский |
| Ростов | фирменный | 17:36 | Казанский |
| Самара | фирменный | 14:20 | Казанский |
| Самара | скорый | 17:40 | Казанский |
| Самара | скорый | 15:56 | Казанский |
| Самара | скорый | 15:56 | Павелецкий |
| Самара | фирменный | 23:14 | Курский |
| Санкт-Петербург | скорый | 8:00 | Ленинградский |
| Санкт-Петербург | скорый | 4:00 | Ленинградский |
| Саратов | скорый | 14:57 | Павелецкий |
| Саратов | пассажирский | 15:58 | Павелецкий |
| Саратов | скорый | 15:30 | Павелецкий |
Сколько записей в данном фрагменте удовлетворяют условию:
(Категория поезда = «скорый») ИЛИ (Вокзал = «Павелецкий»)?
✍ Решение:
- В условии находится логическая операция ИЛИ, которая истинна тогда, кода хоть одно из логических выражений истинно. Для нашего случая это говорит о том, что нужно посчитать те строки, в которых:
1. Категория поезда = «скорый» и Вокзал = любой 2. Категория поезда = «скорый» и Вокзал = «Павелецкий» 3. Категория поезда = любой и Вокзал = «Павелецкий»
Ответ: 9
Разбор задания 3.9:
Ниже в табличной форме представлен фрагмент базы данных «Отправление поездов дальнего следования»:
| Пункт назначения | Категория поезда | Время в пути | Вокзал |
|---|---|---|---|
| Балаково | скорый | 20:22 | Павелецкий |
| Бийск | скорый | 61:11 | Казанский |
| Бишкек | скорый | 121:20 | Казанский |
| Благовещенск | пассажирский | 142:06 | Ярославский |
| Брест | скорый | 14:19 | Белорусский |
| Валуйки | фирменный | 14:57 | Курский |
| Варна | скорый | 47:54 | Киевский |
| Волгоград | скорый | 18:50 | Павелецкий |
| Волгоград | скорый | 24:50 | Курский |
| Воркута | пассажирский | 48:19 | Ярославский |
| Воркута | пассажирский | 48:19 | Ярославский |
| Гродно | скорый | 16:34 | Белорусский |
Сколько записей в данном фрагменте удовлетворяют условию:
(Категория поезда = «скорый») И (Время в пути > 40:00)?
✍ Решение:
- В условии находится логическая операция И, которая истинна только тогда, кода оба (все) выражения истинны. Для нашего случая это говорит о том, что нужно посчитать те строки, в которых:
Категория поезда = «скорый» и Время в пути > 40:00 одновременно
Ответ: 3
Разбор задания 3.10:
Ниже в табличной форме представлен фрагмент базы данных «Отправление поездов дальнего следования»:
| Пункт назначения | Категория поезда | Время в пути | Вокзал |
|---|---|---|---|
| Балаково | скорый | 20:22 | Павелецкий |
| Бийск | скорый | 61:11 | Казанский |
| Бишкек | скорый | 121:20 | Казанский |
| Благовещенск | пассажирский | 142:06 | Ярославский |
| Брест | скорый | 14:19 | Белорусский |
| Валуйки | фирменный | 14:57 | Курский |
| Варна | скорый | 47:54 | Киевский |
| Волгоград | скорый | 18:50 | Павелецкий |
| Волгоград | скорый | 24:50 | Курский |
| Воркута | пассажирский | 48:19 | Ярославский |
| Воркута | пассажирский | 48:19 | Ярославский |
| Гродно | скорый | 16:34 | Белорусский |
Сколько записей в данном фрагменте удовлетворяют условию:
(Пункт назначения = «Волгоград») ИЛИ (Категория поезда = «пассажирский») И (Время в пути < 50:00)?
В ответе укажите одно число — искомое количество записей.
✍ Решение:
- В условии находятся две логических операции: И и ИЛИ. Первой всегда выполняется операция И, затем добавляются записи для операции ИЛИ.
- Операция И истинна только тогда, кода оба (все) выражения истинны.
(Категория поезда = «пассажирский») И (Время в пути < 50:00) одновременно
(Пункт назначения = «Волгоград») добавить к предыдущему результату
Ответ: 4
Разбор задания 3.11:
Ниже в табличной форме представлен фрагмент базы данных «Отправление поездов дальнего следования»:
| Пункт назначения | Категория поезда | Время в пути | Вокзал |
|---|---|---|---|
| Махачкала | скорый | 39.25 | Павелецкий |
| Махачкала | скорый | 53.53 | Курский |
| Мурманск | скорый | 35.32 | Ленинградский |
| Мурманск | скорый | 32.50 | Ленинградский |
| Мурманск | пассажирский | 37.52 | Ленинградский |
| Мурманск | пассажирский | 37.16 | Ленинградский |
| Назрань | пассажирский | 40.23 | Павелецкий |
| Нальчик | скорый | 34.55 | Казанский |
| Нерюигри | скорый | 125.41 | Казанский |
| Новосибирск | скорый | 47.30 | Ярославский |
| Нижневартовск | скорый | 52.33 | Казанский |
| Нижний Тагил | фирменный | 31.36 | Ярославский |
Сколько записей в данном фрагменте удовлетворяют условию:
НЕ (Вокзал = «Ленинградский») И (Время в пути > 50.00)?
✍ Решение:
- В условии находятся две логических операции: НЕ и И.
- Первой всегда выполняется операция НЕ, затем добавляются записи для операции И.
- Операция НЕ обозначает обратное высказывание:
НЕ(Вокзал = «Ленинградский»)
то же самое, что
(Вокзал ≠ «Ленинградский»)
(Вокзал ≠ «Ленинградский») И (Время в пути > 50.00) одновременно
Ответ: 3
Алгебра логики
Алгебра логики
Алгебра логики (англ. algebra of logic) — один из основных разделов математической логики, в котором методы алгебры используются в логических преобразованиях.
Основоположником алгебры логики является английский математик и логик Дж. Буль (1815–1864), положивший в основу своего логического учения аналогию между алгеброй и логикой. Любое высказывание он записывал с помощью символов разработанного им языка и получал «уравнения», истинность или ложность которых можно было доказать, исходя из определенных логических законов, таких как законы коммутативности, дистрибутивности, ассоциативности и др.
Современная алгебра логики является разделом математической логики и изучает логические операции над высказываниями с точки зрения их истинностного значения (истина, ложь). Высказывания могут быть истинными, ложными или содержать истину и ложь в разных соотношениях.
Логическое высказывание — это любое повествовательное предложение, в отношении которого можно однозначно утверждать, что его содержание истинно или ложно.
Например, «3 умножить на 3 равно 9», «Архангельск севернее Вологды» — истинные высказывания, а «Пять меньше трех», «Марс — звезда» — ложные.
Очевидно, что не всякое предложение может быть логическим высказыванием, т. к. не всегда есть смысл говорить о его ложности или истинности. Например, высказывание «Информатика — интересный предмет» неопределенно и требует дополнительных сведений, а высказывание «Для ученика 10-А класса Иванова А. А. информатика — интересный предмет» в зависимости от интересов Иванова А. А. может принимать значение «истина» или «ложь».
Кроме двузначной алгебры высказываний, в которой принимаются только два значения — «истинно» и «ложно», существует многозначная алгебра высказываний. В такой алгебре, кроме значений «истинно» и «ложно», употребляются такие истинностные значения, как «вероятно», «возможно», «невозможно» и т. д.
В алгебре логики различаются простые (элементарные) высказывания, обозначаемые латинскими буквами (A, B, C, D, …), и сложные (составные), составленные из нескольких простых с помощью логических связок, например таких, как «не», «и», «или», «тогда и только тогда», «если … то». Истинность или ложность получаемых таким образом сложных высказываний определяется значением простых высказываний.
Обозначим как А высказывание «Алгебра логики успешно применяется в теории электрических схем», а через В — «Алгебра логики применяется при синтезе релейно-контактных схем».
Тогда составное высказывание «Алгебра логики успешно применяется в теории электрических цепей и при синтезе релейно-контактных схем» можно кратко записать как А и В; здесь «и» — логическая связка. Очевидно, что поскольку элементарные высказывания А и В истинны, то истинно и составное высказывание А и В.
Каждая логическая связка рассматривается как операция над логическими высказываниями и имеет свое название и обозначение.
Логических значений всего два: истина (TRUE) и ложь (FALSE). Это соответствует цифровому представлению — 1 и 0. Результаты каждой логической операции можно записать в виде таблицы. Такие таблицы называют таблицами истинности.
Основные операции алгебры логики
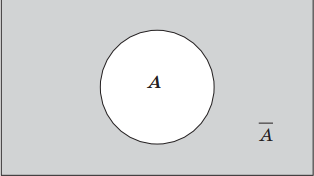
1. Логическое отрицание, инверсия (лат. inversion — переворачивание) — логическая операция, в результате которой из данного высказывания (например, А) получается новое высказывание (не А), которое называется отрицанием исходного высказывания, обозначается символически чертой сверху ($A↖{-}$) или такими условными обозначениями, как ¬, ‘not’, и читается: «не А», «А ложно», «неверно, что А», «отрицание А». Например, «Марс — планета Солнечной системы» (высказывание А); «Марс — не планета Солнечной системы» ($A↖{-}$); высказывание «10 — простое число» (высказывание В) ложно; высказывание «10 — не простое число» (высказывание B ) истинно.
Операция, используемая относительно одной величины, называется унарной. Таблица значений данной операции имеет вид
| A | ¬A |
| истина | ложь |
| ложь | истина |
или
Высказывание $A↖{-}$ ложно, когда А истинно, и истинно, когда А ложно.
Геометрически отрицание можно представить следующим образом: если А — это некоторое множество точек, то $A↖{-}$ — это дополнение множества А, т. е. все точки, которые не принадлежат множеству А.
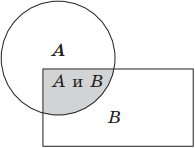
2. Конъюнкция (лат. conjunctio — соединение) — логическое умножение, операция, требующая как минимум двух логических величин (операндов) и соединяющая два или более высказываний при помощи связки «и» (например, «А и В»), которая символически обозначается с помощью знака ∧ (А ∧ В) и читается: «А и В». Для обозначения конъюнкции применяются также следующие знаки: А ∙ В; А & В, А and В, а иногда между высказываниями не ставится никакого знака: АВ. Пример логического умножения: «Этот треугольник равнобедренный и прямоугольный». Данное высказывание может быть истинным только в том случае, если выполняются оба условия, в противном случае высказывание ложно.
Таблица истинности операции имеет вид
| A | B | A ∧ B |
| истина | ложь | ложь |
| ложь | истина | ложь |
| ложь | ложь | ложь |
| истина | истина | истина |
или
| A | B | A ∧ B |
| 1 | 0 | 0 |
| 0 | 1 | 0 |
| 0 | 0 | 0 |
| 1 | 1 | 1 |
Высказывание А ∧ В истинно только тогда, когда оба высказывания — А и В истинны.
Геометрически конъюнкцию можно представить следующим образом: если А, В — это некоторые множества точек, то А ∧ В есть пересечение множеств А и В.
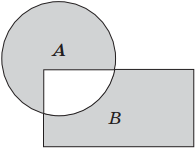
3. Дизъюнкция (лат. disjunction — разделение) — логическое сложение, операция, соединяющая два или более высказываний при помощи связки «или» (например, «А или В»), которая символически обозначается с помощью знака ∨ (А ∨ В) и читается: «А или В». Для обозначения дизъюнкции применяются также следующие знаки: А + В; А or В; А | B. Пример логического сложения: «Число x делится на 3 или на 5». Это высказывание будет истинным, если выполняются оба условия или хотя бы одно из условий.
Таблица истинности операции имеет вид
| A | B | A ∨ B |
| истина | ложь | истина |
| ложь | истина | истина |
| ложь | ложь | ложь |
| истина | истина | истина |
или
| A | B | A ∨ B |
| 1 | 0 | 1 |
| 0 | 1 | 1 |
| 0 | 0 | 0 |
| 1 | 1 | 1 |
Высказывание А ∨ В ложно только тогда, когда оба высказывания — А и В ложны.
Геометрически логическое сложение можно представить следующим образом: если А, В — это некоторые множества точек, то А ∨ В — это объединение множеств А и В, т. е. фигура, объединяющая и квадрат, и круг.
4. Дизъюнкция строго-разделительная, сложение по модулю два — логическая операция, соединяющая два высказывания при помощи связки «или», употребленной в исключающем смысле, которая символически обозначается с помощью знаков ∨ ∨ или ⊕ (А ∨ ∨ В, А ⊕ В) и читается: «либо А, либо В». Пример сложения по модулю два — высказывание «Этот треугольник тупоугольный или остроугольный». Высказывание истинно, если выполняется какое-то одно из условий.
Таблица истинности операции имеет вид
| А | В | А ⊕ B |
| истина | ложь | истина |
| ложь | истина | истина |
| ложь | ложь | ложь |
| истина | истина | ложь |
или
| А | В | А ⊕ B |
| 1 | 0 | 1 |
| 0 | 1 | 1 |
| 0 | 0 | 0 |
| 1 | 1 | 0 |
Высказывание А ⊕ В истинно только тогда, когда высказывания А и В имеют различные значения.
5. Импликация (лат. implisito — тесно связываю) — логическая операция, соединяющая два высказывания при помощи связки «если…, то» в сложное высказывание, которое символически обозначается с помощью знака → (А → В) и читается: «если А, то В», «А влечет В», «из А следует В», «А имплицирует В». Для обозначения импликации применяется также знак ⊃ (A ⊃ B). Пример импликации: «Если полученный четырехугольник квадрат, то около него можно описать окружность». Эта операция связывает два простых логических выражения, из которых первое является условием, а второе — следствием. Результат операции ложен только тогда, когда предпосылка есть истина, а следствие — ложь. Например, «Если 3 * 3 = 9 (А), то Солнце — планета (В)», результат импликации А → В — ложь.
Таблица истинности операции имеет вид
| А | В | А → В |
| истина | ложь | ложь |
| ложь | истина | истина |
| ложь | ложь | истина |
| истина | истина | истина |
или
| А | В | А → В |
| 1 | 0 | 0 |
| 0 | 1 | 1 |
| 0 | 0 | 1 |
| 1 | 1 | 1 |
Для операции импликации справедливо утверждение, что из лжи может следовать все что угодно, а из истины — только истина.
6. Эквивалентность, двойная импликация, равнозначность (лат. aequalis — равный и valentis — имеющий силу) — логическая операция, позволяющая из двух высказываний А и В получить новое высказывание А ≡ В, которое читается: «А эквивалентно B». Для обозначения эквивалентности применяются также следующие знаки: ⇔, ∼. Эта операция может быть выражена связками «тогда и только тогда», «необходимо и достаточно», «равносильно». Примером эквивалентности является высказывание: «Треугольник будет прямоугольным тогда и только тогда, когда один из углов равен 90 градусам».
Таблица истинности операции эквивалентности имеет вид
| А | В | А ∼ В |
| истина | ложь | ложь |
| ложь | истина | ложь |
| ложь | ложь | истина |
| истина | истина | истина |
или
| А | В | А ∼ В |
| 1 | 0 | 0 |
| 0 | 1 | 0 |
| 0 | 0 | 1 |
| 1 | 1 | 1 |
Операция эквивалентности противоположна сложению по модулю два и имеет результат «истина» тогда и только тогда, когда значения переменных совпадают.
Зная значения простых высказываний, можно на основании таблиц истинности определить значения сложных высказываний. При этом важно знать, что для представления любой функции алгебры логики достаточно трех операций: конъюнкции, дизъюнкции и отрицания.
| Сложение по модулю два | А ⊕ В | $(A↖{-} ∧B) ∧ (A ∧ B↖{-})$ |
| Импликация | А → В | $A↖{-} ∨ B$ |
| Эквивалентность | А ∼ В | $(A↖{-} ∧ B↖{-}) ∨ (A ∧ B)$ |
Приоритет выполнения логических операций следующий: отрицание («не») имеет самый высокий приоритет, затем выполняется конъюнкция («и»), после конъюнкции — дизъюнкция («или»).
С помощью логических переменных и логических операций любое логическое высказывание можно формализовать, т. е. заменить логической формулой. При этом элементарные высказывания, образующие составное высказывание, могут быть абсолютно не связаны по смыслу, но это не мешает определять истинность или ложность составного высказывания. Например, высказывание «Если пять больше двух (А), то вторник всегда наступает после понедельника (В)» — импликация А → В, и результат операции в данном случае — «истина». В логических операциях смысл высказываний не учитывается, рассматривается только их истинность или ложность.
Рассмотрим, например, построение составного высказывания из высказываний А и В, которое было бы ложно тогда и только тогда, когда оба высказывания истинны. В таблице истинности для операции сложения по модулю два находим: 1 ⊕ 1 = 0. А высказывание может быть, например, таким: «Этот мяч полностью красный или полностью синий». Следовательно, если утверждение А «Этот мяч полностью красный» — истина, и утверждение В «Этот мяч полностью синий» — истина, то составное утверждение — ложь, т. к. одновременно и красным, и синим мяч быть не может.
Примеры решения задач
Пример 1. Определить для указанных значений X значение логического высказывания ((X > 3) ∨ (X < 3)) → (X < 4) :
1) X = 1; 2) X = 12; 3) X = 3.
Решение. Последовательность выполнения операций следующая: сначала выполняются операции сравнения в скобках, затем дизъюнкция, и последней выполняется операция импликации. Операция дизъюнкции ∨ ложна тогда и только тогда, когда оба операнда ложны. Таблица истинности для импликации имеет вид
| A | B | A → B |
| 1 | 0 | 0 |
| 0 | 1 | 1 |
| 0 | 0 | 1 |
| 1 | 1 | 1 |
Отсюда получаем:
1) для X = 1:
((1 > 3) ∨ (1 < 3)) → (1 < 4) = ложь ∨ истина → истина = истина → истина = истина;
2) для X = 12:
((12 > 3) ∨ (12 < 3) → (12 < 4) = истина ∨ ложь → ложь = истина → ложь = ложь;
3) для X = 3:
((3 > 3) ∨ (3 < 3)) → (3<4) = ложь ∨ ложь → истина = ложь → истина = истина.
Пример 2. Указать множество целых значений X, для которых истинно выражение ¬((X > 2) → (X > 5)) .
Решение. Операция отрицания применена ко всему выражению ((X > 2) → (X > 5)) , следовательно, когда выражение ¬((X > 2) → (X > 5)) истинно, выражение ((X > 2) →(X > 5)) ложно. Поэтому необходимо определить, для каких значений X выражение ((X > 2) → (X > 5)) ложно. Операция импликации принимает значение «ложь» только в одном случае: когда из истины следует ложь. А это выполняется только для X = 3; X = 4; X = 5.
Пример 3. Для каких из приведенных слов ложно высказывание ¬(первая буква гласная ∧ третья буква гласная) ⇔ строка из 4 символов? 1) асса; 2) куку; 3) кукуруза; 4) ошибка; 5) силач.
Решение. Рассмотрим последовательно все предложенные слова:
1) для слова асса получим: ¬(1 ∧ 0) ⇔ 1, 1 ⇔ 1 — высказывание истинно;
2) для слова куку получим: ¬ (0 ∧ 0) ⇔ 1, 1 ⇔ 1 — высказывание истинно;
3) для слова кукуруза получим: ¬ (0 ∧ 0) ⇔ 0, 1 ⇔ 0 — высказывание ложно;
4) для слова ошибка получим: ¬ (1 ∧ 1) ⇔ 0, 0 ⇔ 0 — высказывание истинно;
5) для слова силач получим: ¬ (0 ∧ 0) ⇔ 1, 1 ⇔ 0 — высказывание ложно.
Логические выражения и их преобразование
Под логическим выражением следует понимать такую запись, которая может принимать логическое значение «истина» или «ложь». При таком определении среди логических выражений необходимо различать:
- выражения, которые используют операции сравнения («больше», «меньше», «равно», «не равно» и т. п.) и принимают логические значения (например, выражение а > b , где а = 5 и b = 7, равно значению «ложь»);
- непосредственные логические выражения, связанные с логическими величинами и логическими операциями (например, A ∨ В ∧ С, где А = истина, B = ложь и C = истина).
Логические выражения могут включать в себя функции, алгебраические операции, операции сравнения и логические операции. В этом случае приоритет выполнения действий следующий:
- вычисление существующих функциональных зависимостей;
- выполнение алгебраических операций (вначале умножение и деление, затем вычитание и сложение);
- выполнение операций сравнения (в произвольном порядке);
- выполнение логических операций (вначале операции отрицания, затем операции логического умножения, логического сложения, последними выполняются операции импликации и эквивалентности).
В логическом выражении могут использоваться скобки, которые изменяют порядок выполнения операций.
Пример. Найти значение выражения:
$1 ≤ a ∨ A ∨ sin(π/a – π/b) < 1 ∧ ¬B ∧ ¬(b^a + a^b > a + b ∨ A ∧ B)$ для а = 2, b = 3, A = истина, В = ложь.
Решение. Порядок подсчета значений:
1) ba + ab > a + b, после подстановки получим: 32 + 23 > 2 + 3, т. е. 17 > 2 + 3 = истина;
2) A ∧ B = истина ∧ ложь = ложь.
Следовательно, выражение в скобках равно (ba + ab > a + b ∨ A ∧ B) = истина ∨ ложь = истина;
3) 1≤ a = 1 ≤ 2 = истина;
4) sin(π/a – π/b) < 1 = sin(π/2 – π/3) < 1 = истина.
После этих вычислений окончательно получим: истина ∨ А ∧ истина ∧ ¬В ∧ ¬истина.
Теперь должны быть выполнены операции отрицания, затем логического умножения и сложения:
5) ¬В = ¬ложь = истина; ¬истина = ложь;
6) A ∧ истина ∧ истина ∧ ложь = истина ∧ истина ∧ истина ∧ ложь = ложь;
7) истина ∨ ложь = истина.
Таким образом, результат логического выражения при заданных значениях— «истина».
Примечание. Учитывая, что исходное выражение есть, в конечном итоге, сумма двух слагаемых, и значение одного из них 1 ≤ a = 1 ≤ 2 = истина, без дальнейших вычислений можно сказать, что результат для всего выражения тоже «истина».
Тождественные преобразования логических выражений
В алгебре логики выполняются основные законы, позволяющие производить тождественные преобразования логических выражений.
| Закон | Для ∨ | Для ∧ |
| Переместительный | A ∨ B = B ∨ A | A ∧ B = B ∧ A |
| Сочетательный | A ∨ (B ∨ C) = (B ∨ A) ∨ C | A ∧ (B ∧ C) = (A ∧ B) ∧ C |
| Распределительный | A ∧ (B ∨ C) = (A ∧ B) ∨ (A ∧ C) | A ∨ B ∧ C = (A ∨ B) ∧ (A ∨ C) |
| Правила де Моргана | ${A ∨ B}↖{-}$ = $A↖{-} ∧ B↖{-}$ | ${A ∧ B}↖{-}$ = $A↖{-} ∨ B↖{-}$ |
| Идемпотенции | A ∨ A = A | A ∧ A = A |
| Поглощения | A ∨ A ∧ B = A | A ∧ (A ∨ B) = A |
| Склеивания | (A ∧ B) ∨ (A↖{-} ∧ B) = B | (A ∨ B) ∧ (A↖{-} ∨ B) = B |
| Операция переменной с ее инверсией | $A ∨ A↖{-}$ = 1 | $A ∧ A↖{-}$ = 0 |
| Операция с константами | A ∨ 0 = A A ∨ 1 = 1 |
A ∧ 1 = A A ∧ 0 = 0 |
| Двойного отрицания | $A↖{=}$ = A |
Доказательства этих утверждений производят на основании построения таблиц истинности для соответствующих записей.
Равносильные преобразования логических формул имеют то же назначение, что и преобразования формул в обычной алгебре. Они служат для упрощения формул или приведения их к определенному виду путем использования основных законов алгебры логики. Под упрощением формулы, не содержащей операций импликации и эквивалентности, понимают равносильное преобразование, приводящее к формуле, которая содержит либо меньшее по сравнению с исходной число операций, либо меньшее число переменных.
Некоторые преобразования логических формул похожи на преобразования формул в обычной алгебре (вынесение общего множителя за скобки, использование переместительного и сочетательного законов и т. п.), тогда как другие преобразования основаны на свойствах, которыми не обладают операции обычной алгебры (использование распределительного закона для конъюнкции, законов поглощения, склеивания, де Моргана и др.).
Рассмотрим на примерах некоторые приемы и способы, применяемые при упрощении логических формул:
1) X1 ∧ X2 ∨ X1 ∧ X2 ∪ ¬X1 ∧ X2 = X1 ∧ X2 ∨ ¬X1 ∧ X2 = (X1 ∨ ¬X1) ∧ X2 = 1 ∧ X2 = X2 .
Для преобразования здесь можно применить закон идемпотенции, распределительный закон; операцию переменной с инверсией и операцию с константой.
2) X1 ∨ X1 ∧ X2 = X1 ∨ (1 ∨ 1 ∧ X2) = X1 ∨ (1 ∨ X2) = X1 .
Здесь для упрощения применяется закон поглощения.
3) ¬(X1 ∧ X2) ∨ X2 = (¬X1 ∨ ¬X2) ∨ X2 = ¬X1 ∨ ¬X2 ∨ X2 = ¬X1 ∨ 1 = 1 .
При преобразовании применяются правило де Моргана, операция переменной с ее инверсией, операция с константой
Примеры решения задач
Пример 1. Найти логическое выражение, равносильное выражению A ∧ ¬(¬B ∨ C) .
Решение. Применяем правило де Моргана для В и С: ¬(¬B ∨ C) = B ∧ ¬C .
Получаем выражение, равносильное исходному: A ∧ ¬(¬B ∨ C) = A ∧ B ∧ ¬C .
Ответ: A ∧ B ∧ ¬C.
Пример 2. Указать значение логических переменных А, В, С, для которых значение логического выражения (A ∨ B) → (B ∨ ¬C ∨ B) ложно.
Решение. Операция импликации ложна только в случае, когд а из истинной посылки следует ложь. Следовательно, для заданного выражения посылка A ∨ B должна принимать значение «истина», а следствие, т. е. выражение B ∨ ¬C ∨ B , — «ложь».
1) A ∨ B — результат дизъюнкции — «истина», если хотя бы один из операндов — «истина»;
2) B ∨ ¬C ∨ B — выражение ложно, если все слагаемые имеют значение «ложь», т. е. В — «ложь»; ¬C — «ложь», а следовательно, переменная С имеет значение «истина»;
3) если рассмотреть посылку и учесть, что В — «ложь», то получим, что значение А — «истина».
Ответ: А — истина, В — ложь, С — истина.
Пример 3. Каково наибольшее целое число X, при котором истинно высказывание (35 < X · X) → (X < (X – 3)) ?
Решение. Запишем таблицу истинности для операции импликации:
| A | B | A → B |
| 1 | 0 | 0 |
| 0 | 1 | 1 |
| 0 | 0 | 1 |
| 1 | 1 | 1 |
Выражение X < (X – 3) ложно при любых положительных значениях X. Следовательно, для того чтобы результатом импликации была «истина», необходимо и достаточно, чтобы выражение 35 < X · X также было ложно. Максимальное целое значение X, для которого 35 < X · X ложно, равно 5.
Ответ: X = 5.
Использование логических выражений для описания геометрических областей
Логические выражения могут быть использованы для описания геометрических областей. В этом случае задача формулируется так: записать для заданной геометрической области такое логическое выражение, которое принимает значение «истина» для значений x, y тогда и только тогда, когда любая точка с координатами (x; y) принадлежит геометрической области.
Рассмотрим описание геометрической области с помощью логического выражения на примерах.
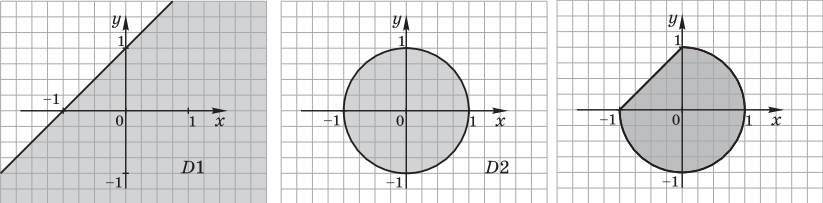
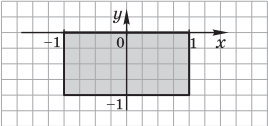
Пример 1. Задано изображение геометрической области. Записать логическое выражение, описывающее множество точек, принадлежащих ей.
1) 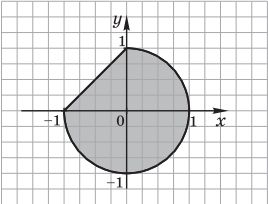
Решение. Заданную геометрическую область можно представить в виде набора следующих областей: первая область — D1 — полуплоскость ${x}/{-1} +{y}/{1} ≤ 1$, вторая — D2 — круг с центром в начале координат $x^2 + y^2 ≤ 1$. Их пересечение D1 $∩$ D2 представляет собой искомую область.
Результат: логическое выражение ${x}/{-1}+{y}/{1} ≤ 1 ∧ x^2 + y^2 ≤ 1$.
2)
Эту область можно записать так: |x| ≤ 1 ∧ y ≤ 0 ∧ y ≥ -1 .
Примечание. При построении логического выражения используются нестрогие неравенства, а это значит, что границы фигур также принадлежат заштрихованной области. Если использовать строгие неравенства, то границы учитываться не будут. Границы, не принадлежащие области, обычно изображаются пунктиром.
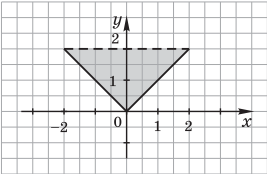
Можно решить обратную задачу, а именно: нарисовать область для заданного логического выражнения.
Пример 2. Нарисовать и заштриховать область, для точек которой выполняется логическое условие y ≥ x ∧ y + x ≥ 0 ∧ y < 2 .
Решение. Искомая область представляет собой пересечение трех полуплоскостей. Строим на плоскости (x, y) прямые y = x; y = –x; y = 2. Это границы области, причем последняя граница y = 2 не принадлежит области, поэтому ее наносим пунктирной линией. Для выполнения неравенства y ≥ x нужно, чтобы точки находились слева от прямой y = x, а неравенство y = –x выполняется для точек, которые находятся справа от прямой y = –x. Условие y < 2 выполняется для точек, лежащих ниже прямой y = 2. В результате получим область, которая изображена на рис.:
Использование логических функций для описания электрических схем
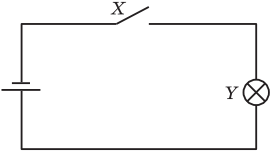
Логические функции очень удобны для описания работы электрических схем. Так, для схемы, представленной на рис., где значение переменной X — это состояние выключателя (если он включен, значение X — «истина», а если выключен — «ложь»), это значение Y — это состояние лампочки (если она горит — значение «истина», а если нет — «ложь»), логическая функция запишется так: Y = X . Функцию Y называют функцией проводимости.
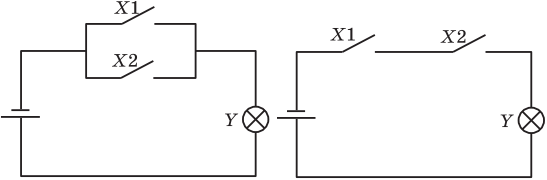
Для схемы, представленной на рис., логическая функция Y имеет вид: Y = X1 ∪ X2, т. к. достаточно одного включенного выключателя, чтобы горела лампочка. В схеме на рис., для того чтобы горела лампочка, должны быть включены оба выключателя, следовательно, функция проводимости имеет вид: Y = X1 ∧ X2 .
Для более сложной схемы функция проводимости будет иметь вид: Y = (X11 ∨ (X12 ∧ X13)) ∧ X2 ∧ (X31 ∨ X32).
Схема также может содержать контакты на замыкание. В этом случае размыкаемый контакт как выключатель обеспечивает загорание лампочки, когда кнопка отпущена, а не нажата. Для таких схем размыкающий выключатель описывается отрицанием.
Две схемы называются равносильными, если через одну из них ток проходит тогда, когда он проходит и через другую. Из двух равносильных схем более простой считается схема, функция проводимости которой содержит меньшее число элементов. Задача нахождения наиболее простых схем среди равносильных очень важна.
Использование аппарата алгебры логики при проектировании логических схем
Математический аппарат алгебры логики очень удобен для описания того, как функционируют аппаратные средства компьютера. Любая информация при обработке на компьютере представляется в двоичной форме, т. е. кодируется некоторой последовательностью 0 и 1. Обработку двоичных сигналов, соответствующих 0 и 1, выполняют в компьютере логические элементы. Логические элементы, которые выполняют основные логические операции И, ИЛИ, НЕ, представлены на рис.
Условные обозначения логических элементов являются стандартными и используются при составлении логических схем компьютера. С помощью этих схем можно реализовать любую логическую функцию, описывающую работу компьютера.
Технически компьютерный логический элемент реализуется в виде электрической схемы, которая представляет собой соединение различных деталей: диодов, транзисторов, резисторов, конденсаторов. На вход логического элемента, который называют также вентилем, поступают электрические сигналы высокого и низкого уровней напряжения, на выход выдается один выходной сигнал также либо высокого, либо низкого уровня. Эти уровни соответствуют одному из состояний двоичной системы: 1 — 0; ИСТИНА — ЛОЖЬ. Каждый логический элемент имеет свое условное обозначение, которое выражает его логическую функцию, но не указывает на то, какая именно электронная схема в нем реализована. Это упрощает запись и понимание сложных логических схем. Работу логических схем описывают с помощью таблиц истинности. Условное обозначение на схеме ИЛИ знак «1» — от устаревшего обозначения дизъюнкции как «>=1» (значение дизъюнкции равно 1, если сумма двух операндов больше или равна 1). Знак «&» на схеме И является сокращенной записью английского слова and.
Из логических элементов составляются электронные логические схемы, выполняющие более сложные логические операции. Набор логических элементов, состоящий из элементов НЕ, ИЛИ, И, с помощью которых можно построить логическую структуру любой сложности, называется функционально полным.
Построение таблиц истинности логических выражений
Для логической формулы всегда можно записать таблицу истинности, т. е. представить заданную логическую функцию в табличном виде. В этом случае таблица должна содержать все возможные комбинации аргументов функции (формулы) и соответствующие значения функции (результаты формулы на заданном наборе значений).
Удобной формой записи при нахождении значений функции является таблица, содержащая, кроме значений переменных и значений функции, также значения промежуточных вычислений. Рассмотрим пример построения таблицы истинности для формулы ${X1}↖{-} ∧ X2 ∨ {X1 ∨ X2}↖{-} ∨ X1$.
| X1 | X2 | ${X1}↖{-}$ | ${X1}↖{-}$ X2 | X1 ∧ X2 | ${X1 ∨ X2}↖{-}$ | ${X1}↖{-}$ ∧ X2 ∨ ${X1 ∨ X2}↖{-}$ | ${X1}↖{-}$ ∧ X2 ∨ ${X1 ∨ X2}↖{-}$ ∨ X1 |
| 1 | 1 | 0 | 0 | 1 | 0 | 0 | 1 |
| 1 | 0 | 0 | 0 | 1 | 0 | 0 | 1 |
| 0 | 1 | 1 | 1 | 1 | 0 | 1 | 1 |
| 0 | 0 | 1 | 0 | 0 | 1 | 1 | 1 |
Если функция принимает значение 1 при всех наборах значений переменных, она является тождественно-истинной; если при всех наборах входных значений функция принимает значение 0, она является тождественно-ложной; если набор выходных значений содержит как 0, так и 1, функция называется выполнимой. Приведенный выше пример является примером тождественно-истинной функции.
Зная аналитическую форму логической функции, всегда можно перейти к табличной форме логических функций. С помощью заданной таблицы истинности можно решить обратную задачу, а именно: для заданной таблицы построить аналитическую формулу логической функции. Различают две формы построения аналитической зависимости логической функции по таблично заданной функции.
1. Дизъюнктивно нормальная форма (ДНФ) — сумма произведений, образованных из переменных и их отрицаний для ложных значений.
Алгоритм построения ДНФ следующий:
- в таблице истинности функции выбирают наборы аргументов, для которых логические формы равны 1 («истина»);
- все выбранные логические наборы как логические произведения аргументов записывают, последовательно соединив их между собой операцией логической суммы (дизъюнкции);
- для аргументов, которые являются ложными, в построенной записи проставляют операцию отрицания.
Пример. Построить функцию, определяющую, что первое число равно второму, используя метод ДНФ. Таблица истинности функции имеет вид
| X1 | X2 | F(X1, X2) |
| 1 | 1 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 0 | 0 | 1 |
Решение. Выбираем наборы значений аргументов, в которых функция равна 1. Это первая и четвертая строки таблицы (строку заголовка при нумерации не учитываем).
Записываем логические произведения аргументов этих наборов, объединив их логической суммой: X1 ∧ X2 ∨ X1 ∧ X2 .
Записываем отрицание относительно аргументов выбранных наборов, имеющих ложное значение (четвертая строка таблицы; второй набор в формуле; первый и второй элементы): X1 ∧ X2 ∨ ${X1}↖{-}$ ∧ ${X2}↖{-}$.
Ответ: F(X1, X2) = X1 ∧ X2 ∨ ${X1}↖{-}$ ∧ ${X2}↖{-}$.
2. Конъюнктивно нормальная форма (КНФ) — произведение сумм, образованных из переменных и их отрицаний для истинных значений.
Алгоритм построения КНФ следующий:
- в таблице истинности выбирают наборы аргументов, для которых логические формы равны 0 («ложь»);
- все выбранные логические наборы как логические суммы аргументов записывают последовательно, соединив их между собой операцией логического произведения (конъюнкции);
- для аргументов, которые являются истинными, в построенной записи проставляют операцию отрицания.
Примеры решения задач
Пример 1. Рассмотрим предыдущий пример, т. е. построим функцию, определяющую, что первое число равно второму, используя метод КНФ. Для заданной функции ее таблица истинности имеет вид
| X1 | X2 | F(X1, X2) |
| 1 | 1 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 0 | 0 | 1 |
Решение. Выбираем наборы значений аргументов, в которых функция равна 0. Это вторая и третья строки (строку заголовка при нумерации не учитываем).
Записываем логические суммы аргументов этих наборов, объединив их логическим произведением: X1 ∨ X2 ∧ X1 ∨ X2 .
Записываем отрицание относительно аргументов выбранных наборов, имеющих истинное значение (вторая строка таблицы, первый набор формулы, второй элемент; для третьей строки, а это второй набор формулы, первый элемент): X1 ∨ ${X2}↖{-}$ ∧ ${X1}↖{-}$ ∨ X2.
Таким образом, получена запись логической функции в КНФ.
Ответ: X1 ∨ ${X2}↖{-}$ ∧ ${X1}↖{-}$ ∨ X2.
Полученные двумя методами значения функций являются эквивалентными. Для доказательства этого утверждения используем правила логики: F(X1, X2) = X1 ∨ ${X2}↖{-}$ ∧ ${X1}↖{-}$ ∨ X2 = X1 ∧ ${X1}↖{-}$ ∨ X1 ∧ X2 ∨ ${X2}↖{-}$ ∧ ${X1}↖{-}$ ∨ ${X2}↖{-}$ ∧ X2 = 0 ∨ X1 ∨ X2 ∨ ${X2}↖{-}$ ∧ ${X1}↖{-}$ ∨ 0 = X1 ∧ X2 ∨ ${X1}↖{-}$ ∧ ${X2}↖{-}$.
Пример 2. Построить логическую функцию для заданной таблицы истинности:
| X1 | X2 | F(X1, X2) |
| 1 | 1 | 1 |
| 1 | 0 | 0 |
| 0 | 1 | 1 |
| 0 | 0 | 0 |
Решение. Используем алгоритм ДНФ для построения исходной функции:
| X1 | X2 | F(X1, X2) | ||
| 1 | 1 | 1 | • | X1 ∧ X2 |
| 1 | 0 | 0 | ||
| 0 | 1 | 1 | • | ${X1}↖{-}$ ∧ X2 |
| 0 | 0 | 0 |
Искомая формула: X1 ∧ X2 ∨ ${X1}↖{-}$ ∧ X2 .
Ее можно упростить: X1 ∧ X2 ∨ ${X1}↖{-}$ ∧ X2 = X2 ∧ (X1 ∨ ${X1}↖{-}$) = X2 ∧ 1 = X2.
Пример 3. Для приведенной таблицы истинности построить логическую функцию, используя метод ДНФ.
| X1 | X2 | X3 | F(X1, X2, X3) | ||
| 1 | 1 | 1 | 1 | • | X1 ∧ X2 ∧ X3 |
| 1 | 0 | 1 | 0 | ||
| 0 | 1 | 1 | 1 | • | ${X1}↖{-}$ ∧ X2 ∧ X3 |
| 0 | 0 | 1 | 0 | ||
| 1 | 1 | 0 | 1 | • | X1 ∧ X2 ∧ ${X3}↖{-}$ |
| 1 | 0 | 0 | 1 | • | X1 ∧ ${X2}↖{-}$ ∧ ${X3}↖{-}$ |
| 0 | 1 | 0 | 0 | ||
| 0 | 0 | 0 | 0 |
Искомая формула: X1 ∧ X2 ∧ X ∨ ${X1}↖{-}$ ∧ X2 ∧ X3 ∨ X1 ∧ X2 ∧ ${X3}↖{-}$ ∪ X1 ∧ ${X2}↖{-}$ ∧ ${X3}↖{-}$.
Формула достаточно громоздка, и ее следует упростить:
X1 ∧ X2 ∧ X3 ∨ ${X1}↖{-}$ ∧ X2 ∧ X3 ∨ X1 ∧ X2 ∧ ${X3}↖{-}$ ∨ X1 ∧ ${X2}↖{-}$ ∧ ${X3}↖{-}$ = X2 ∧ X3 ∧ (X1 ∨ ${X1}↖{-}$) ∨ X1 ∧ ${X3}↖{-}$ ∧ (X2 ∨ ${X2}↖{-}$) = X2 ∧ X3 ∨ X1 ∧ ${X3}↖{-}$.
Таблицы истинности для решения логических задач
Составление таблиц истинности — один из способов решения логических задач. При использовании такого способа решения, условия, которые содержит задача, фиксируются с помощью специально составленных таблиц.
Примеры решения задач
Пример 1. Составить таблицу истинности для охранного устройства, которое использует три датчика и срабатывает при замыкании только двух из них.
Решение. Очевидно, что результатом решения будет таблица, в которой искомая функция Y(X1, X2, X3) будет иметь значение «истина», если какие-либо две переменные имеют значение «истина».
| X1 | X2 | X3 | Y(X1, X2, X3) |
| 1 | 1 | 1 | 0 |
| 1 | 1 | 0 | 1 |
| 1 | 0 | 1 | 1 |
| 1 | 0 | 0 | 0 |
| 0 | 1 | 1 | 1 |
| 0 | 1 | 0 | 0 |
| 0 | 0 | 1 | 0 |
| 0 | 0 | 0 | 0 |
Пример 2. Составить расписание уроков на день, учитывая, что урок информатики может быть только первым или вторым, урок математики — первым или третьим, а физики — вторым или третьим. Возможно ли составить расписание, удовлетворив всем требованиям? Сколько существует вариантов расписания?
Решение. Задача легко решается, если составить соответствующую таблицу:
| 1-й урок | 2-й урок | 3-й урок | |
| Информатика | 1 | 1 | 0 |
| Математика | 1 | 0 | 1 |
| Физика | 0 | 1 | 1 |
Из таблицы видно, что существуют два варианта искомого расписания:
- математика, информатика, физика;
- информатика, физика, математика.
Пример 3. В спортивный лагерь приехали трое друзей — Петр, Борис и Алексей. Каждый из них увлекается двумя видами спорта. Известно, что таких видов спорта шесть: футбол, хоккей, лыжи, плавание, теннис, бадминтон. Также известно, что:
- Борис — самый старший;
- играющий в футбол младше играющего в хоккей;
- играющие в футбол и хоккей и Петр живут в одном доме;
- когда между лыжником и теннисистом возникает ссора, Борис мирит их;
- Петр не умеет играть ни в теннис, ни в бадминтон.
Какими видами спорта увлекается каждый из мальчиков?
Решение. Составим таблицу и отразим в ней условия задачи, заполнив соответствующие клетки цифрами 0 и 1 в зависимости от того, ложно или истинно соответствующее высказывание.
Так как видов спорта шесть, получается, что все мальчики увлекаются разными видами спорта.
Из условия 4 следует, что Борис не увлекается ни лыжами, ни теннисом, а из условий 3 и 5, что Петр не умеет играть в футбол, хоккей, теннис и бадминтон. Следовательно, любимые виды спорта Петра — лыжи и плавание. Занесем это в таблицу, а оставшиеся клетки столбцов «Лыжи» и «Плавание» заполним нулями.
| Футбол | Хоккей | Лыжи | Плавание | Бадминтон | Теннис | |
| Петр | 0 | 0 | 1 | 1 | 0 | 0 |
| Борис | 0 | 0 | 0 | |||
| Алексей | 0 | 0 |
Из таблицы видно, что в теннис может играть только Алексей.
Из условий 1 и 2 следует, что Борис не футболист. Таким образом, в футбол играет Алексей. Продолжим заполнять таблицу. Внесем в пустые ячейки строки «Алексей» нули.
| Футбол | Хоккей | Лыжи | Плавание | Бадминтон | Теннис | |
| Петр | 0 | 0 | 1 | 1 | 0 | 0 |
| Борис | 0 | 0 | 0 | 0 | ||
| Алексей | 1 | 0 | 0 | 0 | 0 | 1 |
Окончательно получаем, что Борис увлекается хоккеем и бадминтоном. Итоговая таблица будет выглядеть следующим образом:
| Футбол | Хоккей | Лыжи | Плавание | Бадминтон | Теннис | |
| Петр | 0 | 0 | 1 | 1 | 0 | 0 |
| Борис | 0 | 1 | 0 | 0 | 1 | 0 |
| Алексей | 1 | 0 | 0 | 0 | 0 | 1 |
Ответ: Петр увлекается лыжами и плаванием, Борис играет в хоккей и бадминтон, а Алексей занимается футболом и теннисом.
Алгебра логики помогает нам понять внутреннее устройство компьютера. Ты уже знаешь, что компьютер обрабатывает информацию только в двоичном коде. Логика поможет тебе понять, как взаимодействуют между собой два состояния: (0) и (1). Процессор компьютера работает за счёт выполнения логических операций, но о них ты узнаешь позже.
Высказывание — это повествовательное предложение, о котором можно сказать, истинно оно или ложно.
Например:
7×8=56
,
26>4
, «Осенние месяцы: сентябрь, октябрь, ноябрь», «Графический планшет — это устройство ввода информации» — это всё истинные высказывания.
«Земля имеет форму квадрата», «Монитор — это устройство для ввода информации»,
3>21
,
15−6=10
— это ложные высказывания.
Высказываниями не могут быть восклицательные и побудительные предложения, определения, уравнения (т. к. там есть переменные), односложные утверждения — «Он хороший» (не для всех непонятный он может быть хорошим).
В алгебре логики высказывания обозначаются латинскими буквами.
Для алгебры логики содержание высказывания не играет никакой роли, главным здесь является, истинно это высказывание или ложно.
Если высказывание истинно, то оно равно (1). Если ложно, то (0).
Например, (A) (=) «Монитор — это устройство для вывода информации» можно записать как
A=1
.
Высказывания могут быть простыми и сложными. Простые состоят из одного высказывания, а сложные — из нескольких высказываний, объединённых логическими операциями.
Например:
(A) (=) «Маша поёт в ансамбле»;
(B) (=) «Маша танцует народные танцы».
Если объединить эти два простых высказывания в одно сложное, можно получить следующее:
(A) или (B) (=) «Маша поёт в ансамбле ИЛИ Маша танцует народные танцы»;
(A) и (B) (=) «Маша поёт в ансамбле И Маша танцует народные танцы».
Подумай! Какая разница между первым и вторым сложными высказываниями?
На этом уроке мы с вами
вспомним, что такое логические величины, проанализируем такие логические
операции, как конъюнкция, дизъюнкция и инверсия. Также поработаем с логическими
выражениями.
В курсе информатики вы
уже проходили логические величины, выражения и операции. Давайте вспомним, что
такое высказывание. Высказывание – это повествовательное предложение на
любом языке, в котором что-либо утверждается или отрицается. То есть любое
высказывание можно определить, как истинное или ложное.
Рассмотрим следующие
предложения:
·
Клавиатура
предназначена для ввода текстовой информации и команд управления компьютером.
·
При
приёме информации происходит процесс переноса информации от источника к
приёмнику.
Эти предложения будут
относится к высказываниям, так как можно точно сказать истины они или
ложны. Первое высказывание является истинным, а второе – ложным.
А вот следующие
предложения:
·
Который
час?
·
Не
поднимай телефон!
Не являются высказываниями,
так как в определении сказано, что высказывание – это повествовательно
предложение.
Для построения
высказываний могут использоваться знаки различных формальных языков:
математики, физики, химии и других.
Числовые выражения не
являются высказываниями. Но, в то же время, если из двух выражений
составить одно и соединить их знаком равенства или неравенства, то новое
выражение будет высказыванием.
Логические высказывания
бывают простыми и составными.
Простое высказывание
– это высказывание, в котором никакая его часть сама не является высказыванием.
Сложное
или же составное высказывание – это высказывание, которое строится
из простых с помощью логических операций.
Логические величины
– это понятия, выражаемые словами Истина (True),
Ложь (False). Истинность
высказывания выражается через логические величины.
Логическая переменная
– это символически обозначенная логическая величина. То есть логическая
величина может обозначаться, например, буквой латинского алфавита. Сама же
буква будет являться переменной логической величины. В свою очередь, она может
принимать только значение Истина или Ложь.
Логическое выражение
– это простое или сложное высказывание. Сложное высказывание, как мы уже знаем,
строиться из простых при помощи логических операций (связок).
К логическим операциям
относятся конъюнкция, дизъюнкция и инверсия (отрицание). Давайте рассмотрим
каждую логическую операцию.
Итак, первая логическая
операция – конъюнкция – логическое умножение.
Конъюнкция
– это логическая операция, которая объединяет два высказывания в одно новое,
которое будет являться ложным тогда, когда хотя бы одно из исходных
высказываний ложно. Конъюнкция – это двухместная операция, то есть в ней
должны присутствовать две логические переменные.
В естественном языке
конъюнкция соответствует союзу «И». В алгебре конъюнкция может обозначаться с
помощью нескольких знаков: знака амперсанда «&», знака конъюнкции «/», а
также знака умножения «·». В языках
программирования для обозначения конъюнкции используется английский союз «AND»,
знак амперсанда «&» или же двойной знак амперсанда «&&».
Следующая операция – дизъюнкция.
Ещё её называют логическим сложением.
Дизъюнкция
– это логическая операция, которая объединяет два высказывания в одно новое,
которое будет истинным тогда, когда хотя бы одно исходное высказывание истинно.
Дизъюнкция также является двухместной операцией, то есть в ней должны
присутствовать две логические переменные.
В различных сферах
применения, дизъюнкция обозначается по-разному. В естественном языке это союз «ИЛИ».
В алгебре высказываний используется следующий знак: «V».
Или знак «+». В программировании в основном используется английское «OR». Но в
некоторых языках программирования дизъюнкция обозначается следующими знаками: «|»,
«||».
И последняя логическая
операция – инверсия – отрицание.
Отрицание
– это логическая операция, которая преобразует исходное высказывание в новое,
значение которого противоположно исходному. А вот отрицание является унарной
(одноместной) операцией.
Давайте посмотрим, как
обозначается инверсия в различных сферах её применения. В естественном языке
инверсии соответствуют речевой оборот «неверно, что» и частица «не». В алгебре
высказывания инверсия обозначается следующими знаками: «¬», «ˉ». А вот в
сфере программирования используется английское слово «NOT».
Давайте составим таблицу
истинности для всех логических операций. В ней И – это истина, Л – Ложь.
В первых двух столбцах
предоставлены всевозможные исходные данные А и B.
В третьем столбце будет
идти ¬А.
Как мы с вами знаем из
определения операция отрицания преобразует исходное выражение в новое, значение
которого противоположно исходному. То есть, если А было истинно, при отрицании
оно станет ложным. И наоборот, если выражение было ложным, то оно станет истинным.
Заполним третий столбец таблицы исходя из данных первого.
Далее идёт конъюнкция.
Здесь мы будем смотреть на значения, которые принимают выражения А и B.
Мы с вами знаем, что при конъюнкции новое высказывание будет являться ложным
тогда, когда хотя бы одно из исходных высказываний ложно. То есть, исходя из
данных нашей таблицы, в первой строке оба высказывания истины, значит и новое
будет истинно. А вот все остальные будут ложными, так как во второй строке
ложно высказывание B, в третьей – А, а в четвёртой
– оба.
И последний, пятый
столбец – дизъюнкция. Снова будем брать значения выражений А и B.
Новое высказывание будет истинным тогда, когда хотя бы одно исходное
высказывание истинно. Значит в первых трёх строках 5 столбца новые выражения
будут истинны, так как в первой строке истинны оба высказывания А и B,
во второй – А, в третьей – B.
А вот в четвёртой строке мы можем видеть, что значения А и B
оба ложны, значит и новое выражение будет ложно.
Логическая формула
– это формула, которая содержит только логические величины и знаки логических
операций. Результатом вычисления такой формулы будет являться истина или ложь.
При выполнении операций в
формуле нужно придерживаться следующего порядка:
1) отрицание;
2) конъюнкция;
3) дизъюнкция.
Но также стоит помнить,
что операции в скобках выполняются в первую очередь. Если же у нас идут
несколько равнозначных операций подряд, то выполнение их будет происходить
слева направо.
Давайте разберёмся на
примере. Вычислить значение логической формулы, если логические переменные
имеют следующие значения: А – Истина, B
– истина, C – Ложь.
A
& (B V
¬C) V
B
Перейдём к решению. Для
начала проставим над каждой операцией номер порядка, в котором она будет
исполняться.
В первую очередь будут
выполняться операции в скобках. А первой будет ¬C.
Затем дизъюнкция: B
V ¬C.
После этого будем
выполнять конъюнкцию: A
& (B V
¬C).
А затем оставшуюся
дизъюнкцию: A & (B
V ¬C)
V B.
Давайте запишем наши
вычисления пошагово:
Первое действие –
отрицание. Переменная С имеет значение Ложь. Смотрим на таблицу истинности и
видим, что при отрицании мы получим значение Истина.
Вторым действием
выполняется дизъюнкция. B =
Истине, ¬C =
Истине. При дизъюнкции двух истин мы получим истину.
Третье действие.
Конъюнкция. А = Истине, B V
¬C =
Истине. При конъюнкции двух истин мы получим истину.
И четвёртое действие –
дизъюнкция. При дизъюнкции двух истин снова получим истину.
Таким образом значение логической
формулы равно истине.
A
& (B V
¬C) V
B = ИСТИНА
А сейчас рассмотрим
логические функции на области числовых значений. Изучением числовых значение
занимается алгебра чисел, а логических функций – алгебра логики.
Две этих науки могут пересекаться в том случае, если необходимо проверить принадлежность
значений алгебраических выражений некоторому множеству. Если нам нужно,
например, проверить принадлежность значения числовой переменной А к множеству
отрицательных чисел, то это можно выразить через высказывание: «А меньше нуля».
В алгебре это можно записать следующим образом:
A < 0.
Такое выражение называется
в алгебре неравенством. А вот в логике – отношением.
Отношение A
< 0 может быть как истинным, так и ложным. Если А – отрицательная величина,
то отношение будет истинным, если же А – положительная число или же равно 0, то
оно – ложно.
Общий вид структуры отношения
такой:
<выражение
1> <знак отношения> <выражение 2>
Выражения 1 и 2 – это
некоторые математические выражения, которые принимаю числовые значения. В
частном случае выражение может представлять собой одну константу или одну
переменную величину. В отношениях могут использоваться следующие знаки: =, <>,
>, <, >=, <=.
Из вышесказанного можно
сделать вывод, что отношение – это простое высказывание, а значит, логическая
величина. Отношение может быть, как постоянным, например, –2<–1 – всегда
Истина, 2·2 = 5 – всегда ложно; так и переменной: x
> y, a2
+
b2 =
c2.
Если в отношение входят
переменные числовые величины, то и значение отношения будет логической
переменной.
Идём дальше. Отношение
также можно рассматривать как логическую функцию от числовых аргументов.
Например, F (x)
= x < 5.
Аргументы определены на
бесконечном множестве действительных чисел, а значения функции – на множестве, состоящем
из двух логических величин: Истина, Ложь. То есть аргумент может принимать
любое числовое значение, а функция только одно из двух: либо Истина, либо Ложь.
Логические функции также
называют термином предикат. В алгоритмах предикаты играют роль условий,
по которым строятся ветвления и циклы. Предикаты могут быть как простыми
логическими функциями, не содержащими логических операций, так и сложными,
содержащими логические операции.
Рассмотрим пример.
Записать предикат (логическую функцию), который будет принимать значение
Истина, если точка на координатной плоскости с координатами (x,y)
лежит внутри фигуры, ограниченной линиями. Рисунок предоставлен.
Перейдём к решению. Наша
фигура имеет 4 границы, которые можно описать с помощью следующих неравенств:
y
> –2;
y
< 2;
x
> –2;
x
< 2;
Из этих четырёх неравенств
можно составить систему.
Наш предикат будет равен
Истине, если точка с координатами (x,
y) будет находится внутри фигуры, то
есть будут удовлетворяться все четыре неравенства системы.
Таким образом все четыре
отношения должны быть одновременно истинными. Поэтому искомый результат будет
выглядеть следующим образом:
А сейчас давайте
рассмотрим логические выражения в языке Pascal.
Как мы с вами уже знаем,
в языке Pascal имеется логический тип данных. К логическим константам относятся
True (истина) и False
(ложь). Все логические переменные будут описываться при помощи типа boolean.
Операции отношения осуществляют сравнение двух операндов и определяют,
истинно или ложно соответствующее отношение между ними.
Давайте ещё раз вспомним,
какие знаки используются в отношениях: равно, не равно, больше, меньше, больше
либо равно, меньше либо равно. В языке программирования они будут выглядеть
следующим образом:
Также в программировании
логические операции записываются не так, как в алгебре логики. Отрицание – not,
конъюнкция (логическое умножение) – and,
дизъюнкция (логическое сложение) – or.
И ещё одна логическая операция – исключающее ИЛИ – xor.
Давайте рассмотрим
таблицу истинности для этих операций, а также заполним столбец для исключающего
ИЛИ. В таблице латинская буква T
обозначает True, а F
– False.
Итак, чтобы заполнить
столбец для исключающего ИЛИ, будем брать данные из первого и второго столбцов.
Исключающее ИЛИ
– это логическая операция, которая объединяет два высказывания в одно новое,
которое будет истинным тогда и только тогда, когда одно из исходных высказываний
истинно, а второе – ложно. Исходя из этого мы можем сделать вывод, что во
второй и третьей строках значение нового высказывания будет равно истине, так
как во второй строке высказывание А – истинно, B
– ложно. В третьей строке наоборот, А – ложно, B
– истинно. В первой и четвёртой строках будет значение – ложь.
Логическое выражение
может состоять из логических констант и переменных, отношений, логических
операций. Также оно будет принимать одно из двух значение: True
или
False.
Давайте запишем выражение
на языке Pascal. А начнём с примера,
который разбирали выше.
A
& (B V
¬C) V
B
Он будет выглядеть следующим
образом:
A
and (B or (not C)) or B
В этом примере переменные
А, B и C
являются переменными типа boolean.
Логические операции выполняются
в следующем порядке:
1) not;
2) and;
3) or/xor.
Если же нам нужно, чтобы
в первую очередь выполнилась операция, которая имеет более низкий приоритет,
необходимо заключать её в скобки. Операции отношения имеют самый низкий
приоритет, поэтому если операндами логической операции являются отношения, то
их нужно заключать в круглые скобки. Например, математическое неравенство:
5
< A ≤ 42.
На языке Pascal
будет
записано так:
(A
> 5) and (A
<= 42).
Также есть такая
логическая функция, как odd
(A). Она принимает значение True,
если значение целочисленного аргумента А является нечётным, и значение False,
если значение аргумента А чётное.
При записи сложного
логического выражения (предиката) нужно учитывать приоритеты арифметических,
логических операций и операций отношений.
1. Арифметические
операции:
1) –
(минус унарный);
2) *,
/;
3) +,
–.
2. Логические
операции:
1) not;
2) and;
3) or,
xor.
3. Операции
отношения: =, <>, >,
<, >=, <=.
Вспомним предикат,
который мы составляли с вами чуть выше. Он выглядит следующим образом:
В нём операции отношений заключены
в скобки, так как они младше логических операций, но выполняться должны раньше.
Подведём итоги урока.
Сегодня мы с вами
вспомнили, что такое высказывание (суждение), логическая величина, логическое
выражение, а также какие бывают основные логические операции.
Также мы узнали, что
логические выражения в языке Pascal
могут принимать одно из двух значений: True
– истина или False – Ложь.
Изучили логические
операции в языке Pascal, а также
расставили приоритеты выполнения действий в логическом выражении на языке Pascal.