Основания правильной усеченной пирамиды представляют собой правильные многоугольники, зная стороны которых можно найти все остальные параметры, такие как внутренний угол, периметр, площадь, радиусы вписанной и описанной окружностей.
γ=180°(n-2)/n
P=n(a+b+d)
S_a=(na^2)/(4 tan〖(180°)/n〗 )
S_b=(nb^2)/(4 tan〖(180°)/n〗 )
r_a=a/(2 tan〖(180°)/n〗 )
r_b=b/(2 tan〖(180°)/n〗 )
R_a=a/(2 sin〖(180°)/n〗 )
R_b=a/(2 sin〖(180°)/n〗 )
Зная высоту усеченной пирамиды, можно найти ее боковое ребро и апофему, рассмотрев прямоугольные трапеции, соединяющие их через радиусы вписанной и описанной окружностей в основаниях. Из прямоугольных трапеций построив дополнительный прямоугольный треугольник, легко вычислить боковое ребро или апофему как гипотенузу, а также найти углы при основаниях. (рис. 50.3, 50.4)
f=√(h^2+(b/2-a/2)^2 )=√(h^2+(b-a)^2/4)
cosβ=(r_b-r_a)/f
α=180°-β
d=√(h^2+(R_b-R_a )^2 )
cosδ=(R_b-R_a)/d
ε=180°-δ
Чтобы найти площадь боковой поверхности, нужно вычислить площадь каждой грани усеченной пирамиды, а затем умножить полученное значение на количество сторон в основаниях. Вычислить площадь полной поверхности усеченной пирамиды, зная стороны и высоту, нужно, преобразовав высоту в апофему по приведенным выше формулам, и сложив площадь боковой поверхности с площадями оснований.
S_(б.п.)=nf (a+b)/2
S_(п.п.)=S_(б.п.)+S_(осн.1,2)=n(f (a+b)/2+a^2/(4 tan〖(180°)/n〗 )+b^2/(4 tan〖(180°)/n〗 ))
Объем усеченной пирамиды, зная стороны и высоту, равен одной трети высоты умноженной на сумму площадей оснований с радикалом из их произведения.
V=1/3 h(S_осн1+S_осн2+√(S_осн1 S_осн2 ))
Данный сайт находится в режиме тестирования, обо всех выявленных проблемах Вы можете сообщить на почту
Формулы усеченной пирамиды
Для расчёта всех основных параметров усеченной пирамиды воспользуйтесь калькулятором.
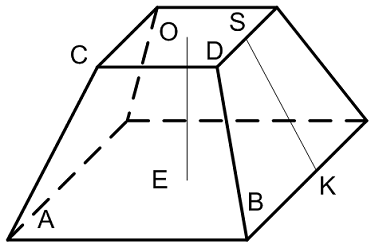
Площадь верхнего основания правильной усеченной пирамиды
$$
S_{верх.основ} = {N * CD^2 over 4 * tan(180/N)}
$$
Площадь нижнего основания правильной усеченной пирамиды
$$
S_{нижн.основ} = {N * AB^2 over 4 * tan(180/N)}
$$
Объём усеченной пирамиды
$$
V = {1 over 3} * OE * (S_{верх.основ} + sqrt{S_{верх.основ} * S_{нижн.основ}} + S_{нижн.основ})
$$
Апофема усеченной пирамиды
Так как боковая сторона усеченной пирамиды – это трапеция, то высота этой трапеции и будет апофемой усеченной пирамиды
$$
SK = sqrt{AC^2 – ({(AB – CD)^2 + AC^2 – BD^2 over 2 * (AB – CD)})^2}
$$
Площадь боковой поверхности
Площадью боковой поверхности усеченной пирамиды является сумма всех боковых сторон, каждая боковая сторона является трапецией
$$
S_{Бок.стороны} = {1 over 2} * SK * (CD + AB)
$$
ВИДЕОУРОК
Усечённой пирамидой ABCDA1B1C1D1 называется часть пирамиды SABCD, заключённая между её основанием и секущей плоскостью, параллельной основанию.

Основаниями усечённой пирамиды называются параллельные грани ABCD и A1B1C1D1 (ABCD – нижнее основание, A1B1C1D1 – верхнее основание).
Высотой усечённой пирамиды называется отрезок прямой, перпендикулярный её основаниям и заключённый между их плоскостями.
Усечённая пирамида называется правильной, если её основания – правильные многоугольники и прямая, соединяющая центры оснований, перпендикулярна плоскости оснований.
Апофемою правильной усечённой пирамиды называют высоту её боковой грани.
Свойства усечённой пирамиды.
Основания – подобные многоугольники.
Боковые грани – трапеции.
Отношение высоты к высоте пирамиды, из которой она получена, равно отношению разности сторон одной грани к длине нижнего основания этой самой грани.
Поверхность усечённой пирамиды.
Площадь боковой поверхности усечённой пирамиды равна сумме площадей её боковых граней.
Полная поверхность усечённой пирамиды равна сумме площади боковой поверхности и площадей оснований.
Боковая поверхность правильной усечённой пирамиды равна произведению полусуммы периметров оснований на апофему.

где Р и Р1 – периметры оснований, m – апофема усечённой пирамиды.
Правильная четырёхугольная усечённая пирамида.

Правильная треугольная усечённая пирамида.

Правильная шестиугольная усечённая пирамида.

ЗАДАЧА:
В правильной четырёхугольной усечённой пирамиде стороны оснований равны 5 и 11 дм, а диагональ пирамиды – 12 дм. Определите боковую поверхность пирамиды.
РЕШЕНИЕ:
В усечённой пирамиде АС1 имеем
А1В1 = В1С1 = С1D1 = D1А1 = 5 дм,
АВ = ВС = СD = DА = 11 дм и
А1С = 12 дм.
Найти боковую поверхность.

Из вершины А1 проведём А1N ⊥ AB и А1M ⊥ AC, тогда А1N – апофема пирамиды.
Боковая поверхность
Sбок = 1/2 (P + P1) × A1N.
где P = 4AB = 44
дм, а
P1 = 4A1B1 = 20
дм.
В квадратах АВСD и А1В1С1D1 по иіх сторонам определяем диагонали
АС = 11√͞͞͞͞͞2 (дм),
A1С1 = 5√͞͞͞͞͞5 (дм).
Рассмотрев равнобедренную трапецию АА1С1С, находим

и соответственно

Тогда из прямоугольного ∆ А1MC находим высоту пирамиды

Из равнобедренного прямоугольного ∆ AMN (∠ ANM = 90°), гипотенуза которого AM = 3√͞͞͞͞͞2 (дм), находим сторону

Апофему данной пирамиды найдём из прямоугольного

Подставляя найденные значения P, P1 и A1N в формулу боковой поверхности пирамиды, получим:
Sбок = 1/2 (44 + 20)×5 = 160 (дм2).
ОТВЕТ:
S = 160 дм2 = 1,6 м2.
ЗАДАЧА:
Высота правильной четырёхугольной усечённой пирамиды
равна 4
см. Стороны оснований равны 2
см и
8 см. Найдите площадь диагональных сечений.
РЕШЕНИЕ:
Начертим чертёж.
Диагональные сечения
AA1C1D и BB1D1D– равные равнобедренные трапеции с высотой ОО1 = h = 4 см и с основаниями
– диагоналями оснований АС и А1С1 та ВD и В1D1 соответственно. ABCD – квадрат, а поэтому
AC2 = AD2 + CD2 =
= 82 + 82 = 128,
AC = √͞͞͞͞͞128 = 8√͞͞͞͞͞2 (cм).
A1B1C1D1 – квадрат, а поэтому
A1C12 = A1D12 + C1D12 = 22 + 22 = 8,
A1C1 = √͞͞͞͞͞8 = 2√͞͞͞͞͞2 (cм).

ОТВЕТ: 20√͞͞͞͞͞2 (cм2)
ЗАДАЧА:
В правильной четырёхугольной усечённой пирамиде высота
равна 2
см, а стороны оснований – 3 см и 5
см. Найдите диагональ этой пирамиды.
РЕШЕНИЕ:
Начертим чертёж.
Диагональным сечением данной пирамиды
является равнобедренная трапеция АА1С1С.
Так как
А1С1 и АС –
диагонали квадратов, А1В1С1D1 и ABCD, то
А1С1 = А1В1 ∙ √͞͞͞͞͞2 = 3√͞͞͞͞͞2 (см) и
АС = АВ ∙ √͞͞͞͞͞2 = 5√͞͞͞͞͞2 (см).
Проведём
А1К ⊥
АС
и С1Н ⊥ АС. Тогда А1С1НК – прямоугольник
и А1С1 =
КН. Так что, прямоугольные треугольники АА1К и СС1Н равны по гипотенузе и катету.
Тогда,
АК = СН = 1/2 (АС – А1С1) =
= 1/2 (5√͞͞͞͞͞2 – 3√͞͞͞͞͞2) = √͞͞͞͞͞2 (см).
Тогда,
СК = АС – АК = 5√͞͞͞͞͞2 – √͞͞͞͞͞2 =
4√͞͞͞͞͞2 (см),
и по
теореме Пифагора в ∆ А1СК:

ОТВЕТ: 6 см
ЗАДАЧА:
В правильной четырёхугольной пирамиде плоскость, проведённая
параллельно основанию, делит высоту пирамиды пополам. Найдите сторону основания,
если площадь сечения равна 36 см2.
РЕШЕНИЕ:
Пусть SABCD – данная правильная пирамида,
основание – квадрат
ABCD, SO – высота, O –
точка пресечения диагоналей квадрата, φ – плоскость сечения, О1 –
точка пересечения φ и SO, φ ∥ (ABC), S = 36 cм2.
Поскольку φ ∥ (ABC),
то прямые пересечения 𝜑 и боковых граней параллельны соответственно рёбрам
основания:
A1B1 ∥ AB, B1C1 ∥ BC, C1D1 ∥ CD,
A1D1 ∥ AD, 𝜑 ⊥ SO,
можно рассмотреть гомотетию с центром S и коэффициентом

которая преобразует квадрат ABCD в квадрат
А1В1С1D1, стороны которого в два раза меньше, а
SABCD = 4SА1В1С1D1 = 4 ∙ 36 (см2).
SABCD = a2 = 4 ∙
36,
a = 2 ∙ 6
= 12 (см).
ОТВЕТ: 12 см
Задания к уроку 10
- Задание 1
- Задание 2
- Задание 3
Другие уроки:
- Урок 1. Прямые и плоскости в пространстве
- Урок 2. Прямая призма
- Урок 3. Наклонная призма
- Урок 4. Правильная призма
- Урок 5. Параллелепипед
- Урок 6. Прямругольный параллелепипед
- Урок 7. Куб
- Урок 8. Пирамида
- Урок 9. Правильная пирамида
- Урок 11. Цилиндр
- Урок 12. Вписанная и описанная призмы
- Урок 13. Конус
- Урок 14. Усечённый конус
- Урок 15. Вписанная и описанная пирамиды
- Урок 16. Сфера и шар
- Урок 17. Комбинация тел
Материал урока.
На прошлых уроках
мы работали с пирамидами. Давайте вспомним, какой многогранник называется
пирамидой, что такое правильная пирамида, вспомним свойства правильной пирамиды.
Многогранник, составленный из -угольника и
треугольников, называется пирамидой.
Пирамида называется правильной,
если ее основание – правильный многоугольник.
Площадь боковой поверхности правильной
пирамиды равна половине произведения периметра основания на апофему.
Все боковые ребра правильной пирамиды
равны, а боковые грани являются равными равнобедренными треугольниками.
Пусть нам дана
пирамида PA1A2…An. Проведем секущую плоскость β,
параллельную плоскости основания пирамиды и пусть эта плоскость пересекает
боковые ребра в точках B1,B2,…,
Bn.
Плоскость β
разбивает пирамиду на две фигуры: пирамиду PB1B2…Bn и многогранник. Многогранник, гранями которого являются n-угольники A1A2…An и B1B2…Bn, расположенные в параллельных плоскостях и n четырехугольников A1A2B2B1, A2A3B3B2,…, AnA1B1Bn называется
усеченной пирамидой.
Вокруг нас много
примеров усеченных пирамид. Вытяжка над кухонной плитой имеет форму усеченной
пирамиды.клавиши клавиатуры и другие предметы.
N-угольники
A1A2…An и B1B2…Bn называются соответственно верхним и нижним основанием.
Четырехугольники A1A2B2B1, A2A3B3B2,…, AnA1B1Bn называются боковыми
гранями.
Отрезки A1B1,…, AnBn называются боковыми рёбрами
усеченной пирамиды.
Усеченную пирамиду
обозначают так A1A2…AnB1B2…Bn. Возьмем на верхнем основании произвольную
точку C и из этой точки опустим перпендикуляр на нижнее
основание. Этот перпендикуляр называется высотой усеченной пирамиды.
Теперь давайте
докажем, что боковые грани усеченной пирамиды – это трапеции.
Для доказательства
рассмотрим грань A1A2B2B1. Понятно,
что для других боковых граней доказательство будет проводится аналогично.
Поскольку секущая
плоскость проводилась параллельно плоскости основания, то можно записать, что A1A2
параллельно B1B2.
Очевидно, что две другие стороны четырехугольника A1A2B2B1 не параллельны (они пересекаются в точке P). Получаем, что этот четырехугольник – трапеция. Очевидно,
что все остальные боковые грани тоже будут трапециями.
Как и в случае с
пирамидой, усеченная пирамида тоже может быть правильной.
Усеченная пирамида
называется правильной, если она получена сечением правильной пирамиды
плоскостью, параллельной основанию.
Основаниями
усеченной пирамиды являются правильные многоугольники, а боковые грани –
равнобедренные трапеции.
Высоты этих трапеций
называются апофемами.
Объединение боковых граней называется боковой
поверхностью усеченной пирамиды, а объединение всех граней называется полной
поверхностью усеченной пирамиды. Тогда площадью боковой поверхности
пирамиды называется сумма площадей ее боковых граней.
А площадью полной поверхности пирамиды называется
сумма площадей всех ее граней.
Теперь давайте
сформулируем и докажем теорему о площади боковой поверхности правильной
усеченной пирамиды.
Площадь боковой
поверхности правильной усеченной пирамиды равна произведению полусуммы
периметров основания на апофему.
Доказательство.
Запишем формулу для
нахождения площади боковой поверхности усеченной пирамиды.
Поскольку усеченная
пирамида правильная, значит, ее гранями будут равнобедренные трапеции.
Площадь равнобедренной
трапеции равна произведению полусуммы оснований на высоту. Высота боковой грани
есть ничто иное как апофема усеченной пирамиды.
Подставим все в
исходную формулу, вынесем половину апофемы за скобки, а в скобках сгруппируем
стороны по основаниям. Тогда получим, что площадь боковой поверхности будет
равна произведению полусуммы периметров оснований усеченной пирамиды на
апофему.
Что и
требовалось доказать.
Решим несколько
задач.
Задача. Стороны
оснований правильной усеченной четырехугольной пирамиды равны
и
. Высота пирамиды
равна . Найти площадь
боковой поверхности.
Решение.
Ответ. 120
см2
Решим еще одну
задачу.
Задача. Пирамида
пересечена плоскостью, параллельной основанию. Доказать что боковые ребра и
высота пирамиды делятся этой плоскостью на пропорциональные части.
Решение.
Что и
требовалось доказать.
Решим еще одну
задачу.
Задача. Правильная
треугольная пирамида с высотой
и стороной основания
равной рассечена плоскостью
, проходящей через
середину высоты
параллельно
основанию . Найти площадь
боковой поверхности полученной усеченной пирамиды.
Решение.
Ответ.
135 см2.
Подведем итоги
урока. Сегодня на уроке мы познакомились с такими понятиями как усеченная
пирамида, правильная усеченная пирамида. Рассмотрели свойства правильной
усеченной пирамиды. Решили несколько задач.
Этот онлайн-калькулятор поможет узнать не только площадь усеченной пирамиды, но и 18 дополнительных значений. Для этого должны быть известны всего 4 значения, такие как: длины сторон верхнего и нижнего основания, общее количество граней, а также один показатель на выбор из следующих: длина ребра, высота, апофема или площадь боковой поверхности усеченной пирамиды. Введя все необходимые значения и нажав на кнопку расчета, можно будет узнать объем усеченной пирамиды, площадь, высоту, угол сторон основания, длину всех ребер и другие величины. Благодаря развернутым формулам в ответах разобраться в расчетах по величинам фигуры не составит труда.
Введите данные:
Сторона верхнего основания (a) *
Сторона нижнего основания (b) *
Количество граней усеченной пирамиды (n) *
Значение ключевого показателя *
Округление:
* – обязательно заполнить