Как найти высоту через проекции сторон

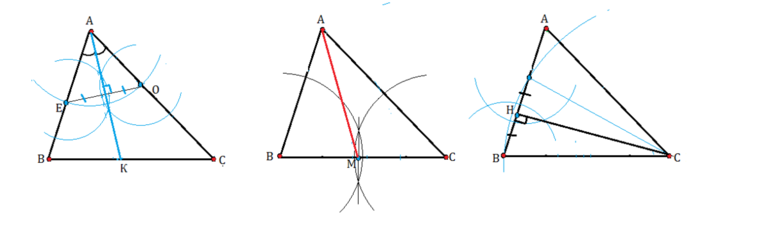
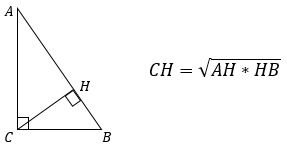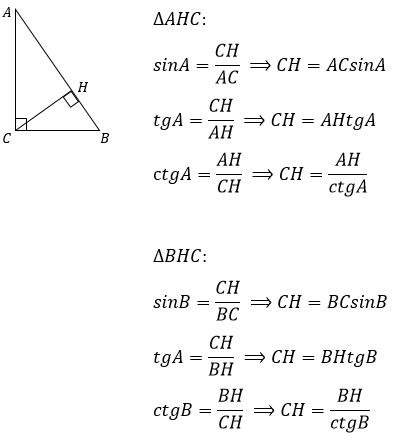Как построить высоту треугольника – основные способы

С применением циркуля

Если нужно нарисовать высоту (перпендикуляр к противоположной стороне) в произвольном треугольнике и измерить её, то лучше всего воспользоваться классическим методом построения. Он предусматривает использование циркуля в качестве основной рабочей принадлежности. Кроме этого, для работы понадобится лист бумаги, небольшая линейка, ластик и простой карандаш.

Способ начертить искомый отрезок:

• На листе бумаги чертят треугольник (можно нарисовать заранее, чтобы сэкономить время).
• Рисунок располагают так, чтобы вершина угла, из которого нужно начертить высоту, находилась сверху, а противоположная ему сторона фигуры была расположена горизонтально (по отношению к ученику).
• Иглу циркуля ставят в вершине любого угла у основания.
• Ножку с грифелем ставят в верхнюю точку треугольника, из которой проводится высота.
• Циркулем рисуют окружность и делают пометку в месте её пересечения с основанием фигуры.
• Аналогичным способом чертят круг из другого угла при основании. При этом важно определить новый радиус, который будет равен длине второй стороны треугольника.
• Делают пометку в месте пересечения начерченных окружностей.
• Ластиком стирают лишние линии, оставляя лишь поставленную точку.
• С помощью карандаша и линейки из неё проводят отрезок к вершине, который и будет высотой треугольника.
• Стирают линии, находящиеся под основанием.

Таким же способом можно с помощью циркуля построить высоту треугольника из любого другого угла.

С помощью линейки

Начертить и обозначить высоту можно и без циркуля. Для этого следует воспользоваться чертёжным угольником, 2 стороны которого перпендикулярны друг другу. Альтернативой этой школьной принадлежности могут стать 2 прямые линейки, соединённые между собой под прямым углом.

В остроугольном треугольнике

Провести высоту в треугольнике, где все углы острые (менее 90 градусов), довольно просто.

Чтобы справиться с этой задачей, нужно подготовить все необходимое и заранее начертить на бумаге геометрическую фигуру.

Правильная последовательность действий:

• Находят вершину, из которой хотят провести перпендикуляр.
• Совмещают угольник с противоположной стороной фигуры.
• Перемещают чертёжную принадлежность до тех пор, пока её перпендикулярная сторона не пройдёт через вершину.
• Простым карандашом проводят линию, которая и будет искомым отрезком.

В тупоугольной фигуре

Трёхсторонняя фигура, у которой один из углов тупой (более 90 градусов) имеет только 1 внутреннюю высоту. Для её проведения используют то же, что и в предыдущем случае.

Порядок действий:

• Располагают чертёж так, чтобы тупой угол оказался у основания.
• Угольник прикладывают к наибольшей стороне фигуры.
• Совмещают перпендикулярную сторону линейки с вершиной тупого угла.
• Соединяют 2 точки простым карандашом, получая искомую линию.

В прямоугольном и равнобедренном

В прямоугольном треугольнике нужно находить только 1 высоту. Две другие будут совпадать с катетами.

Пошаговая инструкция:

• Прикладывают одну из перпендикулярных сторон угольника к гипотенузе.
• Вторую сторону линейки совмещают с вершиной прямого угла.
• Проводят линию, которая будет высотой.

Проще всего проводить перпендикуляр из верхней точки равнобедренного треугольника.

Он будет совпадать с биссектрисой и медианой фигуры. Начертить его можно таким же способом, что и для остроугольной фигуры. Более простой метод предусматривает выполнение следующих действий:

• Линейкой замеряют длину основания.
• Эту величину делят на 2.
• Полученное значение откладывают от вершины одного из углов при основании.
• Отмечают середину стороны и соединяют её с верхней точкой фигуры.

Проведение высоты в треугольнике — это простая задача, с которой легко справится каждый ученик.

Для этого достаточно сделать чертёж геометрической фигуры и воспользоваться одним из существующих способов построения. Такая работа потребует минимум времени и не отнимет у школьника много сил.

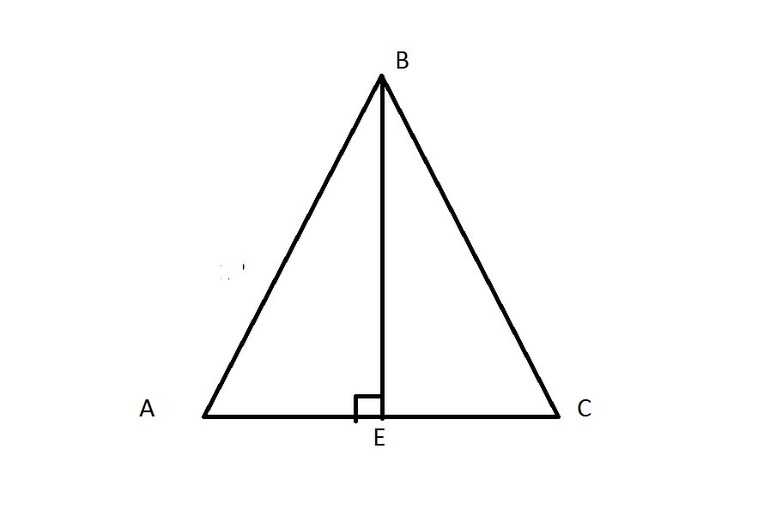
Проекции катетов на гипотенузу

Так как высота, проведенная к гипотенузе, представляет собой проведенный к ней перпендикуляр, то катеты — это наклонные, а отрезки гипотенузы, на которые делит ее высота — проекции катетов на гипотенузу прямоугольного треугольника.

В треугольнике ABC, изображенном на рисунке, AD — проекция катета AC на гипотенузу AB, BD — проекция катета BC на гипотенузу.

Катеты, их проекции на гипотенузу, гипотенуза и высота прямоугольного треугольника связаны между собой формулами.

1) Свойство высоты, проведенной к гипотенузе.

Высота прямоугольного треугольника, проведенная к гипотенузе, есть среднее геометрическое (среднее пропорциональное) между проекциями катетов на гипотенузу.

2) Свойства катетов прямоугольного треугольника.

Катет прямоугольного треугольника есть среднее геометрическое (среднее пропорциональное) между гипотенузой и проекцией этого катета на гипотенузу.

Свойства высоты прямоугольного треугольника

В данной публикации мы рассмотрим основные свойства высоты в прямоугольном треугольнике, а также разберем примеры решения задач по этой теме.

Примечание: треугольник называется прямоугольным, если один из его углов является прямым (равняется 90°), а два остальных – острые ( Содержание скрыть

Свойства высоты в прямоугольном треугольнике

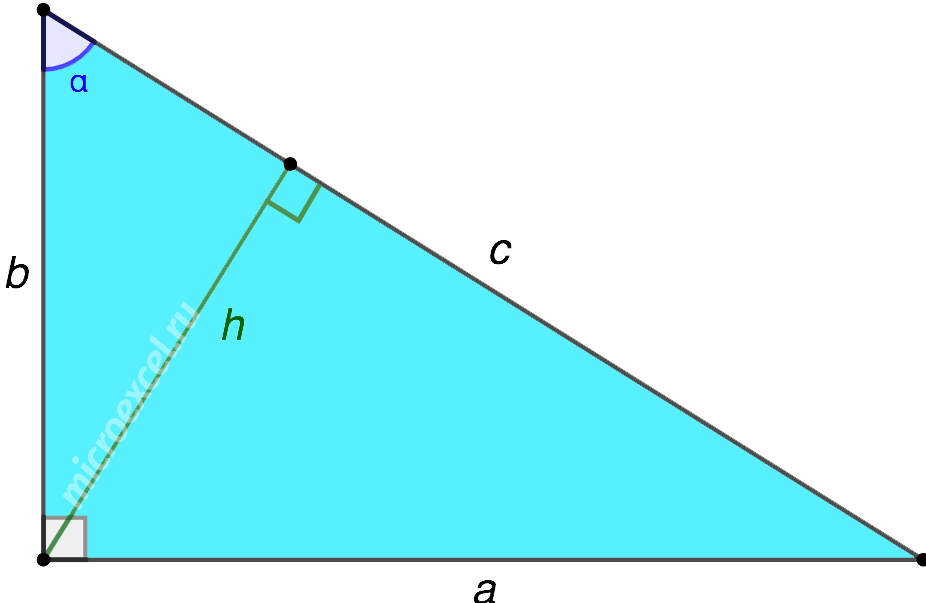
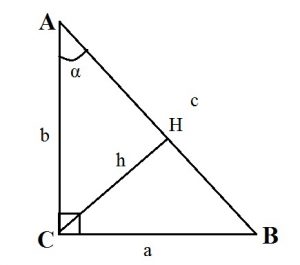
Свойство 1

В прямоугольном треугольнике две высоты (h₁ и h₂) совпадают с его катетами.

Третья высота (h₃) опускается на гипотенузу из прямого угла.

Свойство 2

Ортоцентр (точка пересечения высот) прямоугольного треугольника находится в вершине прямого угла.

Свойство 3

Высота в прямоугольном треугольнике, проведенная к гипотенузе, делит его на два подобных прямоугольных треугольника, которые также подобны исходному.

Аналогичным образом доказывается, что ∠ABD = ∠DAC.

Свойство 4

В прямоугольном треугольнике высота, проведенная к гипотенузе, вычисляется следующим образом:

1. Через отрезки на гипотенузе, образованные в результате ее деления основанием высоты:

2. Через длины сторон треугольника:

Данная формула получена из Свойства синуса острого угла в прямоугольном треугольнике (синус угла равен отношению противолежащего катета к гипотенузе) :

Примечание: к прямоугольному треугольнику, также, применимы общие свойства высоты, представленные в нашей публикации – “Высота в треугольнике abc: определение, виды, свойства”.

Пример задачи

Задача 1
Гипотенуза прямоугольного треугольника поделена высотой, проведенной к ней, на отрезки 5 и 13 см. Найдите длину этой высоты.

Решение
Воспользуемся первой формулой, представленной в Свойстве 4:

Задача 2
Катеты прямоугольного треугольника равны 9 и 12 см. Найдите длину высоты, проведенной к гипотенузе.

Решение
Для начала найдем длину гипотенузы по теореме Пифагора (пусть катеты треугольника – это “a” и “b”, а гипотенуза – “c”):
c 2 = a 2 + b 2 = 9 2 + 12 2 = 225.
Следовательно, с = 15 см.

Теперь можно применить вторую формулу из Свойства 4, рассмотренного выше:

[spoiler title=”источники:”]

[/spoiler]

Высота прямоугольного треугольника, проведенная к гипотенузе

Как и в любом треугольнике прямоугольный треугольник имеет три высоты. Две из них совпадают с катетами, а вот третья высота, проведенная к гипотенузе, постоянно будоражит наши умы.

Поэтому представляю вашему вниманию основные формулы для ее нахождения.

Начну с самой важной.

1. Высота, проведенная к гипотенузе равна корню квадратному из произведения проекций катетов на эту гипотенузу.

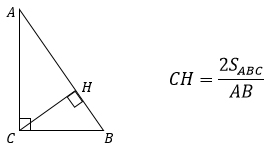
2. Высоту, проведенную к гипотенузе, можно найти, разделив удвоенную площадь прямоугольного треугольника на гипотенузу.

Такая формула получается из классический формулы нахождения площади треугольника: половина произведения основания на высоту, проведенную к этому основанию.

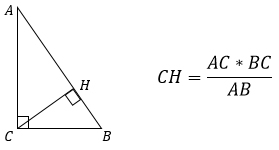
3. Высота, проведенная к гипотенузе, равна произведению катетов, деленному на гипотенузу.

Эта формула получится из второй если заменить площадь на половину произведения катетов.

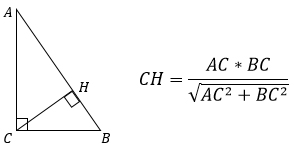
Т.к. АВ – гипотенуза, то ее можно выразить через катеты АС и ВС, используя теорему Пифагора. Тогда формула примет другой вид:

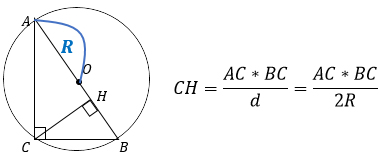
4. Высота, проведенная к гипотенузе, равна произведению катетов, деленному на диаметр описанной вокруг треугольника окружности (или на удвоенный радиус).

Так получается потому, что центр описанной окружности лежит в середине гипотенузы, значит, гипотенуза равна 2R или d.

5. Высоту, проведенную к гипотенузе, можно найти, используя геометрические определения синуса, тангенса и котангенса.

Надеюсь, что данная статья оказалась полезной!)

Готовься к экзамену вместе с нами! Заходи на нашу страницу в ВК.

Треугольник называется прямоугольным, если у него один из углов является прямым. Стороны, прилежащие к прямому углу, называются катетами, а сторона, лежащая напротив прямого угла, гипотенузой.

Прямоугольный треугольник: основные формулы

1. Пусть <A = 30°. Катет, лежащий напротив угла в 30 градусов, равен половине гипотенузы. CB = AB:2.
2. Сумма острых углов прямоугольного треугольника равна 90°. <A + <B = 90°.
3. Теорема Пифагора: квадрат гипотенузы равен сумме квадратов катетов.  AB² = AC² + CB²

Прямоугольный треугольник:  формулы площади и проекции

1. Высота прямоугольного треугольника, проведенная к гипотенузе, равна : h = (ab):c.
2. Высота прямоугольного треугольника, опущенная на гипотенузу, есть среднее пропорциональное между проекциями катетов на гипотенузу: CH² = AH·BH.
3. Катет прямоугольного треугольника — среднее пропорциональное или среднее геометрическое  между гипотенузой и проекцией этого катета на гипотенузу:  CA² = AB·AH;  CB² = AB·BH.
4. Медиана, проведенная к гипотенузе прямоугольного треугольника, равна ее половине.
5. Площадь прямоугольного треугольника равна половине произведения катетов. S = (ab):2.
6. Площадь прямоугольного треугольника равна половине произведения гипотенузы и высоты.  S = (hc):2.

Прямоугольный треугольник:  формулы тригонометрия

1. Косинус острого угла прямоугольного треугольника равен отношению прилежащего катета к гипотенузе.                 cosα  = AC: AB.
2. Синус острого угла прямоугольного треугольника равен отношению противолежащего катета к гипотенузе.           sinα = BC:AB.
3. Тангенс  острого угла прямоугольного треугольника равен отношению противолежащего катета к прилежащему.    tgα  = BC:AC.
4. Котангенс острого угла прямоугольного треугольника равен отношению прилежащего катета к противолежащему.    ctgα  = AC:BC.
5. Основное тригонометрическое тождество:  cos²α + sin²α = 1.
6. Теорема косинусов: b² = a² + c² – 2ac·cosα.
7. Теорема синусов: CB :sinA = AC : sinB = AB.

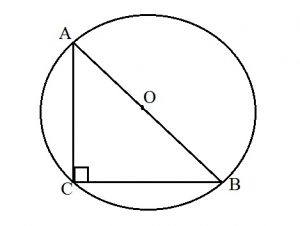
Прямоугольный треугольник:  формулы для описанной окружности

1. Радиус описанной окружности равен половине гипотенузы : R=AB:2.
2. Центр описанной окружности лежит на середине гипотенузы.

Прямоугольный треугольник:  формулы для вписанной  окружности

Радиус окружности, вписанной в прямоугольный треугольник, вычисляется по формуле: r = (a + b  -c):2.

Рассмотрим применение тригонометрических формул прямоугольного треугольника при решении задания 6(вариант 32) из  сборника для подготовки к ЕГЭ по математике профиль автора Ященко.

В треугольнике ABC угол С равен 90°, sinA = 11/14, AC =10√3. Найти АВ.

Решение:

1. Применяя основное тригонометрическое тождество, найдем cosA = 5√3/14.
2. По определению косинуса острого угла прямоугольного треугольника имеем: cosA = AC : AB, AB = AC : cosA = 10√3·14:5√3 = 28.

Ответ: AB = 28.

ЗАДАНИЕ 12 ЕГЭ МАТЕМАТИКА ПРОФИЛЬ( 20 ВАРИАНТ ЯЩЕНКО 2018)