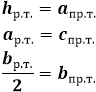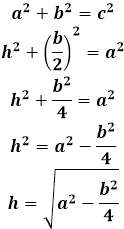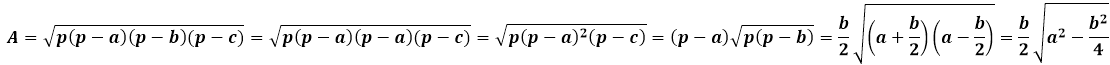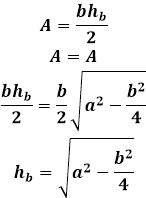Формулы для нахождения высоты треугольника
В данной публикации мы рассмотрим формулы, с помощью которых можно найти высоту в различных видах треугольников, а также разберем примеры решения задач для закрепления материала.
Нахождение высоты треугольника
Напомним, высота треугольника – это отрезок, проведенный перпендикулярно из вершины фигуры к противоположной стороне.
Высота в разностороннем треугольнике
Высоту треугольника abc, проведенного к стороне a, можно найти по формулам ниже:
1. Через площадь и длину стороны
где S – площадь треугольника.
2. Через длины всех сторон
где p – это полупериметр треугольника, который рассчитывается так:
3. Через длину прилежащей стороны и синус угла
4. Через стороны и радиус описанной окружности
где R – радиус описанной окружности.
Высота в равнобедренном треугольнике
Длина высоты ha, опущенной на основание a равнобедренного треугольника, рассчитывается по формуле:
Высота в прямоугольном треугольнике
Высота, проведенная к гипотенузе, может быть найдена:
1. Через длины отрезков, образованных на гипотенузе
2. Через стороны треугольника
Примечание: две остальные высоты в прямоугольном треугольнике являются его катетами.
Высота в равностороннем треугольнике
Для равностороннего треугольника со стороной a формула расчета высоты выглядит следующим образом:
Примеры задач
Задача 1
Найдите высоту треугольника, проведенную из вершины B к стороне AC, если известно, что AB = 7 см, а угол BAC = 45°.
Решение
В данном случае нам поможет формула для нахождения высоты через сторону и синус прилежащего угла:
Задача 2
Найдите длину основания равнобедренного треугольника, если высота, проведенная к нему, равняется 3 см, а боковые стороны – 5 см.
Решение
Вывести формулу для нахождения длины основания можно из формулы расчета высоты в равнобедренном треугольнике:
Все формулы для треугольника
1. Как найти неизвестную сторону треугольника
Вычислить длину стороны треугольника: по стороне и двум углам или по двум сторонам и углу.
a , b , c – стороны произвольного треугольника
α , β , γ – противоположные углы
Формула длины через две стороны и угол (по теореме косинусов), ( a ):
* Внимательно , при подстановке в формулу, для тупого угла ( α >90), cos α принимает отрицательное значение
Формула длины через сторону и два угла (по теореме синусов), ( a):
2. Как узнать сторону прямоугольного треугольника
Есть следующие формулы для определения катета или гипотенузы
a , b – катеты
c – гипотенуза
α , β – острые углы
Формулы для катета, ( a ):
Формулы для катета, ( b ):
Формулы для гипотенузы, ( c ):
Формулы сторон по теореме Пифагора, ( a , b ):
3. Формулы сторон равнобедренного треугольника
Вычислить длину неизвестной стороны через любые стороны и углы
b – сторона (основание)
a – равные стороны
α – углы при основании
β – угол образованный равными сторонами
Формулы длины стороны (основания), (b ):
Формулы длины равных сторон , (a):
4. Найти длину высоты треугольника
Высота– перпендикуляр выходящий из любой вершины треугольника, к противоположной стороне (или ее продолжению, для треугольника с тупым углом).
Высоты треугольника пересекаются в одной точке, которая называется – ортоцентр.

a – сторона, основание
b, c – стороны
β , γ – углы при основании
p – полупериметр, p=(a+b+c)/2
R – радиус описанной окружности
S – площадь треугольника
Формула длины высоты через стороны, ( H ):
Формула длины высоты через сторону и угол, ( H ):
Формула длины высоты через сторону и площадь, ( H ):
Формула длины высоты через стороны и радиус, ( H ):
Способы нахождения высоты треугольника: теорема и формула
Определение высоты треугольника
Геометрия, являющаяся разделом математики, изучает структуры в пространстве и на плоскости. Одним из типов таких фигур являются геометрические фигуры. К ним можно отнести квадрат, прямоугольник, круг, пятиугольник, треугольник и другие. Из них можно делать более сложные фигуры или оставлять в первоначальном виде.
Треугольником является фигура, относящаяся к классу простых фигур, которая образована тремя точками, находящимися не на одной прямой, и соединенными между собой тремя отрезками.
Треугольники могут быть:
- разными по величине углов: прямоугольными, тупоугольными и остроугольными;
- разными по числу равных сторон: равносторонними, равнобедренными и разносторонними.
Помимо трех сторон, важными элементами треугольников являются медианы, высоты и биссектрисы.
Высотой треугольника является перпендикуляр, опущенный из угла треугольника вниз, на противоположную сторону.
В геометрии высота треугольника обозначается буквой h.
В зависимости от типа треугольника высота может:
- падать на противоположную сторону — у остроугольного треугольника;
- находиться вне треугольника — у тупоугольного треугольника;
- совпадать с одной из сторон — у прямоугольного треугольника.
Чтобы сделать высоту графически явной и понятной на рисунке, ее нередко выделяют красной линией.
Для того чтобы определить графическое начертание высоты треугольника, необходимо:
- Найти вершину фигуры.
- Опустить вниз перпендикулярную линию к противоположной стороне.
- Продлить противоположную сторону до пересечения с высотой, если требуется.
Любой треугольник имеет 3 высоты — по числу углов. Их пересечение находится в точке ортоцентра, которая, в зависимости от типа треугольника, может находиться внутри треугольника, снаружи на пересечении продолжений высот или совпадать с вершиной прямого угла.
Все три высоты треугольника обратно пропорциональны сторонам, к которым опущены. Доказательством будет соотношение:
A × H A ÷ B × H B ÷ C × H C = 1 B C ÷ 1 A C ÷ 1 A B
Выглядеть графически это будет так:
Существует множество способов нахождения высоты треугольника в зависимости от имеющихся данных.
Через площадь и длину стороны, к которой опущена высота:
где S — уже известная площадь треугольника,
Через длины всех сторон:
h = 2 p p × a p × b p × c a
где a, b и c — стороны треугольника,
p — его полупериметр.
Данная формула подходит только для нахождения высоты разностороннего треугольника.
Через длину прилежащей стороны и синус угла:
s i n a — синус угла прилежащей стороны.
Данная формула подходит только для нахождения высоты разностороннего треугольника.
Через стороны и радиус описанной окружности.
Решать задачи с треугольником и описанной окружностью для нахождения высоты можно следующим образом:
где b, c — стороны разностороннего треугольника, к которым не опущена высота,
R — радиус описанной окружности.
Данная формула подходит только для нахождения высоты разностороннего треугольника.
Через длины отрезков, образованных на гипотенузе при проведении к ней высоты треугольника:
где C 1 и С 2 — длины отрезков, образованных на гипотенузе, проведенной к ней высотой.
Данная формула подходит только для нахождения высоты прямоугольного треугольника.
Нахождение высоты равнобедренного треугольника через основание и боковые стороны
Равнобедренным треугольником называют треугольник, имеющий одинаковые по длине катеты, которые образуют равные углы с основанием. В таком треугольнике высота будет опускаться ровно в середину основания, образуя с ним прямой угол.
Помимо высоты, проведенная линия будет являться также осью симметрии, биссектрисой вершинного угла и медианой.
Формула для нахождения высоты в этом случае:
где a — основание,
b — равные боковые стороны.
Свойства высоты в равностороннем треугольнике
Равносторонний треугольник — это треугольник, стороны которого, углы, высоты, медианы, оси симметрии и биссектрисы будут равны.
Такой треугольник является частным примером равнобедренного треугольника, но не наоборот.
Высоту в таком треугольнике можно найти с помощью следующей формулы:
где а — сторона равностороннего треугольника.
Главным свойством, которым обладает высота равностороннего треугольника, является тот факт, что она равна медиане и биссектрисе:
а — сторона правильного равностороннего треугольника.
Нахождение высоты прямоугольного треугольника через его катеты
Прямоугольным считается треугольник, у которого один из углов является прямым, то есть равным 90°. Высота, опущенная из такого угла, падает на гипотенузу треугольника и делит его на два прямоугольных треугольника, которые пропорциональны по отношению к большому треугольнику и друг к другу.
Важно отметить, что две другие высоты будут совпадать с катетами треугольника.
Найти высоту в прямоугольном треугольнике, можно через два его катета (a и b) и гипотенузу (c).
Причем гипотенуза также легко находится через катеты по теореме Пифагора:
Расчет высоты идет следующим образом:
где a, b и c — вышеупомянутые стороны треугольника.
[spoiler title=”источники:”]
http://www-formula.ru/2011-10-09-11-08-41
http://wika.tutoronline.ru/geometriya/class/7/sposoby-nahozhdeniya-vysoty-treugolnika-teorema-i-formula
[/spoiler]
Равнобедренным треугольником называется такой треугольник, у которого две из трех сторон равны между собой. Равные стороны считаются боковыми сторонами а, а третья сторона в называется основанием равнобедренного треугольника.
Соответственно, в таком треугольнике можно провести три высоты, две из которых будут равны между собой, аналогично сторонам – это высоты, опущенные на боковую сторону треугольника а, а третья высота опускается на основание. Высота треугольника проводится из угла треугольника к противолежащей стороне под прямым углом. Большинство задач с высотой треугольника решаются через прямоугольные треугольники, которые она образует.
Рассмотрим каждый случай по отдельности.
Высота равнобедренного треугольника, опущенная на основание, обладает рядом индивидуальных свойств, присущих только ей и не распространяющихся на другие высоты в таком треугольнике. В частности, высота, проведенная к основанию равнобедренного треугольника, совпадает с медианой и биссектрисой, проведенным к основанию, следовательно, она не только образует прямой угол с основанием, но и делит его на две равные части, как медиана, и аналогично делит угол пополам, как биссектриса. В итоге, высота является своеобразной осью симметрии треугольника и разделяет его на два конгруэнтных прямоугольных треугольника. В таком треугольнике высота является катетом, и чтобы найти ее длину необходимо соотнести стороны равнобедренного треугольника со сторонами прямоугольного. Боковая сторона равнобедренного треугольника становится гипотенузой, а чтобы определить второй катет, основание равнобедренного треугольника нужно разделить пополам, по свойству медианы.
Длина высоты равнобедренного треугольника равна по теореме Пифагора квадратному корню из суммы квадрата боковой стороны равнобедренного треугольника и четверти квадрата основания равнобедренного треугольника:
Второй случай, когда условиями задачи нужно найти высоту, опущенную на боковую сторону равнобедренного треугольника, раскрывается проще всего через площадь треугольника.
Площадь любого треугольника можно найти несколькими способами – например, через три стороны треугольника по формуле Герона, или через высоту, умножив ее на половину стороны, на которую она опущена. И тем, и другим способом получаются одинаковые значения площади, следовательно обе эти формулы можно друг к другу приравнять и отсюда вывести окончательную формулу высоты, опущенную на боковую сторону равнобедренного треугольника.
Формула Герона для равнобедренного треугольника будет иметь несколько упрощенный вид за счет того, что значения боковых сторон повторяются:
Площадь равнобедренного треугольника через высоту, опущенную к боковой стороне
Эту же формулу можно применять для нахождения любой высоты в равнобедренном треугольнике, если поменять в формуле соответствующие стороны местами.
Формула высоты равнобедренного треугольника через боковую сторону и угол при основании α: h=a sinα
Формула через боковую сторону и угол напротив основания β:
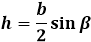
Формула через основание и угол при нем α:
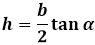
через основание и угол противолежащий ему β:
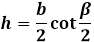
Трапецией принято называть выпуклую четырёхугольную четырехугольник с парой параллельных и двумя не
параллельными сторонами. Отрезки, которые создают параллельные прямы называются «основанием
трапеции», две других стороны играют роль «боковой стороны трапеции». Средняя линия трапеции будет
соединять два центра боковых сторон.
- Высота трапеции через боковую сторону и прилегающий угол
при основании - Высота трапеции через площадь и длины оснований
- Высота трапеции через площадь и среднию линию
- Высота трапеции через основании, диагонали и угол между
диагоналями - Высота трапеции через среднию линию, диагонали и угол между
диагоналями
Как найти высоту при помощи боковой стороны и прилегающего угла при основании
Для вычисления высоты трапеции через боковую сторону и прилегающий угол при основании нужно
воспользоваться нижеприведенной формулой:
h = a · sin α
где h — это искомая высота трапеции, a — известная боковая сторона, sin α — угол
при основании.
Цифр после
запятой:
Результат в:
Пример. Чтобы разобраться с применением формулы, давайте рассмотрим пример. Дана
некая трапеция. Нам известно, что боковая сторона равна 10 сантиметрам, а прилегающих угол
составляет 30 гр. Нам нужно найти высоту данной трапеции. Для решения у нас есть вся нужная
информация и формула выше. Подставляем значения в формулу: h = a · sin, h = 10 · sin 30, h = 10 · 1/2, h = 5 см
Как найти высоту трапецию при помощи длины основания и площади трапеции
Чтобы найти высоту трапеции через известные длины основания и площадь, нужно воспользоваться
формулой:
h = (2S) / (a + b)
где h — это искомая высота трапеции, S — известная площадь фигуры, a и b — длины
обеих оснований.
Цифр после
запятой:
Результат в:
Пример. Закрепим на примере: Нам известно, что в трапеции АВСD основания a и b равны
5 и 10 сантиметров. Площадь фигуры равна 30 квадратных сантиметров. Для решения нужно
воспользоваться формулой. h = (2S) / (a + b), h = (2 х 30) / (5 + 10), h = 60 /15, h = 4 см.
Высота трапеции равна 4 см.
Как найти высоту при помощи диагоналей, углу между диагоналями и средней линией трапеции
Чтобы найти высоту трапеции через среднюю линию, известные диагонали и угол между ними, нужно
прибегнуть к применению выведенной формулы:
h = ((D x d) / (2m)) x sin (α)
где h — это искомая высота трапеции, D и d — известные диагонали, m — средняя
линия, sin(α) — угол между диагоналями.
Цифр после
запятой:
Результат в:
Пример. Закрепим на примере: Дана трапеция с диагоналями 5 и 12 сантиметров.
Известно, что средняя линия фигуры равна 6 см, а угол между диагоналями – 30 градусов. Применив
формулу выше, мы сможем с легкостью найти высоту трапеции. h = ((D x d) / (2m)) x sin (α), h = ((5 x 12) / (2 х 6)) x sin (30), h = (60 /12) x 0.5, h = 2.5 см.
Высота трапеции равна 2.5 см.
Как найти высоту при помощи средней линии и площади трапеции
Чтобы найти высоту трапеции через площадь и среднюю линию воспользуемся выведенной формулой:
h = (2S) / m
где h — это искомая высота трапеции, S — известная площадь фигуры, а m — средняя
линия.
Цифр после
запятой:
Результат в:
Пример. Закрепим на примере: Площадь произвольной трапеции составляет 30 квадратных
сантиметров. Средняя линия фигуры равна 5 см. Нужно найти высоту по формуле. h = (2S) / m, h = (2 х 30) / 5, h = 60 / 5, h = 12 см. 12
см – высота трапеции.
Как найти высоту при помощи известного основания, диагоналей трапеции и угла между диагоналями
Для нахождения высоты трапеции при помощи известного основания, диагонали и углу между диагоналями
используют нижеприведенную формулу:
h = ((Dd) / (a + b)) x sin (α)
где h — это искомая высота трапеции, D и d — известные диагонали, a и b — длины
обеих оснований, sin(α) — угол между диагоналями.
Цифр после
запятой:
Результат в:
Пример. Закрепим на примере: В трапеции ABCD диагонали равны 10 см каждая. Известно,
что сумма основ фигура равна 20 см. Угол, созданный между диагоналями – 30 градусов. Нужно найти
высоту. Для этого нужно воспользоваться выше предоставленной формулой. h = ((Dd) / (a+b)) x sin (α), h = ((10 х 10) / (20)) x sin (30), h = 5 x sin (30), h = 2.5 см.
Высота трапеции равна 2.5 см
Можно выделить 2 разновидности трапеции:
- Трапеция, в которой одна из боковых сторон лежит под перпендикулярным углом с обеими основами
называется прямоугольной. - Трапеции с равными боковыми сторонами называется равнобедренной.
Высотой трапеции принято называть отрезок, которой показывает самое короткое расстояние между верхним
и нижним основанием фигуры. Существует большое количество математических задач разного уровня
сложности, для решения которых активно применяют высоту. Стоит разобраться со всеми возможными
формулами, которые используются для нахождения высоты трапеции.
Download Article
Download Article
To calculate the area of a triangle you need to know its height. To find the height follow these instructions. You must at least have a base to find the height.
-
1
Recall the formula for the area of a triangle. The formula for the area of a triangle is
A=1/2bh.
[1]
- A = Area of the triangle
- b = Length of the base of the triangle
- h = Height of the base of the triangle
-
2
Look at your triangle and determine which variables you know. You already know the area, so assign that value to A. You should also know the value of one side length; assign that value to “‘b'”.
Any side of a triangle can be the base,
regardless of how the triangle is drawn. To visualize this, just imagine rotating the triangle until the known side length is at the bottom.
Example
If you know that the area of a triangle is 20, and one side is 4, then:
A = 20 and b = 4.Advertisement
-
3
Plug your values into the equation A=1/2bh and do the math. First multiply the base (b) by 1/2, then divide the area (A) by the product. The resulting value will be the height of your triangle!
Example
20 = 1/2(4)h Plug the numbers into the equation.
20 = 2h Multiply 4 by 1/2.
10 = h Divide by 2 to find the value for height.
Advertisement
-
1
Recall the properties of an equilateral triangle. An equilateral triangle has three equal sides, and three equal angles that are each 60 degrees. If you
cut an equilateral triangle in half, you will end up with two congruent right triangles.
[2]
- In this example, we will be using an equilateral triangle with side lengths of 8.
-
2
Recall the Pythagorean Theorem. The Pythagorean Theorem states that for any right triangle with sides of length a and b, and hypotenuse of length c:
a2 + b2 = c2.
We can use this theorem to find the height of our equilateral triangle![3]
-
3
Break the equilateral triangle in half, and assign values to variables a, b, and c. The hypotenuse c will be equal to the original side length. Side a will be equal to 1/2 the side length, and side b is the height of the triangle that we need to solve.
- Using our example equilateral triangle with sides of 8, c = 8 and a = 4.
-
4
Plug the values into the Pythagorean Theorem and solve for b2.[4]
First square c and a by multiplying each number by itself. Then subtract a2 from c2.Example
42 + b2 = 82 Plug in the values for a and c.
16 + b2 = 64 Square a and c.
b2 = 48 Subtract a2 from c2. -
5
Find the square root of b2 to get the height of your triangle! Use the square root function on your calculator to find Sqrt(2. The answer is the height of your equilateral triangle!
- b = Sqrt (48) = 6.93
Advertisement
-
1
Determine what variables you know. The height of a triangle can be found if you have 2 sides and the angle in between them, or all three sides. We’ll call the sides of the triangle a, b, and c, and the angles, A, B, and C.
- If you have all three sides, you’ll use
Heron’s formula
, and the formula for the area of a triangle.
- If you have two sides and an angle, you’ll use the formula for the area given two angles and a side.
A = 1/2ab(sin C).[5]
- If you have all three sides, you’ll use
-
2
Use Heron’s formula if you have all three sides. Heron’s formula has two parts. First, you must find the variable
s, which is equal to half of the perimeter of the triangle.
This is done with this formula:
s = (a+b+c)/2.[6]
Heron’s Formula Example
For a triangle with sides a = 4, b = 3, and c = 5:
s = (4+3+5)/2
s = (12)/2
s = 6
Then use the second part of Heron’s formula, Area = sqr(s(s-a)(s-b)(s-c). Replace Area in the equation with its equivalent in the area formula: 1/2bh (or 1/2ah or 1/2ch).
Solve for h. For our example triangle this looks like:
1/2(3)h = sqr(6(6-4)(6-3)(6-5).
3/2h = sqr(6(2)(3)(1)
3/2h = sqr(36)
Use a calculator to calculate the square root, which in this case makes it 3/2h = 6.
Therefore, height is equal to 4, using side b as the base. -
3
Use the area given two sides and an angle formula if you have a side and an angle. Replace area in the formula with its equivalent in the area of a triangle formula: 1/2bh. This gives you a formula that looks like 1/2bh = 1/2ab(sin C). This can be simplified to
h = a(sin C)
, thereby eliminating one of the side variables.[7]
Note that angle C and side a are both positioned across from the height that you need to find (both on the right side from it, or both on the left side).Finding Height with 1 Side and 1 Angle Example
For example, with a = 3, and C = 40 degrees, the equation looks like this:
h = 3(sin 40)
Use your calculator to finish the equation, which makes h roughly 1.928.
Advertisement
Practice Problems and Answers
Add New Question
-
Question
How do I find the area of an equilateral triangle when only the height is given?
H = height, S = side, A = area, B = base. You know that each angle is 60 degrees because it is an equilateral triangle. If you look at one of the triangle halves, H/S = sin 60 degrees because S is the longest side (the hypotenuse) and H is across from the 60 degree angle, so now you can find S. The base of the triangle is S because all the sides are the same, so B = S. Using A = (1/2)*BH, you get A = (1/2)*SH, which you can now find.
-
Question
How do I calculate the height of a right triangle, given only the length of the base and the interior angle at the base?
Look up the tangent of the angle in a trigonometry table. Multiply the tangent by the length of the base.
-
Question
How do I determine the height of a triangle when I know the length of all three sides?
You already know the base, so calculate the area by Heron’s formula. Then, substitute the values you know in the formula. Area=1/2 * base * height or height=2 * Area/base and find your answer.
See more answers
Ask a Question
200 characters left
Include your email address to get a message when this question is answered.
Submit
Advertisement
Video
References
About This Article
Article SummaryX
If you know the base and area of the triangle, you can divide the base by 2, then divide that by the area to find the height. To find the height of an equilateral triangle, use the Pythagorean Theorem, a^2 + b^2 = c^2. Cut the triangle in half down the middle, so that c is equal to the original side length, a equals half of the original side length, and b is the height. Plug a and c into the equation, squaring both of them. Then subtract a^2 from c^2 and take the square root of the difference to find the height. If you want to learn how to calculate the area if you only know the angles and sides, keep reading!
Did this summary help you?
Thanks to all authors for creating a page that has been read 2,398,449 times.
Reader Success Stories
-
“My Geometry teacher is not the best teacher, and I usually have to look up terms and lessons so I can teach myself…” more
Did this article help you?
В данной публикации мы рассмотрим формулы, с помощью которых можно найти высоту в различных видах треугольников, а также разберем примеры решения задач для закрепления материала.
-
Нахождение высоты треугольника
- Высота в разностороннем треугольнике
- Высота в равнобедренном треугольнике
- Высота в прямоугольном треугольнике
- Высота в равностороннем треугольнике
- Примеры задач
Нахождение высоты треугольника
Напомним, высота треугольника – это отрезок, проведенный перпендикулярно из вершины фигуры к противоположной стороне.
Высота в разностороннем треугольнике
Высоту треугольника abc, проведенного к стороне a, можно найти по формулам ниже:
1. Через площадь и длину стороны
где S – площадь треугольника.
2. Через длины всех сторон
где p – это полупериметр треугольника, который рассчитывается так:
3. Через длину прилежащей стороны и синус угла
4. Через стороны и радиус описанной окружности
где R – радиус описанной окружности.
Высота в равнобедренном треугольнике
Длина высоты ha, опущенной на основание a равнобедренного треугольника, рассчитывается по формуле:
Высота в прямоугольном треугольнике
Высота, проведенная к гипотенузе, может быть найдена:
1. Через длины отрезков, образованных на гипотенузе
2. Через стороны треугольника
Примечание: две остальные высоты в прямоугольном треугольнике являются его катетами.
Высота в равностороннем треугольнике
Для равностороннего треугольника со стороной a формула расчета высоты выглядит следующим образом:
Примеры задач
Задача 1
Найдите высоту треугольника, проведенную из вершины B к стороне AC, если известно, что AB = 7 см, а угол BAC = 45°.
Решение
В данном случае нам поможет формула для нахождения высоты через сторону и синус прилежащего угла:
Задача 2
Найдите длину основания равнобедренного треугольника, если высота, проведенная к нему, равняется 3 см, а боковые стороны – 5 см.
Решение
Вывести формулу для нахождения длины основания можно из формулы расчета высоты в равнобедренном треугольнике: