Тема: Высота цилиндра, вписаного в сферу (Прочитано 2435 раз)
0 Пользователей и 1 Гость просматривают эту тему.
Объем шара равен V. В сферу, ограничивающую этот шар, вписан цилиндр наибольшей возможной площади боковой поверхности. Найдите высоту этого цилиндра.
Помогите пожалуйста составить функцию к данной задаче ( что и через что лучше выразить…)
(
V={4/3}{Pi}{R^3}
)
(
S={2}{Pi}{r}{h}
)
На мой взгляд, надо рассматривать окружность, в которую вписан прямоугольник ( длина которого является высотой цилиндра)

Правильно. А теорема Пифагора поможет вам связать диаметр и высоту. Или радиус и высоту. А радиус вычисляется из формулы объема.

Пожалуйста не пишите голое условие! Сначало мы выслушаем Ваши мысли или хотябы вопросы, но конкретные и лишь потом дадим необходимые советы!
Но можете всего этого и не делать, если Вас не интересует результат
Если не хотите разбираться сами закажите решение на сайте.
Я попробывал…

Извините за кривое изображение ( можно на него нажать и там будут функции поворота и увеличения)
Посмотрите,пожалуйста, верно я делаю? Если верно, то не поможете взять производную от этой функции?

Вы не совсем так делаете, как я советовал. Радиус шара (сферы) берется из заданного объема. Высота цилиндра и его диаметр связаны между собой теоремой Пифагора : квадрат диаметра + квадрат высоты = квадрату диаметра сферы. Вот отсюда вы выражаете один параметр через другой. И подставляете в формулу площади поверхности. И исследуете на экстремум именно эту функцию, а не функцию объема. Т.к. объем у вас задан, а наибольшую площадь нужно определить. Вернее высоту цилиндра, обеспечивающую эту наибольшую площадь.

Пожалуйста не пишите голое условие! Сначало мы выслушаем Ваши мысли или хотябы вопросы, но конкретные и лишь потом дадим необходимые советы!
Но можете всего этого и не делать, если Вас не интересует результат
Если не хотите разбираться сами закажите решение на сайте.
Так?

В принципе так. Именно это я и имел в виду. Подстановки и преобразования не проверял.

Пожалуйста не пишите голое условие! Сначало мы выслушаем Ваши мысли или хотябы вопросы, но конкретные и лишь потом дадим необходимые советы!
Но можете всего этого и не делать, если Вас не интересует результат
Если не хотите разбираться сами закажите решение на сайте.

Сфера, вписанная в цилиндр
Сфера называется вписанной в цилиндр, если она касается его оснований и боковой поверхности (касается каждой образующей). При этом цилиндр называется описанным около сферы.
В цилиндр можно вписать сферу, если высота цилиндра равна
диаметру его основания.
Ее центром будет точка O , являющаяся
серединой отрезка, соединяющего центры оснований O 1 и O 2 цилиндра.
В режиме слайдов ответы и решения появляются после кликанья мышкой
Радиус сферы R будет равен
радиусу окружности основания цилиндра.

Упражнение 1
В цилиндр высоты 2 вписана сфера. Найдите ее радиус.
Ответ: 1.

Упражнение 2
В цилиндр вписана сфера радиуса 1. Найдите высоту цилиндра.
Ответ: 2.

Упражнение 3
Радиус основания цилиндра равен 2. Какой должна быть высота цилиндра, чтобы в него можно было вписать сферу?
Ответ: 4.

Упражнение 4
Высота цилиндра равна 2. Каким должен быть радиус основания цилиндра, чтобы в него можно было вписать сферу?
Ответ: 1.

Упражнение 5
Осевым сечением цилиндра является прямоугольник со сторонами 1 и 2. Можно ли в этот цилиндр вписать сферу?
Ответ: Нет.

Упражнение 6
Осевым сечением цилиндра является квадрат. Можно ли в этот цилиндр вписать сферу?
Ответ: Да.

Упражнение 7
Можно ли вписать сферу в цилиндр, осевым сечением которого является ромб?
Ответ: Нет.

Упражнение 8
Можно ли вписать сферу в наклонный цилиндр?
Ответ: Нет.

Упражнение 9
Площадь осевого сечения цилиндра, в который вписана сфера, равна 4 см 2 . Найдите диаметр сферы.
Ответ: 2 см.

Упражнение 10
Периметр осевого сечения цилиндра, в который вписана сфера, равен 8 см. Найдите радиус сферы.
Ответ: 1 см.

Упражнение 1 1
Какой наибольший радиус может быть у сферы, помещающейся в цилиндр, радиус основания которого равен 2, и высота 1.
Ответ: 0,5 см.

Упражнение 12
Можно ли сферу радиуса 1 поместить в наклонный цилиндр, радиус основания которого равен 1, а боковое ребро равно 2 и наклонено к плоскости основания под углом 60 о .
Ответ: Нет.

Упражнение 13
Какой наибольший радиус может быть у сферы, помещающейся в наклонный цилиндр, радиус основания которого равен 1, а боковое ребро равно 2 и наклонено к плоскости основания под углом 60 о .
Ответ:

Сфера, описанная около цилиндра
Цилиндр называется вписанным в сферу, если окружности оснований цилиндра лежат на сфере. При этом сфера называется описанной около цилиндра.
Около любого цилиндра можно описать сферу. Ее центром будет точка O , являющаяся серединой отрезка, соединяющего центры оснований O 1 и O 2 цилиндра.
Радиус сферы R вычисляется по формуле
где h – высота цилиндра, r – радиус окружности основания.
В режиме слайдов ответы и решения появляются после кликанья мышкой

Упражнение 1
Диагональ осевого сечения цилиндра равна 2. Найдите радиус сферы, описанной около этого цилиндра.
Ответ: 1.

Упражнение 2
Около цилиндра высоты 2 и радиуса основания 1 описана сфера. Найдите ее радиус.
Ответ:

Упражнение 3
Около цилиндра, радиус основания которого равен 1, описана сфера радиуса 2. Найдите высоту цилиндра.
Ответ:

Упражнение 4
Около цилиндра, высота которого равна 1, описана сфера радиуса 1. Найдите радиус основания цилиндра.
Ответ:

Упражнение 5
Найдите наименьший радиус сферы, в которую помещается наклонный цилиндр, радиус основания которого равен 1, образующая равна 2 и наклонена к плоскости основания под углом 60 о .
Ответ:

Цилиндр, вписанный в призму
Ц илиндр называется вписанным в призму, если е го основания в писаны в основани я цилиндра. При этом , призма называется описанной около цилиндра
В призму можно вписать цилиндр тогда и только тогда, когда
в ее основание можно вписать окружность.
Радиус основания цилиндра равен
радиусу окружности, вписанной в основание призмы.
В режиме слайдов ответы и решения появляются после кликанья мышкой
Высота цилиндра равна
высоте призмы.

Упражнение 1
Можно ли вписать цилиндр в наклонную призму?
Ответ: Да, наклонный цилиндр.

Упражнение 2
В основании прямой призмы правильный треугольник со стороной 1. Найдите радиус окружности основания цилиндра, вписанного в эту призму.
Ответ:

Упражнение 3
В основании прямой призмы прямоугольный треугольник с катетами 6 и 8. Найдите радиус окружности основания цилиндра, вписанного в эту призму.
Ответ: 2.

Упражнение 4
Найдите радиус окружности основания цилиндра, вписанного в единичный куб.
Ответ:

Упражнение 5
В правильную шестиугольную призму, со стороной основания 1, вписан цилиндр. Найдите радиус окружности основания этого цилиндра.
Ответ:

Цилиндр, описанный около призмы
Ц илиндр называется описанным около призмы, если е го основания о писаны около основани й цилиндра. При этом , п ризма называется вписанной в цилиндр
Около призмы можно описать цилиндр, если около ее оснований можно описать окружности.
Радиус основания цилиндра равен
радиусу окружности, описанной около основания призмы.
В режиме слайдов ответы и решения появляются после кликанья мышкой
Высота цилиндра равна
высоте призмы.

Упражнение 1
Можно ли описать цилиндр около наклонной призмы?
Ответ: Да, наклонный цилиндр.

Упражнение 2
В основании прямой призмы правильный треугольник со стороной 1. Найдите радиус окружности основания цилиндра, описанного около этой призмы.
Ответ:

Упражнение 3
В основании прямой призмы прямоугольный треугольник с катетами 6 и 8. Найдите радиус окружности основания цилиндра, описанного около этой призмы.
Ответ: 5.

Упражнение 4
В основании прямой призмы квадрат со стороной 1. Найдите радиус окружности основания цилиндра, описанного около этой призмы.
Ответ:

Упражнение 5
Около правильной шестиугольной призмы, со стороной основания 1, описан цилиндр. Найдите радиус окружности основания этого цилиндра.
Ответ: 1.

Упражнение 6
Около единичного тетраэдра описан цилиндр так, что вершины тетраэдра принадлежат окружностям оснований цилиндра. Найдите радиус основания и высоту цилиндра.
Ответ:

Упражнение 7
Около единичного октаэдра описан цилиндр так, что две противоположные вершины октаэдра находятся в центрах оснований цилиндра, а остальные вершины принадлежат боковой поверхности цилиндра. Найдите радиус основания и высоту цилиндра.
Ответ:
Если внимательно посмотреть на эту формулу, то можно заметить, что — это формула площади круга, а в нашем случае — площадь основания. Поэтому формулу объема цилиндра можно записать через площадь основания и высоту:
— Если известна площадь бок. поверхности S (б.п.) и высота h цилиндра, радиус будет равен частному от деления S (б.п.) на произведение 2пи на высоту:
1. Через площадь основания и высоту
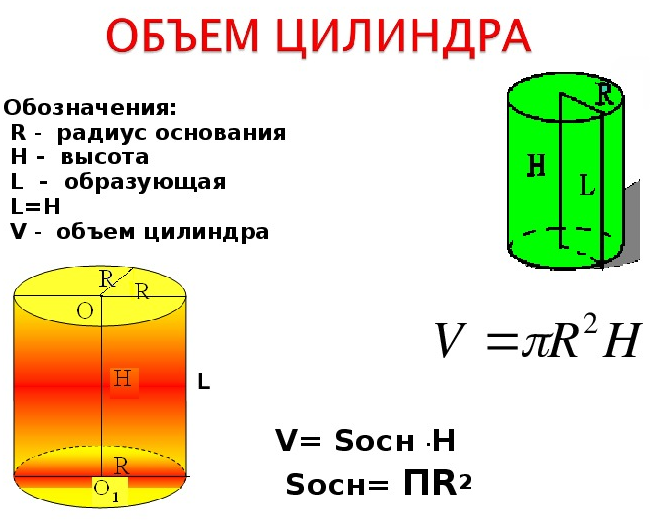
Объем (V) цилиндра равняется произведению его высоты и площади основания.
2. Через радиус основания и высоту
Как мы знаем, в качестве оснований цилиндра (равны между собой) выступает круг, площадь которого вычисляется так: S = π ⋅ R 2 . Следовательно, формулу для вычисления объема цилиндра можно представить в виде:
Примечание: в расчетах значение числа π округляется до 3,14.
3. Через диаметр основания и высоту
Как нам известно, диаметр круга равняется двум его радиусам: d = 2R. А значит, вычислить объем цилиндра можно следующим образом:
Нет сомнений, что все мы со школьных лет помним, как найти высоту цилиндра, формула выглядит так: H=V/πR^2 или 4V/D^2.
То есть получается, что, если разделить объем на площадь основания, получится высота цилиндра.
Можно поступить проще. Для этого нам придется вычислить площадь боковой поверхности искомого цилиндра. Это легко сделать по формуле: S=2πRH. Слегка изменив формулу, получаем: H=S/2πR.
Таким образом, есть уже два способа, которые помогли вспомнить, как найти высоту цилиндра. Это нетрудно, когда перед глазами стройные формулы.
Цилиндр – геометрическое тело, которое получается при вращении прямоугольника вокруг его стороны. Также, цилиндр представляет собой тело, ограниченное цилиндрической поверхностью и двумя параллельными плоскостями, пересекающими ее. Эта поверхность образуется при движении прямой параллельно самой себе. При этом выделенная точка прямой перемещается вдоль определенной плоской кривой (направляющая). Данная прямая называется образующей цилиндрической поверхности.
Формула радиуса цилиндра: 
где V – объем цилиндра, h – высота
Цилиндр – геометрическое тело, которое получается при вращении прямоугольника вокруг его стороны. Также, цилиндр представляет собой тело, ограниченное цилиндрической поверхностью и двумя параллельными плоскостями, пересекающими ее. Эта поверхность образуется при движении прямой параллельно самой себе. При этом выделенная точка прямой перемещается вдоль определенной плоской кривой (направляющая). Данная прямая называется образующей цилиндрической поверхности.
Формула радиуса цилиндра: 
где Sb – площадь боковой поверхности, h – высота
Цилиндр – геометрическое тело, которое получается при вращении прямоугольника вокруг его стороны. Также, цилиндр представляет собой тело, ограниченное цилиндрической поверхностью и двумя параллельными плоскостями, пересекающими ее. Эта поверхность образуется при движении прямой параллельно самой себе. При этом выделенная точка прямой перемещается вдоль определенной плоской кривой (направляющая). Данная прямая называется образующей цилиндрической поверхности.
Формула радиуса цилиндра: 
где S – площадь полной поверхности, h – высота
Площадь боковой поверхности равняется длине окружности основания умноженной на высоту:
где V — объем цилиндра, h — высота.
Полная площадь поверхности цилиндра складывается из сумм площадей его боковой поверхности и двух оснований:
Задание 1
Высота цилиндра равняется 5 см, а объем – 141,3 см 3 . Вычислите его радиус.
Решение:
Воспользуемся соответствующей формулой, подставив в нее известные по условиям задачи значения:

Задание 2
Найдите радиус цилиндра, если площадь его боковой поверхности равна 175,84 см 2 , а высота составляет 7 см.
Задание 3
Рассчитайте радиус цилиндра, если полная площадь его поверхности – 602,88 см 2 , а высота – 10 см.
Sбок. – площадь боковой поверхности цилиндра; равна произведению длины окружности (2 π R), являющейся основанием фигуры, на его высоту:
Формула для нахождения полной поверхности цилиндра через высоту и радиус основания:
, где π — число Пи (3,14159…), r — радиус основания цилиндра, h — высота цилиндра.
Диаметр и высота цилиндра

Свойства
Через диаметр цилиндра можно рассчитать его радиус и периметр основания цилиндра. Радиус будет равен половине диаметра, а периметр – его произведению на число π. r=D/2 P=πD
Зная диаметр и высоту цилиндра, можно узнать площадь, объем, диагональ цилиндра и остальные параметры. Площадь боковой поверхности цилиндра представляет собой площадь прямоугольника, сторонами которого являются периметр основания цилиндра и его высота. Чтобы затем найти площадь полной поверхности цилиндра через диаметр и высоту, нужно к площади боковой поверхности добавить площадь верхнего и нижнего оснований, каждое из которых равно произведению числа π на четверть квадрата диаметра. S_(б.п.)=hP=πDh S_(п.п.)=S_(б.п.)+2S_(осн.)=πDh+(πD^2)/2=πD/2(2h+D) P=πD
Объем цилиндра представляет собой площадь его основания, умноженную на высоту. Чтобы найти объем цилиндра через диаметр и высоту, нужно умножить квадрат диаметра на четверть числа π и на высоту. V=(πD^2 h)/4 P=πD
Диагональ цилиндра находится из прямоугольного треугольника, в котором она является гипотенузой, а катеты представлены высотой и диаметром цилиндра. По теореме Пифагора диагональ цилиндра через высоту и диаметр цилиндра равна квадратному корню из суммы их квадратов. (рис. 25.1) d=√(h^2+D^2 ) P=πD
Чтобы найти радиус сферы вписанной в цилиндр, если его диаметр равен высоте, нужно разделить диаметр цилиндра либо высоту на два, так как радиус вписанной сферы равен радиусу цилиндра. (рис.25.2) r_1=h/2=D/2 P=πD
Радиус сферы, описанной вокруг цилиндра, при соблюдении тех же условий (равенство диаметра цилиндра и его высоты) равен половине диагонали цилиндра.(рис.25.3) R=d/2=√(h^2+D^2 )/2
Высота цилиндра равна длине окружности основания формула
Как найти высоту цилиндра, с помощью данных?
Объем цилиндра формула (через радиус основания и высоту)
r — радиус основания цилиндра,
h — высота цилиндра
Если внимательно посмотреть на эту формулу, то можно заметить, что
— это формула площади круга, а в нашем случае — площадь основания. Поэтому формулу объема цилиндра можно записать через площадь основания и высоту:
S (б.п.) = hP = 2πrh
— Если известна площадь бок. поверхности S (б.п.) и высота h цилиндра, радиус будет равен частному от деления S (б.п.) на произведение 2пи на высоту:
Формула вычисления объема цилиндра
1. Через площадь основания и высоту
Объем (V) цилиндра равняется произведению его высоты и площади основания.
V = S ⋅ H

2. Через радиус основания и высоту
Как мы знаем, в качестве оснований цилиндра (равны между собой) выступает круг, площадь которого вычисляется так: S = π ⋅ R 2 . Следовательно, формулу для вычисления объема цилиндра можно представить в виде:
V = π ⋅ R 2 ⋅ H
Примечание: в расчетах значение числа π округляется до 3,14.
3. Через диаметр основания и высоту
Как нам известно, диаметр круга равняется двум его радиусам: d = 2R. А значит, вычислить объем цилиндра можно следующим образом:
V = π ⋅ (d/2) 2 ⋅ H
Нет сомнений, что все мы со школьных лет помним, как найти высоту цилиндра, формула выглядит так: H=V/πR^2 или 4V/D^2.
Расшифровать формулу просто:
- V – объем цилиндра;
- π – 3,14;
- R – радиус цилиндра;
- D – диаметр.
То есть получается, что, если разделить объем на площадь основания, получится высота цилиндра.
Можно поступить проще. Для этого нам придется вычислить площадь боковой поверхности искомого цилиндра. Это легко сделать по формуле: S=2πRH. Слегка изменив формулу, получаем: H=S/2πR.
Таким образом, есть уже два способа, которые помогли вспомнить, как найти высоту цилиндра. Это нетрудно, когда перед глазами стройные формулы.
Способ расчета радиуса цилиндра:

Цилиндр – геометрическое тело, которое получается при вращении прямоугольника вокруг его стороны. Также, цилиндр представляет собой тело, ограниченное цилиндрической поверхностью и двумя параллельными плоскостями, пересекающими ее. Эта поверхность образуется при движении прямой параллельно самой себе. При этом выделенная точка прямой перемещается вдоль определенной плоской кривой (направляющая). Данная прямая называется образующей цилиндрической поверхности.
Формула радиуса цилиндра: 
где V – объем цилиндра, h – высота

Цилиндр – геометрическое тело, которое получается при вращении прямоугольника вокруг его стороны. Также, цилиндр представляет собой тело, ограниченное цилиндрической поверхностью и двумя параллельными плоскостями, пересекающими ее. Эта поверхность образуется при движении прямой параллельно самой себе. При этом выделенная точка прямой перемещается вдоль определенной плоской кривой (направляющая). Данная прямая называется образующей цилиндрической поверхности.
Формула радиуса цилиндра: 
где Sb – площадь боковой поверхности, h – высота

Цилиндр – геометрическое тело, которое получается при вращении прямоугольника вокруг его стороны. Также, цилиндр представляет собой тело, ограниченное цилиндрической поверхностью и двумя параллельными плоскостями, пересекающими ее. Эта поверхность образуется при движении прямой параллельно самой себе. При этом выделенная точка прямой перемещается вдоль определенной плоской кривой (направляющая). Данная прямая называется образующей цилиндрической поверхности.
Формула радиуса цилиндра: 
где S – площадь полной поверхности, h – высота
S (п.п.) = S (б.п.) + 2S (осн.) = 2πrh + πr2=πr (2h+r)
Площадь боковой поверхности равняется длине окружности основания умноженной на высоту:
R = √V / πh
где V — объем цилиндра, h — высота.
Полная площадь поверхности цилиндра складывается из сумм площадей его боковой поверхности и двух оснований:
Примеры задач
Задание 1
Высота цилиндра равняется 5 см, а объем – 141,3 см 3 . Вычислите его радиус.
Решение:
Воспользуемся соответствующей формулой, подставив в нее известные по условиям задачи значения: 
Задание 2
Найдите радиус цилиндра, если площадь его боковой поверхности равна 175,84 см 2 , а высота составляет 7 см.
Решение:
Применим формулу, в которой задействованы заданные величины: 
Задание 3
Рассчитайте радиус цилиндра, если полная площадь его поверхности – 602,88 см 2 , а высота – 10 см.
Решение:
Используем третью формулу для нахождения неизвестной величины: 
Через площадь боковой поверхности
Радиус цилиндра считается таким образом:

Sбок. – площадь боковой поверхности цилиндра; равна произведению длины окружности (2 π R), являющейся основанием фигуры, на его высоту:
S = 2 π Rh
Площадь полной поверхности цилиндра через радиус основания и высоту

Формула для нахождения полной поверхности цилиндра через высоту и радиус основания:
, где π — число Пи (3,14159…), r — радиус основания цилиндра, h — высота цилиндра.
Высота цилиндра равна длине окружности
537. Диаметр основания цилиндра равен 1 м, высота цилиндра равна длине окружности основания. Найдите площадь боковой поверхности цилиндра.
 Решебник по геометрии за 10 класс (Л.С.Атанасян, 2001 год),
Решебник по геометрии за 10 класс (Л.С.Атанасян, 2001 год),
задача №537
к главе «Глава VI. Цилиндр, конус и шар § 1. цилиндр».
Выделите её мышкой и нажмите CTRL + ENTER
Большое спасибо всем, кто помогает делать сайт лучше! =)
Нажмите на значок глаза возле рекламного блока, и блоки станут менее заметны. Работает до перезагрузки страницы.
Диаметр основания цилиндра равен 1м высота цилиндра равна длине окружности
Диаметр основания цилиндра равен 1м, высота цилиндра равна длине окружности основания. Найдите площадь боковой поверхности цилиндра.
Длина окружности основания равна
Высота цилиндра равна 3.14 м
Площадь боковой поверхности цилиндра равна
S=Lh, где L-длина окружности основания h-высота цилиндра
S=L*L=п*п=3,14*3,14=9,86 кв.м ( хотя наверное лучше оставить п в квадрате, так вроде точнее) п-это пи
Другие вопросы из категории
adef и найдите его периметр
Читайте также
2)Основание пирамиды -прямоугольный треугольник , катет которого равен 20м,а гипотенуза 25м ,высота 10м.Найдите объем пирамиды. 3)Высота правильной четырехугольной пирамиды равна 4 см,а апофема образует с высотой угол 45 градусов. Найдите площадь боковой поверхности пирамиды. 4)Боковое ребро правильной треугольной пирамиды равна 4 корень из 3и наклонено к плоскости основания под углом 60 градусов.Найдите площадь боковой поверхности. 5)В правильной четырехугольной пирамиде MABCD площадь ее основания ABCD равна 32 см ^2, а лощадь треугольника МАС равна 16 см^2.Найдите плоский угол при вершине пирамиды.
2.В правильной 3угольной пирамиде боковое ребро равно 10 см и наклонено к плоскости основы под углом .Найдите высоту пирамиды.
3.В правильной 4угольной пирамиде боковая грань наклонена к основе по д углом , а ее высота равна 12 см.Найтдите апофему пирамиды.
4.Найдите площадь полной поверхности правильной 4угольной
пирамиды, в которой сторона основы равна 6 см, а боковая грань наклонена к основе под углом .
5.Найдите площадь полной поверхности правильной 3угольной пирамиды, в которой апофема равна L и образует с высотой пирамиды угол .
Помогите решить хотя-бы 2 номера..буду благодарна за помощь)
2) Боковое ребро треугольной наклонной призмы равно 8 см, а расстояния между боковыми рёбрами равны 3 см, 4 см, и 5 см. Найдите площадь боковой поверхности призмы
2.) Основанием прямого параллелепипеда служит ромб со стороной а и острым углом Q. Величина угла, образованного меньшей диагональю параллелепипеда с плоскостью его основания, равна 60 градусов. Найдите площадь боковой поверхности этого параллелепипеда.
3.) Основанием пирамиды служит правильный треугольник со стороной 6 см; две боковые грани пирамиды перпендикулярны плоскостью основания; угол, образованной третьей гранью с основанием пирамиды, равен 60 градусам. Найдите площадь полной поверхности пирамиды.
Пожалуйста, напишите все задания с подробными решениями. Заранее спасибо!
точки а до центра основания, содержащего точку б, равно 13м. найдите площадь боковой поверхности цилиндра
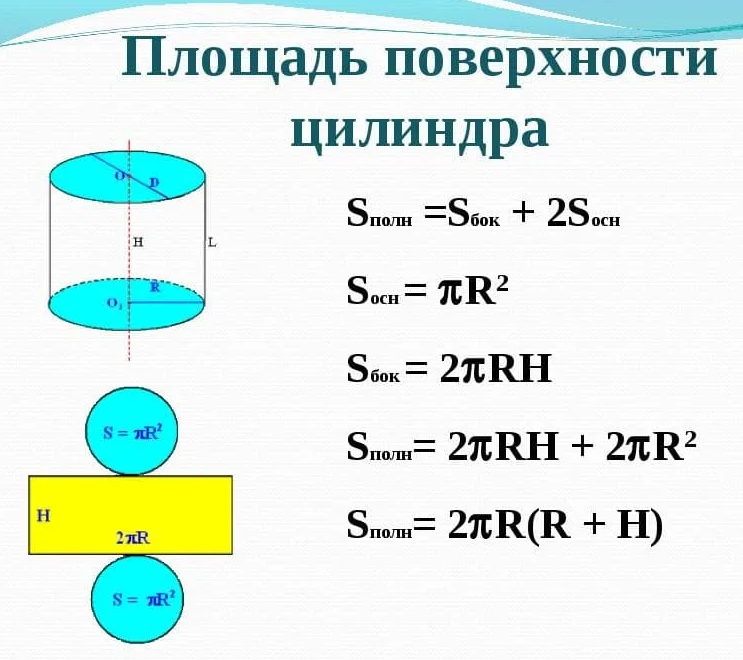
Как найти площадь поверхности цилиндра: боковую, основания, полную
Площадь боковой поверхности цилиндра
Формула площади боковой поверхности цилиндра представляет собой произведение длины основания на его высоту:


Таким образом, используя формулы площади оснований и боковой поверхности фигуры, мы смогли найти полную площадь поверхности цилиндра.
Осевое сечение цилиндра представляет собой прямоугольник, в котором стороны равны высоте и диаметру цилиндра.
Формула площади осевого сечения цилиндра выводится из формулы расчета площади прямоугольника :
Круговой цилиндр
где r – радиус основы, h – высота цилиндра, d – диаметр основы.
Как рассчитать площадь боковой поверхности цилиндра с помощью калькулятора
Калькулятор позволяет определить площадь цилиндра по одному из 2 вариантов исходных данных:
- внешний радиус и высота;
- внешний диаметр и высота.
Выберите соответствующий шаг и введите исходные данные в соответствующие поля.
Также важно указать единицы измерения по условиям задачи.
Расчеты будут выполнены автоматически и конвертированы в основные метрические физические величины площади.
Примеры задач
Задание 1
Найдите площадь боковой поверхности цилиндра, если его радиус равен 11 см, а высота – 8 см.
Решение:
Воспользуемся первой формулой, подставив в нее данные по условиям задачи значения:
S = 2 ⋅ 3,14 ⋅ 11 см ⋅ 8 см = 552,64 см 2 .
Задание 2
Высота цилиндра равна 9 см, а его диаметр – 8 см. Найдите суммарную площадь поверхности фигуры.
Решение:
Если диаметр цилиндра равен 8 см, значит его радиус составляет 4 см (8 см / 2). Применив соответствующую формулу для нахождения площади получаем:
S = 2 ⋅ 3,14 ⋅ 4 см ⋅ (9 см + 4 см) = 326,56 см 2 .
Осевое сечение прямого цилиндра
Осевым называется любое сечение цилиндра, которое содержит его ось. Это определение означает, что осевое сечение будет всегда параллельно образующей линии.
В цилиндре прямом ось проходит через центр круга и перпендикулярна его плоскости. Это означает, что рассматриваемое сечение круг будет пересекать по его диаметру. На рисунке показана половинка цилиндра, которая получилась в результате пересечения фигуры плоскостью, проходящей через ось.

Не сложно понять, что осевое сечение прямого круглого цилиндра представляет собой прямоугольник. Его сторонами являются диаметр d основания и высота h фигуры.
Запишем формулы для площади осевого сечения цилиндра и длины hd его диагонали:
Прямоугольник имеет две диагонали, но обе они равны друг другу. Если известен радиус основания, то не сложно переписать эти формулы через него, учитывая, что он в два раза меньше диаметра.
Введите радиус основания и высоту цилиндра
Радиус:
Высота:

Цилиндр – геометрическое тело, которое получается при вращении прямоугольника вокруг его стороны. Также, цилиндр представляет собой тело, ограниченное цилиндрической поверхностью и двумя параллельными плоскостями, пересекающими ее. Эта поверхность образуется при движении прямой параллельно самой себе. При этом выделенная точка прямой перемещается вдоль определенной плоской кривой (направляющая). Данная прямая называется образующей цилиндрической поверхности.
Площадь полной поверхности цилиндра формула:
S = Sбок + 2 Sосн 2 , где Sбок – площадь боковой поверхности, Sосн – площадь основания
или
S = 2 π R h + 2 π R 2 , где R – радиус оснований, h – высота цилиндра, π – число пи
Площадь полной поверхности цилиндра
Для нахождения полной площади цилиндра нужно к полученной Sбок добавить площади двух окружностей, верха и низа цилиндра, которые считаются по формуле Sо = 2π * r2.
Конечная формула выглядит следующим образом:
Sпол = 2π * r2 + 2π * r * h.
Основные определения и свойства цилиндра
Рассмотрим две паралллельные плоскости паралллельные плоскости α и β и произвольную окружность радиуса r с центром в точке O , лежащую в плоскости α (рис. 1).



Если из каждой точки окружности опустить перпендикуляр на плоскость β , то основания этих перпендикуляров образуют на плоскости β окружность радиуса r , центр O1 которой является основанием перпендикуляра, опущенного из точки O на плоскость β (рис.2).



Отрезок перпендикуляра , опущенного из любой точки окружности с центром O на плоскость β , который заключен между плоскостями α и β , называют образующей цилиндра .
Совокупность всех образующих цилиндра называют цилиндрической поверхностью .
Фигуру, ограниченную цилиндрической поверхностью и плоскостями α и β, называют цилиндром .
Отрезок OO1 называют осью цилиндра .
Радиус окружности Радиус окружности на плоскости α с центром в точке O называют радиусом цилиндра .
Расстояние между плоскостями Расстояние между плоскостями α и β , называют высотой цилиндра .
Круги с центрами O и O1 на плоскостях α и β , называют основаниями цилиндра .
Замечание 1. Цилиндрическую поверхность часто называют боковой поверхностью цилиндра . Боковая поверхность цилиндра и основания цилиндра вместе составляют полную поверхность цилиндра .
Замечание 2. Каждая образующая цилиндра параллельна оси цилиндра, а длина каждой образующей цилиндра равна высоте цилиндра.
Замечание 3. Прямая OO1 является осью симметрии цилиндра, а середина отрезка OO1 является центром симметрии цилиндра.
Геометрическая фигура
Сначала дадим определение фигуре, о которой пойдет речь в статье. Цилиндр представляет собой поверхность, образованную параллельным перемещением отрезка фиксированной длины вдоль некоторой кривой. Главным условием этого перемещения является то, что отрезок плоскости кривой принадлежать не должен.
На рисунке ниже показан цилиндр, кривая (направляющая) которого является эллипсом.

Здесь отрезок длиной h является его образующей и высотой.
Видно, что цилиндр состоит из двух одинаковых оснований (эллипсы в данном случае), которые лежат в параллельных плоскостях, и боковой поверхности. Последней принадлежат все точки образующих линий.
Осевое сечение наклонного цилиндра

Рисунок выше демонстрирует наклонный цилиндр, изготовленный из бумаги. Если выполнить его осевое сечение, то получится уже не прямоугольник, а параллелограмм. Его стороны – это известные величины. Одна из них, как и в случае сечения прямого цилиндра, равна диаметру d основания, другая же – длина образующего отрезка. Обозначим ее b.
Для однозначного определения параметров параллелограмма недостаточно знать его длины сторон. Необходим еще угол между ними. Предположим, что острый угол между направляющей и основанием равен α. Он же и будет углом между сторонами параллелограмма. Тогда формулу для площади осевого сечения наклонного цилиндра можно записать следующим образом:
Диагонали осевого сечения цилиндра наклонного рассчитать несколько сложнее. Параллелограмм имеет две диагонали разной длины. Приведем без вывода выражения, позволяющие рассчитывать диагонали параллелограмма по известным сторонам и острому углу между ними:
l1 = √(d2 + b2 – 2*b*d*cos(α));
l2 = √(d2 + b2 + 2*b*d*cos(α))
Здесь l1 и l2 – длины малой и большой диагоналей соответственно. Эти формулы можно получить самостоятельно, если рассмотреть каждую диагональ как вектор, введя прямоугольную систему координат на плоскости.
Примеры расчета площади поверхности цилиндра
Для понимания приведенных формул попробуем посчитать площадь поверхности цилиндра на примерах.
1. Радиус основания цилиндра равен 2, высота равна 3. Определите площадь боковой поверхности цилиндра.
Sбок. = 2 * 3,14 * 2 * 3
Площадь боковой поверхности цилиндра равна 37,68.
2. Как найти площадь поверхности цилиндра, если высота равна 4, а радиус 6?
S = 2 * 3,14 * 6 2 + 2 * 3,14 * 6 * 4
S = 2 * 3,14 * 36 + 2 * 3,14 * 24
S = 226,08 + 150,72
Площадь поверхности цилиндра равна 376,8.
3. Площадь боковой поверхности прямого кругового цилиндра равна 24π, а диаметр основания — 3. Найдите высоту цилиндра.
Из формулы расчета площади боковой поверхности цилиндра Sбок. = 2πrh следует, что высота равна:
Значение радиуса получаем из формулы: d = 2r
h = 24π / (2π * 0,5d)
h = 24π / (2π * 0,5 * 3)
Высота цилиндра равна 8.
Площадь цилиндра формула через диаметр
Для облегчения расчетов иногда требуется произвести вычисления через диаметр. Например, имеется кусок полой трубы известного диаметра.

Не утруждая себя лишними расчетами, имеем готовую формулу. На помощь приходит алгебра за 5 класс.
Sпол = 2π * r2 + 2π * r * h = 2π * d2/4 + 2π * h * d/2 = π * d2/2 + π * d * h,
Вместо r в полную формулу нужно вставить значение r = d/2.
Площадь боковой поверхности цилиндра через радиус основания и высоту

Формула для нахождения боковой поверхности цилиндра через высоту и радиус основания:
, где π — число Пи (3,14159…), r — радиус основания цилиндра, h — высота цилиндра.
Заключение
В конце статьи назрел вопрос: а так ли необходимы все эти вычисления и переводы одних значений в другие. Зачем все это нужно и самое главное, для кого? Но не стоит пренебрегать и забывать простые формулы из средней школы.
Мир стоял и будет стоять на элементарных познаниях, из математики, в том числе. И, приступая к какой-нибудь важной работе, никогда не лишне освежить в памяти данные выкладки, применив их на практике с большим эффектом. Точность – вежливость королей.
Объем цилиндра
Объем цилиндра, формулы и калькулятор для вычисления объема цилиндра и площади его поверхностей, а также необходимая теория о характеристиках цилиндра.
Объем правильного цилиндра через радиус и высоту цилиндра
Формулы и калькулятор для вычисления объема цилиндра через площадь основания и высоту цилиндра

Формулы и калькулятор для вычисления объема цилиндра через диаметр основания

Объем цилиндрической полости
Объем полости в виде цилиндра равен объему цилиндра, который извлечен из данной полости для ее образования. То есть для вычисления цилиндрической полости можно воспользоваться формулами и калькулятором для расчета простого правильного цилиндра в зависимости от известных исходных данных.
На картинке продемонстрирована цилиндрическая полость, образованная в теле путем извлечения из него цилиндра. Объем извлеченного цилиндра и объем образованной полости равны.
Нужно отметить один важный момент. Несмотря на равенство объемов извлеченного цилиндра и образованной полости, площади поверхностей данных объектов будут отличаться, так как у образованной цилиндрической полости отсутствует верхняя поверхность. То есть суммарная площадь поверхности образованной цилиндрической полости будет меньше суммарной площади извлеченного цилиндра на одну площадь основания цилиндра.
Цилиндр может быть правильным или наклонным  .
.
Правильный цилиндр – это цилиндр, где угол между образующими боковой поверхности и основанием цилиндра равен 90 градусов.
Неправильный или наклонный цилиндр – это цилиндр, где угол между образующими боковой поверхности и основанием цилиндра отличается от 90 градусов.
Рассмотрим правильный цилиндр.
Цилиндр – это тело, образованное вращением прямоугольника вокруг одной из его сторон. Тело цилиндра ограничено двумя кругами, называемыми основанием цилиндра и боковой цилиндрической поверхностью, которая в развертке представляет собой прямоугольник
Цилиндр можно так же описать как тело, состоящее из двух равных кругов, не лежащих в одной плоскости и параллельных между собой, и отрезков, соединяющих все точки одной окружности, с соответствующими точками другой окружности. Данные отрезки называются образующими цилиндра.
Радиус основания цилиндра, является радиусом цилиндра.
Ось цилиндра – это прямая, соединяющая центра оснований цилиндра.
Высота цилиндра – это перпендикуляр, опущенный от одного основания цилиндра к другому.
Поверхности цилиндра
Наружную поверхность цилиндра можно условно разделить на три отдельные поверхности: верхняя, нижняя и боковая.
Верхняя и нижняя поверхности цилиндра имеют форму круга и равны между собой.
Боковая поверхность цилиндра имеет форму прямоугольника. Чтобы это наглядно представить, возьмем боковую наружную поверхность цилиндра и мысленно сделаем вертикальный разрез по образующей цилиндра. Далее развернем поверхность на плоскость. В результате увидим, что боковая поверхность имеет форму прямоугольника (см. на картинке).
Сечения цилиндра

При сечении цилиндра плоскостью, проходящей через оба основания цилиндра под углом в 90 градусов, всегда получатся прямоугольная фигура  .
.
При сечении цилиндра плоскостью, проходящей через оба основания цилиндра под углом отличным от 90 градусов, получатся фигура, похожая на прямоугольник  , но две боковые стороны которого будут являться кривыми линиями.
, но две боковые стороны которого будут являться кривыми линиями.
Если секущая поверхность проходит параллельно основаниям цилиндра, то сечением будет круг  .
.
Если секущая поверхность проходит через боковую поверхность, но при этом не параллельна основанию цилиндра, то в сечении получается эллипс  .
.
Если секущая поверхность проходит через одно основание цилиндра и боковую поверхность, то в сечение будет фигура в виде половины эллипса 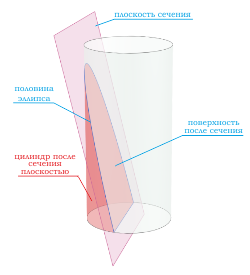 .
.
Что такое объем
Объем тела (геометрической фигуры) – это количественная характеристика, характеризующая количество пространства, занимаемого телом. Объем выражается в кубических единицах измерения, например: мм 3 , см 3 , мл 3 .
Формула вычисления объема цилиндра часто применяются при расчете массы различных цилиндров, например, прутков, заготовок и т.п. Для вычисления массы, необходимо вычисленный объем цилиндра умножить на плотность материала из которого цилиндр.
Так же, вычислить объём цилиндра иногда требуется для определения полости в виде цилиндра (цилиндрическая полость). В данном случае объём полости будет равен объёму цилиндра, который полностью занимает эту полость.
Объем и площадь других видов цилиндров рассмотрен в статьях:
[spoiler title=”источники:”]
http://geleot.ru/education/math/geometry/calc/cylinder/diameter_and_height
http://b4.cooksy.ru/articles/vysota-tsilindra-ravna-dline-okruzhnosti-osnovaniya-formula
[/spoiler]
�������
������� ������ � ������ ��������� �������� ����������� ��ߣ��,
���������� � ����� ������� R .
�������
����� h – ������ ��������, r – ������ ��� ��������� (���.1).
���������� ������� ����� ����������, ���������� ����� ţ ����� O (���.2). �
������� ��������� ���������� ������� R , � ������� ������
������������� ABCD �� ��������� AD = BC = 2r , AB = CD = h � ����������
AC=2R , ���ޣ�
����� O ���������� ��������� � ������� �������������� ABCD . ��
�������������� ������������ ACD �������, ���
4r2 = AD2 = AC2 – CD2 = 4R2 – h2.
����� V(h) – ��ߣ� ��������. �����
V(h) = π r2h = π h(4R2 – h2).
����� �������, ������ �������� � ���������� ����������� ��������
������� V(h) = π h(4R2 – h2) �� ��������� (0;2R) .
����� ��������� V’(h) = 0 , ���ģ� ����������� ����� �������
V(h) . ���������� ������ �� �� ���, ������� ����������� ����������
(0;2R) .
V’(h) = (π h(4R2 – h2))‘
= π(4R2h – h3)‘ = π (R2 –
h2).
���������� (0;2R) ����������� ������������ ������ ����� ���������
h = . ��� �������� ����� ����� h =
����������� ������ ���� � ����� �� �����. ������, �� ����������
(0;) �������
V(h) ����������, � �� ���������� (; 2R) –
�������. �������������, ��� h = ��ߣ� �������� –����������.
��� ����
r = =
= R
.
�����
; R
.
��������� � ���������� �������������
| web-���� | |
| �������� | ������� ����� �� ��������� �.�.������� |
| URL | http://zadachi.mccme.ru |
| ���������� | |
| ����� | 7444 |

