Как найти высоту цылиндра

Как вычислить высоту цилиндра

У цилиндра имеется высота, которая перпендикулярна двум его основаниям. Способ определения ее длины зависит от набора исходных данных. Таковыми могут быть, в частности, диаметр, площадь, диагональ сечения.

Инструкция

Для любых фигур существует такой термин, как высота. Высотой обычно называется измеряемая величина какой -либо фигуры в вертикальном положении. У цилиндра высота -это линия, перпендикулярная двум его параллельным основаниям. Также у него есть образующая. Образующая цилиндра -это линия, вращением которой получается цилиндр. Она, в отличие от образующей других фигур, например конуса, совпадает с высотой.

Рассмотрим формулу, с помощью которой можно найти высоту:

V=πR^2*H, где R – радиус основания цилиндра, H – искомая высота.

Если вместо радиуса дан диаметр, данная формула видоизменяется следующим образом:

V=πR^2*H=1/4πD^2*H

Соответственно, высота цилиндра равна:

H=V/πR^2=4V/D^2

Также высоту можно определить, исходя из диаметра и площади цилиндра. Существует площадь боковой и площадь полной поверхности цилиндра. Часть поверхности цилиндра, ограниченная цилиндрической поверхностью, называют боковой поверхностью цилиндра. Площадь полной поверхности цилиндра включает в себя и площадь его оснований.

Площадь боковой поверхности цилиндра вычисляется по следующей формуле:

S=2πRH

Преобразовав данное выражение, найдите высоту:

H=S/2πR

Если дана площадь полной поверхности цилиндра, вычисляйте высоту несколько иным способом. Площадь полной поверхности цилиндра равна:

S=2πR(H+R)

Вначале преобразуйте данную формулу как показано ниже:

S=2πRH+2πR

Затем найдите высоту:

H=S-2πR/2πR

Через цилиндр можно провести прямоугольное сечение. Ширина этого сечения будет совпадать с диаметрами оснований, а длина – с образующими фигуры, которые равны высоте. Если провести через это сечение диагональ, то можно легко заметить, что образуется прямоугольный треугольник. В данном случае диагональ является гипотенузой треугольника, катет -диаметром, а второй катет- высотой и образующей цилиндра. Тогда высоту можно найти по теореме Пифагора:

b^2 =sqrt (c^2 -a^2)

Источники:

• Как вычислить объем цилиндра?

Войти на сайт

или

Забыли пароль?
Еще не зарегистрированы?

Определение цилиндра: его основание и высота, разновидности

Содержание:

• Что такое цилиндр в геометрии
• Виды цилиндров
• Как найти высоту цилиндра
• Развертка
  • Развертка боковой поверхности
  • Развертка полной поверхности

Разбираемся в особенностях трехмерного геометрического тела под названием цилиндр. Смотрим виды цилиндров, его свойства, какие бывают развертки, а также даем определения составным частям этой фигуры.

Что такое цилиндр в геометрии

Определения

Цилиндр — это трехмерное геометрическое тело, которое ограничено цилиндрической поверхностью и двумя параллельными плоскостями.

Цилиндрическая поверхность — это поверхность, которая образуется за счет движения в пространстве прямой (образующей) параллельно самой себе, пересекающей данную линию (направляющую).

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.

Основания — это одинаковые круги, которые ограничивают цилиндр и находятся параллельно друг другу.

Образующая — отрезок, который соединяет точки окружностей оснований цилиндра и перпендикулярный плоскостям этих оснований. Она равна высоте цилиндра или расстоянию от одного его основания до другого.

Виды цилиндров

Классификация цилиндров может быть разной в зависимости от тех или иных параметров:

• по наклону образующей;
• по форме основания.

У прямого цилиндра образующие строго перпендикулярны основаниям фигуры.

В случае, когда этот угол не равен (90^circ), цилиндр называют наклонным.

Помимо кругов, в основаниях фигуры могут быть еще и эллипсы или другие замкнутые фигуры. Однако, кроме замкнутых форм, основании цилиндру может служить и парабола, и гипербола, и любая друга открытая функция. Такой цилиндр будет называться развернутым.

Как найти высоту цилиндра

Рассмотрим варианты нахождения высоты фигуры, а также длины ее образующей (которая равна этой высоте).

• Первым делом взглянем на формулу: (V=pi R^2times H), где V — объем цилиндра, R — радиус основания, H — высота фигуры.

Через эту формулу можем выразить высоту:

(H=frac V{pi R^2})

Таким образом мы можем узнать H данного геометрического тела, если нам известен его объем и радиус. Если же вместо радиуса мы знаем диаметр, формула расчета будет выглядеть так:

(H=frac{4V}{D^2})

В случае, когда нам известен диаметр и площадь фигуры, мы так же можем найти высоту. Следует обратить внимание, что в зависимости от того, будет ли известна площадь боковой или полной поверхности, формула будет меняться.

Для расчета S боковой поверхности (часть, ограниченная цилиндрической поверхностью) цилиндра мы используем формулу:

(S=2pi RH)

выражаем H и получаем:

(H=frac S{2pi R})

Если известна S полной поверхности (включает в себя площадь оснований фигуры), используем формулу:

(S=2pi R(H+R)=2pi Rtimes H+2pi R^2)

выражаем H и получаем:

(H=frac{S-2pi R^2}{2pi R})

• Для третьего способа нужно будет провести прямоугольное сечение, ширина которого должна будет совпадать с диаметрами оснований, а длина — с образующими цилиндра.

Таким образом, получается прямоугольный треугольник САВ. А так как высота равна образующей, мы можем вычислить ее по теореме Пифагора:

(СВ^2=АС^2-АВ^2)

(H=СВ=sqrt{АС^2-АВ^2})

Развертка

Как уже было упомянуто выше, всего существует две площади поверхности цилиндра: боковой поверхности и полной поверхности. У каждой из них также есть и своя развертка. Разберемся, как они выглядят.

Развертка боковой поверхности

Легче всего представить себе развертку боковой поверхности цилиндра, посмотрев на этикетку пластиковой бутылки. Когда вы ее отклеиваете, то видите прямоугольник. То же самое и с цилиндрическим геометрическим телом: развёрткой его боковой поверхности является прямоугольник. Его длина соответствует длине окружности, лежащей в основании, а ширина — высоте самой трехмерной фигуры.

Развертка полной поверхности

Если развернуть полную поверхность цилиндра, получится примерно то же самое, только с двумя дополнительными элементами в виде окружностей оснований. Выглядит это так:

Текст с ошибкой:

Расскажите, что не так

На этой странице вы узнаете

• Как вода в кружке иллюстрирует сечение цилиндра?
• Как лист бумаги превратить в цилиндр?

Что общего у джентльмена 19 века, Вилли Вонка из «Чарли и шоколадная фабрика», Шерлока Холмса в экранизации «Безобразная невеста» и некоторых сценических костюмов? Цилиндр! О нем, вернее о фигуре цилиндра и поговорим в статье.

Понятие цилиндра

Сейчас мы говорим про мужской головной убор, который был популярен в 19 веке и стал достаточно узнаваем в массовой культуре. Оказывается, в математике также существует цилиндр. И они похожи по форме.

Цилиндр — тело вращения, полученное при вращении прямоугольника вокруг одной из его сторон. 

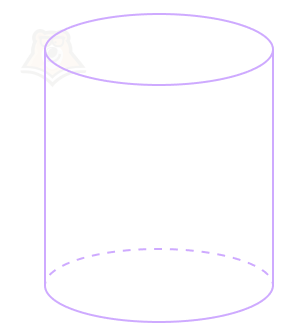
Возможно, для уточнения некоторых терминов вам захочется заглянуть в статью «Тела вращения». 

Если посмотреть на форму шляпы, то она действительно будет похожа на геометрическую фигуру.  Встретить цилиндр можно и в наше время. Обычная кружка является цилиндром.

Прямая, вокруг которой мы крутили прямоугольник, чтобы получить цилиндр, — это ось цилиндра. 

Также, как у Земли есть ось вращения, она есть и у цилиндра. 

Наша кружка стоит на круглом дне. Это дно, как и самый верх кружки, будут называться основаниями цилиндра. 

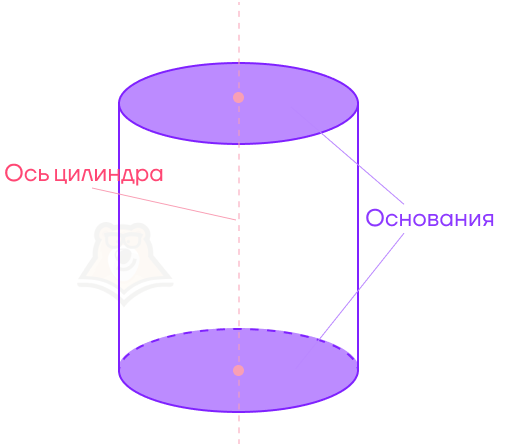
Снова посмотрим на стенки кружки. В цилиндре эта поверхность будет называться цилиндрической поверхностью. Ее также могут называть боковой поверхностью цилиндра. 

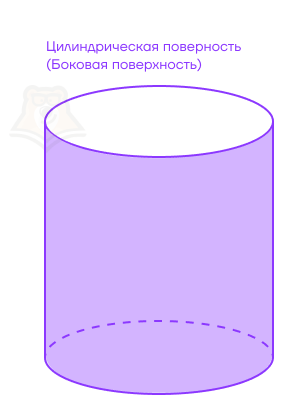
Представим, что наша кружка раскрашена вертикальными линиями. Эти линии будут лежать на цилиндрической поверхности и перпендикулярны основаниям. У них есть название:

Образующая цилиндра — отрезок, соединяющий точки окружностей основания и перпендикулярный плоскостям оснований. 

Все образующие, — а в цилиндре их очень-очень много, —лежат только на цилиндрической поверхности. Эта поверхность и состоит из множества образующих. 

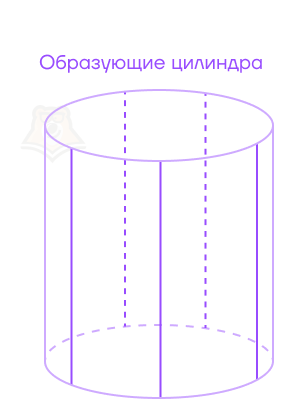
Узнаем ширину кружки. Для этого нужно измерить радиус дна. Этот же радиус будет радиусом основания, а в цилиндре он называется радиусом цилиндра. 

Теперь найдем высоту кружки. Для этого нужно измерить расстояние от дна до самого верха кружки. 

В математике это будет расстоянием между плоскостями, а ищется оно как длина перпендикуляра, опущенного из одной плоскости на другую. Подробнее про это можно прочесть в статье «Расстояния между фигурами». 

Высота цилиндра — перпендикуляр, опущенный из плоскости одного основания на плоскость второго основания. 

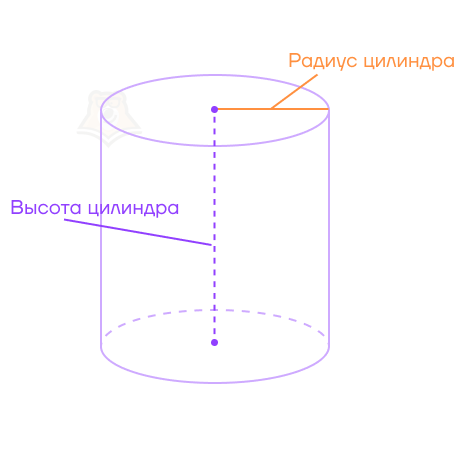
Свойства цилиндра

Рассмотрим, какими свойствами обладает цилиндр. 

Свойство 1. Основания цилиндра равны и параллельны. 

Это всегда два равных круга, лежащих в параллельных плоскостях. 

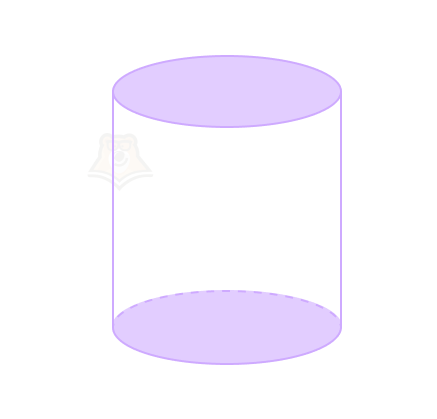
Свойство 2. Образующие цилиндра равны и параллельны. 

Поскольку все образующие перпендикулярны основаниям, то они параллельны между собой по свойству прямой и перпендикулярной ей плоскости. Подробнее про это свойство можно прочесть в статье «Углы в пространстве». 

А равны они потому, что являются перпендикуляром к основаниям, то есть равны высоте цилиндра.

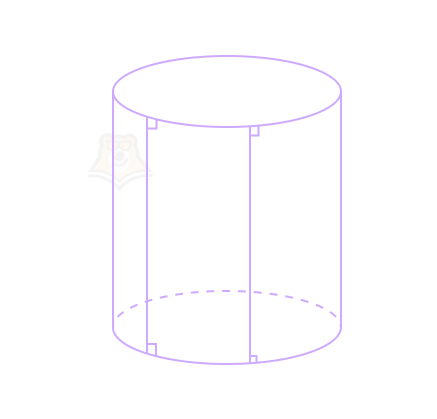
Свойство 3. Сечение цилиндра, проходящее через ось цилиндра, является прямоугольником. Такое сечение в цилиндре будет называться осевым сечением цилиндра. 

Например, если разрезать тортик по диаметру, то место среза как раз будет прямоугольником. 

Подробности про сечения фигур можно найти в статье «Сечения». 

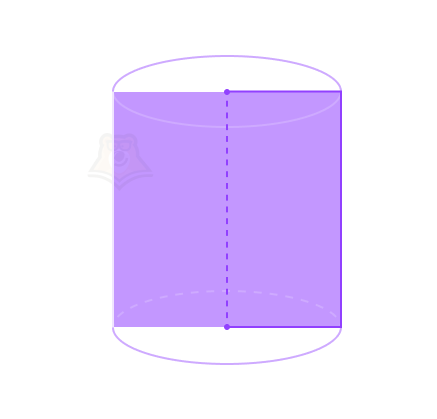
Свойство 4. Сечение цилиндра, проходящее параллельно оси цилиндра и перпендикулярно его основаниям, будет являться прямоугольником. 

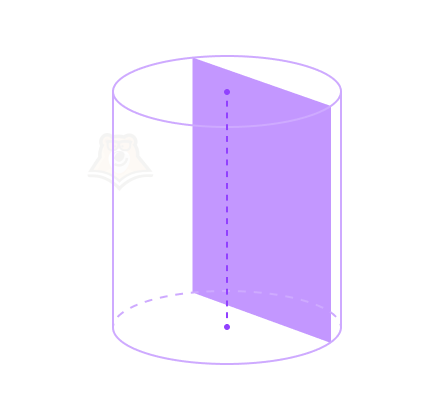
Свойство 5. Сечение цилиндра, перпендикулярное оси цилиндра, является кругом с радиусом, равным радиусу цилиндра. Такое сечение в цилиндре называется перпендикулярным сечением цилиндра. 

Заметим, что все вышеописанные свойства относятся к прямому цилиндру. 

Цилиндр также может быть наклонным. В этом случае ось цилиндра и его образующие не будут перпендикулярны основаниям. 

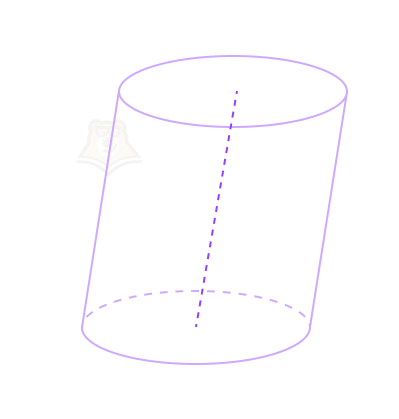
Если мы разрежем поверхность цилиндра по одной из его образующих и как бы “развернем” ее, у нас получится прямоугольник. 

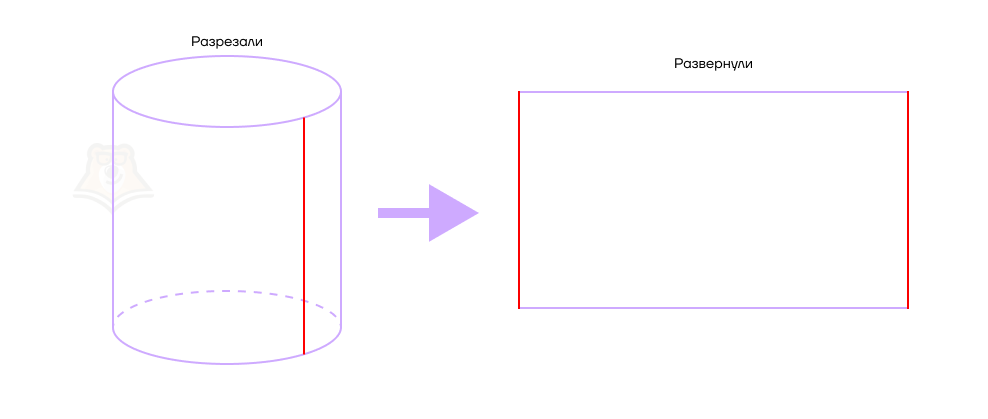
Это также легко увидеть, если вспомнить художников с тубусами. Тубус имеет форму цилиндра, и свернутый прямоугольный лист принимает такую же форму. 

Развертка боковой поверхности цилиндра — прямоугольник, одна сторона которого равна высоте цилиндра, а вторая — длине окружности его основания. 

Формулы цилиндра

А если это прямоугольник, то мы знаем, как найти его площадь. Нам нужно умножить его длину на высоту. Так мы получаем площадь боковой поверхности цилиндра. 

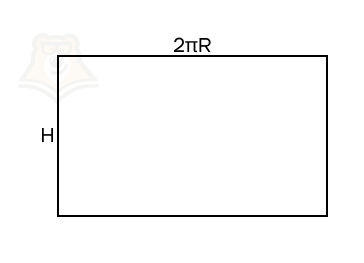
(S_{бок.} = 2 pi RH)

В этой формуле 2R — длина окружности основания, где R — его радиус, а Н — образующая (или высота) цилиндра. Подробнее про площадь прямоугольника и длину окружности (а также про площадь круга) можно прочесть в статьях «Параллелограмм» и «Окружность и круг». 

Мы нашли площадь боковой поверхности. Как же теперь найти площадь полной поверхности?

Для этого нужно сложить площади боковой поверхности и оснований. Следовательно, мы получаем следующую формулу. 

(S = S_{бок.} + 2S_{осн.} = 2 pi RH+2 pi R^2 = 2 pi R(H + R))

Допустим, мы решили сделать чашку очень вкусного чая, но чтобы правильно его заварить нам нужно знать точный объем воды. Для этого вычислим объем цилиндра. Воспользуемся следующей формулой:

(V = S_{осн.}H = pi R^2H)

В этой формуле R — радиус цилиндра, Н — высота. 

Часто формулу объема можно применить для решения жизненных задач. Например, чтобы найти объем детали, погруженной в воду. 

Пример 1. В цилиндрическом сосуде налито 1650 см³ жидкости. В этот сосуд опустили деталь. При этом уровень жидкости увеличился в 1,2 раза. Найдите объем детали. Ответ выразите в см³. 

Решение. 

Шаг 1. Выразим высоту жидкости в первый и второй раз. Пусть вначале уровень жидкости был равен х, значит после того, как в нее опустили деталь, он стал равен 1,2х. 

Шаг 2. Вспомним физику и заметим, что объем жидкости в сосуде после того, как в него опустили деталь, будет равен сумме объемов жидкости и детали: V = V_ж + V_д. 

Шаг 3. С помощью объема жидкости выразим площадь основания сосуда:

V_ж = S_осн.H
1650 = S_осн.x
(S_{осн} = frac{1650}{x})

Шаг 4. Подставим площадь основания в формулу объема жидкости после того, как в нее опустили деталь:

(V = S_{осн.}H = frac{1650}{x} * 1,2x = 1980)

Шаг 5. Тогда объем детали будет равен:

V_д = V — V_ж
V_д = 1980 — 1650 =330 

Ответ: 330 см³

Фактчек

• Цилиндр — тело вращения, полученное при вращении прямоугольника вокруг одной из его сторон. Цилиндр может быть прямым и наклонным. В наклонном цилиндре ось не перпендикулярна основаниям цилиндра. 
• Цилиндр состоит из двух оснований и цилиндрической поверхности (боковой поверхности цилиндра). Основания имеют форму кругов, равны между собой и лежат в параллельных плоскостях. Развертка боковой поверхности имеет форму прямоугольника. 
• Образующая цилиндра — отрезок, соединяющий точки окружностей основания и перпендикулярный плоскостям оснований. В прямом цилиндре образующая равна высоте цилиндра. Образующие равны и параллельны друг другу, а также образуют боковую поверхность цилиндра. 
• Осевое сечение цилиндра проходит через его ось и является прямоугольником. Любое сечение, параллельное осевому, также будет являться прямоугольником. Перпендикулярное сечение проходит перпендикулярно оси цилиндра и параллельно его основаниям. Перпендикулярное сечение имеет форму круга. 

Проверь себя

Задание 1. 
Что такое образующая цилиндра?

1. Ось вращения, с помощью которой получен цилиндр.
2. Диаметр оснований цилиндра.
3. Любой перпендикуляр, проведенный от одного основания к другому.
4. Отрезок, соединяющий точки окружности основания. 

Задание 2. 
Площадь боковой поверхности цилиндра равняется 44. Его радиус равен 8. Найдите высоту цилиндра. 

1. 2,75
2. 5,5
3. (2,75 pi)
4. 2

Задание 3. 
Площадь основания цилиндра равна 16. Его высота равна 4. Найдите площадь полной поверхности цилиндра. 

1. 64
2. (64 pi)
3. 32
4. (32 pi)

Задание 4. 
Объем цилиндра равен 28, а его высота равняется 7. Найдите диаметр основания.

1. 4
2. 2
3. 16
4. 8

Ответы: 1. – 4 2. – 1 3. – 2  4. – 1

Диаметр и высота цилиндра

Свойства

Через диаметр цилиндра можно рассчитать его радиус и периметр основания цилиндра. Радиус будет равен половине диаметра, а периметр – его произведению на число π. r=D/2 P=πD

Зная диаметр и высоту цилиндра, можно узнать площадь, объем, диагональ цилиндра и остальные параметры. Площадь боковой поверхности цилиндра представляет собой площадь прямоугольника, сторонами которого являются периметр основания цилиндра и его высота. Чтобы затем найти площадь полной поверхности цилиндра через диаметр и высоту, нужно к площади боковой поверхности добавить площадь верхнего и нижнего оснований, каждое из которых равно произведению числа π на четверть квадрата диаметра. S_(б.п.)=hP=πDh S_(п.п.)=S_(б.п.)+2S_(осн.)=πDh+(πD^2)/2=πD/2(2h+D) P=πD

Объем цилиндра представляет собой площадь его основания, умноженную на высоту. Чтобы найти объем цилиндра через диаметр и высоту, нужно умножить квадрат диаметра на четверть числа π и на высоту. V=(πD^2 h)/4 P=πD

Диагональ цилиндра находится из прямоугольного треугольника, в котором она является гипотенузой, а катеты представлены высотой и диаметром цилиндра. По теореме Пифагора диагональ цилиндра через высоту и диаметр цилиндра равна квадратному корню из суммы их квадратов. (рис. 25.1) d=√(h^2+D^2 ) P=πD

Чтобы найти радиус сферы вписанной в цилиндр, если его диаметр равен высоте, нужно разделить диаметр цилиндра либо высоту на два, так как радиус вписанной сферы равен радиусу цилиндра. (рис.25.2) r_1=h/2=D/2 P=πD

Радиус сферы, описанной вокруг цилиндра, при соблюдении тех же условий (равенство диаметра цилиндра и его высоты) равен половине диагонали цилиндра.(рис.25.3) R=d/2=√(h^2+D^2 )/2

Высота цилиндра равна длине окружности основания формула

Как найти высоту цилиндра, с помощью данных?

Объем цилиндра формула (через радиус основания и высоту)

r — радиус основания цилиндра,

h — высота цилиндра

Если внимательно посмотреть на эту формулу, то можно заметить, что

— это формула площади круга, а в нашем случае — площадь основания. Поэтому формулу объема цилиндра можно записать через площадь основания и высоту:

S (б.п.) = hP = 2πrh

— Если известна площадь бок. поверхности S (б.п.) и высота h цилиндра, радиус будет равен частному от деления S (б.п.) на произведение 2пи на высоту:

Формула вычисления объема цилиндра

1. Через площадь основания и высоту

Объем (V) цилиндра равняется произведению его высоты и площади основания.

V = S ⋅ H

2. Через радиус основания и высоту

Как мы знаем, в качестве оснований цилиндра (равны между собой) выступает круг, площадь которого вычисляется так: S = π ⋅ R 2 . Следовательно, формулу для вычисления объема цилиндра можно представить в виде:

V = π ⋅ R 2 ⋅ H

Примечание: в расчетах значение числа π округляется до 3,14.

3. Через диаметр основания и высоту

Как нам известно, диаметр круга равняется двум его радиусам: d = 2R. А значит, вычислить объем цилиндра можно следующим образом:

V = π ⋅ (d/2) 2 ⋅ H

Нет сомнений, что все мы со школьных лет помним, как найти высоту цилиндра, формула выглядит так: H=V/πR^2 или 4V/D^2.

Расшифровать формулу просто:

• V – объем цилиндра;
• π – 3,14;
• R – радиус цилиндра;
• D – диаметр.

То есть получается, что, если разделить объем на площадь основания, получится высота цилиндра.

Можно поступить проще. Для этого нам придется вычислить площадь боковой поверхности искомого цилиндра. Это легко сделать по формуле: S=2πRH. Слегка изменив формулу, получаем: H=S/2πR.

Таким образом, есть уже два способа, которые помогли вспомнить, как найти высоту цилиндра. Это нетрудно, когда перед глазами стройные формулы.

Способ расчета радиуса цилиндра:

Цилиндр – геометрическое тело, которое получается при вращении прямоугольника вокруг его стороны. Также, цилиндр представляет собой тело, ограниченное цилиндрической поверхностью и двумя параллельными плоскостями, пересекающими ее. Эта поверхность образуется при движении прямой параллельно самой себе. При этом выделенная точка прямой перемещается вдоль определенной плоской кривой (направляющая). Данная прямая называется образующей цилиндрической поверхности.
Формула радиуса цилиндра:
где V – объем цилиндра, h – высота

Цилиндр – геометрическое тело, которое получается при вращении прямоугольника вокруг его стороны. Также, цилиндр представляет собой тело, ограниченное цилиндрической поверхностью и двумя параллельными плоскостями, пересекающими ее. Эта поверхность образуется при движении прямой параллельно самой себе. При этом выделенная точка прямой перемещается вдоль определенной плоской кривой (направляющая). Данная прямая называется образующей цилиндрической поверхности.
Формула радиуса цилиндра:
где Sb – площадь боковой поверхности, h – высота

Цилиндр – геометрическое тело, которое получается при вращении прямоугольника вокруг его стороны. Также, цилиндр представляет собой тело, ограниченное цилиндрической поверхностью и двумя параллельными плоскостями, пересекающими ее. Эта поверхность образуется при движении прямой параллельно самой себе. При этом выделенная точка прямой перемещается вдоль определенной плоской кривой (направляющая). Данная прямая называется образующей цилиндрической поверхности.
Формула радиуса цилиндра:
где S – площадь полной поверхности, h – высота

S (п.п.) = S (б.п.) + 2S (осн.) = 2πrh + πr2=πr (2h+r)

Площадь боковой поверхности равняется длине окружности основания умноженной на высоту:

R = √V / πh

где V — объем цилиндра, h — высота.
Полная площадь поверхности цилиндра складывается из сумм площадей его боковой поверхности и двух оснований:

Примеры задач

Задание 1
Высота цилиндра равняется 5 см, а объем – 141,3 см 3 . Вычислите его радиус.

Решение:
Воспользуемся соответствующей формулой, подставив в нее известные по условиям задачи значения:

Задание 2
Найдите радиус цилиндра, если площадь его боковой поверхности равна 175,84 см 2 , а высота составляет 7 см.

Решение:
Применим формулу, в которой задействованы заданные величины:

Задание 3
Рассчитайте радиус цилиндра, если полная площадь его поверхности – 602,88 см 2 , а высота – 10 см.

Решение:
Используем третью формулу для нахождения неизвестной величины:

Через площадь боковой поверхности

Радиус цилиндра считается таким образом:

S_бок. – площадь боковой поверхности цилиндра; равна произведению длины окружности (2 π R), являющейся основанием фигуры, на его высоту:

S = 2 π Rh

Площадь полной поверхности цилиндра через радиус основания и высоту

Формула для нахождения полной поверхности цилиндра через высоту и радиус основания:

, где π — число Пи (3,14159…), r — радиус основания цилиндра, h — высота цилиндра.

Высота цилиндра равна длине окружности

537. Диаметр основания цилиндра равен 1 м, высота цилиндра равна длине окружности основания. Найдите площадь боковой поверхности цилиндра.

Решебник по геометрии за 10 класс (Л.С.Атанасян, 2001 год),
задача №537
к главе «Глава VI. Цилиндр, конус и шар § 1. цилиндр».

Выделите её мышкой и нажмите CTRL + ENTER

Большое спасибо всем, кто помогает делать сайт лучше! =)

Нажмите на значок глаза возле рекламного блока, и блоки станут менее заметны. Работает до перезагрузки страницы.

Диаметр основания цилиндра равен 1м высота цилиндра равна длине окружности

Диаметр основания цилиндра равен 1м, высота цилиндра равна длине окружности основания. Найдите площадь боковой поверхности цилиндра.

Длина окружности основания равна

Высота цилиндра равна 3.14 м

Площадь боковой поверхности цилиндра равна

S=Lh, где L-длина окружности основания h-высота цилиндра

S=L*L=п*п=3,14*3,14=9,86 кв.м ( хотя наверное лучше оставить п в квадрате, так вроде точнее) п-это пи

Другие вопросы из категории

adef и найдите его периметр

Читайте также

2)Основание пирамиды -прямоугольный треугольник , катет которого равен 20м,а гипотенуза 25м ,высота 10м.Найдите объем пирамиды. 3)Высота правильной четырехугольной пирамиды равна 4 см,а апофема образует с высотой угол 45 градусов. Найдите площадь боковой поверхности пирамиды. 4)Боковое ребро правильной треугольной пирамиды равна 4 корень из 3и наклонено к плоскости основания под углом 60 градусов.Найдите площадь боковой поверхности. 5)В правильной четырехугольной пирамиде MABCD площадь ее основания ABCD равна 32 см ^2, а лощадь треугольника МАС равна 16 см^2.Найдите плоский угол при вершине пирамиды.

2.В правильной 3угольной пирамиде боковое ребро равно 10 см и наклонено к плоскости основы под углом .Найдите высоту пирамиды.

3.В правильной 4угольной пирамиде боковая грань наклонена к основе по д углом , а ее высота равна 12 см.Найтдите апофему пирамиды.

4.Найдите площадь полной поверхности правильной 4угольной

пирамиды, в которой сторона основы равна 6 см, а боковая грань наклонена к основе под углом .

5.Найдите площадь полной поверхности правильной 3угольной пирамиды, в которой апофема равна L и образует с высотой пирамиды угол .

Помогите решить хотя-бы 2 номера..буду благодарна за помощь)

2) Боковое ребро треугольной наклонной призмы равно 8 см, а расстояния между боковыми рёбрами равны 3 см, 4 см, и 5 см. Найдите площадь боковой поверхности призмы

2.) Основанием прямого параллелепипеда служит ромб со стороной а и острым углом Q. Величина угла, образованного меньшей диагональю параллелепипеда с плоскостью его основания, равна 60 градусов. Найдите площадь боковой поверхности этого параллелепипеда.
3.) Основанием пирамиды служит правильный треугольник со стороной 6 см; две боковые грани пирамиды перпендикулярны плоскостью основания; угол, образованной третьей гранью с основанием пирамиды, равен 60 градусам. Найдите площадь полной поверхности пирамиды.
Пожалуйста, напишите все задания с подробными решениями. Заранее спасибо!

точки а до центра основания, содержащего точку б, равно 13м. найдите площадь боковой поверхности цилиндра

Как найти площадь поверхности цилиндра: боковую, основания, полную

Площадь боковой поверхности цилиндра

Формула площади боковой поверхности цилиндра представляет собой произведение длины основания на его высоту:

Таким образом, используя формулы площади оснований и боковой поверхности фигуры, мы смогли найти полную площадь поверхности цилиндра.
Осевое сечение цилиндра представляет собой прямоугольник, в котором стороны равны высоте и диаметру цилиндра.
Формула площади осевого сечения цилиндра выводится из формулы расчета площади прямоугольника :

Круговой цилиндр

где r – радиус основы, h – высота цилиндра, d – диаметр основы.

Как рассчитать площадь боковой поверхности цилиндра с помощью калькулятора

Калькулятор позволяет определить площадь цилиндра по одному из 2 вариантов исходных данных:

1. внешний радиус и высота;
2. внешний диаметр и высота.

Выберите соответствующий шаг и введите исходные данные в соответствующие поля.

Также важно указать единицы измерения по условиям задачи.

Расчеты будут выполнены автоматически и конвертированы в основные метрические физические величины площади.

Примеры задач

Задание 1
Найдите площадь боковой поверхности цилиндра, если его радиус равен 11 см, а высота – 8 см.

Решение:
Воспользуемся первой формулой, подставив в нее данные по условиям задачи значения:
S = 2 ⋅ 3,14 ⋅ 11 см ⋅ 8 см = 552,64 см 2 .

Задание 2
Высота цилиндра равна 9 см, а его диаметр – 8 см. Найдите суммарную площадь поверхности фигуры.

Решение:
Если диаметр цилиндра равен 8 см, значит его радиус составляет 4 см (8 см / 2). Применив соответствующую формулу для нахождения площади получаем:
S = 2 ⋅ 3,14 ⋅ 4 см ⋅ (9 см + 4 см) = 326,56 см 2 .

Осевое сечение прямого цилиндра

Осевым называется любое сечение цилиндра, которое содержит его ось. Это определение означает, что осевое сечение будет всегда параллельно образующей линии.

В цилиндре прямом ось проходит через центр круга и перпендикулярна его плоскости. Это означает, что рассматриваемое сечение круг будет пересекать по его диаметру. На рисунке показана половинка цилиндра, которая получилась в результате пересечения фигуры плоскостью, проходящей через ось.

Не сложно понять, что осевое сечение прямого круглого цилиндра представляет собой прямоугольник. Его сторонами являются диаметр d основания и высота h фигуры.

Запишем формулы для площади осевого сечения цилиндра и длины hd его диагонали:

Прямоугольник имеет две диагонали, но обе они равны друг другу. Если известен радиус основания, то не сложно переписать эти формулы через него, учитывая, что он в два раза меньше диаметра.

Введите радиус основания и высоту цилиндра

Радиус:

Высота:

Цилиндр – геометрическое тело, которое получается при вращении прямоугольника вокруг его стороны. Также, цилиндр представляет собой тело, ограниченное цилиндрической поверхностью и двумя параллельными плоскостями, пересекающими ее. Эта поверхность образуется при движении прямой параллельно самой себе. При этом выделенная точка прямой перемещается вдоль определенной плоской кривой (направляющая). Данная прямая называется образующей цилиндрической поверхности.

Площадь полной поверхности цилиндра формула:
S = Sбок + 2 Sосн 2 , где Sбок – площадь боковой поверхности, Sосн – площадь основания
или
S = 2 π R h + 2 π R 2 , где R – радиус оснований, h – высота цилиндра, π – число пи

Площадь полной поверхности цилиндра

Для нахождения полной площади цилиндра нужно к полученной Sбок добавить площади двух окружностей, верха и низа цилиндра, которые считаются по формуле Sо = 2π * r2.

Конечная формула выглядит следующим образом:

Sпол = 2π * r2 + 2π * r * h.

Основные определения и свойства цилиндра

Рассмотрим две паралллельные плоскости паралллельные плоскости α и β и произвольную окружность радиуса r с центром в точке O , лежащую в плоскости α (рис. 1).

Если из каждой точки окружности опустить перпендикуляр на плоскость β , то основания этих перпендикуляров образуют на плоскости β окружность радиуса r , центр O₁ которой является основанием перпендикуляра, опущенного из точки O на плоскость β (рис.2).

Отрезок перпендикуляра , опущенного из любой точки окружности с центром O на плоскость β , который заключен между плоскостями α и β , называют образующей цилиндра .

Совокупность всех образующих цилиндра называют цилиндрической поверхностью .

Фигуру, ограниченную цилиндрической поверхностью и плоскостями α и β, называют цилиндром .

Отрезок OO₁ называют осью цилиндра .

Радиус окружности Радиус окружности на плоскости α с центром в точке O называют радиусом цилиндра .

Расстояние между плоскостями Расстояние между плоскостями α и β , называют высотой цилиндра .

Круги с центрами O и O₁ на плоскостях α и β , называют основаниями цилиндра .

Замечание 1. Цилиндрическую поверхность часто называют боковой поверхностью цилиндра . Боковая поверхность цилиндра и основания цилиндра вместе составляют полную поверхность цилиндра .

Замечание 2. Каждая образующая цилиндра параллельна оси цилиндра, а длина каждой образующей цилиндра равна высоте цилиндра.

Замечание 3. Прямая OO₁ является осью симметрии цилиндра, а середина отрезка OO₁ является центром симметрии цилиндра.

Геометрическая фигура

Сначала дадим определение фигуре, о которой пойдет речь в статье. Цилиндр представляет собой поверхность, образованную параллельным перемещением отрезка фиксированной длины вдоль некоторой кривой. Главным условием этого перемещения является то, что отрезок плоскости кривой принадлежать не должен.

На рисунке ниже показан цилиндр, кривая (направляющая) которого является эллипсом.

Здесь отрезок длиной h является его образующей и высотой.

Видно, что цилиндр состоит из двух одинаковых оснований (эллипсы в данном случае), которые лежат в параллельных плоскостях, и боковой поверхности. Последней принадлежат все точки образующих линий.

Осевое сечение наклонного цилиндра

Рисунок выше демонстрирует наклонный цилиндр, изготовленный из бумаги. Если выполнить его осевое сечение, то получится уже не прямоугольник, а параллелограмм. Его стороны – это известные величины. Одна из них, как и в случае сечения прямого цилиндра, равна диаметру d основания, другая же – длина образующего отрезка. Обозначим ее b.

Для однозначного определения параметров параллелограмма недостаточно знать его длины сторон. Необходим еще угол между ними. Предположим, что острый угол между направляющей и основанием равен α. Он же и будет углом между сторонами параллелограмма. Тогда формулу для площади осевого сечения наклонного цилиндра можно записать следующим образом:

Диагонали осевого сечения цилиндра наклонного рассчитать несколько сложнее. Параллелограмм имеет две диагонали разной длины. Приведем без вывода выражения, позволяющие рассчитывать диагонали параллелограмма по известным сторонам и острому углу между ними:

l1 = √(d2 + b2 – 2*b*d*cos(α));

l2 = √(d2 + b2 + 2*b*d*cos(α))

Здесь l1 и l2 – длины малой и большой диагоналей соответственно. Эти формулы можно получить самостоятельно, если рассмотреть каждую диагональ как вектор, введя прямоугольную систему координат на плоскости.

Примеры расчета площади поверхности цилиндра

Для понимания приведенных формул попробуем посчитать площадь поверхности цилиндра на примерах.

1. Радиус ос­но­ва­ния цилиндра равен 2, высота равна 3. Определите площадь боковой поверхности цилиндра.

S_бок. = 2 * 3,14 * 2 * 3

Площадь боковой поверхности цилиндра равна 37,68.

2. Как найти площадь поверхности цилиндра, если высота равна 4, а радиус 6?

S = 2 * 3,14 * 6 2 + 2 * 3,14 * 6 * 4

S = 2 * 3,14 * 36 + 2 * 3,14 * 24

S = 226,08 + 150,72

Площадь поверхности цилиндра равна 376,8.

3. Площадь боковой поверхности прямого кругового цилиндра равна 24π, а диаметр основания — 3. Найдите высоту цилиндра.

Из формулы расчета площади боковой поверхности цилиндра Sбок. = 2πrh следует, что высота равна:

Значение радиуса получаем из формулы: d = 2r

h = 24π / (2π * 0,5d)

h = 24π / (2π * 0,5 * 3)

Высота цилиндра равна 8.

Площадь цилиндра формула через диаметр

Для облегчения расчетов иногда требуется произвести вычисления через диаметр. Например, имеется кусок полой трубы известного диаметра.

Не утруждая себя лишними расчетами, имеем готовую формулу. На помощь приходит алгебра за 5 класс.

Sпол = 2π * r2 + 2π * r * h = 2π * d2/4 + 2π * h * d/2 = π * d2/2 + π * d * h,

Вместо r в полную формулу нужно вставить значение r = d/2.

Площадь боковой поверхности цилиндра через радиус основания и высоту

Формула для нахождения боковой поверхности цилиндра через высоту и радиус основания:

, где π — число Пи (3,14159…), r — радиус основания цилиндра, h — высота цилиндра.

Заключение

В конце статьи назрел вопрос: а так ли необходимы все эти вычисления и переводы одних значений в другие. Зачем все это нужно и самое главное, для кого? Но не стоит пренебрегать и забывать простые формулы из средней школы.

Мир стоял и будет стоять на элементарных познаниях, из математики, в том числе. И, приступая к какой-нибудь важной работе, никогда не лишне освежить в памяти данные выкладки, применив их на практике с большим эффектом. Точность – вежливость королей.

Объем цилиндра

Объем цилиндра, формулы и калькулятор для вычисления объема цилиндра и площади его поверхностей, а также необходимая теория о характеристиках цилиндра.

Объем правильного цилиндра через радиус и высоту цилиндра

Формулы и калькулятор для вычисления объема цилиндра через площадь основания и высоту цилиндра

Формулы и калькулятор для вычисления объема цилиндра через диаметр основания

Объем цилиндрической полости

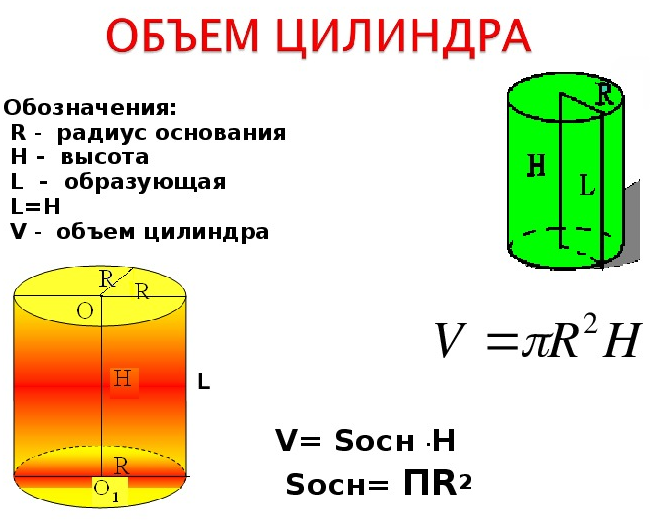
Объем полости в виде цилиндра равен объему цилиндра, который извлечен из данной полости для ее образования. То есть для вычисления цилиндрической полости можно воспользоваться формулами и калькулятором для расчета простого правильного цилиндра в зависимости от известных исходных данных.

На картинке продемонстрирована цилиндрическая полость, образованная в теле путем извлечения из него цилиндра. Объем извлеченного цилиндра и объем образованной полости равны.

Нужно отметить один важный момент. Несмотря на равенство объемов извлеченного цилиндра и образованной полости, площади поверхностей данных объектов будут отличаться, так как у образованной цилиндрической полости отсутствует верхняя поверхность. То есть суммарная площадь поверхности образованной цилиндрической полости будет меньше суммарной площади извлеченного цилиндра на одну площадь основания цилиндра.

Цилиндр может быть правильным или наклонным .

Правильный цилиндр – это цилиндр, где угол между образующими боковой поверхности и основанием цилиндра равен 90 градусов.

Неправильный или наклонный цилиндр – это цилиндр, где угол между образующими боковой поверхности и основанием цилиндра отличается от 90 градусов.

Рассмотрим правильный цилиндр.

Цилиндр – это тело, образованное вращением прямоугольника вокруг одной из его сторон. Тело цилиндра ограничено двумя кругами, называемыми основанием цилиндра и боковой цилиндрической поверхностью, которая в развертке представляет собой прямоугольник

Цилиндр можно так же описать как тело, состоящее из двух равных кругов, не лежащих в одной плоскости и параллельных между собой, и отрезков, соединяющих все точки одной окружности, с соответствующими точками другой окружности. Данные отрезки называются образующими цилиндра.

Радиус основания цилиндра, является радиусом цилиндра.

Ось цилиндра – это прямая, соединяющая центра оснований цилиндра.

Высота цилиндра – это перпендикуляр, опущенный от одного основания цилиндра к другому.

Поверхности цилиндра

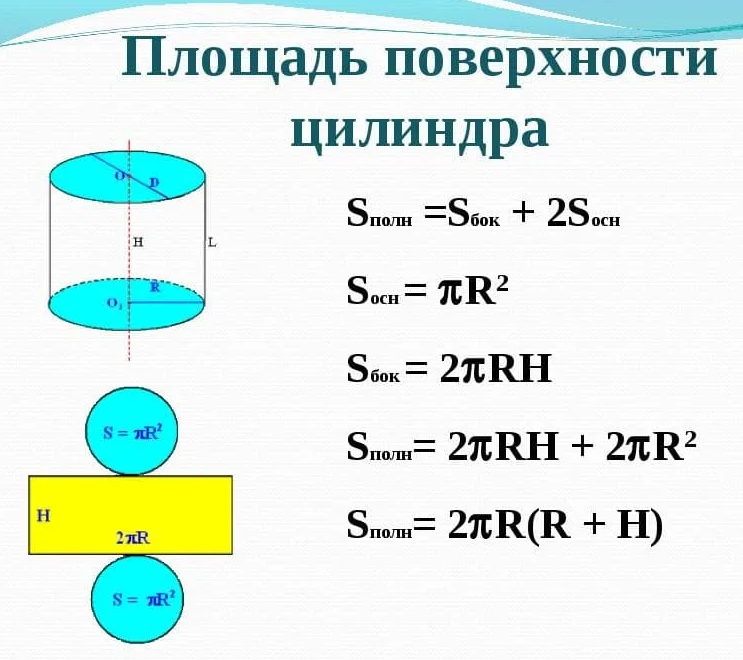
Наружную поверхность цилиндра можно условно разделить на три отдельные поверхности: верхняя, нижняя и боковая.

Верхняя и нижняя поверхности цилиндра имеют форму круга и равны между собой.

Боковая поверхность цилиндра имеет форму прямоугольника. Чтобы это наглядно представить, возьмем боковую наружную поверхность цилиндра и мысленно сделаем вертикальный разрез по образующей цилиндра. Далее развернем поверхность на плоскость. В результате увидим, что боковая поверхность имеет форму прямоугольника (см. на картинке).

Сечения цилиндра

При сечении цилиндра плоскостью, проходящей через оба основания цилиндра под углом в 90 градусов, всегда получатся прямоугольная фигура .

При сечении цилиндра плоскостью, проходящей через оба основания цилиндра под углом отличным от 90 градусов, получатся фигура, похожая на прямоугольник , но две боковые стороны которого будут являться кривыми линиями.

Если секущая поверхность проходит параллельно основаниям цилиндра, то сечением будет круг .

Если секущая поверхность проходит через боковую поверхность, но при этом не параллельна основанию цилиндра, то в сечении получается эллипс .

Если секущая поверхность проходит через одно основание цилиндра и боковую поверхность, то в сечение будет фигура в виде половины эллипса .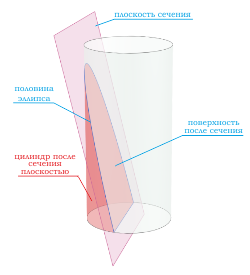

Что такое объем

Объем тела (геометрической фигуры) – это количественная характеристика, характеризующая количество пространства, занимаемого телом. Объем выражается в кубических единицах измерения, например: мм 3 , см 3 , мл 3 .

Формула вычисления объема цилиндра часто применяются при расчете массы различных цилиндров, например, прутков, заготовок и т.п. Для вычисления массы, необходимо вычисленный объем цилиндра умножить на плотность материала из которого цилиндр.

Так же, вычислить объём цилиндра иногда требуется для определения полости в виде цилиндра (цилиндрическая полость). В данном случае объём полости будет равен объёму цилиндра, который полностью занимает эту полость.

Объем и площадь других видов цилиндров рассмотрен в статьях:

[spoiler title=”источники:”]

http://geleot.ru/education/math/geometry/calc/cylinder/diameter_and_height

http://b4.cooksy.ru/articles/vysota-tsilindra-ravna-dline-okruzhnosti-osnovaniya-formula

[/spoiler]