В полевых условиях иногда бывает очень важно и полезно владеть простейшими прикладными способами измерений на местности. Например способами определения высоты дерева или любого другого предмета на местности.
Простые способы определения высоты дерева или любого другого предмета по тени, шесту, лужице или зеркалу, прямоугольному треугольнику.
Высоту дерева или любого другого предмета на местности очень просто можно определить по тени, шесту, лужице или зеркальцу, и прямоугольному треугольнику.
Способ определения высоты дерева или другого предмета по своему росту и длине тени.
Если на ровном месте измерить шагами длину своей тени, а затем длину тени, отбрасываемой деревом илипредметом, то искомую высоту легко вычислить из пропорции :
АК/ак = КЕ/ке
где АК — высота дерева (В), КЕ — тень дерева (D), ак — ваш рост (b), ке — ваша тень (d).
Например длина вашей тени d равна трем шагам, тень дерева D равна девяти шагам, то есть тень дерева длиннее вашей тени в три раза. Если принять ваш рост за 1,5 метра, то высота дерева будет В = 1,5 х 3 = 4,5 метра.
Способ определения высоты дерева или другого предмета по шесту и своему росту.
Этот же способ можно применить при пасмурной погоде, когда тени от предметов не видны. В этом случае для измерения нужно взятьшест, равный длине вашего роста. Шест этот надо установить на таком расстоянии от дерева, чтобы лежа можно было видеть верхушку дерева на одной прямой линии с верхней точкой шеста. Тогда высота дерева равна расстоянию от вашей головы до основания дерева, то есть АС = ВС.
Способ определения высоты дерева или другого предмета по лужице или зеркальцу.
По лужице, зеркальцу илигелиографу высоту дерева или любого другого предмета на местности, можно измерять следующим образом. Станьте так, чтобы лужица поместилась между вами и деревом (В). Найдите точку, из которой видна отраженная в воде вершина дерева. Измеряемоедерево будет во столько раз выше вас, во сколько расстояние от него до лужицы (ВО) больше расстояния от лужицы до вас (АО). Вместо лужицы также можно воспользоваться зеркальцем, положив его горизонтально так, чтобы увидеть вершину дерева.
Способ определения высоты дерева или другого предмета с помощью прямоугольного треугольника с двумя острыми углами по 45 градусов.
С помощью прямоугольного треугольника с двумя острыми углами по 45 градусов, высоту дерева или другогопредмета определяют так. Отходя от дерева на некоторое расстояние и прикладывая треугольник к глазам так, чтобы один из его катетов был параллелен оси дерева, второй — параллелен земной поверхности, а гипотенуза представляла собой линию визирования.
Затем добиваются такого положения, чтобы линия визирования прошла через вершину дерева. В этом случае высота дерева D равна расстоянию от наблюдателя до дерева и плюс рост наблюдателя.
По материалам книги «Карта и компас мои друзья».
Клименко А.И.
Районная учебно – исследовательская конференция школьников
«Первые шаги»
Секция: физика, математика
Тема: «Определение высоты дерева различными физическими способами»
Работу выполнил: Дмитриев Игорь, учащийся 7 класса
Руководитель: Смирнова Светлана Николаевна, учитель физики
Холм 2014 г.
Cодержание
Введение…………………………………………………………………3 – 4 стр.
Основная часть
1. План эксперимента……………………………………………………5 стр.
2. Описание эксперимента……………………………………………….5 стр.
2.1. Поиск различных способов определения высоты дерева,
не срубая его и не влезая на него…………………………………………6-13 стр.
2.2. Выбор оптимальных способов определения высоты дерева……….13 стр.
2.3. Изготовление приборов и сбор подручных средств
для проведения эксперимента……………………………………………..13 стр.
2.4. Проведение эксперимента…………………………………………13-16 стр.
2.5. Анализ результатов, их обоснование,
формулировка выводов…………………………………………………16-18 стр.
Заключение…………………………………………………………………19 стр.
Список использованной литературы……………………………………20 стр.
Введение
Использование различных приборов, механизмов и приспособлений в наше время значительно упрощает жизнь современных людей. Но иногда возникают ситуации, когда нет возможности применить технические средства. Например: часто туристам требуется определить расстояния на местности, оценить размеры предметов для того, чтобы быстро превратить прибрежное дерево в мостик через быструю речку (если, конечно, речь идет не о заповедной зоне или чьем-то участке). Как правило, они не кладут в свои рюкзаки высотомеры. Хотя, казалось бы, уж им эти приборы крайне необходимы.
Но в этом и состоит суть экстремальных увлечений, что они позволяют получать удовольствие от собственных побед — над ленью, обыденностью, интеллектуальной зависимостью от кем-то придуманных технических устройств. Почувствовать себя опытным следопытом или разведчиком может каждый. Стоит только этого захотеть и постараться абстрагироваться от стереотипов. В частности, определить, достаточно ли высоты дерева, чтобы оно, упав, могло перекрыть речку, можно с помощью предметов, которые всегда есть под рукой.
Измерение ширины реки, высоты предмета и определение расстояния до какого – либо объекта часто применимо в нашей повседневной жизни. Выбранная тема актуальна тем, что появляется возможность узнать, как без каких-либо сложных технических устройств можно определить расстояние до недоступных точек. Например, измерить высоту столба, дерева в походе, церкви, зданий, ширину реки, оврага, глубину рек и т.д. Видна в теме практическая значимость.
Проблема: Как определить высоту дерева, не срубая его и не влезая на него?
Гипотеза: Существуют различные способы измерения объектов без специальных измерительных приборов.
Цель эксперимента: определить высоту дерева различными физическими способами без специальных приборов.
Объект исследования: дерево (ель) и здание школы.
Предмет исследования – высота дерева и способы её измерения.
Задачи:
1. Найти всевозможные способы определения высоты дерева без измерительных приборов, не влезая на него и не срубая его.
2. Отобрать наиболее приемлемые и простые способы определения высоты деревьев.
3. Экспериментально проверить использование различных способов определения высоты предмета.
4. Сопоставить результаты исследований и найти наиболее точный способ определения высоты предмета.
Методы исследования:
1.Изучение литературы и ресурсов Интернет
2. Эксперимент
3.Использование технических средств
4. Сравнительный анализ.
Основная часть
-
План эксперимента.
№
План эксперимента
Срок
1.
С помощью различных литературных и Интернет источников найти различные способы измерения высоты дерева, не срубая его.
14 ноября
2.
Выбрать оптимальные способы определения высоты дерева, обсуждение их точности и выполнимости.
15 ноября
3.
Изготовление приборов и сбор подручных средств для проведения эксперимента.
15 ноября
4.
Проведение эксперимента, используя 2 – 3 различных способа (для точности результатов)- экскурсия.
15 ноября
5.
Выполнение расчетов полученных измерений.
16 ноября
6.
Сравнительный анализ результатов, их обоснование, формулировка выводов.
16 ноября
7.
Проверка данных измерений (определение высоты здания школы теми же методами)
27 ноября
8.
Сравнительный анализ данных, определение более точного метода для расчёта высоты объектов
28 ноября
9.
Оформление проекта.
29 – 30 ноября
2. Описание эксперимента
2.1. Поиск различных способов определения высоты дерева, не срубая его и не влезая на него.
Проанализированы различные источники: энциклопедии, Интернет, исторические книги, учебники геометрии, географии, астрономии, физики, журналы и газеты по математике и определены основные способы измерения высоты дерева, не срубая его и не влезая на него.
1. Измерение высоты дерева с помощью «высотомера»
Необходим булавочный прибор для измерения высот – «высотомер».
Использование высотомера: Отойдя от измеряемого дерева, держать прибор так, чтобы один из катетов треугольника был направлен отвесно, для чего можно воспользоваться нитью с грузом, привязанной к верхней булавке. Приближаясь к дереву или удаляясь от него необходимо найти такое место, из которого глядя на булавки а и с нужно увидеть, что они покрывают верхушку дерева С: это значит, что продолжение гипотенузы ас проходит через точку С. Тогда, очевидно, расстояние аВ равно СВ, т . к. угол = 450. Следовательно, измерив расстояние аВ и прибавив ВD, т. е возвышение аА над землёй, получим искомую высоту дерева.
2. Измерение высоты дерева с помощью вешки(шеста) (двумя разными способами).
2.1. Необходимо воткнуть этот шест отвесно в землю так, чтобы выступающая часть была равна нашему росту. Затем необходимо лечь на землю так, чтобы, упираясь ногами в шест, можно было увидеть верхушку дерева на одной прямой линии с верхней точкой кола. Высота дерева будет равна расстоянию от головы наблюдателя до основания дерева.
2.2. Второй способ состоит в следующем.
Взять шест выше своего роста, воткнуть его в землю отвесно на некотором расстоянии от измеряемого дерева. Отойдите от шеста назад, по продолжению Dd до того места А, с которого, глядя на вершину дерева, вы увидите на одной линии с ней верхнюю точку b шеста. Затем, не меняя положения головы, смотрите по направлению горизонтальной прямой аС, замечая точки с и С, в которых луч зрения встречает шест и ствол. Затем необходимо попросить помощника сделать в этих местах пометки, и наблюдение окончено. Остается только на основании подобия треугольников аbс и аВС вычислить ВС из пропорции
ВС : bс = аС : ас,
откуда
ВС = вс(аС/ас).
Расстояния bс. аС и ас легко измерить непосредственно. К полученной величине ВС нужно прибавить расстояние СD (которое тоже измеряется непосредственно), чтобы узнать искомую высоту дерева.
3. Измерение высоты дерева с помощью «высотомера» лесоводов.
Высотомер лесоводов. (очень удобен, если по какой- либо причине подойти к дереву невозможно)
4. Измерение высоты дерева с помощью зеркала.
5. Измерение высоты дерева с помощью его тени.
Необходимо в солнечный день выбрать час, когда длина его собственной тени будет равна его росту. Чтобы воспользоваться тенью для решения задачи, необходимо знать некоторые геометрические свойства треугольника, – именно следующие два:
1) Углы при основании равнобедренного треугольника равны, и обратно – что стороны, лежащие против равных углов треугольника, равны между собою;
2) сумма углов любого треугольника равна 1800 ( т. е. двум прямым углам)
В солнечный день можно воспользоваться любой тенью. Измерив длину шеста (ав) и длину его тени (вс). Затем вычисляют искомую высоту из пропорции: АВ : ав = ВС : вс.
6. Измерение высоты дерева при помощи равнобедренного треугольника.
Приближаясь к предмету (например, к дереву) или удаляясь от него, у
7. Измерение высоты дерева при помощи лужи.

8. Измерение высоты дерева при помощи фотографии.
Возьмём фотографию, на которой изображён измеряемый предмет и мерка. Найдём отношение реальной длины мерки к длине мерки с фотографии, затем полученный результат умножить на длину измеряемого предмета с фотографии? Может быть, мы получим более точный результат.
9. Измерение высоты дерева на глаз ( глазомерно).
Глазомерно – это самый простой и быстрый способ. Главное в нём – тренированность зрительной памяти и умение мысленно откладывать на местности хорошо представляемую постоянную меру (50, 100, 200, 500 метров). Закрепив в памяти эти эталоны, нетрудно сравнивать с ними и оценивать расстояния на местности.
суть: предложить как можно большему числу людей оценить высоту дерева на глаз, установив рядом с деревом вертикально метровую линейку.
10. С помощью воздушного шарика
Суть: сравнить высоту дерева с длиной подходящей нити.
Оборудование: воздушный шарик, наполненный гелием; длинная легкая веревочка (нить); рулетка или т.п. измеритель.
Ход работы:
1) привязать к шарику длинную нитку и выталкивать ее постепенно вверх до тех пор, пока шарик не достигнет верхушки дерева
2) сделать на нитке отметку (например, узелок).
3) вернуть шарик вниз, измерить длину выпущенной части нитки.
11. Метод «Карандаш»
Оборудование: карандаш (пли ручка, или любая палочка), помощник, рулетка.
Ход работы:
1) встать от дерева на такое расстояние, чтобы видеть его целиком – от основания до верхушки. Рядом со стволом установить помощника.
2) вытянуть перед собой руку с карандашом, зажатым в кулаке. Прищурить один глаз и подвести кончик грифеля к вершине дерева. Теперь переместить ноготь большого пальца так, чтобы он оказался под основанием ствола.
3) повернуть кулак на 90 градусов, чтобы карандаш оказался расположен параллельно земле. При этом твой ноготь должен все так же оставаться в точке основания ствола.
4) крикнуть своему помощнику, чтобы он отошел от дерева. Когда он достигнет точки, на которую указывает острие карандаша, подать сигнал, чтобы он остановился.
5) измерить расстояние от ствола до места, где застыл помощник. Оно будет
равняться высоте дерева.
2.2. Выбор оптимальных способов определения высоты дерева.
Обсудили все 11 методов определения высоты дерева. Среди них есть как физические, так и геометрические методы. Отобрали физические методы, применимые к осенним погодным условиям:
с помощью шеста (способ № 2.1.), равнобедренного треугольника (№ 6), фотографии (№ 8), глазомерно (№ 9), используя метод «карандаш» (№11).
2.3. Изготовление приборов и сбор подручных средств для проведения эксперимента.
Для проведения эксперимента потребуется: шест высотой выше нашего роста, рулетка, сделанный из пластика равнобедренный треугольник, цифровой фотоаппарат, принтер.
2.4. Проведение эксперимента.
2.4.1. Определили высоту ели на глаз.
В ходе эксперимента участвовало 4 человека..
Оборудование: метровая линейка.
Ход работы:
1) установить линейку рядом с деревом вертикально;
2) предложить человеку определить высоту дерева на глаз;
3) записать полученное значение в таблицу;
4) для получения среднего значения сумму измерений разделить на количество измерений.
Результат:
12,5 м.
13,0 м.
12,0 м.
14,0 м.
Среднее арифметическое:
12,88 м.
4.4.2. Определение высоты с помощью шеста.
Измерили расстояние от головы Жени, лежащего на земле, и до основания дерева. Оно стало равным 12,5 метрам.
Результат: высота дерева равна 12,5 метрам.
4.4.3. Определение с помощью равнобедренного треугольника.
Взяли равнобедренный треугольник и приложили его к глазу так, чтобы одна его сторона, была параллельна земле, а другая совпадала с верхней точкой дерева. Мы измерили расстояние от ног ученика до основания дерева (оно равно 11,06 метрам), прибавили рост до глаз этого ученика (1,40 метра). Оно оказалось равным 12,46 метрам.
Результат: высота дерева тоже равна 12,46 метрам.
4.4.4. Измерение высоты ёлки по её фотографии.
Чтобы измерить высоту ёлки по её фотографии мы взяли фотографию Жени Бабалова на фоне ёлки. Далее измерили его реальный рост, он равен 1,5 метрам, а высота мерки на фотографии – 1,7 см. Высота ёлки на фотографии 14,5 см. Нашли отношение роста к высоте мерки на фотографии, получили: 150/1,7= 88,24 см (на 1 см – фотографии).
Высота ели на фотографии равна – 14,5 см, значит, настоящая высота дерева находится как произведение отношения роста к высоте мерки на фотографии и высоты ёлки на фотографии, то есть 88,24 * 145 = 12,80 м
Результат: высота ели приближённо равна 12,80 метрам.
4.4.5. Метод «Карандаш»
Измерили расстояние от ствола ели до места, куда встал помощник. Оно и стало равным высоте дерева.
Результат: высота =12,6 м.
4.5. Анализ результатов, их обоснование, формулировка выводов.
Рассмотрены разные способы определения высоты дерева. Реализовали на практике 5 способов: на глаз, измерение высоты с помощью шеста, равнобедренного треугольника, по фотографии, с помощью карандаша.
Все использованные способы показались наиболее простыми и удобными, так как заняли мало времени, минимум приспособлений для решения проблемы и даже плохие погодные условия не помешали провести исследования.
Результаты получились разными.
№ п/п
Метод измерения
Высота дерева
Среднее арифметическое значение
1.
На глаз
12,88 м.
2.
С помощью шеста
12,5 м.
3.
Использование равнобедренного треугольника
12,46 м.
4.
Используя фотографию
12,80 м.
5.
Метод «карандаш»
12,60 м
Ср.арифм. зн.
12,65 м
Видно, что разница между наименьшим и наибольшим значением высоты дерева составляет всего 0,38 метра. Даже с учетом того, что достаточным опытом мы не обладаем и проводили подобную работу впервые, можно утверждать – точность наших измерений высокая.
4.6. Определение более точного способа для определения высоты объекта
От работы получили удовольствие, но не удовлетворение, так как не узнали какой результат у нас более точный, и является действительным. В связи с этим, выбрали другой объект – здание школы, высоту которого мы точно знали по техническому паспорту школы.
Для определения высоты школы использовали те же физические способы, что и для определения высоты ели.

В ходе эксперимента получили следующие результаты:
№ п/п
Метод измерения
Высота здания школы
Погрешность измерений
1.
На глаз
10,00 м.
1.4 м.
2.
С помощью шеста
9,10 м.
0,5 м.
3.
Использование равнобедренного треугольника
9,46 м.
0,86 м.
4.
Используя фотографию
10,60 м.
2 м.
5.
Метод «карандаш»
8,80 м.
0,2 м.
Ср.арифм. зн.
9.60 м.
Реальная высота центральной стены здания – 8,60 м.
Проанализировали результаты, рассчитали погрешность измерений, сравнили с исходными данными и пришли к выводу, что наиболее точным и действенным методом определения высоты здания школы и соответственно высоты дерева является метод «карандаш». Самым неточным способом считаем способ с помощью фотографии.
После всех расчетов пришли к выводу, что высота нашей ёлки – 12,60 м.
Заключение
Конечно, измерение высоты удаленного предмета удобнее делать, когда в наличии имеется специальное измерительное оборудование. Но не каждый раз удается предугадать ситуацию, которая может возникнуть на прогулке или в туристическом походе. Вот тогда такие простые знания пригодятся и даже помогут выйти из затруднительного положения.
В ходе выполнения работы, мы применяли различные способы измерения расстояний недоступных точек. Выбор этих способов сделали не случайно, вычисления в них доступны.
При изучении теоретического материала по этой проблеме познакомились и с другими способами определения недоступных расстояний, например, с помощью зеркала, тени и другие. К сожалению, мы ещё не обладаем геометрическими знаниями, для того, чтобы измерить расстояние данным способом. И, в связи с этим есть планы на будущие эксперименты: рассмотреть и другие способы измерения недоступных высот и расчеты произвести геометрическими способами.
Желающие попробовать определить высоту недоступного объекта могут воспользоваться нашими инструкциями.
Самым доступным и точным способом мы считаем метод карандаша. Он требует минимум оборудования и всего одно измерение.
Своей работой мы удовлетворены, очень заинтересованы, есть планы на будущие исследования, главное мы выполнили поставленные нами задачи и цель работы достигнута.
Список использованной литературы
-
газета: Гумеров И. Измеряем высоту // Математика №3, 2007.
-
газета: Каменева Т. Измерение высоты здания Пермэнерго // Физика в школе №9, 2008.
-
газета: Легенды истории математики // Математика №18, 2006.
-
Злацен Определение высоты предметов [Электронный ресурс] // (1 файл). – http://handly.ru/articles/view:ce.opredelenie-vyisotyi/.
-
Обущак А. Как измерить высоту главного здания [Электронный ресурс] // (1 файл). – http://www.mmforce.net/msu/heart/articles.php.
ПРИЛОЖЕНИЯ
ГБПОУ «Починковский сельскохозяйственный техникум»
Индивидуальный проект по математике на тему:
«Определение высоты предмета различными способами».
Работу выполнил:
студент 1М группы
Бачурин Дмитрий
Проверил:
преподаватель
Абросимова Е.А.
Починки, 2020 г.
Оглавление:
1.Введение
2. Методы измерения в Древней Руси
3. Способы измерения на местности
3.1. Подобие треугольников.
3.2. С помощью вращающейся планки.
3.3. Измерение высоты предмета с помощью тени.
3.4. Измерение высоты предмета при отсутствии тени.
3.5. Измерение высоты предмета с помощью зеркала.
3.6. Измерение высоты предмета с помощью прямоугольного треугольника.
4.Практическая работа. Измерения высоты предметов различными способами
4.1. Измерение высоты предмета с помощью тени.
4.2. Измерение высоты предмета с помощью зеркала.
4.3. Измерение высоты предмета с помощью прямоугольного треугольника.
5.Заключение
-
Введение
«Наука начинается с тех пор, как начинают измерять,
точная наука немыслима без измерения»
Д.И. Менделеев.
Геометрия – одна из древнейших наук, возникших еще до нашей эры. В переводе с греческого слово «геометрия» означает «землемерие». Это название объясняется тем, что его происхождение было связано с различными измерительными работами, которые приходилось выполнять при разметке земельных участков, строительстве зданий и различных сооружений. Другими словами, геометрия возникла из практической деятельности людей и в начале своего развития служила главным образом практическим целям.
Выбранная тема актуальна тем, что можно узнать, как определить высоту объекта без каких-либо специальных технических устройств. В частности, иногда туристам нужно оценить размер дерева, чтобы построить мост через быструю реку. У них нет под рукой высотомера. Чтобы определить, достаточно ли высоты дерева, чтобы упав, оно перекрыло реку, можно использовать предметы, которые всегда под рукой. Или, например, на садовом участке растет дерево, которое мешает по каким – то причинам. Прежде чем его спилить, нужно решить проблему – не достанет ли оно при падении до любого строения, находящегося рядом с ним. И тут снова на помощь приходят различные методы определения высоты дерева с помощью подручных средств.
Гипотеза: в настоящее время измерительные работы на местности играют важную роль.
Цель исследования: определение высоты предмета различными способами.
Объект исследования: измерения на местности.
Предмет исследования: способы измерений на местности.
Задачи:
– изучить какие способы измерения длины были в древности;
– рассмотреть различные способы измерения высоты предмета;
– экспериментально проверить использование различных способов определения высоты предмета;
– проанализировать полученные данные и определить наиболее точный способ измерения высоты предмета.
Методы исследования:
– сбор информации из энциклопедий, книг, системы Интернет;
– эксперимент;
– сравнение;
– анализ.
-
Методы измерений Древней Руси.
В древности человеку приходилось постепенно постигать не только искусство счета, но и измерений. Когда древний человек, уже мыслящий, попытался найти для себя пещеру, он вынужден был соразмерить длину, ширину и высоту своего будущего жилища с собственным ростом. А ведь это и есть измерение. Изготовляя простейшие орудия труда, строя дома, добывая пищу, возникает необходимость измерять расстояния, а затем площади, емкости, массу, время. Наш предок располагал только собственным ростом, длиной рук и ног. Если при счете человек пользовался пальцами рук и ног, то при измерении расстояний использовались руки и ноги. Не было народа, который не изобрел бы своих единиц измерения.
В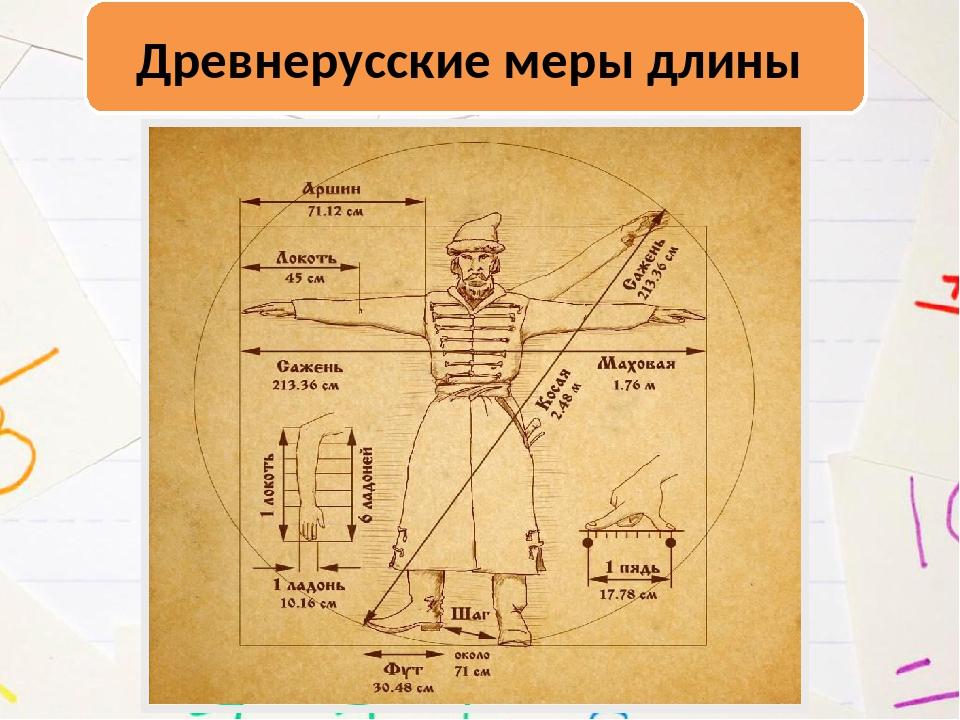
Небольшие расстояния на Руси измерялись четвертями, пядями и аршинами. Четверть — расстояние между раздвинутыми большим и указательным пальцами, пядь — расстояние от конца большого пальца до конца мизинца при наибольшем возможном их раздвижении. Четыре четверти составляли аршин, который, в свою очередь, трижды вмещался в косую сажень.
3. Способы определения высоты предмета
Существует множество различных способов производить определение высоты предмета при помощи весьма незамысловатых приборов и даже без всяких приспособлений.
Для своей работы я отобрал только те, которые просты в применении.
3.1. Подобие треугольников
Способы определения высоты предмета с помощью подручных средств основаны на применении такого важного понятия геометрии, как подобие треугольников.
Д
Соответственные стороны – это стороны, лежащие напротив равных углов.
Коэффициент подобия – это число k, равное отношению соответственных сторон. При решении задач на местности чаще всего применяют первый признак подобия треугольников: если два угла одного треугольника равны соответственно двум углам другого треугольника, то такие треугольники подобны.
3.2. Измерение высоты предмета с помощью вращающейся планки.
Предположим, что нам нужно определить высоту какого – нибудь предмета, например высоту столба А 1 С 1. Для этого поставим на некотором расстоянии от столба шест АС с вращающейся планкой и направим планку на верхнюю точку С 1 столба. Отметим на поверхности земли точку В, в которой прямая А 1 А пересекается с поверхностью земли. Прямоугольные треугольники А 1 С 1 В и АСВ подобны по первому признаку подобия треугольников (угол А 1 = углу А = 90 о, угол В – общий). Из подобия треугольников следует;
Измерив расстояния ВА 1 и ВА (расстояние от точки В до основания столба и расстояние до шеста с вращающейся планкой), зная длину АС шеста, по полученной формуле определяем высоту А 1 С 1 столба.

3.3. Измерение высоты предмета с помощью тени.
Этот способ называется способом Фалеса. В честь греческого мудреца Фалеса Милетского, который еще за шесть веков до нашей эры научил египтян определять высоту пирамиды по длину ее тени.
Измерение следует проводить в солнечную погоду. Например, для измерения длины дерева. Для этого измерим длину тени дерева и длину тени человека. Построим два прямоугольных треугольника, они подобны. Используя подобие треугольников, составим пропорцию (отношение соответственных сторон), из которой и найдём высоту дерева.
3. 4. Измерение высоты предмета при отсутствии тени.
При отсутствии тени высота вертикальных предметов определяется следующим образом. Рядом с измеряемым предметом установить вертикально палку известной длины и отойти на 25 – 30 шагов. В вытянутой руке держать перед глазами вертикально карандаш или ровную палочку. Отметить на карандаше высоту вертикальной палки и измерить это расстояние. Мысленно умножить это расстояние на измеренный предмет. Умножив полученное количество раз на длину палки, можно получить искомую величину.
3.5. Измерение высоты предмета с помощью зеркала.
Д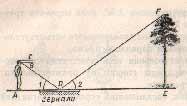
3
На уровне глаз расположим прямоугольный равнобедренный треугольник, направив один катет горизонтально поверхности земли, другой катет, направив на предмет, высоту которого измеряем. Отходим от предмета на такое расстояние, чтобы второй катет совпадал с верхней точкой предмета, которого измеряем, т.к. треугольник равнобедренный, то высота предмета равна расстоянию от человека до основания предмета (прибавив рост человека).
Если треугольник не равнобедренный, то используется снова подобие треугольников, измеряя катеты треугольника и расстояние от человека до предмета (используется и построение прямоугольных треугольников в выбранном масштабе). Если треугольник имеет угол в 30 0 , то используется свойство прямоугольного треугольника: против угла в 30 0 лежит катет вдвое меньше гипотенузы.
4. Практическая работа. Измерение высоты предметов различными способами.
4.1. Измерение высоты предмета с помощью тени
Помимо измерительной ленты нам нужен солнечный день, чтобы получить свою четкую тень, и тень предмета. Зная свой рост, измерив, тень предмета и свою тень и используя основное свойство пропорции можно вычислить высоту предмета.
1) Высота дерева:
Я встал рядом с деревом. Тень дерева и моя тень образовали параллельные прямые. Потом измерил тень дерева и мою тень.
Мой рост 177см
Моя тень 259см
Тень дерева 1100см
Высота дерева x
По свойствам пропорции:
177: 259 = x : 1100
x = (177*1100):259=752см=7,52м
Ответ: высота дерева 7,52м
2) Высота столба.
Мой рост 177см
Моя тень 215см
Тень столба 1000см
Высота столба x м
Составили пропорцию и вычислили искомую высоту.
177: 215= х: 1000
х = (177 *1000): 215 = 8,2м
Ответ: высота столба
8,2 м.
Таким образом, я измерил высоту дерева, и высоту столба.
4.2.Измерение высоты предмета с помощью зеркала
Я положил зеркало на землю, отошел в сторону до того момента, пока в зеркале не отразится верхушка дерева. Измерил расстояния от себя до зеркала, от зеркала до дерева и свой рост до глаз.
Мой рост до уровня глаз 165см
Расстояние от меня до зеркала 100см
Расстояние от зеркала до дерева 900см
Высота дерева x
По свойствам пропорции: x=(165*900):100=1485 см=14.8 м
Ответ: высота дерева 14.8 м
4.3. Измерение высоты предмета с помощью прямоугольного треугольника.
Для реализации этого способа, я взял равнобедренный треугольник и приложил его к глазу так, чтобы одна его сторона была параллельна земле, а другая совпадала с верхней точкой здания (моего дома). Я измерил расстояние от дома до места где я стоял, плюс мой рост до уровня глаз 6400+165=6605 см, оно оказалось равным 6, 60м, значит и высота дома тоже равна 6,60метрам.
1.Держа равнобедренный прямоугольный треугольник на уровне глаз вертикально, отойдите от дома на такое расстояние, чтобы, глядя вдоль гипотенузы, видно было верх дома.
2.Измерить расстояние от места измерения до дома
3.Измерить катет треугольника.
4.Измерить рост до уровня глаз.
Геометрическая постановка задачи. Рассмотреть по двум углам треугольники АВС и А1В1С1 и составить отношение соответственных сторон , где АС – расстояние от точки измерения до основания дерева, А1С1 – длина катета равнобедренного прямоугольного треугольника, ВС – искомая величина, В1С1 – длина катета равнобедренного прямоугольного треугольника .
5. Заключение
В данной работе рассмотрены различные способы определения высоты предмета, некоторые из методов были реализованы на практике.
Выполняя практические задания на местности, я научился видеть подобные треугольники в разных ситуациях; правильно записывать соотношения соответственных сторон; используя свойство пропорции, вычислять неизвестные элементы.
Во время эксперимента самым простым для меня способом было измерить высоту дома с помощью равнобедренного прямоугольного треугольника, так как это занимает минимум времени и не требует большого количества приборов.
Относительная погрешность измерений, полученных в ходе эксперимента, различна. Наиболее точным оказался метод определения высоты с помощью треугольника, а наименее точным – по тени. Трудно сказать, каким способом лучше пользоваться для определения высоты объекта. Все зависит от имеющихся подручных средств, от места положения объекта, от точности, которая необходима. Таким образом, поставленные задачи были выполнены и цель работы достигнута.
Эта работа ясно показывает, что геометрия – это не просто школьный предмет, а наука, которая используется в жизни.
Список используемых источников:
1. Болтянский В.Г. Элементарная геометрия. – М.: Просвещение, 1982
2. Перельман Я.И. Занимательная геометрия. – М.: АСТ, 2005
3.Энциклопедический словарь юного математика. – М.: Педагогика, 1983
4. Большая Российская Энциклопедия.М, том 11,2008
5. Виленкин Н.Я., Шибасов Л.Т. «За страницами учебника
математики» – М.: Просвещение: АО «Учеб. лит.», 1996.
6. http:// festival.1september.ru
7. http://www.pandia.ru/
Как определить высоту предмета
- Авторы
- Руководители
- Файлы работы
- Наградные документы
Цветов А.Э. 1
1МБОУ СШ №16 г.Павлово Нижегородской области
Захарова Т.Н. 1
1МБОУ СШ №16 г.Павлово Нижегородской области
Текст работы размещён без изображений и формул.
Полная версия работы доступна во вкладке “Файлы работы” в формате PDF
Введение
Геометрия – одна из древнейших наук, возникших еще до нашей эры. В переводе с греческого слово «геометрия» означает «землемерие». Это название объясняется тем, что его происхождение было связано с различными измерительными работами, которые приходилось выполнять при разметке земельных участков, строительстве зданий и различных сооружений. Другими словами, геометрия возникла из практической деятельности людей и в начале своего развития служила главным образом практическим целям. [6]
На уроках геометрии в 8-м классе при изучении темы «Подобные треугольники» я заинтересовался ее практическим применением, в частности использованием подобия при измерении высоты объекта.
Выбранная тема актуальна тем, что можно узнать, как определить высоту объекта без каких-либо специальных технических устройств. В частности, иногда туристам нужно оценить размер дерева, чтобы построить мост через быструю реку. У них нет под рукой высотомера. Чтобы определить, достаточно ли высоты дерева, чтобы упав, оно перекрыло реку, можно использовать предметы, которые всегда под рукой. Или, например, на садовом участке растет дерево, которое мешает по каким – то причинам. Прежде чем его спилить, нужно решить проблему – не достанет ли оно при падении до любого строения, находящегося рядом с ним. И тут снова на помощь приходят различные методы определения высоты дерева с помощью подручных средств.
Проблема: как определитьвысоту предмета с помощью подручных средств.
Цель исследования: определение высоты предмета различными способами.
Объект исследования: дом, в котором я живу.
Предмет исследования: высота дома.
Задачи:
– рассмотреть различные способы измерения высоты предмета;
– экспериментально проверить использование различных способов определения высоты предмета, определив высоту дома, в котором я живу;
– проанализировать полученные данные и определить наиболее точный способ измерения высоты предмета.
Методы исследования:
– изучение литературы и ресурсов Интернет;
– эксперимент;
– сравнение;
– анализ.
Глава I. Способы определения высоты предмета
В своей профессиональной деятельности строители, архитекторы, лесоводы, военные для определения высоты предмета используют специальные сложные и дорогостоящие приборы – высотометры. В книге Я.И.Перельмана «Занимательная геометрия» [5], а также на сайте «Лесная промышленность» [7] можно найти различные способы определения высоты предмета с помощью подручных средств на примере определения высоты дерева.
В школьных учебниках геометрии также есть практические задачи на определение высоты дерева. Например, в учебнике Л.С.Атанасяна «Геометрия 7-9» [1] в №581 рассмотрен способ измерения высоты дерева с помощью зеркала, а в учебнике А.Г.Мерзляка «Геометрия – 8» [4] в №472 – с помощью тени (рис.1).
рис.1
Изучив литературу [3] и ресурсы сети Интернет, я выделил несколько способов определения высоты предмета и разработал пошаговые инструкции по применению каждого из них на примере измерения высоты дерева.
1. Подобие треугольников
Способы определения высоты предмета с помощью подручных средств основаны на применении такого важного понятия геометрии, как подобие треугольников. [2]
Два треугольника называются подобными, если их углы соответственно равны, и стороны одного треугольника пропорциональны соответственным сторонам другого треугольника (рис.2)
рис.2
Соответственные стороны – это стороны, лежащие напротив равных углов.
Коэффициент подобия – это число k, равное отношению соответственных сторон (рис.3).
рис.3
При решении задач на местности чаще всего применяют первый признак подобия треугольников: если два угла одного треугольника равны соответственно двум углам другого треугольника, то такие треугольники подобны (рис.4).
рис.4
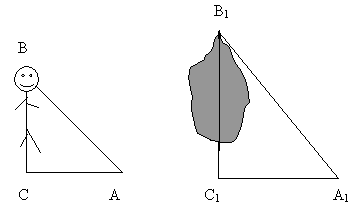
2. Определение высоты с помощью тени
Этот способ называется способом Фалеса. В честь греческого мудреца Фалеса Милетского, который еще за шесть веков до нашей эры научил египтян определять высоту пирамиды по длину ее тени.
Инструкция:
1.Встаньте рядом с деревом так, чтобы были видны тени и дерева, и человека (рис.5).
2.Измерьте тень человека и тень дерева.
3.Измерьте рост человека.
рис.5
Геометрическая постановка задачи. Рассмотрите подобные по двум углам треугольники АВС и А1В1С1 (рис.5) и составьте отношение соответственных сторон , где АВ – искомая высота дерева, А1В1 – рост человека, ВС – длина тени дерева, В1С1 – длина тени человека. Подставьте измерения и найдите величину АВ. Это и будет искомая высота дерева.
3. Определение высоты с помощью равнобедренного прямоугольного треугольника
Инструкция:
1.Держа равнобедренный прямоугольный треугольник на уровне глаз вертикально, отойдите от дерева на такое расстояние, чтобы, глядя вдоль гипотенузы, видно было верхушку дерева (рис.6).
2.Измерьте расстояние от места измерения до дерева.
3.Измерьте катет треугольника.
4.Измерьте рост человека до уровня глаз.
рис.6
Геометрическая постановка задачи. Рассмотрите подобные по двум углам треугольники АВС и А1В1С1 (рис.5) и составьте отношение соответственных сторон , где АС – расстояние от точки измерения до основания дерева, А1С1 – длина катета равнобедренного прямоугольного треугольника, ВС – искомая величина, В1С1 – длина катета равнобедренного прямоугольного треугольника (рис.7).
рис.7
Подставьте измерения и найдите величину ВС. К полученной величине прибавьте рост человека до уровня глаз. Это и будет искомая высота дерева.
4. Определение объекта с помощью зеркала
Инструкция:
1.Положить зеркало горизонтально на ровную землю на некотором расстоянии от измеряемого дерева (рис.8).
2.Отойти от зеркала на такое расстояние, чтобы видеть в зеркале верхушку дерева.
3.Измерить расстояние от зеркала до основания дерева и до точки измерения.
рис.8
Затем измеряется расстояние от основания дерева до зеркала и расстояние от зеркала до измерителя.
Геометрическая постановка задачи. Способ основан на законе отражения света. Вершина отражается в точке так, что АВ = В. Из подобия треугольников ВС и СЕD следует, что . В этом отношении необходимо только заменить В равным АВ. Решив пропорцию, найдем высоту дерева АВ (рис.9).
рис.9
5. Определение высоты с помощью булавочного прибора
Булавочный прибор можно изготовить из дощечки и трех булавок. На дощечке или куске коры отмечают три точки – вершины равнобедренного прямоугольного треугольника, и в эти точки втыкают по булавке (рис.10).
рис.10
Инструкция:
1.Держа булавочный прибор на уровне глаз так, чтобы один из катетов треугольника был направлен вниз, отойдите от дерева на такое расстояние, чтобы, глядя на булавки А1 и С1, можно увидеть верхушку дерева (рис.11).
2.Измерьте расстояние от основания дерева до точки измерения.
рис.11
Геометрическая постановка задачи. Из подобия треугольников АВС и АВ1С1 следует отношение соответственных сторон , где АВ – расстояние от точки измерения до основания дерева, АВ1 – длина катета равнобедренного прямоугольного треугольника, ВС – искомая величина, В1С1 – длина катета равнобедренного прямоугольного треугольника (рис.11).
Решив пропорцию, находим ВС. Для того, чтобы найти высоту дерева, необходимо к этой величине прибавить рост человека до уровня глаз.
6. Определение высоты с помощью фотографии
Инструкция:
1.Сделайте фотографию человека на фоне дерева (рис.12).
2.Измерьте рост человека.
3.Измерьте на фотографии высоту дерева и рост человека.
рис.12
Составьте отношение соответственных сторон:
Подставьте измерения и найдите реальную высоту дерева.
Глава II. Проведение эксперимента
1.Измерение высоты дома, в котором я живу
Разработанные инструкции для определения высоты предмета с помощью подручных средств я решил применить на практике, измерив высоту дома, в котором живу (Приложение 1, рис.13).
1)Измерение высоты дома по его тени (Приложение 1, рис.14).
Такое измерение лучше проводить в солнечные дни.
Необходимое оборудование: рулетка.
Результаты измерения: мой рост – 160 см, длина моей тени – 173 см, длина тени дома – 500 см.
Составляем и решаем пропорцию: .
см
Искомая высота дома в данном случае равна 4,62 м.
2) Измерение высоты дома с помощью зеркала (Приложение 1, рис.15).
Оборудование: зеркало, рулетка.
Результаты измерения: мой рост – 160 см, расстояние от зеркала до основания дома – 680 см, расстояние от зеркала до точки измерения – 220 см.
Составляем и решаем пропорцию: .
см
Искомая высота дома в данном случае равна 4,94 м.
3) Измерение высоты дома с помощью равнобедренного прямоугольного треугольника (Приложение 1, рис.16).
Оборудование: рулетка, равнобедренный прямоугольный треугольник.
Результаты измерения: длина катета равнобедренного прямоугольного треугольника – 38 см, расстояние от дома до точки измерения – 350 см.
Составляем и решаем пропорцию: .
см
Чтобы найти высоту дома, необходимо к полученному значению прибавить мой рост до уровня глаз: 350 см + 150 см = 500 см. Итак, искомая высота дома в данном случае равна 5 м.
4) Измерение высоты дома с помощью булавочного прибора (Приложение 1, рис.17).
Оборудование: рулетка, булавочный прибор (Приложение 1, рис.18).
Результаты измерения: длина катета булавочного прибора – 5 см, расстояние от дома до точки измерения – 370 см.
Составляем и решаем пропорцию: .
см
Чтобы найти высоту дома, необходимо к полученному значению прибавить мой рост до уровня глаз: 370 см + 150 см = 520 см. Итак, искомая высота дома в данном случае равна 5,2 м.
5) Измерение высоты дома с помощью фотографии (Приложение 1, рис.19).
Оборудование: линейка, фотоаппарат.
Результаты измерения: мой рост – 160 см, высота дома на фотографии – 10,5 см, мой рост на фотографии – 3,5 см.
Составляем и решаем пропорцию: .
см
Искомая высота дома в данном случае равна 4,8 м.
2. Определение наиболее точного способа измерения
Посмотрев технический план нашего дома, я выяснил, что его реальная высота – 4,85 м.
Измерив высоту дома различными способами, я решил проверить, насколько мои измерения точны. Для этого я вычислил относительную погрешность измерений по формуле , где х – точное значение величины, а а – приближенное значение (табл.1). Относительную погрешность измерений я вычислял в процентах.
Таблица 1. Относительная погрешность измерения
|
Метод измерения |
Результат измерений |
Фактическое значение |
Относительная погрешность |
|
С помощью тени |
4,62 м |
4,85 м |
|
|
С помощью зеркала |
4,94 м |
4,85 м |
|
|
С помощью равнобедренного прямоугольного треугольника |
5 м |
4,85 м |
|
|
С помощью булавочного прибора |
5,2 м |
4,85 м |
|
|
С помощью фотографии |
4,8 м |
4,85 м |
Из данной таблицы видно, что наиболее точными оказались метод определения высоты дома с помощью фотографии и с помощью зеркала, а наименее точными – с помощью тени и с помощью булавочного прибора. Нужно отметить, что имели свое значение и не очень благоприятные условия: неровная, неудобная местность. Сказывалось и отсутствие опыта проведения практических измерений.
Заключение
В данной работе рассмотрены различные способы определения высоты предмета, описанные в научной литературе, и составлены инструкции по применению каждого из этих методов. Все рассмотренные методы были реализованы на практике.
Выполняя практические задания на местности, я научился видеть подобные треугольники в разных ситуациях; правильно записывать соотношения соответственных сторон; используя свойство пропорции, вычислять неизвестные элементы. Мой интерес к предмету геометрии также возрос. Длительное пребывание на свежем воздухе помогло укрепить мое здоровье.
Во время эксперимента самым простым для меня способом было измерить высоту дома с помощью равнобедренного прямоугольного треугольника, так как это занимает минимум времени и не требует большого количества приборов. Но я также столкнулся с трудностями: это неровный рельеф местности, пасмурная погода (высоту дома с помощью тени можно определить только в солнечную погоду).
Относительная погрешность измерений, полученных в ходе эксперимента, различна. Наиболее точным оказался метод определения высоты дома по фотографии и с помощью зеркала, а наименее точным – по тени и с помощью булавочного прибора.
Таким образом, поставленные задачи были выполнены и цель работы достигнута.
Желающие, кто хочет попробовать определить высоту предмета, могут воспользоваться инструкциями, приведенными в этой работе. Эта работа ясно показывает, что геометрия – это не просто школьный предмет, а наука, которая используется в жизни.
Библиографический список
Атанасян Л.С. и др. Геометрия: учебник для 7-9 кл. общеобразовательных учреждений. – М.: Просвещение, 2017
Болтянский В.Г. Элементарная геометрия. – М.: Просвещение, 1982
Ганьшин В.Н. Простейшие измерения на местности. – М.: Недра, 1983
Мерзляк А.Г., Полонский В.Б., Якир М.С. и др. Геометрия 8 класс: учеб. для общеобразоват. организаций.- М.: Вентана-Граф, 2018
Перельман Я.И. Занимательная геометрия. – М.: АСТ, 2005
Энциклопедический словарь юного математика. – М.: Педагогика, 1983
http://wood-prom.ru/ – сайт Лесная промышленность
Приложение 1
Фотоотчет проведения эксперимента
рис.13. Объект измерения
рис.14. Измерение высоты дома с помощью тени
рис.15. Измерение высоты дома с помощью зеркала
рис.16. Измерение высоты дома с помощью равнобедренного прямоугольного треугольника
рис.17. Измерение высоты дома с помощью булавочного прибора
рис.18. Булавочный прибор
рис.19. Измерение высоты дома с помощью фотографии
Просмотров работы: 4025
Текущая страница: 10 (всего у книги 11 страниц) [доступный отрывок для чтения: 2 страниц]
Не приближаясь к дереву
Случается, что почему-либо неудобно подойти вплотную к основанию измеряемого дерева. Можно ли в таком случае определить его высоту?
Вполне возможно. Для этого придуман остроумный прибор, который, как и предыдущие, легко изготовить самому. Две планки аb и cd (см. рис. 56) скрепляются под прямым углом так, чтобы аb равнялось bc, a bd составляло половину ab. Вот и весь прибор. Чтобы измерить им высоту, держат его в руках, направив планку cd вертикально (для чего при ней имеется отвес – шнурок с грузиком), и становятся последовательно в двух местах: сначала (рис. 56) в точке А, где располагают прибор концом с вверх, а затем в точке А‘, подальше, где прибор держат вверх концом d. Точка А избирается так, чтобы, глядя из а на конец с, видеть его на одной прямой с верхушкой дерева. Точку же А’ отыскивают так, чтобы, глядя из а’ на точку d’, видеть ее совпадающей с В. В отыскании этих двух точек А и А’[36]36
Точки эти непременно должны лежать на одной прямой с основанием дерева.
[Закрыть]
заключается все измерение, потому что искомая часть высоты дерева ВС равна расстоянию АА’. Равенство вытекает, как легко сообразить, из того, что аС = ВС, а а’С = 2ВС; значит,
а’С – аС = ВС.
Рис. 56. Применение простейшего высотомера, состоящего из двух планок
Вы видите, что, пользуясь этим простым прибором, мы измеряем дерево, не подходя к его основанию ближе его высоты. Само собою разумеется, что если подойти к стволу возможно, то достаточно найти только одну из точек – А или А’, чтобы узнать его высоту.
Вместо двух планок можно воспользоваться четырьмя булавками, разместив их на дощечке надлежащим образом; в таком виде «прибор» еще проще.
При помощи зеркала
Задача
Вот еще своеобразный способ определения высоты дерева при помощи зеркала. На некотором расстоянии (рис. 57) от измеряемого дерева, на ровной земле в точке С кладут горизонтально зеркальце и отходят от него назад в такую точку D, стоя в которой наблюдатель видит в зеркале верхушку А дерева.
Рис. 57. Измерение высоты при помощи зеркала
Тогда дерево (АВ) во столько раз выше роста наблюдателя (ED), во сколько раз расстояние ВС от зеркала до дерева больше расстояния CD от зеркала до наблюдателя. Почему?
Решение
Способ основан на законе отражения света. Вершина А (рис. 58) отражается в точке А’ так, что АВ = А’В. Из подобия же треугольников ВСА’ и CED следует, что
A’B: ED = BC: CD.
В этой пропорции остается лишь заменить A’В равным ему АВ, чтобы обосновать указанное в задаче соотношение.
Рис. 58. Геометрическое построение к способу измерения высоты при помощи зеркала
Этот удобный и нехлопотливый способ можно применять во всякую погоду, но не в густом насаждении, а к одиноко стоящему дереву.
Задача
Как, однако, следует поступать, когда к измеряемому дереву невозможно почему-либо подойти вплотную?
Решение
Это – старинная задача, насчитывающая за собою свыше 500 лет. Ее рассматривает средневековый математик Антоний де Кремона в сочинении «О практическом землемерии» (1400 г.).
Задача разрешается двукратным применением сейчас описанного способа – помещением зеркала в двух местах. Сделав соответствующее построение, нетрудно из подобия треугольников вывести, что искомая высота дерева равна возвышению глаза наблюдателя, умноженному на отношение расстояния между положениями зеркала к разности расстояний наблюдателя от зеркала.
Прежде чем окончить беседу об измерении высоты деревьев, предложу читателю еще одну «лесную» задачу.
Две сосны
Задача
В 40 м одна от другой растут две сосны. Вы измерили их высоту: одна оказалась 31 м высоты, другая, молодая – всего 6 м.
Рис. 59. Как велико расстояние между вершинами сосен?
Можете ли вы вычислить, как велико расстояние между их верхушками?
Решение
Искомое расстояние между верхушками сосен (рис. 59) по теореме Пифагора равно
Форма древесного ствола
Теперь вы можете уже, прогуливаясь по лесу, определить – чуть не полдюжиной различных способов – высоту любого дерева. Вам интересно будет, вероятно, определить также и его объем, вычислить, сколько в нем кубических метров древесины, а заодно и взвесить его – узнать, можно ли было бы, например, увезти такой ствол на одной телеге. Обе эти задачи уже не столь просты, как определение высоты; специалисты не нашли способов точного ее разрешения и довольствуются лишь более или менее приближенной оценкой. Даже и для ствола срубленного, который лежит перед вами очищенный от сучьев, задача разрешается далеко не просто.
Дело в том, что древесный ствол, даже самый ровный, без утолщений, не представляет ни цилиндра, ни полного конуса, ни усеченного конуса, ни какого-либо другого геометрического тела, объем которого мы умеем вычислять по формулам. Ствол, конечно, не цилиндр, – он суживается к вершине (имеет «сбег», как говорят лесоводы), – но он и не конус, потому что его «образующая» не прямая линия, а кривая, и притом не дуга окружности, а некоторая другая кривая, обращенная выпуклостью к оси дерева[37]37
Всего ближе эта кривая подходит к так называемой «полукубической параболе» (y3 = ax2); тело, полученное вращением этой параболы, называется «нейлоидом» (по имени старинного математика Нейля, нашедшего способ определять длину дуги такой кривой). Ствол выросшего в лесу дерева по форме приближается к нейлоиду. Расчет объема нейлоида выполняется приемами высшей математики.
[Закрыть]
.
Поэтому более или менее точное вычисление объема древесного ствола выполнимо лишь средствами интегрального исчисления. Иным читателям покажется, быть может, странным, что для измерения простого бревна приходится обращаться к услугам высшей математики. Многие думают, что высшая математика имеет отношение только к каким-то особенным предметам, в обиходной же жизни применима всегда лишь математика элементарная. Это совершенно неверно: можно довольно точно вычислить объем звезды или планеты, пользуясь элементами геометрии, между тем как точный расчет объема длинного бревна или пивной бочки невозможен без аналитической геометрии и интегрального исчисления.
Но наша книга не предполагает у читателя знакомства с высшей математикой; придется поэтому удовлетвориться здесь лишь приблизительным вычислением объема ствола. Будем исходить из того, что объем ствола более или менее близок либо к объему усеченного конуса, либо – для ствола с вершинным концом – к объему полного конуса, либо, наконец, – для коротких бревен – к объему цилиндра. Объем каждого из этих трех тел легко вычислить. Нельзя ли для однообразия расчета найти такую формулу объема, которая годилась бы сразу для всех трех названных тел? Тогда мы приближенно вычисляли бы объем ствола, не интересуясь тем, на что он больше похож – на цилиндр или на конус, полный или усеченный.
Шестиногие богатыри
Удивительные создания муравьи! Проворно взбегая по стебельку вверх с тяжелой для своего крошечного роста ношей в челюстях (рис. 60), муравей задает наблюдательному человеку головоломную задачу: откуда у насекомого берется сила, чтобы без видимого напряжения втаскивать груз в десять раз тяжелее его самого? Ведь человек не мог бы взбегать по лестнице, держа на плечах, например, пианино (рис. 60), а отношение веса груза к весу тела у муравья примерно такое же. Выходит, что муравей относительно сильнее человека!
Так ли?
Без геометрии здесь не разобраться. Послушаем, что говорит специалист (проф. А.Ф. Брандт), прежде всего, о силе мускулов, а затем и о поставленном сейчас вопросе соотношения сил насекомого и человека:
«Живой мускул уподобляется упругому шнурку; только сокращение его основано не на упругости, а на других причинах, и проявляется нормально под влиянием нервного возбуждения, а в физиологическом опыте от прикладывания электрического тока к соответствующему нерву или непосредственно к самому мускулу.
Рис. 60.
Шестиногий богатырь
Опыты весьма легко проделываются на мускулах, вырезанных из только что убитой лягушки, так как мускулы холоднокровных животных весьма долго и вне организма, даже при обыкновенной температуре, сохраняют свои жизненные свойства. Форма опыта очень простая. Вырезают главный мускул, разгибающий заднюю лапу, – мускул икр – вместе с куском бедренной кости, от которой он берет начало, и вместе с концевым сухожилием. Этот мускул оказывается наиболее удобным и по своей величине, и по форме, и по легкости препаровки. За обрезок кости мускул подвешивают на станке, а сквозь сухожилие продевают крючок, на который нацепляют гирю. Если до такого мускула дотрагиваться проволоками, идущими от гальванического элемента, то он моментально сокращается, укорачивается и приподнимает груз.
Постепенным накладыванием дополнительных разновесок легко определить максимальную подъемную способность мускула. Свяжем теперь по длине два, три, четыре одинаковых мускула и станем раздражать их сразу. Этим мы не достигнем большей подъемной силы, а груз будет подниматься лишь на большую высоту, соответственно суммированию укорочений отдельных мускулов. Зато если свяжем два, три, четыре мускула в пучок, то вся система будет при раздражении поднимать и в соответственное число раз больший груз. Точно такой же результат, очевидно, получился бы и тогда, если бы мускулы между собою срослись. Итак, мы убеждаемся в том, что подъемная сила мускулов зависит не от длины или общей массы, а лишь от толщины, т. е. поперечного разреза.
После этого отступления обратимся к сличению одинаково устроенных, геометрически подобных, но различных по величине животных. Мы представим себе двух животных; первоначальное и вдвое увеличенное во всех линейных измерениях. У второго объем и вес всего тела, а также каждого из его органов будет в 8 раз больше; все же соответственные плоскостные измерения, в том числе и поперечное сечение мускулов, лишь в 4 раза больше. Оказывается, мускульная сила, по мере того как животное разрастается до двойной длины и восьмерного веса, увеличивается лишь в четыре раза, т. е. животное сделалось относительно вдвое слабее. На этом основании животное, которое втрое длиннее (с поперечными сечениями, в 9 раз обширнейшими, и с весом, в 27 раз большим), оказывалось бы относительно втрое слабее, а то, которое вчетверо длиннее, – вчетверо слабее и т. д.
Законом неодинакового нарастания объема и веса животного, а вместе с тем и мускульной силы объясняется, почему насекомое, – как мы это наблюдаем на муравьях, хищных осах и т. д., может тащить тяжести, в 30, в 40 раз превосходящие вес собственного их тела, тогда как человек в состоянии тащить нормально – мы исключаем гимнастов и носильщиков тяжестей – лишь около 9/10, а лошадь, на которую мы взираем как на прекрасную живую рабочую машину, и того меньше, а именно лишь около 7/10 своего веса»[38]38
Подробно об этом см. «Занимательную механику» Я.И. Перельмана, главу десятую «Механика в живой природе».
[Закрыть]
.
После этих разъяснений мы другими глазами будем смотреть на подвиги того муравья-богатыря, о котором И.А. Крылов насмешливо писал:
Какой-то муравей был силы непомерной,
Какой не слыхано и в древни времена;
Он даже (говорит его историк верный)
Мог поднимать больших ячменных два зерна.
Глава пятая
Геометрия у реки
Измерить ширину реки
Не переплывая реки, измерить ее ширину – так же просто для знающего геометрию, как определить высоту дерева, не взбираясь на вершину. Неприступное расстояние измеряют теми же приемами, какими мы измеряли недоступную высоту. В обоих случаях определение искомого расстояния заменяется промером другого расстояния, легко поддающегося непосредственному измерению.
Из многих способов решения этой задачи рассмотрим несколько наиболее простых.
1. Для первого способа понадобится уже знакомый нам «прибор» с тремя булавками на вершинах равнобедренного прямоугольного треугольника (рис. 61). Пусть требуется определить ширину АВ реки (рис. 62), стоя на том берегу, где точка В, и не перебираясь на противоположный. Став где-нибудь у точки С, держите булавочный прибор близ глаз так, чтобы, смотря одним глазом вдоль двух булавок, вы видели, как обе они покрывают точки В и А. Понятно, что, когда это вам удастся, вы будете находиться как раз на продолжении прямой АВ.
Рис. 61. Измерение ширины реки булавочным прибором
Теперь, не двигая дощечки прибора, смотрите вдоль других двух булавок (перпендикулярно к прежнему направлению) и заметьте какую-нибудь точку D, покрываемую этими булавками, т. е. лежащую на прямой, перпендикулярной к АС. После этого воткните в точку С веху, покиньте это место и идите с вашим инструментом вдоль прямой CD, пока не найдете на ней такую точку Е (рис. 63), откуда можно одновременно покрыть для глаза булавкой b шест точки С, а булавкой а – точку А. Это будет значить, что вы отыскали на берегу третью вершину треугольника АСЕ, в котором угол С – прямой, а угол Е равен острому углу булавочного прибора, т. е. ½ прямого. Очевидно, и угол А равен ½ прямого, т. е. АС = СЕ. Если вы измерите расстояние СЕ хотя бы шагами, вы узнаете расстояние AC, a отняв ВС, которое легко измерить, определите искомую ширину реки.
Рис. 62. Первое положение булавочного прибора
Рис. 63. Второе положение булавочного прибора
Довольно неудобно и трудно держать в руке булавочный прибор неподвижно; лучше поэтому прикрепить эту дощечку к палке с заостренным концом, которую и втыкать отвесно в землю.
Рис. 64. Пользуемся признаками равенства треугольников
2. Второй способ сходен с первым. Здесь также находят точку С на продолжении АВ и намечают при помощи булавочного прибора прямую CD под прямым углом к СА. Но дальше поступают иначе (рис. 64). На прямой CD отмеряют равные расстояния СЕ и EF произвольной длины и втыкают в точки Е и F вехи. Став затем в точке F с булавочным прибором, намечают направление FG, перпендикулярное к FC. Теперь, идя вдоль FG, отыскивают на этой линии такую точку Н, из которой веха Е кажется покрывающей точку А. Это будет означать, что точки Н, Е и А лежат на одной прямой.
Задача решена: расстояние FH равно расстоянию АС, от которого достаточно лишь отнять ВС, чтобы узнать, искомую ширину реки (читатель, конечно, сам догадается, почему FH равно АС).
Этот способ требует больше места, чем первый; если местность позволяет осуществить оба приема, полезно проверить один результат другим.
3. Описанный сейчас способ можно видоизменить: отмерить на прямой CF не равные расстояния, а одно в несколько раз меньше другого. Например (рис. 65), отмеряют FE в четыре раза меньше ЕС, а далее поступают по-прежнему: по направлению FG, перпендикулярному к FC, отыскивают точку Н, из которой веха Е кажется покрывающей точку А. Но теперь уже FH не равно АС, а меньше этого расстояния в четыре раза: треугольники АСЕ и EFH здесь не равны, а подобны (имеют равные углы при неравных сторонах). Из подобия треугольников следует пропорция
AC: FH = CE: EF = 4: 1.
Значит, измерив FH и умножив результат на 4, получим расстояние АС, а отняв ВС, узнаем искомую ширину реки.
Этот способ требует, как мы видим, меньше места и потому удобнее для выполнения, чем предыдущий.
Рис. 65. Пользуемся признаками подобия треугольников
4. Четвертый способ основан на том свойстве прямоугольного треугольника, что если один из его острых углов равен 30°, то противолежащий катет составляет половину гипотенузы. Убедиться в правильности этого положения очень легко. Пусть угол В прямоугольного треугольника АВС (рис. 66, слева) равен 30°; докажем, что в таком случае АС =½АВ. Повернем треугольник АВС вокруг ВС так, чтобы он расположился симметрично своему первоначальному положению (рис. 66, справа), образовав фигуру ABD; линия ACD – прямая, потому что оба угла у точки С прямые. В треугольнике ABD угол А = 60°, угол ABD, как составленный из двух углов по 30°, тоже равен 60°. Значит, AD = BD как стороны, лежащие против равных углов. Но АС = ½AD; следовательно, АС =½AB.
Желая воспользоваться этим свойством треугольника, мы должны расположить булавки на дощечке так, чтобы основания их обозначали прямоугольный треугольник, в котором катет вдвое меньше гипотенузы. С этим прибором мы помещаемся в точке С (рис. 27) так, чтобы направление АС совпадало с гипотенузой булавочного треугольника. Смотря вдоль короткого катета этого треугольника, намечают направление CD и отыскивают на нем такую точку Е, чтобы направление ЕА было перпендикулярно к CD (это выполняется при помощи того же булавочного прибора). Легко сообразить, что расстояние СЕ – катет, лежащий против угла 30°, – равно половине АС. Значит, измерив СЕ, удвоив это расстояние и отняв ВС, получим искомую ширину АВ реки.
Рис. 66. Когда катет равен половине гипотенузы
Рис. 67. Схема применения прямоугольного тpeyгольника с углом в 30°
Вот четыре легковыполнимых приема, при помощи которых всегда возможно, не переправляясь на другой берег, измерить ширину реки со вполне удовлетворительной точностью. Способов, требующих употребления более сложных приборов (хотя бы и самодельных), мы здесь рассматривать не будем.
Длина острова
Задача
Теперь нам предстоит задача более сложная. Стоя у реки или у озера, вы видите остров (рис. 68), длину которого желаете измерить, не покидая берега. Можно ли выполнить такое измерение?
Рис. 68. Как определить длину острова
Хотя в этом случае для нас неприступны оба конца измеряемой линии, задача все же вполне разрешима, притом без сложных приборов.
Решение
Рис. 69. Пользуемся признаками равенства прямоугольных треугольников
Пусть требуется узнать длину АВ (рис. 69) острова, оставаясь во время измерения на берегу. Избрав на берегу две произвольные точки Р и Q, втыкают в них вехи и отыскивают на прямой PQ точки М и N так, чтобы направления AM и BN составляли с направлением PQ прямые углы (для этого пользуются булавочным прибором). В середине О расстояния MN втыкают веху и отыскивают на продолжении линии AM такую точку С, откуда веха О кажется покрывающей точку В. Точно так же на продолжении BN отыскивают точку D, откуда веха O кажется покрывающей конец А острова. Расстояние СD и будет искомой длиной острова.
Доказать это нетрудно. Рассмотрите прямоугольные треугольники АМО и OND; в них катеты МО и NO равны, а кроме того, равны углы АОМ и NOD — следовательно, треугольники равны, и AO = OD. Сходным образом можно доказать, что ВО = ОС. Сравнивая затем треугольники АВО и COD, убеждаемся в их равенстве, а значит, и в равенстве расстояния АВ и CD.
Энергия реки
Ты знаешь край, где все обильем дышит,
Где реки льются чище серебра,
Где ветерок степной ковыль колышет,
В вишневых рощах тонут хутора.А.К. Толстой
Реку, длина которой не более 100 км, принято считать малой. Знаете ли вы, сколько таких малых рек в бывшем СССР? Очень много – 43 тысячи!
Если эти реки вытянуть в одну линию, то получилась бы лента длиною 1 300 000 км. Такой лентой земной шар можно тридцать раз опоясать по экватору (длина экватора примерно 40 000 км).
Неторопливо течение этих рек, но оно таит в себе неистощимый запас энергии. Специалисты полагают, что, если сложить скрытые возможности всех малых рек, которые протекают по нашей Родине, получится внушительное число – 34 миллиона киловатт! Эту даровую энергию необходимо широко использовать для электрификации хозяйства селений, расположенных вблизи рек.
Пусть свободная течет река, —
Если в плане значится, плотина
Гребнем каменным по всем глубинам
Преградит дорогу на века.С. Щипачев
Вы знаете, что это осуществляется при помощи гидроэлектростанций (ГЭС), и можете проявить много инициативы и оказать реальную помощь в подготовке строительства небольшой ГЭС. В самом деле, ведь строителей ГЭС будет интересовать все, что относится к режиму реки: ее ширина и скорость течения («расход воды»), площадь поперечного сечения русла («живое сечение») и какой напор воды допускают берега. А все это вполне поддается измерению доступными средствами и представляет сравнительно нетрудную геометрическую задачу.
К решению этой задачи мы сейчас и перейдем.
Но прежде приведем здесь практический совет специалистов, инженеров В. Яроша и И. Федорова, относящийся к выбору на реке подходящего места для строительства будущей плотины.
Небольшую гидроэлектростанцию мощностью в 15–20 киловатт они рекомендуют строить не дальше чем в 5 км от селения.
«Плотину ГЭС нужно строить не ближе чем в 10–15 км и не дальше чем в 20–40 км от истока реки, потому что удаление от истока влечет за собой удорожание плотины, которое вызывается большим притоком воды. Если же плотину располагать ближе чем в 10–15 км от истока, гидроэлектростанция в силу малого притока воды и недостаточного напора не сможет обеспечить необходимой мощности. Выбранный участок реки не должен изобиловать большими глубинами, которые тоже увеличивают стоимость плотины, требуя тяжелого фундамента».
Сколько воды протекает в реке
Вы всегда можете определить скорость, с какой течет вода в реке, поделив расстояние, которое пройдет по воде поплавок, на время, за которое он одолеет нужный участок (S: t = v). Труднее выполнять определение площади поперечного разреза воды. Чтобы найти величину этой площади, – того, что принято называть «живым сечением» реки, – надо изготовить чертеж этого сечения. Делается подобная работа следующим образом.
Первый способ
В том месте, где вы измерили ширину реки, вы у самой воды вбиваете на обоих берегах по колышку. Затем садитесь с товарищем в лодку и плывете от одного колышка к другому, стараясь все время держаться прямой линии, соединяющей колышки. Неопытный гребец с такой задачей не справится, особенно в реке с быстрым течением. Ваш товарищ должен быть искусным гребцом; кроме того, ему должен помогать и третий участник работы, который, стоя на берегу, следит, чтобы лодка не сбивалась с надлежащего направления, и в нужных случаях дает гребцу сигналами указания, в какую сторону ему нужно повернуть. В первую переправу через речку вы должны сосчитать лишь, сколько ударов веслами она потребовала, и отсюда узнать, какое число ударов перемещает лодку на 5 или 10 м. Тогда вы совершаете второй переезд, вооружившись на этот раз достаточно длинной рейкой с нанесенными на ней делениями, и каждые 5—10 м (отмеряемые по числу ударов веслами) погружаете рейку отвесно до дна, записывая глубину речки в этом месте.
Таким способом можно промерить «живое сечение» только небольшой речки; для широкой, многоводной реки необходимы более сложные приемы; работа эта выполняется специалистами. Любителю приходится избирать себе задачу, отвечающую его скромным измерительным средствам.
Второй способ
На узкой неглубокой речке и лодка не нужна.
Между колышками вы натягиваете перпендикулярно к течению бечевку со сделанными на ней через 1 м пометками или узлами и, опуская рейку до дна у каждого узла, измеряете глубину русла.
Рис. 70. «Живое сечение» реки
Когда все измерения закончены, вы прежде всего наносите на миллиметровую бумагу либо на лист из ученической тетради в клетку чертеж поперечного профиля речки. У вас получится фигура вроде той, какая изображена на рис. 70. Площадь этой фигуры определить весьма несложно, так как она расчленяется на ряд трапеций (в которых вам известны оба основания и высота) и на два краевых треугольника также с известными основанием и высотой. Если масштаб чертежа 1:100, то результат получаем сразу в квадратных метрах.
Теперь вы располагаете уже всеми данными для расчета количества протекающей воды. Очевидно, через «живое сечение» реки протекает каждую секунду объем воды, равный объему призмы, основанием которой служит это сечение, а высотой – средняя секундная скорость течения. Если, например, средняя скорость течения воды в речке 0,4 м в секунду, а площадь «живого сечения», скажем, равна 3,5 кв. м, то ежесекундно через это сечение переносится
3,5 · 0,4 = 1,4 куб. м воды,
или столько же тонн[39]39
1 куб. м пресной воды весит 1 т (1000 кг).
[Закрыть]
. Это составляет в час
1,4 · 3600 = 5040 куб. м,
а в сутки
5040 · 24 = 120 960 куб. м,
свыше 100 000 куб. м. А ведь река с живым сечением 3,5 кв. м – маленькая речка: она может иметь, скажем, 3,5 м ширины и 1 м глубины, вброд перейти можно, но и она таит в себе энергию, способную превратиться во всемогущее электричество. Сколько же воды протекает в сутки в такой реке, как Нева, через живое сечение которой ежесекундно проносится 3300 куб. м воды! Это – «средний расход» воды в Неве у Ленинграда. «Средний расход» воды в Днепре у Киева – 700 куб. м.
Молодым изыскателям и будущим строителям своей ГЭС необходимо еще определить, какой напор воды допускают берега, т. е. какую разность уровней воды может создать плотина (рис. 71). Для этого в 5—10 м от воды на берегах вбивают два кола, как обычно – по линии, перпендикулярной к течению реки.
Рис. 71. Гидроэлектростанция мощностью 80 киловатт Бурмакинской сельскохозяйственной артели; дает энергию семи колхозам
Двигаясь затем по этой линии, ставят маленькие колышки в местах характерных изломов берега (рис. 72). С помощью реек с делениями замеряют возвышение одного колышка над другим и расстояния между ними. По результатам измерений вычерчивают профиль берегов аналогично построению профиля русла реки.
Рис. 40. Измерение профиля берегов
По профилю берегов можно судить о величине допустимого напора.
Предположим, что уровень воды может быть поднят плотиной на 2,5 м. В таком случае вы можете прикинуть возможную мощность вашей будущей ГЭС.
Для этого энергетики рекомендуют 1,4 (секундный «расход» реки) умножить на 2,5 (высота уровня воды) и на 6 (коэффициент, который меняется в зависимости от потерь энергии в машинах). Результат получим в киловаттах. Таким образом,
1,4 · 2,5 · 6 = 21 киловатт.
Так как уровни в реке, а следовательно, и расходы меняются в течение года, то для расчета надо узнать ту величину расхода, которая характерна для реки бóльшую часть года.













































