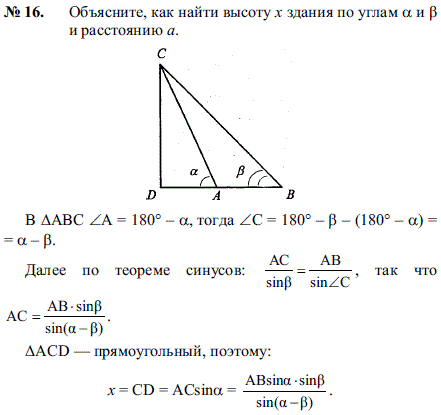Как найти высоту дома геометрия

Скачать материал

Скачать материал

Описание презентации по отдельным слайдам:

• 

  1 слайд

  Как измерить высоту здания без специальных приборов?
  Исследовательскую работу выполнила ученица 6 класса
  Тимофеева Екатерина.
  Руководитель- учитель математики-Грачёва Т.В.
  гУжур
  2017г

• 

  2 слайд

  Содержание
  Ведение.
  Цели и задачи.
  Гипотеза. Методы исследования.
  Вывод
  Литература.

• 

  3 слайд

  Введение.
  Каждый день мы входим в здание нашей школы и не можем ответить на вопросы: когда было построено здание, какова его высота, периметр…Результаты опроса учащихся моего класса показали, что ни один ученик не знает точную высоту школы. Заинтересовавшись ответом на этот вопрос об измерении недоступных высот, я определила цель и задачи моего исследования. Тема моей работы звучит так: « Как измерить высоту здания без специальных приборов?».

• 

  4 слайд

  Цели и задачи.
  Цель  работы : определить высоту здания школы разными способами без специальных приборов.
  Для достижения цели необходимо решить следующие задачи:
  — по литературным и интернет — источникам рассмотреть различные способы определения высоты выбранного здания;
  — провести соответствующие измерения высоты;
  — проанализировать и определить наиболее точный способ измерения высоты здания.

• 

  5 слайд

  Гипотеза. Методы исследования.
  Я выдвинула гипотезу: если я смогу измерить высоту здания не специальными приборами, то она будет правдива?

  Методы исследования: анкетирование, эксперимент, сравнение, анализ, фотосъемка.

• 

  6 слайд

  План работы.
  1.Ознакомиться с современными приборами, которые позволяют измерить высоту зданий.
  2. Выбрала способы измерения высоты здания школы.
  а) измерение с помощью фотографии;
  б) способ, в основе которого лежит знание длины своего шага и длины тени;
  в) способ «карандаша»; г) с помощью зеркала
  д) измерение с помощью запуска воздушного шарика.
  3.Выполнить необходимые расчёты.
  4. Сравнить полученные данные, выбрать наиболее
  точный способ.

• 

  7 слайд

  Измерение с помощью фотографии
  Измерение с помощью фотографии процесс несложный нужно сфотографироваться на фоне здания. Измерить свой рост и высоту здания на фото, вычислить во сколько раз высота школы больше моего роста, значит во столько раз и высота школы будет больше чем мой рост В результате у меня получилось: на фото мой рост –  12мм, высота школы на фото- 73мм,значит высота школы больше 6,08 раз. Мой рост 170см умножаю на 6, получается −10м 40см

• 

• 

  9 слайд

  Определение высоты здания с помощью тени.
  Самый древний способ ,которым греческий мудрец Фалес за шесть веков до нашей эры определил высоту пирамиды. Он воспользовался её тенью. Во сколько раз тень пирамиды больше его тени, во столько же раз высота пирамиды больше его роста. Наши результаты : тень школы – 58м 40см,моя тень – 8м 85см,мой рост – 170см.Делим тень школы на мою тень:5840:835=6.99(раз) Умножаем мой рост на это число получаем 11м89см.

• 

• 

  11 слайд

  Способ “Карандаша»
  Мне очень понравился способ «карандаша». Нужно встать от здания на такое расстояние , чтобы видеть его целиком. Я встала рядом со зданием . Надо вытянуть руку с карандашом, зажатым в кулаке. Прищурить один глаз и подвести грифель карандаша к крыше здания. Основание карандаша должно совпадать с основанием школы и помошника. Повернуть карандаш в горизонтальное положение, причём основание карандаша должно оставаться на месте. Затем я прошла расстояние на которое указало острие карандаша. Пока мне не подали сигнал. Измерив длину этого расстояния мы вычислили высоту школы-. Наш результат -11м60см.

• 

• 

  13 слайд

  Измерение высоты здания при помощи зеркала.
  Кладем зеркало на землю так, как показано на фото, отходим в сторону до того момента, пока в зеркале не отразится верхушка измеряемого объекта. Измеряем необходимые расстояния от человека до зеркала, от зеркала до школы, и делаем вычисления .Во стколко раз расстояние от школы до зеркала больше, чем расстояние от меня до зеркала, значит во столько же раз высота школы больше моего роста. Наши данные измерения: от меня до зеркала-190см.от центра зеркала до школы 13м10см. 1310:190=6.89(раз). Мой рост 170см*6,89=11м71см

• 

• 

  15 слайд

  Измерение высоты при помощи шарика.
  Привязала к шарику длинную нитку и запустила шарик в небо, дала ему подняться на высоту здания, у основания здания сделала на нитке узелок, а затем, намотав нитку на школьную линейку, я узнала высоту здания школы 1ом 80см.

• 

• 

• 

• 

• 

  20 слайд

  Вывод.
  Сейчас имеется точный способ измерения высоты здания при помощи лазарной рулетки ей пользуются работники БТИ при измерении периметров, площадей и высот зданий, к сожалению я не смогла им воспользоваться для измерения высоты нашей школы, но проделав много опытов по определению высоты здания я поняла, что существует много интересных легко доступных способов измерения высоты. В нашем случае с учётом предоставленного паспорта школы высота школы более точно была измерена с помощью метода фотографии и с помощью шарика.

• 

• 

• 

  23 слайд

  Литература.
  1.Н. Н. Аменицкий, И. П. Сахаров Забавная арифметика Москва «Наука» 1997
  2.Я. И. Перельман. Занимательная геометрия. – Москва  «АСТ» 2005
  3. http://piterhunt.ru/pages/nk-os/5/15.htm сайт «Питерский охотник»
  4. В. Н. Русанов Математические олимпиады младших школьников Москва «Просвещение» 1990
  5. http://www.scouts.ru «Центральный сайт скаутов-разведчиков России»

Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:

6 257 142 материала в базе

• Выберите категорию:

• Выберите учебник и тему

• Выберите класс:

• Тип материала:

  • Все материалы

  • Статьи

  • Научные работы

  • Видеоуроки

  • Презентации

  • Конспекты

  • Тесты

  • Рабочие программы

  • Другие методич. материалы

Найти материалы

Вам будут интересны эти курсы:

• Курс повышения квалификации «Изучение вероятностно-стохастической линии в школьном курсе математики в условиях перехода к новым образовательным стандартам»

• Курс профессиональной переподготовки «Экономика: теория и методика преподавания в образовательной организации»

• Курс повышения квалификации «Разработка бизнес-плана и анализ инвестиционных проектов»

• Курс повышения квалификации «Финансы: управление структурой капитала»

• Курс повышения квалификации «Особенности подготовки к сдаче ОГЭ по математике в условиях реализации ФГОС ООО»

• Курс профессиональной переподготовки «Математика и информатика: теория и методика преподавания в образовательной организации»

• Курс повышения квалификации «Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО»

• Курс повышения квалификации «Методы и инструменты современного моделирования»

• Курс профессиональной переподготовки «Черчение: теория и методика преподавания в образовательной организации»

• Курс повышения квалификации «Учебная деятельность по предметной области «Черчение»: основы предмета и реализация обучения в условиях ФГОС»

• Курс профессиональной переподготовки «Уголовно-правовые дисциплины: теория и методика преподавания в образовательной организации»

• Курс профессиональной переподготовки «Теория и методика музейного дела и охраны исторических памятников»

• Курс профессиональной переподготовки «Стандартизация и метрология»

---

---

Нашли ошибку? Сообщите в комментариях (внизу страницы)

Раздел: Геометрия Полное условие: Объясните, как найти высоту x здания по углам а и b и расстоянию a. Решение, ответ задачи 2157 из ГДЗ и решебников: Этот учебный материал представлен 1 способом: Для просмотра в натуральную величину нажмите на картинку Идея нашего сайта – развиваться в направлении помощи ученикам школ и студентам. Мы размещаем задачи и решения к ним. Новые задачи, которые недавно добавляются на наш сайт, временно могут не содержать решения, но очень скоро решение появится, т.к. администраторы следят за этим. И если сегодня вы попали на наш сайт и не нашли решения, то завтра уже к этой задаче может появится решение, а также и ко многим другим задачам. основной поток посетителей к нам – это из поисковых систем при наборе запроса, содержащего условие задачи

Счетчики: 2392 | Добавил: Admin

Добавить комментарий Добавлять комментарии могут только зарегистрированные пользователи. [ Регистрация | Вход ]

Доброго дня, уважаемые гости и подписчики!

Сегодня хотел бы осветить тему использования тригонометрии в строительстве, так как математика очень тесно взаимодействует с этой сферой.

Величины углов и сторон любого будь-то равнобедренного, равностороннего или разностороннего треугольника связываются между собой определенными тригонометрическими соотношениями, основные из которых выделяют как “теорема синусов” и “теорема косинусов”.

Благодаря великим математикам древних времен, выведены формулы, позволяющие по ТРЁМ элементам ЛЮБОГО треугольника – ВОССТАНОВИТЬ остальные три!

Далее немного теории из школьного курса (очень кратко):

Значения длин сторон треугольника пропорциональны синусам противолежащих углов:

Она обобщает теорему Пифагора на произвольные треугольники, таким образом теорема Пифагора – становится частным случаем теоремы косинусов.

Так, для любого треугольника, справедлива зависимость:

После преобразований, мы можем найти косинус любого угла треугольника:

и установить следующее:

И если угол является прямым (второй случай), то теорема косинусов превращается в теорему Пифагора.

После значительных раскладок и преобразований доказывается “формула Герона”, по которой зная только стороны треугольника, мы можем вычислить площадь:

Выше приведенные соотношения и вычисления используются там, где требуется расчет каких-либо элементов со значительными размерами, которые невозможно измерить угломерными линейками или доставляет много неудобств использование рулетки.

Примеры задач, решаемых с помощью таких теорем

Зная длину ската и угол наклона кровли мы можем получить остальные значения всех составляющих элементов, будь то высота кровли до конька или длина здания:

И наоборот, зная угол наклона кровли и длину здания с кровельным свесом – высчитывается в пару действий как длина стропильных ног, так и высота крыши:

А точная высота дома? – Да не вопрос!

?/Sin40° = 10/Sin50°

? = (10 х Sin40°)/Sin50° = 10 х 0,643 : 0,766 = 8,4 м.

Определение угла наклона ската

Определить угол наклона ската с точностью до 1 градуса с земли тоже совершенно не напрягаясь можно сделать: для этого требуется занять положение наблюдателю так, чтобы плоскость ската легла в одну линию с линией направления взгляда.

Теперь зная высоту дома (a) и расстояние (b), а соответственно по теореме Пифагора и гипотенузу (с), мы можем посчитать величину синуса или косинуса угла А (формула на рисунке выше).

Далее таблица Брадиса в помощь! ))) Находим значение в колонке Синуса и сопоставляем с соответствующим углом!

Так же решаются задачи с устройством фронтонов в скат основной кровли (рисунок ниже)! Зная только угол наклона основной кровли, мы можем рассчитать длины стропил и основание врезаемого фронтона, чтобы углы были равны между собой!

Для возведения зданий и различных сооружений с помощью таких формул рассчитывается разница высот на участке, а так же углы в разных плоскостях с помощью геодезических приборов, работающих на основании той же тригонометрии – теодолит, тахеометр и тригонометрический нивелир.

И это лишь малая часть приведенных примеров, где нужны знания тригонометрии…

Похоже учителя были правы, когда говорили, что “Математика пригодится!!!” ))).

На этом всё, спасибо Вам за внимание!

1. “Варианты построения прямых углов при строительстве дома и проверка углов при уже возведенном сооружении.”

2. “3 способа небольшой экономии на ленточном фундаменте без потери качества.”

3. Что делать, если запорный шаровой кран под давлением вышел из строя? Пошаговое руководство по замене.

____________________

Если Вам понравилась моя статья, ставьте лайк и подписывайтесь на канал

Как определить высоту предмета

• Авторы
• Руководители
• Файлы работы
• Наградные документы

Текст работы размещён без изображений и формул.
Полная версия работы доступна во вкладке “Файлы работы” в формате PDF

Введение

Геометрия – одна из древнейших наук, возникших еще до нашей эры. В переводе с греческого слово «геометрия» означает «землемерие». Это название объясняется тем, что его происхождение было связано с различными измерительными работами, которые приходилось выполнять при разметке земельных участков, строительстве зданий и различных сооружений. Другими словами, геометрия возникла из практической деятельности людей и в начале своего развития служила главным образом практическим целям. [6]

На уроках геометрии в 8-м классе при изучении темы «Подобные треугольники» я заинтересовался ее практическим применением, в частности использованием подобия при измерении высоты объекта.

Выбранная тема актуальна тем, что можно узнать, как определить высоту объекта без каких-либо специальных технических устройств. В частности, иногда туристам нужно оценить размер дерева, чтобы построить мост через быструю реку. У них нет под рукой высотомера. Чтобы определить, достаточно ли высоты дерева, чтобы упав, оно перекрыло реку, можно использовать предметы, которые всегда под рукой. Или, например, на садовом участке растет дерево, которое мешает по каким – то причинам. Прежде чем его спилить, нужно решить проблему – не достанет ли оно при падении до любого строения, находящегося рядом с ним. И тут снова на помощь приходят различные методы определения высоты дерева с помощью подручных средств.

Проблема: как определитьвысоту предмета с помощью подручных средств.

Цель исследования: определение высоты предмета различными способами.

Объект исследования: дом, в котором я живу.

Предмет исследования: высота дома.

Задачи:

– рассмотреть различные способы измерения высоты предмета;

– экспериментально проверить использование различных способов определения высоты предмета, определив высоту дома, в котором я живу;

– проанализировать полученные данные и определить наиболее точный способ измерения высоты предмета.

Методы исследования:

– изучение литературы и ресурсов Интернет;

– эксперимент;

– сравнение;

– анализ.

Глава I. Способы определения высоты предмета

В своей профессиональной деятельности строители, архитекторы, лесоводы, военные для определения высоты предмета используют специальные сложные и дорогостоящие приборы – высотометры. В книге Я.И.Перельмана «Занимательная геометрия» [5], а также на сайте «Лесная промышленность» [7] можно найти различные способы определения высоты предмета с помощью подручных средств на примере определения высоты дерева.

В школьных учебниках геометрии также есть практические задачи на определение высоты дерева. Например, в учебнике Л.С.Атанасяна «Геометрия 7-9» [1] в №581 рассмотрен способ измерения высоты дерева с помощью зеркала, а в учебнике А.Г.Мерзляка «Геометрия – 8» [4] в №472 – с помощью тени (рис.1).

рис.1

Изучив литературу [3] и ресурсы сети Интернет, я выделил несколько способов определения высоты предмета и разработал пошаговые инструкции по применению каждого из них на примере измерения высоты дерева.

1. Подобие треугольников

Способы определения высоты предмета с помощью подручных средств основаны на применении такого важного понятия геометрии, как подобие треугольников. [2]

Два треугольника называются подобными, если их углы соответственно равны, и стороны одного треугольника пропорциональны соответственным сторонам другого треугольника (рис.2)

рис.2

Соответственные стороны – это стороны, лежащие напротив равных углов.

Коэффициент подобия – это число k, равное отношению соответственных сторон (рис.3).

рис.3

При решении задач на местности чаще всего применяют первый признак подобия треугольников: если два угла одного треугольника равны соответственно двум углам другого треугольника, то такие треугольники подобны (рис.4).

рис.4

2. Определение высоты с помощью тени

Этот способ называется способом Фалеса. В честь греческого мудреца Фалеса Милетского, который еще за шесть веков до нашей эры научил египтян определять высоту пирамиды по длину ее тени.

Инструкция:

1.Встаньте рядом с деревом так, чтобы были видны тени и дерева, и человека (рис.5).

2.Измерьте тень человека и тень дерева.

3.Измерьте рост человека.

рис.5

Геометрическая постановка задачи. Рассмотрите подобные по двум углам треугольники АВС и А₁В₁С₁ (рис.5) и составьте отношение соответственных сторон , где АВ – искомая высота дерева, А₁В₁ – рост человека, ВС – длина тени дерева, В₁С₁ – длина тени человека. Подставьте измерения и найдите величину АВ. Это и будет искомая высота дерева.

3. Определение высоты с помощью равнобедренного прямоугольного треугольника

Инструкция:

1.Держа равнобедренный прямоугольный треугольник на уровне глаз вертикально, отойдите от дерева на такое расстояние, чтобы, глядя вдоль гипотенузы, видно было верхушку дерева (рис.6).

2.Измерьте расстояние от места измерения до дерева.

3.Измерьте катет треугольника.

4.Измерьте рост человека до уровня глаз.

рис.6

Геометрическая постановка задачи. Рассмотрите подобные по двум углам треугольники АВС и А₁В₁С₁ (рис.5) и составьте отношение соответственных сторон , где АС – расстояние от точки измерения до основания дерева, А₁С₁ – длина катета равнобедренного прямоугольного треугольника, ВС – искомая величина, В₁С₁ – длина катета равнобедренного прямоугольного треугольника (рис.7).

рис.7

Подставьте измерения и найдите величину ВС. К полученной величине прибавьте рост человека до уровня глаз. Это и будет искомая высота дерева.

4. Определение объекта с помощью зеркала

Инструкция:

1.Положить зеркало горизонтально на ровную землю на некотором расстоянии от измеряемого дерева (рис.8).

2.Отойти от зеркала на такое расстояние, чтобы видеть в зеркале верхушку дерева.

3.Измерить расстояние от зеркала до основания дерева и до точки измерения.

рис.8

Затем измеряется расстояние от основания дерева до зеркала и расстояние от зеркала до измерителя.

Геометрическая постановка задачи. Способ основан на законе отражения света. Вершина отражается в точке так, что АВ = В. Из подобия треугольников ВС и СЕD следует, что . В этом отношении необходимо только заменить В равным АВ. Решив пропорцию, найдем высоту дерева АВ (рис.9).

рис.9

5. Определение высоты с помощью булавочного прибора

Булавочный прибор можно изготовить из дощечки и трех булавок. На дощечке или куске коры отмечают три точки – вершины равнобедренного прямоугольного треугольника, и в эти точки втыкают по булавке (рис.10).

рис.10

Инструкция:

1.Держа булавочный прибор на уровне глаз так, чтобы один из катетов треугольника был направлен вниз, отойдите от дерева на такое расстояние, чтобы, глядя на булавки А₁ и С₁, можно увидеть верхушку дерева (рис.11).

2.Измерьте расстояние от основания дерева до точки измерения.

рис.11

Геометрическая постановка задачи. Из подобия треугольников АВС и АВ₁С₁ следует отношение соответственных сторон , где АВ – расстояние от точки измерения до основания дерева, АВ₁ – длина катета равнобедренного прямоугольного треугольника, ВС – искомая величина, В₁С₁ – длина катета равнобедренного прямоугольного треугольника (рис.11).

Решив пропорцию, находим ВС. Для того, чтобы найти высоту дерева, необходимо к этой величине прибавить рост человека до уровня глаз.

6. Определение высоты с помощью фотографии

Инструкция:

1.Сделайте фотографию человека на фоне дерева (рис.12).

2.Измерьте рост человека.

3.Измерьте на фотографии высоту дерева и рост человека.

рис.12

Составьте отношение соответственных сторон:

Подставьте измерения и найдите реальную высоту дерева.

Глава II. Проведение эксперимента

1.Измерение высоты дома, в котором я живу

Разработанные инструкции для определения высоты предмета с помощью подручных средств я решил применить на практике, измерив высоту дома, в котором живу (Приложение 1, рис.13).

1)Измерение высоты дома по его тени (Приложение 1, рис.14).

Такое измерение лучше проводить в солнечные дни.

Необходимое оборудование: рулетка.

Результаты измерения: мой рост – 160 см, длина моей тени – 173 см, длина тени дома – 500 см.

Составляем и решаем пропорцию: .

см

Искомая высота дома в данном случае равна 4,62 м.

2) Измерение высоты дома с помощью зеркала (Приложение 1, рис.15).

Оборудование: зеркало, рулетка.

Результаты измерения: мой рост – 160 см, расстояние от зеркала до основания дома – 680 см, расстояние от зеркала до точки измерения – 220 см.

Составляем и решаем пропорцию: .

см

Искомая высота дома в данном случае равна 4,94 м.

3) Измерение высоты дома с помощью равнобедренного прямоугольного треугольника (Приложение 1, рис.16).

Оборудование: рулетка, равнобедренный прямоугольный треугольник.

Результаты измерения: длина катета равнобедренного прямоугольного треугольника – 38 см, расстояние от дома до точки измерения – 350 см.

Составляем и решаем пропорцию: .

см

Чтобы найти высоту дома, необходимо к полученному значению прибавить мой рост до уровня глаз: 350 см + 150 см = 500 см. Итак, искомая высота дома в данном случае равна 5 м.

4) Измерение высоты дома с помощью булавочного прибора (Приложение 1, рис.17).

Оборудование: рулетка, булавочный прибор (Приложение 1, рис.18).

Результаты измерения: длина катета булавочного прибора – 5 см, расстояние от дома до точки измерения – 370 см.

Составляем и решаем пропорцию: .

см

Чтобы найти высоту дома, необходимо к полученному значению прибавить мой рост до уровня глаз: 370 см + 150 см = 520 см. Итак, искомая высота дома в данном случае равна 5,2 м.

5) Измерение высоты дома с помощью фотографии (Приложение 1, рис.19).

Оборудование: линейка, фотоаппарат.

Результаты измерения: мой рост – 160 см, высота дома на фотографии – 10,5 см, мой рост на фотографии – 3,5 см.

Составляем и решаем пропорцию: .

см

Искомая высота дома в данном случае равна 4,8 м.

2. Определение наиболее точного способа измерения

Посмотрев технический план нашего дома, я выяснил, что его реальная высота – 4,85 м.

Измерив высоту дома различными способами, я решил проверить, насколько мои измерения точны. Для этого я вычислил относительную погрешность измерений по формуле , где х – точное значение величины, а а – приближенное значение (табл.1). Относительную погрешность измерений я вычислял в процентах.

Таблица 1. Относительная погрешность измерения

Метод измерения	Результат измерений	Фактическое значение	Относительная погрешность
С помощью тени	4,62 м	4,85 м
С помощью зеркала	4,94 м	4,85 м
С помощью равнобедренного прямоугольного треугольника	5 м	4,85 м
С помощью булавочного прибора	5,2 м	4,85 м
С помощью фотографии	4,8 м	4,85 м

Из данной таблицы видно, что наиболее точными оказались метод определения высоты дома с помощью фотографии и с помощью зеркала, а наименее точными – с помощью тени и с помощью булавочного прибора. Нужно отметить, что имели свое значение и не очень благоприятные условия: неровная, неудобная местность. Сказывалось и отсутствие опыта проведения практических измерений.

Заключение

В данной работе рассмотрены различные способы определения высоты предмета, описанные в научной литературе, и составлены инструкции по применению каждого из этих методов. Все рассмотренные методы были реализованы на практике.

Выполняя практические задания на местности, я научился видеть подобные треугольники в разных ситуациях; правильно записывать соотношения соответственных сторон; используя свойство пропорции, вычислять неизвестные элементы. Мой интерес к предмету геометрии также возрос. Длительное пребывание на свежем воздухе помогло укрепить мое здоровье.

Во время эксперимента самым простым для меня способом было измерить высоту дома с помощью равнобедренного прямоугольного треугольника, так как это занимает минимум времени и не требует большого количества приборов. Но я также столкнулся с трудностями: это неровный рельеф местности, пасмурная погода (высоту дома с помощью тени можно определить только в солнечную погоду).

Относительная погрешность измерений, полученных в ходе эксперимента, различна. Наиболее точным оказался метод определения высоты дома по фотографии и с помощью зеркала, а наименее точным – по тени и с помощью булавочного прибора.

Таким образом, поставленные задачи были выполнены и цель работы достигнута.

Желающие, кто хочет попробовать определить высоту предмета, могут воспользоваться инструкциями, приведенными в этой работе. Эта работа ясно показывает, что геометрия – это не просто школьный предмет, а наука, которая используется в жизни.

Библиографический список

Атанасян Л.С. и др. Геометрия: учебник для 7-9 кл. общеобразовательных учреждений. – М.: Просвещение, 2017

Болтянский В.Г. Элементарная геометрия. – М.: Просвещение, 1982

Ганьшин В.Н. Простейшие измерения на местности. – М.: Недра, 1983

Мерзляк А.Г., Полонский В.Б., Якир М.С. и др. Геометрия 8 класс: учеб. для общеобразоват. организаций.- М.: Вентана-Граф, 2018

Перельман Я.И. Занимательная геометрия. – М.: АСТ, 2005

Энциклопедический словарь юного математика. – М.: Педагогика, 1983

http://wood-prom.ru/ – сайт Лесная промышленность

Приложение 1

Фотоотчет проведения эксперимента

рис.13. Объект измерения

рис.14. Измерение высоты дома с помощью тени

рис.15. Измерение высоты дома с помощью зеркала

рис.16. Измерение высоты дома с помощью равнобедренного прямоугольного треугольника

рис.17. Измерение высоты дома с помощью булавочного прибора

рис.18. Булавочный прибор

рис.19. Измерение высоты дома с помощью фотографии

Просмотров работы: 4025