Задача о теплице, входит в первые пять заданий огэ по математике, и является практико-ориентированной задачей. Сложность данной задачи заключается в том, что в 5 задании требуется найти приближенное значение арифметического квадратного корня, и попасть в интервал ответов.
Вот текст задачи:
По этому тексту, нужно ответить на 5 вопросов.
1) Какое наименьшее количество дуг, нужно нужно заказать, чтобы расстояние между соседними дугами было не более 70 см.
Из первого предложения текста задачи, мы узнаем, что длина теплицы составляет 6 метров. Поэтому, первым делом находим количество интервалов, между дугами.
Теперь найдем, сколько будет дуг. Количество дуг = количество интервалов +1 = 9+1 = 10 дуг. Ответ 10
2) Сколько упаковок плитки необходимо купить для дорожек между грядками, она продается в упаковках по 14 штук?
Для этого вопроса, информация в тексте задачи дана в последнем предложении “Между грядками будут дорожки шириной 50 см, для которых необходимо купить тротуарную плитку размером 25х25”
Поскольку у нас ширина дорожки 50 см, а ширина плитки 25 см, то в ширину дорожки можно уложить 2 плитки. Длина у нас 6 метров, что составляет 600 см, поэтому в длину уместится 24 плитки. Тогда во всей дорожке будет 48 плитки. а в двух дорожках 96 штук.
Расчет количества упаковок приведен ниже.
3) Найдите ширину теплицы. Ответ дайте в метрах до сотых.
Ширина теплицы – это отрезок АD. Поскольку теплица состоит из дуг, то АD- это диаметр окружности.
Диаметр окружности связан с длиной окружности следующей формулой:
В этой формуле, L-длина окружности, D- диаметр окружности, “пи”=3,14
Длину окружности, найдем из следующей информации: “….металлические дуги в форме полуокружности длиной 5,53 метра….”
Поскольку известна длина полуокружности – 5,53 м, то длина окружности равна:
Из этих расчетов получаем, что ширина теплицы (с округлением до сотых) равна 3,52
4) Найти ширину центральной грядки, если она в два раза больше ширины узкой грядки. Ответ дайте до десятков, с точностью до десятков.
Для ответе на этот вопрос, сделаем схематический чертеж:
В этой задаче, за Х взяли ширину узкой грядки. Тогда широкая грядка будет 2Х. В задаче у нас две дорожки, что показано на схеме, которые составляю по 50 см.
По схеме составим уравнение:
Поскольку в задаче написано условие, что результат нужно округлить до десятков, поэтому получаем ответ 130.
5)Найти высоту входа в теплицу. Ответ дайте в сантиметрах.
Для расчета высоты теплицы, нам необходимо сделать дополнительные построения. Проводим ОС1. Получаем прямоугольный треугольник, ОС1С. Дальше по теореме Пифагора, выразим СС1. Для этой задачи, покажу три разных варианта завершения задачи.
Первый вариант:
При таком решении, получаем неизвлекаемый корень из 3. На экзамене, хорошо, что хоть кто нибудь вспомнит, что примерно он равен 1,7. Но такого значения не достаточно, поскольку мы получаем, что высота входа равна 149,6. Но такой ответ нас не устраивает, поскольку верный ответ находится в интервале от 150-160 см
Поэтому в этой задаче, чем точнее ответ, тем больше вероятность, что ответ будет не верный, не попадете в интервал правильного ответа.
Второй вариант:
В этом варианте, мы не будем раскладывать числа до последнего множителя, а будем раскладывать число на множители таким образом, что бы получилось приближенное число из таблицы квадратов. В этом случае, 23232 можно поделить на 16 (признак делимости на 4, если последние два числа делятся на 4)
Как видите, оба ответа, 152 и 156 подходят под наш интервал решения.
Третий вариант: воспользуемся канадской формулой вычисления приближенного значения квадратного корян.
Как видим, эту формулу. так же можно использовать для решения этой задачи.
Вы меня очень поддержите, если поставите лайк и подпишитесь на мой блог.
Чтобы правильно рассчитать количество поликарбоната на теплицу, нужно учесть не только ширину и длину, но и высоту теплицы, и её форму. Ниже мы остановимся на этом подробно, а сначала рассмотрим «идеальный» случай – арочную теплицу шириной 3 метра.
Именно такая теплица, шириной в 3 м, высотой от 2 до 2,1 м и длиной от 4 до 6 м, и стала самой популярной среди дачников и в небольших частных хозяйствах.
Популярная арочная теплица 3х4 м
Стандартный размер листа поликарбоната составляет 2,1 х 6 метра, такой размер выбран производителями не случайно. Реже встречается лист 2,1 на 12 м, представляя собой, по сути, вдвое увеличенный по длине 6-метровый лист.
Расчет полукруглой теплицы
Инструкции для калькулятора расчета материалов арочной теплицы
Укажите необходимый масштаб чертежей.
Заполните параметры теплицы в миллиметрах:
X – Ширина теплицы выбирается исходя из бюджета, наличия свободного места для размещения на участке, а также Ваших пожеланий и целей. Стандартная ширина теплиц заводского изготовления находится в пределах 1800-6000 мм. Оптимальное значение X для комфортной работы в теплице не меньше 2400 мм. Такой размер позволяет оборудовать в теплице проход шириной 600 мм (что оптимально), поставить стеллажи с рассадой или оборудовать грядки по обе стороны до 900 мм (сложно ухаживать за растениями дотягиваясь дальше указанного расстояния).
Z – Длина парника, может быть любой, если позволяют размеры участка. При выборе значения Z следует учитывать стандартные размеры материала, который будет применяться для остекления. Например, если используется полиэтиленовая пленка значение длины Z должно быть кратным 1000 мм, а если поликарбонат – кратным 2100 мм.
Один из решающих аспектов, влияющих на выбор ширины и длины теплицы, это ширина покрытия. Стандартная ширина листа поликарбоната 2100 мм это максимально допустимая ширина, при которой не происходит провисание под собственным весом, при условии обеспечении упора краями материала на каркас. Теплица, покрытая материалом максимальной ширины более светлая, поскольку в таком случае используется меньше стоек. Однако при определении оптимального количества стоек каркаса также следует учитывать климатические особенности Вашего региона (снеговые и ветровые нагрузки).
Y – Высота теплицы выбирается исходя из удобства работы в ней (определяющим фактором является рост работника). Значение Y влияет на длину дуги каркаса (больше высота – длиннее дуга и большее количество материала необходимо для остекления). Оптимальная высота теплицы 2000 – 2200 мм.
При выборе основных параметров теплицы следует учитывать рекомендации СП 107.13330.2012 «Теплицы и парники» (актуализированная редакция СНиП 2.10.04-85).
A – Количество вертикальных секций на фасаде теплицы, следует выбирать с учетом геометрических размеров материала для обшивки.
E – Число вертикальных сегментов стен, зависит от размеров используемого для обшивки материала и длины парника. Например, для шести метровой теплицы остекленной поликарбонатом стандартной ширины, значение E следует принимать не меньше 3.
D – Количество ячеек в вертикальном сегменте принимается с учетом свойств материала остекления и прочности каркаса. Если используется поликарбонат, достаточно значения D=3 (поскольку в конструкции он согнут и напряжен, то хорошо воспринимает нагрузки на растяжение-сжатие), для парниковой пленки следует принимать значение D больше чтобы исключить провисание.
У Вас есть возможность подобрать оптимальные размеры секций и ячеек изменяя их количество, при этом размеры будут отображены на чертежах теплицы.
Нажмите «Рассчитать»
Калькулятор поможет посчитать площадь, объем и периметр полукруглой теплицы. А также площади крыши, боковых стен и фасадов и полную площадь остекления, что необходимо для закупки материала обшивки в нужном количестве. Кроме того вы узнаете длину дуг теплицы (их количество) и длину материалов для изготовления каркаса. Использование данного онлайн калькулятора позволит Вам достаточно точно рассчитать материалы для изготовления арочной теплицы своими руками и оценить финансовые вложения в ее постройку. Также будет произведен расчет длины и дуги арки теплицы.
Важно: при использовании поликарбоната для остекления теплицы его следует сгибать поперек ребер жесткости.
Найдите длину дуги расширяющейся дуги для угла 7pi / 5 радиан на окружности радиуса 3.
Джеймс Дж.
задано • 25.08.17
Определите длину дуги для исходящей дуги, описанной в вопросе.
Больше
с = rθ
с = 3 (7π / 5)
с = 21π / 5
Все еще ищете помощь? Получите правильный ответ быстро.
ИЛИ
Найдите онлайн-репетитора сейчас
Выберите специалиста и познакомьтесь онлайн. Никаких пакетов или подписок, платите только за необходимое время.
¢ € £ ¥ ‰ μ · • § ¶ ß « » ≤ ≥ — — ¯ ~ ¤ | ¨ ¡ ¿ ~ ° — ± ÷ / × ƒ ∫ Σ ∞ √ ~ ≅ ≈ ≠ ≡ ∈ ∉ ∋ Π ∧ ∨ ¬ ∩ ∪ ∂ ∀ ∃ ∅ ∇ * α ∠ ‘ ¸ ª º † ‡ À Á Â Ã Ä Å Æ БЗ Э. É Ê Ë Я Я Я Я Ð ЦТС Ò Ó Ф Õ Ö Ø О.Н Š Ù Ú Û Ü Ý Ÿ Þ à á â ã ä å æ ç è é ê ë я я я я ð ñ ò ó ô õ ö ø œ š ù ú û ü ý þ ÿ Α Β Γ Δ Ε Ζ Η Θ Ι Κ Λ Μ Ν Ξ Ο Π Ρ Σ Τ Υ Φ Χ Ψ Ω α β γ δ ε ζ η θ ι κ λ μ ν ξ ο π ρ ς σ τ υ φ χ ψ ω ℵ π ℜ Υ ℘ ℑ ← ↑ → ↓ ↔ ↵ ⇐ ⇑ ⇒ ⇓ ⇔ ∴ ⊂ ⊃ ⊄ ⊆ ⊇ ⊕ ⊗ ⊥ ⋅ ⌈ ⌉ ⌊ ⌋ ◊ ,
Полукруглая теплица
Полукруглая Теплица — отапливаемый парник, представляющий собой защитное сооружение полукруглой (арочной) формы, как правило, из поликарбоната для выращивания ранней рассады.
Полугруглые теплицы из поликарбоната получили широкое распространение среди садоводов из за быстроты сборки и установки, но при этом имеют сложность в проветривании, из-за покатой крыши сложнее сделать открывающиеся окна (форточки). Таким образом, целесообразнее делать два входа в теплицу для лучшего проветривания.
Установка полукруглой теплицы из поликарбоната осуществляется на неглубокий ленточный фундамент (30-50 см).
Калькулятор расчета материалов для полукруглой теплицы
Онлайн калькулятор расчета необходимых материалов для сооружения полукруглой теплицы из поликарбоната. С помощью калькулятора возможно рассчитать площадь и объем теплицы, площадь ее остекления, количество материалов для каркаса, периметр для фундамента.
Формулы расчета полукруглой теплицы
Площадь полукруглой теплицы (м 2 ) = X/1000*Z/1000; Периметр полукруглой теплицы (м) = X/1000*2+Z/1000*2; Объем полукруглой теплицы (м 3 ) = X/1000*Z/1000*(Y/1000-(X/1000)/2)+((3.14*X/1000/2*Z/1000/2)/2)*Z/1000; Площадь крыши и боковых стен (м 2 ) = ((Y/1000-(X/1000)/2)*2+3.14*X/1000)*(Z/1000); Площадь фасадов (м 2 ) = (X/1000*(Y/1000-(X/1000)/2)+(3.14*X/1000/2*X/1000/2)/2)*2 Полная площадь остекления (м 2 ) = Площадь фасадов + Площадь крыши и боковых стен Длина дуг (м): (Y/1000-(X/1000)/2)*2+3.14*X/1000 Общая длина материалов каркаса (м) = √(Полная площадь остекления)*(√(E*D*2+A*D*2))*2
где,
- Ширина (мм.) — X;
- Длина (мм.) — Z;
- Высота (мм.) — Y;
- Секций по фасаду — A;
- Секций стен — E;
- Ячеек в секциях — D;
Конструкция полукруглой теплицы с обшивкой из сотового поликарбоната получается значительно легче, долговечнее и прочнее, даже в сравнении со стеклянным покрытием, не говоря о плёнке. Лист материала из поликарбоната, благодаря своей структуре, удерживает тепло лучше, чем полиэтиленовая плёнка или одинарное стекло.
Синонимы: оранжерея, тепличка, огород под крышей, огород под стеклом, теплый огород, зимний огород, парник, крытый огород.
Определение длины дуги — математическая открытая ссылка
Определение длины дуги — математическая открытая ссылка Определение: расстояние по изогнутой линии, составляющей дуга
Попробуйте это Перетащите одну из оранжевых точек, определяющих конечные точки синей дуги. Длина дуги будет постоянно рассчитываться.
Длина дуги — это мера расстояния по изогнутой линии, образующей дуга. Он длиннее, чем расстояние по прямой между его конечными точками (что было бы аккорд)
Существует сокращенный способ записать длину дуги: Это читается как «Длина дуги AB равна 10».
Строчная буква L спереди коротка от слова «длина». Однако во многих случаях буква L и даже изогнутая линия над AB опускаются, если нет сомнений в том, что имеется в виду.
Центральный угол в градусах
Формула измерения дуги: где: C
— это центральный угол дуги в градусов
R
— это радиус дуги
π
равен Пи, приблизительно 3,142
Напомним, что 2πR — это длина окружности всего круга, поэтому формула просто уменьшает это значение на соотношение угла дуги на полный угол (360).Путем транспонирования приведенной выше формулы вы находите радиус, центральный угол или длину дуги, если вам известны любые два из них.
Центральный угол в радианах *
Если центральный угол равен радиан, формула проще: где: C
— центральный угол дуги в радиан.
R
— это радиус дуги
Это то же самое, что и версия с градусами, но в случае с градусами 2π / 360 преобразует градусы в радианы.
*
Радианы — это еще один способ измерения углов вместо градусов. Один радиан составляет примерно 57,3 ° Подробнее об этом см. Определение радианов.
Другие темы кружка
Общие
Уравнения окружности
Углы по окружности
Дуги
(C) Открытый справочник по математике, 2011 г. Все права защищены.
,
Калькулятор расчета полукруглой теплицы
Инструкции для калькулятора расчета материалов полукруглой теплицы
Все параметры указываем в миллиметрах
Z – Теплица в длину.
X — Ширина парника.
Y – Высота.
A — Число вертикальных сегментов по периметру фасада.
D — Количество ячеек в секциях вертикальных.
E – Число вертикальных сегментов стен.
Изменяя количеств ячеек или секций, можно подобрать оптимальный размер.
Все вычисления будут отображены на чертеже.
Параметры ячеек рассчитываются автоматически.
Программа поможет Вам выполнить точный расчет материалов, которые необходимы для возведения полукруглой теплицы.
По результатам вычисления Вы узнаете объем и площадь теплицы, периметр для фундамента, количество материалов для каркаса и площадь ее остекления.
Как построить полукруглую теплицу своими руками
Технология монтажа парника из поликарбоната достаточно проста, но требует соблюдать ряд условий. Для каждого отдельного проекта, следует учесть ряд особенностей, чтобы будущая теплица была максимально функциональной и комфортной в эксплуатации.
Как рассчитать оптимальные размеры теплицы из поликарбоната с учетом задач
Высокая стоимость поликарбоната в качестве покрытия тепличного каркаса заставляет задуматься, как можно сэкономить на этой статье расхода. Достаточно часто начинающие овощеводы пытаются уменьшить начальные затраты за счет минимизации габаритов своей первой теплицы. При этом они упускают из виду несколько факторов, ведущих к существенным потерям урожая.
Как влияют размеры теплицы из поликарбоната на ее рентабельность, и что следует учесть еще на этапе проектирования?
Что влияет на размеры и как их правильно рассчитать
Решая, какой по размеру должна быть ваша теплица, нужно исходить не столько из размеров участка, сколько из ее предназначения. Разные растения требуют разных условий, которые возможно обеспечить только при определенных габаритах закрытого грунта.
Тем не менее, малоопытные огородники почему-то забывают о цели, для которой создают теплицу, и строят конструкцию с заранее неподходящими размерами.
Зависимость размеров от целей огородника
Так, для выращивания зелени в стеллажах требуется достаточно много света, недостаток которого придется компенсировать искусственно. Поэтому каркас теплицы под зеленные культуры не должен перекрывать солнечный свет, и само сооружение должно быть небольшим – примерно 3х6 м. Его досвечивание в облачные дни не будет выливаться в круглую сумму, а необходимого объема урожая можно добиться за счет правильной организации пространства.
Томаты, особенно высокорослые, нуждаются в большом пространстве – некоторым сортам может понадобиться теплица высотой 2,5, а то и 3 м. Конечно, ради нескольких кустов не стоит выстраивать такую конструкцию, иначе счет за отопление перекроет всю материальную выгоду от тепличного хозяйства. Но, если вы планируете получить завидный урожай от среднерослых растений, заложите высоту теплицы не менее 2 м.
То же правило касается и огуречников: для выращивания огурцов в полном цикле, а не только рассады, теплица должна обеспечивать комфортные условия для ухода за ними.
Поэтому и для мало-, и для среднерослых кустов стоит поднять крышу постройки до 2–2,5 м именно из соображений эргономики.
Что касается соотношения ширины и длины теплицы, то можно обойтись и стандартными размерами, выведенными на практике опытными овощеводами: 3х6 м, 3х8 м или 4х8 м.
Впрочем, и здесь существуют некоторые нюансы, которые стоит взять во внимание в зависимости от того, какая форма, и как будет осуществляться вентиляция и полив в теплице.
Габариты теплицы в зависимости от формы и технического обустройства
Арочные постройки при всех достоинствах имеют существенный недостаток – соорудить боковые форточки в них весьма затруднительно, и владельцу приходится ограничиваться лишь сквозным проветриванием, организованным через входные двери и торцевые фрамуги.
Качественно провентилировать таким образом сооружение длиной более 6 м сложно, поэтому оптимальный размер теплицы из поликарбоната в форме арки составляет: 3х4, 3х6 или 4х6.
Односкатный закрытый огород, размещенный около глухой стены, стоит делать широким (4–5 м) – так солнце сможет лучше освещать большую его часть, на которой можно будет выращивать светолюбивые культуры. Размеры двускатных теплиц обычно варьируются в более широких пределах, но владельцы длинных конструкций часто жалуются на некоторые проблемы, возникающие при их обслуживании:
- сложности в организации полива, в частности, ручного или с помощью шланга – поливать вручную 100–120 кустов через каждые 2–3 дня, мягко говоря, утомительно, а шлангом есть постоянный риск сломать куст;
- медленное снижение температуры – в теплице из поликарбоната под ярким солнцем моментально становится жарко, и для улучшения микроклимата приходится регулярно включать мощную вентиляцию, что приводит к удорожанию конечной продукции.
Совсем другая картина наблюдается в постройках, размеры которых не превышают 4–5 м в длину – при условии правильного расположения теплицы относительно розы ветров принудительная вентиляция бывает нужна только в полный штиль.
Легкие парники из дуг с укрывным материалом
На большей территории России холодное время суток, в среднем, больше, чем тёплых, но различные конструкции в виде парника или теплицы позволяет получить урожай. Парник, в отличие от теплицы, имеет относительно маленькие размеры и используется сезонно. Для защиты рассады от неблагоприятных погодных условий, а также для увеличения периода вегетации, хорошо подойдёт переносной парник, состоящий из дуг с укрывным материалом.Разберёмся, какие бывают конструкции, и как их собирать.
Нержавеющие дуги для парника
Конструкция не будет поддаваться разложению в отличие от дерева. Парник из дуг имеет лёгкий вес и легко будет транспортироваться и складываться. Такой арочный парник можно сделать своими руками абсолютно разной длины и высоты.
Парники из дуг с укрывным материалом имеют ряд преимуществ:
- Экономичность конструкции;
- Долговечность;
- Гигиеничность;
- Практичность.
Во многих садоводческих магазинах имеются в продаже дуги поштучно, в наборе, дуги составляющие каркас, вшитыми в виде гармошки, а также, как комплект с плёнкой для сборки всей теплицы.
Дуги для парника могут быть выполнены из пластика, металла или ПВХ.
Самые дешёвые дуги стоят в среднем от 40 руб (из ПВХ). В Леруа Мерлен (есть фото и видео каталог) пластиковые дуги для парника стоят от 25 руб за 1 шт. Если выбирать дуги в комплекте с плёнкой, то в среднем 500 руб, однако ценовой диапазон может отличаться, в зависимости от региона, а также от габаритов конструкции. Чтобы миновать расчёты всех составных частей парника, можно воспользоваться комплектом, состоящим из дуг, которые состоят из металлических трубок, покрытых в полимерной оболочкой, соединительных элементов, изготовленных из пластика. Такие сборно-разборные наборы парников могут быть от 2 м до 4 м. Перед тем как приобретать дуги и укрывной материал, необходимо замерить габариты грядок. Также нужно учесть высоту будущего каркаса, в зависимости от высоты растения.
Способы крепления дуг парника
Чтобы приступить к закреплению дуг, нужно выбрать место под будущую теплицу, она должна быть хорошо освещена (солнечная сторона), место безветренное. Если выбрать голое, ветреное место, то парник может просто сорвать или опрокинуть, далее сильные порывы ветра могут навредить рассаде, что снизит урожай.
Необходимо учитывать:
- Высоту дуг;
- Чем выше будет теплица, тем лучше её нужно закрепить;
- Закапывая, как можно глубже, усиливается прочность.
Все дуги одной теплицы должны быть заданных размеров, перед креплением к почве, необходимо вбить колышки в тех местах, где будут располагаться опорные части дуги. Колышки могут быть деревянные или металлические, если дуга из трубки, то диаметр колышка должен быть меньше, чем внутренний диаметр трубы, чтобы было возможно надеть трубки на колышки. Внимание, не делайте теплицу очень высокой, иначе конструкция просто развалится от сильных ветров или дождя.
Как согнуть трубу без трубогиба для навеса. Гнём трубу без трубогиба. Как сделать, делаем навес.
Отзывы:
Александр Трутнев
пишет: Сначала подумал, что сеньёр ёбу дал и хочет согнуть эту здоровенную квадратную трубу.
евгений абрамов
пишет: говносеры и тут повылазили никак не угомонятся. из за таких п….ров нормальные люди не будут делиться своими идеями. если не нравится смотри порнуху и учи как нужно ноги расставлять
Владелен Букамбаев
пишет: так и зайцев наловить можно.
Павел Ко
пишет: не сгибание получилось а натягивание как тетива лука. Очень хитро) буду делать навес таким способом.. автору спасибо.
Сергей Харитонов
пишет: Всё супер, но всё-таки маску нужно использовать. Глаз то запасных нет…
Составляя своими руками чертёж оранжерейной либо парниковой конструкции, следует не только лишь высчитать, сколько будет нужно расходного материала, да и сделать очень четкие расчёты накрывного материала, в качестве которого допускается внедрение листового пластика, стекла либо полиэтиленовой плёнки. Чертежи могут полагать сборку конструкции без сварки, с внедрением для закрепления каркаса только крепёжных частей. Преимуществом такового материала является не только лишь универсальность, да и то, что каркас теплицы из трубы профильной можно сделать фактически хоть какой формы.
Оранжерейные и парниковые конструкции можно сделать своими руками односкатными, двускатными, арочной формы или шатровыми. Готовые чертежи самых удачных конструкций размещены в свободном доступе на строительных сайтах. Использование современных технологий и материалов позволяет на основе индивидуального чертежа сделать максимально удобные конструкции. Каркас теплицы из профильной трубы можно сделать цельным, сварным или разборным.
В 2022 учебном году выпускники 9 классов будут сдавать ОГЭ по обновлённым заданиям. Представляем вам вариант тренировочной работы по математике в формате ОГЭ от СтатГрада. Обычно статградовские задания, используемые на пробных тестированиях в школах, максимально приближены к реальным экзаменационным вариантам. Рассказываем, как работать с новыми заданиями про теплицу.
Хотите БЕСПЛАТНО разобрать с опытным преподавателем все детали новых усложнённых вариантов ОГЭ по математике 2023 года – приходите на пробное занятие в Lancman School. Решите продолжить готовиться к ОГЭ вместе с нами весь год – дадим скидку после бесплатного пробного занятия.
Любой вопрос смело пишите сюда. Мы 13 лет готовим к ОГЭ на высокие баллы. Прокачиваем знания даже самых слабых учеников. Гаранитруем получение оценки “5” на ОГЭ. Офисы Курсов ОГЭ Lancman School есть на каждой ветке московского метро.
Если хотите сэкономить, но получить при этом качественную подготовку, записывайтесь на наши онлайн-курсы ОГЭ-2023 по русскому языку, математике, обществознанию и английскому языку.
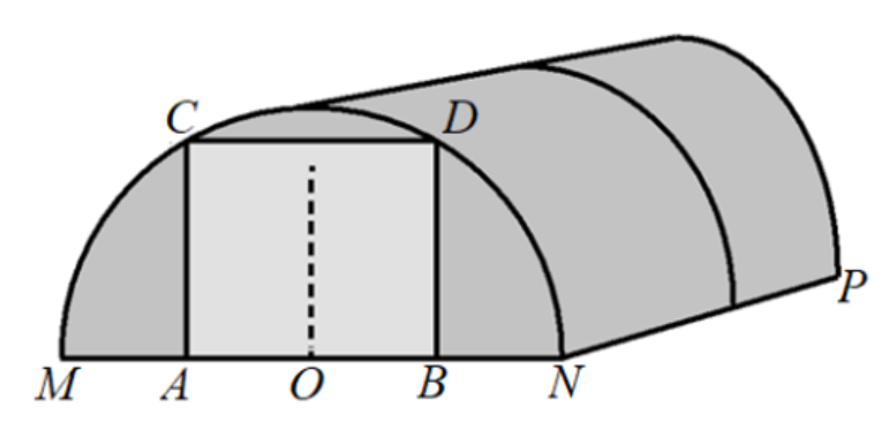
Алексей Юрьевич решил построить на дачном участке теплицу длиной NP = 4,5 м. Для этого он сделал прямоугольный фундамент. Для каркаса теплицы Алексей Юрьевич заказывает металлические дуги в форме полуокружностей длиной 5,2 м каждая и плёнку для обтяжки. В передней стенке планируется вход, показанный на рисунке прямоугольником ACDB. Точки A и B — середины отрезков MO и ON соответственно.
1. Какое наименьшее количество дуг нужно заказать, чтобы расстояние между соседними дугами было не более 60 см?
Решение:
Решать подобные задания лучше наглядным способом, то есть нарисовать предварительно дугу и делать на ней необходимые пометки.
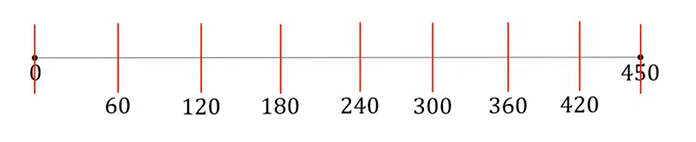
Ответ: 9.
2. Найдите примерную ширину MN теплицы в метрах. Число π возьмите равным 3,14. Результат округлите до десятых.
Решение:
Длину МN необходимо искать, исходя из дуги, используя формулу длины окружности. Поскольку MN – это полуокружность, то ее длина равна πR.
πR=5,2
3,14R=5,2
R=5,2/3,14
MN=2 × 520/314=520/157
MN=3,31
Ответ: 3,3
3. Найдите примерную площадь участка внутри теплицы в квадратных метрах. Ответ округлите до целых.
Решение:
Площадь участка внутри теплицы представляет собой прямоугольник, и его площадь равна MN × NP.
S=520/157 × 4,5= 2340/157=14,9… При округлению получаем 15.
Можно взять ответ в 3,3 из предыдущего задания для решения.
S=3,3 × 4,5=14,85. При округлении тоже получаем 15.
Ответ: 15.
4. Сколько квадратных метров плёнки нужно купить для теплицы с учётом передней и задней стенок, включая дверь? Для крепежа плёнку нужно покупать с запасом 10 %. Число π возьмите равным 3,14. Ответ округлите до целых.
Решение:
Для начала необходимо посчитать площадь крыши теплицы. Она представляет собой прямоугольник со сторонами, равными 4,5 и 5,2.
S крыши=5,2 × 4,5=23,4
Остаётся посчитать площадь двух полуокружностей (перед и задняя часть теплицы). Вместе это одна окружность – значит, можно не считать площадь 2 раза.
S стенок=3,14 × (260/157)в квадрате=314/100 × 260/157 × 260/157=1352/157
К данной площади необходимо добавить 10%, поскольку плёнки надо купить с запасом. Прибавляем по 10% к уже имеющимся цифрам.
S крыши=25,74
S стенок=9,47…
Складываем и округляем. Получаем примерно 35 метров плёнки.
Ответ: 35.
5. Найдите примерную высоту входа в теплицу в метрах. Число π возьмите равным 3,14. Ответ округлите до десятых.
Решение:
Задача геометрическая: нам надо представить, что перед нами равносторонний треугольник.
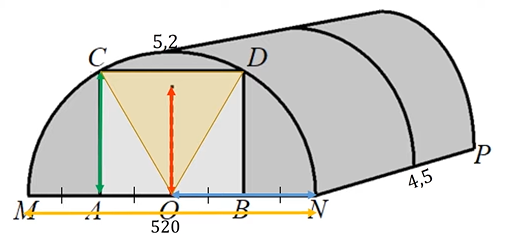
Итак, перед нами равносторонний треугольник СOD. Найдя его высоту, мы найдём высоту входа в теплицу. Будем использовать формулу высоты равностороннего треугольника. Сторона треугольника COD равна радиусу окружности, которую мы уже знаем (260/157).
h=1,40… Округляем до 1,4.
Ответ: 1,4.
Ваш ребёнок – школьник 1-11 класса? Вы учитель? Отлично! Мы пишем для вас. Узнавайте от нас первыми новости образования, актуальную информацию об экзаменах и просто полезные советы. Кнопка подписки прямо под постом!
Фото: pixabay.com
Прочитайте внимательно текст и выполните залдания 1 — 5.
Сергей Петрович решил построить на дачном участке теплицу длиной 4 м. Для этого он сделал прямоугольный фундамент.
Задание 1 (ОГЭ 2020)
Какое наименьшее количество дуг нужно заказать, чтобы расстояние между соседними дугами было не более 60 см?
Решение: Длина теплицы составляет 4 м = 400 см. Рассчитаем количество дуг для теплицы, соблюдая условие: расстояние между соседними дугами меньше или равно 60 см. Разделим 400 на 60. Получится 6 дуг и в остатке 40 см. Учитывая две крайние дуги, получается:6 + 2 = 8 (дуг).
Ответ: 8.
Задание 2 (ОГЭ 2020)
Сколько упаковок плитки необходимо купить для дорожек между грядками, если она продается в упаковках по 6 штук?
Решение: Из условия задачи имеем, что грядок в теплице планируется 3. Дорожек будет 2. Длина дорожки совпадает с длиной теплицы, то есть 4 м = 400 см. Ширина дорожки — 40 см. Найдем площадь двух дорожек. 2 * 40 * 400 = 32000 (кв. см).
Площадь одной плитки: 20 * 20 = 400 (кв. см).
32000 : 400 = 80 (штук) плиток нужно купить для двух дорожек.
80 : 6 = 13 (остаток 2).
Понадобится 13 + 1 = 14 упаковок плитки.
Ответ: 14.
Задание 3 (ОГЭ 2020)
Найдите ширину теплицы. Ответ дайте в метрах с точностью до десятых.
Решение:
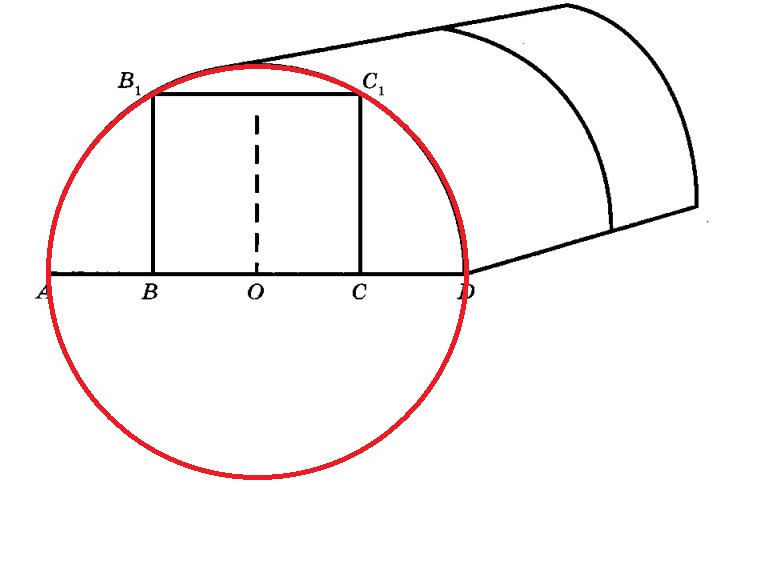
Дуги для теплицы имеют форму полуокружности. Чтобы найти ширину теплицы, нужно достроить окружность и найти радиус окружности OD.
Ширина теплицы AD является диаметром окружности. AD = 2 * OD.
Длина дуги теплицы равна 5 м и вычисляется по формуле П * OD (это длина полуокружности).
OD = 5 : 3,14 = 1,6 (м).
AD = 2 * OD = 2 * 1,6 = 3,2 (м).
Ответ: 3,2.
Задание 4 (ОГЭ 2020)
Найдите ширину центральной грядки, если она в два раза больше ширины узкой грядки. Ответ дайте в сантиметрах с точностью до десятых.
Решение: Ширина теплицы 3,2 м = 320 см. В теплице есть 2 дорожки по 40 см и три грядки. Пусть ширина узкой грядки х см, тогда широкой грядки — 2х см.
Составим уравнение 2х + х + х + 2 * 40 = 320 и решим его.
4х + 80 = 320,
4х = 320 — 80,
4х = 240,
х = 60 (см) — ширина узкой грядки.
Найдем ширину центральной грядки (широкой). 2х = 2 * 60 = 120 (см).
Ответ: 120.
Задание 5 (ОГЭ 2020)
Найдите высоту входа в теплицу. Ответ дайте в сантиметрах.
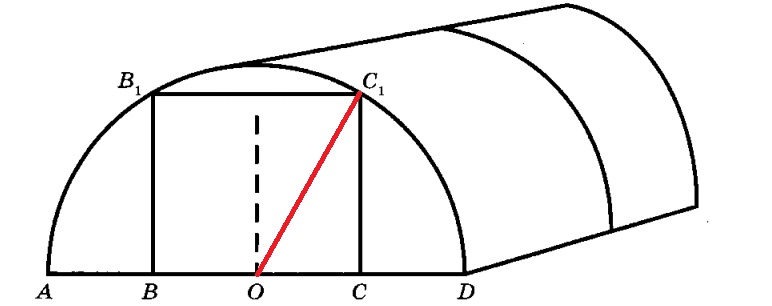
Чтобы найти высоту входа в теплицу,нужно рассмотреть прямоуголный треугольник OC1A. Применив теорему Пифагора, вычислим высоту CC1 теплицы.
По условию AB = BO = OC = CD = 320 см : 4 = 80 см.
ОС1 = OD = 160 см — радиусы.
По теореме Пифагора имеем: СС1 = 80√3 см = 136 см.
Ответ: 136.
Подробный ОГЭ 2020 — земледелец устраивает на склонах гор терассы — задания 1 — 5.
Алексей Юрьевич решил построить на дачном участке теплицу длиной
NP = 6,5 м. Для этого он сделал прямоугольный фундамент. Для каркаса
теплицы Алексей Юрьевич заказывает металлические дуги в форме
полуокружностей длиной 6,1 м каждая и плнку для обтяжки. В передней
стенке планируется вход, показанный на рисунке прямоугольником ACDB.
Точки A и B — середины отрезков MO и ON соответственно.
Задание 1.Какое наименьшее количество дуг нужно заказать чтобы расстояние между соседними дугами было не более 75 см?
Ответ: ______________
Задание 2.Найдите примерную ширину MN теплицы в метрах. Число π возьмите равным 3,14. Результат округлите до десятых.
Ответ: ______________
Задание 3.Найдите примерную площадь участка внутри теплицы в квадратных метрах. Ответ округлите до целых.
Ответ: ______________
Задание 4.Сколько квадратных метров плнки нужно купить для теплицы с учетом передней и задней стенок, включая дверь? Для крепежа пленку нужно покупать с запасом 10%. Число π возьмите равным 3,14. Ответ округлите до целых.
Ответ: ______________
Задание 5.Найдите примерную высоту входа в теплицу в метрах. Число π возьмите равным 3,14. Ответ округлите до десятых.
Ответ: ______________
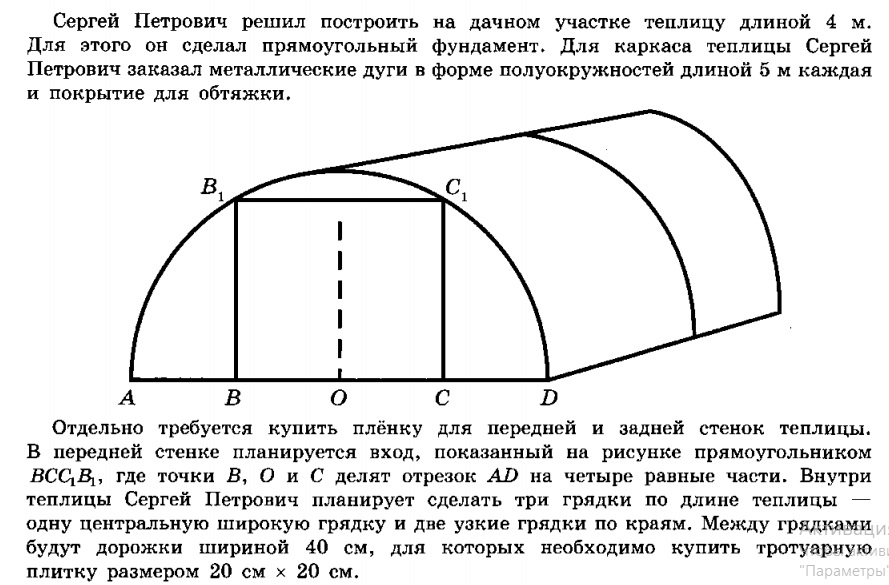
Сергей Петрович решил построить на дачном участке теплицу длиной 4 м. Для этого он сделал прямоугольный фундамент. Для каркаса теплицы Сергей Петрович заказал металлические дуги в форме полуокружностей длиной 5 м каждая и покрытие для обтяжки.
Отдельно требуется купить плёнку для передней и задней стенок теплицы. Внутри теплицы Сергей Петрович планирует сделать три грядки по длине теплицы — одну центральную широкую грядку и две узкие грядки по краям. Между грядками будут дорожки шириной 40 см, для которых необходимо купить тротуарную плитку размером 20 см х 20 см. Высота теплицы показана на рисунке отрезком HF.
Задание 1.
Сколько упаковок плитки необходимо купить для дорожек между грядками, если она продаётся в упаковках по 12 штук?
Задание 2.
Какое наименьшее количество дуг нужно заказать, чтобы расстояние между соседними дугами было не более 70 см?
Задание 3.
Найдите высоту теплицы. Ответ дайте в метрах с точностью до десятых.
Задание 4.
Найдите площадь участка, отведённого под теплицу. Ответ дайте в квадратных метрах. Результат округлите до целых.
Задание 5.
Сколько квадратных метров плёнки необходимо купить для передней и задней 1 стенок, если с учётом крепежа её нужно брать с запасом 10 %? Ответ округлите до десятых.
1. Какое наименьшее количество дуг нужно заказать, чтобы расстояние между соседними дугами было не более 60 см?
Длина теплицы 4 м = 400 см.
Чтобы узнать наименьшее количество дуг найдем количество секторов, которые получатся при установке дуг на расстояние 60 см. Для этого разделим длину теплицы на максимальное расстояние между дугами.
400 : 60 ≈ 6,6, т.е. 7 секторов.
Если вы схематично нарисуете 7 секторов и отметите дуги, то заметите, что дуг будет на одну больше.
Ответ: 8.
2. Сколько упаковок плитки необходимо купить для дорожек между грядками, если она продаётся в упаковках по 6 штук?
Длина дорожек соответствует длине теплицы и равна 400 см. Ширина дорожек равна 40 см.
Площадь одной дорожки равна 400 · 40 = 16 000 см2, а площадь одной плитки равна 202 = 400 см2.
На одну дорожку потребуется 16 000 : 400 = 40 плиток, следовательно, на две дорожки потребуется 80 плиток.
Т.к. плитка продается в упаковках по 6 штук, то упаковок надо закупить 80 : 6 = 14 штук.
Ответ: 14.
3. Найдите ширину теплицы. Ответ дайте в метрах с точностью до десятых.
Шириной теплицы будет диаметр окружности с центром в точке О. Из условия задачи нам известно, что длина металлической дуги равна 5 м. А металлическая дуга является полуокружностью, значит, длина всей окружности с центром в точке О равна 10.
Длина окружности находится по формуле L = πd, где d = AD — диаметр.
Найдем АD.
АD = 10 : 3,14 ≈ 3,2 м.
Ответ: 3,2.
4. Найдите ширину центральной грядки, если она в два раза больше ширины узкой грядки. Ответ дайте в сантиметрах с точностью до десятков.
Пусть ширина узкой грядки равна х, тогда ширина центральной грядки — 2х. Т.к. общая ширина двух дорожек равна 80 см = 0,8 м и ширина теплицы равна 3,2 м, то составим и решим уравнение:
х + х + 2х + 0,8 = 3,2;
4х = 2,4;
х = 0,6 м — ширина узкой грядки.
0,6 · 2 = 1,2 м = 120 см- ширина центральной грядки.
Ответ: 120.
5. Найдите высоту входа в теплицу. Ответ дайте в сантиметрах.
ВО = ОС = ¼АD = ¼ · 3,2 = 0,8 м, значит, ВС = В1С1 = 0,8 ·2 = 1,6 м (из условия задачи).
ОВ1 — радиус, который равен половине диаметра AD, т.е. ОВ1 = 3,2 : 2 = 1,6 м.
Пусть точка О1 — середина В1С1, тогда треугольник ОВ1О1 — прямоугольный и имеет гипотенузу ОВ1 = 1,6 м и катет В1О1 = 1,6 : 2 = 0,8 м.
По теореме Пифагора найдем второй катет, и по совместительству, высоту входа теплицы ОО1, предварительно переведя метры в сантиметры.
ОО12 = ОВ12 — В1О12 = 1602 — 802 = 19 200
ОО1 = √19200. Корень не извлекаемый.
Возведем в квадрат число 140: 1402 = 19 600 — многовато.
1392 = 19 321
1382 = 19 044
Вообще, если у вас есть книжечка с этой задачей, то вы можете увидеть в ответах некоторый промежуток. Любое число из этого промежутка будет являться правильным ответом. Я возьму число 139, т.к. его квадрат находится ближе к 19 200.
Ответ: 139.
Не можешь найти нужную задачу? Предложи свою! Наша группа в VK.
Рассмотрим первые пять задач Варианта 16 из ОГЭ. Математика: типовые экзаменационные варианты:36 вариантов /под ред . И.В. Ященко на нахождение неизвестных величин теплицы.
Сергей Петрович решил построить на дачном участке теплицу длиной 6 м. Для этого он сделал прямоугольный фундамент. Для каркаса теплицы Сергей Петрович заказал металлические дуги в форме полуокружностей длиной 5 м каждая и покрытие для обтяжки.
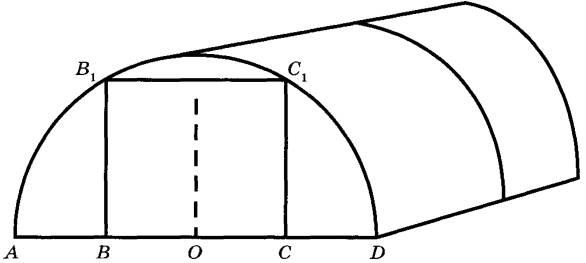
Отдельно требуется купить плёнку для передней и задней стенок теплицы. В передней стенке планируется вход, показанный на рисунке прямоугольником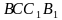 
, где точки B, O и C делят отрезок AD на четыре равные части. Внутри теплицы Сергей Петрович планирует сделать три грядки по длине теплицы — одну центральную широкую грядку и две узкие грядки по краям. Между грядками будут дорожки шириной 50 см, для которых необходимо купить тротуарную плитку размером 25 см х 25 см.
Задание 1. Какое наименьшее количество дуг нужно заказать, чтобы расстояние между соседними дугами было не более 80 см?
Решение.
Длина теплицы 6 м = 600 см. Разделим эту длину на 80 см и округлим результат до ближайшего наибольшего целого, получим:
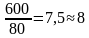
то есть, нужно заказать 8 дуг + 1 первая дуга = 9 дуг.
Ответ: 9.
Задание 2. Сколько упаковок плитки необходимо купить для дорожек между грядками, если она продаётся в упаковках по 10 штук?
Решение.
В теплице 3 грядки, между которыми будут две дорожки. Длина каждой дорожки равна длине теплицы – 600 см, а ширина – 50 см.
Площадь одной дорожки 600∙50 = 30 000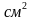 
,
тогда площадь двух дорожек 2∙30 000 = 60 000 .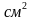
Тротуарная плитка имеет размеры 25х25 см площадь одной плитки 625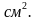
Найдем сколько плиток необходимо для дорожек
площадь двух дорожек : площадь одной плитки
60 000:625 = 96 плиток
Так как плитки продаются в упаковках по 10 штук, то необходимо купить
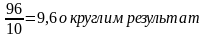
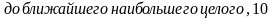упаковок
Ответ: 10.
Задание 3. Найдите ширину теплицы. Ответ дайте в метрах с точностью до десятых.
Решение.
Ширина теплицы определяется диаметром полуокружности длиной 5 метров. Для вычисления радиуса такой полуокружности можно воспользоваться формулой длины окружности L=2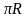
. Нам дана длина полуокружности =5м, следовательно
полная длина окружности будет 10м. Подставим
2*3,14R=10
R=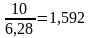
ширина теплицы равна диаметру , поэтому 2*1,592=3,184.
Ответ дать в метрах с точностью до десятых 3,2 м.
Ответ: 3,2.
Задание 4. Найдите ширину узкой грядки, если ширина центральной грядки относится к ширине узкой грядки как 5:3. Ответ дайте в сантиметрах с точностью до десятков.
Решение.
Условно представим теплицу с грядками: две по краям с шириной 3x см и одна центральная с шириной в 5х см. Между ними дорожки шириной 50 см.
Учитывая, что вся ширина теплицы примерно 3,2 м = 320 см, получаем уравнение:
3х+50+5х+50+3х=320,
11х=320-50-50,
Х=220/11
Х=20. Найдите ширину узкой грядки 3х=3*20=60 см.
Ответ: 60.
Задание 5. Сколько квадратных метров пленки необходимо купить дл передней и задней стенок, если с учетом крепежа ее нужно брать с запасом 15% ? Ответ округлите до десятых.
Решение. Ширина теплицы 3,2 м , а радиус 1,6 м
Так как передние и задние части стенок теплицы являются полуокружностями ,то вместе они образуют круг. Площадь круга S=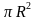
= 3,14*
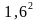= 8,0384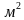 
С учетом крепежа ее нужно брать с запасом 15%
8,0384+0,15*8,0384=9,24416 Ответ округлите до десятых 9,2
Ответ: 9,2
